Sequence–structure relationships in RNA loops: establishing the basis for loop homology modeling

Abstract

The specific function of RNA molecules frequently resides in their seemingly unstructured loop regions. We performed a systematic analysis of RNA loops extracted from experimentally determined three-dimensional structures of RNA molecules. A comprehensive loop-structure data set was created and organized into distinct clusters based on structural and sequence similarity. We detected clear evidence of the hallmark of homology present in the sequence–structure relationships in loops. Loops differing by <25% in sequence identity fold into very similar structures. Thus, our results support the application of homology modeling for RNA loop model building. We established a threshold that may guide the sequence divergence-based selection of template structures for RNA loop homology modeling. Of all possible sequences that are, under the assumption of isosteric relationships, theoretically compatible with actual sequences observed in RNA structures, only a small fraction is contained in the Rfam database of RNA sequences and classes implying that the actual RNA loop space may consist of a limited number of unique loop structures and conserved sequences. The loop-structure data sets are made available via an online database, RLooM. RLooM also offers functionalities for the modeling of RNA loop structures in support of RNA engineering and design efforts.

INTRODUCTION

RNA function is encoded within its three-dimensional (3D) structure. This especially holds for the ability of binding to proteins and nucleic acids, as well as small metabolite molecules [e.g. (1)] with high specificity and sensitivity. The highly specific molecule binding has been extensively assessed by the technique of in vitro selection (SELEX) (2) for the past two decades. It has been determined that most of this binding functionality resides in regions of an RNA that lack canonical base pairing and, therefore, are seen as unstructured at the secondary structure level. These regions are either single-stranded segments (e.g. bulges or the individual strands in internal loops and multi-loops) connecting two distinct helical elements or hairpin loops bridging the gap between the two strands of a single helix. Analogously to loops in protein structures, we call these single-stranded segments ‘loops’. Prominent examples include the pyrimidine- and phosphate-sensor bulges of the thiamine riboswitch (3), the core region of the hammerhead ribozyme (4) and the tRNA anticodon loops. The absence of the stabilizing canonical base pairs in loops introduces flexibility into the overall structure, therefore allowing for local bending and thus the formation of structural motifs such as stacked helices. In contrast to helical regions, which are constrained by their helical shape and, therefore, can be easily modeled based on well-known geometrical parameters, loops are not as constrained and can, at least theoretically, adopt a wide range of 3D structures. This situation is similar to protein structure modeling, where loop modeling is an integral part of the structure prediction process (5).

As for proteins, there still is a wide gap between known sequences and the knowledge of their associated 3D. Compared to ∼1.15 million known sequences in the Rfam database (Version 9.1 January 2009) (6), only ∼4300 distinct, but partially redundant, RNA structures are available in the Nucleic Acid Database (June 2009) (7). Hence, the ability of properly modeling RNA 3D structures, and to thereby close the gap, is of high importance not only for the prediction of complete RNA 3D structures but also for molecular engineering as well. An essential step towards understanding the folding mechanisms of RNA and applying this knowledge to structure prediction is the careful and exhaustive exploration and analysis of the currently known 3D structural space. In recent years, several research groups have performed thorough studies of RNA structures and the underlying intramolecular interactions. Analyses of loop structures were conducted by Huang et al. (8) applying cluster analysis on distance comparisons of full-backbone superpositionings of tetraloop hairpins. Lisi and Major investigated sequence–structure relations in triloop 5-mers using supervised machine-learning techniques and the structure motif detection and analysis capabilities of the MC-Tools software suite (9). Sykes and Levitt analysed nucleotide doublet libraries (10), and Richardson et al. (11) studied possible backbone conformations of RNA. One of the most important recent advances in RNA structure research was the discovery of base pair isostericity by Leontis and Westhof (12). The possibility to exchange two different base pairs without disrupting the local backbone geometry allows for a deeper understanding of the formation of RNA structure, as well as for the development of new modeling approaches based on non-sequence homologuous template libraries. The recent extension of the formerly qualitative method to a quantitative measure (13) might even be of use in the development of RNA knowledge-based potentials applicable for RNA threading algorithms.

Beyond these seminal contributions, the field of RNA 3D structure prediction has recently experienced a boost in activity. Here, the focus is shifting from the time-consuming manual structure building [e.g. structure manipulation via MANIP (14), S2S/Paradise (15) or helix building via NAB (16) or 3DNA (17)] to approaches based on database-derived potentials and ab initio modeling. Other approaches aim to predict the functional class, and thus structural class of RNA molecules from sequence alone using abstractions of predicted secondary structures such as graphs [e.g. (18,19)]. Four methods (or their successful application to a modeling problem) have been published in recent years. FARNA (20) uses potentials derived from ribosome structures and is based on the successful protein modeling approach ROSETTA. Two simplified ab initio bead-string model approaches have been developed by Ding et al. (21) in 2008 [available as web server iFoldRNA (22)] and Jonikas et al. (23) in 2009 (NAST/C2S). The former approach uses discrete molecular dynamics simulations, while the latter is purely geometrical, but allows for the incorporation of certain constraints, such as secondary or tertiary structure or information on the general shape of the target into the modeling process. Finally, Parisien and Major (24) applied a novel secondary structure model of nucleotide cyclic motifs for a highly accurate prediction of small (up to 47 nucleotides) RNA structures using a prediction pipeline based on MC-Fold and MC-Sym. Because of their functional importance and structural diversity, computational means for the proper modeling of loop regions are particularly desirable. By contrast, assuming correct secondary structure predictions, structural modeling of helical regions presents less of a challenge given their canonical structures. As for proteins, the notion of homology modeling may be used to model RNA loop regions. Towards this end, first, a knowledge base (i.e. a data set of determined loop structures) needs to be established. Examples of current RNA 3D structural motif databases that can form a possible foundation for such a knowledge base are the Structural Classification of RNA database (25), the RNAjunction database (26), the RNA FRABASE (27) and the DARTS database (28). Second, the sequence–structure relationships have to be explored. Up to what degree of sequence divergence can RNA loops be expected to assume a similar structure? And is there a similar sequence-means-similar structure rule, comparable to the one in protein structure, in RNA loops at all? It is a priori not clear, whether such a rule exists for RNA structures given their different alphabet (building blocks) and the correspondingly different physical forces and principles determining the structure of RNA molecules. To address these questions, we generated and analysed a comprehensive data set of loop structures extracted from experimentally determined RNA structures. We observed that there is indeed evidence of sequence–structure relationships in RNA loops that are consistent with the notion of homology. Up to a surprisingly sharply defined degree of sequence divergence, loops are observed to assume very similar structures. Based on the extracted data set, we developed a modeling pipeline allowing the user to execute a range of different tasks in automatic RNA loop modeling. First and foremost, the application allows to browse and explore the structural space of RNA loops by querying the database for sequences and structural patterns. Secondly, as a step towards semi-automated homology modeling, we implemented a homology-based loop modeling service similar to the one devised by Michalsky et al. (29) for protein structures (LIP). Third, the modeling application allows to answer questions in RNA engineering, such as how well different loop structures fit into a given 3D structure and whether there are loop structures available that mimic the structure of the native loop regardless of sequence similarity. Our web application allows to insert loop regions in RNA solved structures or structure models. Our results shed light on the evolution of RNA sequences and lend further support for homology-based modeling efforts.

MATERIALS AND METHODS

Creation of the loop structure database

Using the software MC-Annotate (30), we computed structural parameters such as sugar pucker and glycosidic bond configuration as well as base pairs and stacked bases for 1371 RNA-containing chains from the Protein Data Bank (PDB) (31) (December 2008) excluding 137 chains without loops (e.g. from DNA/RNA hybrid helices). Based on the set of canonical base pairs, we then assigned the secondary structure of the RNA, making the following assumptions:

• cis-Watson–Crick GU/UG-wobble base pairs are considered being part of the secondary structure.

• The minimum stack size for a helix is two base pairs. Single canonical base pairs are considered not to belong to a secondary structural element, since they are less stable due to the lack of stacking interactions with subsequent base pairs.

• Pseudoknots are considered to be part of the tertiary structure. Base pairs and stacks of base pairs that conflict with the nested definition of secondary structure are therefore not considered being part of the secondary structure, regardless of their base pair family.

These assumptions, together with the commonly accepted formal definitions of RNA secondary structure [e.g. (32)], allowed us to extract the atomic coordinates for each detected secondary structural motif. This yielded three preliminary data sets of connecting structural elements: hairpin loops, bulges/internal loops and multi-branched loops. To cover a wider and more diverse structural space, we created a fourth set (segments) and allowed its contents to partially overlap with the internal loop and multi-branched loop sets. We moved all bulges to the segments set and then added all individual single-stranded regions from the internal loop and multi-branched loop sets to this set. In addition to the unpaired regions of a loop (i.e. one for hairpins and single-stranded segments, two for internal loops and up to n for n-branched multi-loops), we extracted the flanking bases on either side of the unpaired regions. These extra nucleotides (anchors) are required for the insertion of a loop into a target structure. For each loop, we stored its atomic coordinates as well as its MC-Annotate annotation in a MySQL database.

Structural clustering

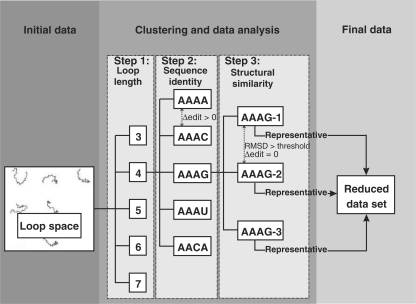
For each loop type, we created subsets according to the sequence length. We limited these sets to hairpins and segments of three (or, respectively, 1 for segments) to 30 bases, as well as internal and multi-loops with individual unpaired regions between 0 (i.e. the 5′-base of the succeeding helix is directly connected to the 3′-base of the current helix on the backbone, but forms a base pair with a base that is not part of the current helix) and 30 bases. This upper limit of 30 bases, especially for internal loop segments, is commonly used in RNA structure computations [e.g. the Mfold server (33)] since longer unpaired regions tend to disrupt the stability of an RNA molecule. In addition, the known structural space above loop length 30 only consists of a handful of structures. We assessed the structural similarity between members in each subset by computing their pairwise root mean square deviation (RMSD) of the superpositions of the reduced backbones (P, O5′, C5′, C4′, C3′ and O3′ atoms) over the full length of the loop including the anchors. To reduce redundancy, we generated clustered sets based on both sequence (100% identity; i.e. all members are required to have the same sequence except for the anchors) and structural similarity [RMSD < 0.5 Å (0.5 seqid set) or, respectively, RMSD <1.0 Å (1.0 seqid set)], assigning all loops fulfilling these criteria to a common cluster. The data creation workflow is illustrated in Figure 1. For each cluster, we computed the centroid structure and chose the member structure as cluster representative that showed the highest structural similarity to the centroid. In addition, we generated six additional clustered sets using incremental RMSD ranges from 0.5 Å to 3.0 Å with a step size of 0.5 Å) and irrespective of sequence identity.

Figure 1.

Data set creation workflow. All structures of the available loop structural space are grouped according to their loop length (Step 1). Within these length groups, structures are further divided by their sequence identity (Step 2) and structural similarity according to a certain RMSD threshold (Step 3). The representative structures of the resulting clusters are then put into a new data set with reduced redundancy. Step 2 is omitted for the creation of non-seqid sets.

Structural comparisons

First, we assessed sequence-related structural diversity of the known RNA loop structural space (i.e. do sequence-identical loops assume the same structure?) by comparing the loop structures of all sequence-identical representative structures of the 0.5 Å (seqid) set with loop lengths between 1 (or, respectively, 3 for hairpins) and 30 bases. We computed the pairwise backbone RMSD between all structures of the same sequence and grouped the medians of those comparisons according to their loop length. We then compared the structural and sequence similarity among all representative structures, regardless of sequence identity.

For each possible pair of loops L_i,L_j of the same length, we computed the loop–loop comparison 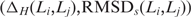, where Δ_H is the sequence dissimilarity as given by the number of differing bases between two loops of the same length (the Hamming distance) and RMSD_s is the structural similarity as given by the RMSD of the superposition of the reduced backbones. We then computed all 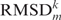, the median RMSD_s for all loop–loop comparisons 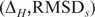with Δ_H = k; i.e. for all loop–loop comparisons with the same sequence dissimilarity. Finally, for all loops of length n, we normalized all 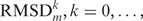by dividing by

i.e. the average of the median structural similarities associated with the loop–loop comparisons with the three greatest Hamming distances. We plotted them against the sequence dissimilarity as given by the percentage of the maximum possible Hamming distance; i.e. the loop length n itself.

Analysis of isosteric contact patterns

We examined base pair patterns within the representative structures of the reduced redundancy 0.5 Å (seqid) set. Analogously to Lisi and Major (9), we assigned loops that exhibited the same base pair pattern to a common group. In contrast to the aforementioned work, however, we focused on base pairs of the 12 Leontis/Westhof families (12) to which the definition of base pair isostericity can be applied. For two distinct loop structures to be assigned to a common cluster, they have to share all their base pairs; i.e. all base pairs occurring in one structure have to be present in the other one. Furthermore, both loop structures do not necessarily have to share the same sequence, as long as their common base pairs are isosteric.

Comparison with the Rfam database

To evaluate the coverage of the currently known loop sequence space by the currently known loop structural space, we compared our loop database with the sequences contained in the Rfam database. We took the seed alignments (1372 RNA families) from the Rfam database (version 9.1) and extracted the sequences for all unstructured regions (as given by the consensus structure) up to a length of 30 bases. To obtain the sequence space covered by the currently known loop structural space, we then generated all isosteric [according to the latest definition of isostericity by Stombaugh et al. (13)] sequences for each loop in our database, taking into account all intraloop canonical and non-canonical base pairs that can be grouped into one of the twelve Leontis/Westhof families.

RNA loop modeling

We modified the homology-based method by Michalsky et al. (29) (LIP) for application to nucleic acid structures. Given an RNA structure and a target sequence for the loop target, our method finds the loop templates that fit best into a target site specified by two nucleotide positions (anchors). We achieve this by performing an anchor fitting according to the method by Kabsch (34). As a quality measure, we compute the RMSD of the reduced backbone atoms of the anchors of template and target (RMSD_a). To determine, whether a loop template fits into a target structure without steric clashes, we compute all pairwise atomic distances between the inserted loop template and target structure, with the exception of atoms that are parts of the anchors. Atom distances below a user-specified threshold (default 4 Å) imply a clash, while templates with high RMSD_a imply loop structures that do not fit well into the target site. While the latter templates are rejected if their RMSD_a exceeds a user-specified threshold (default 5 Å), clashing templates might still be accepted as valid candidates. The reason for this is that we only compute whether (and if, then how well) a loop template fits into the gap between the anchors of a target structure and attach the template in a rigid fashion. The resulting structures have thus to be subjected to energy minimization, which might remove the clash without significantly changing the structure of the template. In contrast, structures with mismatching anchors (as revealed by high RMSD_a values) might require a significant change in their backbone conformation to fit properly into the target site, which would defeat the purpose of a template library.

RESULTS

Generation of a loop-segment structural data set

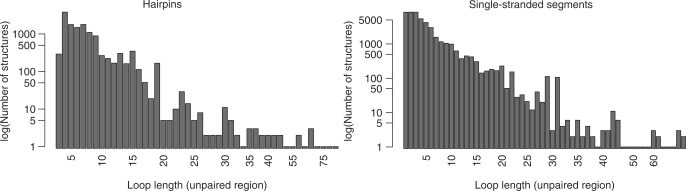
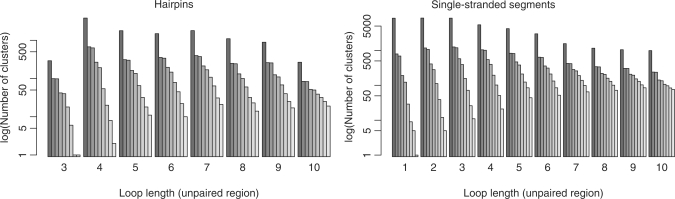
We computed secondary structures for and extracted loop regions from 1371 of the 1544 RNA-containing chains contained in the PDB (December 2008). This leaves 137 chains within the PDB unused as they represented ‘unstructured’ molecules, e.g. small single-stranded fragments or purely helical structures. Table 1 lists the sizes of the unclustered and clustered loop data sets. The initial, redundant loop data sets contained 13 085 hairpins and 46 361 segments with loop lengths ranging between 3 and 32 bases including the two anchors. The initial internal loop and multi-loop data sets contained 17 133 and 5756 structures, respectively. Figure 2 displays the length distribution of all found hairpin loops and single-stranded segments. The effect of structural clustering on the initial data is illustrated in Figure 3. It shows the distribution of hairpin loops from 3 to 10 bases and single-stranded segments from one to ten bases. For each loop length, the set sizes of the unfiltered and eight clustered sets (from left to right: unfiltered, 0.5 Å (seqid), 0.5 Å, 1.0 Å (seqid), 1.0 Å, 1.5 Å, 2.0 Å, 2.5 Å and 3.0 Å) are given as bar plots. From these figures, as well as from Table 1, the high degree of redundancy in the available RNA 3D structural space becomes apparent. We can observe large set sizes in the unfiltered sets and significantly decreased numbers at the transitions between the 0.5 Å, 1.0 Å and 1.5 Å sets.

Table 1.

Loop database data set sizes

	Hairpin	Segment	Internal	Multi-loop
All structures	13 085	46 361	17 133	5756
0.5 Å (seqid) cluster	2916	8216	2371	1520
0.5 Å cluster	2807	7870	2247	1499
1.0 Å (seqid) cluster	1486	4181	2275	989
1.0 Å cluster	1215	3412	870	912
1.5 Å cluster	705	2139	421	745
2.0 Å cluster	456	1552	259	691
2.5 Å cluster	316	1212	186	673
3.0 Å cluster	234	976	137	668

Set sizes of the unclustered data set and eight clustered data sets. Names of cluster sets represent the cutoff value for inclusion into the cluster. seqid refers to cluster sets where 100% sequence identity is an additional requirement for cluster membership.

Figure 2.

Distribution of loop lengths. Left: hairpin loops, right: single-stranded segments.

Figure 3.

Effect of structural clustering on loop length distribution. Left: hairpin loops, right: single-stranded segments. For each loop length, the set sizes of the nine cluster sets (from left to right: unfiltered, 0.5 Å (seqid), 0.5 Å, 1.0 Å (seqid), 1.0 Å, 1.5 Å, 2.0 Å, 2.5 Å and 3.0 Å).

Analysis of isosteric contact patterns

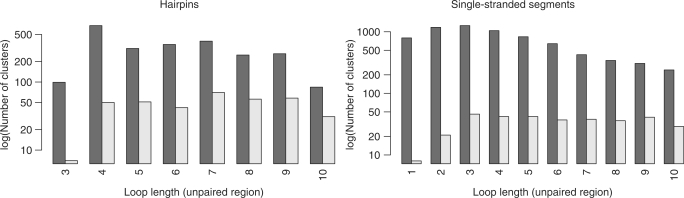
Following the filtering of the representative structures of the 0.5 Å (seqid) set using base pair isostericity information (see ‘Materials and Methods’ section for details), we can observe huge decreases (of up to 99%) in the number of unique structures as can be seen in Figure 4. By way of example, we provide detailed information on the base pair patterns in tetraloop hairpins. In Table 2, we list the 16 largest contact pattern clusters. In total, there are 50 clusters, of which the remaining 34 are singleton clusters and thus correspond to unique sequences including a number of loops with an GNRA sequence motif. The largest two clusters correspond to ‘unstructured’ loops that only contain the closing cis-Watson–Crick base pair between the anchors. The largest cluster represents loops with {A,U} or {C,G} closing pairs, while the second largest represents those loops that are closed by a UG-wobble pair. An interesting finding is that while there is still some higher structural diversity in the unstructured loops (maximum pairwise distance 5.08 Å), at least half of the structures for most clusters have a structural similarity of ≤2.0 Å according to the backbone RMSD. Additionally, we can observe highly similar structures (≤0.5 Å) between non-sequence-identical loops as given by the minimum pairwise distances. An example can be found in Supplementary Figure S1.

Figure 4.

Effect of base pair information on loop set sizes. Left: hairpin loops, right: single-stranded segments, dark grey: sizes of the 0.5 Å (seqid) sets of loop lengths from three to ten bases, light grey: set sizes after additional filtering using base pair contact and isostericity information.

Table 2.

Contact patterns and consensus sequences in tetra-loop hairpins

Contacts	#members	#total	Range	μ ± s	Median	Consensus
(1,6,WWc)	520	3035	[0.14, 5.08]	1.88 ± 0.58	1.87	nNNNNn
(1,6,WWc)	45	410	[0.28, 3.63]	2.10 ± 0.89	2.12	uNNNNg
(1,6,WWc), (2,5,SHt)	24	25	[0.53, 3.11]	1.22 ± 0.40	1.12	nDNRKn
(1,6,WWc), (2,5,WWt)	18	114	[0.32, 2.63]	1.29 ± 0.48	1.14	bUWCGv
(1,6,WWc), (2,5,SHt)	6	12	[0.62, 3.01]	1.62 ± 0.96	1.14	uGHRAg
(1,6,WWc), (2,5,SWt)	5	9	[0.54, 2.47]	1.49 ± 0.72	1.11	cMWKSg
(1,6,WWc), (2,5,WHt)	3	3	[1.67, 2.48]	2.01 ± 0.42	1.87	cGWGAg
(1,6,WWc), (2,4,WHc)	3	4	[1.10, 2.31]	1.88 ± 0.68	2.23	yUYYBr
(1,6,WWc), (4,5,SWc)	2	6	[0.97, 0.97]	0.97 ± 0.00	0.97	cUWCGg
(1,6,WWc), (1,2,WSt)	2	8	[1.07, 1.07]	1.07 ± 0.00	1.07	sMKAKs
(1,6,WWc), (2,5,SWc)	2	2	[1.39, 1.39]	1.39 ± 0.00	1.39	cUUAUg
(1,6,WWc), (2,5,HWt)	2	2	[1.56, 1.56]	1.56 ± 0.00	1.56	sMYSRs
(1,6,WWc), (2,5,SHt)	2	3	[1.59, 1.59]	1.59 ± 0.00	1.59	kGKKGm
(1,6,WWc), (2,5,SHt)	2	7	[1.52, 1.52]	1.52 ± 0.00	1.52	cMWACg
(1,6,WWc), (2,5,WWc)	2	2	[1.22, 1.22]	1.22 ± 0.00	1.22	cUMWUg
(1,6,WWc), (2,5,HWt)	2	2	[2.77, 2.77]	2.77 ± 0.00	2.77	cMYKRg

The table contains the 16 largest contact pattern clusters for tetra-loop hairpins based on the 0.5 Å (seqid) set. For each cluster, the contact pattern, the cluster size; i.e. number of representative sequences from the 0.5 Å set that belong to the cluster (#members), and the total number of redundant structures represented by the cluster (#total) are given. Furthermore, we provide (in Å) the range, mean ± standard deviation and median of the pairwise backbone superposition distances of the cluster members, as well as the cluster consensus sequence (using IUPAC nucleic acid ambiguity codes; anchors in lowercase letters). Contacts are given by the indices of the pairing bases and their base pair family (W = Watson–Crick edge, H = Hoogsteen edge, S = sugar edge, c = cis, t = trans).

Sequence–structure relationships in loops

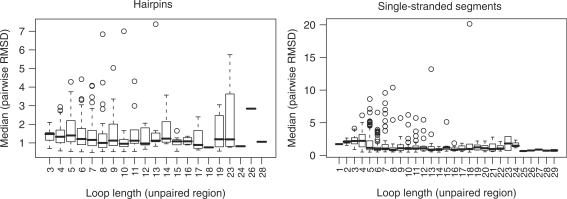
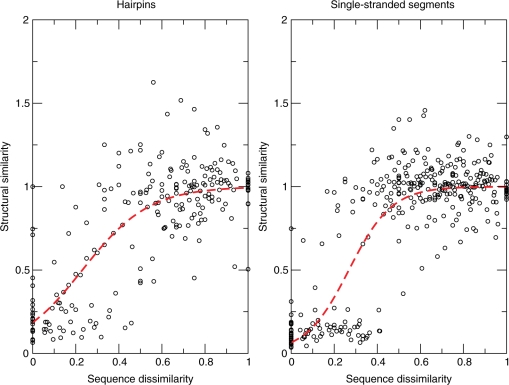
The generated comprehensive data sets of loop structures enabled us to investigate the sequence–structure relationships in RNA loops. In particular, we were interested in the question whether similar loop sequences imply similar structure as well; i.e. whether the basis for homology modeling is actually fulfilled in RNA loop structures. We first compared sequence-identical loops of different length (Figure 5). The median RMSD stays rather constant between 1.0 Å and 2.0 Å, instead of increasing together with the loop length. However, we can also observe large (RMSD > 6.0 Å) structural differences among the outliers, for instance in the octa-, deca- and tridecaloop hairpin sets and for most of the segments between four and 13 bases. Thus, loops of identical sequence and independent of loop length adopt—by and large—very similar structures. Next, we examined whether increasing sequence divergence is reflected by an associated increasingly significant structural change. The expectation would be that few changes can be tolerated and the corresponding loops adopt very similar structures, while increasing sequence changes will, at some point, cause structural differences. Figure 6 shows the results of systematic pairwise comparisons of structural and sequence similarity over all loops between 3 (or four for segments) and 30 bases (see ‘Materials and Methods’ section for details). For the single-stranded segments (Figure 6, right-hand graph), we can observe a sharp transition from structural similarity maintained up to ∼40% sequence dissimilarity to structural dissimilarity at greater sequence divergence levels. For hairpin loops (Figure 6, left-hand graph), the behaviour is similar, albeit less pronounced. We fitted a logistic curve, lc, with 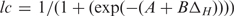, where Δ_H is the normalized Hamming distance and A and B the fitted parameters of the curve, to the data points to qualitatively and quantitatively capture the overall association. Qualitatively, the more sigmoidal the curve, the sharper the transition from similar to dissimilar structures as a function of increasing sequence divergence. Quantitatively, the inflection point of the logistic curve (lc = 0.5) may operationally mark the point of structural transition from similar to different. Surprisingly, while representing different structural elements, the inflection point is very similar for both the single-stranded segment motif—the inflection point is located at Δ_H = 27% dissimilarity for single-stranded segments—and hairpin loops—inflection point at 24% dissimilarity.

Figure 5.

Structural diversity among sequence-identical loops. Left: hairpin loops, right: single-stranded segments. Median values of pairwise RMSD comparisons of the 0.5 Å (seqid) cluster set.

Figure 6.

Structural similarity of RNA loops as a function of their sequence divergence. Left: hairpin loops, right: single-stranded segments. Structural similarity over sequence diversity resulting from pairwise structural and sequence comparisons among structures of the same length. Structural similarity is given by the normalized median RMSD (see text) and sequence dissimilarity is given as fraction of maximum Hamming distance. Dashed lines correspond to a logistic curve fit (see text).

Coverage of Rfam loop structures

According to the Rfam consensus secondary structures, the Rfam database contains unique sequences of 16 545 hairpin loops and 17 705 single-stranded segments, whereas the sequence space of our database contains the structures of 821 different hairpin sequences and of 2135 different single-stranded segments with sequence lengths of up to 30 bases. Including the artificially generated isosteric sequences (see ‘Materials and Methods’ section for details), our database covers 31 335 different hairpins and 14 725 different single-stranded segments. Of the predicted loop sequences in Rfam, only a small fraction is currently covered by actual structural data (numbers for the sequence space including the artifical isosteric sequences are given in parentheses), namely 337 (872) hairpins and 722 (1089) single-stranded segments. For 16 208 [98.0% (15 673 (94.7%)] hairpins and 16 983 [95.9% (16 616 (93.9%)] single-stranded segments in the Rfam database, no 3D-structural data are available so far. Additionally, there are 3D structures available in the PDB that do not occur in the Rfam database: 484 (30 463) hairpins and 1413 (13 636) single-stranded segments in the PDB are not represented among the loop sequences extracted from the Rfam consensus structures. We then tested, whether these non-covered sequences occur in the Rfam database [in both the seed (27 292 sequences) and full (1 149 685 sequences) data sets] at all, irrespective of the consensus structure. Interestingly, we only found 60 (326) hairpin and 88 (298) single-stranded segment sequences within the seed set, spread over 1117 and, respectively, 950 Rfam sequences. Within the full set, we found 112 (1407) hairpins (in 17 437 Rfam sequences) and 217 (950) single-stranded segments (in 16 384 Rfam sequences).

RLooM—an RNA loop modeling web application

We developed a publicly accessible web interface to our loop database and implemented a basic loop modeling method. Using the loop modeling, web application requires submitting a 3D RNA structure (e.g. from homology modeling) to the server and specifying a target sequence and, optionally, a target site. Omission of the target site prompts the application to scan the structure for suitable target sites using a base pair annotation by MC-Annotate. It reports all anchor sites of secondary structure motifs and unpaired regions (=loops). For a given structure and specified target site and associated sequence, RLooM proposes loop structures from the loop library that geometrically fit best to either replace the current loop or add a new one, for instance, at the end of a helix. The target sequence may contain nucleotide wildcard characters and the number of allowed mismatches can be adjusted (default 0). Additionally, a ‘forced’ target sequence can be submitted, leading to the automatic mutation of the bases of a template to the desired sequence. We also allow for structural searches using MC-Search scripts, thus enabling the user to explicitely specify base pair patterns to be included in the template candidates. The application is controlled using an XML-like scripting language (RLML, cf. Supplementary Data). Three parameters can be adjusted: the template data set that should be used, the maximum distance between the anchors of a loop and a target structure such that the inserted loop gives a valid model and the threshold distance defining when a clash occurs between the new loop and the target molecule. The web application and database interface are available under http://rloom.mpimp-golm.mpg.de.

Loop modeling experiments

Since there are no suitable benchmark sets available for checking the quality of RNA structure prediction and modeling methods, we hand-selected a few examples from the pool of available structures with known and important functions: the D—(AGUUGGGA), anticodon (ACUGAAGAU) and TΨC (or L, UUCGAUC)—hairpins of a tRNA (1evv), a hexaloop hairpin from a viral RNA pseudoknot (1L2X, CACCGU), a GNRA hairpin (GAGA) from the malachite green binding aptamer (1Q8N), the 23S rRNA sarcin/ricin domain hairpin (1Q9A, UAGUACGAGAGGACC), a hammerhead ribozyme GNRA (GCAA) hairpin (1RMN), the pyrimidine sensor bulge of the Arabidopsis thi-box riboswitch (2CKY, UGAGAAAGU) and a Group II intron tri-segment (2F88, AAG). We used the 0.5 (seqid) set as loop library for our experiments. If the cluster containing the target loop coincides with the best fitting result, we give the second best result instead. For comparison to an existing ab initio approach, we submitted the target sequences to the iFoldRNA web server (http://troll.med.unc.edu/ifoldrna/), using default parameters and requesting ten models for each query in order to compare ab initio models with our homology-based database. For hairpin targets, we included the three base pairs flanking the loop, and for segment targets, we included the anchors. The reasons for including these extra bases were firstly, to allow the hairpin sequences to fold into a hairpin by adding a set of bases at the 5′- and 3′-ends that should fold into a stack of Watson–Crick base pairs. Secondly, the extra flanking bases include/are the anchors, without which it would not have been possible to determine, whether and how well the ab initio modeled loops fit into the target structure. Figure 7 displays an example modeling result for the tRNA D-loop and Table 3 lists the results of both homology-based and ab initio modelings. More detailed results can be found in Supplementary Table S1. We give three quality measures, all based on reduced backbone fittings: RMSD_a (the RMSD between the anchors), which is used by our method to rank the templates, RMSD_b (the RMSD between the whole loops after superposing the anchors) and RMSD_s (the structural similarity as given by the RMSD resulting from superposing both loops). Best hits that are marked with an asterisk denote results, where the method originally found the cluster with the native structure as best result.

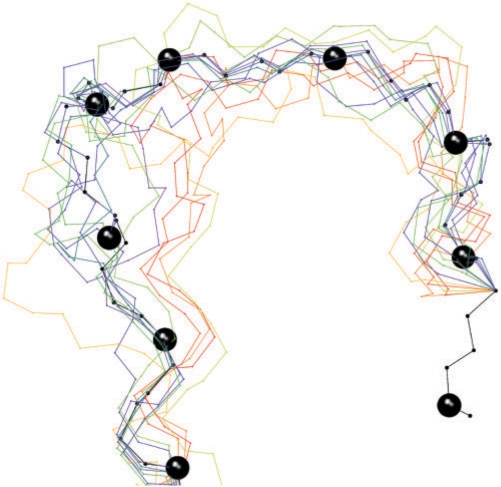
Figure 7.

Modeling a tRNA D-Loop. Reduced backbone representation of target (PDB: 1EVV:A, 13–22) and suitable template structures superposed on the anchors. The target structure is coloured in black and its C3′-atoms are represented by spheres.

Table 3.

Loop modeling results

PDB id	tRNA(phe)			viralb	m. aptamerc	sarc./ric.d	hammerh.e	thi box	gII intron
	D-loop	ac-loopa	L-loop	hexaloop	GNRA loop	15-mer	GNRA loop	Y-sensorf	tri-bulge
	1evv	1evv	1evv	1l2x	1q8n	1q9a	1rmn	2cky	2f88
Bases	13–22	30–40	53–61	7–14	14–19	6–22	16–21	26–36	23–27
Best hits
RLooM	1ehz*	1mj1	2k4c*	1l3d*	1m90*	2d3o*	3bbn*	3d2x*	1jzx*
RMSDa	0.14	0.00	0.15	0.90	0.48	0.16	0.20	0.25	0.44
RMSDb	1.04	0.78	1.11	1.72	4.12	2.76	3.12	0.53	1.58
RMSDs	0.98	0.69	0.90	0.75	2.05	1.05	1.71	0.38	1.34
iFoldRNA
RMSDa	1.08	0.30	1.21	0.50	0.48	2.58	0.60	1.39	1.01
RMSDb	10.88	3.90	4.72	4.40	1.26	23.19	2.51	9.21	1.45
RMSDs	6.19	6.42	6.90	5.43	5.31	8.75	5.68	6.31	1.18

Modeled structures are indicated by their PDB identifier and are located in chain A. RMSD_a, RMSD between anchors; RMSD_b, RMSD between reduced backbones given anchor superposition; RMSD_s, structural similarity—RMSD between reduced backbones given optimal superposition, values are given in Å, *: second best template (cf. text).

^aAnticodon loop.

^bBeet western yellow virus pseudoknot.

^cMalachite green binding aptamer.

^d23S rRNA sarcin/ricin loop.

^eHammerhead ribozyme.

^fPyrimidine sensor bulge.

DISCUSSION

Capturing diversity within structural clusters

The 0.5 Å (seqid) clustered sets reduce redundancies in the available structural space by at least 78% (hairpins). This removes certain redundancies resulting from similar structures that are represented by different chains in the same PDB entry. Nevertheless, redundancies resulting from similar structures with slight structural differences (e.g. contained in different PDB entries) will persist, since the corresponding structures will still be classified as different structures. By contrast, the high-threshold (RMSD ≥ 1.5 Å) clustered sets, are more likely to create clusters of actually different structures. Moderate set sizes of 8931, 6409 and 4010 structures, with highly reduced structural redundancy while retaining diversity, are obtained in the 1.0 Å (seqid), 1.0 Å and 1.5 Å clustered sets. These sets provide a suitable basis for the homology modeling of RNA loops, while the 0.5 Å and 0.5 Å (seqid) sets provide additional structural data with a slightly higher degree of variability.

Isostericity reveals relations between different sequences

Grouping together loop structures according to their contact patterns results in a template data set with significantly reduced size. Additionally, we found non-sequence-identical structures that contain the same contact pattern according to the definition of base pair isostericity. These structures with a common contact pattern generally show high structural similarity (as given by pairwise backbone RMSD), thus resulting in a reduced set of structures not based on sequence similarity. Here, we only examined contacts that belong to one of the twelve Leontis/Westhof families. The inclusion of stacked bases and other tertiary structure contacts might result in further subdivisions of available loop structures into small sets with highly similar backbone structure as well as identical or near-identical contact patterns. For application in structure modeling, this means that a basic set of sequence-independent template structures can be used to model target structures with different sequences.

Loop structures tolerate limited sequence diversity

Based on the rather low variability of the median RMSD between the backbones of sequence-identical loop structures, the global structural diversity for both loop types seems to be rather limited. This suggests that the global fold space for unpaired regions could be highly constrained by the base sequence, which appears to be the case for most of the sequences in the PDB. However, the diversity among the outliers also makes it clear that this does not generally apply to all possible sequences of the sequence space. Our assessment of the structural diversity among loops of the same length supports these findings. We found a clear partitioning of the structural space by sequence similarity. Loop structures with <25% sequence dissimilarity fold into highly similar, if not identical structures, while more divergent sequences rarely adopt similar structures. For single-stranded segments, this is particularly interesting, because of the almost complete absence of a transitional space; i.e. individual RNA loop structures that are located between the two clusters and as such represent loops that either adopt similar structures with a sequence dissimilarity slightly higher than the cutoff or that fold into less similar structures despite having highly similar sequences. The observed cutoff is less pronounced for hairpins, which can possibly be explained by their higher constrained structure space, due to their closing base pair. Furthermore, although loops and segments of various lengths are represented in Figure 6, a clear sigmoidal shape of the logistic curve is evident nonetheless, especially for single-stranded segments. Thus, we observed evidence of a relative—rather than absolute; i.e. number of changes—sequence tolerance threshold below which structure is conserved. The 25% sequence dissimilarity structural transition point may serve as an effective threshold for the selection of suitable template structures for RNA modeling. For proteins, it has been shown that there exists a sharp sequence identity threshold above which proteins fold similarly (35). For RNA structures, an equivalent threshold has not been determined yet. Here, we focused on structural comparisons of same-sized loops. It is possible that shorter loops adopt structural motifs that recur also in longer loops. However, an extension of the current study to the comparison of different-sized loops may not be straightforward as the combinatorial explosion associated with all possible structural alignments would have to be addressed. In conclusion, RNA loops—as protein loops for which a clear structural similarity between similar sequences has been observed as well [e.g. (36,37)]—preserve their structure when the sequences are homologous. It should be borne in mind that local RNA loop structure will also be influenced by the spatial surrounding and structural context within the RNA molecule. A corresponding study to investigate the interplay between local and global structural determinants appears worthwhile.

Discrepancies between sequence and structural space

Only a fraction of the loop sequences in the PDB actually exists within the Rfam database. A certain number of bases in RNA loops are modified and thus simply cannot occur within a sequence database. Yet, the low overlap between Rfam and PDB is surprising. Furthermore, the large numbers of artificially generated isosteric sequences that do not occur in the Rfam could suggest that the actual RNA loop space (as sampled by the Rfam database) might mainly consist of a limited number of unique loop structures with rather conserved sequences.

Loop modeling

For each examined target structure, we could find a number of well fitting candidate templates among the loops in our template library. In most cases, the cluster containing the target loop was the best fitting result, it was, however, possible to find at least one different structure in all the cases, except for one: the pyrimidine-sensor bulge of the Arabidopsis thi-box riboswitch. This motif is a highly specific sequence found conserved in multiple organisms and, therefore, occurs only in related structures within the set of templates. Our homology-based method could find better templates in all cases than the ab initio-based iFoldRNA. Although lacking properly formed base pairs, the structures generated by iFoldRNA still have anchors that fit well into the target site. However, the overall structural similarity to the target loop of these ab initio structures is, except for the case of the tri-segment, always >4.5 Å, which corresponds to the range of structural quality of the discrete-molecular-dynamics-based ab initio models reported by Ding et al. (21). The high RMSD_b of query structure 1Q9A (a 17-mer) is explained by the fact that although the anchors can be superposed reasonably well, the protruding loop regions are oriented into opposite directions (cf. Supplementary Figure S2). This effect can be observed quite frequently (cf. Supplementary Table S1).

For sequences with known structural templates, our method outperforms ab initio modeling in general as tested with the iFoldRNA web server. We assume that the ab initio results would be better if the method had not failed to form proper base pairs between the flanking regions, which would have limited the possible conformational space for the unpaired regions.

CONCLUSION

We found evidence suggesting a sequence-constrained structural fold space for RNA loops, indicating that RNA loops with <25% sequence diversity fold into similar structures while almost no similar structures are found at higher levels of sequence diversity. Our findings support the application of homology modeling for RNA loop structure modeling. In addition, we applied the concept of isostericity as a comparison method for loop structures, confirming the capacity of different RNA sequences to fold into similar structures. Finally, as an application of homology modeling for RNA loops, we presented a homology-based method for the modeling of RNA loop structures as well as a comprehensive loop structure database. Our web application RLooM provides a useful step in the direction of semi-automated homology-based loop modeling for both structure prediction and RNA engineering. The structure coverage of our database, and thus the performance and accuracy of our modeling application is expected to improve over time with the increase of experimentally solved RNA 3D structures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

German Federal Ministry of Education and Research (GoFORSYS Grant number 0313924 to P.M. and D.W.). Funding for open access charge: The Max Planck Society.

Conflict of interest statement. None declared.