Abstract
We explore the question of whether local effects (originating from the amino acids intrinsic secondary structure propensities) or nonlocal effects (reflecting the sequence of amino acids as a whole) play a larger role in determining the fold of globular proteins. Earlier circular dichroism studies have shown that the pattern of polar, non polar amino acids (nonlocal effect) dominates over the amino acid intrinsic propensity (local effect) in determining the secondary structure of oligomeric peptides. In this article, we present a coarse grained computational model that allows us to quantitatively estimate the role of local and nonlocal factors in determining both the secondary and tertiary structure of small, globular proteins. The amino acid intrinsic secondary structure propensity is modeled by a dihedral potential term. This dihedral potential is parametrized to match with experimental measurements of secondary structure propensity. Similarly, the magnitude of the attraction between hydrophobic residues is parametrized to match the experimental transfer free energies of hydrophobic amino acids. Under these parametrization conditions, we systematically explore the degree of frustration a given polar, non polar pattern can tolerate when the secondary structure intrinsic propensities are in opposition to it. When the parameters are in the biophysically relevant range, we observe that the fold of small, globular proteins is determined by the pattern of polar, non polar amino acids regardless of their instrinsic secondary structure propensities. Our simulations shed new light on previous observations that tertiary interactions are more influential in determining protein structure than secondary structure propensity. The fact that this can be inferred using a simple polymer model that lacks most of the biochemical details points to the fundamental importance of binary patterning in governing folding.
Keywords: secondary structure propensity, sequence periodicity, coarse grained protein model, four helical bundle, energetic frustration
Introduction
The burial of non polar residues in the protein core, and the formation of hydrogen-bonded, secondary structure elements such as α helices and β sheets play a fundamental role in stabilizing the native structure of globular, solvated proteins.1 Although the hydrophobic effect is responsible for the formation of the protein core, the emergence of secondary structure is typically driven by both local and nonlocal interactions. Local interactions are reflected in the intrinsic propensities of the single amino acid towards adopting a particular secondary structure. These propensities appear to arise from both enthalpic factors (steric interactions between the amino acid side chain and backbone atoms within the same residue and/or between neighboring residues along the chain), and entropic factors (loss of side chain conformational entropy).2–5 Several methods, based on experiments as well as on statistical analyses of the protein database have been proposed to rank amino acids according to their propensities to form α helices and β sheets.6–12
Local interactions alone do not fully determine the formation of α helices and/or β sheets in proteins. Long range interactions between amino acids distant in sequence space can also be the key players in determining the secondary structure in the folded protein. Hence, it is important to consider not only the intrinsic propensities of the amino acids composing the sequence, but also the sequence as a whole. In particular, the pattern of polar and non polar residues in solvated proteins appears to be tuned such as to accomodate a particular secondary structure while satisfying the requirement for burial of hydrophobic residues in the core of the protein. For example, for an amphiphilic α helix structure with a natural repeat of 3.6 amino acids per turn, a matching periodicity of polar and non polar amino acids will have a non polar residue every three or four positions. This will lead to a solvent exposed hydrophilic face and a buried hydrophobic face. In the same vein, in an amphiphilic β sheet, polar and non polar residues will alternate every other residue.13
Database analyses of α helical structures (Ref. 14 and our results in Section I of the Supporting Information Material) confirm that non polar amino acids appear in the protein sequence most frequently, every 3–4 amino acid positions and in the sequences of solvent exposed β-sheets every 2 amino acid positions. Another statistical study by Schwartz and King15 also showed that a length of 2 is the most probable for blocks of non polar amino acids in helical structures whereas a length of 1 is the most probable for blocks of non polar amino acids in β sheets.
Several experimental studies have shown that it is possible to design four-helix bundle proteins with native-like properties considering principally the intrinsic propensities and the pattern of polar and non polar amino acids.16–21 It is worth noting that all these protein design studies relied also on the rational choice of specific interresidue contacts (to optimize the packing within the hydrophobic core) as well as on the explicit definition of the turn regions.
A more general, combinatorial approach to de novo protein design was introduced by Hecht and coworkers who synthesized several four-helix bundle proteins, with native-like properties, using sequences composed from a set of amino acids with high helical propensities and with fold-appropriate patterning.22–27 In these sequences, the precise identities of the single amino acids (within the chosen set), and the specificity of the interresidue contacts were not specified. Only the polar and non polar nature of the amino acids13,28,29 was considered. The protein sequences were composed of four strands, with periodicity of generic polar and non polar amino acids matching the α helix structure, connected by three short interhelical turns. The degenerate codons NTN and NAN (N = A,G,T,C) were used to fill polar and non polar positions along the helical strands with the amino acids in the sets (Glu, Asp, Lys, Asn, Gln, His) and (Phe, Leu, Ile, Met, Val), respectively. The interhelical turns were the only regions in the sequences that were defined explicitly (with specific interresidue contacts and no degeneracy).
The idea of using intrinsic propensity and a generic polar, non polar patterning has also been exploited in coarse grained, computational models of protein folding.30 Both the four-helix bundle and the four β sheet bundle motifs have been successfully studied using a simplified representation of the protein chain and considering only three types of residues: H for hydrophobic, L for polar, and N for “neutral” groups used to build the turn regions.31–38 In these models, the secondary structure intrinsic propensity is introduced explicitly in the force field either via a dihedral potential term or via a “helical wheel” potential term. In all these coarse grained models, the generic HL pattern and the “intrinsic propensity” potential term both favor the same secondary structure motif (α helix or β sheet), which is consistent with the target fold.
The question arises whether secondary structure intrinsic propensity or polar, non polar patterning is more important in determining the overall fold. For short peptides, it appears that intrinsic propensities can govern the fold. For instance, in the case of polyalanine, the intrinsic propensity of this amino acid alone (in the absence of patterning) is sufficient to drive folding to a helical structure.39,40 The importance of patterning, however, starts to emerge in the folding of proteins with well-defined hydrophobic cores.41 Hecht and coworkers investigated this question by studying two different peptide sequences containing the same pattern of polar and non polar amino acids. This pattern was designed to form single amphiphilic α helices. One of the sequences was composed by amino acids with high α helical propensity (peptide 1A) while the other was composed of amino acids with low α helical propensity (peptide 2A). It was found that both sequences had α helix-like CD spectra (at high enough concentration so that oligomers could form). At these concentrations, peptides would adopt a secondary structure that allowed them to bury their hydrophobic residues regardless of the intrinsic propensities of the amino acids composing the sequence. A similar experiment was carried out on two sequences with the polar, non polar pattern, matching the β sheet secondary structure (peptide 1B composed by residues with high β-sheet propensity and peptide 2B composed by residues with low β sheet propensity). Both peptide 1B and peptide 2B had β sheet CD spectra. The results of Hecht and coworkers show that the secondary structure correlates with the polar, non polar periodicity of the amino acids in the sequence even when this secondary structure is not consistent with their intrinsic propensities.
Although these results may, at first glance, seem to indicate that patterning trumps intrinsic propensity, experiments did not answer the following fundamental question: how much “frustration” (in terms of incorrect secondary structure propensity) can a given pattern tolerate? This question can be studied in a rational manner using simple computational models. One important goal of the present study is to determine the degree of “propensity frustration” for which the polar, non polar patterning can no longer dictate the secondary structure in a globular, solvated protein.
In this article, we introduce a coarse grained protein model that enables us (i) to decouple local and nonlocal factors governing the fold and (ii) to control the amount of “propensity frustration” in a quantitative way. Our protein model is based on the Honeycutt-Thirumalai model42,43 and consists of hydrophobic (H), polar (L), and neutral (N) residues. Inspired by the work of Hecht and coworkers, we chose as first target fold the four helix bundle. We selected a sequence (which we refer to as A16) consisting of four identical “strands” of 16 residues with a helical favoring pattern,20,35 separated by three neutral residues for the turn regions. As a reference point, we also studied a second sequence (B16), with a pattern favoring the formation of an amphiphilic four strands β barrel (See Fig. 1). The force field consists of bonded terms (bond length, bond angle, and dihedral) and nonbonded terms involving generic attractive interactions between the hydrophobic residues and repulsive interactions between all other residues. The model does not have any tertiary structure bias to a given native fold (see Methods Section for details).
Figure 1.
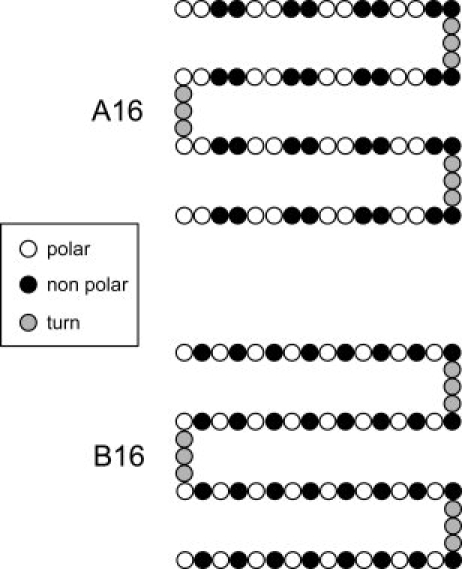
Sequences considered in our REX-LD simulations. The two sequences considered in our simulations are both composed by four identical “strands” contaning polar and non polar beads, connected by short flexible regions (turns) made up by three beads of type N, each. The binary pattern composing the strands in the A16 sequence is consistent with the burying of the non polar residues in four-helix bundle proteins. Similarly, the binary pattern composing the strands in the B16 sequence is consistent with the burying of the non polar residues in four-β strands structures.
The dihedral potential term in our force field allows us to modulate the intrinsic secondary structure propensity. This potential can be tuned to favor helical or β states or it can be adjusted so as to make the α helix and the β sheet secondary structures equally favored. This ability to effectively “turn off” the amino acids secondary structure propensity is key to resolving the relative roles of propensity versus patterning in determining the overall fold. Using replica exchange molecular dynamics simulations, we study the folding thermodynamics of the A16 and B16 proteins with sequences corresponding to five different levels of “propensity frustration.” For each of the two sequences A16 and B16, we study (a) “underfrustrated systems” where both the dihedral potential term (intrinsic propensity) and the polar, non polar pattern favor the same secondary structure; (b) “superfrustrated systems” where the dihedral potential term favors a secondary structure which is in opposition to the one favored by the polar, non polar patterning; (c) “frustrated system” where the fold is “entirely” driven by the polar, non polar patterning, with the dihedral term equally favoring the α helix and the β sheet secondary structure (See Force Field Section for details).
Results and Discussion
16 sequences form four-helix bundles and B16 sequences form four-β-strands bundles
Regarless of the degree of frustration, our simulations show that sequences with the A16 pattern fold to a four-helix bundle. We find two families of four-helix bundles: A “U-bundle” topology and a “Z-bundle” topology that differ in the position of the terminal strands with respect to the second turn (shown schematically in Fig. 2). Each topology has two subtopologies arising from different conformations of the second turn. We denote these structures as UA1 and UA2 (for the “U-bundle”) and ZA1 and ZA2 (for the “Z-bundle”). The four lowest energy structures corresponding to these topologies, along with their RMSD value from UA1 are shown in Figure 2. All four structures have very similar potential energies.
Figure 2.
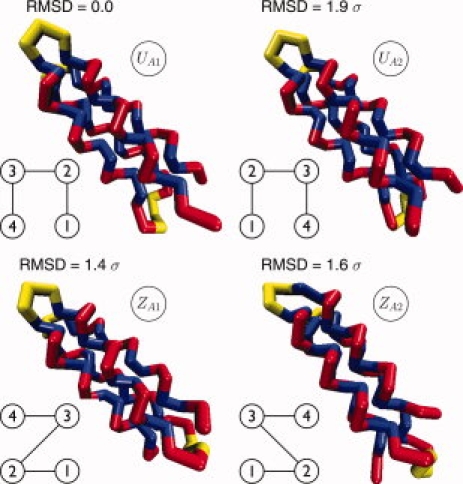
Native structures for the sequence A16 obtained from REX-SC simulations (blue: non polar, red: polar). These structures are common to all five systems AUF2, AUF1, AF, ASF1, ASF2 (See Table IV). Structures UA1 and UA2 have both the terminal beads of the chain on one side and the second turn on the other side (U geometry). They differ in the conformation of the second turn. Structures ZA1 and ZA2 have the terminal beads of the chain on opposite sides respect to the second turn (Z geometry). As in structures UA1 and UA2, structures ZA1 and ZA2 differ in the conformation of the second turn. For each structure, we also show the RMSD from UA1 and a schematic of the helical strands connectivity. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Similarly, the B16 pattern also folds so as to bury the hydrophobic residues and expose the hydrophilic ones to the surface. For the B16 patterning, this results in the formation of four-β-strands bundles (regarless of the degree of frustration), again with' “U-bundle and Z-bundle topologies” (see Fig. 3).
Figure 3.

Native structures for the sequence B16 obtained from REX-SC simulations (blue: non polar, red: polar). These structures are common to all five systems BUF2, BUF1, BF, BSF1, BSF2 (See Table IV). Structure UB1 has both the terminal beads of the chain on one side and the second turn on the other side (U geometry). Structures ZB1, ZB2 have the terminal beads of the chain on opposite sides respect to the second turn (Z geometry). The difference between ZB1 and ZB2 resides in two different conformations of the second turn. For each structure, we also show the RMSD from UB1. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The reason that even the less frustrated sequences for the A16 and B16 cases (AUF2 and BUF2) fold to two alternate topologies (Z and U) is due to the fact that we have not specified any constraints in the turn regions. In nature, amino acids in turns (such as prolines) have conformations preferences that will favor either the U and Z topologies. Simulations by Skolnick and Thirumalai using coarse grained models31,35 have also observed the presence of U and Z four-helix bundles, and showed that adding an “energetic bias” in the turn region would favor one topology over the other. In the present study, we are not unduly concerned by the turns as our goal was to examine the role of pattern and secondary structure frustration in the strands on folding.
Four-β-strand bundles are not common structures in natural proteins (they only appear in the core of the Greek key motif),36 nevertheless, they were studied in several coarse grained simulations as minimal representations of more complex β barrel motifs.31,36,42–44 Conversely, four helix bundles are a common structural motif in both natural and designed proteins.16,25,45 For this reason, we will focus the rest of our analysis on A16-based systems (systems with four-helix bundles as native-like structures). The B16-based systems (systems with four-β-strand bundles as native-like structures) will be considered as an essential benchmark set of systems for extending the validity of our model to both α helix and β strand folds.
Loss of folding cooperativity with increasing secondary structure frustration
The nature of the folding and collapse transitions of the A16 sequence with varying degrees of secondary structure frustration was monitored by considering the specific heat and temperature denaturation curves (Fig. 4). The temperature denaturation curves g(T) (Fraction Folded vs. Temperature) yield the folding temperature TF of the protein from the midpoint in the curves (temperature corresponding to 0.5 fraction folded). The fraction folded g(T) was defined as the statistical weight of the structures with both RMSD(UA1) and RMSD(ZA1) < 2.11 σ. This definition comes from considering the joint 2D probability distributions of the root mean square deviation from structure UA1 [RMSD(UA1)] and structure ZA1 [RMSD(ZA1)], for the systems AUF2, AUF1, AF, ASF1, and ASF2 at low temperature. This cutoff definition encompasses all the four low energy structural families shown in Figure 2. Plots of the specific heat as a function of temperature give the collapse temperature TC from the location of the peak in the curve.
Figure 4.
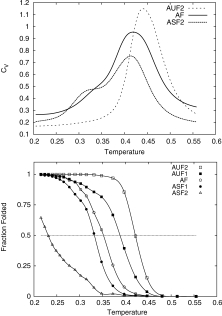
Top: Heat capacity versus temperature calculated from our REX-LD simulations for systems AUF2, AF, and ASF2. Bottom: Temperature denaturation curves calculated from our REX-LD simulations. Systems AUF2, AUF1, AF, and ASF1 exhibit sigmoidal denaturation curves indicating cooperative behavior whereas system ASF2 (the system with the highest degree of energetic frustration) shows a gradual conformational change, and therefore, no cooperativity during denaturation.
For the least frustrated sequence (high intrinsic helical propensities, potential α2 in Fig. 5), the denaturation curve shows a well defined sigmoidal shape and the heat capacity shows a single peak. The values of TF and TC obtained from these graphs coincide, a signature of a cooperative folding process, in which folding and collapse occur simultaneously.
Figure 5.
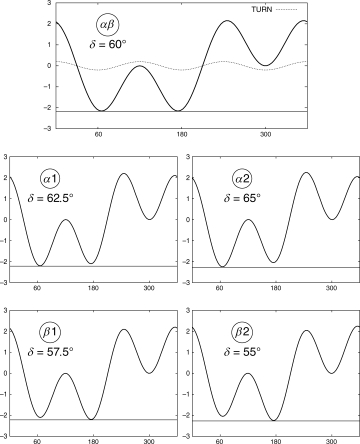
Dihedral potentials used in our simulations. Top: Dihedral potential αβ. This potential favors equally α helix and β strand conformations. Middle: Dihedral potentials α1 and α2. These potentials favor the α helix conformation (intrinsic α helix propensity). Bottom: Dihedral potentials β1 and β2. These potentials favor the β strand conformation (intrinsic β strand propensity).
As secondary structure frustration increases, the denaturation curves remain sigmoidal, but the sigmoidal nature becomes less defined. For the highest level of frustration studied (ASF2), the sigmoidal nature breaks down and the folded populations barely reached 50% even at low temperatures. ASF2 appears to have exceeded the level of frustration that the A16 pattern can tolerate to fold in a “well-behaved” cooperative manner to a four-helix bundle. We also observe that the folding temperature decreases with increasing frustration, indicating a lowering of the stability of the protein. In parallel, the heat capacity curves start to become broader and eventually show two distinct peaks at ASF2. The first peak corresponds to the collapse temperature, and does not show dramatic variations with increasing frustration. The second peak corresponds to a second folding transition. Overall, cooperativity decreases with increasing secondary structure frustration.
Experimental protein denaturation curves for two-state folders (as a function of temperature or of denaturant concentration) typically show a sigmoidal shape indicating the cooperative nature of the folding process.46–49 With the exception of the most frustrated system, the curves for the other systems considered (ASF1, AF, AUF1, and AUF2) exhibit sigmoidal shapes in qualitative agreement with experimental thermal denaturation curves obtained from protein design experiments.26,27
The folding and collapse temperatures for the A16 systems are listed in Table I together with the correspondent percentages of α helix and β sheet secondary structure content. It is interesting to note that at 50% folded (TF), the helical content for all the A16 systems is ≈70% while at 100% folded (lowest temperature TL), the α helical content is ≈ 80−82% (data not shown) for ASF1, AF, AUF1, and AUF2 and ≈70% for system ASF2 where TL ≈ TF. Hence, for ASF1, AF, AUF1, and AUF2, a small relative difference in α helical content (≈10−12%) between temperatures TL and TF leads to a large change in structure population.
Table I.
Collapsing Temperatures TC Calculated from the Heat Capacity Data
| System name | TC (CV) | TF (RMSD) | %α | %β |
|---|---|---|---|---|
| AUF2 | 0.44 | 0.42 | 73 | 16 |
| AUF1 | 0.45 | 0.39 | 74 | 15 |
| AF | 0.42 | 0.35 | 73 | 16 |
| ASF1 | 0.43 | 0.33 | 73 | 16 |
| ASF2 | 0.42 | 0.23 | 69 | 18 |
| BUF2 | 0.51 | 0.50 | 24 | 67 |
| BUF1 | 0.46 | 0.46 | 27 | 62 |
| BF | 0.44 | 0.44 | 29 | 61 |
| BSF1 | 0.40 | 0.37 | 16 | 72 |
| BSF2 | 0.38 | 0.36 | 17 | 71 |
Folding temperatures TF calculated from the joint probability distributions of RMSD (ZA1) and RMSD (UA1). For the folding temperatures calculated from the RMSD probability distributions, we also list the correspondent percentages of α helix and β sheet secondary structure contents. Because of the presence of the turn regions, in the A16 systems, the maximum percentage value for the α helix secondary structure content, calculated from simple statistical considerations, is 82%. The 95% confidence intervals for the calculated folding temperatures and for the collapsing temperatures are < 0.01. The relative experimental error in the percentages of secondary structure content is < 1%.
Similar results were observed for the B16 sequence, with loss of stability and cooperativity upon increase of secondary structure frustration (data not shown). TF, TC, and helical and beta contents for the B16 system are tabulated in Table I. We also observed that when the same degree of energetic frustration is applied, the systems based on the B16 sequence (β strand folders) are more stable than the corresponding systems based on the A16 sequence (α helix folders). Analysis of the distributions of distances between non polar beads in A16-based and B16-based systems shows that the average nearest-neighbor distance is smaller in β structures than in α helix bundles (data not shown). This leads to a more compact and “energetically efficient” packing of the hydrophobic core in β structures, and therefore, to a higher stability.
Free energy surfaces at TF
In Figure 6, we plot the two-dimensional free energy landscapes as functions of RMSD(ZA1) and RMSD(UA1), for the systems AUF2, AUF1, AF, ASF1, ASF2, at their respective folding temperatures. At folding temperature, the protein populates both unfolded and folded conformations. For AUF2, AUF1, AF, and ASF1, the four basins corresponding to the U and Z topologies are well-defined. It is remarkable that three of these basins are still clearly seen for the most frustrated sequence ASF2, despite its “poor folder” nature. Representative structures of the unfolded states are shown in Figure 6.
Figure 6.
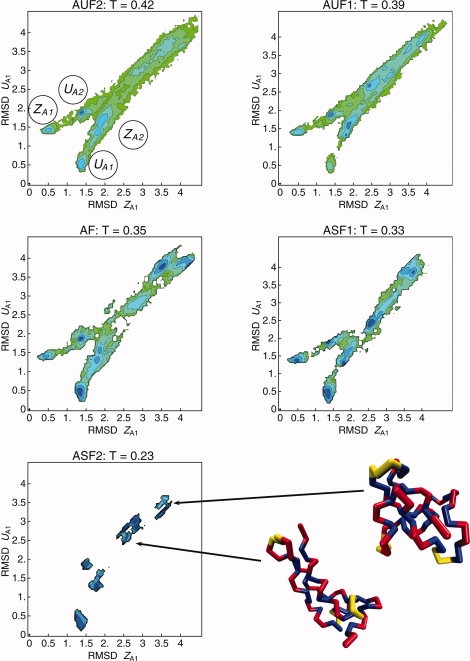
Free energy landscape as a function of the two order parameters RMSD (ZA1) and RMSD (UA1) obtained from REX-LD simulations for the systems AUF2, AUF1, AF, ASF1, and ASF2, at their respective folding temperatures (See Table I). The four energy basins in the top left plot have been labeled after the correspondent native-like structures in Figure 2. Two representative structures for the basin of the non-native, compact structures for system ASF2 are shown at the bottom right corner. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
CD spectra and ensembles of structures
In Figure 7, we plotted the free energy maps for the systems AUF2, AF, and ASF2 together with their CD spectra at T = 0.35 (the folding temperature of the AF system). The CD spectra at T = 0.35 for the AUF2 (least frustrated), AF, and ASF2 (most frustrated) were calculated following the protocol reported in the Supporting Information.50 The three spectra show the typical signature of the α helix secondary structure, namely, a global maximum at λ ≈ 190 nm, a crossover at λ ≈ 200 nm, and two minima at λ ≈ 208 nm and λ ≈ 222 nm.50
Figure 7.
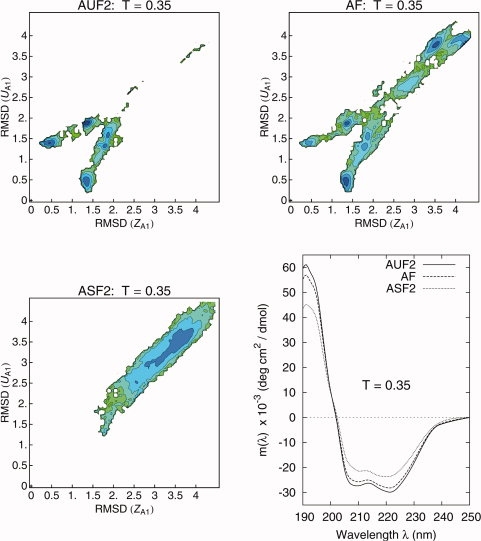
Free energy landscape as a function of the two order parameters RMSD (ZA1) and RMSD (UA1) obtained from REX-LD simulations for the systems AUF2 (top left), AF (top right), and ASF2 (bottom left), at the folding temperature of the system AF (T = 0.35). As the energetic frustration increases from AUF2 to AF and ASF2, the basins correspondent to unfolded, non-native structures increase its statistical weight. Bottom right: CD spectra for the systems AUF2, AF, and ASF2 at T = 0.35 (folding temperature for the AF system). Dramatic differences in the structure population translate into small differences in the the CD profiles. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
As can be seen from the free energy maps in Figure 7, the population of native structures varies wildly between AUF2 and ASF2 at T = 0.35. At this temperature, the AUF2 shows 100% folded population, AF 50% and ASF2 0%. The helical contents are 80% for AUF2, 74% for AF, and 56% for ASF2. Despite these dramatic differences, the CD profiles of AUF2 and AF look the same while the CD profile of ASF2 shows a slight upward shift and shallowing of the basins (and slight decrease in the 190 nm peak) with increasing frustration. Experiments by Hecht and coauthors observed similar differences between CD spectra of helical peptides designed using (i) amino acids with high α helix propensity (correspondent to our AUF2 system) and (ii) amino acids with low α helix propensity (correspondent to our ASF2 system).51 The persistence of secondary structure in heat-denatured states, as observed in the CD spectrum of the ASF2 system, has been seen experimentally by CD spectroscopy data.52,53
What simulations are adding to these experiments is a “picture” of the ensemble of structures underlying a given CD spectrum. We can explicitely see (in the case of ASF2) that a collection of non-native, compact conformations, with no well-defined tertiary structure, but with some helical content, can produce a spectra that is easily mistaken for one of a “folded” protein.47
Comparison with energetic frustration in de novo peptides
Our model allows us to directly explore the effect of using torsion-angle forces (local interactions, secondary structure propensity), which oppose the secondary structure favored by the pattern of polar and non polar amino acids in the sequence (nonlocal interactions), and therefore, to add energetic frustration to the model. A similar type of frustration has been introduced by Xiong and coauthors51 who designed a peptide with helical (polar, non polar) pattern using amino acids with low helical propensity, that is, with high β sheet forming propensity (“peptide 2A”). In the same experimental study, a control system consiting of a de novo peptide (“peptide 1A”) with the same helical pattern and composed by amino acids with high α helical propensity was used for comparison. Both peptide 1A and 2A contain 16 amino acids.
We offer an estimate of the energetic frustration introduced in peptide 2A, respect to peptide 1A, by calculating the difference in energetic stability between the two peptides from the values Ui,α in Table II (see Section “Knowledge-based estimates of α helix and β sheet propensities” for details). We define this difference as:
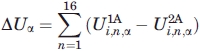 |
(1) |
where 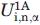 and
and 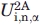 are the free energy costs of introducing amino acid i at position n in peptide 1A and peptide 2A, respectively. In Table II, we compare the value of ΔUα calculated from Eq. (1) with analogous calculations where we consider helical propensity scales obtained from single-point mutation experiments.8,54,56 The third column in Table III contains the predicted values of ΔUα normalized over the number of dihedral angles in our Cα peptide model
are the free energy costs of introducing amino acid i at position n in peptide 1A and peptide 2A, respectively. In Table II, we compare the value of ΔUα calculated from Eq. (1) with analogous calculations where we consider helical propensity scales obtained from single-point mutation experiments.8,54,56 The third column in Table III contains the predicted values of ΔUα normalized over the number of dihedral angles in our Cα peptide model 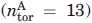 and can be directly related with the dihedral angle frustration in our computational model. The value of this energetic frustration introduced in our systems ASF1 and ASF2 (compared to systems AUF1 and AUF2) and in systems BSF1 and BSF2 (compared to systems BUF1 and BUF2) can be calculated directly from Eq. (5) and varies between 0.17 ε and 0.34 ε. This is consistent with the results in Table III for ε = 1 − 2 Kcal mol.−1 It is worth reminding that, for ε ≤ 2.9 Kcal mol,−1 we observe full consistency between the net intrinsic secondary structure propensity in our force field and an analogous quantity calculated from the PDB repository (see Section “Force Field” and Table II).
and can be directly related with the dihedral angle frustration in our computational model. The value of this energetic frustration introduced in our systems ASF1 and ASF2 (compared to systems AUF1 and AUF2) and in systems BSF1 and BSF2 (compared to systems BUF1 and BUF2) can be calculated directly from Eq. (5) and varies between 0.17 ε and 0.34 ε. This is consistent with the results in Table III for ε = 1 − 2 Kcal mol.−1 It is worth reminding that, for ε ≤ 2.9 Kcal mol,−1 we observe full consistency between the net intrinsic secondary structure propensity in our force field and an analogous quantity calculated from the PDB repository (see Section “Force Field” and Table II).
Table II.
Estimates of ΔUα
| Ui,α estimation method | ΔUα (Kcal mol−1) |
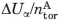 (Kcal mol−1) (Kcal mol−1) |
|---|---|---|
| This study: Table I, column 5 | −1.824 | −0.140 |
| O'Neil and Degrado54 (α helical dimer peptide) | −3.09 | −0.24 |
| Horovitz et al.8 (Barnase, site 32) | −3.66 | −0.28 |
| Blaber et al.55 (T4 Lysozyme, site 44) | −0.84 | −0.065 |
| Myers et al.56 (helical peptide from RNase T1, pH 7) | −2.50 | −0.19 |
ΔUα is the Change in helical stability between peptides 1A and 2A used by Xiong et al51, predicted using a variety of empirical (this study) and experimental helical propensity scales. The third column is the predicted change in stability normalized over the number of dihedral degrees of freedom in our model peptides and can be directly compared with our simulations results (See Section “Comparison with energetic frustration in de novo peptides”).
Table III.
Amino Acid Frequency in α Helices and β Sheets
| AA | P(i|α) (%) | P(i|β) (%) | P(i) (%) | Ui,α (Kcal mol−1) | Ui,β (Kcal mol−1) | Ui,α − Ui,β |
|---|---|---|---|---|---|---|
| Ala | 12.050 ± 0.043 | 6.813 ± 0.046 | 8.326 ± 0.020 | −0.220 | 0.120 | −0.34 |
| Arg | 6.372 ± 0.032 | 4.454 ± 0.038 | 5.257 ± 0.016 | −0.115 | 0.099 | −0.214 |
| Asn | 3.044 ± 0.023 | 2.171 ± 0.027 | 4.147 ± 0.014 | 0.184 | 0.386 | −0.202 |
| Asp | 4.958 ± 0.029 | 2.457 ± 0.028 | 5.881 ± 0.017 | 0.102 | 0.520 | −0.418 |
| Cys | 1.065 ± 0.014 | 1.673 ± 0.023 | 1.246 ± 0.008 | 0.093 | −0.176 | 0.269 |
| Gln | 4.808 ± 0.028 | 2.520 ± 0.029 | 3.639 ± 0.013 | −0.166 | 0.219 | −0.385 |
| Glu | 9.733 ± 0.039 | 4.637 ± 0.038 | 7.004 ± 0.018 | −0.196 | 0.246 | −0.442 |
| Gly | 3.243 ± 0.024 | 4.714 ± 0.039 | 7.286 ± 0.018 | 0.483 | 0.260 | 0.223 |
| His | 2.039 ± 0.019 | 2.146 ± 0.026 | 2.374 ± 0.011 | 0.091 | 0.060 | 0.031 |
| Ile | 6.399 ± 0.033 | 11.030 ± 0.057 | 5.878 ± 0.017 | −0.051 | −0.375 | 0.324 |
| Leu | 12.536 ± 0.044 | 11.598 ± 0.058 | 9.563 ± 0.021 | −0.161 | −0.115 | −0.046 |
| Lys | 6.591 ± 0.033 | 3.943 ± 0.035 | 5.775 ± 0.017 | −0.079 | 0.228 | −0.307 |
| Met | 2.118 ± 0.019 | 1.826 ± 0.024 | 1.687 ± 0.009 | −0.136 | −0.047 | −0.089 |
| Phe | 3.997 ± 0.026 | 6.026 ± 0.043 | 4.089 ± 0.014 | 0.014 | −0.231 | 0.245 |
| Pro | 1.161 ± 0.014 | 1.484 ± 0.022 | 4.606 ± 0.015 | 0.821 | 0.675 | 0.146 |
| Ser | 4.470 ± 0.027 | 4.492 ± 0.038 | 5.825 ± 0.017 | 0.158 | 0.155 | 0.003 |
| Thr | 4.010 ± 0.026 | 6.075 ± 0.043 | 5.324 ± 0.016 | 0.169 | −0.079 | 0.248 |
| Trp | 1.446 ± 0.016 | 1.819 ± 0.024 | 1.376 ± 0.008 | −0.030 | −0.166 | 0.136 |
| Tyr | 3.392 ± 0.024 | 5.076 ± 0.040 | 3.514 ± 0.013 | 0.021 | −0.219 | 0.24 |
| Val | 6.559 ± 0.033 | 15.043 ± 0.065 | 7.195 ± 0.018 | 0.055 | −0.440 | 0.495 |
As detailed in the Methods section, we use a representative sample of chains from the PDB database. P(i|α) is the conditional probability that a randomly chosen amino acid from the subset of amino acids belonging to α helices is of type i (where “i” represents one of the 20 standard amino acids). From these probabilities, we estimate the free energy penalty for belonging to a helix, Ui,α, using: exp(−Ui,α/kBT) = P(i|α)/P(i), where P(i) is the probability that an amino acid found in this set of proteins is of type i. (Here, we have assumed T = 300°K, kB = 0.0019872 Kcal mol−1 K−1. See Table I in the Supporting Information for comparison with experimental α helix propensity scales.) P(i|β) and Ui,β are defined in an analogous way.
Xiong and coauthors51 also studied two peptides both with the pattern of polar and non polar amino acids favoring the β sheet secondary structure and composed by nine amino acids with high α helical propensity (“peptide 1B”) and with high β sheet propensity (“peptide 2B”). The energetic frustration introduced in peptide 1B is calculated following the same method used for peptides 1A and 2A (aforementioned in this Section) and is found to be 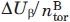 = 0.125 ± 0.005 Kcal mol−1, where
= 0.125 ± 0.005 Kcal mol−1, where 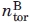 = 6 is the number of torsional degrees of freedom for a nine amino acid peptide in the Cα representation.
= 6 is the number of torsional degrees of freedom for a nine amino acid peptide in the Cα representation.
Methods
Geometry and sequences
Each amino acid in the model protein is represented by a single bead (with diameter σ) that can be polar (L), non polar (H), or neutral (N). Each bead has mass m (m is the mass unit) and is connected to the neighboring beads in the peptide chain by harmonic “springs” (See Section “Force Field”). In this study, we analyze two different “amino acid” sequences named A16 and B16, both composed by four identical “strands” contaning L and H beads and connected by short flexible regions (turns) made up by three beads of type N, each. The A16 sequence is: (LLHH)4N3(HHLL)4N3(LLHH)4N3(HHLL)4 whereas the B16 sequence is: (LH)8N3(HL)8N3(LH)8N3(HL)8. The two “amino acid” sequences A16 and B16 are shown in Figure 1. The pattern of polar (L) and non polar residues (H) in the A16 sequence (non polar residues every three or four positions) is consistent (i) with the structural periodicity of 3.6 residues/turn typical of α helices and (ii) with the “burying” of the non polar residues H in an amphiphilic four-helix bundle. Similarly, the B16 sequence (non polar residues every two positions) is consistent with (i) the typical structural periodicity of β sheets and (ii) with the burial of the non polar residues in an amphiphilic four-strands β barrel.14,20,35,51
Force Field
The Hamiltonian includes the following terms:
- Non-bonded Interactions
where λLj = λNj = 0.0 (j = H, L, N) and λHH = 1.0, ε defines the energy scale and σ defines the length scale. The pair, nonbonded, interactions involving L and N beads are purely repulsive whereas HH pairs interact via a “full” Lennard-Jones (LJ) potential comprising both a soft repulsive core and a short-range attractive tail. We observe that the energy contribution from an HH contact in our model is consistent with free energies of transfer from non polar solvent to water, for hydrophobic amino acids, if ɛ in the LJ potential is between 1 and 3 Kcal mol−1.57–61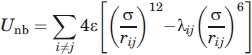
(2) - Bond length potential
where Kb = 4813 ε · σ−2 and r0 = σ.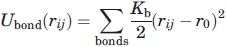
(3) - Bond angle potential
where Kθ = 66.6 ε and θ0 = 105°.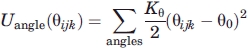
(4) Dihedral angle potential
Dihedral angles γ defined by different quadruplets composed of H and L beads are constrained by the potential energy term:
| (5) |
where C = 1.2 ε. The dihedral potential Udihe has three minima: ∼60°, ∼180°, and ∼ −60°, correspondent to α helix, β strand, and left helix conformations, respectively. In our simulations, we consider five different dihedral potentials differing in the value of the phase δ. The profiles of the dihedral potentials are plotted in Figure 5. On the top line of Figure 5, we plot the potential labeled as αβ (where δ = 60.0°). This potential favors equally α helix and β strand conformations, that is, the α helix and the β strand minima have the same depth and ΔUdihe = ∥Udihe(γα) − Udihe(γβ)∥ = 0.0, where γα ≈ 60° is the location of the α helix minimum and γβ ≈ 180° is the location of the β sheet minimum.
The potentials labeled as α1 and α2 (where δ = 62.5° and δ = 65.0°, respectively) favor the α helix conformation, that is, they introduce in the Hamiltonian an “intrinsic” propensity for the α helix secondary structure (see middle line of Fig. 5). In a similar way, the potentials labeled as β1 and β2 (where δ = 57.5° and δ = 55.0°, respectively) favor the β strand conformation, that is, they introduce in the Hamiltonian an “intrinsic” propensity for the β strand secondary structure (See bottom line of Fig. 5). For the potentials α1 and β1, ΔUdihe = 0.085 ɛ, whereas for potentials α2 and β2, ΔUdihe = 0.17 ε. Hence, in our model the net energy contribution from the amino acid intrinsic propensity, expressed as a difference between α helix and β strand secondary structures, varies between 0 and 0.17 ε (ΔUdihe ε [0,0.17]ε). To relate ΔUdihe to real proteins, we analyzed a recent snapshot of the PDB repository and obtained: |ΔUdihe| ≡ ∥Ui,α − Ui,β∥ ε [0.01,0.495] Kcal mol−1 (See Table III and the details of our calculation in Sections “Knowledge-based estimates of α helix and β sheet propensities” and “Comparison with energetic frustration in de novo peptides”). We observe that the energy contribution from the net intrinsic secondary structure propensity in our model (dihedral potential) is consistent with the results obtained from the PDB repository for values of ε up to ∼2.9 Kcal mol.−1
Dihedral angles involving one or more N beads are considered as parts of the “turn regions”. The dihedral potential energy term for the turn regions is:
| (6) |
where D = 0.2 ɛ. The small value for the energy constant D in 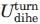 makes the “turn regions” highly flexible, in terms of rotational degrees of freedom, when compared with the α helix and β strand regions (See Fig. 5, top line).
makes the “turn regions” highly flexible, in terms of rotational degrees of freedom, when compared with the α helix and β strand regions (See Fig. 5, top line).
Nomenclature
We performed replica exchange Langevin dynamics (REX-LD) simulations for studying the thermodynamics of folding of 10 different model proteins differing in the “sequence propensity,” defined by the pattern of polar and non polar beads (α helix for sequence A16 and β sheet for sequence B16), and in the intrinsic secondary structure propensity, defined by the value of the phase δ in Eq. (5). The names of the protein systems together with their “amino acid” sequence, sequence propensity, secondary structure propensity, and the corresponding value of the “dihedral” phase δ are given in Table IV. We will refer to the different systems as follows: (i) “frustrated” (F) in which the dihedral potential favors equally the α helix or the β strand (δ = 60°); (ii) “underfrustrated” (UF) in which the “intrinsic” secondary structure propensity (dihedral potential) and the binary patterning favor the same secondary structure; and (iii) “superfrustrated” (SF) where the “intrinsic” secondary structure propensity (dihedral potential) opposes the binary patterning (in other words, a sequence composed of amino acids with a high β strand propensity, but with a binary pattern favoring a helix, and vice versa). We will consider two “underfrustrated” systems (UF1 and UF2) and two “superfrustrated” systems (SF1 and SF2). The “energetic frustration” in the different systems follows the order: UF2 < UF1 < F < SF1 < SF2. Energies are expressed in units of ε and distances in units of σ.
Table IV.
Different Systems Studied in Our Simulations and Their Correspondent Sequence, Sequence Propensity, Secondary Structure Propensity, and Value of the “Dihedral” Phase δ
| System name | Sequence | Sequence propensity | Secondary structure propensity | δ (deg) |
|---|---|---|---|---|
| AUF2 | A16 | Alpha | Alpha (α2) | 65.0 |
| AUF1 | A16 | Alpha | Alpha (α1) | 62.5 |
| AF | A16 | Alpha | None (αβ) | 60.0 |
| ASF1 | A16 | Alpha | Beta (β1) | 57.5 |
| ASF2 | A16 | Alpha | Beta (β2) | 55.0 |
| BUF2 | B16 | Beta | Beta (β2) | 55.0 |
| BUF1 | B16 | Beta | Beta (β1) | 57.5 |
| BF | B16 | Beta | None (αβ) | 60.0 |
| BSF1 | B16 | Beta | Alpha (α1) | 62.5 |
| BSF2 | B16 | Beta | Alpha (α2) | 65.0 |
The labels in brackets correspond to the different dihedral potentials plotted in Figure 5. The first character in the system name corresponds to the sequence (A for sequence A16 and B for sequence B16). The last three characters in the system name identify the degree of “frustration”: UF, underfrustrated; F, frustrated; SF, superfrustrated. The degree of “frustration” in the different systems follows the order: UF2 < UF1 < F < SF1 < SF2. See Section “Force Field” and Figure 5 for further details.
Simulations details
An “extended” conformation for the protein chain was generated by running a short LD simulation at a temperature T = 1.0 (in reduced units) with the intramolecular interactions being purely repulsive. The conformation of the protein chain at the end of this preliminary run was taken as the starting conformation in the 10 independent REX-LD simulations. We ran the REX-LD simulations using 16 (B16-based systems) or 20 (A16-based systems) replicas with temperatures in the interval [0.22, 0.55] (in reduced units). The time step was ts ≈ 0.008 τ, where τ = (mσ2/ɛ) is the time unit. The cutoff for the nonbonded interactions was fixed at 4 σ and the damping coefficient in the Langevin integrator was set to b = 0.8 τ−1, Swaps between the different replicas were attempted every 2 × 104 time steps, the acceptance ratio varied between 40% and 60% and the total simulation time for each replica varied between 5 × 105 τ and 106 τ. We considered the second half of the trajectories as the production runs. Additional replica exchange simulations combined with “slow cooling” (REX-SC) were used to obtain the lowest energy structures, at zero temperature, for the different systems listed in Table IV. REX-SC simulations used the same set of parameters as in REX-LD simulations. Every 10 replica swaps, the temperatures were lowered of a quantity ΔT, calculated so to have all the replicas reaching ≈ zero temperature at the end of the REX-SC simulations. The NAMD software62 was used for all the simulations. The VMD software was used for part of the analysis.63
Knowledge-based estimates of α helix and β sheet propensities
Inspired by earlier research on empirical potentials,64–66 in Table III, we attempt to estimate the relative α helix and β sheet propensity of the standard amino acids, by considering the probability that each amino acid is found in α helices and β sheets in nature. We associate a free energy penalty Ui,α to amino acid i in a helix with the probability P(i|α) that this amino acid occurs in helices (relative to the probability that a random mutation would produce the same amino acid):
| (7) |
where T = 300°K, kB = 0.0019872 Kcal mol−1 K−1) and P(i) is the probability that the amino acid i is found in nature, regardless of secondary structure. The P(i|α)/P(i) values correlate well with experimental measures of α-helical propensity (with correlation coefficient R ranging from 0.6 to 0.87; see Supporting Information)54–56 as well as with other knowledge-based propensity scales.7,67,68 The analogous quantities for β sheets, Ui,β and P(i|β), were calculated using the same method.
The probabilities P(i|α) and P(i|β) were estimated from a representative sample of sequences from the PDB database consisting of Ntot = 1,986,157 amino acids, Nα = 886,428 of which belong to α-helices, and Nβ = 471,407 to β sheets (See Section I in the Supporting Information for database details). In details, P(i|α) is the conditional probability that the amino acid i belongs to a helix (P(i|β) was calculated analogously.) In an effort to eliminate noise from the data set, the first and last two amino acids of every helix, and the first and last amino acid of every strand of every β sheet were ignored in the calculations of P(i|α) and P(i|β), respectively. We found that these terminal residues were occasionally proline and glycine residues, which are normally found in turns. The results of these calculations are shown in Table III.
Conclusions
A large body of experimental work has focused on identifying the key elements that govern folding to a given three-dimensional native structure. In this article, we have used a coarse grained Cα model consisting of three types of residues (hydrophobic, polar, and neutral) to investigate the relative importance of sequence patterning (a long-range effect) and intrisic secondary structure propensity (a local effect) in determining a protein's fold.
The intrinsic secondary structure propensity is introduced in our model via a dihedral potential term that can be adjusted (1) to favor a particular conformation (α helix or β sheet) and (2) to explore the “ideal” condition in which both the α helix and the β sheet secondary structures are equally favored. The “adaptability” of this dihedral potential term allowed us to quantitatively analyze the separate contributions of local and nonlocal factors (intrinsic propensity and polar, non polar patterning, respectively) in determining the folded structure of both a four-helix bundle protein and a four β sheet bundle.
Our simulations allow us to systematically explore the degree of frustration a given polar, non polar pattern can tolerate when the secondary structure intrinsic propensities are in opposition to it. We showed that the range of “propensity” frustration that we studied in our simulation can be correlated to experiments through a statistical analysis of the PDB repository data. For values of the intrinsic secondary structure propensities commensurate with those used in experiments by Xiong and coauthors51 on aggregating peptides, (see Section “Comparison with energetic frustration in de novo peptides”), we find that the binary patterning trumps the propensities in determining the secondary structure.
Our simulations augment experiments in two manners. First, they allow us to determine for which degree of intrinsic secondary structure frustration the patterning can no longer determine the structure. In the experiments of Xiong and coauthors,51 the frustrated sequence still adopted the correct secondary structure, and hence, no conclusions could be drawn about whether there existed a threshold level of frustration that the patterning could no longer tolerate. Second, they directly target how patterning and propensity affect the overall fold of the protein. The experiments by Xiong and coauthors,51 in which intrinsic secondary structure frustration was introduced, focused uniquely on short peptides that aggregate into oligomers with a given secondary structure. Here, we considered a model of an actual protein, with a well defined tertiary structure. As such, our results qualitatively extend experimental findings by examining the relative roles of polar and non polar patterning, and intrinsic propensity in determining not only the secondary structure content but also the native fold of single domain proteins.
It is quite remarkable that our simple computational model, in which the fine chemical details of the amino acids are not considered, quantitatively agrees with experimental results. This points to the fact that sequence patterning is a fundamental physical property, and, as such, can be captured in models obeying basic polymer physics principles.
Acknowledgments
Simulations were performed in part by using the computational resources of the California Nanosystem Institute. The authors thank Michael Hecht (Princeton University) and David Shortle (Johns Hopkins University) for helpful advice.
References
- 1.Ventura S, Serrano L. Designing proteins from the inside out. Proteins. 2004;56:1–10. doi: 10.1002/prot.20142. [DOI] [PubMed] [Google Scholar]
- 2.Ramachandran G, Sasisekharan V. Conformation of polypeptides and proteins. Adv Protein Chem. 1968;23:283–437. doi: 10.1016/s0065-3233(08)60402-7. [DOI] [PubMed] [Google Scholar]
- 3.Creamer TP, Rose GD. Side-chain entropy opposes alpha-helix formation but rationalizes experimentally determined helix-forming propensities. Proc Natl Acad Sci USA. 1992;89:5937–5941. doi: 10.1073/pnas.89.13.5937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Street A, Mayo S. Intrinsic beta-sheet propensities result from van der waals interactions between side chains and the local backbone. Proc Natl Acad Sci USA. 1999;96:9074–9076. doi: 10.1073/pnas.96.16.9074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Richardson JM, Lopez MM, Makhatadze GI. Enthalpy of helix-coil transition: missing link in rationalizing the thermodynamics of helix-forming propensities of the amino acid residues. Proc Natl Acad Sci USA. 2005;102:1413–1418. doi: 10.1073/pnas.0408004102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Creamer TP, Rose GD. Alpha-helix-forming propensities in peptides and proteins. Proteins. 1994;19:85–97. doi: 10.1002/prot.340190202. [DOI] [PubMed] [Google Scholar]
- 7.Chou PY, Fasman GD. Empirical predictions of protein conformation. Annu Rev Biochem. 1978;47:251–276. doi: 10.1146/annurev.bi.47.070178.001343. [DOI] [PubMed] [Google Scholar]
- 8.Horovitz A, Matthews JM, Fersht AR. Alpha-helix stability in proteins. II. Factors that influence stability at an internal position. J Mol Biol. 1992;227:560–568. doi: 10.1016/0022-2836(92)90907-2. [DOI] [PubMed] [Google Scholar]
- 9.Pace CN, Scholtz JM. A helix propensity scale based on experimental studies of peptides and proteins. Biophys J. 1998;75:422–427. doi: 10.1016/s0006-3495(98)77529-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim CA, Berg JM. Thermodynamic beta-sheet propensities measured using a zinc-finger host peptide. Nature. 1993;362:267–270. doi: 10.1038/362267a0. [DOI] [PubMed] [Google Scholar]
- 11.Minor DL, Kim PS. Measurement of the beta-sheet-forming propensities of amino acids. Nature. 1994;367:660–663. doi: 10.1038/367660a0. [DOI] [PubMed] [Google Scholar]
- 12.Smith CK, Withka JM, Regan L. A thermodynamic scale for the beta-sheet forming tendencies of the amino acids. Biochemistry. 1994;33:5510–5517. doi: 10.1021/bi00184a020. [DOI] [PubMed] [Google Scholar]
- 13.Brändén C-I, Tooze J. Introduction to protein structure. 2nd ed. New York, NY: Garland Pub; 1999. [Google Scholar]
- 14.West M, Hecht MH. Binary patterning of polar and non polar amino acids in the sequences and structures of native proteins. Protein Sci. 1995;4:2032–2039. doi: 10.1002/pro.5560041008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schwartz R, King J. Frequencies of hydrophobic and hydrophilic runs and alternations in proteins of known structure. Protein Sci. 2006;15:102–112. doi: 10.1110/ps.051741806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schafmeister CE, LaPorte SL, Miercke LJ, Stroud RM. A designed four helix bundle protein with native-like structure. Nat Struct Biol. 1997;4:1039–1046. doi: 10.1038/nsb1297-1039. [DOI] [PubMed] [Google Scholar]
- 17.Regan L, DeGrado WF. Characterization of a helical protein designed from first principles. Science. 1988;241:976–978. doi: 10.1126/science.3043666. [DOI] [PubMed] [Google Scholar]
- 18.Hecht MH, Richardson JS, Richardson DC, Ogden RC. De novo design, expression, and characterization of felix: a four-helix bundle protein of native-like sequence. Science. 1990;249:884–891. doi: 10.1126/science.2392678. [DOI] [PubMed] [Google Scholar]
- 19.Handel TM, Williams SA, DeGrado WF. Metal ion-dependent modulation of the dynamics of a designed protein. Science. 1993;261:879–885. doi: 10.1126/science.8346440. [DOI] [PubMed] [Google Scholar]
- 20.Munson M, O'Brien R, Sturtevant JM, Regan L. Redesigning the hydrophobic core of a four-helix-bundle protein. Protein Sci. 1994;3:2015–2022. doi: 10.1002/pro.5560031114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Raleigh DP, Betz SF, DeGrado WF. A de novo designed protein mimics the native state of natural proteins. J Am Chem Soc. 1995;117:7558–7559. [Google Scholar]
- 22.Kamtekar S, Schiffer J, Xiong H, Babik J, Hecht M. Protein design by binary patterning of polar and non polar amino acids. Science. 1993;262:1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
- 23.Wei Y, Kim S, Fela D, Baum J, Hecht M. Solution structure of a de novo protein from a designed combinatorial library. Proc Nat Acad Sci USA. 2003;100:13270–13273. doi: 10.1073/pnas.1835644100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wei Y, Liu T, Sazinsky S, Moffet D, Pelczer I, Hecht M. Stably folded de novo proteins from a designed combinatorial library. Protein Sci. 2003;12:92–102. doi: 10.1110/ps.0228003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Go A, Kim S, Baum J, Hecht MH. Structure and dynamics of de novo proteins from a designed superfamily of 4-helix bundles. Protein Sci. 2008;17:821–832. doi: 10.1110/ps.073377908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Roy S, Ratnaswamy G, Boice J, Fairman R, McLendon G, Hecht M. A protein designed by binary patterning of polar and non polar amino acids displays native-like properties. J Am Chem Soc. 1997;119:5302–5306. [Google Scholar]
- 27.Roy S, Hecht M. Cooperative thermal denaturation of proteins designed by binary patterning of polar and non polar amino acids. Biochemistry. 2000;39:4603–4607. doi: 10.1021/bi992328e. [DOI] [PubMed] [Google Scholar]
- 28.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 29.Engelman DM, Steitz TA, Goldman A. Identifying non polar transbilayer helices in amino acid sequences of membrane proteins. Annu Rev Biophys Biophys Chem. 1986;15:321–353. doi: 10.1146/annurev.bb.15.060186.001541. [DOI] [PubMed] [Google Scholar]
- 30.Dill KA, Bromberg S, Yue K, Fiebig KM, Yee DP, Thomas PD, Chan HS. Principles of protein folding: a perspective from simple exact models. Protein Sci. 1995;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Guo Z, Thirumalai D. Kinetics and thermodynamics of folding of a de novo designed four-helix bundle protein. J Mol Biol. 1996;263:323–343. doi: 10.1006/jmbi.1996.0578. [DOI] [PubMed] [Google Scholar]
- 32.Guo Z, Thirumalai D. Kinetics of protein folding:- nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36:83–102. [Google Scholar]
- 33.Sorenson JM, Head-Gordon T. Matching simulation and experiment: a new simplified model for simulating protein folding. J Comput Biol. 2000;7:469–481. doi: 10.1089/106652700750050899. [DOI] [PubMed] [Google Scholar]
- 34.Brown S, Fawzi NJ, Head-Gordon T. Coarse-grained sequences for protein folding and design. Proc Natl Acad Sci USA. 2003;100:10712–10717. doi: 10.1073/pnas.1931882100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rey A, Skolnick J. Computer modeling and folding of four-helix bundles. Proteins. 1993;16:8–28. doi: 10.1002/prot.340160103. [DOI] [PubMed] [Google Scholar]
- 36.Kolinski A, Galazka W, Skolnick J. Computer design of idealized beta-motifs. J Chem Phy. 1995;103:10286–10297. [Google Scholar]
- 37.Nymeyer H, Garcia AE, Onuchic JN. Folding funnels and frustration in off-lattice minimalist protein landscapes. Proc Natl Acad Sci USA. 1998;95:5921–5928. doi: 10.1073/pnas.95.11.5921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shea J-E, Nochomovitz YD, Guo Z, Brooks CL., III Exploring the space of protein folding hamiltonians: the balance of forces in a minimalist beta-barrel model. J Chem Phys. 1998;109:2895–2903. [Google Scholar]
- 39.Spek E, Anders Olson C, Shi Z, Kallenbach N. Alanine is an intrinsic alpha-helix stabilizing amino acid. J Am Chem Soc. 1999;121:5571–5572. [Google Scholar]
- 40.Heitmann B, Job GE, Kennedy RJ, Walker SM, Kemp DS. Water-solubilized, cap-stabilized, helical polyalanines: calibration standards for nmr and cd analyses. J Am Chem Soc. 2005;127:1690–1704. doi: 10.1021/ja0457462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Minor DLJ, Kim PS. Context-dependent secondary structure formation of a designed protein sequence. Nature. 1996;380:730–734. doi: 10.1038/380730a0. [DOI] [PubMed] [Google Scholar]
- 42.Honeycutt J, Thirumalai D. Metastability of the folded states of globular proteins. Proc Nat Acad Sci USA. 1990;87:3526–3529. doi: 10.1073/pnas.87.9.3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Honeycutt J, Thirumalai D. The nature of folded states of globular proteins. Biopolymers. 1992;32:695–709. doi: 10.1002/bip.360320610. [DOI] [PubMed] [Google Scholar]
- 44.Friedel M, Sheeler D, Shea J. Effects of confinement and crowding on the thermodynamics and kinetics of folding of a minimalist beta-barrel protein. J Chem Phys. 2003;118:8106–8113. [Google Scholar]
- 45.Harris NL, Presnell SR, Cohen FE. Four helix bundle diversity in globular proteins. J Mol Biol. 1994;236:1356–1368. doi: 10.1016/0022-2836(94)90063-9. [DOI] [PubMed] [Google Scholar]
- 46.Chan HS, Sarina B, Dill KA. Models of cooperativity in protein folding. Philos Trans R Soc London Ser B. 1995;348:61–70. doi: 10.1098/rstb.1995.0046. [DOI] [PubMed] [Google Scholar]
- 47.Betz SF, Raleigh DP, DeGrado WF. De novo protein design: from molten globules to native-like states. Curr Opin Struct Biol. 1993;3:601–610. [Google Scholar]
- 48.Betz SF, Bryson JW, DeGrado WF. Native-like and structurally characterized designed alpha-helical bundles. Curr Opin Struct Biol. 1995;5:457–463. doi: 10.1016/0959-440x(95)80029-8. [DOI] [PubMed] [Google Scholar]
- 49.Kaya H, Chan HS. Polymer principles of protein calorimetric two-state cooperativity. Proteins. 2000;40:637–661. doi: 10.1002/1097-0134(20000901)40:4<637::aid-prot80>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 50.Greenfield N, Fasman GD. Computed circular dichroism spectra for the evaluation of protein conformation. Biochemistry. 1969;8:4108–4116. doi: 10.1021/bi00838a031. [DOI] [PubMed] [Google Scholar]
- 51.Xiong H, Buckwalter B, Shieh H, Hecht M. Periodicity of polar and non polar amino acids is the major determinant of secondary structure in self-aseembling oligomeric peptides. Proc Nat Acad Sci USA. 1995;92:6349–6353. doi: 10.1073/pnas.92.14.6349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shortle D. Denatured states of proteins and their roles in folding and stability. Curr Opin Struct Biol. 1993;3:66–74. [Google Scholar]
- 53.Tamura A, Kimura K, Takahara H, Akasaka K. Cold denaturation and heat denaturation of streptomyces subtilisin inhibitor. Part 1. cd and dsc studies. Biochemistry. 1991;30:11307–11313. doi: 10.1021/bi00111a017. [DOI] [PubMed] [Google Scholar]
- 54.O'Neil KT, DeGrado WF. A thermodynamic scale for the helix-forming tendencies of the commonly occurring amino acids. Science. 1990;250:646–651. doi: 10.1126/science.2237415. [DOI] [PubMed] [Google Scholar]
- 55.Blaber M, Zhang XJ, Matthews BW. Structural basis of amino acid alpha helix propensity. Science. 1993;260:1637–1640. doi: 10.1126/science.8503008. [DOI] [PubMed] [Google Scholar]
- 56.Myers JK, Pace CN, Scholtz JM. Helix propensities are identical in proteins and peptides. Biochemistry. 1997;36:10923–10929. doi: 10.1021/bi9707180. [DOI] [PubMed] [Google Scholar]
- 57.Wolfenden R. Experimental measures of amino acid hydrophobicity and the topology of transmembrane and globular proteins. J Gen Physiol. 2007;129:357–362. doi: 10.1085/jgp.200709743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Creighton TE. Proteins: structure and molecular principles. New York: W.H. Freeman and Company; 1983. [Google Scholar]
- 59.Wolfenden R, Andersson L, Cullis PM, Southgate CC. Affinities of amino acid side chains for solvent water. Biochemistry. 1981;20:849–855. doi: 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
- 60.Nozaki Y, Tanford C. The solubility of amino acids and two glycine peptides in aqueous ethanol and dioxane solutions. Establishment of a hydrophobicity scale. J Biol Chem. 1971;246:2211–2217. [PubMed] [Google Scholar]
- 61.Tanford C. Contribution of hydrophobic interactions to the stability of the globular conformation of proteins. J Am Chem Soc. 1962;84:4240–4247. [Google Scholar]
- 62.Phillips J, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel R, Kale L, Schulten K. Scalable molecular dynamics with namd. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Humphrey W, Dalke A, Schulten K. Vmd: visual molecular dynamics. J Mol Graph. 1996;14:33. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 64.Shortle D. Propensities, probabilities, and the boltzmann hypothesis. Protein Sci. 2003;12:1298–1302. doi: 10.1110/ps.0306903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Finkelstein AV, Badretdinov AYa, Gutin AM. Why do protein architectures have boltzmann-like statistics? Proteins. 1995;23:142–150. doi: 10.1002/prot.340230204. [DOI] [PubMed] [Google Scholar]
- 66.Sippl MJ. Boltzmann's principle, knowledge-based mean fields and protein folding. An approach to the computational determination of protein structures. J Comput Aided Mol Des. 1993;7:473–501. doi: 10.1007/BF02337562. [DOI] [PubMed] [Google Scholar]
- 67.Chou PY, Fasman GD. Conformational parameters for amino acids in helical, beta-sheet, and random coil regions calculated from proteins. Biochemistry. 1974;13:211–222. doi: 10.1021/bi00699a001. [DOI] [PubMed] [Google Scholar]
- 68.Kallberg Y, Gustafsson M, Persson B, Thyberg J, Johansson J. Prediction of amyloid fibril-forming proteins. J Biol Chem. 2001;276:12945–12950. doi: 10.1074/jbc.M010402200. [DOI] [PubMed] [Google Scholar]


