Controlled surface-induced flows from the motion of self-assembled colloidal walkers

Abstract

Biological flows at the microscopic scale are important for the transport of nutrients, locomotion, and differentiation. Here, we present a unique approach for creating controlled, surface-induced flows inspired by a ubiquitous biological system, cilia. Our design is based on a collection of self-assembled colloidal rotors that “walk” along surfaces in the presence of a rotating magnetic field. These rotors are held together solely by magnetic forces that allow for reversible assembly and disassembly of the chains. Furthermore, rotation of the magnetic field allows for straightforward manipulation of the shape and motion of these chains. This system offers a simple and versatile approach for designing microfluidic devices as well as for studying fundamental questions in cooperative-driven motion and transport at the microscopic level.

Nature has engineered a variety of ways to control the transport of fluids and matter in biological organisms that range from classic pumps, such as the heart, to complex arrays of filaments that beat synchronously to induce flow. The need to use such different approaches is due to the broad spectrum of length scales at which the various processes occur. In particular, at microscopic length scales the irrelevance of inertia implies that any cyclic motion will result in zero net translation. To rectify fluid motion at the microscopic scale, it is necessary to break the symmetry of the system (1). In this respect, nature has devised several mechanisms to transport materials in the microscopic realm, such as flagellar rotation and ciliary beating (2). The former breaks the symmetry by using a spiral filament that functions in a similar fashion to a corkscrew, and is the primary locomotion mechanism used by some bacteria to move and search for nutrients (e.g,. E. Coli) (1, 3). In the case of cilia, filaments are anchored at the surface of the cells and symmetry breaking occurs due to the filament flexibility. Asymmetry arises from the velocity-dependence of cilia deformation that results in different filament geometries for the fast, forward stroke compared to that for the slow, backward stroke (4–6). Cilia carpets perform tasks such as the locomotion of unicellular eukaryotes (e.g., Paramecium) (7), the transport of mucus in the trachea (8), the development of microscopic flows during the early stages of embryonic development (9), and even the directed transport of the egg along the mammalian oviduct into the uterus (10). One particularly interesting feature of an individual filament, as well as the cooperative motion of cilia carpets (cilium), is the creation of a local and dynamic flow that can transport nutrients or other substances in a controlled fashion over length scales hundreds of times the size of a single filament. The details of the flow are nevertheless dictated by using the particular actuation protocol and can be tuned to create the desired flow profile (5, 6).

Cilia-based transport is an incredible example of the fine level of control of flows in biological systems. The dynamics of the fluid in the vicinity of a ciliated surface can be spatially and temporally modulated, such as in the case of metachronal waves (11, 12). It is thus of great interest to gain a more profound understanding of these systems via the development of unique approaches to create bioinspired flows. Studies in this field will also lead to advances in microfluidics and sensing, where bioinspired locomotion could facilitate elegant design and precise control substantially beyond current technologies.

In recent years there have been important advances in creating systems that mimic flows similar to those generated by cilia carpets. For example, scientists have been successful at creating a “forest” of magnetic rods that pulsate in a similar fashion as cilia when driven by using magnetic fields (13), diodes that rely on induced elecroosmosis to move nearby fluid (14, 15), and even carpets of fixed bacteria that exploit the machinery already present in biology to create complex flows (16).

Here, we present an alternative approach to create controlled, surface-induced flows based on magnetic self-assembled chains composed of superparamagnetic beads that walk on surfaces. Both experimental and theoretical studies show that the velocity, direction, and particular flow characteristics can be controlled by direct manipulation of the magnetic field that drives the motion of these “surface walking” assemblies. These assemblies are dynamic because they exist only in the presence of an external magnetic field and their shape is strongly controlled by the magnetic field (e.g., they undergo drag-induced fragmentation transitions at high frequencies). This system represents a completely reversible, self-assembled, active material that can be used on demand and does not require complex fabrication techniques.

Results and Discussion

Single Surface Walker: Assembly and Dynamics.

The basic unit of a carpet of surface walkers is a single chain of beads, and it proves convenient to first analyze the behavior of a single chain in the absence of other surrounding chains. A chain is driven to assemble upon application of an external field caused by the induction of magnetic moments in the superparamagnetic beads. The chains then behave as elongated magnetic dipoles that align with the applied magnetic field. Turning off the field results in the facile disassembly of the aggregates, allowing for the possibility of reassembly under different conditions. This characteristic will also allow for breakup of the filaments and self-regulation of the walking speed depending on the frequency and strength of the field. This contrasts with recent designs of microscopic swimmers where strings of beads have been held together by using irreversible DNA linkages (17, 18).

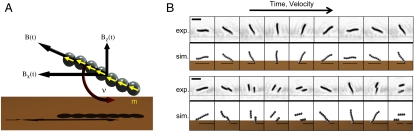
Upon rotation of the field, the assembled chains become μm-sized rotors. Fig. 1A shows a schematic of the system. The chain cohesion and rotation speed can be simply controlled by the strength, B, and frequency of rotation, ν, of the magnetic field, respectively. In particular, we will only consider a field that rotates at a constant frequency in the x-z plane, but other protocols are equally feasible.

Fig. 1.

(A) The geometry of “surface walkers”. Each chain is composed of superparamagnetic beads that move according to the dynamics of the magnetic field B that induces a magnetic moment m in each bead. In particular, we focus on rotation along the x-z plane at a frequency ν. (B) Top: The aggregate moves along the surface in both experiment (frames taken 16 ms apart in a 5 Hz rotating field, scale bar is 5 μm) and simulation upon confinement at the surface. Bottom: When the field rotation is raised to 7 Hz, the rotors fragment periodically. Notice that the agreement is excellent between both experiments and theory, even in the shape of the fragmented aggregates.

To induce motion, we require asymmetry because simple rotors do not undergo translational motion when they rotate in the bulk. One attractive scheme that has gained considerable interest lately is to use surfaces to locally hinder the mobilities of particles near the surface (19). Very recently this approach has been used to move, in a controlled fashion, irreversibly-bound dimers (18) and slightly longer chains on paramagnetic substrates to enhance friction (20). A simple way to understand this concept is to think of the lower bead (the one closest to the surface) as a hinge on which the rest of the chain rotates. This is an oversimplification because friction near the surface remains finite and the bead is allowed to move, but it conveys the essential concept underlying the coupling of rotational motion and translational motion near a surface (21, 22). In this article we exploit this mechanism to rectify the motion of the chains, converting them into surface walkers. Furthermore, by utilizing a large number of these surface walkers we are capable of moving objects in a very precise manner over large distances. To keep the beads near the surface we make use of gravity; however, other methods like electric fields, magnetic fields, or chemical gradients are equally applicable.

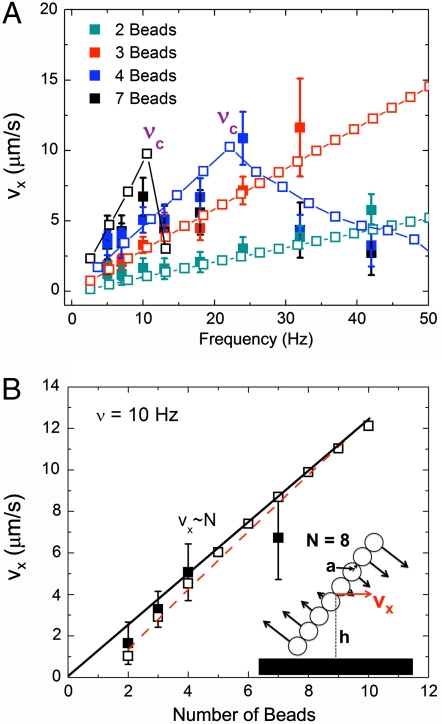
The behavior of the self-assembled rotors was investigated using simulation, theory, and experiment, all of which are described in detail in SI Text. Fig. 1B shows a series of snapshots of a typical rotor over time for two different rotation frequencies at a fixed magnetic field strength. We note that both experiment and simulation are presented and exhibit excellent agreement, demonstrating the accuracy of our theoretical approach that is free of adjustable parameters (movies of the experiment and the simulation are available in SI Movies). At low frequencies (upper sequences) the chain simply follows the field and exhibits small deformation. However, if the frequency is high enough, the drag force acting on the beads surpasses the magnetic force holding the chain together. This induces a fragmentation transition (lower sequences) (23). In simple terms, fragmentation can be understood by noting that the drag force experienced by the beads scales linearly with the rotational velocity and, hence, it scales linearly with the frequency ν at which the chains rotate. On the other hand, the maximum torque applied to the system is independent of the frequency and only depends on the magnitude of the magnetic field and the size of the aggregate that are both assumed to remain constant. Thus, above some critical fragmentation frequency, ν_c, the drag force will overcome the cohesive forces and chain breakup will occur. We will make this argument more quantitative in the following section. The typical sequence of events upon exceeding ν_c is that the system initially breaks in half, and as the frequency is increased even further the system breaks into three fragments, then four, and so forth. This mechanism has a strong effect on the translational velocity of the rotor that is clearly shown in Fig. 2A where we plot the average translational velocity of the center of mass of the rotors versus frequency. Each trace corresponds to chains with different numbers of beads. Note the two regimes: a linear regime at low frequencies where the velocity increases linearly with the frequency, and a fragmentation regime that appears as a sudden dip in velocity above ν_c. The strong reduction in translational velocity is due to the breakup of the chain into n fragments. Also plotted in Fig. 2A is the data taken from computer simulations corresponding to our experimental setup (open symbols). Again, we find excellent agreement despite the fact that there are no adjustable parameters in the simulation.

Fig. 2.

(A) Graph of average translational chain velocity, v_x, versus frequency, ν, as a function of the number of beads. Both experimental (filled symbols) and simulation (open symbols) results are shown. Lines between simulation points are a guide to the eye. At high ν both the experimental and simulation data suddenly decay to a low-velocity regime due to the onset of chain breakup. (B) Graph of the velocity at ν = 10 Hz versus the number of beads in the chain from experiments (filled symbols), simulation (open, black symbols), and the analytical equation derived in SI Text (red dashed line). The data quickly approaches the linear regime predicted by using the long-chain limit of the analytical equation (Eq. 1) as demonstrated by the fit line. The schematic shown in the inset is a diagram of the geometric variables used in this paper: a is the bead radius, h is the rotor height (measured from the surface), N is the number of beads, and v_x is the translational velocity of the rotor.

Characterization of Rotor Velocity and Fragmentation.

Upon initial observation, it is apparent that these rotors display predictable and controllable behavior in the linear (“low” frequency) regime. Furthermore, the velocity-frequency response as a function of chain length is similarly well-behaved, as shown in Fig. 2B. In this plot we show the velocity as a function of chain length at a fixed frequency (in this case 10 Hz). To further understand this system, we analyze the hydrodynamic forces acting on a rotor in the presence of a no-slip wall, such as the one depicted in the inset of Fig 2B. We assume that the forces acting on each bead are perpendicular to the axis of the filament and proportional to the distance from the center of mass to ensure that the angular velocity of each of the beads is the same. The force along the parallel direction does not lead to motion and is neglected. Furthermore, we include all terms due to the images as originally introduced by Blake to account for the no-slip boundary condition at the surface (for a complete description of the image system see ref. 24). In fact, it is these images that are responsible for the movement of the chains because they emulate the effect of the wall. The image forces, are analogous to the image charges in electrostatics used to solve for the electric field near a boundary but are more complicated in our case. The final form of the velocity of a single rotating chain near a wall can then be shown to scale as (see SI Text for a detailed derivation):

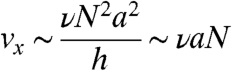[1]

where v is the average translational velocity of a chain consisting of N beads of radius a, ν is the frequency of rotation, and h is the distance from the center of the rotor to the surface. To obtain the last expression, we have made two assumptions. First, the height of the center of mass scales with the length of the chain that is based on the experimental and simulation results. Second, we approximate the chain as a dumbbell with each bell consisting on N/2 beads, and the distance between bells is also proportional to N. The latter approximation is confirmed by calculating analytically the velocity of a chain of N beads and evaluating numerically the results (see the red, dashed curve in Fig. 2B). In the large N limit it is found that Eq. 1 is the correct scaling relation (see SI Text). Our simulation data closely follows the linear relationship between ν and v (as presented before), and quickly converges to the linear relationship between v and N, as described by Eq. 1, which also demonstrates the symmetry breaking effect of the surface with the velocity going to zero in the limit of infinite h (bulk regime).

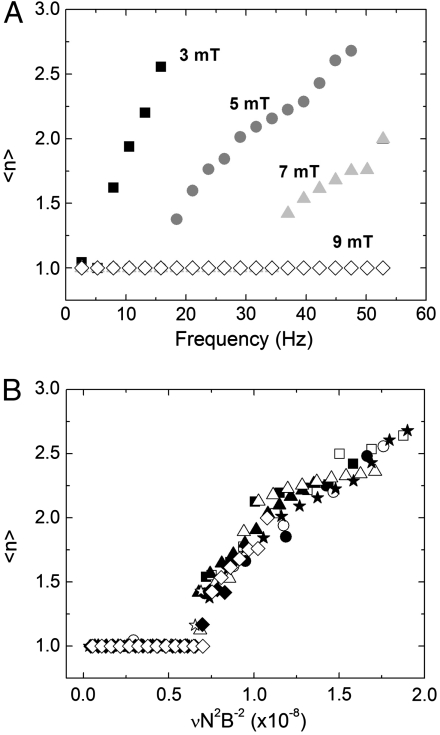
To further characterize the fragmentation transition (the “high” frequency regime), we introduce a quantity that tracks the average number of chain fragments 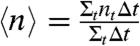as a function of ν and B, as shown in Fig. 3A, for a typical 10-bead system. As the field strength is lowered or the frequency increased, the number of breaking fragments increases. Remarkably, this fragmentation behavior is universally scalable for all chain lengths and field strengths through the simple relationship:

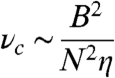[2]

as shown in Fig. 3B. Eq. 2 corresponds to an effective Mason number for our system that simply compares the maximum magnetic torque that can be applied to the system τ_B = m × B ∼ NB² to the torque due to the hydrodynamic drag forces τ_F ∼ νηa³N³ (see SI Text for more details). When this ratio becomes of order unity, that is τ_B/τ_F ∼ 1, we expect the system to undergo a fragmentation transition that also defines the critical frequency ν_c.

Fig. 3.

(A) The time-average number of chain fragments, 〈n〉, versus magnetic field rotation frequency, ν, as a function of magnetic field strength for a N = 10 bead chain. At higher B values, the ν required to break the chain becomes larger. (B) Simulations of chains of N = 7–10 at B = 3–7 mT as a function of the rescaled frequency 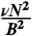. This interplay between the magnetic and frictional forces is well described by using the scaling law in Eq. 2 by observing that all the data collapses to a master curve. Conditions plotted are: N = 10, B = 7 mT (⋄), N = 9, B = 5 mT (△), N = 8, B = 3 mT (□), N = 8, B = 7 mT (☆), N = 10, B = 3 mT (○), N = 9, B = 3 mT (•), N = 8, B = 5 mT (▴), N = 7, B = 3 mT (▪), N = 10, B = 5 mT (★), N = 9, and B = 7 mT (⧫).

Controlled Surface-Induced Flows and Transport Using Ensembles of Rotors.

In what follows we turn our attention to a collection of chains. This case is nontrivial because the system is polydisperse; however, we assume the properties are well-described by using the average chain size, a value that we expect to be strongly correlated to the magnetic field strength. The velocity profile surrounding a single chain can be extracted from the simulations by noting that the velocity at an arbitrary point r_i can be evaluated as (25)

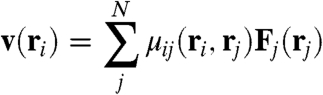[3]

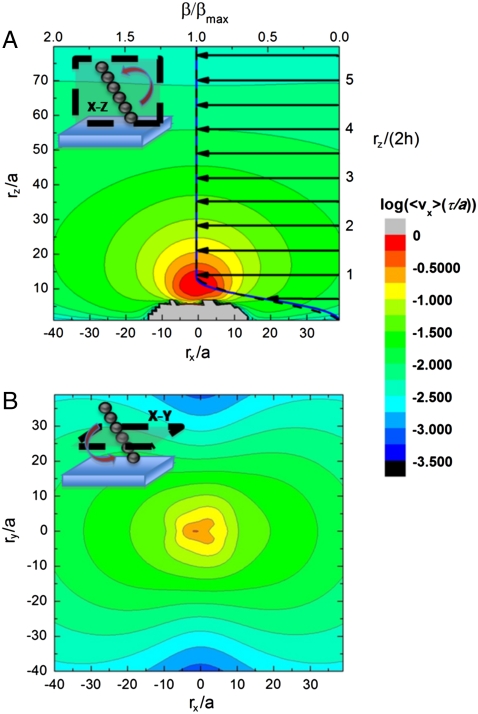
where μ_ij corresponds in our case to the Blake tensor, and F_j(r^′) represents the force on bead j that is located at r_j. A typical average velocity profile (per cycle) around a chain is shown in the contour plots of Fig. 4.

Fig. 4.

The logarithmic intensity of the x direction of the velocity field immediately surrounding a single seven-bead rotating chain (measured from the chain center of mass), in both the x-z (A) and x-y (B) planes (geometry shown in the cartoon in the upper left corners). We also plot on the x-z plane the function β (normalized by β_max) as a function of z that is proportional to the mean velocity profile of a collection of rotors as represented in Eq. 5. Both the simulation (black dashed) and analytical (blue solid) results for β are shown with the arrows representing the direction of the flow. Both profiles are indistinguishable above z = h. We note that β tends towards zero near the surface, due to the no-slip condition, and resembles a plug flow profile. The gray area in (A) represents flow that opposes the predominating flow direction and cannot be plotted in the logarithmic scale.

From the single chain velocity profile we can calculate the average flow profile along the z axis for a collection of chains that are homogeneously distributed in the plane. This is done by integrating the velocity at a given height z above the surface as

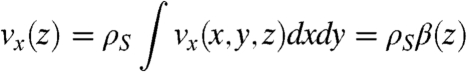[4]

where ρ_S corresponds to the surface density of chains and is assumed to be homogeneous, and the function β(z) = ∫v_x(x,y,z)dxdy simply corresponds to the integral of the single chain velocity field v_x along a given z plane. The function β(z) depends on the number of beads, N, and the height, h, at which the chain is rotating. From the experiments and simulations, the latter has been observed to be approximately half the length of the rotor (i.e., h = Na), and this is the value we use here. The function β(z) calculated from the simulation is displayed in Fig. 4A as the dashed, black curve (upper and left axis). For clarity, we have normalized the data with the maximum value of the flow, namely β_max. This allows us to also present an analytical formula for this profile that can be derived directly from the model used to solve for the walking velocity (see SI Text for the derivation). The analytical form of β(z) for the geometry in our simulations is given by

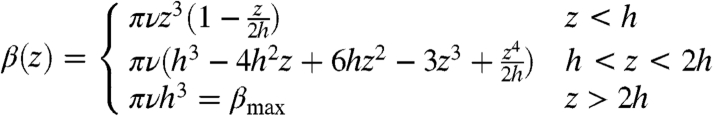[5]

that is also plotted in Fig. 4A (solid blue curve). Notice the excellent agreement between the simulation and analytical equation that are essentially indistinguishable above z = h. One can see from both of these curves that there is considerable fluid flow in the direction of chain motion, and that it closely resembles a plug flow profile above the rotors, similar to the case of electroosmosis (14, 15, 26). Also, notice that the value of the maximum velocity is ρ_s ∼ νh³ ∼ ρ_sν(aN)³, implying that the flow can be strongly affected by changing the effective (or average) length of the chains, and thus can be modified by simply changing the strength of the magnetic field. The numerical value of the β_max in the simulations is slightly larger than the one calculated analytically, but they both show the same behavior as a function of N, as shown in SI Text.

To probe the effect of this surface-induced current on larger objects, we placed fluorescently-labeled vesicles filled with a heavier liquid (so that they would sediment on the surface) in a solution containing the superparamagnetic beads. By applying the rotating magnetic field at 32 Hz we observed that the large vesicles moved with the rotating chains at a velocity ∼10 μm/s, as shown in the snapshots (Fig. 5). Comparing our calculations to the experiments, we estimate the surface density of rotors to be of the order of ρ_s ∼ 10^-2 μm^-2 being driven at ∼30 Hz. At this particular frequency, we expect all the chains to be highly fragmented given that the field was kept below 10 mT. Using our result for the two bead case for β_max and multiplying by ρ_s, we find the velocity above the surface to be approximately 10 μm/s, which is on the right order of magnitude observed in the experiment.

Fig. 5.

The presence of a velocity field created by using the rotors enables the transport of large, dispersed objects like the vesicles in this figure (large dark circle). The flow is created by using a carpet of surface walkers randomly positioned (bright, short, chain-like regions) actuated at 32 Hz. The snapshots are taken from the top, as indicated in the cartoon. The scale bar represents 20 μm, and the time between frames is 0.5 s.

The motion of the vesicles could be extremely well controlled and we could even make them dance a Bavarian waltz (see SI Movies). In particular, we note that the vesicle motion responds almost immediately to both the initiation and cessation of the field rotation in either direction, allowing for precise manipulation of the vesicle position. This suggests that both the magnitude and the direction of the flow is also precisely manipulated. In the present work we only considered rotation along a given plane, but extrapolation of this effect to incorporate full two-dimensional control of the system would be trivial upon addition of one extra pair of coils along the remaining perpendicular plane. Furthermore, it is possible to envision that small spatial gradients in the magnetic field, that do not induce considerable motion by themselves, could be used to create gradients in the lateral velocity field. This can be achieved by exploiting the fragmentation instability. As just shown before, the average number of segments in a chain, and thus the overall velocity of the fluid, vary considerably if one changes the frequency and magnitude of the magnetic field. Hence, if one imposes a small gradient on the magnitude of the magnetic field along, for example, the y direction, with the field rotating on the x-z plane, it is possible to create shear velocity gradients along the y direction by exploiting the fragmentation instability. The high velocity region would correspond to the region of higher field and the lower velocities will occur in the lower field region where, presumably, the fragments size is much smaller. Finally, it is important to mention that our system is very simple and only requires a pair of Helmholtz coils and superparamagnetic beads, both of which are cheap and commercially available.

In summary, we have developed a system to create controllable, surface-induced flows based on the completely reversible self-assembly of superparamagnetic particles. This method does not require complex fabrication techniques, and is well-controlled by using the facile manipulation of an external magnetic field. We envision that such precise control of fluids will be of particular use in the emerging field of nano- and micro-fluidic devices, providing the ability to drive the motion of dispersed particles such as vesicles (as in our work), droplets, or even biological cells. The strong response of the chain fragmentation behavior to the strength of a magnetic field adds a further dimension of control to this system. Due to this effect, an improved experimental setup allowing for small B gradients in the proximity of this fragmentation transition, together with a particle tracking and feedback mechanism, could, in principle, allow for a complete control of a number of different entities simultaneously. Such control could be used to probe local environments at interfaces such as those occurring in cell-cell interactions (27, 28). It can also be employed to study complex flow dynamics and hydrodynamically mediated synchronization (29). In fact, the proposed setup is much more versatile than current methods that rely on complex flow geometries inherent in the device itself or on specific characteristics of the particles to be transported.

From the more fundamental perspective, the use of the hydrodynamic, no-slip condition at a surface to generate asymmetry is a unique approach to create surface-induced currents to be studied in future works. We expect this mechanism to be critical in biological systems where surfaces represent a major motif. Furthermore, our approach could be extrapolated to analogous cases in different environments where instead of using the gravitational force to confine the rotors to the surface, one could use electric fields or chemical interactions. Finally, the reversible assembly adds dimension to the behavior of “swimming” or “walking” aggregates that are typically held together through irreversible DNA tethers.

Materials and Methods

Experimental Setup.

The assembly of superparamagnetic particles was achieved by creating a magnetic field using a pair of Helmholtz coils, each with 300 windings at a radius of 45 mm (see Fig. S.1). To induce a rotating magnetic field we use a π/2 phase-shifted sinusodial signal for each coil. The signal was amplified by using a low-frequency amplifier to gain an electric current of adequate strength to achieve a maximum magnetic field of 10 mT. The frequency could be varied between 5–1,000 Hz. The sample is enclosed by using the Helmholtz coils and is mounted on an inverted fluorescent microscope equipped with phase contrast (Zeiss, Axiovert 200M). The microscope can be tilted by 90 ° and therefore samples can be observed from the side.

Materials.

Magnetic beads were purchased by Invitrogen (Dynabeads MyOne Carboxylic Acid) in aqueous solution. The phospholipid vesicles were prepared by using electroswelling (30). In all experiments we used the lipid 1,2-Dioleoyl-sn-Glycero-3-Phosphocholine (DOPC, Avanti Polar Lipids) without further purification. We added a small amount (0.1% wt/wt) of the fluorescently-labeled lipid, Texas Red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (Texas Red DHPE, Invitrogen) to the DOPC lipid. The vesicles were swollen in a 200 mM sucrose solution and injected into an isoosmotic glucose filled chamber for the experiments. Due to the slightly higher density of sucrose, the vesicles settle down on the bottom of the sample chamber.

Computer Simulations.

We simulate the assembly and dynamic response of the magnetic beads using Brownian Dynamics. This simulation involves integrating the following Langevin equation:

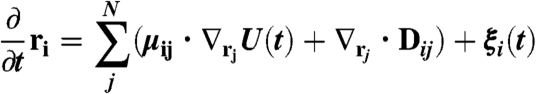[6]

where r_i is the position of bead i, μ_ij is the mobility matrix given by the Rotne–Prager–Blake tensor (19, 26, 31), U(t) is the time-dependent potential (that takes into account the gravitational, steric, and magnetic forces), D_i,j is the diffusion tensor, and ξ_i is a stochastic random force. Detailed descriptions of the integration procedure and of the various parameters are presented in detail in SI Text.