Abstract
Coordinated spiking activity in neuronal ensembles, in local networks and across multiple cortical areas, is thought to provide the neural basis for cognition and adaptive behavior. Examining such collective dynamics at the level of single neuron spikes has remained, however, a considerable challenge. We found that the spiking history of small and randomly sampled ensembles (~20–200 neurons) could predict subsequent single neuron spiking with substantial accuracy in the sensorimotor cortex of humans and nonhuman behaving primates. Furthermore, spiking was better predicted by the ensemble’s history than by the ensemble’s instantaneous state (Ising models), emphasizing the role of temporal dynamics leading to spiking. Notably, spiking could be predicted not only by local ensemble spiking histories, but also by spiking histories in different cortical areas. These strong collective dynamics may provide a basis for understanding cognition and adaptive behavior at the level of coordinated spiking in cortical networks.
Single-neuron action potential (spiking) activity depends on intrinsic biophysical properties and the neuron’s interactions in neuronal ensembles. In contrast with ex vivo/in vitro preparations, cortical pyramidal neurons in intact brain each commonly receive thousands of synaptic connections arising from a combination of short- and long-range axonal projections in highly recurrent networks1–3. Typically, a considerable fraction of these synaptic inputs is simultaneously active in behaving animals, resulting in ‘high-conductance’ membrane states4; that is, lower membrane input resistance and more depolarized membrane potentials. The large number of synaptic inputs and the associated high-conductance states contribute to the high stochasticity of spiking activity and the typically weak correlations observed among randomly sampled pairs of cortical neurons. Nevertheless, previous studies5–11 have suggested that some of a single neuron’s spiking activity might be explained by measured ongoing network states. We used cortical microelectrode array recordings in humans and monkeys to determine the predictability of single-neuron spiking on the basis of the recent (<100 ms) spiking history of small, randomly sampled neuronal ensembles from the same (intra) or from a different (inter), but connected, cortical area. In addition, we also compared the predictive power of ensemble spiking histories and instantaneous collective states. Substantial predictability in these small and randomly sampled ensembles would imply strong collective dynamics, with implications for both cortical processing and the experimental endeavor of studying coordinated spiking in large, distributed cortical networks.
We studied tens to hundreds of randomly and simultaneously sampled neurons in small (4 × 4 mm) patches in arm-related areas of primary motor (M1), parietal (5d) and ventral premotor (PMv) cortices while humans (M1) and monkeys (M1-PMv and M1-5d) performed sensorimotor tasks. Beyond their local connectivity, M1-PMv and M1-5d are known to be bidirectionally connected12,13 (their coordination is thought be important for reaching and grasping14,15), allowing us to study not only local, but also inter-areal, ensemble–based prediction. Point process models16–18 were fitted to express the spiking probability at any 1-ms time interval conditioned on the past 100 ms of the neuron’s own (intrinsic) spiking history and the past 100 ms of the spiking history of the neuronal ensemble. On the basis of this conditional spiking probability, we predicted whether or not a target neuron would spike in any given 1-ms time bin. When examining the predictive power of the ensemble’s simultaneous spiking state, we defined simultaneity at two levels of temporal resolution, 1 and 10 ms. These instantaneous collective states could result from common inputs or from synchronization patterns arising from the neuronal network’s intrinsic dynamics. Pair-wise maximum entropy (Ising) models7 were used to approximate the distributions of these instantaneous collective states. Detailed receiver operating characteristic (ROC) curve analyses19 allowed us to quantify and compare the predictive power of intrinsic and ensemble histories, intra- and inter-areal ensemble activity, and spiking histories and instantaneous collective states.
RESULTS
We analyzed 12 neuronal datasets recorded from two human clinical trial participants with tetraplegia (hS1 and hS3) and four monkeys (mLA, mCL, mCO and mAB). These included M1 recordings taken while human participants performed two sessions of a ‘neural cursor’ center-out task (that is, a task where the participant used, via a neural interface, his or her own recorded M1 spiking activity to move a computer cursor to targets radially positioned on the computer screen), M1 recordings from two monkeys (mLA and mCL), each performing two sessions of a task requiring planar point-to-point reaches toward targets randomly placed in the workspace, simultaneous M1 and PMv recordings from a monkey (mCO) performing two sessions of a task that required reach and grasp toward moving objects in a three-dimensional workspace, and simultaneous M1 and 5d recordings from a monkey (mAB) performing two sessions of a pursuit tracking task that required planar hand movements. The 12 datasets used in the analyses included 1,187 neuronal recordings. Minimum inter-electrode distance in the 10 × 10 microelectrode array was 400 µm. Maximum inter-electrode distance, including electrodes in two arrays, was ~2 cm (Supplementary Fig. 1).
To assess the predictive power of spiking histories, we first computed the probability that any given ith neuron xi,t was going to spike at time t, conditioned on spiking histories ℋt from the past 100 ms up to (but not including) time t. Without further constraints, direct estimation of conditional probability distributions for high-dimensional systems is typically an intractable problem, leading to combinatorial explosion and requiring amounts of data that grow exponentially with the number of neurons in the ensemble. Instead, we took advantage of the fact that this conditional probability can be computed as16
| equation (1) |
where λi(t| ℋt) is the instantaneous spiking rate (conditional intensity function) of the neuron and Δ = 1 ms in our discrete time representation, and used a simplified model to capture the relationship between the instantaneous rate and spiking histories
| equation (2) |
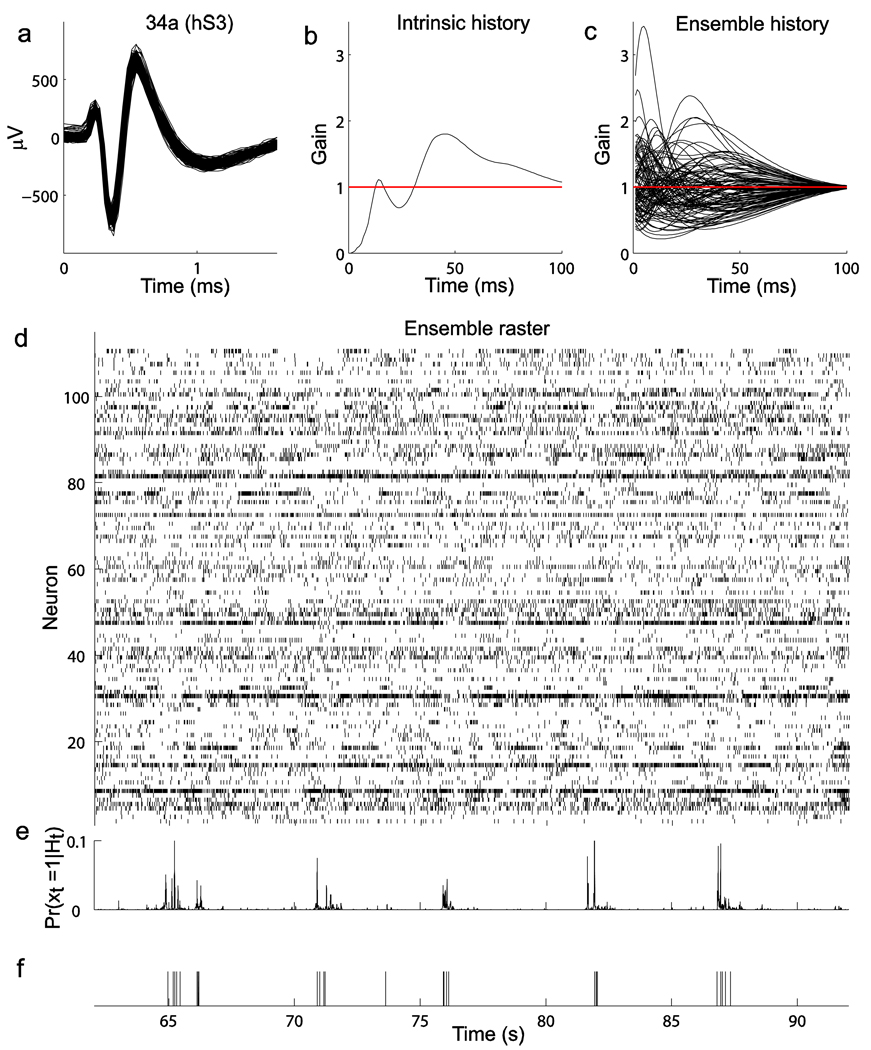
The term µi relates to a background level of spiking activity, xi is the spiking history in the specified time interval for the ith neuron, i = 1, 2,…, n recorded neurons, and K1,i and K2,i,j denote temporal filters related to intrinsic and ensemble history effects, respectively. These temporal filters were approximated via basis functions9,16,18 (see Online Methods). Once an instantaneous spiking rate model was fitted, the estimated probability of a spike at any given time bin, conditioned on intrinsic and ensemble spiking histories, was easily computed using equation (1) (the spike prediction approach is shown using cell 34a (hS3) as the example target neuron; Fig. 1).
Figure 1.
History point process models, intrinsic and ensemble history effects, and conditional spiking probabilities. Neuron 34a (hS3, session 2) was chosen as the example target neuron. (a) Waveforms corresponding to all sorted spikes for neuron 34a used in these analyses are shown. (b) Intrinsic spiking history. The curve represents the estimated temporal filter for the intrinsic history. Values below or above 1 correspond to a decrease or increase, respectively, in spiking probability contributed by a spike at a previous time specified in the horizontal coordinate. Refractory and recovery period effects after a spike, followed by an increase in spiking probability at longer time lags (40–100 ms), can be seen. This late intrinsic history effect might also reflect network dynamics. (c) Ensemble spiking history effects. Each curve represents the temporal filter corresponding to a particular input neuron to cell 34a. Many input neurons contributed biphasic effects: for example, an increase in spiking probability followed by a decrease, or vice-versa. All of the examined target neurons in our datasets showed qualitatively similar temporal filters. (d) Spike raster for all of the 110 neurons recorded in hS3 over a short, continuous time period. (e) Predicted spiking probabilities for the target neuron 34a were computed from the estimated intrinsic and ensemble temporal filters and the spike trains shown in b, c and d, respectively. (f) Observed spike train for neuron 34a in the same period.
Predictive power of ensemble spiking histories in M1
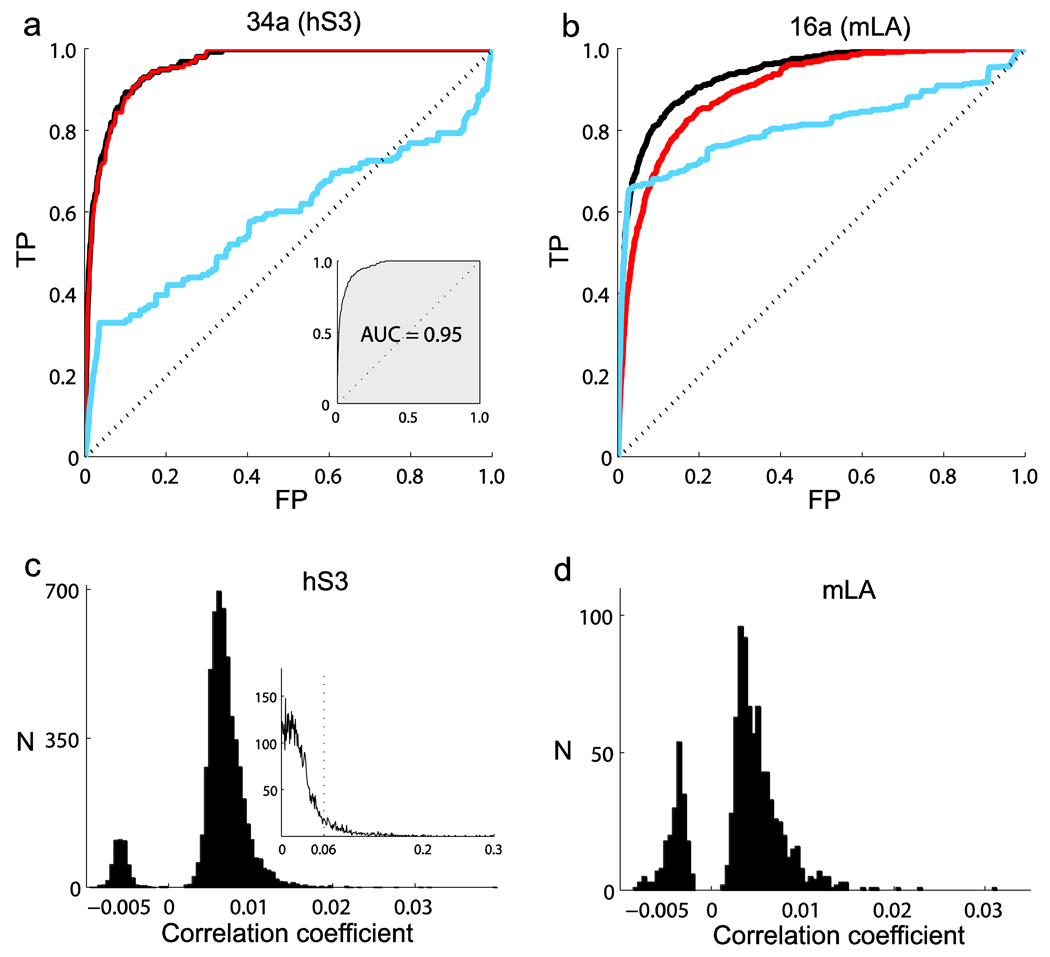
On the basis of the estimated conditional spiking probabilities, we used a standard tool, the ROC curve analysis19, to assess the predictive power of spiking history models (see Online Methods). Spike prediction in 1-ms time bins based on spiking histories was substantial. Intra-areal ensemble history–based predictions in M1 resulted in high true-positive rates while maintaining low numbers of false positives. For example, it was possible to correctly predict 80% of spikes in neuron 34a (participant hS3) with a false-positive rate of less than 5% (Fig. 2a). Similarly, an 80% true-positive rate was obtained for neuron 16a (monkey mLA) with a less than 10% false-positive rate (Fig. 2b). This predictability was substantial despite the weak pair-wise correlations that we observed among all neuronal pairs in the recorded datasets for hS3 and mLA (Fig. 2c,d). We confirmed this observation in our datasets for all subjects, areas and tasks.
Figure 2.
Prediction of single-neuron spiking and weak pair-wise correlations. (a) ROC curves for neuron 34a (human participant hS3, n = 110 neurons, session 2, 240,000 samples). FP and TP denote false- and true-positive prediction rates, respectively. The diagonal line corresponds to the expected chance prediction. The black, red and blue ROC curves correspond to the prediction based on full history models, only the ensemble histories, or only the neuron’s own spiking history, respectively. The inset shows the AUC corresponding to the ROC curve for the ensemble history model. (b) ROC curves for neuron 16a (monkey mLA, n = 45, session 2, 1,230,857 samples). 95% confidence intervals for the AUC chance level resulted in 0.51 ± 0.004 and 0.51 ± 0.017 for target neurons 16a and 34a, respectively. These narrow confidence intervals (data not shown) were typical for the recorded neurons. (c) Distribution of Pearson correlation coefficients computed over all of the neuron pairs for hS3 (1-ms time bins). N corresponds to the number of neuron pairs. Each of these correlation coefficients corresponds to the extremum value of the cross-correlation function computed for time lags in the interval ± 500 ms. Inset, normalized absolute (extremum) correlation coefficients for all of the neuronal pairs in the ensemble from hS3 computed for spike counts in 50-ms time bins; about 90% of the pairs had a correlation value smaller than 0.06 (vertical line). (d) Distribution of correlation coefficients computed over all of the neuron pairs for mLA (1-ms time bins).
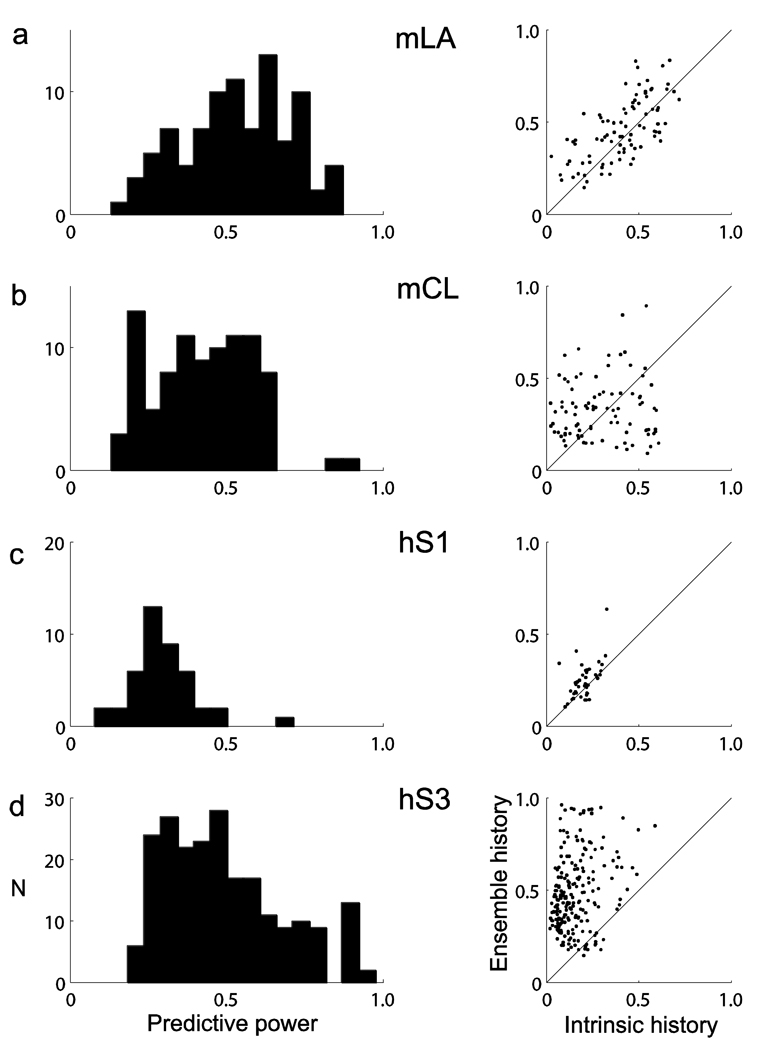
We obtained a more comprehensive assessment of predictive performance by computing the area under the ROC curve. The area under the curve (AUC) is a global summary statistic; that is, it depends on both the true- and false-positive rates and on all of the possible thresholds on the spiking probability. The AUC gives the probability that, when two samples are randomly drawn from the data (one containing a spike, the other not), the conditional intensity model will assign a higher probability (i.e. a higher instantaneous spiking rate) to the sample with a spike20. It therefore provides an assessment of the discriminatory power for predictive variables under a given model. It approaches 0.5 for a chance level predictor, that is, a predictor having false- and true-positive rates along the diagonal, and it equals 1 for a perfect predictor. For example, the AUC for neuron 34a was 0.95 (Fig. 2a). We further corrected the AUC by subtracting chance-level predictions estimated from the actual data and scaled it to obtain a quantity that ranged from 0 (no predictive power) to 1 (perfect prediction). We refer to this corrected and normalized AUC measure as the predictive power (see Online Methods). More than 50% of examined neurons in monkey mLA showed a predictive power higher than 0.5 (median = 0.55, range = 0.1–0.89) (Fig. 3). Prediction in subjects mCL and hS3 showed similar performances, with medians of 0.45 and 0.49 and ranges of 0.18–0.91 and 0.23–0.97, respectively. Predictive power was lower for participant hS1 (median = 0.30, range = 014–0.69). We conjectured that this was probably a result of the smaller number of neurons (n = 21, n = 22) that were recorded and used for prediction in this participant. To test this conjecture, we computed the predictive power on the basis of several smaller ensemble subsets (n = 22 neurons) randomly chosen out of the 110 neurons from hS3’s dataset (session 2). Data from hS3 provided a good reference, as neurons were recorded from M1 under the same task condition as for hS1. The distribution of predictive power values, based on this collection of smaller ensemble subsets, was similar to the one obtained for hS1, supporting our hypothesis (Supplementary Fig. 2 and Supplementary Note).
Figure 3.
Predictive power of intra-areal (M1) ensemble histories. (a–d) Prediction was substantial, as shown by the distributions of predictive power corresponding to target neurons from subjects mLA (a), mCL (b), hS1 (c) and hS3 (d). Each distribution includes target neurons recorded in two different sessions (mLA: n = 45, n = 45; mCL: n = 47, n = 44; hS1: n = 22, n = 21; hS3: n = 108, n = 110). The left column shows the distribution of predictive power based on the full history model and the right column compares the predictive power of the two (intrinsic and ensemble) history components separately. The predictive power measure is based on the AUC scaled and corrected for chance level prediction. It ranges from 0 (no predictive power) to 1 (perfect prediction). For many neurons, the predictive power of separate components (intrinsic and ensemble) could add to a value larger than 1 or result in a larger predictive power than that obtained by the full history model. This indicates that there was some redundancy in the information conveyed by these two components. The numbers of predicted samples (1-ms time bins) were 864,657 and 1,230,857 for mLA, 1,220,921 and 1,361,811 for mCL, 240,000 in both sessions for hS1 and 240,000 in both sessions for hS3.
These predictive power levels were obtained using the full history models, that is, the instantaneous spiking rate of each neuron conditioned on both intrinsic and ensemble histories. We further compared the predictive power of each of these two components separately (Fig. 3). For the majority of neurons in all of the subjects, the predictive power obtained exclusively from the ensemble histories was larger than the predictive power from intrinsic histories. In addition, it is possible that some of the intrinsic history effects, beyond refractory and recovery period effects, could also reflect network dynamics. Thus, these results indicate that the collective ensemble activity, rather than refractory and recovery dynamics, was the main source of the observed predictive power of spiking histories.
The predictive power of these M1 spiking history models in monkeys mLA and mCL was also higher than the predictive power of relevant kinematic covariates, such as hand position and velocity (Supplementary Fig. 3 and Supplementary Note). We used pathlet models21 to estimate spiking probabilities conditioned on kinematics; that is, the instantaneous spiking rate was expressed as function of hand position and velocity trajectory in the time interval (−200 ms, 300 ms) with respect to spiking time. Furthermore, the predictive power values of spiking history and pathlet models were not strictly additive (Supplementary Fig. 4). This result indicates that there was some level of redundancy between the information conveyed by these two models about single-neuron spiking: some of the spiking activity that was predicted by the spiking history models could also be predicted by the examined kinematics.
Predictive power of M1 instantaneous collective states
Beyond examining the predictive power of ensemble spiking histories, we were also interested in the predictive power of instantaneous collective states in the recorded ensemble, that is, simultaneous states at either 1- or 10-ms temporal resolution. Instantaneously correlated states could result from common inputs and/or from synchronization patterns arising from the neuronal network’s own dynamics. Strong instantaneous collective states7 could still be consistent with the weak pair-wise instantaneous interactions that we observed in our datasets (Fig. 2c,d). We estimated the joint probability distribution of these instantaneous collective states by fitting maximum entropy22,23 point process models constrained by empirical mean spiking rates and zero time-lag pair-wise correlations. That is, these maximum entropy distribution models were consistent with the observed mean spiking rates and zero time-lag pair-wise correlations, but made no additional assumptions (see Online Methods). This pair-wise maximum entropy probability model, also known as the Ising model in statistical mechanics24,25, has been shown to capture most of the instantaneous interdependency structure in ex vivo/in vitro neuronal ensemble preparations7,8,10.
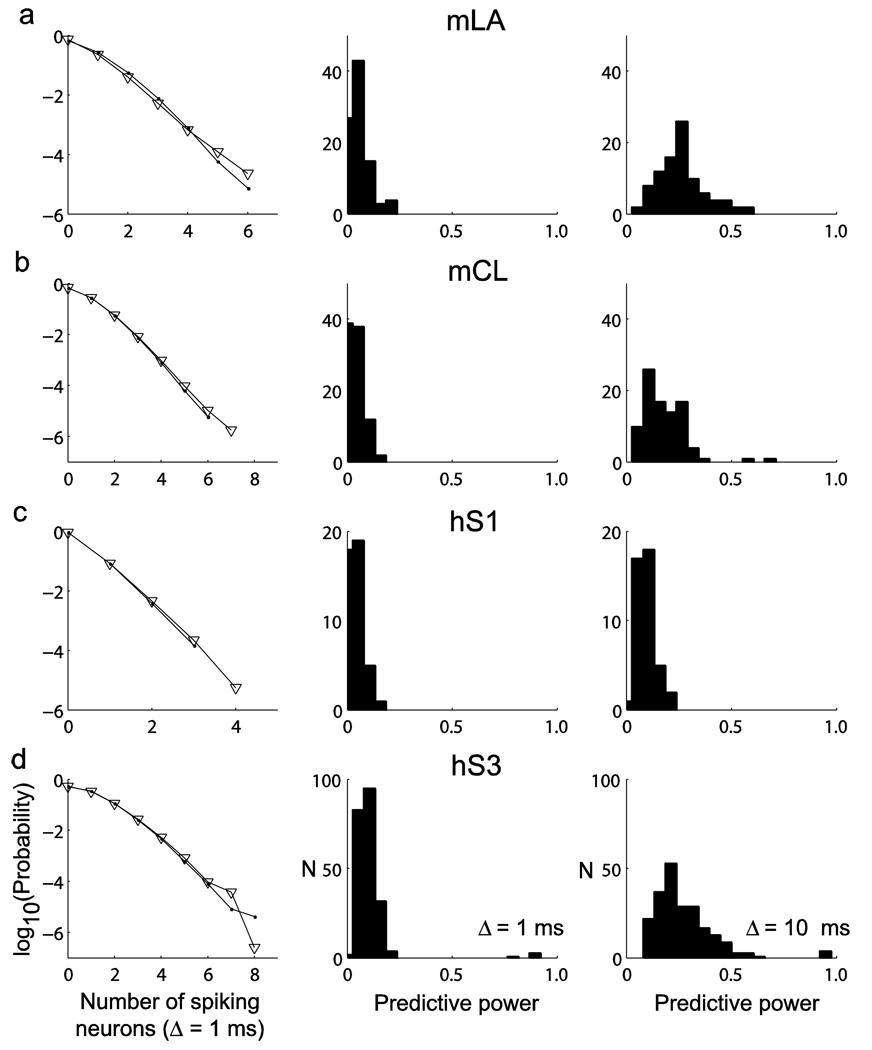
Besides satisfying the pair-wise correlation structure in the examined datasets, the estimated models also accounted well for the distribution of multiple-neuron spike coincidences, as seen in the comparison of the empirical distribution and the distribution generated from the model via Gibbs sampling26 (Fig. 4). Nevertheless, the predictive power of this pair-wise correlation structure was considerably poorer than the predictive power of intrinsic and ensemble spiking histories, as captured by the models (Fig. 4). Across the four subjects, the predictive power values of pair-wise maximum entropy models corresponded to 0.10 ± 0.17, while the spiking history models yielded values of 0.50 ± 0.40 (mean ± s.d.). The predictive power of spiking history models were still higher when we considered instantaneous states at a coarser 10-ms temporal resolution (Fig. 4), which resulted in predictive power values of 0.26 ± 0.27 (mean ± s.d.).
Figure 4.
Predictive power of instantaneous collective states (Ising models). (a–d) The distributions of instantaneous collective states were approximated via maximum entropy distributions constrained on empirical mean spiking rates and zero time-lag pair-wise correlations. The left column shows the empirical distribution of the observed number of multi-neuron spike coincidences in the ensemble (Δ = 1 ms) and the distribution generated from the maximum entropy model via Gibbs sampling (∇). The middle column shows the distribution of predictive power values. Predictive power was computed for each target neuron separately, with the instantaneous or simultaneous collective state defined at a temporal resolution of 1 ms. For each given neuron, predictions were determined by a conditional spiking probability derived from the maximum entropy joint distribution model and knowledge of all of the (n – 1) neurons’ simultaneous states. The right column shows the distribution of predictive power when the instantaneous state was defined at a coarser temporal resolution of 10 ms. In that case, time bins containing more than one spike were set to 1. For each monkey and human participant, data from two sessions were used in these analyses. The rows correspond to mLA (n = 45, n = 45, a), mCL (n = 47, n = 44, b), hS1 (n = 22, n = 21, c) and hS3 (n = 108, n = 110, d).
Intra and inter-areal spike prediction: M1↔PMv and M1↔5d
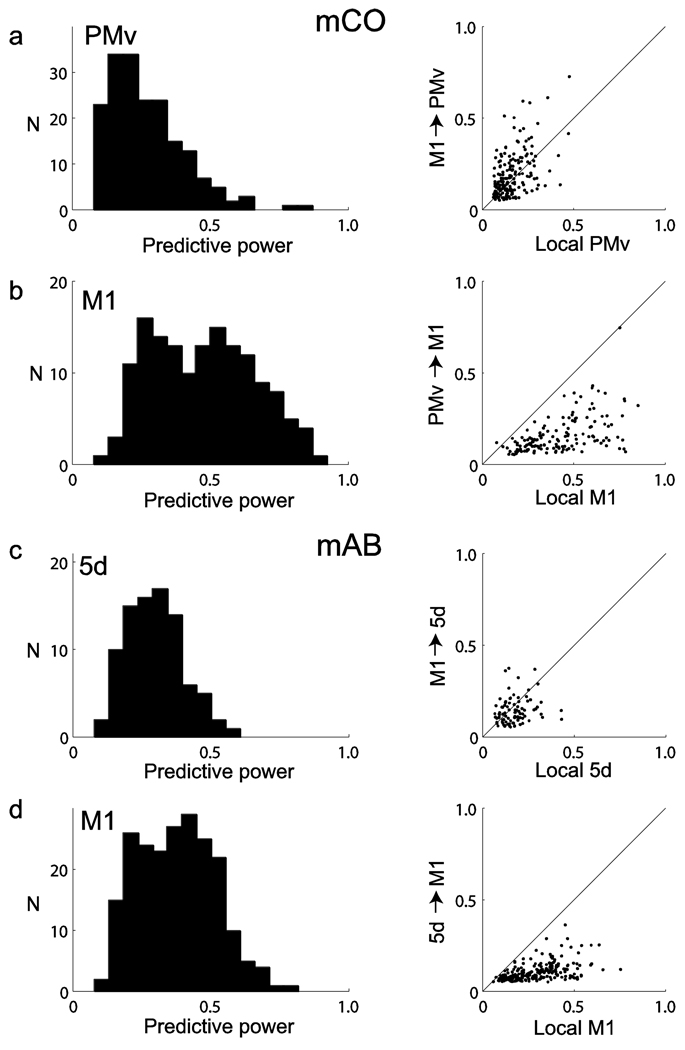
We performed the same predictive power analysis for areas PMv and 5d and compared predictions based on ensemble histories recorded from the same or a different cortical area in the connected pairs M1↔PMv and M1↔5d (Fig. 5). Predictive power, based on both local and inter-areal spiking histories, corresponding to target neurons in PMv (mCO; Fig. 5a) and 5d (mAB; Fig. 5c) had medians of 0.27 and 0.32 and ranges of 0.11–0.86 and 0.13–0.62, respectively. Predictive power corresponding to target neurons in M1, based on both local and inter-areal spiking histories, had medians of 0.50 and 0.40 and ranges of 0.15–0.93 and 0.11–0.83 for monkeys mCO and mAB, respectively (Fig. 5b,d). The inter-areal predictive power could also be substantial in both directions, M1–PMv and M1–5d (Fig. 5). Medians were 0.15, 0.13, 0.13 and 0.09 and ranges were 0.05–0.73, 0.06–0.75, 0.06–0.37 and 0.05–0.37 for M1→PMv, PMv→M1, M1→5d and 5d→M1, respectively.
Figure 5.
Predictive power of intra- and inter-areal neuronal ensemble histories. Predictive power of inter-areal ensemble history was also substantial. (a) Left, distribution of predictive power values for target neurons in area PMv (subject mCO), which were recorded during free reach-grasp movements. Predictive power was computed from full history models that also included spiking histories in M1. Right, comparison of the power of intra (PMv, n = 77, n = 109) and inter-areal (M1, n = 148, n = 109) ensemble histories to predict spiking in PMv. The predictive power M1→PMv tended to be higher than the local PMv→PMv in this case, where the number of neurons recorded in M1 was larger than in PMv. In contrast, additional analyses using balanced-size ensembles indicated that intra-areal predictive power was actually slightly higher (Supplementary Fig. 5). (b) Left, distribution of predictive power for target neurons in M1. Predictive power was computed from full history models that also included spiking histories in PMv. Right, comparison of the power of the intra (M1) and inter-areal (PMv) ensemble histories to predict spiking in M1. (c,d) Data are presented as in a and b, but were computed for parietal 5d (n = 41, n = 47) and M1 (n = 104, n = 110), recorded from monkey mAB during a planar pursuit tracking task. The numbers of predicted samples were 212,028 and 99,008 for mCO (sessions 1 and 2, respectively) and 416,162 and 472,484 for mAB (sessions 1 and 2, respectively).
Furthermore, the predictive power from one area to target neurons in the other, especially from M1→PMv, could be larger than the predictive power of local ensembles (Fig. 5a,c). We speculated that the higher predictive power of M1→PMv in some of these cases could simply reflect the larger number of recorded neurons in M1, rather than the relative strength of feedforward and feedback connections between these two areas. A supplementary analysis using ensembles of equal size suggested that this was the case (Supplementary Fig. 5 and Supplementary Note). This analysis also indicated that intra-areal predictive power was slightly higher than inter-areal predictive power when ensembles of equal size were considered.
As shown before for subjects mLA and mCL, the predictive power of spiking history models for areas M1, 5d and PMv also tended to be higher than the predictive power of pathlet models (Supplementary Fig. 3). The medians and ranges of predictive power values for pathlet models corresponded to 0.25 and 0.21, and 0.01–0.77 and 0.01–0.75 for mCO and mAB, respectively.
Predictability, spiking irregularity and information rates
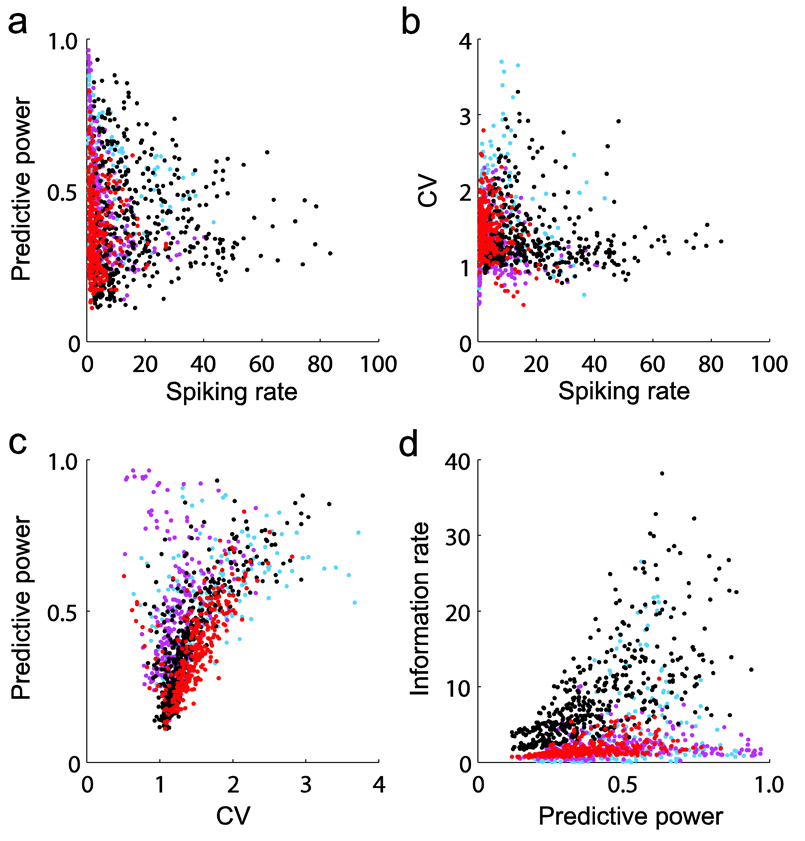
The predictive power of spiking history models varied broadly across the 1,187 neurons in the 12 datasets. We examined whether this variation could be easily explained by simple features of the predicted spiking activity. The predictive power of history models did not appear to depend, at least in a simple manner, on the mean spiking rate or on the level of irregularity of the predicted spiking activity (Fig. 6a–c). Assessments of spike train irregularity were based on the coefficient of variation3 of the interspike time intervals. We also assessed how much information was involved in the prediction of single neuron spiking.
Figure 6.
Predictive power, mean spiking rates, spike train irregularity and information rates. Each dot corresponds to one of the 1,187 target neurons recorded from two human participants and four monkeys, three different cortical areas and four different tasks. Each color relates to one of the different tasks. (a) The predictive power of full history models versus the mean spiking rate (in spikes per s) of the target neurons is shown. (b) Coefficient of variation (CV) of the inter-spike time intervals versus spiking rates. (c) Predictive power of full history models versus coefficients of variation of the predicted spiking activity. Lower coefficients indicate more regular spike trains. Coefficients around 1 and below tended to correspond to a broad range of predictive power, whereas higher coefficients tended to cluster around intermediate predictive power values. In summary, the predictive power of history models did not seem to depend, in a simple manner, on mean spiking rates or on the level of irregularity of the spiking activity. (d) Predictive power versus the information rate (in bits per s) involved in the prediction. Approximately equal predictive power could relate to a broad range of information rates. Blue: point-to-point reaching, monkeys mLA and mCL, area M1; purple: neural cursor control, participants hS1 and hS3, area M1; black: free reach and grasp task, monkey mCO, areas M1 and PMv; red: pursuit tracking task, monkey mAB, areas M1 and 5d.
In principle, the same level of prediction accuracy could be achieved for two different target neurons while involving different amounts of information. We examined this possibility by asking how much information about a neuron spiking or not at any given time was gained by modeling the intrinsic and ensemble history effects compared with knowing only the mean spiking rate of the process. This information gain can be estimated as the normalized difference between the log-likelihood under the estimated history model and the log-likelihood under a homogenous Poisson process with given mean spiking rate (see Online Methods). Our analysis confirmed that similar predictive power values (in the prediction of different target neurons) could involve a wide range of information rates (Fig. 6d).
DISCUSSION
Our findings reveal that single-neuron spiking in the cortex of humans and monkeys performing sensorimotor tasks can be substantially predicted by the spiking history of small, randomly sampled neuronal ensembles. The fact that this predictability was based on small neuronal ensembles, randomly sampled out of millions of neurons in the cortex, suggests that strongly coordinated activity underlies the generation of single-neuron spikes. This finding is notable if one considers the properties of cortical neuronal networks. Cortical neurons are embedded in large, sparsely connected recurrent networks in which the high number of synaptic inputs and high-conductance states typically induce weak coupling between randomly sampled neuron pairs. Not surprisingly, revealing and understanding these large scale and dynamic interactions has been challenging. On the basis of only the weak pair-wise correlations observed amongst cortical neurons in our datasets, one would have underestimated the strength of the statistical interdependencies induced by the collective dynamics. Furthermore, we believe our estimates of predictive power for these small neuronal ensembles should be taken as lower-bound values. There are at least a few factors that could have diminished predictive performance. For example, even though we were careful to include only trials or time segments in which the hand was moving or when the human participants were controlling a computer cursor, it is possible that the network’s functional connectivity was nonstationary within and across trials. Also, we avoided more complex, and thus potentially more predictive, point process history models for computational tractability.
The fact that spiking was better predicted by the ensemble’s history than by the ensemble’s simultaneous collective state, estimated via pair-wise maximum entropy models, emphasizes the temporal dynamics leading to spiking. This finding, however, should not be taken as a limitation of pair-wise maximum entropy models. It is possible that multiple time-lag pair-wise correlation maximum entropy models11,27 might capture most of the history effects detected in our data and therefore provide a simpler, minimal model. Our goal here was not, however, to provide such a minimal model for the temporal and instantaneous collective dynamics, but to determine the existence and strength of such dynamics in the cortex of humans and behaving monkeys. This is, nevertheless, an important issue that should be addressed.
In previous studies, we and others have shown that the spiking activity of small, simultaneously and randomly sampled neuronal ensembles in motor cortex can be used to predict (decode) subsequent complex behavioral variables such as arm kinematics28–32. Here, we found that the activity of these same neuronal ensembles can also be used to predict subsequent single-neuron spiking with substantial accuracy, implying the presence of strong collective dynamics in sensorimotor cortex. One may then ask how these collective dynamics relate to behavior. Although a comprehensive analysis of this problem is beyond the scope of this study, our results indicate that these collective dynamics do not simply reflect background coherent states that are completely unrelated to behavior and, conversely, do not simply reflect ‘trivial common inputs’, such as those usually considered in studies involving stimulus-driven activities of early sensory neurons. Regarding the background coherent states, our data indicate that the predictive power of models based only on ensemble history and of models based only on kinematics are not strictly additive (Supplementary Fig. 4). In other words, there is some level of redundancy between the information (about single-neuron spiking) conveyed by ensemble spiking histories and information conveyed by kinematics variables. Therefore, the detected collective dynamics cannot simply reflect background coherent states that are entirely unrelated to behavior. Nonetheless, it is still possible, if not likely, that part of the detected collective dynamics may reflect ongoing internal processes that are not related to behavioral variables. Regarding common inputs, we note that kinematics and other features of voluntary movements are controlled in large part (either directly, or indirectly via spinal and muscle activations) by the coordinated activity of sensorimotor cortical neurons. It is, therefore, not surprising that these behavioral variables can also achieve substantial explanatory power for spiking activity. Even so, the fact that kinematics (pathlet) models were less predictive than ensemble history models suggests that the latter carried extra information about single-neuron spiking (Supplementary Fig. 3). Given these considerations, the detected collective dynamics are unlikely to be explained as the simple reflection of trivial common inputs. In sum, we believe that these strong collective dynamics reflect the intra and inter-areal coordinated activity of neuronal ensembles distributed in the many different cortical and subcortical areas that participate in voluntary control of movement.
We hypothesize that the detected collective dynamics and ensemble influences on spiking activity reflect information transfer and computation in cortical networks. Collective dynamics and functional connectivity, as captured by connectivity matrices derived from ensemble history models, as well as predictive power levels, should vary as information transfer and computation change during behaviors that engage cortical areas. On the basis of current computational theories of motor control14,15, one could predict, for example, that M1↔5d spiking predictability will manifest primarily during the initial phase of reaching movements, whereas M1↔PMv spiking predictability will peak during the hand-shaping phase of object grasping. A related and more general inquiry will be to examine the relationship of collective dynamics at this ‘microscopic’ spatial scale to neural activities reflected in meso- and macroscopic scale signals, such as local field potentials and electrocorticograms.
Our results also have implications for neural decoding theory and intracortical neural interfaces for motor prostheses. Collective dynamics add redundancy and, therefore, error-correcting properties to neural codes7. In addition, these dynamics might also account for variability of neural responses5, which is otherwise usually attributed to noise. Therefore, it seems that ensemble history effects should be taken into consideration when decoding kinematics (or other variables) from the spiking activity of neuronal ensembles. One would predict that decoding algorithms that take into account ensemble spiking histories will outperform algorithms that treat spiking activity of different neurons as, conditioned on decoded variables, independent processes.
Our findings suggest the presence of strong collective dynamics that are fundamental to the experimental endeavor of determining coordinated spiking in cortical networks. Networks responsible for specialized cortical function are likely to be contained in the spiking patterns of millions of neurons distributed across multiple cortical areas. Current and developing recording technologies measure the spiking activity of hundreds to thousands of neurons, a very small fraction of these networks. Without strong collective dynamics (that is, if neurons in small randomly sampled ensembles behaved seemingly independently), there would be little hope of determining how the coordinated propagation of action potentials in large-scale recurrent networks leads to computation and information processing. We believe, therefore, that the existence of these collective dynamics offers a basis for understanding cognition and adaptive behavior at the level of coordinated spiking in cortical networks.
METHODS
Methods and any associated references are available in the online version of the paper at http://www.nature.com/natureneuroscience/.
Supplementary Material
ACKNOWLEDGMENTS
We thank M. R. Fellows, C. Vargas-Irwin and B. Philip for collecting the nonhuman primate data. We thank our clinical trial participants for their dedication to this research, G. Friehs for his role as surgical investigator for the pilot clinical trial, J. Mukand for his role as clinical investigator for the pilot clinical trial, and A. Caplan, M. Serruya, M. Saleh and other employees of Cyberkinetics Neurotechnology Systems for data collection, manufacturing and clinical trial management. This study was based on work supported in part by the Office of Research and Development, Rehabilitation R&D Service, Department of Veterans Affairs (L.R.H. and J.P.D.). This work was supported by the National Institute of Neurological Disorders and Stroke (5K01NS057389-02 to W.T. and NS-25074 (Javits Award) to J.P.D.), the National Institute of Child Health and Human Development/National Center for Medical Rehabilitation Research (N01-HD-53403, subcontract to L.R.H.), the Massachusetts General Hospital Deane Institute (L.R.H.), the Doris Duke Charitable Foundation (L.R.H) and the National Institute on Deafness and Other Communication Disorders (R01-DC-009899 to L.R.H.).
Footnotes
AUTHOR CONTRIBUTIONS
W.T. conceived the study’s central ideas and conducted the data analyses. W.T. wrote the paper with contributions from L.R.H. and J.P.D. L.R.H. and J.P.D. contributed to the clinical research design. L.R.H. was the principal investigator for the pilot clinical trial. J.P.D. supervised the nonhuman primate experiments.
COMPETING INTERESTS STATEMENT
The authors declare competing financial interests: details accompany the full-text HTML version of the paper at www.nature.com/natureneuroscience/.
Reprints and permissions information is available online at http://www.nature.com/reprintsandpermissions/.
Note: Supplementary information is available on the Nature Neuroscience website.
References
- 1.Braitenberg V, Schüz A. Cortex: Statistics and Geometry of Neuronal Connectivity. New York: Springer-Verlag; 1998. [Google Scholar]
- 2.Elston GN, Rockland KS. The pyramidal cell of the sensorimotor cortex of the macaque monkey: phenotypic variation. Cereb. Cortex. 2002;12:1071–1078. doi: 10.1093/cercor/12.10.1071. [DOI] [PubMed] [Google Scholar]
- 3.Dayan P, Abbott LF. Theoretical Neuroscience. Cambridge, Massachusetts: MIT Press; 2001. [Google Scholar]
- 4.Destexhe A, Rudolph M, Paré D. The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- 5.Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- 6.Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- 7.Schneidman E, Berry M, Segev R, Bialek W. Weak pair-wise correlations imply strongly correlated network states in a neural population. Nature. 2006;440:1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shlens J, et al. The structure of multi-neuron firing patterns in primate retina. J. Neurosci. 2006;26:8254–8266. doi: 10.1523/JNEUROSCI.1282-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pillow JW, et al. Spatio-temporal correlations and visual signaling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yu S, Huang D, Singer W, Nikolic D. A small world of neuronal synchrony. Cereb. Cortex. 2008;18:2891–2901. doi: 10.1093/cercor/bhn047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tang A, et al. A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. J. Neurosci. 2008;28:505–518. doi: 10.1523/JNEUROSCI.3359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jones EG, Coulter JD, Hendry SH. Intracortical connectivity of architectonic fields in the somatic sensory, motor and parietal cortex of monkeys. J. Comp. Neurol. 1978;181:291–347. doi: 10.1002/cne.901810206. [DOI] [PubMed] [Google Scholar]
- 13.Shimazu H, Maier MA, Cerri G, Kirkwood PA, Lemon RN. Macaque ventral premotor cortex exerts powerful facilitation of motor cortex outputs to upper limb motoneurons. J. Neurosci. 2004;24:1200–1211. doi: 10.1523/JNEUROSCI.4731-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kalaska JF, Scott SH, Cisek P, Sergio LE. Cortical control of reaching movements. Curr. Opin. Neurobiol. 1997;7:849–859. doi: 10.1016/s0959-4388(97)80146-8. [DOI] [PubMed] [Google Scholar]
- 15.Shadmehr R, Krakauer JW. A computational neuroanatomy for motor control. Exp. Brain Res. 2008;185:359–381. doi: 10.1007/s00221-008-1280-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble and extrinsic covariate effects. J. Neurophysiol. 2005;93:1074–1089. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- 17.Paninski L, Pillow J, Lewi J. Statistical models for neural encoding, decoding, and optimal stimulus design. Prog. Brain Res. 2007;165:493–507. doi: 10.1016/S0079-6123(06)65031-0. [DOI] [PubMed] [Google Scholar]
- 18.Truccolo W. Stochastic point process models for multivariate neuronal spike train data: collective dynamics and neural decoding. In: Grün S, Rotter S, editors. Analysis of Parallel Spike Trains. New York: Springer; 2009. [Google Scholar]
- 19.Fawcett T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006;27:861–874. [Google Scholar]
- 20.Bamber D. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. J. Math. Psychol. 1975;12:387–415. [Google Scholar]
- 21.Hatsopoulos NG, Xu Q, Amit Y. Encoding of movement fragments in the motor cortex. J. Neurosci. 2007;27:5105–5114. doi: 10.1523/JNEUROSCI.3570-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jaynes ET. On the rationale of maximum entropy methods. Proc. IEEE. 1982;70:939–952. [Google Scholar]
- 23.Cover TM, Thomas JA. Elements of Information Theory. New York: Wiley & Sons; 1991. [Google Scholar]
- 24.Landau LD, Lifshitz EM. Statistical Physics. 3rd edn. Oxford: Butterworth & Heinemann; 1980. [Google Scholar]
- 25.Amit DJ. Modeling Brain Function. Cambridge: Cambridge University Press; 1989. [Google Scholar]
- 26.Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984;6:721–724. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 27.Marre O, El Boustani S, Fregnac Y, Destexhe A. Prediction of spatiotemporal patterns of neural activity from pair-wise correlations. Phys. Rev. Lett. 2009;102:138101. doi: 10.1103/PhysRevLett.102.138101. [DOI] [PubMed] [Google Scholar]
- 28.Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. Spatiotemporal tuning of motor neurons for hand position and velocity. J. Neurophysiol. 2004;91:515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
- 29.Wessberg J, et al. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408:361–365. doi: 10.1038/35042582. </jrn>. [DOI] [PubMed] [Google Scholar]
- 30.Serruya MD, Hatsopoulos NG, Paninski L, Fellows MR, Donoghue JP. Instant neural control of a movement signal. Nature. 2002;416:141–142. doi: 10.1038/416141a. [DOI] [PubMed] [Google Scholar]
- 31.Hochberg LR, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- 32.Truccolo W, Friehs GM, Donoghue JP, Hochberg LR. Primary motor cortex tuning to intended movement kinematics in humans with tetraplegia. J. Neurosci. 2008;28:1163–1178. doi: 10.1523/JNEUROSCI.4415-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.