NMR, IR/Raman, and Structural Properties in HNO and RNO (R = alkyl and aryl) Metalloporphyrins with Implication for the HNO-myoglobin Complex

Abstract

Structural and functional details of heme protein complexes with HNO and the isoelectronic RNO (R = alkyl and aryl) molecules (metabolic intermediates) are largely unknown. We report a quantum chemical investigation of three characteristic spectroscopic properties, ¹H and ¹⁵N NMR chemical shifts and NO vibrational frequencies in synthetic HNO and RNO heme complexes, with theory-versus-experiment correlation coefficients R² = 0.990–0.998. A new density functional theory (DFT) method was found to yield excellent predictions of experimental structures of HNO, RNO, and NO heme systems. Interestingly, this method also helps the identification of an excellent linear quantitative structure observable relationship between NO vibrational frequencies and bond lengths in all these NO-containing systems. This suggests that NO vibrations are largely local effects of the NO bonds in these complexes and may help deduce the NO bond lengths from using experimental vibrational data in these systems. The NO vibrational frequencies in HNO, RNO and NO metalloporphyrins were found to follow a general trend of NO > RNO > HNO complexes, as a result of the electron populations in the anti-bonding NO orbitals of NO < RNO < HNO complexes. Investigations of the NMR and IR/Raman spectroscopic data in HNO metal complexes show that HNO is a strong π-acid. In addition, we performed the first quantum chemical investigation of the hydrogen bond effect on HNO in MbHNO (Mb = myoglobin) models. Based on comparisons with experimental ¹H and ¹⁵N NMR results and NO vibrational frequency in MbHNO, a dual hydrogen bond mode for HNO in MbHNO was proposed. The enhanced stability from this dual hydrogen bonding may provide a basis for the unusual stability of MbHNO observed experimentally. These results should facilitate spectroscopic characterizations and structural investigations of HNO and RNO heme proteins and models.

Introduction

HNO, nitroxyl or nitrosyl hydride, is a sibling molecule of the well-known signaling agent nitric oxide (NO), yet their chemistries are quite different.¹ For instance, HNO and NO can lead to increases in the biochemical messengers cyclic adenosine monophosphate (cAMP) and cyclic guanosine monophosphate (cGMP), respectively.² HNO participates in many physiological and pathological processes.^2–8 With a more favorable vasodilative effect than NO and an increased contractility effect, HNO donors offer a promising new class of vasodialtors and heart failure treatment.⁹ HNO has also been suggested as a potential pharmacological treatment for reduction of neuronal damage, for instance, during stroke.² These observations strongly suggest that HNO has distinctive roles in biology and medicine. Heme proteins have long been proposed to mediate the physiological activity of HNO, since the early studies of biological denitrification processes in plants, bacteria, and fungi catalyzed by nitrite and nitric oxide reductases.^{10, 11} HNO has also been proposed in the catalytic cycles of the heme enzyme nitric oxide synthase, peroxidase, and cytochrome P450.^12–15 The isoelectronic RNO molecules (R = alkyl or aryl groups) that are metabolic intermediates of the amines, hydroxylamines, and organic nitro compounds have been found to bind with a number of heme proteins, such as myoglobin, soluble guanylyl cyclase, catalase, and cytochrome P450.^16–18 However, many structural and functional details of HNO or RNO protein complexes are still unknown.

Spectroscopic investigations of HNO and RNO protein complexes and synthetic models can provide useful information to help characterize these systems. Recently, an unusually stable HNO adduct of myoglobin (MbHNO) was isolated, ^{19, 20} which enabled NMR, resonance Raman, and x-ray absorption spectroscopic characterizations.^{21, 22} The ¹H NMR chemical shift of 14.8 ppm is a unique feature for the HNO moiety in MbHNO. A more recent investigation of HNO complexes with other oxygen-binding hemoglobins support that this proton NMR shift can serve as a sensitive probe of the heme active site.²³ Interestingly, this shift also varies with the metal center and ligand set in synthetic HNO metal complexes,^24–33 suggesting a useful role in characterizing synthetic HNO metal systems, too. The ¹⁵N NMR chemical shifts of the HNO moieties in a number of HNO heme protein complexes were also found to vary with the specific protein environment²³ and they are different from the nitrogen shifts observed in RNO iron porphyrin complexes.³⁴ In addition, experimental studies suggest that the NO vibrational frequency, ν_NO, is another useful probe of the metal environment in both HNO and RNO heme complexes. For example, ν_NO in MbHNO is 1385 cm⁻¹, which is quite different from that of the nitrosyl ferrous Mb, 1613 cm⁻¹, and that of the nitrosyl ferric Mb, 1927 cm⁻¹.²² The experimental NO vibrational frequencies in HNO metal complexes have a broad range of 1335 – 1493 cm⁻¹, with that in a heme model system (1380 cm⁻¹) being close to the value seen in MbHNO.^24–33 In contrast, the NO vibrational frequencies in RNO iron porphyrin complexes^{35, 36} (1400–1445 cm⁻¹) are relatively higher than those in HNO heme complexes. Therefore, the ¹H and ¹⁵N NMR chemical shifts and NO vibrational frequencies are important spectroscopic probes to investigate HNO and RNO heme systems.

However, there are no quantum chemical investigations of the characteristic ¹H NMR shifts in HNO protein or model systems. For the ¹⁵N NMR shifts in HNO or RNO protein and model systems, there is a previous computational investigation of some RNO metallophorphyrins, which provides a useful analysis of the solid-state ¹⁵N NMR results, yet the predicted isotropic shifts in many iron porphyrins have 30 ppm or larger errors.³⁴ Regarding ν_NO calculations, a recent investigation of MbHNO using the simple [Fe(Por)(ImH)(HNO)] (Por = porphyrinate) model suggests that quantum chemical investigations may be helpful to understand the experimental vibrational spectra,³⁷ as with other NO heme complexes.^38–41 However, errors of 31–32 cm⁻¹ for the NO vibrational frequency in MbHNO from the best reported calculations clearly indicate the insufficiency of the used model or method. Another report of the gas phase ν_NO calculation is for a synthetic HNO metal complex Ru(HNO)(‘py^buS₄’) (‘py^buS₄’ = 2,6-bis(2-mercapto-3,5-di-tert-butylphenylthio)dimethyl-pyridine),³⁰ with an error of 155 cm⁻¹ and a surprisingly large effect of ~120 cm⁻¹ on the calculated ν_NO from using hydrogen bonds. In addition, there are no reports of quantum chemical investigations of NO vibrational frequencies in RNO heme models. Overall, high accuracy predictions of the ¹H and ¹⁵N NMR chemical shifts and NO vibrational frequencies as important spectroscopic probes to investigate HNO and RNO heme systems have not been reported yet.

Previous investigations show that the high accuracy predictions of some characteristic spectroscopic observables can help understand, assign, and sometimes correct experimental spectra,^{42, 43} help understand relevant electronic structures,^{42, 44–52} and provide a valuable venue to refine or determine protein structures^{46, 48, 49, 51, 53, 54} using a way we now call the integrated quantum mechanics and spectroscopy (QM/S) approach. This is based on an intrinsic mathematical relationship between a spectroscopic observable of a given molecule and its molecular structure. According to a fundamental theorem in the density functional theory (DFT) – the Hohenberg-Kohn theorem,⁵⁵ any property can be expressed by a functional of the molecular system’s electron density. Therefore, a spectroscopic observable property (e.g. NMR chemical shift) is a functional of the electron density, ρ(r₁, r₂,…r_n), which is determined by the molecular structure or spatial arrangement of the atoms (n atoms) in this molecule, (r₁, r₂,…r_n). In many cases, this quantitative structure observable relationship (QSOR) cannot be expressed explicitly, so quantum chemical geometry optimization is needed to find the optimal structure that can minimize the prediction errors for some key experimental spectroscopic observables.^{48, 49, 53} In addition to the use of this implicit QSOR approach, sometimes, numerical explicit QSOR may be constructed and a probability surface can be used to directly find the optimal geometric parameters.^{46, 54} The easiest way to determine a geometric parameter from using the experimental spectroscopic data may be the use of an analytic QSOR, which is actually not uncommon, e.g. the well-known Karplus relationship.⁵⁶

Here, we report a quantum chemical investigation of the ¹H and ¹⁵N NMR chemical shifts and NO vibrational frequencies in synthetic HNO and RNO heme complexes, with prediction errors ~2–3% of the experimental data ranges, using a new DFT method based on a comprehensive investigation. An analytic QSOR was found between the NO vibrational frequencies and the NO bond lengths in all HNO, RNO, and NO heme systems investigated here. In addition, based on comparisons with these three experimental spectroscopic data of MbHNO, a dual hydrogen bond mode for HNO in MbHNO was proposed for the first time, using model systems. These results should facilitate future studies of HNO and RNO metalloporphyrins and heme proteins.

Computational Details

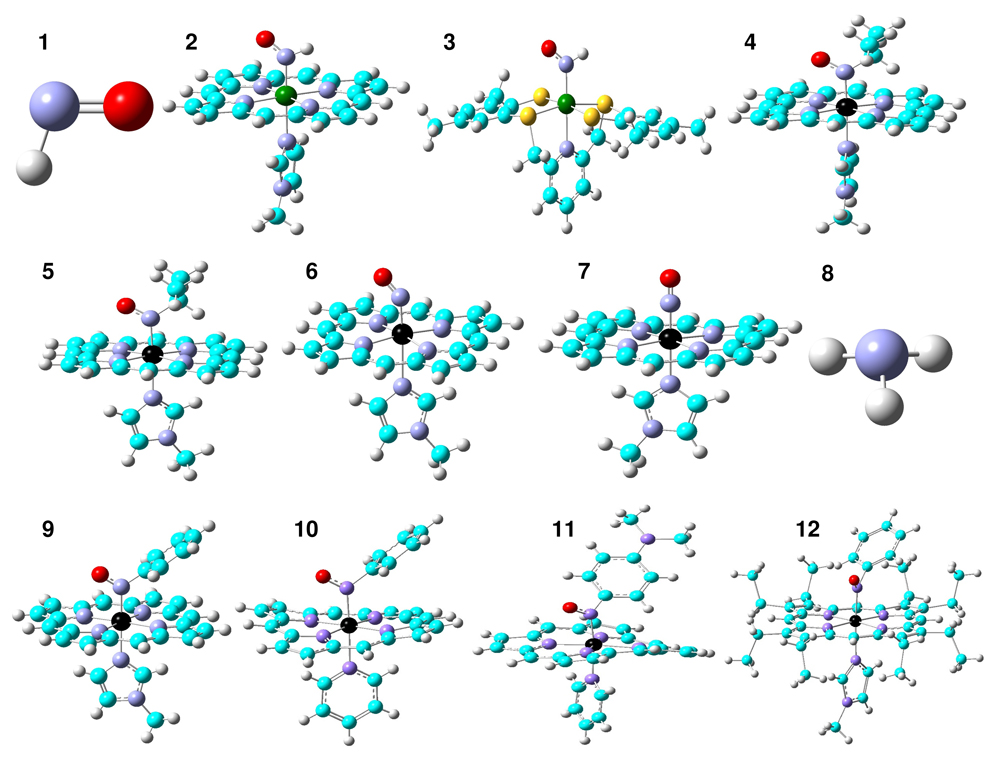
As shown in Figure 1, sixteen molecules were investigated to evaluate the predictions of the characteristic spectroscopic probes in HNO and RNO heme models and other relevant systems: HNO (1), Ru(TTP)(HNO)(1-MeIm) (2), Ru(HNO)(‘py^buS₄’) (3), Fe(TPP)(ⁱPrNO)(1-MeIm) (4), Fe(OEP)(ⁱPrNO)(1-MeIm) (5), Fe(TPP)(NO)(1-MeIm) (6), [Fe(OETPP)(NO)(1-MeIm)]⁺ (7), NH₃ (8), Fe(TPP)(PhNO)(1-MeIm) (9), Fe(TPP)(PhNO)(py) (10), Fe(TPP)(NODMA)(py) (11), Fe(OEP)(PhNO)(1-MeIm) (12), Fe(Por)(HNO)(5-MeIm) (13), Fe(Por)(HNO…H₂O)(5-MeIm) (14), Fe(Por)(H₂O…HNO)(5-MeIm) (15), and Fe(Por)(H₂O…HNO…H₂O)(5-MeIm) (16), where TTP = 5,10,15,20-tetratolylporphyrinato, TPP = 5,10,15,20-tetraphenyl-porphyrinato, OEP = 2,3,7,8,12,13,17,18-octaethylporphyrinato, OETPP = 2,3,7,8,12,13,17,18-octaethyl-5,10,15,20-tetraphenylporphy-rinato, 1-MeIm = 1-methylimidazole, py = pyridine, and NODMA = 4-nitroso-N,N-dimethylaniline. The peripheral substituents on the porphyrin rings were replaced by hydrogen atoms as in the previous work^{42, 44–46, 49, 54, 57} unless otherwise indicated. Molecules 1–8 and 13–16 were subject to full geometry optimizations and subsequent frequency calculations to verify that they are the minimum energy states in their potential energy surfaces. No scaling factors were used in the reported vibrational frequencies. The solution NMR chemical shifts calculations and atomic charges from the natural population analysis⁵⁸ (NPA) were done using the fully optimized structures. Solid state NMR chemical shifts results of complexes 9–12 were predicted using the corresponding x-ray crystal structures.³⁴ The calculated ¹H and ¹⁵N NMR chemical shifts are referenced to the calculated chemical shieldings in experimentally used reference standards TMS and NH₃, respectively.

Figure 1.

Structures of the molecules (1–16) investigated in this work. Atom color scheme: Ru-dark green, Fe-black, C-cyan, N-blue, O-red, S-yellow, H-grey.

A comprehensive investigation on the computational methods was performed to evaluate the predictions of structures and various spectroscopic properties of molecules 1–12 and the selected methods were then used to investigate MbHNO models 13–16. In addition to the use of two commonly used hybrid Hartree-Fock/density functional theory methods B3LYP⁵⁹ and mPW1PW91,⁶⁰ we examined three series of customized combinations of pure DFT methods. The first series uses the Becke⁶¹ (abbreviated as B) exchange functional with the following correlation functionals: VWN,⁶² VWN5,⁶² LYP,⁶³ PL,⁶⁴ P86,⁶⁵ B95,⁶⁶ PBE,⁶⁷ TPSS,⁶⁸ as implemented in Gaussian 03.⁶⁹ The second series uses the Perdew-Wang 1991 exchange functional as modified by Adamo and Barone (mPW)⁶⁰ exchange functional, with above correlation functionals. The third series of pure DFT methods was built by using the following exchange functionals with the P86⁶⁵ correlation functional: G96,⁷⁰ PW91,⁷¹ PBE,⁶⁷ and O⁷² as implemented in Gaussian 03. For non-metal elements, 30 Pople-type basis sets (from 6-311G(d) to 6-311++G(3df,3pd)) as well as four Dunning’s correlation consistent basis sets⁷³ (cc-pvdz, aug-ccpvdz, aug-ccpvtz, aug-ccpvqz) were used. For metal elements, both the all electron basis sets (Wachters’ ^{74, 75} and DGDZVP⁷⁶) and the effective core potential basis sets (LanL2DZ,⁷⁷ CEP-121G,⁷⁸ SDD⁷⁹) were studied.

The use of pure or hybrid DFT methods with different exchange and correlation functionals and different basis sets all affect the predictions. For HNO calculations, among all 74 computational methods used in this work (see supporting information for details), a new pure DFT method mPWVWN with a 6-311++G(2d,2p) basis was chosen based on its best performance in predictions of experimental geometric parameters and vibrational frequencies^{80, 81} (vide infra). This mPWVWN method was then used in geometry optimizations and frequency calculations of all HNO, RNO, and NO heme model complexes investigated here (2–7, 13–16), with the 6-311++G(2d,2p) basis for HNO and the first coordination shell atoms, while the rest atoms were treated with a 6-31G(d) basis for computational efficiency. This is designated as 6-311++G(2d,2p)|metal’s basis|6-31G(d) in this work. Among a number of all electron and effective core potential basis sets examined here (see supporting information for details), the use of the DGDZVP for Ru and Wachters’ for Fe was found to yield the best predictions of vibrational data. For calculations of the proton NMR chemical shifts, δ_H, in the HNO moieties of the HNO metal complexes, we used the method that previously yielded excellent predictions of ¹H NMR shifts in various metal-containing systems,⁸² i.e., the B3LYP/6-311++G(2d,2p)|metal’s basis|6-31G(d) method. Ru and Fe were treated with the DGDZVP and LanL2DZ bases, respectively. In ¹⁵N NMR property predictions, the OP86/6-311++G(2d,2p) method for the experimental reference system NH₃ and the OP86/6-311++G(2d,2p)|LanL2DZ|6-31G(d) method for iron porphyrin systems, were chosen (see supporting information for details). Based on these calculations for HNO and RNO heme model complexes as well as additional results in supporting information, we used the following methods for ν_NO, δ_H, and δ_N predictions in MbHNO models (13–16): mPWVWN/6-311++G(2d,2p)|Wachters|6-31G(d), B3LYP/6-311++G(2d,2p)|LanL2DZ|6-31G(d), and OP86/6-311++G(2d,2p)|LanL2DZ|6-31G(d), respectively.

Results and Discussion

Vibrational and Structural Properties in HNO and RNO Heme Model Complexes

We first investigated HNO to see for this small molecule how well we can improve over the previous predictions of the geometric structures and vibrational frequencies,³⁷ which will build a basis for subsequent calculations for synthetic HNO metal complexes. Clearly, as seen from Table 1 (selected results) and Table S1 (all results), the use of pure or hybrid DFT methods with different exchange and correlation functionals and different basis sets all affect the predictions. We first performed calculations with the widely used hybrid HF-DFT method B3LYP using a number of different basis sets (see Table S1), which resulted in large errors of 88–110 cm⁻¹ for ν_NO predictions, as found in the previous report. ³⁷ We then used another hybrid method mPW1PW91 which contains more HF exchange component compared to B3LYP to examine the effect of HF exchange on such kind of calculations. As shown in Table S1, results are even worse, e.g. the errors in ν_NO predictions are 143–170 cm⁻¹. These results suggest that the methods with less or no HF exchange may perform better in the investigation of HNO vibrations, which was confirmed by additional pure DFT calculations (see Table S1). Among all 74 different methods examined here, a new pure DFT method mPWVWN with a 6-311++G(2d,2p) basis produces the best predictions with 1 and 0 cm⁻¹ errors for ν_NO and ν_HNO, and 0.006 Ådeviations from experimental NO and NH bond lengths. ^{80, 81} Interestingly, this method was also found to perform well in our recent investigation of other molecules.⁸³

Table 1.

Errors in Selected Results of Geometry Optimizations and Frequency Calculations for HNO

Entrya	DFT method	Basis	ΔRNO	ΔRNH	ΔνNO	ΔνHNO
			(Å)	(Å)	(cm−1)	(cm−1)
b	B3LYP	6-311G(2d,2p)	−0.010	0.000	90	73
b	BLYP	6-311G(2d,2p)	0.007	0.019	−6	−11
9	B3LYP	6-311++G(2d,2p)	−0.010	−0.003	88	65
18	mPW1PW91	6-311++G(2d,2p)	−0.018	−0.006	143	84
46	BVWN5	6-311G(2d,2p)	0.008	0.011	2	−6
56	mPWVWN5	6-311G(2d,2p)	0.007	0.011	3	−14
67	mPWVWN	6-311++G(2d,2p)	0.006	0.006	1	0

^aThe entry number corresponds to that in Table S1, which includes full results.

^bRef. ³⁷.

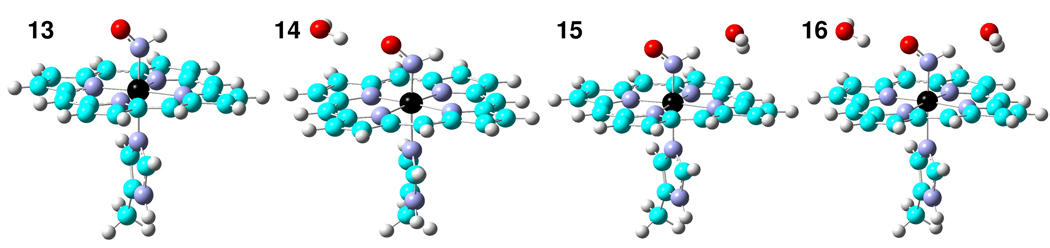
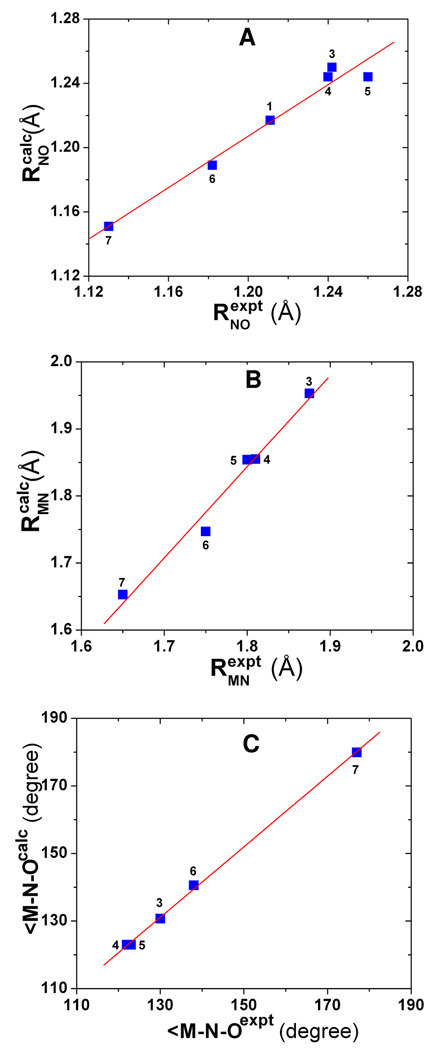
As shown in Table 2, for the only HNO heme model complex reported to date, Ru(TTP)(HNO)(1-MeIm) (2), an error of 2 cm⁻¹ was obtained for ν_NO. We also investigated Ru(HNO)(‘py^buS₄’) (3), which compared to other known HNO metal complexes characterized by IR and NMR techniques^{24–29, 31, 32} is closest to a heme model environment by having a relatively rigid ligand set in the equatorial plane and a nitrogen-coordinated ligand in the axial position. An error of 12 cm⁻¹ is much improved over the 155 cm⁻¹ error in the previous work.³⁰ In addition, we performed the first computational vibrational analysis of RNO heme model systems: Fe(TPP)(ⁱPrNO)(1-MeIm) (4) and Fe(OEP)(ⁱPrNO)(1-MeIm) (5), for which the predicted ν_NO values deviate from experiment by −5 and 6 cm⁻¹, respectively. For comparison, we also investigated the ferrous and ferric NO heme models: Fe(TPP)(NO)(1-MeIm) (6) and [Fe(OETPP)(NO)(1-MeIm)]⁺ (7), for which the predicted geometric parameters and NO vibrations are again in good accord with experiment,^84–86 Table 2. Now, for all HNO, RNO, and NO systems (1–7) investigated here, as shown in Figure 2A–C, there are good agreements between theory and experiment: R² = 0.968 and SD = 0.008 Å for R_NO, R² = 0.978 and SD = 0.020 Å for R_MN, and R² = 0.999 and SD = 0.9° for ∠M-N-O. In addition, as demonstrated in Figure 3A, an excellent agreement between computational and experimental ν_NO data can be found with R² = 0.998 and a SD = 9 cm⁻¹, or 1.8% of the whole 513 cm⁻¹ range seen experimentally. These results indicate that the new pure DFT method mPWVWN is able to yield accurate geometries and NO vibrations in a number of HNO, RNO, and NO metalloporphyrins.

Table 2.

NMR, IR/Raman, Structural, and Charge Properties in Molecules 1–16

	System		RNO	RNH	RMN	∠H-N-O	∠M-N-O	νNO	δH	δN	QNO	QH	Ref.
			(Å)	(Å)	(Å)	(°)	(°)	(cm−1)	(ppm)	(ppm)	(e)	(e)
1	HNO	Expt	1.211	1.063				1565					80, 81
		Calc	1.217	1.069		108.6		1566	30.06	1237	−0.233	0.233
2	Ru(TTP)(HNO)(1-MeIm)	Expt						1380	13.64				33
		Calc	1.248	1.039	1.940	112.0	132.1	1382	13.18		−0.383	0.284
3	Ru(HNO)(‘pybuS4’)	Expt	1.242		1.875		130	1358	19.56				30
		Calc	1.250	1.040	1.953	111.7	130.7	1370	19.98		−0.421	0.279
4	Fe(TPP)(iPrNO)(1-MeIm)	Expt	1.24		1.81		122	1433					35
		Calc	1.244		1.855		123.0	1428			−0.198
5	Fe(OEP)(iPrNO)(1-MeIm)	Expt	1.26		1.80		123	1423					35
		Calc	1.244		1.854		123.0	1429			−0.199
6	Fe(TPP)(NO)(1-MeIm)	Expt	1.182		1.750		138	1630					84, 85
		Calc	1.189		1.747		140.6	1614			−0.057
7	[Fe(OETPP)(NO)(1-MeIm)]+	Expt	1.130		1.650		177.0	1871					86
		Calc	1.151		1.653		179.9	1874			0.348
8	NH3	Expt		1.015						0.00			87
		Calc		1.015						0.74
9	Fe(TPP)(PhNO)(1-MeIm)	Expt	1.254		1.800		124.8			605			34
		Calc								616
10	Fe(TPP)(PhNO)(py)	Expt	1.249		1.819		123.9			607			34
		Calc								632
11	Fe(TPP)(NODMA)(py)	Expt	1.252		1.859		119.8			607			34
		Calc								590
12	Fe(OEP)(PhNO)(1-MeIm)	Expt	1.264		1.806		123.3			593			34
		Calc								616
	MbHNO	Expt	1.241		1.820		131.0	1385	14.80	661			22, 23
13	Fe(Por)(HNO)(5-MeIm)	Calc	1.245	1.040	1.804	112.4	132.4	1400	15.42	607	−0.307	0.289
14	Fe(Por)(HNO…H2O)(5-MeIm)	Calc	1.252	1.038	1.795	111.5	133.8	1379	14.61	596	−0.304	0.303
15	Fe(Por)(H2O…HNO)(5-MeIm)	Calc	1.247	1.043	1.805	112.0	130.6	1400	15.54	643	−0.284	0.337
16	Fe(Por)(H2O…HNO…H2O)(5-MeIm)	Calc	1.253	1.042	1.800	111.2	131.6	1382	14.63	642	−0.323	0.340

Figure 2.

Computed vs. experimental geometric parameters. A) NO bond lengths; B) MN bond lengths; C) ∠M-N-O bond angles.

Figure 3.

A) Computed vs. experimental NO vibrational frequencies in 1–7 and MbHNO model 16. B) Calculated NO vibrational frequencies vs. NO bond lengths in 1–7 and 13– 16; C) Calculated NO vibrational frequencies vs. NPA charges of NO in metal complexes 2–7 and 13–16. Green data points are for MbHNO models.

To further compare with the performance of this new mPWVWN method, additional calculations of the HNO, RNO, and NO heme models (2–4, 6–7) using the next two favorable methods BVWN5/6-311G(2d,2p) and mPWVWN5/6-311G(2d,2p) were also carried out. These two methods result in errors of 2 and 3 cm⁻¹ for ν_NO predictions of HNO respectively, compared to the 1 cm⁻¹ error from using the mPWVWN/6-311++G(2d,2p) method, see Table 1. As shown in Table S3, their mean absolute errors of ν_NO predictions for the metal complexes are 12.8 cm⁻¹, which is ca. 70% larger than that from using the mPWVWN method described above for the same set of metal complexes, 7.6 cm⁻¹. These results further support the use of the new pure DFT method mPWVWN in investigating HNO, RNO, and NO heme systems.

As shown in Table 2, both experimental and computational results show that the NO vibrations in these three types of NO-containing heme complexes follow a general trend of NO > RNO > HNO complexes. Interestingly, the computational results offer a couple of insights into the origin of this trend. As demonstrated in Figure 3B, there is an excellent linear QSOR between ν_NO and R_NO with R² = 0.977 in all of these NO-containing molecules with a trend of NO < RNO < HNO complexes for NO bond lengths, which supports the opposite trend seen for NO vibrational frequencies. This also indicates that NO vibrations are mainly local effects of the NO bonds and the NO bond lengths may be deduced directly from using the NO vibrational frequencies in all of these NO-containing systems, including some MbHNO models (vide infra). In addition, an excellent relationship between NO vibrational frequencies and NPA charges of the NO groups in all the metal complexes (Q_NO) with R² = 0.953 was found, as shown in Figure 3C. This shows that there is a common bonding behavior in the NO moieties in all these different NO-containing systems: with more electrons populated in the antibonding π_NO* orbital, the NO bonds become weakened, resulting in longer NO bond lengths and smaller NO vibrational frequencies. HNO and RNO have an extra electron compared to NO, which results in weaker NO bonds and consequently smaller NO vibrational frequencies seen in HNO and RNO heme model complexes compared to NO heme systems. The negative charges of HNO moieties in the HNO heme model complexes (see Table 2) indicate that HNO acts as a π acid, receiving back donation from the metal center, which is the same as in other non-heme type HNO metal complexes.²⁷ For the isoelectronic HNO and RNO species, the observed smaller NO vibrational frequencies in HNO metal complexes compared to RNO complexes suggest that HNO is a stronger π acid than RNO, in agreement with the calculated charges of NO groups in these systems.

NMR Properties in HNO and RNO Heme Model Complexes

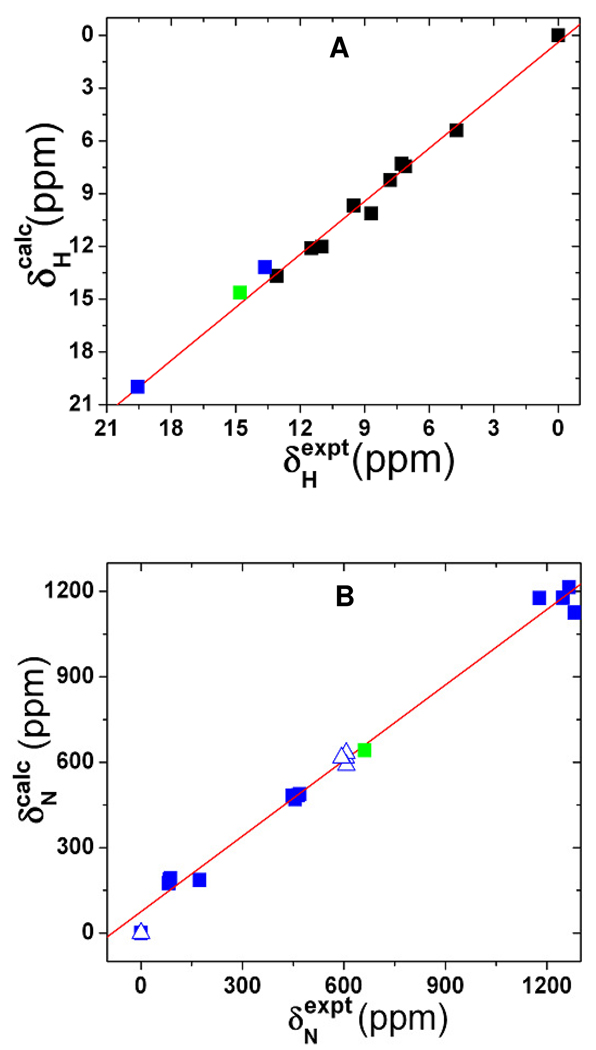
As shown in Table 2, for the two synthetic HNO complexes 2 and 3, the errors in proton NMR shift predictions are 0.46 and 0.42 ppm, respectively. These results indicate that in these first reports of the ¹H NMR shift predictions for HNO metal complexes, the errors are similar to those seen with other metal complexes using basically the same method.⁸² Indeed, as demonstrated in Figure 4A, there is an excellent agreement between experiment and calculation for all these systems with R² = 0.990 and SD = 0.52 ppm, or 2.6% of the whole 19.89 ppm range seen experimentally. This suggests that the method used here works well for a number of different metal complexes.

Figure 4.

A) Computed vs. experimental ¹H NMR chemical shifts. Blue, black and green data points are for synthetic HNO metal complexes, other metal complexes and ligands from ref. 82, and MbHNO model 16. B) Computed vs. experimental ¹⁵N NMR chemical shift tensor results. The triangle data points are the corresponding isotropic values and the green data point is for MbHNO model 16.

We then moved to the predictions of ¹⁵N NMR chemical shifts in RNO heme model complexes.³⁴ For the experimental reference system NH₃ (8), the predicted shift by using the OP86/6-311++G(2d,2p) method has an error of 0.74 ppm compared to the experimental result.⁸⁷ For the RNO heme model complex 9, an error of 11 ppm was obtained, Table 2, which is much improved over the previously reported error of 23 ppm.³⁴ This kind of computational error is close to that seen in solution ¹⁵N NMR experiments for investigating protein systems due to a number of experimental effects.⁸⁸ An overall comparison with the experimental ¹⁵N NMR shifts for 8–12 shows R² = 0.996 and SD of 19 ppm or 3.1% of the studied experimental range. In addition, the predicted ¹⁵N NMR chemical shift tensor elements (see supporting information for details) are also in excellent agreement with experimental data, with R² = 0.991 and 3.5% error over the entire experimental range of 1281 ppm. These results are demonstrated in Figure 4B.

Compared to the predicted ¹H NMR shift of 30.06 ppm and ¹⁵N NMR shift of 1237 ppm in free HNO, both the proton and nitrogen NMR shifts in HNO metal complexes are much upfield, suggesting a strong effect from metal coordination. As shown in Table 2, large electron densities in the HNO moiety (Q_NO+Q_H) in HNO metal complexes were found in comparison to that in free HNO, which result in larger NMR chemical shieldings and consequently the smaller NMR chemical shifts seen experimentally in HNO metal systems. The extra electron densities gained through the metal coordination in these HNO metal complexes reflects the π-acidity nature of HNO in these complexes. The strong π-acid effect of HNO seen from these NMR results is also consistent with above results and discussion on NO vibrations in HNO metal complexes.

MbHNO Model Calculations

In order to obtain a preliminary understanding of the structural effects especially the previously unexplored hydrogen bond effect in MbHNO on the three spectroscopic “fingerprints”: ν_NO, δ_H, and δ_N, we carried out a series of calculations on the following models: Fe(Por)(HNO)(5-MeIm) (13), Fe(Por)(HNO…H₂O)(5-MeIm) (14), Fe(Por)(H₂O…HNO)(5-MeIm) (15), and Fe(Por)(H₂O…HNO…H₂O)(5-MeIm) (16). As shown in Figure 1, in these models, the HNO adopts a perpendicular conformation with respect to the axial His ligand (modeled as 5-MeIm here), since this was found in a previous experimental work²¹ and there is no significant difference between the perpendicular and parallel conformations in both geometries and predicted spectroscopic properties.³⁷ As the HNO molecule has both terminal hydrogen and oxygen atoms available to form hydrogen bonds, models 14, 15, and 16 were used to investigate the effects of HNO act as a hydrogen bond acceptor, hydrogen bond donor, and both. Here, the water molecule is used as a hydrogen bond probe because of its simplicity, capability of acting as both hydrogen bond donor and acceptor, and viability in the protein systems.

As shown in Table 2, for the hydrogen bond free model 13, though the ν_NO calculation error has been greatly reduced in comparison to an early work,³⁷ the overall errors in these three spectroscopic properties are large enough to preclude this model for MbHNO. Interestingly, when HNO acts as a hydrogen bond acceptor (14), both ν_NO and δ_H predictions of 1379 cm⁻¹ and 14.61 ppm become close to the experimental data of 1385 cm⁻¹ and 14.80 ppm. ^{22, 23} However, the ¹⁵N NMR shift prediction error is enlarged, indicating that although this model corrects some problems, it still misses one or more essential structural feature(s) in MbHNO. In the case of HNO acting as a hydrogen bond donor (15), an exactly opposite phenomenon was observed, see Table 2. The calculated ¹⁵N NMR chemical shift was improved by 36 ppm, yet there is no improvement or even a little deterioration for ν_NO and δ_H predictions. These results suggest that in MbHNO, these two hydrogen bonding structural effects may be applicable at the same time. Indeed, as shown for the dual hydrogen bond model (16) in Table 2, all these three characteristic spectroscopic property predictions were improved simultaneously. This can also been seen from Figure 3 and Figure 4 for δ_NO, δ_H, and δ_N plots, where the predicted values of the dual hydrogen bond model (16) fit well with results of related HNO/RNO systems. This suggests that the HNO moiety in MbHNO may be involved in two hydrogen bonds as found in the HNO dimer⁸⁹ and synthetic HNO metal complex.³⁰ In MbHNO, the distal His residue and a possible water molecule in the active site can form the two hydrogen bonds with HNO. Since the experimental NMR studies indicates that a wide range of active site residues may be involved in the interactions with HNO,²¹ an extensive examination of these effects in MbHNO towards an accurate picture of the HNO interactions in a heme protein environment is under investigation in our group.

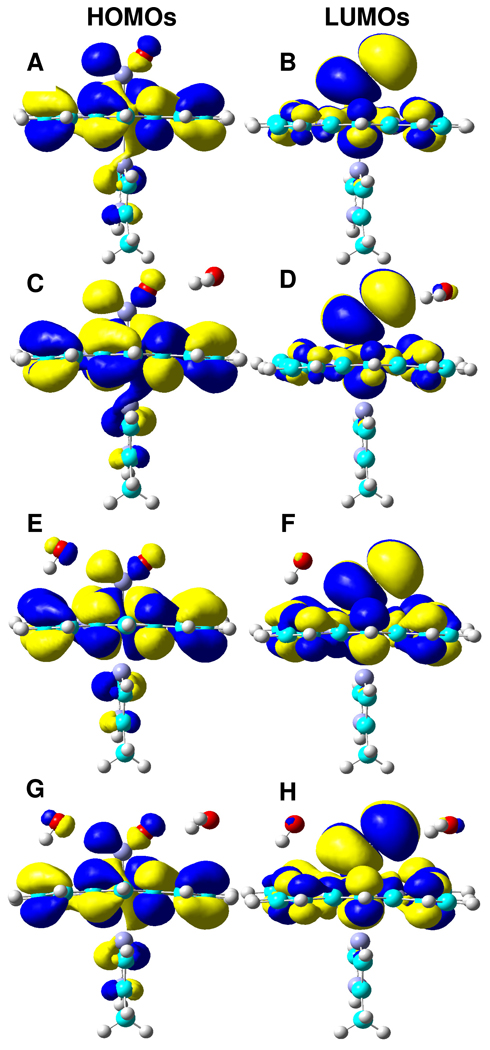
The capability of forming dual hydrogen bonds for HNO may provide a basis for the unusual stability of MbHNO observed experimentally.¹¹ As shown in Figure 5, the HOMOs and LUMOs are essentially the same for all MbHNO models studied here (13– 16), with a σ_NH orbital acting as the hydrogen bond donor and a π_NO* orbital acting as the hydrogen bond acceptor. The hydrogen bond distances of O_water…H_HNO are 2.028 Åin 15 and 2.012 Å in 16, and the distances of O_HNO…H_water are 2.072 Å in 14 and 2.070 Å in 16. Clearly, the hydrogen bond distances in the dual hydrogen bond model 16 are shortened in comparison to those in the single hydrogen bond models 14 and 15. This suggests that the hydrogen bonds are not simply added together in 16, but have a synergetic, strengthening effect, consistent with the additional stabilization energies of 8–9 kcal/mol in 16 than in 14 and 15. This kind of dual hydrogen bonding capability of HNO is unique and has not been seen in heme protein complexes with other small molecules such as O₂, which may be responsible for the stronger binding affinity of Mb for HNO than the native substrate dioxygen.¹¹

Figure 5.

Isosurface representations of HOMOs and LUMOs for 13 (A,B), 14 (C,D), 15 (E,F), and 16 (G,H), respectively, with contour values = ± 0.01 au.

Conclusion

The results we have described above are of interest for a number of reasons. First, based on a comprehensive methodological investigation, a new pure DFT method mPWVWN was found to yield excellent predictions of key geometric parameters around the NO groups (R_NO, R_MN, ∠M-N-O) in the HNO, RNO, and NO heme model complexes with R² = 0.968–0.999. Second, for the three characteristic spectroscopic properties ¹H and ¹⁵N NMR chemical shifts and NO vibrational frequencies in synthetic HNO and RNO heme complexes, excellent correlations with experimental results were found with R² = 0.990–0.998. Third, an excellent linear QSOR was found between ν_NO and R_NO with R² = 0.977 in all of the HNO, RNO, and NO heme model complexes investigated here, which may help deduce the NO bond lengths from experimental NO vibrational data. ν_NO data has a general trend of NO > RNO > HNO complexes, resulting from the opposite trend of the electron populations in the anti-bonding NO orbitals. Investigations of the NMR and IR/Raman spectroscopic data in HNO metal complexes show that HNO is a strong π-acid. Fourth, we performed the first quantum chemical investigation of the hydrogen bond effect on HNO in MbHNO models. Based on comparisons with experimental ¹H and ¹⁵N NMR results and NO vibrational frequency in MbHNO, a dual hydrogen bond mode for HNO was proposed. The enhanced stability from this dual hydrogen bonding may account for the unusual stability of MbHNO observed experimentally. Taken together, these results are of broad general interest since they represent the first accurate quantum chemical investigations of some characteristic NMR and IR/Raman spectroscopic results in HNO and RNO heme complexes, which should facilitate spectroscopic characterizations and structural investigations of HNO and RNO heme proteins and models.