Modulation of Axonal Excitability by High-Frequency Biphasic Electrical Current

Abstract

The modulation of axonal excitability by high-frequency biphasic (HFB) electrical current was analyzed using a lumped circuit model of the myelinated axon based on Schwarz-Reid-Bostock (SRB) equations. The results show that axonal excitability could be either increased or decreased by HFB current depending on the current intensity. The increase of axonal excitability is due to the high level of sodium channel activation, whereas the activation of both fast and slow potassium channels plays an important role in decreasing axonal excitability. As the HFB current intensity increases, the location determining the axonal excitability changes from the nodes under the electrode within the “main lobe” region of the activating function to the nodes away from the electrode in the “side lobe” region of the activating function. This simulation study also shows that the modulation of axonal excitability by HFB electrical current could be potentially useful to selectively activate the small nerve fibers in a compound nerve trunk without activating the large fibers. Understanding how HFB electrical current modulates the axonal excitability will further elucidate the possible mechanisms underlying the nerve conduction block induced by HFB electrical current.

I. INTRODUCTION

Previous studies have shown that high-frequency (kHz) biphasic (HFB) electrical current applied to a nerve can block the conduction of action potentials [1]-[11], indicating that axonal excitability must be reduced by the application of high-frequency blocking stimulation. However, the axonal region where conduction failure occurs may not necessarily be unexcitable. Applying an extracellular electrical pulse to the axonal region of blockage may still be able to induce an action potential if the stimulus pulse is strong enough. Currently, there is no publication that has investigated how axonal excitability is modulated by the HFB electrical current, although recently many studies investigated the nerve conduction block induced by HFB current [1]-[7][12]-[17]. A reversible nerve blocking method employing electrical current will find many clinical applications [1]-[6]. Understanding how axonal excitability is modulated by HFB current and the possible mechanisms underlying this modulation could help to further understand the nerve conduction block phenomenon and promote the clinical application of HFB electrical current to induce blockade of the peripheral nerves.

In addition, selective activation of small nerve fibers in a compound nerve trunk without activating large nerve fibers would be very useful in the design of neural prostheses [18][19]. For example, by stimulating small diameter axons first and then gradually activating large diameter axons, a well-graded and fatigue-resistant force could be generated in the innervated muscles [20], which could be used to restore functional movement in patients with motor disability. Selective activation of small nerve fibers could also be used to induce bladder contraction without activating the urethral sphincter during sacral anterior root stimulation in order to restore micturition function after spinal cord injury [21]. The difficulty in selectively activating the small nerve fibers without activating the large nerve fibers in a compound nerve trunk is due to the fact that the large fibers have lower thresholds than the small fibers. However, the excitability of small or large nerve fibers might be modulated differently by HFB electrical current resulting in a condition in which the small fibers become more excitable than the large fibers. Thus, understanding how HFB electrical current modulates axonal excitability could be very helpful in designing new selective stimulation methods.

It will be very difficult to reveal the mechanisms underlying the modulation of axonal excitability by HFB electrical current in animal experiments. This is due to: (1) the high frequency electrical noise caused by the HFB electrical current; and (2) the technical difficulty in recording activity from every axonal node along a single nerve fiber. Therefore, in this study we used the Schwarz-Reid-Bostock (SRB) axonal membrane model, which was derived from human axonal data, to investigate the modulation of axonal excitability induced by HFB electrical current in an attempt to further understand the underlying mechanisms at the single cell level.

II. METHODS

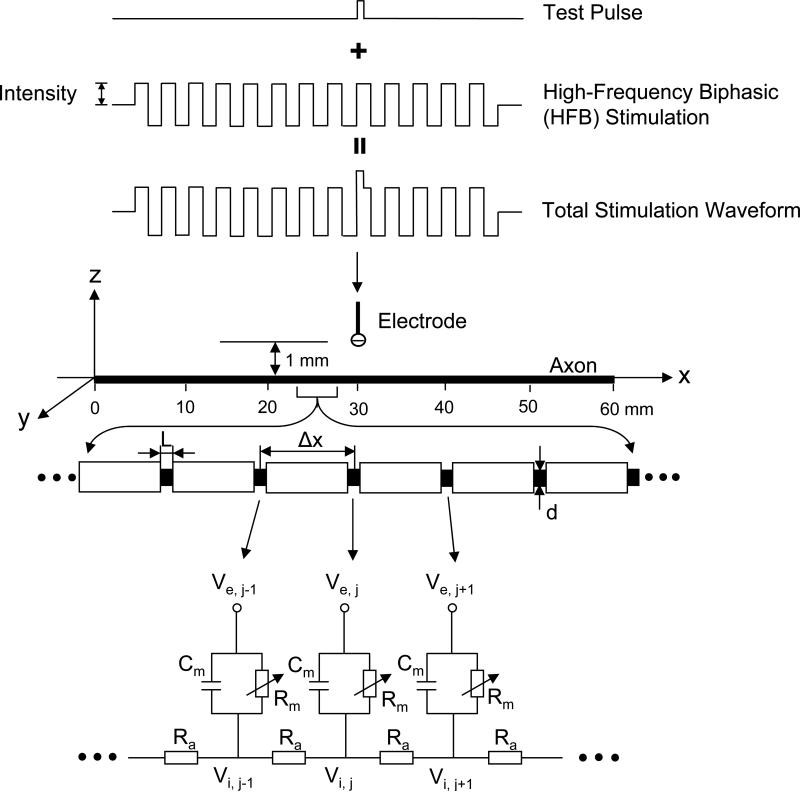
Fig.1 shows the nerve model. A 60 mm long myelinated axon is modeled with an inter-node length Δx = 100d (where d is the axon diameter) and d = 0.7D (where D denotes the axon external myelin diameter)[28][32]. The inter-nodal myelin sheath is modeled as an isolator (i.e. no current passing through). The nodal length is denoted by L. Each node of the axon is modeled by a membrane capacitance (C_m) and a variable membrane resistance (R_m). R_a is the inter-node axoplasm resistance. The ionic currents passing through the variable membrane resistance are described by the SRB model (see Appendix and [22]). A single point electrode (with the indifferent electrode at infinity) is placed at 30 mm location along the axon at a 1 mm distance from the axon (Fig. 1). The HFB rectangular electrical current as shown in Fig. 1 used to modulate the axonal excitability is delivered via the point electrode. After 30 ms of HFB modulation, a uniphasic test pulse (see Fig. 1) is added to the HFB electrical current to determine axonal excitability, i.e. the excitation threshold that is represented by the minimal intensity of the test pulse to induce an action potential. The HFB electrical current always starts with a cathodal phase first. The test pulse is always cathodal, and starts with the upstroke of a cathodal HFB pulse (see Fig. 1).

Fig. 1.

Myelinated axonal model used to simulate the modulation of axonal excitability by high-frequency biphasic (HFB) electrical stimulation. The inter-node length Δx = 100d; d is the axon internal myelin diameter. L is the nodal length. Each node is modeled by a resistance-capacitance circuit based on SRB model. R_a: inter-nodal axoplasm resistance; R_m : nodal membrane resistance; C_m : nodal membrane capacitance; V_i,j : intracellular potential at the j^th node; V_e,j: extracellular potential at the j^th node.

We assume that the axon is in an infinite homogeneous medium (extracellular resistivity ρ_e = 0.3 k Ω·cm). After neglecting the small influence induced by the presence of the axon in the medium, the extracellular potential V_e,j at the j^th node along the axon can be calculated by:

$$V_{e,j}\left(t\right)=\frac{{\rho }_e}{4\pi }\left[\frac{I_{HFB}\left(t\right)+I_{test}\left(t\right)}{\sqrt{{(j\Delta x-x_0)}^2+z_0^2}}\right]$$

where I_HFB(t) and I_test(t) are the HFB electrical current and the uniphasic test pulse respectively that are delivered to the stimulation electrode at location x₀ = 30 mm, z₀ = 1 mm.

The change of the membrane potential V_j at the j^th node is described by [28]:

$$\frac{d{V}_j}{dt}=\frac{1}{c_m}\left[\frac{d}{4{\rho }_{i}L\Delta x}(V_{j-1}-2V_j+V_{j+1}+V_{e,j-1}-2V_{e,j}+V_{e,j+1})-i_{i,j}\right]$$

where V_j = V_i,j–V_e,j–V_rest ; V_i,j is the intracellular potential at the j^th node; V_e,j is the extracellular potential at the j^th node; V_rest is the resting membrane potential; c_m is the membrane capacitance per unit area; ρ_i is the intracellular axoplasm resistivity; i_i,j is the ionic current density at the j^th node described by SRB equations (see Appendix in [26]).

The SRB model was derived from the total nodal current instead of current density. In order to normalize the model, the axon diameter used to develop SRB model needs to be estimated, which was not given in the original SRB model [22]. The duration of the action potential recorded at 25°C is 1.4 ms in SRB model [22]. According to Paintal's experimental data [23], the conduction velocity v is estimated to be 64 m/s in SRB model. Based on v = D×5.7×10⁶ given by Boyd and Kalu [24], the estimated axon external myelin diameter D is 11.23 μm in SRB model. Therefore, the axon diameter d = 0.7D = 7.86 μm was used in this study to convert the parameters in original SRB model to the values per unit area (see Table 1).

Table 1.

The parameters used in the SRB model

Symbol	Description	Value
Vrest (mV)	resting membrane potential	−84
EK (mV)	potassium equilibrium potential	−84
EL (mV)	leakage ion equilibrium potential	−84
gKf (mS/cm2)	fast potassium conductance per unit area	60.75
gKs (mS/cm2)	slow potassium conductance per unit area	121.51
gL (mS/cm2)	leakage conductance per unit area	121.51
cm (μF/cm2)	membrane capacitance per unit area	5.67
PNa (cm/s)	sodium permeability	0.01426
[Na]o (mmole/l)	extracellular sodium concentration	154
[Na]i (mmole/l)	intracellular sodium concentration	35
L (cm)	nodal length	1.0*10−4
F (C/mole)	Faraday constant	96485
R (mJ/K/mole)	gas constant	8314.4
ρe (kΩ•cm)	extracellular resistivity	0.3
ρi (kΩ•cm)	intracellular resistivity	0.11
T (Kelvin)	temperature	310.15

The axonal model was solved by the Runge-Kutta method [25] with a time step of 0.001 ms. The simulation was always performed with the initial condition V_j = 0 mV and the temperature T = 37 °C. The membrane potentials at the two end nodes of the modeled axon were always equal to the membrane potentials of their closest neighbors, which implemented sealed boundary conditions (no longitudinal currents) at the two ends of the modeled axon. During the simulation, a current resolution of 0.2 mA was initially used for the HFB stimulation to identify 3 different intensity ranges for axonal conduction, repetitive firing, and conduction block. Then, the intensity thresholds for the HFB stimulation to induce repetitive firing or conduction block were further determined at a resolution of 0.01 mA. The current resolution for the HFB stimulation to test axonal excitability was varied between 0.1 mA and 1 mA depending on the changing rate of the excitability. The test pulse threshold was determined at a current resolution of 0.1 mA.

III. RESULTS

A. Modulation of Axonal Excitability by HFB Electrical Current

Axonal excitability can be significantly modulated by the HFB electrical current. As the intensity of a 10 kHz HFB current increases from 0 mA to 10 mA, the threshold intensity of the test pulse (0.1 ms pulse width) to excite an axon of diameter 2 μm first decreases gradually from 2.2 mA to 0 mA, and then starts to increase again (see Fig. 2A). Figs. 2B-D show 3 examples of the threshold modulation at 3 different conditions marked by symbols “B”, “C”, and “D” in Fig. 2A. The HFB current and the test pulse are also schematically plotted in Fig. 2B for clarity. The HFB current does not induce an initial action potential as shown in Fig. 2B, but still modulates the axonal excitability (Fig. 2A). But, at a higher intensity (6 mA) as shown in Fig. 2C, the HFB current alone induces repetitive firing at a frequency of approximately 600 Hz without the test pulse (i.e. the test pulse intensity is 0 mA). The HFB current only induces an initial action potential without repetitive firing when the intensity is further increased above 8.3 mA (see Fig. 2D for 9 mA).

Fig. 2.

Test pulse (TP) threshold modulated by high-frequency biphasic (HFB) stimulation at different intensities. A: TP threshold changes with the intensity of HFB stimulation. The axonal activity at the 3 stimulation conditions marked by symbols “B”, “C”, and “D” in A is shown in B, C, and D respectively. B: TP induced an action potential while HFB stimulation did not. HFB/TP=3 mA/1.6 mA. For clarity, the TP and HFB stimulation are also schematically plotted in B. C: The HFB stimulation induced repetitive firing. HFB/TP=6 mA/0 mA. D: TP induced an action potential while HFB stimulation only induced an initial action potential. HFB/TP=9 mA/0.9 mA. The short arrows in B, C, and D mark the electrode locations along the axon. TP width: 0.1 ms; HFB stimulation frequency: 10 kHz; Axon diameter: 2 μm.

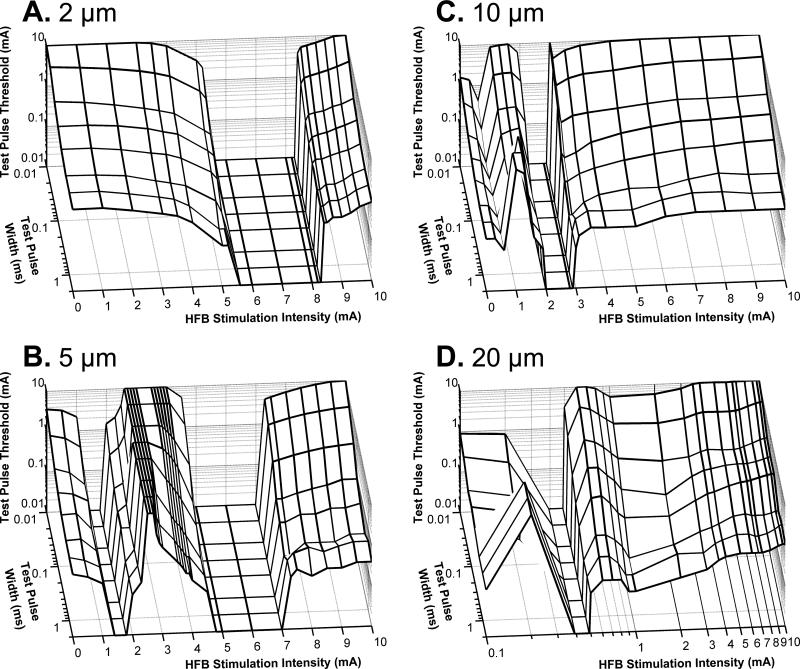
The modulation of axonal excitability by different intensities of HFB current was also investigated using different test pulse widths (0.01-2 ms) and different axon diameters (2-20 μm)(Fig. 3). As the 10 kHz HFB electrical current increases in intensity from 0 mA to 10 mA, there is only a single intensity range where it can induce repetitive firing of a 2 μm axon without applying the test pulse (see Fig. 3A). However, for a 5 μm axon the HFB current can cause repetitive firing in two intensity ranges (see Fig. 3B). The low HFB intensity range for the 5 μm axon is much lower than the range to induce repetitive firing of a 2 μm axon (see Fig. 3A-B). As the axon diameter increases to 10-20 μm, the intensities to induce repetitive firing become a single range again (Figs. 3C-D).

Fig. 3.

Influence of test pulse width (0.01-2 ms) and axon diameter (2 μm, 5 μm, 10 μm, and 20 μm) on the modulation of axonal excitability by HFB current. The test pulse threshold and width are drawn in logarithmic scale. HFB stimulation frequency: 10 kHz. Note: Different from A-C, the HFB stimulation intensity in D is drawn in logarithmic scale for clarity.

B. Reversing Excitation Thresholds for Small and Large Diameter Axons

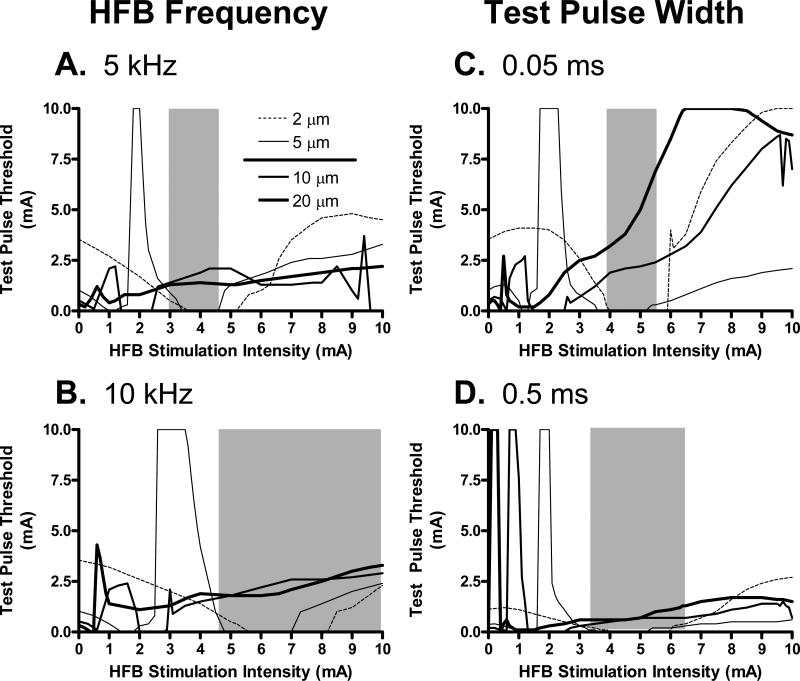
Since the HFB current can differentially modulate the excitability of different diameter axons (see Fig. 3), further studies were conducted to evaluate the conditions that shift the excitation threshold of small axons to a lower value than that of large axons. The effective intensity range of HFB current to invert the axonal thresholds of small and large axons is influenced by the frequency of HFB stimulation (Fig. 4A-B), and by the test pulse width (Fig. 4 C-D). These effective intensity ranges are indicated by the grey areas in Fig. 4A-D. At 5 kHz and 3-4.5 mA (Fig. 4A), HFB current excited small diameter axons (2-5 μm) at lower threshold than the threshold for axons of large diameters (10-20 μm). At longer pulse widths and higher frequencies, the range of HFB stimulus intensities that produces this reversal of test pulse thresholds is generally broader and shifts to higher stimulus intensities (Fig. 4A-D).

Fig. 4.

Selective activation of the small axon group (2-5 μm) without activation of large axon group (10-20 μm) is influenced by HFB stimulation frequency (A and B) and test pulse width (C and D). The legend in A also applies to B, C, and D. Small and large axon groups are separated by a solid line in the legend. The region marked by the grey area in each figure indicates the HFB stimulation intensity range where the test pulse threshold for the small axon group is smaller than the threshold for the large axon group. In A and B, the test pulse width is 0.05 ms. In C and D, the HFB stimulation frequency is 6 kHz.

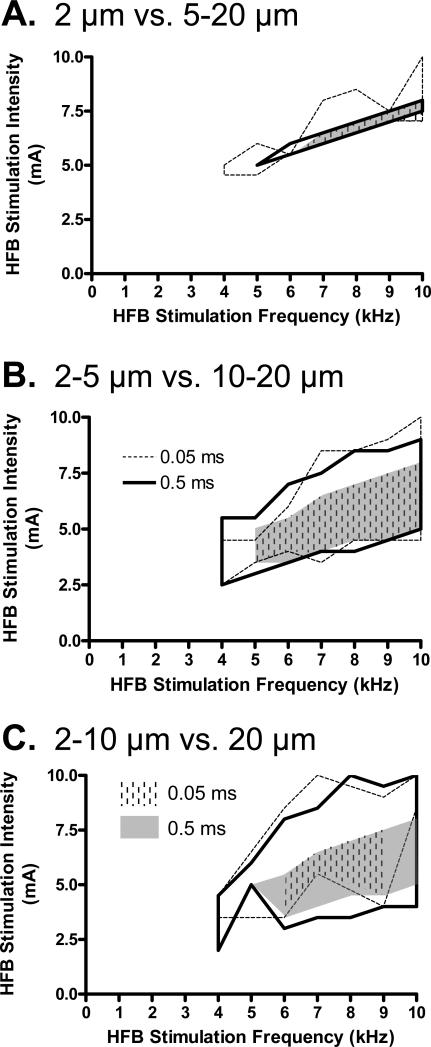
The effective intensity and frequency for the HFB current to reverse the excitation thresholds for 2 groups of axons with different diameters plotted in Fig. 5 for different test pulse widths (0.05 or 0.5 ms). By comparing Figs. 5A-C, it is obvious that the range of modulatory stimulus intensities that selectively activates small axons becomes smaller as the diameters of the small axon group decreases. It is also worth noting that the effective frequency for HFB current to reverse the axonal thresholds is always greater than 4 kHz, and repetitive firing of small axons can occur as indicated in Fig.5 by the grey or dashed areas.

Fig. 5.

HFB stimulation frequencies, intensities, and test pulse widths for selectively activating different groups of smaller axons without activating larger axons: A. 2 μm vs. 5-20 μm; B. 2-5 μm vs. 10-20 μm; C. 2-10 μm vs. 20 μm. The legends in B and C indicate different test pulse widths which apply to all graphs. The stimulation parameters enclosed by thick or dashed lines are suitable for activating the small axons without activating the large axons. The grey or dashed areas indicate the regions where the small axons fire action potentials repetitively.

C. Mechanisms Underlying the Modulation of Axonal Excitability

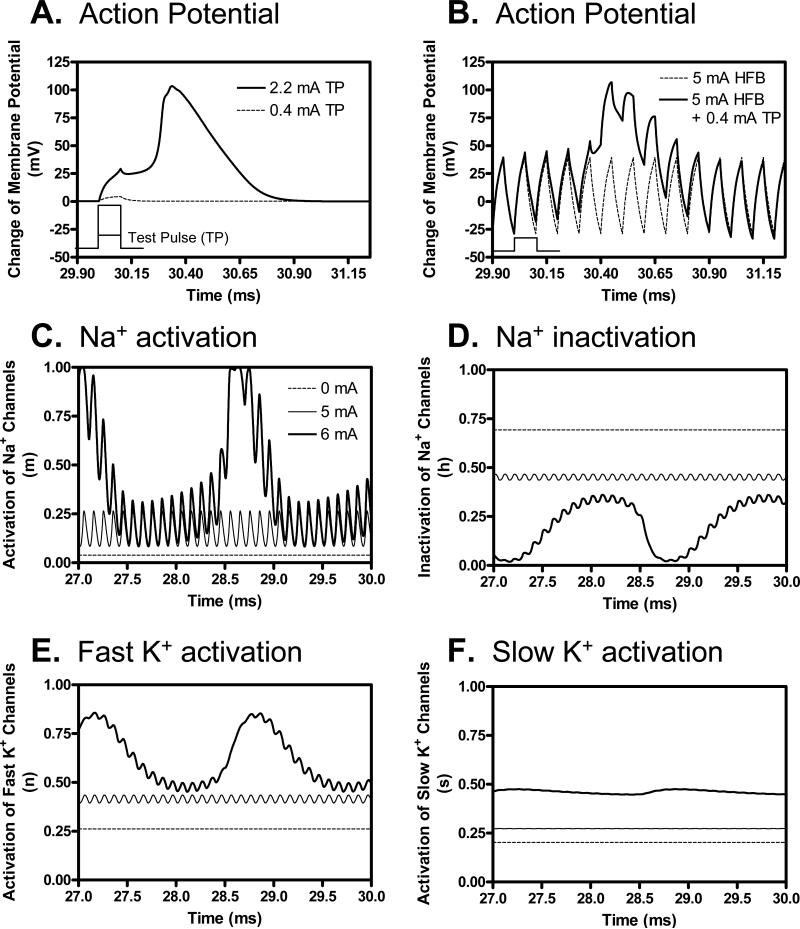
The membrane potentials and ion channel activities at the node under the stimulation electrode at different HFB stimulation intensities (Fig. 6) provide some insights into the mechanism for HFB modulation of axonal threshold. Fig. 6A shows the change of membrane potential induced by the test pulse alone (0.1 ms pulse width) at the threshold intensity (2.2 mA) and a sub-threshold intensity (0.4 mA) without the presence of HFB current. Fig. 6B further shows that the sub-threshold test pulse (0.4 mA) becomes super-threshold and induces an action potential after a modulatory HFB current (10 kHz, 5 mA) is applied for 30 ms. Figs. 6C-F show the ion channel activities at the node under the electrode just before the application of test pulse (27-30 ms). As the intensity of HFB current increases from 0 mA to 5 mA, the activation (m) of sodium channels also increases (Fig. 6C) resulting in an increase of axonal excitability (i.e. a decrease of threshold as shown in Fig. 2A). Although the inactivation (h) of sodium channels (Fig. 6D) and the activation of fast (n) and slow (s) potassium channels (Fig. 6E-F) also increase, their effects on axonal excitability are dominated by sodium channel activation (Fig. 6C). When the intensity of HFB current increases to 6 mA, the activation/inactivation of ion channels fluctuates (Fig. 6C-F) resulting in a repetitive firing of action potentials (Fig. 2C).

Fig. 6.

Mechanism underlying the increase of axon excitability shown in Fig. 2A as the HFB stimulation intensity increases from 0 mA to 6 mA. A 0.4 mA sub-threshold test pulse (A) induced an action potential after 30 ms modulation by a 5 mA, 10 kHz HFB current (B). Test pulse is schematically plotted in A and B to show the timing. The ionic channel activities just before the application of test pulse (27-30 ms) at the node under the electrode are shown in C-F at different intensities of HFB current (0-6 mA). The legend in C also applies to D-F. HFB frequency: 10 kHz; Axon diameter: 2 μm.

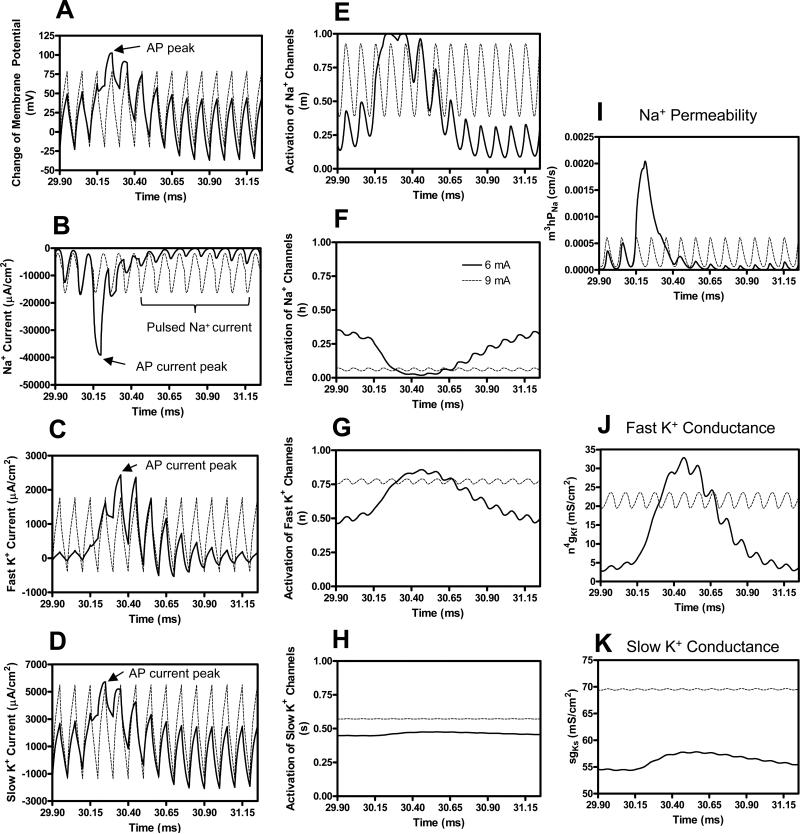
Figure 7 shows the change of membrane potential, ionic currents, and activation/inactivation of ion channels under the stimulation electrode when the HFB current increases from 6 mA to 9 mA. Test pulse is not applied in Fig. 7. At 6 mA the HFB current induces repetitive firing (see Fig. 2C) due to the fluctuation of the ion channels as shown in Fig. 6 (also shown in Fig. 7E-H). Each action potential (Fig. 7A) is accompanied by a large inward sodium current (Fig. 7B) followed by large potassium currents (Fig. 7C-D). However, when the HFB current increases to 9 mA, the activation (m) of sodium channels oscillates at a high level (Fig. 7E) while the inactivation (h) of sodium channels remains at a relatively low level (Fig. 7F), resulting in a pulsed inward sodium current (Fig. 7B). However, this pulsed inward sodium current fails to further depolarize the membrane and induce an action potential. This is due to the fact that the activation of both fast (n) and slow (s) potassium channels becomes constantly high (Fig. 7G-H) resulting in large pulsed outward fast and slow potassium currents (Fig. 7C-D). These large outward potassium currents oppose the inward sodium current, which causes action potential failure at the node under the stimulation electrode leading to the disappearance of repetitive firing. At 9 mA the HFB current can also cause nerve conduction block, which has been reported in detail in our previous study [26].

Fig. 7.

Mechanism underlying the disappearance of the repetitive firing as shown in Fig. 2C-D when the HFB stimulation intensity increases from 6 mA to 9 mA. No test pulse is applied in this figure. Axonal activities at the node under the electrode are shown in A-H. The legend in F indicates the HFB stimulation intensity. HFB stimulation frequency: 10 kHz; Axon diameter: 2 μm. AP – action potential. Note: the AP duration lasts for several cycles of the HFB stimulation.

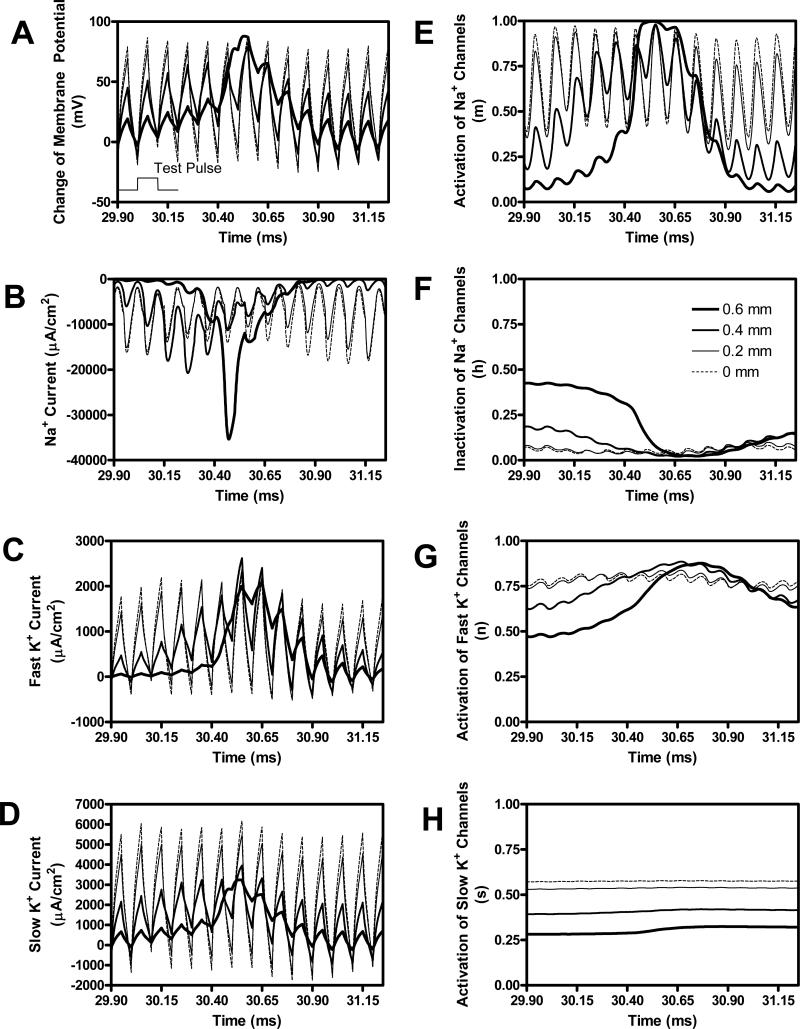
Although 9 mA HFB current can stop the repetitive firing (Fig. 2D and Fig. 7) and cause nerve conduction block, a 0.9 mA test pulse (0.1 ms pulse width) can still excite the axon and induce an action potential propagating away from the stimulation electrode (see Fig. 2D). However, the action potential does not originate from the node under the stimulation electrode (see Fig. 8). The node under the electrode (0 mm as shown in Fig.8) and the node 0.2 mm away from the electrode are still unexcitable. The ion channel activity at the node under the electrode as shown in Fig. 8 is similar to the activity in the absence of the test pulse as shown in Fig. 7. However, an action potential is clearly initiated by the test pulse at the node 0.6 mm away from the stimulation electrode (see Fig. 8A), which is also clearly indicated by a large pulsed inward sodium current followed by the delayed potassium currents. The ion channel activity at the 0.6 mm node is also very similar to the activity at the node under the electrode as shown in Fig. 7 for the 6 mA HFB current. It is less clear whether the action potential originates from the node 0.4 mm away from the electrode (see Fig. 8A), but the ion channel activity seems to indicate that the action potential might start at the 0.4 mm node (see Fig. 8E-G).

Fig. 8.

Site of action potential initiation induced by the test pulse as shown in Fig. 2D is at a nearby node close to the stimulation electrode. The legend in F indicates the distance of the node from the stimulation electrode. The thinnest dashed line (0 mm) corresponds to the node under the electrode (i.e. at 30 mm location). The thickest solid line (0.6 mm) corresponds to the node at the greatest distance from the electrode (i.e. at 29.4 mm location). The test pulse is shown in A to indicate the timing. Test pulse intensity: 0.9 mA; Test pulse width: 0.1 ms; HFB stimulation intensity: 9 mA; HFB stimulation frequency: 10 kHz; Axon diameter: 2 μm.

Figure 9 shows the activity of ion channels at the node 0.6 mm away from the stimulation electrode for 9 mA and 10 mA HFB currents. The activation (m) of sodium channels oscillates at almost same level for 9 mA or 10 mA HFB current (Fig. 9A). However, the 10 mA HFB current induces more inactivation (h) of sodium channels (Fig. 9B) and more activation of both fast (n) and slow (s) potassium channels (Figs. 9C-D) than the 9 mA HFB current, causing the node at the 0.6 mm less excitable. Since the test pulse needs to activate this node in order to induce an action potential as shown in Fig. 8, this explains why the threshold intensity of the test pulse increases when the HFB current increases from 9 mA to 10 mA as shown in Fig. 2A.

Fig. 9.

Mechanism underlying the decrease of axonal excitability shown in Fig. 2A as the HFB stimulation intensity increases from 9 mA to 10 mA. The ionic channel activity at the node 0.6 mm away from the stimulation electrode is shown in A-D. The legend in A indicates HFB stimulation intensity. HFB stimulation frequency: 10 kHz; Axon diameter: 2 μm.

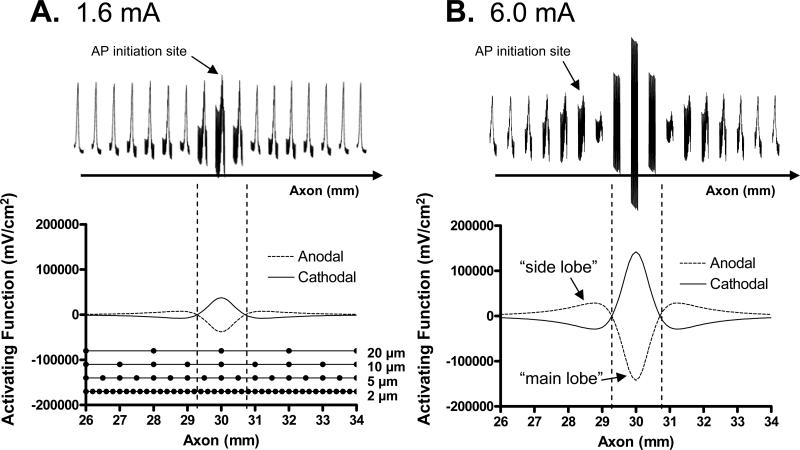
Figures 6-9 reveal the mechanisms underlying the HFB modulation of axonal excitability as shown in Fig. 2A and Fig. 3A for 2 μm diameter axon. There is only a single intensity range for producing repetitive firing in a 2 μm diameter axon (Fig. 3A). However, in a 5 μm diameter axon there are two intensity ranges for HFB current to induce repetitive firing (Fig. 3B). A possible explanation for this response is provided in Fig. 10 using the “side lobe” effect of the activating function (Δ²V_e,j/Δx²) [27][28]. In Fig. 10 the 1.6 mA intensity represents the low intensity range in Fig. 3B, while 6.0 mA represents the high intensity range in Fig. 3B. At a low HFB current intensity (1.6 mA), the repetitive firing of a 5 μm diameter axon is initiated at the node under the electrode at the 30 mm location (Fig. 10A). But at a high HFB current intensity (6.0 mA) the repetitive firing is initiated at the node 1.5 mm away from the electrode (i.e., at the 28.5 mm location, see Fig. 10B). This is due to the fact that at 6 mA the range of membrane potential oscillation at the 28.5 mm location was approximately equivalent to that at the 30 mm location when stimulation intensity was 1.6 mA. The activating functions during the anodal or cathodal phase of the HFB currnt are both plotted in Fig. 10 for current intensities of 1.6 mA and 6.0 mA respectively. A positive value of the activating function depolarizes the axonal membrane, whereas a negtive value hyperpolarizes the membrane [27][28]. It can be seen that the range between the anodal and cathodal activating functions at the 28.5 mm location (i.e. the “side lobe” region) when current intensity is 6.0 mA (Fig. 10B) is about same as the range at the 30 mm location (i.e. the “main lobe” region) when stimulation intensity is 1.6 mA (Fig. 10A). This causes the node at the 28.5 mm location to be alternatively depolarized and hyperpolarized by the 6.0 mA HFB current to the same extent as the node at the 30 mm location during 1.6 mA HFB stimulation. Therefore, the low intensity range for HFB current to induce repetitive firing of a 5 μm diameter axon (Fig. 3B) is due to the modulation of excitability of nodes under the electrode within the “main lobe” region of the activating function, while the high intensity range is due to the modulation of excitability of nodes adjacent to the electrode in the “side lobe” region of the activating function. It is worth noting that the activating function is symmetric for a monopolar electrode resulting in the “side lobe” effect occurring on both sides of the electrode (i.e. at the 28.5 mm and the 31.5 mm locations, see Fig. 10B).

Fig. 10.

Excitation locations and activating functions at HFB stimulation intensities of 1.6 mA (A) and 6.0 mA (B) for a 5 μm axon. The upper traces show the action potentials at 8 nodes on each side of the electrode. The upper trace shares the same horizontal axis as the lower trace showing the activating functions. The activating functions for both anodal and cathodal pulses are shown. The stimulation electrode is located at 30 mm. A: The action potential is generated at the node under the stimulation electrode. B: The action potential is generated at the node 1.5 mm away from the stimulation electrode in the “side lobe” region (at 28.5 mm location). HFB stimulation frequency: 10 kHz; The node locations for 2 μm, 5 μm, 10 μm, and 20 μm axons are also drawn as black dots in A. AP – action potential.

The high intensity range for HFB current to induce repetitive firing is shifted to a lower intensity for the large axons of 10-20 μm diameters (Figs. 3C-D) due to the lower excitation thresholds for larger axons. This causes the “side lobe” effect to occur before the node under the electrode could generate repetitive firing, resulting in the repetitive firing only occurring in a single intensity range (see Figs. 3C-D).

IV. DISCUSSION

This simulation study employing a mammalian myelinated axonal model based on SRB equations investigated the modulation of axonal excitability by high frequency (1-10 kHz) biphasic (HFB) electrical currents. The results indicate that the effects of HFB current can be facilitatory or inhibitory and are frequency and intensity dependent. As the intensity of HFB current increases, the excitability of a small axon (2 μm) first increases and then decreases (Fig. 3A). The increase of excitability is determined by the node under the electrode (Fig. 6), but the decrease is occurring at the nodes adjacent to the electrode (Fig. 8). The increase of axonal excitability is due to a higher level of sodium channel activation (m) (Fig. 6), whereas activation of fast (n) and slow (s) potassium channels play an important role in the decrease of axonal excitability (Fig. 9). For larger axons (5-20 μm), this modulation is bimodal occurring at low as well as high intensities (Figs. 3B-D). At low intensity range, the modulation of axonal excitability occurs at the nodes under the stimulation electrode. But, at high intensity range it occurs at the nodes in the “side lobe” region of the activating function (Fig. 10).

Only a monopolar point electrode is investigated in this study in order to elucidate the mechanisms underlying the modulation of axonal excitability in a relatively simple way. Different geometries of the stimulation electrode (monopolar, bipolar, or tripolar) will produce a significantly different shape of the activating function [27][28]. This may result in a “side lobe” effect that is very different from what is shown in Fig. 10. However, as long as the extracullular potential field generated by the bipolar/tripolar electrode is not symmetric, the “side lobe” effect will exist. Therefore, the geometry of stimulation electrode needs to be considered when applying HFB current to modulate axonal excitability. The results presented in this study for a monopolar electrode could be used as the basic elements to analyze bipolar/tripolar electrode since multi-polar electrode configuration could be considered as a combination of multiple monopolar electrodes.

The difference in the modulation of axonal excitability as shown in Fig.3 A-D is mainly due to the scaling effect of different axon diameters (i.e. a larger axon has a lower excitation threshold). Therefore, for a larger axon the “valley” in Fig.3 moves to a lower stimulation intensity range. Similar scaling effect also occurs as the electrode distance increases or decreases. Changing the electrode distance could change the excitation threshold [16] resulting in a shift of the HFB intensity ranges shown in Fig. 3. Fig. 10A shows the number of axonal nodes within the “main lobe” region of the activating function for axons of different diameters (2-20 μm) when electrode distance is 1 mm. Increasing electrode distance will not only increase the excitation threshold but also lead to more axonal nodes in the “main lobe” region causing the intensity ranges for inducing repetitive firing of the large axons (10-20 μm) to become similar to those of smaller axon (5 μm) at a closer electrode distance. Therefore, if electrode distance is increased, there would be a bimodal intensity range as shown for a 5 μm axon in Fig. 3B that would induce repetitive firing in 10-20 μm axons. Meanwhile, if the stimulation electrode is placed closer to a 2 μm axon, there would also be a bimodal intensity range to cause repetitive firing instead of a single range of intensities as illustrated in Fig. 3A. In addition to the electrode distance, other parameters including nodal position relative to the electrode, and temperature, etc. could also influence the axonal excitation threshold and the modulation of axonal excitability. These influential parameters were not investigated in this study.

Previous studies have shown that the HFB electrical current can reversibly block nerve conduction [1]-[11]. Our recent simulation study [26] revealed that the likely blocking mechanism involves the constant activation of both fast and slow potassium channels. This study further shows that the activation of potassium channels also causes the disappearance of repetitive firing (see Fig. 7) and the increase of the excitation threshold (Fig. 9). At the intensity ranges where the excitation thresholds increase as shown in Fig. 3, the HFB current can also induce nerve conduction block [26]. Furthermore, this study reveals that the blocking locations might be different for axons of different diameters. For a small axon of 2 μm diameter, the blocking location is under the electrode within the “main lobe” region of the activating function (Fig. 3A and Fig. 7). For a large axon (10-20 μm diameters), the blocking location is further away from the electrode at the “side lobe” region (Figs. 3C-D and Fig. 10). However, for a 5 μm diameter axon, the blocking location will change from the location under the electrode to a location in the “side lobe” region as the intensity of HFB current increases (Fig. 3B and Fig. 10). These blocking locations will also change as the electrode distance increases or decreases as discussed above in regard to repetitive firing.

The results shown in Fig. 5 indicate that the modulation of axonal excitability by HFB current might be used to selectively activate the small nerve fibers in a nerve trunk without activating the large nerve fibers. Animal experiments are still needed to prove the effectiveness of this putative selective stimulation method. It might be difficult to identify the parameters of HFB modulatory current that would allow the test pulse to selectively activate only the smallest axons, for example, the 2 μm axon as shown in Fig. 5A. However, if this method is successful it could be very useful in the applications of neuroprosthetic devices. It is worth noting that this selective stimulation method fails at HFB frequencies below 4 kHz (Fig. 5). Since this method will only be effective with certain stimulation parameters to selectively activate certain groups of nerve fibers (see Fig. 5), it will be necessary to determine the effective stimulation parameters in different applications to accommodate the different composition of axons in different types of nerves. It is also worth noting that the small axons, which fire repetitively in the absence of a test pulse, might limit the clinical application of the selective stimulation/block method to the situations where axonal firing rate is not critical, for example, in urological applications to control bladder and urethral sphincter [1][2].

It is worth noting that this study used a McNeal type axonal model that did not incorporate a detailed representation of the internodal region. However, this study and previous studies using McNeal type models have sucessfully simulated both axonal excitation [18,27,28] and conduction block phenomena [14,15,17,26] observed in animal studies [1]-[11]. Our previous studies of axonal conduction block [14,15,17,26] using McNeal type models also produced the results similar to the study [16] using MRG model that incorporated a detailed representation of the internodal region, indicating that the internodal region might not be involved in the possible mechanisms underlying the nerve conduction block induced by high-frequency biphasic electrical current. However, the study using MRG model [16] indicated that the nerve conduction block might be due to Na+ inactivation caused by depolarization, which is different from the K+ activation mechanism revealed in our studies using McNeal type models [14,15,17,26]. The axonal model in this paper produced a relatively slow conduction velocity, i.e. about 24 m/s for an axon of diameter 7.86 μm instead of 64 m/s. Reducing the membrane capacity to 2 μF/cm² [16][27][28] could produce a more accurate conduction velocity. However, we decided to use the membrane capacity estimated from human axon data (see table 1) [22]. The inaccuracy of conduction velocity should not significantly influence the conclusions in this paper.

Methods to reversibly block nerve conduction or to selectively activate small nerve fibers in a compound nerve trunk will find many applications both in clinical treatments such as neuroprostheses and in basic neuroscience studies. Understanding the biophysics and mechanisms underlying the modulation of axonal excitability by HFB electrical current could promote these applications and possibly develop new stimulation waveforms using less current to block or selectively activate nerves. Simulation studies using more complex axon models [30][31] that incorporate more realistic extracellular space, glial buffering, and ion pumps may further reveal the mechanisms by which alternation in potassium channels leads to a modulation of axonal excitability by HFB electrical current. Although previous simulation studies [4][7][12]-[17][26] showed that the specific firing pattern of an axon responding to HFB electrical stimulation might vary depending on the different nodal membrane models used, the nerve conduction block phenomenon could be successfully simulated as long as the potassium channel was included in the models [7][15]. Simulation analysis using computer models provides a useful tool to reveal the possible mechanisms and may help to design animal experiments to further test the new stimulation methods.