Abstract
The function of many proteins involves equilibria between conformational substates, and to elucidate mechanisms of function it is essential to have experimental tools to detect the presence of conformational substates and to determine the time scale of exchange between them. Site-directed spin labeling (SDSL) has the potential to serve this purpose. In proteins containing a nitroxide side chain (R1), multicomponent electron paramagnetic resonance (EPR) spectra can arise either from equilibria involving different conformational substates or rotamers of R1. To employ SDSL to uniquely identify conformational equilibria, it is thus essential to distinguish between these origins of multicomponent spectra. Here we show that this is possible based on the time scale for exchange of the nitroxide between distinct environments that give rise to multicomponent EPR spectra; rotamer exchange for R1 lies in the ≈0.1–1 μs range, while conformational exchange is at least an order of magnitude slower. The time scales of exchange events are determined by saturation recovery EPR, and in favorable cases, the exchange rate constants between substates with lifetimes of approximately 1–70 μs can be estimated by the approach.
1 Introduction
By the early 1970s substantial experimental evidence had accumulated showing proteins as dynamic structures in solution [1–4], and Cooper [5] had pointed out that thermodynamic fluctuations are an inherent property of systems with dimensions on the order of globular proteins. In this same period, Frauenfelder and co-workers [6] proposed the existence of multiple conformational states in equilibrium to account for the dynamics of ligand binding to myoglobin. Extensive studies of myoglobin reaction kinetics ultimately led to the idea of a hierarchy of protein dynamics [7] (Fig. 1), in which a particular functional protein state is made up of a number of conformational substates (or “taxonomic” substates in the nomenclature of Frauenfelder [6]). At this level in the energetic hierarchy, the number of conformational substates is generally few and their microsecond–millisecond lifetimes are long enough to be described in molecular detail. Within each conformational substate are a multitude of short-lived (ps–ns) statistical substates, each corresponding to the same global conformation but having different torsional states of bonds in the backbone and side chains. A transition between any of the various substates is referred to as “exchange”; conformational exchange gives rise to low-frequency (kHz–MHz) “breathing” modes of proteins, while exchange between statistical substates yields low-amplitude, high-frequency (GHz–THz) fluctuations of the backbone. This general view of protein dynamics has been strongly supported by the elegant methods of modern solution nuclear magnetic resonance (NMR) [8–10].
Fig. 1.
Hierarchy of protein dynamics. A protein in a given state resides in a global free energy minimum in multidimensional conformational space, here represented by a single conformational coordinate (top panel). Within the global conformation of a given state, there exist taxonomic substates in equilibrium, with exchange lifetimes on the μs–ms time scale (center panel). Within each taxonomic substate, there exist statistical substates of very short lifetimes, on the ps–ns time scale (bottom panel). Transitions between taxonomic substates correspond to conformational exchange, while transitions between statistical substates correspond to backbone fluctuations about the average structure of the substate
There is little doubt now that the flexibility of proteins on the μs–ms time scale, in many cases, is related to function. An example is provided by the exchange between the open and closed conformational substates of molecular gates in protein–ligand systems [11] that coordinate ligand binding and dissociation reactions. In other cases, conformational substates may correspond to specific intermediates exhibited during enzyme catalysis [12, 13], generate the diversity of ligand recognition in antibodies [14, 15], or result in promiscuity in protein–protein recognition in signal transduction [16, 17]. Of particular interest is a recent NMR study that showed the conformational substates explored by ubiquitin in solution to constitute the complete manifold of substates involved in promiscuous binding interactions [18].
Flexibility on the ps-ns time scale, due to transitions between statistical substates, plays a role in protein–ligand and protein–protein interactions [19–21], and provides for flexible regions that enable the larger scale conformational exchange events [22]. A remarkable recent discovery is that a substantial number of proteins exist in a completely unstructured state (“intrinsically disordered proteins”) [23, 24], characterized by high backbone flexibility; such proteins adopt a particular conformation only upon binding to a structured partner [25]. The intrinsically disordered nature allows for rapid search-and-bind kinetics as well as the potential for recognition of multiple partners [26].
To explore molecular mechanisms of protein function, it is apparent that experimental techniques capable of monitoring dynamic protein modes over a wide range of time scales are required. NMR has led the way in solution-phase studies of relatively small proteins, but equivalent measurements on larger soluble proteins, membrane-bound proteins, and transient complexes remain challenging, and so new methodologies would be welcome to both extend and complement NMR.
Site-directed spin labeling (SDSL) has the potential to provide information on protein motions taking place on the above time scales without limitations regarding the size or complexity of the system. Moreover, picomole quantities of soluble or membrane proteins can be investigated under physiological conditions in a native-like environment. In SDSL, a nitroxide side chain is introduced in a site-specific manner; the most widely used is that designated R1, although others have been developed and were also employed in the present study (Fig. 2) [27–29]. Motions of the R1 nitroxide group on the ps–ns time scale result in magnetic relaxation that determines the transverse relaxation time (T2) and hence the electron paramagnetic resonance (EPR) spectral line shape. Backbone fluctuations that occur on the nanosecond time scale can thus directly affect the EPR spectrum, and SDSL has been shown to provide a measure of fast backbone dynamics [30, 31]. This capability should prove invaluable in locating disordered domains within proteins, identifying intrinsically disordered proteins and monitoring their interactions with binding partners [32].
Fig. 2.
Spin labeling of a cysteine side-chain in a protein. A cysteine residue can be modified by the methanthiosulfonate reagent [(1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl) methanethiosulfonate] HO-225 or its variants HO-1943, HO-2101, HO-1944, reagent yielding the R1 (a), R1b (b), R1f (c), or RX (d) side-chains, respectively. In the case of the RX side-chain, two cysteine sites in close proximity are cross-linked by this reagent
Although fast backbone motions are directly revealed in the EPR line shape, detection of conformational exchange on the μs–ms time scale requires a different approach, because such motions are too slow to produce relaxation effects that reveal themselves in the spectra. If R1 is in a region where it undergoes slow conformational exchange between chemically unique environments (Fig. 3a), the EPR spectrum is simply a weighted sum of the spectra corresponding to each substate. Such multicomponent spectra are referred to as “complex”. Complex spectra can also be the result of the R1 side chain existing in multiple rotameric states, with unique environments for each state (Fig. 3b), as established by X-ray crystallography, mutagenic and EPR studies [33–35]. Therefore, in using SDSL to identify conformational exchange processes, it is necessary to be able to distinguish with certainty protein conformational equilibria from R1 rotameric equilibria as the origin of complex spectra. In this report, we show that the exchange rate of the nitroxide between the environments identified in a complex spectrum provides the required means of discrimination between rotameric and conformational equilibria.
Fig. 3.
Structural origin of complex spectra of R1. a Hypothetical example of conformational exchange between two states (“A” and “B”) related to each other by the outward rotation of a domain. In “B” the nitroxide is buried and has little motion relative to protein, giving rise to a characteristic broad line shape (magenta trace). When the domain rotates out, motional constraints on the nitroxide are relieved, giving rise to a mobile state, “A”, with a relatively sharp line shape (cyan trace). In an equilibrium mixture, with slow exchange between states, the spectrum is a sum of the two components in proportion to their population (green trace). b Models of two R1 rotamers, in which the nitroxide makes immobilizing contacts with the protein in one configuration, while the nitroxide retains high mobility in the other. This situation will also give rise to a complex spectrum similar to that shown due to the simultaneous presence of both rotamers. Rotamer model is based on 115R1 in T4 Lysozyme, Protein Data Bank: 2OU9
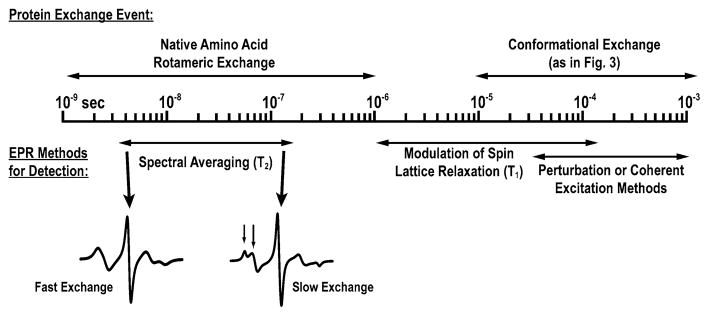
Figure 4 shows some experimental strategies in X-band EPR for determining exchange rates of nitroxides between different environments reflected by a complex spectrum, together with the time scale for rotamer exchange in native side chains and for conformational exchange in proteins, both as determined from NMR [9]. For exchange on the 1–100 ns time scale, spectral components are averaged to various degrees, as illustrated in Fig. 4, and the exchange rate can be extracted from simulations (the program NLSL.SRLS.EXCH for simulating exchange effects on continuous-wave (CW) spectra is available from the ACERT Center at Cornell University, http://www.acert.cornell.edu/index_files/acert_ftp_links.php). Exchange on the μs–ms time scale, corresponding to protein conformational exchange, is too slow to influence line shapes. However, exchange on the 1–100 μs time scale, relevant to fast conformational exchange events in proteins, provides a mechanism for modulating the nitroxide spin–lattice relaxation rate, W = (2T1)−1, where T1 is the spin–lattice relaxation time. Thus, the measurement of W for R1 can, in principle, provide a means of measuring protein conformational exchange kinetics. Exchange events occurring on a slower time scale (long μs to ms and beyond) can be measured in real time with perturbation methods employing temperature or pressure jumps, or coherent excitation methods [36–38].
Fig. 4.
Time scale for EPR exchange spectroscopy and some exchange events in proteins. Together, various EPR detection methods span a wide time range, encompassing part or all of the events of interest in proteins. For short lifetimes (on the T2 time scale), exchange leads to spectral averaging, illustrated by the merging of resolved peaks in the CW EPR spectrum (arrows, lower right spectrum). Rotamer lifetimes for some native side chains fall in this time domain [74]. Pulsed saturation recovery and relaxation spectroscopy (T- or P-jump) cover the range of lifetimes expected for protein conformational exchange inferred from NMR [9]
Spin–lattice relaxation times at physiological temperatures are conveniently measured by the pulsed technique saturation recovery (SR) EPR, developed by Hyde and co-workers [39, 40]. Inversion recovery methods employing spin echo detection are not generally applicable due to the very short T2 relaxation rates of nitroxides in proteins near room temperature (ca. 60 ns) [41]. In SR-EPR, an intense saturation pulse of microwave radiation is delivered at a frequency corresponding to the central resonance line of the nitroxide (mI = 0 of 14N), and the return of spectral intensity is monitored with a weak CW observing microwave field at the same frequency. Within the context of a two-component system with two relaxation rates, the relaxation to equilibrium is in general bi-exponential, where the relaxation rate constants are functions of the intrinsic T1 values and exchange rates. Long-pulse SR-EPR has been previously employed to measure exchange rates of a lipid spin label between two environments in biological membranes [42], and exchange rates between bound and unbound states of a protein [43]. Here we present a new application of the general method to distinguish rotamer from conformational exchange in proteins and, in ideal cases, estimate exchange rate constants for conformational exchange.
2 Theory and Experimental Design
2.1 Determination of Exchange Rate Constants by Saturation Recovery
For nitroxides in proteins, the rates of spectral diffusion due to nitrogen nuclear relaxation and rotational diffusion are much greater than electron relaxation rates, and for long-pulse SR-EPR, the recovery of a given nitroxide state can be treated assuming a single pair of spin energy levels corresponding to ms = ±½[42, 44–47], simplifying the formulation of the theory. The spin–lattice relaxation rates exhibited in such a system can be derived from the exact solutions of the Bloch–McConnell equations [48, 49] or by solving the rate equations describing the exchanging system [50], both yielding analogous expressions.
The expression for the SR-EPR signal, i(t), of an R1 residue in a protein that explores two distinct environments (with distinct T1s) via conformational or rotameric exchange is derived in Appendix A. The result for the relaxation rates is a special case of that derived by Kawasaki et al. [42], which included Heisenberg exchange, but the expressions in Appendix A include the exponential amplitudes which are determined in full by using initial conditions.
The general result for the saturation recovery signal of a nitroxide in exchange between states α and β is:
| (1) |
The quantities γ, δ, X, Y and Z are defined in terms of the intrinsic relaxation rates of the nitroxide in the two states (Wα = (2T1α)−1 and Wβ = (2T1β)−1), the fractional population of state α (fα), the exchange rate constant (k) and constant quantities ρ, c and Ctot (see Appendix A):
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where kαβ and kβα are the first-order rate constants for the forward and reverse steps, respectively, in the exchange equilibrium.
SR-EPR studies typically focus on the measurement and analysis of the two exponential time constants X + Y ± Z, and ignore the exponential amplitudes γ/Z ± δ, which are also dependent on X, Y, Z and, hence, the exchange rate constant [42, 45–47, 50]. Although the amplitude expressions involve quantities that can also be obtained from the relaxation rates, they are important for estimating the range of exchange rates accessible by the method (see below and Appendix B).
In the slow-exchange limit, where k ≪ |Wα − Wβ|, the relaxation rates approach the individual intrinsic rates of the two states:
In the limit of fast exchange, where k ≫ |Wα − Wβ|,
However, k cannot be experimentally determined from the first of these expressions because the exponential amplitude of the X + Y + Z term goes to zero as k approaches the fast-exchange limit (see Appendix B).
In the intermediate exchange case (k ≈ |Wα − Wβ|), the exponential time constants X + Y + Z and X + Y − Z depend on k, Wα, Wβ and fα [see Eqs. (6)–(8)]. Thus, there are four unknown quantities and only two measured relaxation rates, so the problem is underdetermined. The fractional population of each state can be estimated from spectral simulations [51], reducing the unknown quantities by one, but still more information is needed. A similar problem was encountered in measuring lipid exchange, and the solution, suggested by Kawasaki et al. [42], is to differentially vary Wα and Wβ by the addition of a fast relaxation agent, such as molecular oxygen or nickel (II) ethylenediaminediacetic acid (EDDA). These reagents increase the relaxation rate in proportion to the collision rate of the nitroxide with the reagent, and, hence, to the concentration of a relaxation agent [42, 45, 52, 53]:
| (10) |
where T1α,0 and T1α,RA are the T1s of state α in the absence and presence of the relaxation agent (RA), respectively, and jα,RA is the “accessibility constant” of state α to collision with RA. Similarly for state β:
| (11) |
Quite generally, the accessibilities of the two states α and β to collision with either NiEDDA or oxygen will be different [45], and the addition of either relaxation agent will differentially modulate the intrinsic T1s of the two states. By determining the experimental relaxation times as a function of relaxation agent concentration, Eqs. (1)–(8) can be globally solved for Wα, Wβ, the accessibility constants and k. There are independent experimental checks on the results of this procedure that will be discussed below. For the fast- and slow-exchange limits, exchange rates are linear functions of [RA], whereas a nonlinear dependence identifies intermediate exchange. As shown in detail in Appendix B, the range of exchange lifetimes accessible by this strategy is limited to approximately 1–70 μs. This has traditionally been a difficult range to access with solution NMR techniques, but recent studies have now revealed that important conformational exchange events populate this time domain [18, 54–56].
3 Materials and Methods
3.1 T4L Mutants and Sample Preparation
Preparations of the single cysteine substitution mutants of T4 Lysozyme (T4L), the general method for spin labeling with methanethiosulfonate reagents, and the protein purification have been previously reported [27, 33, 34, 57]. The syntheses of spin labeling reagents HO-225, HO-1943, HO-2101, and HO-1944 (Fig. 2) have been previously reported [27, 28, 58, 59]. The preparation of double cysteine mutant T4L 131C/135C, with which HO-1944 reacts, will be published elsewhere (Fleissner, M.R., Cascio, D., Kalai, T., Hideg, K., Hubbell, W.L.).
All samples were prepared such that the final concentration of spin-labeled protein was between 150 and 500 μM. Each spectrum was recorded in 25% w/w Ficoll 70 to remove the effect of rotational diffusion and to reveal the spectrum corresponding to motion of the nitroxide relative to the protein. Ficoll has no effect on the internal motion of the side chain [60]. Ficoll-containing protein solutions (25% w/w) were prepared by two-fold dilutions of the spin-labeled protein solution with a 50% w/w Ficoll-70 solution in 25 mM 3-(N-morpholino)propanesulfonic acid buffer at pH 6.8. Nickel (II) EDDA (“NiEDDA”) was synthesized according to Oh et al. [61]. Protein-NiEDDA solutions were prepared such that the final concentration of NiEDDA ranged from 0.3 to 1.5 mM. Typically, a series of solutions with final NiEDDA concentrations of 0.3, 0.6, 0.9, 1.2 and 1.5 mM was measured for each T4L Mutant.
3.2 CW and Pulse SR-EPR
In all studies approximately 3 μl of a given sample were loaded into a gas-permeable TPX capillary (methylpentene polymer, inner diameter of 0.6 mm, Molecular Specialties Inc., Milwaukee, WI, USA). Prior to recording spectra, gas and temperature equilibration were allowed to occur for at least 15 min.
All CW-EPR spectra were recorded at X-band on a Bruker E-580 spectrometer fitted with a two-loop one-gap resonator (Medical Advances, Milwaukee, WI, USA) [62] over a field range of 100 G, at 2.0 mW incident power, a modulation frequency of 100 kHz and a modulation amplitude of 1 G. Temperature and atmosphere around the sample during measurement were controlled by the commercial Bruker temperature control unit, which employs nitrogen flow from a liquid nitrogen boiler and heater apparatus. All samples containing NiEDDA were equilibrated with a nitrogen atmosphere to ensure no relaxation effects due to the presence of oxygen.
Most of the SR-EPR spectra reported herein were measured on the Bruker 580 spectrometer fitted with a Stanford Research Instruments amplifier (Part #SR445A) in place of the video amplifier originally supplied with the spectrometer. Data acquisition was under the control of Bruker-supplied software, and selection of parameters for the long-pulse experiments followed the general guidelines provided by Hyde [63, 64]. The sample container, resonator and temperature control were as described above for CW spectroscopy. The 250 mW, 500 ns pump pulse provided by the electron-electron double resonance (ELDOR) source was set to the maximum absorbance of the mI = 0 hyperfine line of the 14N nitroxide spectrum. The CW observe power was 100 μW at the same frequency as the pump pulse. The defense pulse length was 280 ns. Each SR curve was acquired with 2048 points at 50 MHz, with an analog bandwidth of 20 MHz. Typically 65536 accumulations were acquired on- and off-resonance using a 1 Hz field step of −10 G upfield. The total number of accumulations was 2.10 million over the course of approximately 10 min; each measurement was independently repeated 3–5 times. Some saturation recovery measurements were made on the saturation recovery spectrometer at the National Biomedical EPR Center in Milwaukee, WI, with the following instrument settings: pulse length = 300 ns, pulse power = 140 mW, CW observe power = 31.5 μW, points per spectrum = 2048 at 50 MHz with an analog bandwidth of 25 MHz. Use of molecular oxygen as a relaxation agent (performed in Milwaukee) required equilibration of the samples with a mixture of dry air and the compressed nitrogen gas used for temperature control, adjusted using gas-flow gauges [53]. For samples that were compared on the Bruker 580 and Milwaukee instruments, there was excellent agreement in the measured T1s (less than 5% variation).
3.3 CW-Spectral Simulations, SR Curve Fitting, and the Determination of Exchange Rate Constant Using T1 Versus Relaxation Agent Dependence
CW spectra were fit using the microscopic order-macroscopic disorder (MOMD) model of Freed and co-workers as implemented in the nonlinear least-squares stochastic Liouville (NLSL) program [51]. Starting values for the elements of the A and g magnetic tensors were Axx = 6 G, Ayy = 6 G, Azz = 37 G, gxx = 2.0078, gyy = 2.0055, gzz = 2.0023, and the fitting procedure is described in detail elsewhere [57].
For experimental saturation recovery data, 10–60 data points (out of 2048) were trimmed from the beginning of the relaxation curves to remove remnants of the instrumental defense pulse. The data were then fit with a least-squares criterion to the equation
with Aα, Aβ, Wα, Wβ and i0 as parameters using GraphPad Prism v5.02 data analysis software for Windows (GraphPad Software, San Diego California USA, www.graphpad.com). For each sample, 3–5 data sets were fitted using this method and a weighted average was determined. In all cases, T1 values from each data set deviated no more than 0.5 μs from the average.
For complex spectra with bi-exponential saturation recovery curves, the above analysis was carried out for data collected at different concentrations of exchange reagent ([RA]), either NiEDDA or O2. Simulation of the corresponding CW spectra provided values for the fractional populations fα, fβ = 1 − fα, independent of the exchange reagent concentration. Thus, a series of values was obtained for the parameter set {Wα, Wβ, [RA], fα}, with fα being constant for a given sample. These values provided a corresponding set of equations for X + Y + Z and X + Y − Z (given by Eqs. (6)–(11) above), which were globally fitted in a least-squares sense for the parameters T1α, T1β, jα,RA, jβ,RA and k, again using the GraphPad Prism software. When fits produced a k value less than ca. 0.015 MHz, it was concluded that the system was in the slow-exchange regime. In situations where only one relaxation time was recorded, global fitting to data obtained for a series of RA concentrations provided the accessibility constant jRA for the R1 site.
Independent checks on the validity of T1α, T1β, jα,RA and jβ,RA values obtained by this procedure are available. For example, the intrinsic T1s should be consistent with those expected from the mobility of the two components (Fig. 5d) and the exchange rate, and the accessibility constants should be consistent with those published for R1 at sites of similar topography [45, 52].
Fig. 5.
Dependence of the spin–lattice relaxation time on effective correlation time for R1 in T4L. a Ribbon model of T4L showing the sites (black spheres) where spin-labeled side chains were introduced, one at a time (except for 131RX135, in which two cysteine mutations were introduced for cross-linking by reagent HO-1944, see Fig. 2). b CW EPR spectra (black traces) of the nitroxide side chains at the indicated sites recorded at 298 K in 25% w/w Ficoll 70, which has no effect on the internal motion of the side chain [60]. In addition, the spectra simulated by the MOMD model are shown (dashed traces). In each case, the effective T1 determined for the protein in a nitrogen atmosphere under the same conditions for the CW spectrum is indicated. Below each simulated spectrum are provided the rotational correlation time and order parameter in the format {τR,S}, determined from the simulation. Arrows above the spectrum for 150R1 indicate the resolved hyperfine components A⊥ and A|| due to uniform anisotropic motion. c Representative saturation recovery curve for T4L 131R1 in nitrogen atmosphere at 298 K (black trace) with the exponential least-squares best fit (white trace) and the tenfold-magnified (10×) residual of this fit below. The inset shows the linear dependence of the 131R1 spin–lattice relaxation rate (W) on [O2] (diamonds). The line is a least-squares fit of the data to a straight line. d Plot of the spin–lattice relaxation rate for these sites versus the rotational correlation time of the nitroxide (τR) extracted from the MOMD simulations. Errors in τR are estimated during the MOMD simulation process and reflect the strong correlation between the fitting parameters corresponding to the order and rotational correlation time
4 Results
4.1 Spin–Lattice Relaxation Rates for R1 Residues with a Single Dynamic Mode; Dependence of T1 on Correlation Time
The exchange rate of a nitroxide between two states reflected in a complex spectrum can be estimated by the strategy presented above, provided that the T1s and solvent accessibilities are different in the two states. As illustrated in Fig. 3, complex spectra arise from the presence of two or more states of different mobility. Because the T1s of small nitroxides in solution depend on rotational correlation time (τR) [65–67], the states corresponding to the two CW spectral components of R1 are expected to have different intrinsic T1s.
To examine the dependence of T1 on the rotational correlation time for spin labels in proteins, sites were selected in T4 Lysozyme (T4L) for which the spectra reflect a single dynamic state of the nitroxide, as determined from simulations using the MOMD model (see Sect. 3). In this case, single-exponential recoveries are expected, and the relaxation rates are the intrinsic rates unaffected by exchange events on the μs or slower time scale.
The location of the sites and the corresponding EPR spectra are shown in Fig. 5a and b, respectively; in each case, the spectrum can be fitted to a single dynamic component (dashed traces, Fig. 5b). The features that might be interpreted as multiple dynamic components (in all spectra, save for 48R1) are the parallel and perpendicular orientations of the nitroxide that are resolved in the uniform z-axis anisotropic motion (arrows above spectrum for 150R1, Fig. 5b) [27, 68]. Figure 5c shows a representative saturation recovery curve for T4L 131R1 under a nitrogen atmosphere (black trace), together with the fit to a single-exponent (white trace) and the residual to the fit below. The inset to Fig. 5c shows the linear increase in the single relaxation rate as a function of added molecular oxygen; the slope of this line is the accessibility constant, jO2 for 131R1. The relaxation rate also increases linearly with NiEDDA concentration (data not shown). Similar results are found for R1 at each of the sites in Fig. 5b, i.e., the SR curve is best fitted by a single-exponent, and the relaxation rates are linear in added relaxation reagent, either oxygen or NiEDDA. The relationship between the intrinsic relaxation rates of R1 at these sites (W = (2T1) −1) and the rotational correlation times (τR), as estimated from spectral simulations, is shown in Fig. 5d. The relaxation rate increases by a factor of 3–4 from the most immobilized state of R1 (133R1) to the most mobile (48R1). Extrapolation of this plot to longer correlation times is likely not valid, because the apparent linearity holds over a limited range of τR, and the curve flattens at longer τR [66].
Although the dynamic range of intrinsic T1 for R1 in proteins is small, it is sufficient to resolve two states in the usual case, where the nitroxide of one has contact interactions with nearby groups leading to strong nitroxide immobilization, while the other will project into solvent and have a high mobility determined by side chain internal motions (e.g., Fig. 3). This distinction also guarantees that the two states will have different accessibilities with respect to collision with NiEDDA and O2 [45, 52].
4.2 Spin–Lattice Relaxation Rates for R1 with Two Dynamic Modes; Fast Rotamer Exchange
Figure 6a is a ribbon model of T4L identifying sites, at which the spectra of R1 have two components of different mobility, and Fig. 6b shows the corresponding complex EPR spectra; these spectra cannot be simulated on the assumption of a single component. In each case, relatively mobile (α) and immobile (β) components are identified by spectral intensity in the corresponding shaded regions of Fig. 6b. These spectra illustrate essentially the full range of complex spectra observed for R1 in proteins. X-ray crystallographic and mutagenic studies of spin-labeled T4L mutants 44R1 [33], 115R1 [34] and 119R1 [35] suggest that their complex spectra arise from two rotamers of the R1 side chain. This result is understandable because these sites are in well-ordered domains in T4L, and two-component spectra thus arise exclusively from rotamer equilibria. Similarly, it is tentatively assumed that the two-component spectra for 61R1, 109R1, and 127R1 in T4L also arise from rotamer exchange, although this remains to be proven.
Fig. 6.
Spin–lattice relaxation for cases of R1 with rotamer exchange. a Ribbon model of T4L showing the sites where R1 was introduced (black spheres). b EPR spectra of R1 at the indicated sites. The shaded areas identify regions where spectral intensity corresponds to relatively mobile (α, light gray) and immobilized (β, darker gray) states. Values for the experimentally determined effective spin–lattice relaxation times are provided. c Representative saturation recovery curve for T4L 44R1 in nitrogen atmosphere at 298 K (black trace), with the exponential least-squares best fit to a single component (white trace) and the tenfold-magnified (10×) residual of this fit below. The inset shows the spin–lattice relaxation rate (W) dependence of 44R1 on molecular oxygen concentration (diamonds) against a straight-line least-squares fit of the data
Figure 6c shows a representative saturation recovery curve from 44R1, along with the fit to a single-exponential and its residual (a two-exponential fit gives no improvement). Similar results are seen for R1 at each of the sites shown in Fig. 6a, and the values experimentally determined for the single effective spin–lattice relaxation time, T1eff, are given in Fig. 6b.
The field separation between the resolved spectral features that correspond to the different dynamic modes for R1 in proteins is typically about 5–10 G, and exchange rates in the neighborhood of 109 s−1 would be required for spectral averaging. Since such averaging is not evident, the resolution of two states in the spectral line shape but a single T1 implies that
| (12) |
where ΔW is the difference in the spin–lattice relaxation rates of the two sites, as defined above. This implies that the rotamer exchange rate constants are approximately within the range 109 Hz > k > 106 Hz.
For 44R1, 61R1, 115R1, 119R1, and 127R1, the spectra all have an immobilized component (β) with τR in the range of 10–16 ns (Fig. 6b), corresponding to T1 ≈ 5–8 μs from Fig. 5d. The substantially shorter relaxation times observed for R1 at these sites (ca. 1.5–4 μs) provide added evidence for the exchange process. As stated above, in the fast-exchange limit, the “effective” measured spin–lattice relaxation is,
| (13) |
Using populations and correlation times of the individual components obtained from CW spectral simulation, it is possible to estimate T1eff for comparison with experimental results. As an example, consider the relaxation behavior of 44R1. Simulations of T4L 44R1 give for the mobile component, fα = 0.7, τR = 1.9 ns and for the immobile component, fβ = 1 − fα = 0.3 and τR = 13 ns [33]. From Fig. 5d, the estimated intrinsic T1s are T1α = 2.6 μs and T1β = 6.5 μs, giving a T1eff of 3.2 μs, in reasonable agreement with the measured value of 3.4 μs (Fig. 6c). Other sites, for which this calculation can be carried out, give similar levels of agreement.
In the fast-exchange limit, Weff is predicted to be linear in NiEDDA or O2 concentration, but if the rate of collisions with the paramagnetic relaxation agent becomes sufficiently large for one of the states but not the other, ΔW could increase such that the inequality of the right-hand side of Eq. (12) could become invalid. In this case, the system could transition to intermediate exchange, where two relaxation times appear (see below). The experimental plot for Weff versus [NiEDDA] for 44R1 is linear in NiEDDA (Fig. 6c, inset), indicating that rotameric exchange processes for R1 are, indeed, in the fast-exchange limit.
4.3 Spin–Lattice Relaxation Rates for R1 with Two Dynamic Modes; Slow Conformational Exchange
The above results show that exchange between two rotamer states, at least for the examples investigated, is in the fast limit with respect to T1. The other extreme, the slow-exchange limit,
is the case for many examples of exchange between conformational substates, where NMR methods have estimated millisecond exchange rates [22, 69–71]. For a two-state system in this limit, two relaxation times are observed that correspond to the intrinsic spin–lattice relaxation times for the individual states, and each relaxation rate is linear in the concentration of added paramagnetic reagent.
Many single-point mutants of T4L with dramatically decreased thermal stability have been prepared and characterized [72]. It is likely that the destabilized state of the protein exists as a manifold of fluctuating conformations [73], some of which likely reflect partially unfolded states that should be detectable by SDSL methods. One example is T4L mutant L46A, which is destabilized by nearly 3 kcal/mol relative to the wild-type protein [72]. Residue 46 is located at the buried surface of helix B (Fig. 7a). This short helix has a relatively small buried surface area and it is not surprising that mutations at this site lead to significant destabilization, at least locally in helix B. In an earlier study, Leucine 46 was replaced with the larger R1 side chain, leading to substantial overpacking of the core [33], destabilizing the protein by ≈4 kcal/mol (J.J. McCoy, W.L. Hubbell, unpubl.), similar to that produced by the L46A cavity-creating mutation. The EPR spectrum of 46R1, reproduced in Fig. 7b (black trace), is striking and reveals a highly mobile component in addition to an immobilized state characteristic of a buried site (e.g., 133R1, Fig. 5b). The best fit of the 46R1 spectrum to a two-component model is shown in Fig. 7b (dashed trace); the correlation times for the two components estimated from the fit are 8.4 ns and 1.1 ns for the immobilized and mobile components, respectively.
Fig. 7.
Spin–lattice relaxation for slow conformational exchange. a Ribbon model of T4L showing the location of the buried leucine-46 residue (dark gray CPK spheres) that was mutated to a cysteine for spin labeling. b EPR spectrum of T4L 46R1 (black trace) with a two-component MOMD fit (dashed trace) to the data. Rotational correlation times and order parameters for the individual components determined from the fit are given in the format {τR,S} below the simulated spectrum. c Saturation recovery curve for T4L 46R1 in nitrogen atmosphere at 298 K (black trace), with a double-exponential least-squares fit (white trace) and the tenfold-magnified (10×) residuals to single- and double-exponential fits below. The inset shows the linear spin–lattice relaxation rate (Wα and Wβ) dependence of 46R1 on NiEDDA concentration for the fast and slow SR components (open diamonds and solid squares, respectively, plotted on separate axes). The lines are straight-line fits to the data
The saturation recovery for 46R1 is well fitted with two exponents (Fig. 7c) with individual relaxation times of 4.8 and 2.3 μs, showing that the exchange between the two states is not in the fast-exchange limit. Assuming a slow-exchange limit, estimates for T1 based on Fig. 5d and the rotational correlation times given above are 5.3 and 1.8 μs, respectively, in reasonable agreement with the experimental values. On the basis of this result and the linearity of the individual relaxation times with NiEDDA concentration (inset Fig. 7c), we tentatively conclude that 46R1 is in the slow-exchange limit consistent with exchange between two local conformations of helix B.
4.4 Spin–Lattice Relaxation Rates for R1 with Two Dynamic Modes; Intermediate Microsecond Exchange
The cases presented above illustrate the two extremes expected to be commonly encountered for R1 in exchange, namely, the fast- and slow-exchange limits. Due to the limited range of T1s observed for R1 in proteins, the range for detecting intermediate exchange and numerically evaluating the exchange rates is limited approximately to 0.014–1 MHz, corresponding to lifetimes of 1–70 μs. The hallmark of intermediate exchange is a nonlinearity in the dependence of exchange rates on the concentration of added paramagnetic reagent.
Using the methodology described in the Sect. 2, a few cases have been found, for which R1 is apparently in intermediate exchange when located in the region of proteins known to be in conformational exchange. These cases are still under study, and detailed accounts will be presented elsewhere, but one example will be illustrated with T4L 130R1.
A crystal structure of T4L 130R1 [29] shows the R1 side chain to occupy a single rotamer at a contact site between two helices (Fig. 8a). On the other hand, the EPR spectrum has two well-resolved components (Fig. 8b) and two spin–lattice relaxation rates (Fig. 8c), corresponding to effective T1s of 2.6 and 5.8 μs in the absence of relaxation reagents at 298 K. The dependence of relaxation rates on [NiEDDA] for both components is nonlinear, with concave and convex curvatures for the slow and fast components, respectively (inset, Fig. 8c). The traces are from the fit of the data to Eqs. (1)–(11) with k = 0.036 ± 0.017 MHz, and the straight dashed lines that define the initial slopes are provided to emphasize the curvature. Possible physical origins of the exchange process for 130R1 will be discussed below.
Fig. 8.
Spin–lattice relaxation in the intermediate exchange regime. a Model of 130R1 in T4L based on the crystal structure [29]. b EPR spectrum of T4L 130R1 in 25% w/w Ficoll 70 at 298 K (black trace), along with a two-component MOMD spectral simulation (dashed trace). The spectra of the individual components α and β, determined by the simulation, are also given below with intensities scaled by the relative populations. Rotational correlation times and order parameters determined from the simulation are given below each spectrum as {τR,S}. c A representative saturation recovery curve for T4L 130R1 in a nitrogen atmosphere under the same conditions as for the CW spectrum (black trace), with a double-exponential fit (white trace) and the tenfold-magnified (10×) residuals to single- and double-exponential fits below. The inset shows the dependence of the spin–lattice relaxation rate (Wα and Wβ) on [NiEDDA] for the fast and slow SR components of 130R1 (open diamonds and solid squares, respectively, plotted on separate axes). The lines here are from a fit of Eqs. (1)–(8) with a nonzero average exchange rate, k. Dashed lines on each trace are placed to emphasize the nonlinearity of the fits
5 Discussion and Conclusions
The single most important conclusion of this study is that exchange between R1 rotamers that give rise to complex spectra takes place on a time scale at least an order of magnitude faster than protein conformational exchange events characterized so far. As a result, complex spectra arising from rotamer exchange have a single T1 observed in saturation recovery, while such spectra arising from protein conformational exchange have two or more spin–lattice relaxation times. This qualitative result offers a great simplification in interpreting the EPR of R1 in terms of protein structure and dynamics.
This simple and gratifying picture assumes that all conformational exchange processes in proteins will be slow on the T1 time scale and all rotamer exchange events of R1 will be fast. The first assumption is so far supported by NMR relaxation studies, but there is no precedent for the second. Clearly, more experiments are needed to verify that all R1 rotamer exchange events are in the fast limit. Nevertheless, the cases investigated in this first study include examples of rotamer exchange that likely involve rotations about different bonds in the R1 side chain as well as distinct interactions of the nitroxide with the environment that must be broken or made concomitant with the rotamer exchange; these interactions range from largely polar in the case of 44R1 [33] to hydrophobic in the case of 115R1 [34]. This suggests that exceptions to fast exchange will be unusual, and the linear trend seen in the plot of Weff versus [NiEDDA] for T4L 44R1 agrees with this suggestion (Fig. 6c). It is estimated that the R1 rotamer exchange rate falls in the approximate range of 1–100 MHz. For comparison, the rotamer exchange rates of some methyl-containing native side chains have been found to be on the GHz (or faster) time scale [74, 75]. However, at such high rates spectral averaging would occur in CW EPR, and complex spectra would not be observed for R1 (bottom Fig. 4). It is thus likely that the slower rotamer exchange of R1 compared to that of native methyl-containing side chains is due to unique intraresidue interactions of R1 with the protein backbone, and to the interactions of the nitroxide ring with nearby side chains that give rise to multiple spectral components [33–35, 57].
In principle, it might be possible to determine an exchange rate between rotamers at a reduced temperature, at which it becomes sufficiently slow to move into the intermediate exchange regime. However, saturation recovery curves for all six of the sites shown in Fig. 6 remain mono-exponential down to 270 K, at which point the motion of R1 in both states moves into the slow-motion limit and spectral resolution between states is lost (data not shown). At the other extreme of slow exchange, illustrated by 46R1, raising the temperature to 310 K increases side chain mobility, which causes the two spectral components to merge, and does not drive the system into the intermediate-exchange regime. The limitation in both cases is the loss of spectral resolution between states due to the temperature dependence of the internal motion of R1.
In early studies, using the first saturation recovery instrument, Percival and Hyde [63] showed that nitroxide T1s were dependent on the rotational diffusion rate. On the basis of this result, Robinson et al. [76] and Eaton et al. [77] carried out detailed and systematic studies of the dependence of nitroxide T1s on the rotational diffusion rate. More recently, Sato et al. [66, 67] found that the dependence of T1 on isotropic τR near room temperature for small nitroxides in water-glycerol mixtures could be accounted for by modulation of the electron-nuclear dipolar interaction, assuming a Cole–Davidson spectral density function to describe the frequency distribution of the isotropic motion. On a log–log plot, the W1 versus τR trend is roughly linear in the range 1 ns < τR < 20 ns, which is the typical range of τR encountered for R1 side chains in proteins. Figure 5d shows that a similar plot ((2T1) −1 vs. τR) for R1 in a protein is also roughly linear. However, it should be noted that the data in Fig. 5d was derived from nitroxides undergoing anisotropic motion (except for the most immobilized cases of 131R1f, 131RX135 and 133R1, which are assumed to be purely isotropic).
The dependence of T1 on motion, although relatively weak, is useful in providing an independent check on exchange models used in data analysis. For example, in the case of fast exchange, one can estimate the effective spin–lattice relaxation time from Eq. (13) by using fα and τR values from CW spectral simulation and intrinsic T1 values from the above determined τR and Fig. 5d. Such estimates can be compared with the experimental relaxation rate as a check on the fast exchange model, as shown above for the T4L 44R1 case. In the case of slow exchange, the measured relaxation times should be the intrinsic T1s determined from the estimated τRs and Fig. 5d, while in intermediate exchange, one expects relaxation rates somewhat faster than the estimated intrinsic T1s.
The case of 46R1, for which R1 is in slow exchange between two states, deserves comment. The SR relaxation data clearly require two exponents for a reasonable fit (Fig. 7c), and this guided the choice of a two-component simulation for the EPR spectrum (Fig. 7b). However, the fit is not perfect, as can be seen when comparing the data to the simulation around the low-field line, and could be improved by including a third component that contributes to spectral intensity between the α and β components. However, the dynamic range of the nitroxide T1 is too small to reliably use a three-exponential fit; the T1 of the third component would be quite close to that of the α component.
The 46R1 mutation destabilizes the protein by about 3–4 kcal/mole as measured by thermal unfolding detected with circular dichroism, although the melting may not correspond to a simple two-state transition (J.J. McCoy, W.L. Hubbell, unpubl.). The 46R1 residue is located on the buried surface of the short B helix in the C-terminal domain (Fig. 7a), and substantially overpacks the hydrophobic core of this small domain. Considering that the N-terminal domain is relatively unstable compared to the C-terminal domain [78, 79] and that the substantial destabilization is due to the mutation, it is likely that the mobile component in the EPR spectrum (Fig. 7b) corresponds to a complete unfolding of the B helix, and perhaps the entire N-terminal domain. In this case it would be easy to understand slow exchange between the states of R1 at this site as well as the existence of intermediate states that could give rise to additional components in the EPR spectrum.
As stressed above, the most important result of the current work is to provide a simple criterion for distinguishing rotamer from conformational exchange. However, it is also possible to determine numerical estimates for the exchange rate constant for exchange events that occur on the time scale of 1–70 μs, a time domain of considerable interest in protein science [18, 54–56]. A single example is provided by the case of 130R1 in T4L, for which an exchange rate constant of ≈0.04 MHz, corresponding to a 20 μs average lifetime, was found to account for the relaxation data at 298 K. Nitroxide scanning in helix H, in which the site 130 resides, revealed that this helix has higher flexibility than the neighboring helix G [33]. Moreover, one of the cavities in the wild-type T4L interior is located beneath helix H [72].
The CW spectrum of 130R1 clearly reveals two components, although the crystal structure of the spin-labeled protein shows a single rotamer, at least at cryogenic conditions where the data were collected (100 K). Modeling suggests that the two components could possibly arise from two rotamers about the X4 dihedral (second bond from the ring). In one rotamer, that observed in the crystal, the nitroxide has immobilizing interactions with an adjacent helix, while in the other (modeled) rotamer, the ring projects into solution and would be relatively mobile [29]. However, evidence presented above makes it unlikely that such a simple rotamer exchange process would be slow. A more attractive model is one in which helix H has two (or more) conformations, due to the destabilizing cavity mentioned above, perhaps, together with some degree of destabilization due to the presence of R1 at a helix-helix contact site [28]. One conformation of the helix could be as in the crystal structure, with another related to the first by a simple helix rotation, for example, that would position R1 away from the intrahelical contact site. Further studies are needed to fully understand this exchange and to exclude an unusually slow rotamer exchange, but 130R1 offers here an initial example of an event that lies within the accessible time domain of the saturation recovery method.
In summary, the data and analysis presented above provide the basis of a general and powerful approach for differentiating fast rotameric and slow conformational exchange in proteins and, in some cases, quantifying it. We envision in the future that both CW and SR data will be routinely obtained on the same sample, in the same resonator, on the same spectrometer. This is currently feasible on the commercial Bruker 580 spectrometer using either the Bruker split-ring resonators, or a loop-gap resonator. A set of experiments, in which an R1 side chain is placed on the outside surface of a protein to sample the principal structural elements, would then provide data related to both T1 and T2, which would allow one to map the regions of the protein with fast backbone dynamics [31] as well as those in slow conformational exchange. As a final comment, the EPR time scale is particularly attractive in that neither rotamer nor conformational exchange is sufficiently fast to average the CW line shape, so structural information on the exchanging partners is available via established SDSL principles [30]. On the other hand, the T1 range for nitroxide side chains attached to proteins overlaps an important time domain for protein conformational exchange, enabling direct measurement by saturation recovery techniques, as illustrated here.
Acknowledgments
This work was supported by National Institute of Health grants EY05216, T32 EY07026 and 5P41EB001980, the Jules Stein Professorship endowment, and the Hungarian National Research Fund OTKA T048334. We are particularly grateful to the National Biomedical EPR Center in Milwaukee, WI, for providing the outstanding facility and support staff for several of the SR measurements reported here. We also thank Wojciech Froncisz for discussions on the technique and surrounding theory, and Christian Altenbach and Mark Fleissner for helpful comments on the manuscript. Additionally, we thank Mark Fleissner, Carlos López, and John McCoy for graciously providing some of the spin-labeled T4 Lysozyme mutants reported herein.
Appendix A
Derivation of the Pulse Saturation Recovery Signal Expression
In the following, it is assumed that both nitrogen nuclear relaxation and protein rotational diffusion rates are much faster than electron spin–lattice relaxation rates, and this is generally the case for small spin-labeled proteins in solution (even in the presence of 25% Ficoll), as previously discussed [45]. In this case, the spin-½ nitroxide can be treated as a single set of energy levels [46] in a magnetic field as shown in Fig. 9, which includes the possibility of exchange between two states of the nitroxide within the protein (α and β); the first-order exchange rate constants are kαβ and kβα. In the usual case of dilute protein solutions (≤1 mM), there is negligible Heisenberg exchange, which would otherwise connect energy levels 1 with 4 and 2 with 3.
Fig. 9.
Energy level diagram for an exchanging spin-½ system. For the present purposes, this is a nitroxide radical attached to a protein, where spectral diffusion rates (14N nuclear relaxation and rotational diffusion) are much faster than the spin–lattice relaxation rate [76], and where the saturating pulse is long relative to spectra diffusion events. Under these conditions the nuclear manifold collapses to a single state, leaving only the two conformationally inequivalent states, α and β. The concentrations of proteins are sufficiently dilute that there is no Heisenberg exchange between them
The complex spectra encountered for R1 in proteins typically have 2 resolved components corresponding to states of different mobility, i.e., a “mobile” and “immobile” state. Let state α be the mobile state and state β be the immobile state. As discussed above, states α and β have different spin–lattice relaxation rates (W) characterized by their spin–lattice relaxation times (T1):
Let ni and Ni be the instantaneous and equilibrium populations of the spins in energy level ‘i’, respectively. In the derivation below, Eqs. (14)–(18) follow Yin et al. [46]. The rate equations for the spin populations are:
| (14) |
| (15) |
Let fi be the mole fraction of component ‘i’, where fα + fβ = 1 and fi > 0, and Ctot is the total concentration of spin. The absolute amounts of each state are:
| (16) |
| (17) |
The Boltzmann population ratios of each state are:
From Eqs. (16) and (17), and the above ratios bα and bβ, the population differences of the two states are:
| (18) |
| (19) |
where
Note that at 298 K and 3000 G, c = 6.77 × 10−4. Variation of the field by ± 25 G yields only a 1% change in this value. Thus, it is safe to approximate c ≈ d. The observable SR signals are:
| (20) |
| (21) |
By combining Eqs. (14), (15), (17) and (21) and simultaneously solving the resulting pair of equations, we get:
| (22) |
| (23) |
where
Equations (22) and (23) are equivalent to the relaxation expressions for exchange given elsewhere, if the Heisenberg exchange rate is set to zero [42, 46]. Using initial conditions, the coefficients I1 and I2 can be determined and the pre-exponential terms simplified. Immediately after the saturating pulse is applied (t = 0), from Eqs. (18)–(21) above we get:
| (24) |
| (25) |
where ρα and ρβ are the degrees of saturation of the α and β components, respectively, following the saturating pulse. If ρi = −1, the net magnetization of the ith component has been inverted; if ρi = 0, the system is completely saturated; if ρi = +1, it is unchanged from its Boltzmann equilibrium distribution. These definitions follow Yin et al. [46].
Inputting t = 0 into Eqs. (22) and (23) above and setting them equal to Eqs. (24) and (25), respectively, we get:
| (26) |
| (27) |
Letting
the coefficients I1 and I2 are:
| (28) |
| (29) |
Note that ELDOR spectroscopy could be employed to study a two-state system in exchange. In the ideal case with perfect spectral resolution, one would pump one population and probe the other (e.g., ρα = 0 and ρβ = 1, observe i2). In this case, the two exponents extracted from the data are identical to those that would be taken from an SR experiment. Only the relative amplitudes of the components would change, occasionally in sign (but not always). Thus the ELDOR experiment has little to offer in the measurement of exchange rates in two-component systems. This is in direct contrast to the utility of ELDOR in the measurement of collisional Heisenberg exchange rates.
The experimentally observed SR curve will be the sum of iα and iβ, weighted according to their relative CW amplitudes at the field, where the recovery is observed. Thus, the observed SR signal will be
| (30) |
where ρ1 and ρ2 represent the intensities of each component contributed to the total signal at the field of observation (ρj = 0 corresponds to zero contribution from the jth component to the observed signal, ρj = 1 corresponds to full signal intensity of that component). Combining Eqs. (22), (23), and (28)–(30), with some rearrangement, we arrive at Eqs. (1)–(8) given in the text.
Appendix B
The Use of SR-EPR Amplitudes to Determine Relative Concentration Ratios and the Limits of Exchange Rates That Can Be Measured
The amplitudes of the exponents in the SR signal [Eqs. (1)–(8)] can be used to estimate the practical range of the exchange measurement as described above, and can also be used to determine the component fractions for each state in the absence of exchange. Note that the signal amplitude of each component is not solely dependent on its mole fraction, and thus relative amplitudes do not, in general, give the relative populations of the states in a straightforward manner.
In the following, the average exchange rate constant is defined as
and throughout the text is referred to simply as the exchange rate constant. Note that this definition is different by a factor of two from that in some NMR literature [54, 56]. Only when k = 0, do the amplitudes directly reflect fα.
In a typical long-pulse, sufficiently high power saturation recovery experiment, the following assumptions apply:
The first assumption is valid since the two spectral components completely overlap in the central resonance line, and thus both are fully saturated by the long pulse. The second assumption states that, at our designated field of detection, both components contribute their full spectral amplitude to the observed signal (the zero-crossing of the center first derivative line, mI = 0). ‘cCtot’ is a concentration- and spin-label dependent term, only important when dealing with measurement of absolute signal amplitudes. Normalization of the slow and fast component amplitudes, Aslow and Afast, respectively, removes the dependence on this term, and simplifies analysis using amplitudes:
| (31) |
| (32) |
These normalized amplitudes can be extracted from a two-component typical saturation recovery curve, however, special care must be taken to ensure that the signals from the earliest times after the pulse are not lost due to instrumentation settings (e.g., long defense pulses, etc.) by properly extrapolating the amplitudes to t = 0.
Let
“Q” is the ratio of the exchange rate constant to the difference in the two spin–lattice relaxation rates. Derivation of the SR amplitudes in terms of this quotient allows one to determine the upper limit of exchange rate, while still observing two separate exponential recovery curves, i.e., the range of Q values, which allow one to measure exchange using T1 modulation by the addition of relaxation agents such as NiEDDA or molecular oxygen. Thus,
From the normalized amplitudes, which range from 0 to 1 and sum to unity, two important points can be gleaned:
As Q increases, ANfast goes to zero;
To obtain a fast-component amplitude within two orders of magnitude (1%) of that of the slow component, Q must be less than ca. 5.
Point 1 shows that the limit to measuring two separate exponential recovery curves by the technique described above, as exchange rate increases, is dictated in part by the relative amplitudes: if the average exchange rate constant (k) between two components is sufficiently large relative to the difference in spin–lattice relaxation rates (ΔW), the SR technique will only reveal one exponent due to reduction in amplitude of the faster component. This means that, using the approximate upper boundary for Q given in Point 2 and for a two-state sample with intrinsic T1s of 2 and 20 μs (extrema in spin-labeled proteins), the fastest average exchange rate constant determinable by this technique is ca. 1 MHz (an exchange lifetime of approximately a microsecond). On the other end of the exchange spectrum, using the exponential time constants in Eqs. (1) and (6)–(8), X + Y + Z and X + Y − Z, we estimate that with intrinsic T1s of 4 and 8 μs (typical values in spin-labeled proteins for two similar states), it would be difficult to measure an exchange rate constant slower than ca. 0.014 MHz (an exchange lifetime of ~70 μs).
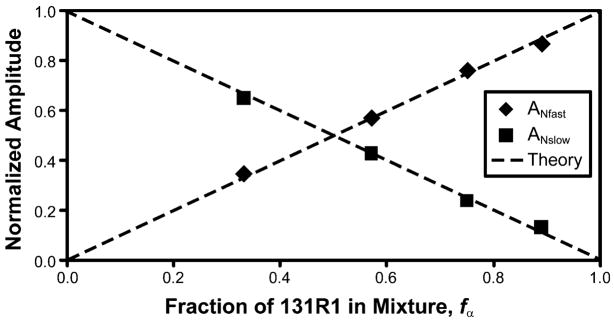
Note that when Q goes to zero, ANslow and ANfast are 1 − fα and fα, respectively. To show that the amplitudes correctly give the relative populations of states in this limit, two samples of different T1s were mixed in varying ratios, effectively creating an artificial spin-labeled protein sample with two states in the zero-exchange regime (k = 0 = Q). The proteins in the mixture were T4L mutants 131R1 and 133R1, each having only one dominant spectral component and a single spin–lattice relaxation time (Fig. 5). The experimental saturation recovery curve was fitted to two exponents, each agreeing well with the T1s of the isolated proteins (Fig. 5b). The fit was extrapolated to t = 0, and the absolute amplitudes of the two components were determined and normalized to the total amplitude change of the saturation recovery signal. Figure 10 shows that the experimental data are in close agreement with predictions for a two-component system in the absence of exchange.
Fig. 10.
Normalized SR signal amplitudes measured for mixtures of T4L 131R1 and 133R1 of varying relative concentrations. The dashed black lines are the expected normalized amplitudes based on ANslow = 1 − fα and ANfast = fα, when k = 0 (from Eqs. (1)–(5))
Footnotes
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Englander SW, Downer NW, Teitelbaum H. Annu Rev Biochem. 1972;41:903–924. doi: 10.1146/annurev.bi.41.070172.004351. [DOI] [PubMed] [Google Scholar]
- 2.Grinvald A, Steinberg IZ. Biochemistry. 1974;13:5170–5178. doi: 10.1021/bi00722a019. [DOI] [PubMed] [Google Scholar]
- 3.Lakowicz JR, Weber G. Biochemistry. 1973;12:4171–4179. doi: 10.1021/bi00745a021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Molday RS, Englander SW, Kallen RG. Biochemistry. 1972;11:150–158. doi: 10.1021/bi00752a003. [DOI] [PubMed] [Google Scholar]
- 5.Cooper A. Proc Natl Acad Sci USA. 1976;73:2740–2741. doi: 10.1073/pnas.73.8.2740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Austin RH, Beeson KW, Eisenstein L, Frauenfelder H, Gunsalus IC. Biochemistry. 1975;14:5355–5373. doi: 10.1021/bi00695a021. [DOI] [PubMed] [Google Scholar]
- 7.Frauenfelder H, Sligar SG, Wolynes PG. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 8.Mittermaier A, Kay LE. Science. 2006;312:224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
- 9.Henzler-Wildman K, Kern D. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 10.Palmer AG, 3rd, Massi F. Chem Rev. 2006;106:1700–1719. doi: 10.1021/cr0404287. [DOI] [PubMed] [Google Scholar]
- 11.Hodsdon ME, Cistola DP. Biochemistry. 1997;36:2278–2290. doi: 10.1021/bi962018l. [DOI] [PubMed] [Google Scholar]
- 12.Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 13.Huang YL, Hsu YH, Han YT, Meng M. J Biol Chem. 2005;280:13153–13162. doi: 10.1074/jbc.M412619200. [DOI] [PubMed] [Google Scholar]
- 14.James LC, Roversi P, Tawfik DS. Science. 2003;299:1362–1367. doi: 10.1126/science.1079731. [DOI] [PubMed] [Google Scholar]
- 15.Keskin O. BMC Struct Biol. 2007;7:31. doi: 10.1186/1472-6807-7-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ma YC, Huang XY. Cell Mol Life Sci. 2002;59:456–462. doi: 10.1007/s00018-002-8438-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Woodside DG, Obergfell A, Talapatra A, Calderwood DA, Shattil SJ, Ginsberg MH. J Biol Chem. 2002;277:39401–39408. doi: 10.1074/jbc.M207657200. [DOI] [PubMed] [Google Scholar]
- 18.Lange OF, Lakomek NA, Fares C, Schroder GF, Walter KFA, Becker S, Meiler J, Grubmuller H, Griesinger C, de Groot BL. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 19.Adams PD, Loh AP, Oswald RE. Biochemistry. 2004;43:9968–9977. doi: 10.1021/bi0490901. [DOI] [PubMed] [Google Scholar]
- 20.Palmer AG. Curr Opin Struct Biol. 1997;7:732–737. doi: 10.1016/s0959-440x(97)80085-1. [DOI] [PubMed] [Google Scholar]
- 21.Duggan BM, Dyson HJ, Wright PE. Eur J Biochem. 1999;265:539–548. doi: 10.1046/j.1432-1327.1999.00781.x. [DOI] [PubMed] [Google Scholar]
- 22.Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. Nature. 2007;450:913–927. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 23.Fink AL. Curr Opin Struct Biol. 2005;15:35–41. doi: 10.1016/j.sbi.2005.01.002. [DOI] [PubMed] [Google Scholar]
- 24.Dunker AK, Silman I, Uversky VN, Sussman JL. Curr Opin Struct Biol. 2008;18:756–764. doi: 10.1016/j.sbi.2008.10.002. [DOI] [PubMed] [Google Scholar]
- 25.Wright PE, Dyson HJ. Curr Opin Struct Biol. 2009;19:31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eliezer D, Palmer AG., 3rd Nature. 2007;447:920–921. doi: 10.1038/447920a. [DOI] [PubMed] [Google Scholar]
- 27.Columbus L, Kalai T, Jeko J, Hideg K, Hubbell WL. Biochemistry. 2001;40:3828–3846. doi: 10.1021/bi002645h. [DOI] [PubMed] [Google Scholar]
- 28.Mchaourab HS, Lietzow MA, Hideg K, Hubbell WL. Biochemistry. 1996;35:7692–7704. doi: 10.1021/bi960482k. [DOI] [PubMed] [Google Scholar]
- 29.Fleissner MR. Ph.D. Thesis. University of California; Los Angeles, USA: 2007. [Google Scholar]
- 30.Columbus L, Hubbell WL. Trends Biochem Sci. 2002;27:288–295. doi: 10.1016/s0968-0004(02)02095-9. [DOI] [PubMed] [Google Scholar]
- 31.Columbus L, Hubbell WL. Biochemistry. 2004;43:7273–7287. doi: 10.1021/bi0497906. [DOI] [PubMed] [Google Scholar]
- 32.Sugase K, Dyson HJ, Wright PE. Nature. 2007;447:U1011–U1021. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- 33.Guo ZF, Cascio D, Hideg K, Hubbell WL. Protein Sci. 2008;17:228–239. doi: 10.1110/ps.073174008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guo ZF, Cascio D, Hideg K, Kalai T, Hubbell WL. Protein Sci. 2007;16:1069–1086. doi: 10.1110/ps.062739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Langen R, Oh KJ, Cascio D, Hubbell WL. Biochemistry. 2000;39:8396–8405. doi: 10.1021/bi000604f. [DOI] [PubMed] [Google Scholar]
- 36.Kitahara R, Royer C, Yamada H, Boyer M, Saldana JL, Akasaka K, Roumestand C. J Mol Biol. 2002;320:609–628. doi: 10.1016/s0022-2836(02)00516-8. [DOI] [PubMed] [Google Scholar]
- 37.Pearson DS, Holtermann G, Ellison P, Cremo C, Geeves MA. Biochem J. 2002;366:643–651. doi: 10.1042/BJ20020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Knierim B, Hofmann KP, Ernst OP, Hubbell WL. Proc Natl Acad Sci USA. 2007;104:20290–20295. doi: 10.1073/pnas.0710393104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Huisjen M, Hyde JS. Rev Sci Instrum. 1974;45:669–675. [Google Scholar]
- 40.Percival PW, Hyde JS. Rev Sci Instrum. 1975;46:1522–1529. [Google Scholar]
- 41.Bonora M, Pornsuwan S, Saxena S. J Phys Chem B. 2004;108:4196–4198. [Google Scholar]
- 42.Kawasaki K, Yin JJ, Subczynski WK, Hyde JS, Kusumi A. Biophys J. 2001;80:738–748. doi: 10.1016/S0006-3495(01)76053-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sarewicz M, Borek A, Daldal F, Froncisz W, Osyczka A. J Biol Chem. 2008;283:24826–24836. doi: 10.1074/jbc.M802174200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hyde JS, Yin JJ, Subczynski WK, Camenisch TG, Ratke JJ, Froncisz W. J Phys Chem B. 2004;108:9524–9529. [Google Scholar]
- 45.Pyka J, Ilnicki J, Altenbach C, Hubbell WL, Froncisz W. Biophys J. 2005;89:2059–2068. doi: 10.1529/biophysj.105.059055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yin JJ, Feix JB, Hyde JS. Biophys J. 1988;53:525–531. doi: 10.1016/S0006-3495(88)83132-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yin JJ, Pasenkiewiczgierula M, Hyde JS. Proc Natl Acad Sci USA. 1987;84:964–968. doi: 10.1073/pnas.84.4.964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hansen DF, Led JJ. J Magn Reson. 2003;163:215–227. doi: 10.1016/s1090-7807(03)00062-4. [DOI] [PubMed] [Google Scholar]
- 49.Leigh JS. J Magn Reson. 1971;4:308. [Google Scholar]
- 50.Yin JJ, Hyde JS. J Magn Reson. 1987;74:82–93. [Google Scholar]
- 51.Budil DE, Lee S, Saxena S, Freed JH. J Magn Reson Ser A. 1996;120:155–189. [Google Scholar]
- 52.Altenbach C, Froncisz W, Hemker R, Mchaourab H, Hubbell WL. Biophys J. 2005;89:2103–2112. doi: 10.1529/biophysj.105.059063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kusumi A, Subczynski WK, Hyde JS. Proc Natl Acad Sci USA. 1982;79:1854–1858. doi: 10.1073/pnas.79.6.1854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Akke M, Liu J, Cavanagh J, Erickson HP, Palmer AG. Nat Struct Biol. 1998;5:55–59. doi: 10.1038/nsb0198-55. [DOI] [PubMed] [Google Scholar]
- 55.Chattopadhyay K, Saffarian S, Elson EL, Frieden C. Proc Natl Acad Sci USA. 2002;99:14171–14176. doi: 10.1073/pnas.172524899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Evenas J, Malmendal A, Akke M. Structure. 2001;9:185–195. doi: 10.1016/s0969-2126(01)00575-5. [DOI] [PubMed] [Google Scholar]
- 57.Fleissner MR, Cascio D, Hubbell WL. Protein Sci. 2009;18:893–908. doi: 10.1002/pro.96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Berliner LJ, Grunwald J, Hankovszky HO, Hideg K. Anal Biochem. 1982;119:450–455. doi: 10.1016/0003-2697(82)90612-1. [DOI] [PubMed] [Google Scholar]
- 59.Kalai T, Balog M, Jeko J, Hideg K. Synthesis. 1999;95:973–980. [Google Scholar]
- 60.Lopez CJ, Fleissner MR, Guo ZF, Kuznetzow AK, Hubbell WL. Protein Sci. 2009;18:1637–1652. doi: 10.1002/pro.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Oh KJ, Altenbach C, Collier RJ, Hubbell WL. Methods Mol Biol. 2000;145:147–169. doi: 10.1385/1-59259-052-7:147. [DOI] [PubMed] [Google Scholar]
- 62.Hubbell WL, Froncisz W, Hyde JS. Rev Sci Instrum. 1987;58:1879–1886. [Google Scholar]
- 63.Percival PW, Hyde JS. J Magn Reson. 1976;23:249–257. [Google Scholar]
- 64.Hyde JS. In: Time Domain Electron Spin Resonance. Kevan L, Schwartz RN, editors. Wiley; New York: 1979. pp. 1–30. [Google Scholar]
- 65.Mailer C, Nielsen RD, Robinson BH. J Phys Chem A. 2005;109:4049–4061. doi: 10.1021/jp044671l. [DOI] [PubMed] [Google Scholar]
- 66.Sato H, Bottle SE, Blinco JP, Micallef AS, Eaton GR, Eaton SS. J Magn Reson. 2008;191:66–77. doi: 10.1016/j.jmr.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sato H, Kathirvelu V, Spagnol G, Rajca S, Rajca A, Eaton SS, Eaton GR. J Phys Chem B. 2008;112:2818–2828. doi: 10.1021/jp073600u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hubbell WL, Mcconnell HM. Proc Natl Acad Sci USA. 1969;64:20–27. doi: 10.1073/pnas.64.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Evenas J, Forsen S, Malmendal A, Akke M. J Mol Biol. 1999;289:603–617. doi: 10.1006/jmbi.1999.2770. [DOI] [PubMed] [Google Scholar]
- 70.Grey MJ, Wang CY, Palmer AG. J Am Chem Soc. 2003;125:14324–14335. doi: 10.1021/ja0367389. [DOI] [PubMed] [Google Scholar]
- 71.Hernandez G, Jenney FE, Adams MWW, LeMaster DM. Proc Natl Acad Sci USA. 2000;97:3166–3170. doi: 10.1073/pnas.040569697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Eriksson AE, Baase WA, Zhang XJ, Heinz DW, Blaber M, Baldwin EP, Matthews BW. Science. 1992;255:178–183. doi: 10.1126/science.1553543. [DOI] [PubMed] [Google Scholar]
- 73.Beeser SA, Goldenberg DP, Oas TG. J Mol Biol. 1997;269:154–164. doi: 10.1006/jmbi.1997.1031. [DOI] [PubMed] [Google Scholar]
- 74.Chou JJ, Case DA, Bax A. J Am Chem Soc. 2003;125:8959–8966. doi: 10.1021/ja029972s. [DOI] [PubMed] [Google Scholar]
- 75.Hu H, Hermans J, Lee AL. J Biomol NMR. 2005;32:151–162. doi: 10.1007/s10858-005-5366-0. [DOI] [PubMed] [Google Scholar]
- 76.Haas DA, Sugano T, Mailer C, Robinson BH. J Phys Chem. 1993;97:2914–2921. [Google Scholar]
- 77.Owenius R, Terry GE, Williams MJ, Eaton SS, Eaton GR. J Phys Chem B. 2004;108:9475–9481. [Google Scholar]
- 78.Cellitti J, Bernstein R, Marqusee S. Protein Sci. 2007;16:852–862. doi: 10.1110/ps.062632807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Llinas M, Marqusee S. Protein Sci. 1998;7:96–104. doi: 10.1002/pro.5560070110. [DOI] [PMC free article] [PubMed] [Google Scholar]