Abstract
We derive simple analytical expressions for the error and computational efficiency of simulated tempering (ST) simulations. The theory applies to the important case of systems whose dynamics at long times is dominated by the slow interconversion between two metastable states. An extension to the multistate case is described. We show that the relative gain in efficiency of ST simulations over regular molecular dynamics (MD) or Monte Carlo (MC) simulations is given by the ratio of their reactive fluxes, i.e., the number of transitions between the two states summed over all ST temperatures divided by the number of transitions at the single temperature of the MD or MC simulation. This relation for the efficiency is derived for the limit in which changes in the ST temperature are fast compared to the two-state transitions. In this limit, ST is most efficient. Our expression for the maximum efficiency gain of ST simulations is essentially identical to the corresponding expression derived by us for replica exchange MD and MC simulations [E. Rosta and G. Hummer, J. Chem. Phys. 131, 165102 (2009)] on a different route. We find quantitative agreement between predicted and observed efficiency gains in a test against ST and replica exchange MC simulations of a two-dimensional Ising model. Based on the efficiency formula, we provide recommendations for the optimal choice of ST simulation parameters, in particular, the range and number of temperatures, and the frequency of attempted temperature changes.
INTRODUCTION
Molecular dynamics (MD) and Monte Carlo (MC) simulations are powerful tools to explore the configuration space of molecular systems. However, for many systems the sampling efficiency is limited by the slow rate of interconversion between different conformational basins on the energy surface. To accelerate the conformational sampling, a variety of extended ensemble schemes have been developed. Among the most widely used ones are simulated tempering (ST),1, 2 replica exchange Monte Carlo (REMC),3, 4 and replica exchange molecular dynamics (REMD).5, 6 Replica exchange is also known as parallel tempering. These extended ensemble methods aim to establish an equilibrium between canonical systems at different temperatures (or, more generally, systems with different Hamiltonians7), an idea that can be traced back to the seminal papers by Bennett,8 and Swendsen and Wang.9 By coupling simulations at a low temperature of interest with simulations at high temperatures where the relaxation is fast, one hopes to transfer the improved sampling efficiency at the higher temperature down to the lower temperature.
In ST simulations,1, 2 the reference thermostat temperature is itself a dynamic variable. At fixed intervals along an otherwise regular MD or MC simulation, attempts are made to change the current reference temperature Ti to a trial temperature Tj picked from a discrete set (e.g., Ti±1 in a series of temperatures T1,T2,…,TN). These attempted temperature changes are accepted with a criterion designed to maintain detailed balance for canonical distributions. In a long run (assuming mixing in the resulting Markov chain), canonical distributions will be obtained at each of the temperatures Ti. In REMD (Refs. 5, 6) and REMC,3, 4 MD and MC simulations of N identical molecular systems are performed in parallel. Each replica is thermostatted at a different temperature Ti to establish corresponding canonical distributions.10 With a given frequency, one attempts to exchange the configurations of replica pairs, i↔j (typically i↔i±1). These replica exchanges are accepted with a probability that conserves the respective canonical distributions. ST and REMD have been proven particularly useful to enhance the sampling of biomolecular systems.5, 6, 11, 12, 13, 14, 15
Key questions in ST, REMD, REMC, or other extended ensemble simulations are as follows: (1) How large is the possible gain in computational efficiency, (2) for which simulation parameters can this maximum gain be realized, and (3) how do the different methods compare with respect to their efficiency gains? We have previously developed a simple analytical formula for the efficiency gain in REMD and REMC simulations16 for the important case that the slow dynamics of the system of interest can be described by two-state transitions. Here, we derive a formula for the error and computational efficiency of ST simulations. The formula applies to systems with two-state dynamics at long-time scales (with an extension to the multistate case being discussed). For the sake of concreteness, we will frequently refer to two-state protein folding, but the theory is general. We measure the error in the estimator of an equilibrium property by its variance over repeated simulations. The computational efficiency is then defined as the rate with which the variance in the estimator decreases with length of the simulations.
The main result of this paper is that the relative efficiency of a ST simulation compared to a regular MD (or MC) simulation of the same duration tsim, run at the temperature Tm of interest alone, is
| (1) |
independent of the property of interest. In the ST simulation, the system spends a fraction Qi at each of the N temperatures T1,T2,…,TN, with . Equation 1 is valid for systems whose slow dynamics can be described by two-state transitions, and in the asymptotic limit of long simulation times tsim. The lifetimes of the system in its two long-lived (unfolded and folded) states at temperature Ti are and , where and are the corresponding (folding and unfolding) rates. A ST simulation is more efficient than a MD simulation of the same duration at temperature Tm if ηm>1.
We can interpret Eq. 1 for the relative efficiency of ST simulations as the ratio of the net reactive fluxes given by the number of folding and unfolding transitions per unit time in the ST simulation, and in the MD simulation: is the expected number of two-state transitions in MD and in the ST simulation. Remarkably, Eq. 1 is essentially identical to the efficiency formula obtained by us for REMD (Ref. 16) on a different, more involved route. We will show that this is no coincidence: The derivation followed here for ST can be adapted for replica exchange. Practically, the equivalence of the efficiency formulas means that at least asymptotically for two-state systems and ignoring any issues of computational overhead, ST and REMD have the same efficiency.
To illustrate and test the efficiency formula, we perform MC simulations of a two-dimensional (2D) Ising system at zero magnetic field. Below the critical temperature of the infinite system, a finite spin system will only slowly interconvert between the “up” and “down” states of the net magnetization, if only single spin flips are attempted in the MC sampling. We show that the slow sampling of the net magnetization of a finite system is accurately captured by our theory. We also show that Eq. 1 quantitatively reproduces the observed gains in efficiency from using ST, and that the large predicted gains in efficiency can indeed be realized for the 2D Ising system with its thermally activated transition in magnetization. In conclusion, we discuss procedures to accelerate the sampling of temperature space and strategies to optimize the choice of parameters.
THEORY
Rate model of simulated tempering
Building on our recent work on REMD,10 we will analyze the statistical error and efficiency of ST simulations for the important case of systems whose dynamics at long times is governed by a single slow exponential relaxation process. Even though complex molecular systems normally have multiple states, and thus a broad spectrum of relaxation processes, at sufficiently long times the relaxation to equilibrium is often dominated by a single slow exponential process. The folding of small “two-state” proteins is a specific example, with measured relaxation times that range from microseconds to seconds.
For such systems, a reduced two-state description captures the long-time dynamics. For the sake of concreteness, here we will refer to protein folding and unfolding as the slow processes, but the results are general. In the following, we assume that the interconversion between the same two states U and F dominate the relaxation at low and high temperatures (but we note that this may not always be the case). In the absence of ST temperature changes, we assume that the interconversion between the folded and unfolded states Fi and Ui, respectively, at each of the temperatures Ti follows first-order kinetics,
| (2) |
At temperature Ti, the equilibrium folded and unfolded populations are and qi=1−pi, respectively.
In ST simulations,1, 2 one periodically attempts to change the simulation temperature from Ti to Tj. These changes are accepted with a probability that maintains detailed balance with respect to a canonical ensemble at each temperature. If E=E(x) is the energy of a configuration x, a change from temperature Ti to Tj is accepted with probability
| (3) |
where kB is Boltzmann’s constant. Here we assume that the generation probabilities for changes Ti→Tj and Tj→Ti are identical. If x is a purely configurational coordinate of the system, as in typical MC sampling, E is the potential energy; in contrast, if x is a position in phase space, as in MD simulations, E is the total energy. Alternatively, in ST combined with MD simulations, one can also use the potential energy E in the acceptance criterion, combined with either rescaling momenta or redrawing them from a Maxwell–Boltzmann distribution at the new temperature Tj upon acceptance. The fi are constants that determine the fraction Qi of time spent at temperature Ti in long runs,
| (4) |
where Zi=∫dxe−E(x)∕kBTi is the partition function at Ti and 0<Qi≤1 with . Note that otherwise the Qi are arbitrary, determined by the specific choice of ST simulation parameters. In practice, the coefficients fi can be gradually optimized to achieve a targeted distribution, e.g., Qi=1∕N. These optimization strategies are typically based on the average energies at the different temperatures.2, 17 Here, we will instead solve the N−1 coupled linear equations
| (5) |
for with g1=1, is the observed fraction at Ti in a preliminary run with weight factors , and are the new weight factors for subsequent runs.
To model ST with a kinetic model with 2N states, we allow changes in the temperature along the simulation trajectory. Here, we focus on the case of very frequent temperature change attempts (which will result in the highest possible efficiency gains). In this limit of fast ST, we can use a rate model also for changes in the temperature in ST, not just for the two-state transitions of the system,
| (6) |
In the kinetic model, the rates and ( and ) for temperature changes in a folded (unfolded) structure should satisfy detailed balance to maintain the proper equilibria,
| (7) |
where r is a constant rate that will be chosen large enough to ensure frequent temperature changes. To model an actual simulation, the rate coefficients can be estimated from the acceptance probabilities pacc, given the folding state of the system, and the time intervals Δt between attempted changes of a certain type, e.g., . In our ST implementations, we will also consider non-nearest-neighbor transitions, for which temperature change rates can be estimated by analogy. Similar master-equation descriptions resulting in simple first-order kinetic models have previously been used to model replica exchange simulations.16, 18, 19, 20, 21
Error and efficiency of MD and ST simulations
Calculating equilibrium properties is the main goal in both MD, MC, and ST simulations. We accordingly define the computational efficiency of the simulations as the rate with which the statistical error in the estimate of the property of interest decreases with the simulation time. Following our earlier work on the efficiency of REMD simulations,16 we note that for simulation times tsim long compared to the overall longest relaxation time of the system, the central limit theorem implies that the error in the estimate of the exact mean ⟨A⟩ of any property A decreases as , where indicates the variance about the true mean in multiple simulations of the same duration tsim. The constant c depends on the simulation method (MD versus ST). Note that we do not consider the approach of to equilibrium for a given (“nonequilibrium”) initial condition. This approach to the true mean ⟨A⟩ occurs asymptotically as 1∕tsim, faster than the decrease in the statistical error (tsim−1∕2).
The ratio of the variances of the estimators from MD and ST simulation methods allows us to compare their respective efficiencies. Even though we explicitly consider only the case of two-state protein folding, the results apply generally to systems with two metastable states that interconvert slowly compared to the relaxation processes within each state. Importantly,16 in the two-state case the relative computational efficiencies will not depend on the particular property A. In such systems, A will quickly relax to the average values ⟨A⟩F and ⟨A⟩U in folded and unfolded states F and U, respectively. If those averages differ, then , where s indicates the folding state with s=1 if the system is folded, and s=0 if it is unfolded, such that ⟨s⟩i=pi at temperature Ti. It thus suffices to compare the convergence of estimates of the fraction folded, ⟨s⟩1, at the temperature T1 of interest.
For regular MD (and, by analogy, MC) simulations, one finds either directly16 or from the theory of statistical errors in single-molecule experiments22, 23 that the estimator , defined as the fraction of time spent in the folded state in a simulation of duration tsim has a variance of
| (8) |
at the temperature T1 of interest. Equation 8 applies in the asymptotic limit of .
For ST simulations, we consider the limit of very frequent temperature changes (r large). In this fast ST limit, the different temperatures will be visited frequently before a change in the folding state occurs at any one of the temperatures Ti. We can thus describe the kinetics of the folding state with effective folding and unfolding rates,
| (9) |
where p(i|U) and p(i|F) are the probabilities of being at temperature Ti, given that the system is unfolded and folded, respectively. From Bayes’ theorem, p(i|U)=p(U|i)p(i)∕p(U) with p(U|i)=qi, p(i)=Qi, and [and analogous relations for p(i|F)] it follows that
| (10) |
where
| (11) |
and is the net fraction folded irrespective of temperature. In the last expression, we substituted the lifetimes for the rates of interconversion.
To estimate the sampling error, we define the estimator x1 of p1≡⟨s⟩1 (i.e., the fraction folded at the temperature T1 of interest) as x1=tF1∕(tF1+tU1), where tF1 and tU1 are the times spent folded and unfolded, respectively, at temperature T1 during a simulation of duration tsim. In the following, we will calculate the variance of x1 over repeated ST simulations of duration tsim.
In the limit of fast ST, we have effective two-state behavior with folding and unfolding rates and , respectively. We define tF and tU=tsim−tF as the total time folded and unfolded in the simulation, irrespective of the temperature. Then, in the limit of fast ST, we have tF1=p(1|F)tF and tU1=p(1|U)tU, i.e., perfect sampling of the fractions of time spent at temperature T1 for given times tF and tU spent folded and unfolded, respectively,
| (12) |
We further assume that the simulation time tsim is sufficiently long compared to the characteristic time 1∕keff, where is the effective folding relaxation rate irrespective of temperature. We can then use the asymptotic formula22, 23 for the variance of tF and linear error propagation,
| (13) |
| (14) |
After differentiating Eq. 12 with respect to tF, and substituting p(1|F)p+p(1|U)(1−p)=p(1)=Q1 and ⟨tF⟩=ptsim, we find that
| (15) |
Substituting Eqs. 14, 15 into Eq. 13 results in
| (16) |
Comparing this expression to the corresponding variance of the estimator in a regular MD simulation at temperature T1, Eq. 8, we find that
| (17) |
In the last expression, we used Eq. 11 for κ and for the rate coefficients. By rewriting Eq. 17 in terms of the ratio of variances for a more general temperature of interest, Tm instead of T1, we obtain our main result, Eq. 1, for the relative efficiency of ST simulations compared to MD simulations using the same computational resources.
We note that one obtains the same result by using error propagation, including covariances. Specifically, if one defines covariances of the times spent folded and unfolded irrespective of temperature as Cαβ=⟨tαtβ⟩−⟨tα⟩⟨tβ⟩ with α,β∊{F,U}, then
| (18) |
With this procedure it is possible to extend the efficiency analysis worked out above for two-state systems to systems whose slow dynamics involves M>2 states. In the limit of fast ST, one can again determine effective transition rates from state β to α, averaged over the different temperatures Ti, analogous to Eq. 9. From the resulting effective rate matrix Keff, the matrix of correlation coefficients,
| (19) |
of the times tα and tβ spent in states α,β and β irrespective of temperature (α=1,2,…,M) can be determined in the asymptotic limit of large tsim as
| (20) |
where P=(p1,p2,…,pN)T(1,1,…,1) is a projector onto the equilibrium distribution, P′ is a diagonal matrix,, and a is a an arbitrary nonzero number with dimensions of reciprocal time. Equation 20 corresponds to Eq. (12) in Ref. 24, noting that ταβ in that paper is related to Cαβ through Cαβ=−2tsimpαταβpβ for α≠β andCαα=2tsimpαταα(1−pα). If we define as the estimator of the relative population p(α|T1) in state α at temperature T1, then
| (21) |
where p(α) is the fraction in state α averaged over all temperatures. Substitution of Eqs. 20, 21 into Eq. 18 allows us to evaluate the variance of the estimator xα1 for a system with more than two states.
Relation to REMD and REMC
Equation 1 is identical to our previous result for the relative efficiency of REMD simulations16 if we identifyQi=1∕N. In REMD simulations, the different temperatures indeed have equal weights by construction. As a consequence, REMD and ST have the same computational efficiency for the systems studied here in the asymptotic limit of long simulations, and if the sampling of temperature space is uniform in ST. However, the methods are only equivalent in the limits of fast temperature changes in ST, and fast replica exchanges in REMC and REMD simulations (and for a large number of replicas).
The efficiency result for REMD simulations was derived by us on a very different route. Specifically, in Ref. 16 we studied the global relaxation dynamics of the total number n(t) of folded replicas at time t, requiring us to estimate the first nonzero eigenvalue of a large rate matrix. In the following, we sketch a rederivation of the efficiency formula for REMD (and, by analogy, REMC) simulations following the route in the present paper.
In REMD and REMC simulations, every replica is statistically equivalent.25 So if we follow each replica, as it travels through temperature space, we have in effect the same dynamics as we have here for a single ST run (except that in REMC and REMD, Qi=1∕N is fixed). In particular, if temperature changes are fast compared to folding and unfolding, the folding dynamics can be described with the effective rates in Eq. 10. As a consequence, in a REMD simulation of duration tsim∕N (which is N times shorter than a MD or ST simulation using the same resources), the variance in the estimator x from an individual replica will be N times larger than that in Eq. 17. However, in the limit of a large number of replicas, the estimators from different replicas are statistically independent. As a consequence of the central limit theorem, the variance in the estimator x obtained by pooling all N replicas is thus reduced by a factor N, and we arrive at Eq. 17 also for REMD, with Qi=1∕N. We note, however, that in the case of replica exchange the efficiency formula is only approximate (because of the assumption of statistical independence of the estimators), even in the limit of fast replica exchange, whereas it is exact for ST in the fast limit. We note further that in REMC and REMD, one gets weights Qi different from 1∕N simply by running more replicas at a certain temperature.
As an interesting note, we showed in Ref. 16 that the estimators of all typical observables in a REMD simulation (and, in particular, the total number of folded replicas) relax at long times with a characteristic rate . This rate is different from the relaxation rate predicted for ST, . However, keff should give the relaxation of the estimator evaluated for an individual replica in REMD (or REMC), as it performs its random walk through temperature space.
RESULTS
Error and efficiency in simulated tempering
To test Eq. 1 for the efficiency, we have performed MC simulations of a 2D Ising model with Hamiltonian,
| (22) |
The sum extends over all distinct pairs (i,j) of neighboring spins σi=±1 on a periodic square lattice of size K×K. In a canonical ensemble with Boltzmann factor exp(−H∕T) and partition function ∑{σi}exp(−H∕T) (with kB=1 in this section), in the absence of an external magnetic field, and below the critical temperature Tc=2∕ln(1+21∕2)≈2.3 for the infinite system, finite 2D Ising models exhibit bistability with respect to their reduced magnetization m=∑iσi∕K2. At sufficiently low temperatures, m fluctuates between m≈−1 and 1.
The dynamics of this interconversion between up and down states of m will depend on the chosen MC move set. If in the MC sampling the move set is restricted to flips of single spins, the relaxation time of m will be long, measured in units of MC steps (one attempted move per spin) or MC passes (one attempted move for each of the K2 Ising spins). The reason is that intermediate states with m≈0 are energetically unfavorable.
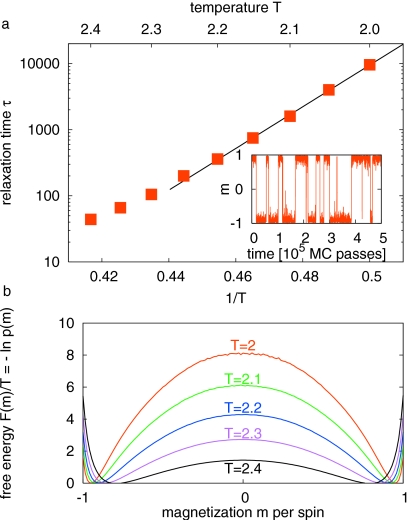
The inset in Fig. 1a shows the magnetization m(t) for a trajectory segment at T=2 of a 2D periodic Ising systems with 12×12 spins obtained from a regular MC simulation with single spin flips. From the decay of the autocorrelation function of m(t) at temperatures between 2 and 2.45 we have determined the relaxation time τ(T). The Arrhenius plot of τ(T) in Fig. 1a shows that the relaxation time grows exponentially with 1∕T at low temperatures. As a consequence, sampling of ⟨m⟩ with naive MC is challenging at low temperatures. The slow interconversion rate of the up and down states of m at low temperatures is also reflected in a high barrier at m=0 in the free energy profile F(m)∕T=−ln p(m), where p(m) is the probability density of m [Fig. 1b].
Figure 1.
Magnetization of the 12×12 2D Ising model. (a) Arrhenius plot of relaxation time τ(T) of magnetization m in units of MC passes vs 1∕T. Symbols: MC data; line: Arrhenius fit. Inset: MC trajectory segment of the reduced magnetization m(t) at T=2. (b) Free energy profileF(m)∕T=−ln p(m) of the reduced magnetization m at temperaturesT=2,2.1,…,2.4 (top to bottom at m=0).
In addition to the regular MC simulations, we have also performed ST simulations at temperatures Ti=2+(i−1)∕20, i=1,2,…. We have run simulations for N=2 (T1=2, T2=2.05), N=3 (T1=2, T2=2.05, T3=2.1), etc., up to N=10 (with T1=2 and T10=2.45). The weight factors fi determining the relative populations Qi of the different temperatures in the ST runs are adjusted by solving Eq. 5 such thatQi=1∕N. After every MC pass, we randomly pick a trial temperature Tj (j=1,2,…,i−1,i+1,…,N) different from the current temperature Ti, and accept the change from Ti to Tj according to Eq. 3.
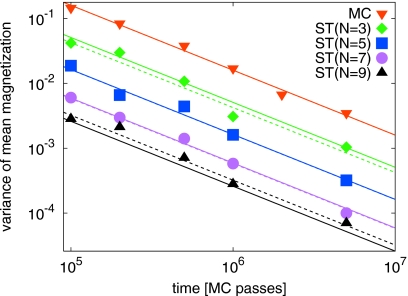
From each of the simulations, we estimated the average magnetization at the lowest temperature, T=2, as the simple mean of the instantaneous magnetization along the trajectory. In the limit of perfect sampling, converges to the exact limit ⟨m⟩=0. From multiple ST simulations of the same duration (number of MC passes between tsim=105 and 5×106) we have determined the variance of the estimator and confirmed that it scales as for both regular MC (N=1) and ST simulations (N>1). The coefficients cN are determined from a fit, with c1 being the coefficient that determines the rate of convergence for regular MC, c2 for ST with two temperatures, T1=2 and T2=2.05, etc. As shown in Fig. 2, the fitted coefficients cN are in excellent agreement with the theoretical predictions from Eq. 8 for regular MC, and Eq. 17 for the ST simulations.
Figure 2.
Variance in the estimator of the mean magnetization as a function of the simulation length tsim measured in units of MC passes. The symbols show the results of a regular MC simulation (top, inverted triangles) and ST simulations with N=3, 5, 7, and 9 temperatures (top to bottom) and corresponding upper temperatures TN=2.1, 2.2, 2.3, and 2.4. The solid lines are the theoretical predictions, cN∕tsim, with cN=(⟨m⟩+−⟨m⟩−)2var(x1)=⟨2|m|⟩2var(x1) and defined in Eq. 8 for the MC data (N=1) and in Eq. 17 for the ST data (N>1). The dashed lines are fits of cN∕tsim. Note that for N=9, the actual error is slightly larger than predicted.
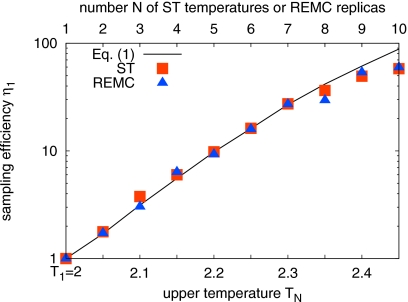
Figure 3 plots the relative computational efficiencies η1=c1∕cN of the ST simulations compared to a regular MC simulation at temperature T=2, with the ci obtained from fits. Also plotted is the relative efficiency gain η1 predicted from Eq. 1 using the life times , where τ(Ti) is the relaxation time of the magnetization m at temperature Ti plotted in Fig. 1a. We find that the relative efficiencies of sampling in the actual ST and MC simulations is accurately predicted by Eq. 1 up to an upper temperature of TN=2.3 (with N=7 temperatures, resulting in an efficiency gain of a factor of ≈30). For upper temperatures TN>2.3, Eq. 1 slightly overestimates the efficiency gain. At these high temperatures, the magnetization is barely bimodal [Fig. 1b, with a low barrier of only ≈1kBT in the free energy profile along m], and both the assumption of two-state dynamics and fast temperature change begin to break down.
Figure 3.
Efficiency gain η1 in ST (squares) and REMC simulations (triangles) over regular MC sampling of the magnetization m of the finite 2D Ising model at T1=2. The theoretical prediction, Eq. 1, is shown as a line. The bottom axis indicates the upper temperature TN in the ST and REMC simulations. The top axis indicates the corresponding number of evenly spaced temperatures in the ST simulations, and replicas in the REMC simulations.
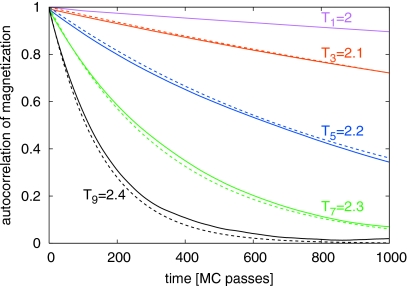
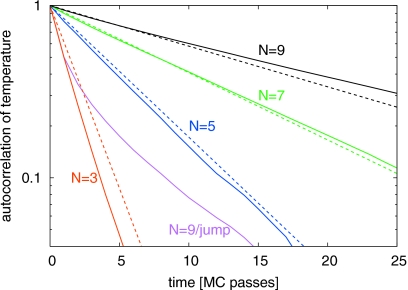
A comparison of the normalized autocorrelation function of the magnetization C(t) from simulations and theory further demonstrates the quantitative accuracy of the kinetic model of ST (Fig. 4). We find that C(t)=⟨Δm(t)Δm(0)⟩∕⟨Δm2⟩ with Δm(t)=m(t)−⟨m⟩, as obtained from the ST simulations, matches the theoretical prediction of with defined in Eq. 9. The correlation functions are calculated from the time series of m(t) irrespective of the instantaneous temperatures in the ST simulations. Figure 4 shows that the magnetization relaxes exponentially with a rate of keff, with only small deviations even at a high upper temperature of T9=2.4.
Figure 4.
Normalized autocorrelation function C(t) of the magnetizationm(t) irrespective of temperature in ST simulations (solid lines) with N=3, 5, 7, and 9 evenly spaced temperatures and upper temperatures of TN=2.1, 2.2, 2.3, and 2.4. Dashed lines show the theoretical predictions C(t)=exp(−kefft). For reference, the top curve shows C(t) for a regular MC run at temperature T1=2.
Comparison to replica exchange Monte Carlo
For comparison, we have also run REMC simulations with replicas at the same temperatures as in the ST simulations. Figure 3 shows that the resulting efficiency gains for sampling the magnetization at T1=2 are nearly identical to those of the ST simulations, and again in full agreement with Eq. 1 up to an upper temperature of TN=2.3.
Effect of tempering protocol
To test the influence of slowing down the sampling of the different temperatures Ti (i.e., the diffusion in temperature space), we have also performed ST simulations in which temperature changes are only allowed with neighboring temperatures (j=i±1) instead of picking the trial temperature Tj randomly from the whole temperature range. For upper temperatures TN<2.3, the efficiency gains are identical to those in ST simulations with random choice of the trial temperature Tj (not shown); for higher temperatures TN, the efficiency gains fall below the theoretical limit of Eq. 1 and those in ST simulations with faster sampling of temperature space. We found that for TN=2.45, the relaxation time of the temperature in the ST simulations with neighbor switching is comparable to the relaxation time of the magnetization at TN. As a consequence, the assumption of fast temperature change is no longer valid, explaining the reduced gain in efficiency. In essence, with temperature relaxation being slow, transitions between positive and negative magnetizations at a high temperature have a high probability of reverting before the ST system “cools down” to the temperature of interest.
Effect of the number of temperatures
A somewhat surprising prediction from the efficiency formula equation 1 is that for a fixed temperature range T1 to TN, and with a given distribution of temperatures (e.g., uniform), the efficiency gain ηm will approach a constant in the limit of large N.16 This means that even though the fraction Qm of time spent at the target temperature decreases as 1∕N, the sampling efficiency ηm is predicted to be unaffected. However, Eq. 1 applies only in the limit of fast temperature change, which may not be the case for large N, depending on the tempering protocol used. If temperature changes are only performed between nearest neighbors in temperature, then for large N the mean first passage time (in units of attempted temperature changes) to diffuse from a high temperature TN to a low temperature T1 will scale as N2. Specifically, for uniform weights Qi=1∕N, we can estimate the relaxation time of the temperature from the corresponding time for diffusion on a finite interval,
| (23) |
where Δt is the time between attempted temperature changes in the same direction (e.g., up), and is the average probability of acceptance. Here we assume to be independent of temperature and the state of the system and p(Ti|F) to be roughly constant. We found Eq. 23 to be an excellent approximation for the relaxation time of the temperature (Fig. 5).
Figure 5.
Normalized autocorrelation function of the temperature in ST simulations with nearest-neighbor temperature exchanges (solid lines), N=3, 5, 7, and 9 evenly spaced temperatures and upper temperatures of TN=2.1, 2.2, 2.3, and 2.4. Dashed lines show the theoretical predictions exp(−t∕τT) with τT from Eq. 23. Also shown is the curve for N=9 with global temperatures changes (i→1,2,…,i−1,i+1,…,N) permitting distant jumps in the temperature.
For large N with only nearest-neighbor temperature exchanges the assumption of fast temperature change will be violated. We tested this prediction by performing simulations with a fixed temperature range, but covered with different numbers N of uniformly spaced temperatures. For T1=2 and TN=2.4 with nearest-neighbor exchange, we found a significant gain in efficiency when using only N=3 or 5 temperatures (η1≈53) instead of 9 (η1≈30), but still somewhat lower than what is obtained by picking the trial temperature Tj at random from N=9 uniformly spaced temperatures (η1≈59). In contrast, global temperature changes,i→1,2,…,i−1,i+1,…,N, result in much faster temperature relaxation (Fig. 5). In practice, one should monitor andoptimize the rate of temperature relaxation [e.g., from the autocorrelation function of T(t)] and compare it to the rate of relaxation of the two-state process. Fast temperature change is essential to achieve the maximum possible efficiency.
Effect of temperature weights
According to Eq. 1, the computational efficiency can be increased by giving higher weights Qi to temperatures Ti, where is small and the system crosses frequently between the states. Typically, these will be the higher temperatures. We have tested Eq. 1 for nonuniform Qi by running ST simulations of the Ising system with linearly increasing weights, . We again find excellent agreement between the predicted and observed gains in efficiency up to about N=7 with an upper temperature of T7=2.3 (data not shown). For higher upper temperatures, the gains are somewhat below those predicted, as with uniform weights. Overall, using a linear bias toward higher temperatures results in gains ≈35% higher than those for uniform weights. Gains from increasing the weight of the higher temperatures were previously observed in simulations by Zhang and Ma.26
Accelerated tempering protocol
We have also tested a scheme to speed up the temperature relaxation. Instead of first picking the temperatures Tj from 1,2,…,i−1,i+1,…,N (or from j=±1) and then accepting a change from Ti to Tj according to Eq. 1, we choose the temperatures Tj at random according to their probability for a given conformation with energy E,
| (24) |
To sample Tj from this distribution, we calculate the cumulative distribution , with P0=0 and PN=1. We then draw a random number r with uniform distribution between 0 and 1. The new temperature Tj is determined suchthat Pj−1<r≤Pj. Care has to be taken to avoid over-∕underflows in the numerical calculation, e.g., by adding a suitable constant to all energies E. As an alternative, one can also repeatedly apply the standard ST temperature change protocol for a fixed configuration of energy E, and with detailed balance properly enforced.
In simulations of the Ising model with N=10 temperatures, and T1=2 and T10=2.45, the efficiency gains from this protocol over picking trial temperatures at random are negligible [η1≈58 in both cases, compared to η1=88 from Eq. 1]. We conclude from this result (and similar results from simulations run with attempted temperature changes after every attempted spin flip) that the gradual breakdown of the two-state assumption is primarily responsible for the actual efficiency being slightly lower than predicted for upper temperatures TN>2.3.
CONCLUDING REMARKS
We have derived an analytical expression for the relative computational efficiency of ST simulations over regular MC or MD simulations. The expression, Eq. 1, applies to the important case that the slow dynamics of the system can be described by the relaxation between two metastable states, and is derived under the assumption that the temperature change in ST is fast compared to the transitions between the two states. We also sketch an extension to systems requiring more than two states. In our efficiency calculation, we have not considered the possibility of reweighting the data collected at the different temperatures. Combining data from all temperatures, for instance, by using the weighted histogram method,27, 28 can further enhance the sampling efficiency at the temperature of interest, in particular if ST is not in the fast limit; but gains should be minimal if ST is fast with respect to the property of interest.
We have tested the expression for the efficiency gain against MC calculations of the magnetization in a 2D Ising model. We have found that Eq. 1 predicts the efficiency gains quantitatively. Only at the highest upper temperatures TN considered, the observed sampling efficiency gains are somewhat below those predicted. The reasons for this drop are, on the one hand, that the assumption of fast temperature change is increasingly violated at high TN (where the relaxation between up and down magnetizations becomes faster than the relaxation from high to low temperatures); and, on the other hand, that the two-state assumption for the magnetization breaks down as the temperature TN exceeds Tc.
Interestingly, the formula equation 1 for the efficiency gain in ST simulations is essentially identical to that derived previously on a very different route for REMD and REMC simulations. However, in the limit of fast exchange and a large number N of replicas, we have shown that the equivalence of the two approaches follows from simple statistical arguments. As an interesting consequence, in the asymptotic limit running multiple ST simulations in parallel without communication is as efficient as running REMD or REMC simulations with communication for replica exchange. This makes ST particularly useful for distributed computing.15
Our analytical result for the efficiency gain in ST simulations has practical implications in the setup of ST simulations as follows.
Temperature range T1 to TN
As in REMC and REMD simulations,16 one should cover a range of temperatures Ti, where the sum of relaxation times is smaller than at the temperature of interest, Tm. In this way, the more frequent transitions (corresponding to a higher reactive flux) at the higher temperatures result in improved sampling at the lower temperatures of interest. To further maximize ηm with respect to T1 and TN, the strategies discussed in Sec. II.E of our previous work16 for REMD and REMC can be adapted.
Importantly, because the sum of lifetimes enters the efficiency formula equation 1, not the relaxation rate , ST, REMC, and REMD are not as powerful to enhance the sampling of entropy dominated processes such as protein folding as they are for enthalpy dominated transitions. Over a fairly broad range of temperatures, the folding rate of proteins is often found to be nearly constant or even slowing down with increasing temperature. Despite the acceleration of the enthalpy dominated unfolding process at high temperatures, the efficiency gain is limited by the unaccelerated folding process, resulting in long lifetimes of the unfolded state.
Temperature weights
Traditionally, one attempts to find weight factors fi to ensure equal sampling Qi≈1∕N for all temperatures. From the perspective of sampling efficiency, equal weighting is not optimal. Based on Eq. 1, it is advantageous to give higher weights to temperatures Ti at which is smaller than at the temperature of interest, Tm. In typical problems, one would thus want to give a disproportionally high weight to the higher temperatures. However, any optimization of the target weights Qi has to consider that the relaxation in temperature space should be fast, as discussed next.
Temperature relaxation
In addition to choosing the optimal temperature range, it is important to ensure that temperature relaxation is fast compared to the relaxation of the system state at any given temperature [as has been found before for REMD (Refs. 16, 19, 20, 21)]. Temperature relaxation can be accelerated by spacing the temperatures Ti more narrowly (if the acceptance of temperature changes is low), by making more frequent temperature change attempts, by using nonlocal temperature change moves (that must, however, satisfy detailed balance, e.g., by picking the trial temperatures Tj at random), or by picking temperatures Tj according to Eq. 24. Alternative implementations of ST,14, 29, 30 often related to approaches in REMD and REMC simulations,31 may also help enhance the sampling of temperature space, and in turn configuration space.
There has been some discussion in the literature of the optimal frequency of attempted temperature exchanges, in particular, in the context of replica exchange simulations.21, 32, 33 On formal grounds, and consistent with other studies,21, 26, 33 we conclude that it is optimal to attempt temperature changes in ST, and temperature exchanges in REMC and REMD, as frequent as possible (as long as the computational cost of the exchange itself can be ignored). However, in practical implementations it is important that exchanges maintain a proper Boltzmann distribution. This is a particular concern in MD simulations, where one should use proper thermostats10 and integrators that evaluate positions and momenta at the same time step, such as velocity Verlet,34 for proper rescaling (or redrawing) of the momenta.
Number N of temperatures
Interestingly, for a large number of temperatures N spaced according to a given distribution in a fixed range T1 to TN, the efficiency gain becomes independent of N, as long as the temperature change is fast. As a consequence, there is no loss in sampling efficiency from increasing the number N of temperatures, as long as the temperature relaxation rate does not suffer. However, circumventing the N2 scaling of the temperature relaxation time for large N will require nonlocal temperature changes [such as the use of Eq. 24].
In summary, we have shown that ST can substantially enhance the sampling efficiency over regular MC and MD simulations, as measured by a decrease in the simulation time required to achieve a certain statistical accuracy. In the limit of fast temperature change, this gain is largest, and equivalent to that in REMD and REMC simulations covering the same temperatures. Achieving high computational efficiency in ST simulations requires a careful selection of the simulation parameters, a process that can be guided by the analytical expression Eq. 1 for the maximum gain achievable.
ACKNOWLEDGMENTS
We thank Dr. Attila Szabo for many helpful and stimulating discussions and Dr. William Swope for discussions about the effects of integrators. This research was supported by the Intramural Research Program of the NIDDK, NIH.
References
- Lyubartsev A. P., Martsinovski A. A., Shevkunov S. V., and Vorontsov-Velyaminov P. N., J. Chem. Phys. 96, 1776 (1992). 10.1063/1.462133 [DOI] [Google Scholar]
- Marinari E. and Parisi G., Europhys. Lett. 19, 451 (1992). 10.1209/0295-5075/19/6/002 [DOI] [Google Scholar]
- Geyer C. J., Computing Science and Statistics: Proceedings of the 23rd Symposium on the Interface (American Statistical Association, New York, 1991), pp. 156–163.
- Hukushima K. and Nemoto K., J. Phys. Soc. Jpn. 65, 1604 (1996). 10.1143/JPSJ.65.1604 [DOI] [Google Scholar]
- Sugita Y. and Okamoto Y., Chem. Phys. Lett. 314, 141 (1999). 10.1016/S0009-2614(99)01123-9 [DOI] [Google Scholar]
- García A. E. and Sanbonmatsu K. Y., Proc. Natl. Acad. Sci. U.S.A. 99, 2782 (2002). 10.1073/pnas.042496899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunishi H., Watanabe O., and Takada S., J. Chem. Phys. 116, 9058 (2002). 10.1063/1.1472510 [DOI] [Google Scholar]
- Bennett C. H., J. Comput. Phys. 22, 245 (1976). 10.1016/0021-9991(76)90078-4 [DOI] [Google Scholar]
- Swendsen R. H. and Wang J. -S., Phys. Rev. Lett. 57, 2607 (1986). 10.1103/PhysRevLett.57.2607 [DOI] [PubMed] [Google Scholar]
- Rosta E., Buchete N. -V., and Hummer G., J. Chem. Theory Comput. 5, 1393 (2009). 10.1021/ct800557h [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansmann U. H. E. and Okamoto Y., Phys. Rev. E 54, 5863 (1996). 10.1103/PhysRevE.54.5863 [DOI] [PubMed] [Google Scholar]
- Hansmann U. H. E. and Okamoto Y., J. Comput. Chem. 18, 920 (1997). [DOI] [Google Scholar]
- Mitsutake A., Sugita Y., and Okamoto Y., Biopolymers 60, 96 (2001). [DOI] [PubMed] [Google Scholar]
- Rauscher S., Neale C., and Pomés R., J. Chem. Theory Comput. 5, 2640 (2009). 10.1021/ct900302n [DOI] [PubMed] [Google Scholar]
- Huang X. H., Bowman G. R., and Pande V. S., J. Chem. Phys. 128, 205106 (2008). 10.1063/1.2908251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosta E. and Hummer G., J. Chem. Phys. 131, 165102 (2009). 10.1063/1.3249608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S. and Pande V. S., Phys. Rev. E 76, 016703 (2007). 10.1103/PhysRevE.76.016703 [DOI] [PubMed] [Google Scholar]
- Zheng W., Andrec M., Gallicchio E., and Levy R. M., Proc. Natl. Acad. Sci. U.S.A. 104, 15340 (2007). 10.1073/pnas.0704418104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadler W. and Hansmann U. H. E., J. Phys. Chem. B 112, 10386 (2008). 10.1021/jp805085y [DOI] [PubMed] [Google Scholar]
- Nadler W. and Hansmann U. H. E., Phys. Rev. E 75, 026109 (2007). 10.1103/PhysRevE.75.026109 [DOI] [PubMed] [Google Scholar]
- Sindhikara D., Meng Y. L., and Roitberg A. E., J. Chem. Phys. 128, 024103 (2008). 10.1063/1.2816560 [DOI] [PubMed] [Google Scholar]
- Boguñá M., Berezhkovskii A. M., and Weiss G. H., J. Phys. Chem. A 105, 4898 (2001). 10.1021/jp004023b [DOI] [Google Scholar]
- Berezhkovskii A. M., Szabo A., and Weiss G. H., J. Chem. Phys. 110, 9145 (1999). 10.1063/1.478836 [DOI] [Google Scholar]
- Gopich I. V. and Szabo A., J. Chem. Phys. 118, 454 (2003). 10.1063/1.1523896 [DOI] [Google Scholar]
- Nymeyer H., J. Chem. Theory Comput. 4, 626 (2008). 10.1021/ct7003337 [DOI] [PubMed] [Google Scholar]
- Zhang C. and Ma J. P., J. Chem. Phys. 129, 134112 (2008). 10.1063/1.2988339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrenberg A. M. and Swendsen R. H., Phys. Rev. Lett. 63, 1195 (1989). 10.1103/PhysRevLett.63.1195 [DOI] [PubMed] [Google Scholar]
- Chodera J. D., Swope W. C., Pitera J. W., Seok C., and Dill K. A., J. Chem. Theory Comput. 3, 26 (2007). 10.1021/ct0502864 [DOI] [PubMed] [Google Scholar]
- Stolovitzky G. and Berne B. J., Proc. Natl. Acad. Sci. U.S.A. 97, 11164 (2000). 10.1073/pnas.97.21.11164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denschlag R., Lingenheil M., Tavan P., and Mathias G., J. Chem. Theory Comput. 5, 2847 (2009). 10.1021/ct900274n [DOI] [PubMed] [Google Scholar]
- Liu P., Kim B., Friesner R. A., and Berne B. J., Proc. Natl. Acad. Sci. U.S.A. 102, 13749 (2005). 10.1073/pnas.0506346102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J. and Gready J. E., J. Chem. Theory Comput. 4, 1119 (2008). 10.1021/ct800016r [DOI] [PubMed] [Google Scholar]
- Periole X. and Mark A. E., J. Chem. Phys. 126, 014903 (2007). 10.1063/1.2404954 [DOI] [PubMed] [Google Scholar]
- Swope W. C., Andersen H. C., Berens P. H., and Wilson K. R., J. Chem. Phys. 76, 637 (1982). 10.1063/1.442716 [DOI] [Google Scholar]