PRIMO/PRIMONA: A coarse-grained model for proteins and nucleic acids that preserves near-atomistic accuracy

Abstract

The new coarse graining model PRIMO/PRIMONA for proteins and nucleic acids is proposed. This model combines one to several heavy atoms into coarse-grained sites that are chosen to allow an analytical, high-resolution reconstruction of all-atom models based on molecular bonding geometry constraints. The accuracy of proposed reconstruction method in terms of structure and energetics is tested and compared with other popular reconstruction methods for a variety of protein and nucleic acid test sets.

Introduction

Computational methods are increasingly being employed for addressing the challenges in biological systems. Recent technological advances have enabled simulations of small proteins in explicit aqueous environment up to microsecond time scales^1–3, and the large scale modeling of proteins and protein-DNA complexes over tens of nanoseconds in atomistic detail. However, many relevant interactions in biology typically involve large macromolecular complexes of proteins, lipids and nucleic acids and time scales of micro- to milliseconds or longer. Such dynamic processes are generally not accessible with current atomistic models. Coarse-grained (CG) models are being increasingly applied to address these issues. The concept of CG models is not a new idea and was employed for studying protein folding already in the 1970s⁴. In recent times, there has been a dramatic increase in the development and application of CG models. Several types of CG models have been proposed for proteins^5–12, lipids¹³, and nucleic acids^14–20.

The recipe for coarse-graining essentially involves two steps: first, the resolution (number of interaction sites) is chosen for the CG model, and second, suitable interaction schemes need to be developed for that model. In the case of proteins, the resolution of CG model varies drastically from one CG particle per amino acid which is usually either located at the C_α-position^5,6,21 or at the side chain center^9,22 to two CG particles^5,6,12 or more than three atoms per residue.^{5–7,10,11,23} There are also models where multiple residues are combined into CG sites ²⁴. CG models of DNA and RNA have been proposed by several groups, either for DNA alone¹⁶, in the context of protein-DNA docking¹⁷, to understand the dynamics of the nucleosome particle^18,19, to gain insights into RNA folding mechanism^14,15, or to probe DNA packaging into viral capsids²⁰. Most of these nucleic acid CG models employ a highly coarse-grained representation with one¹⁹ or more²⁰ nucleotides per bead, but models with three particles per nucleotide (one each for phosphate, sugar and base) have also been proposed^14–16,18 and in the context of protein-DNA docking a model with five to six CG sites per nucleotides has been used to provide a better description of the binding interface¹⁷.

The choice of the model resolution fundamentally limits the accuracy of a given CG model and its applicability in increasingly popular multi-scale techniques^25,26 where different resolutions of the system (typically CG and atomistic models) are used in a single simulation. Furthermore, the level of coarse-graining largely determines to what extent physically-motivated transferable interaction potentials can be devised instead of empirical, often system-specific potentials^24,27,28. A key feature in this respect is how well CG and atomistic models can be inter-converted. The generation of CG models from atomistic models is generally straightforward, but may involve the optimization of suitable interaction sites in highly coarse-grained representations. The reconstruction of atomistic models from CG models (referred to as “reverse mapping”), on the other hand, is a more difficult problem that has been studied extensively^29–32. The reverse mapping algorithm depends on the resolution of CG model. For CG models which contain one CG particle (usually the C_α-atom) the backbone is reconstructed using analytical methods³³, using protein fragments or structures from the PDB database³⁰ or knowledge-based methods^31,34. Though different strategies^{29,31,32,34,35} have been explored for placing the side chain on the reconstructed backbone, generally a rotamer library is used to limit the conformational search space³⁶. The accuracy of C_α-based reconstruction schemes are usually at 1.5–2 Å RMSD from the underlying atomistic model²⁹. CG models that include side chain centers facilitate the selection of sidechain rotamers and also improve the reconstruction of the backbone. As a result an accuracy of near 1 Å RMSD can be achieved with such models^31,34. On the other hand, the reconstruction of atomistic models from mesoscopic models where several residues are combined into CG particles is even more difficult. The limited accuracy of all-atom reconstructions from commonly employed CG models compromises the ability of CG models to study biomolecular systems where mechanistic questions often need to be ultimately understood at the atomistic level. At the same time, the development of multi-scale modeling schemes is significantly complicated in the absence of a bi-directional one-to-one correspondence between CG and atomistic models. Most reconstruction schemes are also too time consuming for multi-scale simulation schemes where rapid interconversion between different resolutions is typically required^25,27. Often, a reconstructed model is initially subjected to minimization to remove energetically-unfavorable contacts introduced during the reconstruction process^31,32,34. Especially the reverse mapping from non- native structures generated during CG simulations may require extensive minimization^{18,25,27,29,37}.

In this work, we describe a new CG model that was developed specifically to allow rapid, near-exact reconstruction of atomistic representations for proteins and nucleic acids based on analytical functions while at the same time minimizing the number of CG interaction sites. The model and reconstruction procedure relies on standard molecular bonding geometries according to the hybridization states of different atoms. The resulting model, called PRIMO (Protein Intermediate Model) for proteins and PRIMONA for the protein/nucleic-acid version, involves three to eight sites per amino acid residue and twelve to thirteen sites per nucleotide. The model is presented next in more detail, followed by a description of the analytical reverse mapping scheme to rebuild atomistic models. The model and reconstruction procedure is then tested for a number of test sets and compared to other commonly used reconstruction methods for CG models at different resolutions.

Materials and Methods

Design of PRIMO/PRIMONA CG Model

The PRIMO CG model is constructed as a minimal model that allows all-atom reconstruction with an analytical formalism at negligible loss of accuracy (defined as a reconstruction accuracy of 0.1 Å or better). This is accomplished by taking advantage of geometric constraints under the assumption that standard molecular bonding geometries are maintained. Additional design principles are applied to facilitate the later development of interaction potentials that are compatible with and comparable to all-atom force fields: 1) PRIMO sites either correspond directly to heavy atoms or the center of geometry for a group of heavy atoms. 2) CG sites are arranged so that space is filled uniformly. 3) Chemical specificity is preserved to maintain hydrogen bond donors and acceptors and the location of charges on charged residues.

As a result PRIMO may not represent the absolute minimal model that allows all-atom reconstruction with quasi-atomistic accuracy. However, as described below, PRIMO is significantly reduced compared to other models that offer quasi-atomistic resolution, such as united-atom models while offering similar computational advantage as other coarse-grained models that do not achieve quasi-atomistic accuracy.

Although PRIMO is designed with molecular mechanics-type interaction potentials in mind, it is primarily meant to preserve the structural features of peptides and proteins and is therefore expected to be equally applicable for statistical interaction potentials..

PRIMO Model for Proteins

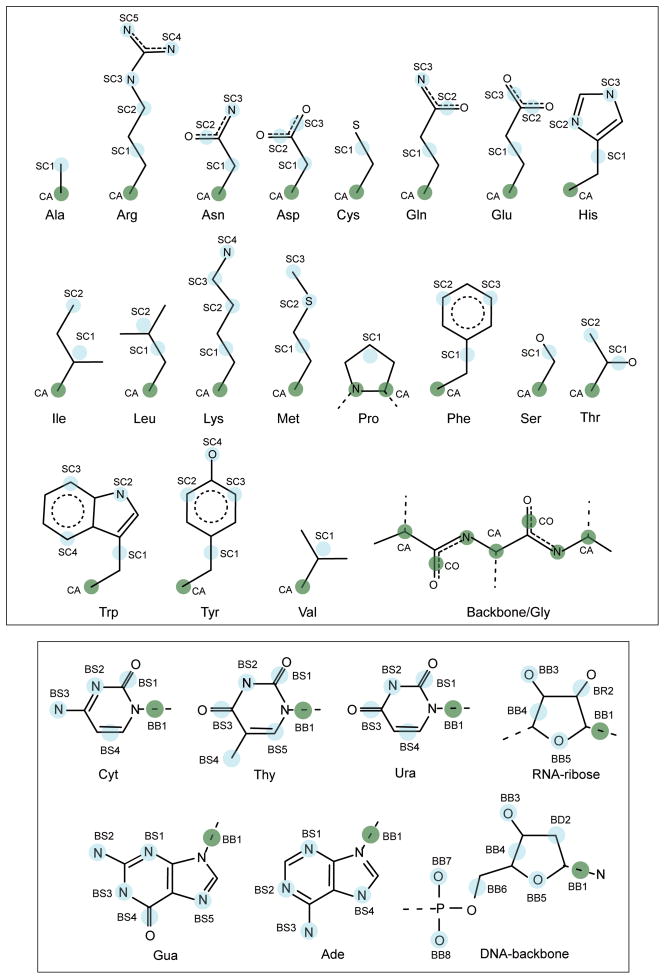
The CG interaction sites for amino acids are illustrated in Figure 1. Table 1A lists the mapping between all-atom and PRIMO CG levels. The backbone is represented with N, C_α and a combined carbonyl site (CO) placed at the geometric center of the carbonyl C and O atoms. As a result, backbone hydrogen bonding interactions can be preserved, which is essential for an accurate description of the secondary structures of proteins.

Figure 1.

PRIMO/PRIMONA model for proteins and nucleic acids with PRIMO/PRIMONA CG sites are represented as cyan spheres on a template of atomistic models. For proteins, the backbone C_α and N atoms are shown as green spheres. The side chain CG sites for each residue are named as SCn where n varies from 1 to 5 depending on the type of the residue. For nucleic acids, the sugar-phosphate backbone of DNA and RNA units are labeled as BBx and the nitrogenous bases are labeled as BSx. The CG site representing the glycosidic bond is shown as green spheres.

Table 1.

Table 1A. CG mapping scheme for proteins. PRIMO CG sites and their mapping to all-atom space. A CG particle consisting of more than one atom is placed at the geometric center of its constituent atoms.
Residue	PRIMO	All-atom
Backbone	N	N
	Ca	Ca
	CO	C+O
Ala	SC1	Cβ
Arg	SC1	Cβ+Cγ
	SC2	Cδ
	SC3	Nε
	SC4	Nη1
	SC5	Nη2
Asn	SC1	Cβ
	SC2	Cγ+Oδ1
	SC3	Nδ2
Asp	SC1	Cβ
	SC2	Cγ+Oδ1
	SC3	Cγ+Oδ2
Cys	SC1	Cβ+Sγ
Gln	SC1	Cβ+Cγ
	SC2	Cδ+Oε1
	SC3	Nε2
Glu	SC1	Cβ+Cγ
	SC2	Cδ+Oε1
	SC3	Cδ+Oε2
His	SC1	Cβ+Cγ
	SC2	Nδ1
	SC3	Nδ2
Ile	SC1	Cβ+Cγ1+Cγ2
	SC2	Cδ
Leu	SC1	Cβ+Cγ
	SC2	Cγ+Cδ1+Cδ2
Lys	SC1	Cβ+Cγ
	SC2	Cδ
	SC3	Cε
	SC4	Nζ
Met	SC1	Cβ+Cγ
	SC2	Sδ
	SC3	Cε
Phe	SC1	Cβ+Cγ
	SC2	Cε1
	SC3	Cε2
Pro	SC1	Cβ+Cγ+Cδ
Ser	SC1	Cβ+Oγ
Thr	SC1	Cβ+Oγ1
	SC2	Oγ2
Trp	SC1	Cβ+Cγ
	SC2	Nε1
	SC3	Cε3
	SC4	Cζ2
Tyr	SC1	Cβ+Cγ
	SC2	Cε1
	SC3	Cε2
	SC4	Oη
Val	SC1	Cβ+Cγ1+Cγ2

Table 1B CG mapping scheme for nucleic acids. PRIMONA CG sites and their mapping to all-atom space. A CG particle consisting of more than one atom is placed at the geometric center of its constituent atoms.
Residue	PRIMONA	All-atom
Backbone Phosphate	BB8	O2P
	BB7	O1P
	BB6	O5′+C5′
Backbone Sugar	BB5	O4′
	BB4	C4′+C3′
	BB3	O3′
	BD2/BR2	C2′
	BB1	C1′+N9 (purine) C1′+N1 (pyrimidine)
Ade	BS1	N3
	BS2	N1
	BS3	N6
	BS4	N7
Gua	BS1	N3
	BS2	N2
	BS3	N1
	BS4	C6+O6
	BS5	N7
	BS1	C2+O2
	BS2	N3
	BS3	N4
	BS4	C5+C6
Thy	BS1	C2+O2
	BS2	N3
	BS3	C4+O4
	BS4	C5M
	BS5	C6
Ura	BS1	C2+O2
	BS2	N3
	BS3	C4+O4
	BS4	C5+C6

Non-glycine side chains are represented with one to five CG sites (referred to as SCn, where n is the index of the CG side chain site). The amino acids Ala, Cys, Pro, Ser, and Val have only one SC1 particle; the amino acids Ile, Leu and Thr are modeled with SC1 and SC2 sites; the amino acids Asn, Asp, Gln, Glu, His, Met, and Phe have three SC sites; the amino acids Lys, Trp and Tyr have four SC particles; while Arg side chain has five SC interaction sites.

Reconstruction of all-atom models from PRIMO

The reconstruction of an all-atom model from PRIMO is accomplished by assuming standard bonding geometries as described by bond distances, angles and dihedrals. These geometric parameters were derived from long explicit water molecular dynamics (MD) simulations. For the amino acid parameterization, we performed 150 ns explicit water simulations of blocked dipeptides using the CHARMM22 force field³⁸ with the CMAP correction term³⁹. The details of these simulations are described elsewhere⁴⁰. MD results were chosen instead of ab initio data or experimental structures in order to account for the influence of aqueous solvent and maximize compatibility with an all-atom force field. The latter is especially important for the development of multi-scale methods. The resulting bonding parameters that were used for reconstructing various amino acid heavy atoms are given in Table 2A.

Table 2.

Table 2A Bonding parameters used for protein reconstruction. Bond distance, angle, and dihedral parameters used in scheme 1 for PRIMO protein reconstructions. The constructed and constrained atoms correspond to atoms A, B, C and D respectively as discussed in the main text. For Ile and Val, the dihedral angle χ is defined by backbone N, Cα, the reconstructed side chain Cβ atom, and SC1 (combined Cβ, Cγ1 and Cγ2 atoms); for Leu, χ is defined by reconstructed Cα, reconstructed Cβ, Cγ atoms and SC1 (combined Cγ, Cδ1 and Cδ2 atoms). All parameters are obtained from all atom explicit solvent simulations of dipeptides.
Residue	Constructed Atom	Constrained Atoms/ CG Sites	Bond Length b (Å)	Bond Angle θ (°)	Dihedral φ(°)
Backbone	Ci	COi, Ni+1, Cαi	0.617	41.30	0.0
Arg	Cβ	Cα, N, C	1.550	110.70	−121.0
Asn	Cγ	SC2, SC3, Cβ	0.617	41.30	0.00
Cys	Cβ	Cα, N, C	1.553	110.50	−122.3
Gln	Cβ	Cα, N, C	1.555	110.80	−121.9
	Cδ	SC2, SC3, Cγ	0.617	41.30	0.00
Glu	Cβ	Cα, N, C	1.552	110.55	−123.5
His	Cβ	Cα, N, C	1.553	110.40	−122.5
	Cε1	SC3, SC2, Cγ	1.325	33.77	180.0
	Cε2	SC3, SC2, Cγ	1.378	73.35	0.0
Ile	Cβ	Cα, N, C	1.535	112.00	−124.5
	Cγ2	Cα, Cβ, N	1.550	108.00	χ1 − 60.0
	Cγ1	Cα, Cβ, N	1.547	112.40	χ1 + 60.0
Leu	Cβ	Cα, N, C	1.555	110.50	−122.5
	Cδ1	Cγ, Cα, Cβ	1.535	108.00	χl − 60.0
	Cδ2	Cγ, Cα, Cβ	1.535	108.00	χl + 60.0
Lys	Cβ	Cα, N, C	1.555	110.70	−123.0
Met	Cβ	Cα, N, C	1.552	110.50	−123.0
Phe/Tyr	Cβ	Cα, N, C	1.555	111.00	−122.2
	Cδ1	SC2, SC3, Cγ	1.405	89.90	0.0
	Cδ2	SC3, SC2, Cγ	1.405	89.90	0.0
	Cζ	SC3, Cδ2, Cγ	1.405	119.80	0.0
Pro	Cβ	Cα, N, C	1.530	104.00	−122.0
	Cδ (Non N-term)	Ni, Cαi, Ci−1	1.470	111.05	180.0
	Cδ (N-term)	N, Ca, C	1.470	111.05	−15.0
Ser	Cβ	Cα, N, C	1.555	112.00	−123.00
Thr	Cβ	Cα, N, C	1.525	113.00	−124.00
Trp	Cβ	Cα, N, C	1.555	110.50	−123.5
	Cδ2	SC3, SC4, SC2	1.400	59.80	0.0
	Cε2	SC2, SC4, SC3	1.365	25.10	0.0
	Cδ1	SC2, Cε2, Cδ2	1.375	109.50	0.0
	Cζ3	SC3, Cδ2, Cε2	1.400	118.50	0.0
	Cη2	SC4, Cε2, Cδ2	1.390	118.10	0.00
	Cβ	Cα, N, C	1.530	112.00	−125.00
Val	Cγ1	Cβ, Cα, N	1.545	110.50	χv − 60.0
	Cγ2	Cβ, Cα, N	1.545	110.50	χv + 60.0

Table 2B Bonding parameters used for nucleic acid reconstruction. Bond distance, angle, and dihedral parameters used in scheme 1 for PRIMONA nucleic acid reconstructions. The constructed and constrained atoms correspond to atoms A, B, C and D respectively as discussed in the main text. All parameters except dihedrals, are obtained from all atom explicit solvent simulations of B-from DNA and RNA duplex.
Residue	Constructed Atom	Constrained Atoms	Bond Length b (Å)	Bond Angle θ (°)	Dihedral φ (°)
Backbone phosphate	P	BB8, BB3, BB7	1.480	36.500	−33.0
	O5′	P, BB7, BB8	1.570	109.000	−125.0
Sugar ring	C4′	BB5, C5′, BB4	1.460	36.000	33.5
	C2′ (RNA)	C3′, C1′, BR2	1.530	39.000	33.5
Ade	N9	BS4, BS2, BS1	2.240	80.700	0.0
	C8	N9, BS4, BS2	1.370	32.500	180.0
	C4	N9, C8, BS4	1.375	106.000	0.0
	C5	BS4, C8, N9	1.390	104.000	0.0
	C2	BS1, C4, C5	1.340	110.500	0.0
	C6	BS2, C2, BS1	1.360	118.600	0.0
Gua	N9	BS5, BS3, BS1	2.240	79.700	0.0
	C8	N9, BS5, BS3	1.370	32.500	180.0
	C4	N9, C8, BS5	1.375	106.000	0.0
	C5	BS5, C8, N9	1.390	104.000	0.0
	C2	BS2, BS3, BS1	1.320	32.750	180.0
	C6	BS3, C2, BS1	1.390	125.300	0.0
Cyt	N1	BS2, BS3, BS4	2.375	119.600	0.0
	C6	N1, BS2, BS3	1.380	90.000	0.0
	C4	C5, C6, N1	1.430	117.700	0.0
	C2	N1, C6, C5	1.396	119.425	0.0
Thy	N1	BS5, BS2, BS1	1.380	60.400	0.0
	C5	BS5, N1, BS1	1.340	123.200	0.0
	C4	C5, BS5, N1	1.440	117.800	0.0
	C2	N1, BS5, C5	1.380	121.200	0.0
Ura	N1	BS2, BS3, BS4	2.315	110.800	0.0
	C6	N1, BS2, BS3	1.380	88.400	0.0
	C4	C5, C6, N1	1.430	119.600	0.0
	C2	N1, C6, C5	1.380	120.400	0.0

Before the reconstruction procedure is described for each amino acid is described in detail, a number of general schemes are described that are applied to different atoms/residues:

Scheme 1

The reconstruction of an atomic site A (r⃗_A) based on the distance A–B (b), the angle A-B-C (θ), and the dihedral A-B-C-D (φ) is accomplished as follows: The position of atom A in a local coordinate system ( ${\overrightarrow{r}}_A^l$) can be represented in spherical coordinates according to the transformation:

$${\overrightarrow{r}}_A^l=\left[\begin{array}{c}bsin(\theta )sin(\phi )\\ bsin(\theta )cos(\phi )\\ bcos(\theta )\end{array}\right]$$ (1)

Note, that the Cartesian transformation corresponds to that of a left-handed coordinate system.

To obtain r⃗_A (global coordinate system) in terms of local coordinates ${\overrightarrow{r}}_A^l$ one has to determine a transformation matrix (T) which maps atoms B, C and D to a local coordinate system where B is placed at origin, C on the z-axis and D in the y-z plane. We need the inverse of the transformation matrix (I) to compute r⃗_A. The details of how to calculate the inverse transformation matrices are given in the supplementary information. Here we give the final result

$$\begin{array}{c}I=\left[\begin{array}{cccc}{u}^x& u^y& u^z& 0\\ v^x& v^y& v^z& 0\\ w^x& w^y& w^z& 0\\ {r_B}^x& {r_B}^y& {r_B}^z& 1\end{array}\right]\\ {\overrightarrow{r}}_A=I·{\overrightarrow{r}}_A^l\end{array}$$ (2)

where û, v̂ and ŵ are unit vectors of local coordinate system which are functions of position vectors of B(r⃗_B), C(r⃗_C) and D(r⃗_D).

Scheme 2

If a CG site consists of a combination of atoms A and B and if the position of one of them is known (say B, r⃗_B), the position of the other site (r⃗_A) is estimated as

$${\overrightarrow{r}}_A=2{\overrightarrow{r}}_{AB}-{\overrightarrow{r}}_B$$ (2)

where r⃗_AB is the distance between A and B CG sites.

Scheme 3

If atoms A, B, C and D lie in a plane and atom pairs B/C and B/D are combined into CG particles, then the positions of atoms B (r⃗_B), C(r⃗_C) and D(r⃗_D) are estimated as

$$\begin{array}{l}{\overrightarrow{r}}_{\mathit{ABCD}}={\overrightarrow{r}}_{\mathit{ABC}}+{\overrightarrow{r}}_{\mathit{ABD}}-2{\overrightarrow{r}}_A\\ {\overrightarrow{r}}_B={\overrightarrow{r}}_A+d_{AB}{\widehat{r}}_{\mathit{ABCD}}\\ {\overrightarrow{r}}_C=2({\overrightarrow{r}}_{BC}-{\overrightarrow{r}}_B)+{\overrightarrow{r}}_B\\ {\overrightarrow{r}}_D=2({\overrightarrow{r}}_{BD}-{\overrightarrow{r}}_B)+{\overrightarrow{r}}_B\end{array}$$ (3)

where r⃗_A is the unit vector in direction of A, r⃗_BC and r⃗_BD are the position vectors of CG particles BC and BD, respectively, r⃗_ABC is the bond vector between atom A and the BC particle, r⃗_ABD is the bond vector between atom A and the BD particle and d_AB is the bond distance between A and B.

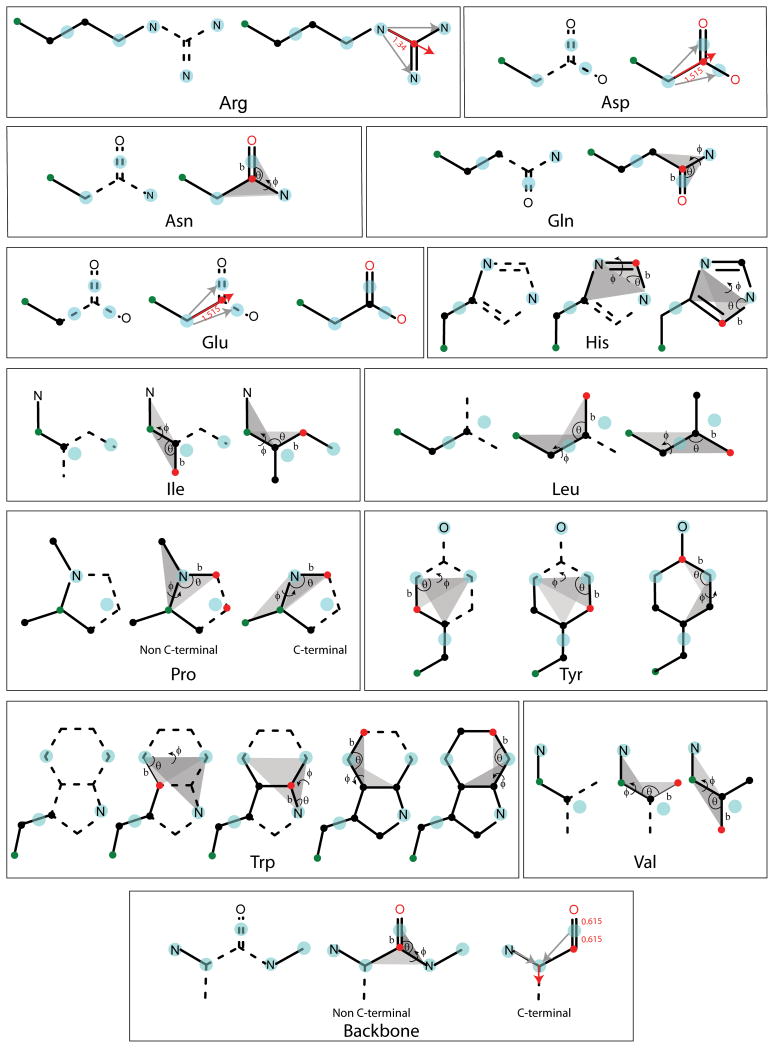
Backbone reconstruction requires only the reconstruction of carbonyl C and O atoms from the combined CO particle (see Fig. 2). The main assumption is that C, O, N and C_α atoms all lie in the same plane. For non C-terminal residues, the carbonyl C atom is estimated according to scheme 1 from the CO, C_α (i), and N(i+1) sites. The carbonyl O position is then calculated according to scheme 2 using Eq. 1 and the positions of the CO and C particles. For C-terminal residues where N(i+1) is not available, the reconstruction is slightly more complicated. First the C_α-N and C_α-CO bond vectors are averaged The resulting normalized vector is used to define the direction of the C and O atom from the CO particle. C and O positions are estimated based on the standard C-O bond length. The reconstruction of the C and O in C-terminal residues places the C and O atoms in the same plane as the C_α and N particles, which is not correct in general but serves as a reasonable approximation for C-terminal residues. As a result, the position of C-terminal carbonyl atoms is estimated with less accuracy as for non-C-terminal residues.

Figure 2.

Protein all-atom reconstruction sequence is shown for all relevant amino acids. The CG sites are shown in cyan, existing (reconstructed) atomistic sites in black and atoms to be reconstructed in red. The backbone C_α atom is also shown in green. For reconstruction according to scheme 1, the associated bond lengths, angles and dihedrals are denoted by b, θ and φ respective. Also shown are the planes defining the dihedral angle φ. For the reconstructions using scheme 3, the r⃗_ABC and r⃗_ABD vectors are denoted in grey and r⃗_ABCD is denoted in red (see text for details). For clarity resonance of double bonds is not shown.

In rebuilding side chains, the C_β atom is reconstructed for all residues except Ala, Asn, Asp, Gly and Val, where C_β is either absent (Gly) or corresponds directly to a CG site based on scheme 1 from the backbone atoms C_α, N and C using the bonding parameters given in Table 2. C_γ atoms of residues Arg, Gln, Glu, His, Leu, Lys, Met, Phe, Trp and Tyr, and the S_γ atom of Cys, the O_γ atom of Ser and the O_γ1 atom of Thr are estimated using scheme 2 (Eq. 1) from the position of the SC1 particle and the reconstructed C_β atom.

C_γ and O_δ1atoms of Asn and C_δ and O_ε1atoms of Gln are reconstructed like the backbone using scheme 1 based on positions of C_β, SC2 (combination of C_γ and O_δ1atoms), and SC3 (N_δ2atom) for Asn and C_δ atom, SC2 (combination of C_δ and O_ε1atoms) and SC3 (N_ε2atom) for Gln (See Fig. 2).

In the case of Asp and Glu with indistinguishable SC2 and SC3 particles, scheme 3 (Eq. 2) is employed for the reconstruction of the C_γ, O_δ1, O_δ2and C_δ, O_ε1, O_ε2atoms, respectively. This scheme uses C_β, SC2 (combination of C_γ and O_δ1), and SC3 (combination of C_γ and O_δ2) for Asp and C_γ, SC2 (combination of C_δ and O_ε1), SC3 (combination of C_δ and O_ε2) for Glu (see Fig. 2)

The C_ε1and C_δ2atoms of His are also estimated using scheme 1 from the positions of SC2 (N_ε2), SC3 (N_δ1) and the C_γ atom (see Fig. 2).

In the case of Ile and Val, the SC1 particle is located at the midpoint of the virtual triangle spanned by the C_β, C_γ1and C_γ2atoms. In order to reconstruct C_γ1and C_γ2using scheme 1, values of the dihedral C_γ1-C_β-C_α-N and the dihedral C_γ2-C_β-C_α-N are required. It is possible to get these dihedral values by using the position of SC1 particle and calculating the virtual dihedral between the N, C_α, C_β and SC1 sites (χ). Because the relative torsion between the two planes (C_α, C_β, C_γ1, C_γ2) is 120°, the dihedrals for reconstructing the C_γ1and C_γ2atoms are χ ± 60° (see Table 2). The same procedure also applies for the reconstruction of C_δ1and C_δ2atoms in Leu with the only difference that C_γ, C_β and C_α atoms are used as input as shown in Fig. 2.

For non N-terminal Pro, the C_δ atom is reconstructed using scheme 1 from positions of N(i), C_α(i) and C(i−1) atoms. In case of N-terminal Pro, the C_δ atom is estimated from the positions of the N, C_α and C_β atoms using scheme 1 (see Table 2). The C_γ atom in either of above cases is rebuilt from the positions of the reconstructed C_β and C_δ atoms and the SC1 particle similar to scheme 2.

The C_δ1and C_δ2atoms of Phe and Tyr residues are reconstructed using scheme 1 from the positions of the SC2 (C_ε1) and SC3 (C_ε2) particles and the reconstructed C_γ position. The C_ζ atom of Tyr is estimated in same way using the positions of the reconstructed C_γ and C_δ1atoms and the SC2 particle.

In case of Trp, the position of C_δ2is estimated according to scheme 1 from the positions of the SC3 (C_ε3), SC4 (C_ζ2), and SC2 (N_ε1) particles; C_ε2is obtained from the SC2, SC4, and SC3 particles; C_δ1is obtained from SC2 and the C_ε2and C_δ2atoms; C_ζ3 is obtained from SC3, and the C_δ2, and C_ε2atoms; C_η2atom is obtained from SC4, and the C_ε2and C_δ2atoms.

PRIMONA Model for Nucleic Acids

The CG model for nucleic acids is illustrated in Figure 1 and the mapping of the CG particles to all-atom space is listed in Table 1B. The CG particles are chosen to preserve the polar/charged particles of the sugar-phosphate backbone and also the hydrogen bond donors and acceptors of the base moiety. Some charged atoms are combined with the neighboring carbon atom to achieve good space filling at the CG level. The CG particles representing the sugar-phosphate backbone are named as BBx, while those belonging to the base are named as BSx (where, ‘x’ is the number denoting the particle), with the exception of the particle that represents sugar ring C2′ in DNA (known as BDx) or C2′-O2′ in RNA (known as BRx). The backbone for both DNA and RNA consists of 8 CG particles, with particles BB8, BB7, BB3 and BB5 placed at the atomic centers of the two phosphate oxygens, O3′ and the ribose O4′. Apart from these particles, a combined CG particle BB6 represents O5′ and C5′, while BB4 combines C4′ and C5′. The particle BB4 does not contribute significantly towards the electrostatic potential of the nucleic acid backbone, but is essential to maintain proper space filling and a better description of the sugar pucker, which is an important structural signature for differentiating polymorphic double-helical forms of DNA and RNA. The CG particle BD2 represents sugar atom C2′ of DNA, while BR2 is a combined particle of C2′ and O2′ of RNA. Finally, BB1 is located at the center of the glycosidic bond between the ribose and the nucleotide bases combining C1′ and N9 in purines and C1′ and N1 pyrimidines.

The guanine base is represented by five CG particles, four of which correspond to the atomic centers of the nitrogenous hydrogen bond donor/acceptors (BS1, BS2, BS3 and BS5). The CG particle BS4 represents the carbonyl group by combining C6 and O6.

Adenine is represented by four CG particles, all of them located on the atomic positions of the ring nitrogen atoms (BS1, BS2, BS3 and BS4).

Cytosine is represented with four CG particles with BS1 representing the carbonyl group C2-O2, BS2 and BS3 corresponding to the ring nitrogen atoms, and BS4 combining the ring carbons C5 and C6. The particle BS4 maintains the space filling of the cytosine base but is not essential for accurate all-atom reconstruction.

Thymine has five CG particles: BS1 and BS2 represent the two carbonyl groups; BS2 corresponds to the ring nitrogen; BS4 and BS5 represent the methyl group and ring carbon C6, respectively. Again BS5 is used for proper space filling and to preserve the hydrophobicity and bulkiness of the methyl group that leads to many sequence specific interactions of ligands with nucleic acids.

Finally, uracil consists of four CG particles: BS1 and BS3 represent the two carbonyl groups, BS2 corresponds to the ring nitrogen and BS4 combines the ring carbons C5 and C6.

Reconstruction Scheme for Nucleic Acids

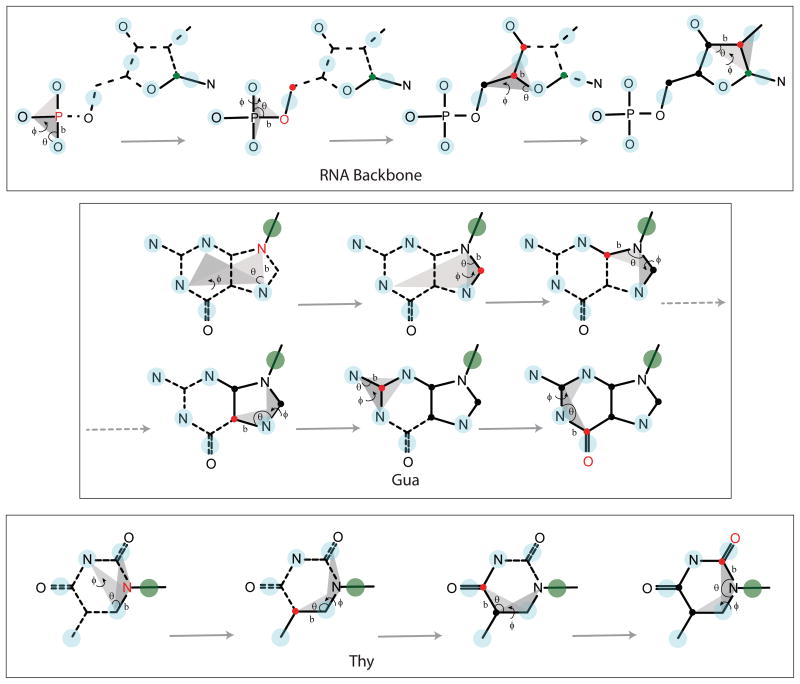
The DNA and RNA nucleotides are reconstructed using scheme 1 and scheme 2 as described in the protein reconstruction section. Most of the nucleic acid particles are reconstructed using scheme 1, which requires atomic positions of three particles to reconstruct the unknown atom. As in the protein model, the nucleic acid CG particles are designed in such a way that all heavy atoms could be reconstructed using standard bonding geometries. The distance, angle and dihedral values used for the reconstruction are taken from long MD simulations of DNA and RNA duplexes in explicit water and are tabulated in Table 2B. A schematic diagram describing the reconstruction procedure for the RNA backbone and for the purine and pyrimidine bases are provided in Figure 3. As an example, nucleic acid backbone atom P is reconstructed using the bond length P-O2P, the angle P-O2P-O3′, and the dihedral P-O2P-O3′-O1P which involves the phosphate group of the nucleotide. Scheme 1 is used to construct P using the atomic positions of BB8 (O2P), BB3 (O3′) and BB7 (O1P) with standard bond length, angle, and dihedral values.

Figure 3.

Nucleic acid reconstruction procedure with the same nomenclature and coloring scheme as that of Figure 2. The position C1′ is shown in green for backbone reconstructions, while CG particle BB1 is shown in green for base reconstructions.

Similarly, O5′ is constructed using the position of the newly reconstructed P, BB7 and BB8. The position of C5′ is calculated using scheme 2 and the positions of O5′ and the CG particle BB6 (the combined particle of C5′ and O5′). C4′ is reconstructed using scheme 1 and the particle BB5 (O4′), the atom C5′ and BB4 (the combined particle of C4′ and C3′). C3′ is rebuilt using scheme 2 and the position of C4′ and the CG particle BB4.

The sugar ring atoms are not used to reconstruct the atom C1′ as that would involve the non-planar atoms of the sugar ring defining the ring pucker which can vary for different nucleic acid conformations. Instead, the glycosidic bond atom N9 (for purine) is first constructed using the distance N9-N7, the angle N9-N7-N1 and the dihedral N9-N7-N1-N3 (which is zero for the planar base atoms). The CG particles representing ring nitrogen atoms of Ade or Gua are used in this case.

The distance and angle used for the reconstruction of base atoms have constant values for a specific base geometry, while the dihedral is either 0 or 180 according to the definition of the planes used for the dihedral. Like N9, the atom N1 for Cyt is reconstructed using the distance N1-BS2, the angle N1-BS2-BS3 and the dihedral N1-BS2-BS3-BS4, where BS4 is the combined particle of C5 and C6. The atom N1 for Thy is reconstructed using the distance N1-BS5 (BS5 is the ring atom C6), the angle N1-BS5-BS2 and the dihedral N1-BS5-BS2-BS1, where BS1 represents the C2-O2 carbonyl group. The atom N1 for Ura is reconstructed using the distance N1-BS2, the angle N1-BS2-BS3 and the dihedral N1-BS2-BS3-BS4, where BS3 and BS4 are the combined particles for the two carbonyl groups. After calculating the position of N9 or N1 atom for purine or pyrimidine, the ring atom C1′ is constructed using scheme 2 and the position of N9/N1 and the CG particle BB1, which is a combination of two atoms defining the glycosidic bond. While this completes the reconstruction of the sugar-phosphate backbone of the DNA bases, for RNA, the atom C2′ is reconstructed using scheme 1 and the bond C2′-C3′, the angle C2′-C3′-C1′, and the dihedral C2′-C3′-C1′-BR2, where BR2 is the combined particle of C2′ and O2′. Finally, the position of O2′ is obtained using scheme 2 and position of C2′ and the CG particle BR2.

The base ring atom C8 of purine is reconstructed using scheme 1 and atoms N9, N7, and N1, where the CG particle representing N7 and N1 is used for Ade or Gua. The atom C4 is constructed using atoms N9, C8, and N7, while C5 is constructed using N7, C8, and N9. The atom C2 is reconstructed using N2, N1, and N3 for Gua, while N3, C4, and C5 are used for Ade. The position of atom C6 is reconstructed using N1, C2, and N3 in purines. For Gua, the atom O6 is reconstructed using scheme 2 and the position of N6 and CG particle BS4 (the combined particle of N6 and O6).

The atom C6 for cytosine is reconstructed using scheme 1 and N1, BS2, and BS3, while C5 is obtained using scheme 2 and positions of C6 and the CG particle BS4 (the combined particle of C5 and C6). Reconstruction of C4 is then followed using scheme 1 and atoms C5, C6, and N1. The atom C2 is further reconstructed using scheme 1 and atoms N1, C6 and C5, while O2 is obtained from C2 and CG particle BS1 (combined particle of C2 and O2).

The reconstruction of thymine is started by obtaining the position of C5 using scheme 1 and atoms BS5, N1, and BS1, where BS1 is the combined particle for the carbonyl group C2-O2. C4 is reconstructed using C5, BS5, and N1, while O4 is constructed using scheme 2 from the positions of C4 and the CG particle BS3, which is a combination of C4 and O4. This is followed by the reconstruction of C2 using scheme 1 with the atoms N1, BS5, and C5. The final atom O2 is obtained using scheme 2 and the positions of C2 and the CG particle BS1, which is the combined particle of C2 and O2.

Uracil is obtained by reconstructing C6 using scheme 1 with N1, BS2, and BS3. This is followed by the construction of C5 from the positions of C6 and the CG particle BS5, which is the combination of C6 and C5. C4 is obtained from C5, C6, and N1, while O4 is reconstructed using C4 and the CG particle BS3 (the combined particle of C4 and O4). Similarly, C2 is reconstructed from N1, C6, and C5 using scheme 1, followed by the atom O2 from C2 and the CG particle BS1 (combination of C2 and O2) using scheme 2.

PRIMO Software

Programs for the generation of PRIMO/PRIMONA models and to carry out the all-atom reconstructions described here have been implemented as extensions to the MMTSB Tool Set⁴¹. These tools are freely available from the authors upon request and will be distributed as part of future releases of the MMTSB Tool Set.

All-atom reconstruction from other protein CG models

The all-atom reconstruction from PRIMO is compared here also to all-atom reconstructions from other types of CG models. In particular, CG models consisting only of C_α atoms (CA), only backbones (BB), only side chain centers (SICHO), and side chain centers plus C_α (SICHO/CA) are considered to cover the most commonly used coarse-graining schemes. From SICHO and SICHO/CA models, all-atom models were reconstructed using the reconstruction procedure implemented in the MMTSB Tool Set⁴¹. It should be noted, that although the original SICHO model was projected onto lattice for computational efficiency⁹, we used here an off-lattice version. SCWRL 4.0³⁵ was used to reconstruct all-atom structures from BB models. In order to reconstruct all-atom structures from C_α-only models, a backbone was first completed with the MMTSB Tool Set⁴¹ and SCWRL 4.0³⁵ was then used to reconstruct the all-atom structures from the completed backbone. The different methods were also compared in terms of timing. All timing results were obtained on a single-core 2.8 GHz Xeon processor.

Test Sets

The reconstruction procedure of the protein version of PRIMO was tested with a set of 611 non-homologous proteins of varying sizes from 19 to 839 residues (average size: 113 residues) and 120 folded, mis-folded, and unfolded conformations of chicken villin head piece. The structures in the non-homologous decoy set were first minimized to with the CHARMM22 force field to relieve steric clashes and add missing atoms. The decoy set for villin head piece consisting of 120 structures was generated with SICHO model and later converted to atomic resolution with the MMTSB Tool Set. Both test sets are described in more detail previously⁴¹ and are available upon request from the authors. In all cases, reconstructed structures were compared to the structures of the test sets and not to the original X-ray structures.

Reconstruction of nucleic acids was tested with DNA and RNA duplexes and 15 diverse DNA-protein and RNA-protein complexes. The choice of these structures involves large protein-DNA complexes like the nucleosome core particle and mismatch repair protein complex on one hand and complicated RNA structures like the ribonuclease, ribosomal and viral capsid protein-RNA complexes on the other. The complexes contain nucleic acids with 24 to 298 base pairs and proteins with 84 to 1761 amino acids. 5′-phosphate groups were added if missing in the nucleic acid structures. The PRIMONA model can only handle regular nucleotides at this time and hence our dataset for nucleic acid-protein complexes did not include any structures containing modified nucleotides such as tRNA.

Results and Discussion

Reconstruction of protein structures

In order to determine the reconstruction accuracy, structures from a number of test sets were compared to all-atom models that were reconstructed from CG representation of the same structures. Furthermore, the reconstruction accuracy of PRIMO are also compared to other CG representations (see results in Table 3).

Table 3. Comparison of reconstructed models from PRIMO, SICHO/CA, SICHO and BB, and CA.

Average all-atom RMSD values obtained from various reconstruction methods in Å along with standard deviations in brackets.

	PRIMO	SICHO/CA	SICHO	BB	CA
All	0.099 (0.04)	0.885 (0.26)	1.280 (0.24)	1.454 (0.31)	1.703 (0.31)
back	0.046 (0.02)	0.590 (0.20)	0.988 (0.19)	0 (0)	0.564 (0.15)
side	0.131 (0.06)	1.111(0.33)	1.526 (0.30)	2.082 (0.43)	2.366 (0.42)
Cα	0 (0)	0 (0)	0.760 (0.18)	0 (0)	0 (0)
Cα+Cβ	0.075 (0.03)	0.376 (0.20)	0.940 (0.21)	0.065 (0.03)	0.345 (0.10)
Arg	0.056 (0.04)	1.215 (0.50)	1.634 (0.48)	3.045 (0.87)	3.322 (0.94)
Asn	0.011 (0.01)	1.275 (0.44)	1.562 (0.44)	1.825 (0.64)	1.967 (0.62)
Asp	0.018 (0.01)	0.966 (0.43)	1.299 (0.41)	1.691 (0.61)	1.837 (0.58)
Cys	0.105 (0.06)	0.586 (0.57)	1.079 (0.57)	0.967 (0.62)	1.234 (0.67)
Gln	0.067 (0.05)	1.192 (0.48)	1.543 (0.47)	2.290 (0.65)	2.490 (0.69)
Glu	0.098 (0.05)	0.984 (0.50)	1.385 (0.42)	2.049 (0.53)	2.294 (0.55)
His	0.075 (0.04)	1.412 (0.45)	1.652 (0.52)	2.119 (1.06)	2.525 (1.13)
Ile	0.244 (0.15)	0.842 (0.53)	1.484 (0.48)	1.166 (0.59)	1.433 (0.59)
Leu	0.205 (0.13)	0.915 (0.48)	1.264 (0.43)	1.306 (0.55)	1.589 (0.62)
Lys	0.067 (0.04)	1.025 (0.45)	1.507 (0.44)	2.399 (0.61)	2.673 (0.69)
Met	0.067 (0.04)	1.262 (0.78)	1.697 (0.65)	1.954 (0.74)	2.472 (1.00)
Phe	0.059 (0.03)	1.149 (0.60)	1.613 (0.60)	1.967 (1.22)	2.352 (1.21)
Pro	0.110 (0.07)	0.471 (0.43)	1.042 (0.41)	0.313 (0.17)	0.686 (0.40)
Ser	0.114 (0.06)	0.621 (0.46)	1.066 (0.41)	1.154 (0.36)	1.342 (0.40)
Thr	0.136 (0.05)	0.836 (0.50)	1.420 (0.47)	1.075 (0.51)	1.333 (0.49)
Trp	0.053 (0.03)	1.171 (0.89)	1.972 (0.80)	2.679 (1.70)	3.131 (1.72)
Tyr	0.059 (0.03)	1.277 (0.75)	1.760 (0.76)	2.156 (1.47)	2.718 (1.51)
Val	0.291 (0.16)	0.669 (0.42)	1.145 (0.38)	0.726 (0.39)	0.928 (0.38)

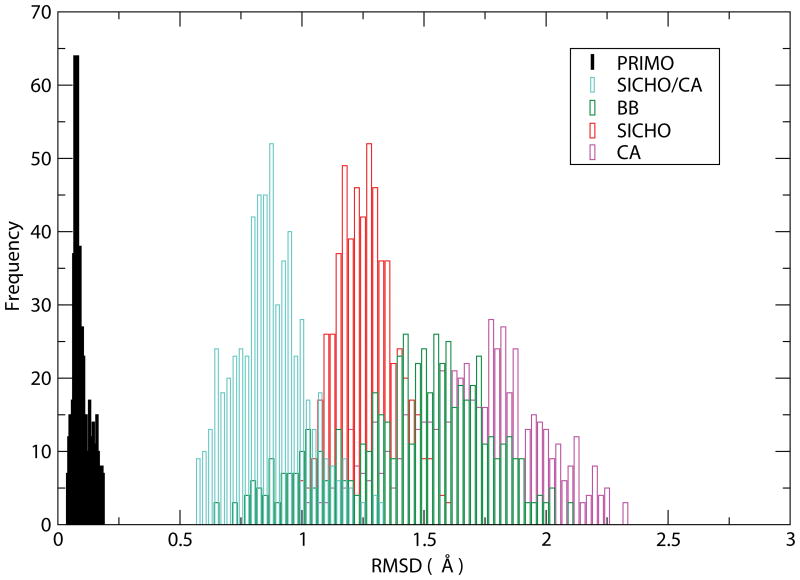
The overall average all-atom RMSD (excluding hydrogens that were not reconstructed) for all-atom structures rebuilt from PRIMO was 0.099 Å. This value is much smaller than all-atom reconstructions from all of the other CG representations that range from 0.885 Å for SICHO/CA to 1.703 Å for C_α-only models. Such a small RMSD with PRIMO indicates that PRIMO does indeed preserve near-atomistic accuracy despite a significant reduction in the number of interaction sites. The distribution of deviations of reconstructed structures is shown in the histograms in Figure 4. It can be seen that the accuracy of models reconstructed from PRIMO remains within the narrow range of 0.05–0.25 Å which indicates uniformly high accuracy across different structures and places an upper limit of 0.25 Å in terms of the accuracy that can be expected from PRIMO. Both the average and distribution of reconstruction accuracies are much greater for other CG representations. Reconstructions from BB or C_α-only models, for example, may exceed 2 Å RMSD for some structures which means that a clear one-to-one correspondence to all-atom models cannot be established with such CG models. It should be noted that a number of other reconstruction procedures are available to rebuild all-atom models from C_α traces^30,34, backbones^31,35,36, or side chains³¹. However, to the best of our knowledge none of these methods provide a substantially better performance in terms of reconstruction accuracy compared to the methods tested here.

Figure 4.

RMSD histograms for protein reconstruction accuracy for PRIMO, SICHO/CA, BB, SICHO, and CA models.

Table 3 also provides information about the variation of the reconstruction accuracy as a function of backbone and sidechains. The reconstruction of the backbone from PRIMO is more accurate than the reconstruction of the side chains (0.047 Å vs. 0.137 Å). The backbone reconstruction is still significantly more accurate than other models (about 0.6 Å accuracy), except for the BB model where the backbone is preserved in full detail.

PRIMO reconstruction accuracy for side chains varies considerably from 0 Å for Ala to 0.29 Å for Val. Four side chains have RMSDs significantly above the average: Ile (0.244 Å), Leu (0.205 Å) and Val (0.290 Å). In these residues, three heavy atoms are combined into a CG site which involves multiple steps in the reconstruction procedure and thus introduces additional uncertainties. The larger uncertainties for Ile, Leu, and Val could be addressed by introducing additional interaction sites, however, because of the hydrophobic nature of these residues, the side chain interactions are less specific than for polar or charged residues and a somewhat larger uncertainty in individual atomic positions is acceptable as long as the overall side chain packing is preserved.

The reconstruction procedure was also tested for different conformations of the chicken villin headpiece. While detailed results are given in Table S1 in the supplementary material, basically the same conclusions can be made that reconstruction from PRIMO preserves atomistic details within deviations of about 0.1 Å RMSD while reconstruction from other CG models is near 1 Å accuracy or worse. However, we also used these two test sets to examine the practically more relevant question of whether reconstructed structures are located in the same energetic minimum as the original structures. This was tested by comparing free energy estimates according to the CHARMM22 all-atom force field in combination with generalized Born implicit solvent⁴² before and after coarse-graining/all-atom reconstruction. We find that none of the reconstruction schemes yield a good correlation between the energies of the original and reconstructed models. Even although the reconstructed PRIMO models on average differ by only 0.1 Å all-atom RMSD the energies are only moderately correlated (r=0.369) due to several outliers which have large energies due to small deviations from standard bonding values.

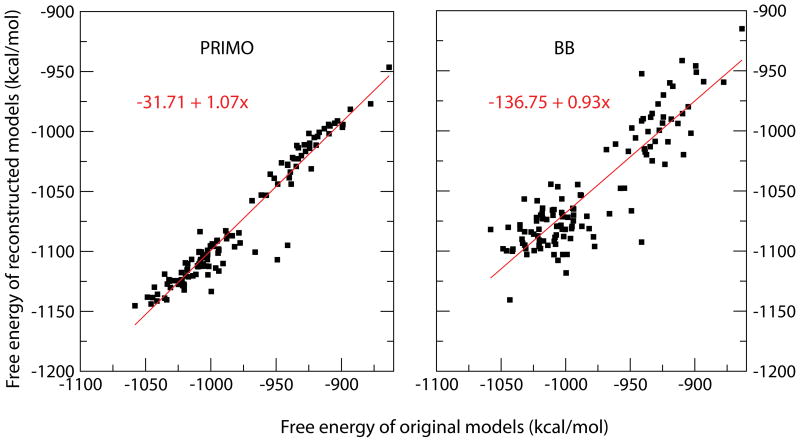
To find out whether a short minimization can rectify problems with reconstructed structures, we subjected the reconstructed models to 25 steps of steepest decent minimization. Figure 5 shows that a reasonable energetic correlation is observed after such a short minimization both when reconstructing from PRIMO models and from BB models using SCWRL. However, the correlation and slope is significantly better with the models generated from PRIMO despite the exact reproduction of the backbone and extensive optimization that is part of the SCWRL reconstruction procedure. PRIMO achieves a correlation coefficient of 0.967 and a slope of 1.07 vs. a correlation coefficient of 0.887 and a slope of 0.93 with BB models reconstructed using SCWRL (see Fig. 5).

Figure 5.

Correlation of all-atom free energy estimates for original and structures reconstructed from PRIMO (top) and BB (bottom) models for villin head piece after short minimization.

Reconstruction from SICHO and SICHO/CA models resulted in poor energetic correlation after brief minimization. However, a longer minimization protocol consisting of 25 steps of steepest decent (SD) followed by 100 steps of adopted-basis Newton-Raphson (ABNR) minimization was able to restore some energetic correlation with the SICHO-based models. After such a more extended optimization, correlation coefficients were 0.947 for PRIMO reconstruction, 0.893 for BB models, 0.754 for SICHO/CA, 0.725 for SICHO models, and 0.811 for CA models of villin conformations.

From the above results it is clear that PRIMO allows near-atomistic reconstruction with highly correlated energetics to all-atom force fields after very brief minimization. However, the additional cost due to any minimization limits the ability to use CG models in multi-scale models. It is possible to devise an alternate reconstruction scheme where all bonded parameters in the reconstructed model are constrained to minima in the force field so that the resulting all-atom models are at low energies. However, such a scheme would violate the one-to-one correspondence between the all-atom and CG levels in the sense that a PRIMO model generated from a reconstructed all-atom model would deviate from the initial PRIMO model used for the reconstruction. Whether such fuzziness in matching CG and all-atom models has practical consequences in the context of multi-scale modeling schemes is unclear at this time. Such issues go beyond the scope of the present paper and will be revisited in the future when exploring the application of PRIMO within multi-scale frameworks.

Reconstruction of protein-nucleic acid complexes

We have tested the reconstruction accuracy of PRIMONA on DNA and RNA duplexes and a number of DNA-protein or RNA-protein complexes. Table 4A tabulates the average RMSD values for different types of nucleic acid residues while Table 4B shows the average RMSD for each of the structures from the test set. The comparison between the initial all-atom structures and the PRIMONA-reconstructed structures show very low RMSD values with an average of 0.066 for all five nucleotides. The best accuracy is achieved for guanine (0.045 Å RMSD), the worst for uracil (0.092 Å RMSD). Generally, the RNA residues have slightly larger RMSD compared to those of DNA (average RMSD of 0.077 for RNA and 0.051 for DNA). Apart from greater uncertainty with uracil this is a consequence of combining C2′-O2′ into a single particle in RNA vs. C2′ in DNA which is mapped directly onto a CG site. RMSD values for protein-nucleic acid complexes that are also reported in Table 4B highlight that both macromolecules (protein as large as 1761 residues in 2O8B, DNA as large as 294 base pairs in 1KX5 and RNA as large as 298 base pairs in 2A64) can be represented at the coarse-grained level while preserving quasi-atomistic accuracy with our reconstruction procedure.

Table 4.

Table 4A. Average RMSD deviations in Å for reconstructed DNA and RNA duplexes and selected protein-nucleic acid complexes.
Nucleic acid Type	PDB	Type of complex	RMSD in Å with PRIMONA
			All	Nucleic acid	Protein
DNA	7BNA	B-DNA dodecamer	0.069	0.069	-
	1NVP	TFIIA/TBP-DNA complex	0.076	0.048	0.082
	1L3S	DNA-polymerase I fragment-DNA complex	0.069	0.046	0.070
	1KX5	Nucleosome core particle	0.067	0.046	0.079
	1JB7	Telomeric protein-DNA G- quartets complex	0.072	0.045	0.075
	1J75	Z-DNA-protein complex	0.101	0.056	0.111
	1GT0	POU/HMG/DNA ternary complex	0.082	0.047	0.096
	1BPX	Human polymerase Beta- DNA complex	0.166	0.078	0.181
	2O8B	Human MSH2/MSH6- mismatch-DNA complex	0.107	0.079	0.109
RNA	3CZW	RNA duplex	0.086	0.086	-
	3BNP	Human mitochondrial ribosomal decoding site	0.078	0.078	-
	1KUQ	16S rRNA-ribosomal protein complex	0.100	0.078	0.129
	1I6U	16S rRNA-S8 ribosomal protein complex	0.073	0.078	0.069
	1A34	Satellite tobacco mosaic virus-RNA complex	0.094	0.103	0.091
	2A64	Bacterial ribonuclease P RNA	0.075	0.075	-

Table 4B. Average RMSD deviations in Å for different nucleic acid types in reconstructed DNA and RNA.
All nucleic acid residues		0.066 (0.020)
DNA	All residues	0.051 (0.020)
	Ade	0.045 (0.009)
	Gua	0.048 (0.011)
	Thy	0.048 (0.010)
	Cyt	0.064 (0.034)
RNA	All residues	0.077 (0.011)
	Ade	0.073 (0.007)
	Gua	0.071 (0.006)
	Ura	0.092 (0.012)
	Cyt	0.078 (0.006)

To our knowledge, this is the first reconstruction scheme for a CG model that can handle both DNA and RNA structures and provides atomic-level accuracy. At the same time, the coarse-graining scheme of PRIMONA preserves the ability to represent diverse sugar puckers and backbone dihedral conformations that are important for nucleic acid structures.

Timing

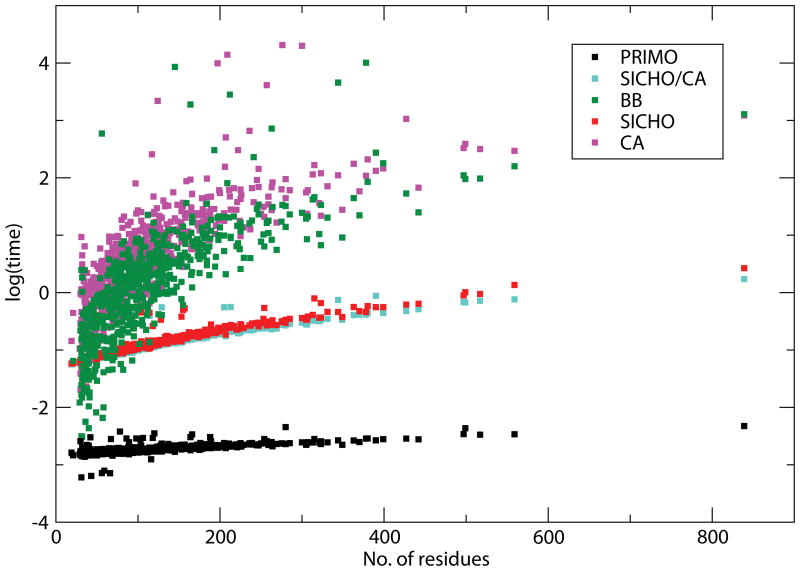
An important consideration in multi-scale schemes is the time it takes to interconvert between different resolutions. While the generation of CG representations is generally rapid, all-atom reconstruction schemes typically take at least seconds which is too long for use in a tightly coupled MM/CG scheme where all-atom representations need to be recalculated for example at every time step in a multi-scale molecular dynamics simulation. We therefore compared the timing of each of the reconstruction methods used here. The results are shown in Fig. 6. From the graph it is evident that PRIMO reconstruction is the only method that can be accomplished in negligible time and almost independent of molecular size because of the analytical nature of the reconstruction procedure. The average time for all-atom reconstructions with PRIMO is 0.08 seconds. In comparison, the average times for reconstruction from other models are 0.33, 0.35, 2.43 and 2.10 seconds for SICHO/CA, SICHO, BB and C_α-only reconstructions respectively. These numbers were obtained by averaging timing for 100 reconstructions and by subtracting time for input/output operations. It is found that reconstruction times involving SCWRL increase significantly with the number of residues. SICHO and SICHO/CA timings are considerably faster than that of SCWRL because rotamer selection from the library is faster due to a prior knowledge of side chain (rotameric) center.

Figure 6.

Comparison of timing for different reconstruction methods as a function of residue size. PRIMO: black, SICHO/CA: cyan, SICHO: red, BB: green, CA: purple. The time (in seconds) is shown in logarithmic scale.

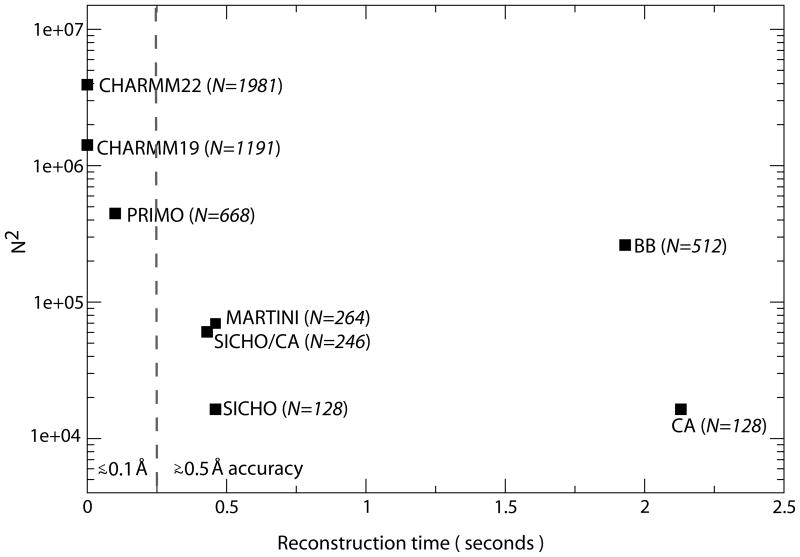
The time to reconstruct all-atom models may be put in relation to anticipated simulation speeds with a given models. While actual simulation speeds depend on interaction potentials, sampling methods, integration time steps, and treatment of solvent environment, a common point of comparison is the number of particles for a given protein system and a hypothetical computational cost that scales as O(N²), the scaling for non-truncated pairwise interactions. Fig. 7 shows such a comparison for a 128-residue protein for the different models discussed here. In addition the popular Martini force field is included. All-atom reconstruction from the Martini model was achieved by generating an approximate side chain center from the side chain particles and following the SICHO/C_α reconstruction procedure. It can be seen that PRIMO falls into the intermediate regime between all-atom and united-atom models (that do not any cost to reconstruct all-atom models) and more coarse-grained models that require significant time for all-atom reconstruction. If the accuracy of the reconstruction is taken into account, PRIMO distinguishes itself from the other coarse-grained models and thereby reflects a new type of coarse-grained models with a significantly reduced number of interaction sites but very fast and accurate all-atom reconstruction.

Figure 7.

Number of interaction sites vs. all-atom reconstruction speed for a variety of different models. The number of interaction sites is shown as N² to indicate the relative cost of non-truncated pairwise interactions.

Conclusions

In this work we have introduced a new coarse-graining scheme for proteins and nucleic acids, called PRIMO and PRIMONA, respectively. The PRIMO model is the first CG model that offers near-atomistic resolution while still significantly reducing the number of interaction sites by a factor of three to four over fully atomistic models. The high-accuracy reconstruction to within 0.1 Å RMSD of all-atom structures is accomplished by relying on assumptions of standard molecular bonding geometries and is achieved solely with analytical functions without the need for geometric optimizations. Furthermore, the energies of reconstructed all-atom structures become highly correlated with the original structures after brief minimization. Because of the close correspondence between the CG and all-atom levels, the PRIMO/PRIMONA model is ideally suited for the development of transferable coarse-grained models of proteins and nucleic acids through close parameterization based on all-atom force fields and for applications within multi-scale frameworks.