Predicting the reaction coordinates of millisecond light-induced conformational changes in photoactive yellow protein

Abstract

Understanding the dynamics of large-scale conformational changes in proteins still poses a challenge for molecular simulations. We employ transition path sampling of explicit solvent molecular dynamics trajectories to obtain atomistic insight in the reaction network of the millisecond timescale partial unfolding transition in the photocycle of the bacterial sensor photoactive yellow protein. Likelihood maximization analysis predicts the best model for the reaction coordinates of each substep as well as tentative transition states, without further simulation. We find that the unfolding of the α-helical region 43–51 is followed by sequential solvent exposure of both Glu46 and the chromophore. Which of these two residues is exposed first is correlated with the presence of a salt bridge that is part of the N-terminal domain. Additional molecular dynamics simulations indicate that the exposure of the chromophore does not result in a productive pathway. We discuss several possibilities for experimental validation of these predictions. Our results open the way for studying millisecond conformational changes in other medium-sized (signaling) proteins.

Investigation of the dynamics of large conformational changes in proteins leads to a better understanding of their functioning. Molecular simulation can complement experiments by modeling the dynamical time evolution of biomolecular systems in atomistic detail. Yet, even though straightforward all-atom molecular dynamics (MD) can now access the microsecond regime, simulating the kinetics of folding and other large conformational changes in proteins at ambient conditions has been limited to relatively small (model) proteins (1). Here we show how the transition path sampling technique enables investigation of the atomistic dynamical pathways for the millisecond timescale partial unfolding transition in a biologically relevant signaling protein, the photoactive yellow protein (PYP). Moreover, analysis of the ensembles of unbiased molecular trajectories allows the extraction of the (possibly complex) reaction coordinates.

PYP is a water soluble blue-light photo receptor from Halorhodospira halophila (2, 3) composed of 125 amino acids and a covalently bound chromophore (para-coumaric acid, pCA) (4). The protein folds into a Per–Arnt–Sim core capped by an N-terminal domain (5, 6). Upon the absorption of a blue-light photon, PYP undergoes many different conformational rearrangements, culminating in the formation of the signaling state. The first steps in signaling state formation are the isomerization of pCA, on a picosecond timescale (7), followed by a proton transfer, taking place within microseconds (8, 9). These reactions result in an intermediate pB ^′ with pCA in a strained configuration and a negative charge on a buried glutamate (Glu46) (10, 11). As a consequence, the protein partially unfolds to expose pCA and Glu46 to bulk water (12 –14), completing the formation of the signaling state pB.

PYP is an excellent model signaling protein because it is easily accessible for the application of a wide variety of experimental techniques, and hence, many of its characteristics have been elucidated. For example, the initial events of the photocycle have become much clearer with the use of ultrafast spectroscopy techniques (15) and time-resolved x-ray crystallography (16). Still, revealing the structural and dynamical details of the poorly understood mechanism of the submillisecond unfolding process at high resolution, e.g., by time-resolved NMR, remains elusive (13). As stated above, molecular simulation can provide atomistic detail for protein conformational change, complementary to experiments (17). For instance, a recent study using QM/MM showed that proton transfer can only occur when the negative charge on Glu46 is sufficiently stabilized (18). Molecular simulation also provided insights into the formation of the signaling state pB. Replica exchange MD (REMD) simulations indicated that the formation of pB involves the unfolding of the α-helical region 43–51 and the solvent exposure of Glu46 and pCA (14). The predicted signaling state showed remarkable agreement with the NMR structure of the pB state of the N-terminally truncated mutant Δ₂₅-PYP (13, 19).

Notwithstanding the success of the signaling state prediction, the room temperature kinetic mechanism by which pB is formed remained hidden due to the nature of the REMD sampling method. In this work we aim to provide mechanistic details at atomistic resolution of the submillisecond unfolding process of PYP by molecular simulation. However, while the conformational transitions occur too fast for high-resolution experimental methods, they are too slow to occur spontaneously in fully atomistic MD simulations. These long timescales originate from relatively high free-energy barriers between (meta)stable states, hampering efficient sampling of conformational space when using conventional MD. Moreover, protein conformational changes in general can occur via a myriad number of pathways, and hence, observation of a single event will not be conclusive. To avoid the long waiting times inherent in conventional MD of activated processes, many rare event simulation techniques have been developed (20). Whereas these methods are well suited for computing free-energy barriers and other thermodynamic properties, they often fail to yield mechanistic insight at ambient conditions. Examples are the artificial acceleration of the dynamics by raising the temperature (e.g., REMD 21) and methods that bias the system toward the barrier region along a predefined reaction coordinate (RC). In the latter case, the RC can be complex, and a poor choice might lead to a wrong reaction mechanism, bad sampling statistics, and a poor estimate of the rate constants (22). The transition path sampling (TPS) (23) algorithm avoids both these drawbacks by collecting an ensemble of short reactive trajectories (in our case, several ns) connecting a predefined initial and final state, without prior knowledge of the transition state region. In contrast, a straightforward MD trajectory would require many microseconds to achieve the same. The TPS method enables evaluation of the mechanism, the transition state ensemble, and the RC in terms of order parameters (22). A good RC must be able to predict the so-called committor (24). This can be tested by performing a committor analysis (22 –24), which requires running multiple additional MD simulations from putative transition state configurations. More efficient committor analysis algorithms include a GNN approach (25), a Bayesian path statistical analysis (26), and a likelihood maximization (LM) method (27, 28). The latter approach has the advantage of requiring only the results from a TPS simulation.

We employ TPS simulations to investigate the mechanisms underlying the transition from the folded pB ^′ state to the unfolded signaling state pB of PYP (see Fig. 1). Starting in the intermediate state pB ^′, instead of in the receptor state, allows us to use classical force fields, thus avoiding prohibitively costly quantum chemical computations. Any TPS simulation requires definitions for the initial and final states and an initial trajectory connecting these states, which can be provided by, for instance, REMD simulations (14, 19). Starting from the pB ^′ state, we sampled four transitions to end up in the pB state (see Fig. 1). Our findings indicate that productive signaling state formation starts with losing α-helical content in the chromophore binding pocket, followed by solvent exposure of Glu46, and subsequent exposure of pCA. The state with only pCA solvent exposed is an off-pathway intermediate. Whether pCA or Glu46 become solvent exposed first correlates with the presence of a salt bridge between Asp20 an Lys55.

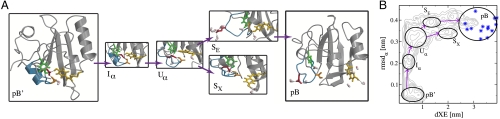
Fig. 1.

The reaction network of the pB ^′ to pB transition. (A) Structures of metastable states in the pB ^′ to pB transition (see main text for a description). The helix α3 is rendered blue, and the stick models represent relevant residues: pCA (yellow), Glu46 (red), Tyr42 (green) and Thr50 (orange). Black dotted lines indicate hydrogen bonds. Water molecules are shown as pink and white stick models. (B) Free-energy profile projected in the dXE - rmsd _α plane. The labeled ellipses roughly indicate the location of the metastable states. The gray contour lines indicate the free-energy profile obtained from a previous REMD simulation, separated by 1k _B T (19). The blue stars indicate the conformations obtained by time-resolved NMR on a mutant of PYP (13).

This work shows that TPS enables the sampling of millisecond timescale processes at room temperature and at atomistic detail. Additional LM analysis can predict relevant reaction coordinates for each conformational rearrangement in PYP. For the loss of α-helical content, we find that the best RC involves the overall deviation from the folded helix, but also a helical hydrogen bond and the distance between Pro54 and Ala44. RCs of the exposure of pCA and Glu46 involve the breaking of hydrogen bond interactions in the chromophore binding pocket, between pCA, Glu46 and Tyr42. The reaction coordinates we found for the various transitions do not directly involve (bulk) water order parameters. Nevertheless, bulk water provides additional stabilization of the negatively charged Glu46 and the hydrophilic chromophore, leading to their solvent exposure. Indeed, the formation of pB is slowed down and dramatically reduced at lowered humidity (29).

Our findings provide previously undescribed insights in the mechanism of light-induced unfolding in PYP, which potentially can be tested by experiments. Probing the existence of the predicted off-pathway intermediate experimentally requires sensitive time-resolved measurements that specifically target either pCA or Glu46, and preferably both. By isotopically labeling pCA and/or Glu46, vibrational shifts, due to changes in the local environment of these residues, can be monitored using FTIR (30) or resonance Raman spectroscopy (31). Furthermore, the fluorescence of the single tryptophan in PYP is quenched by energy transfer to pCA and strongly reflects changes in orientation of either pCA or Trp119 (32). Other techniques, such as time-resolved THz spectroscopy (33) and time-resolved optical rotatory dispersion (34), might be sensitive enough to detect the intermediates. The prediction that a salt bridge is correlated with the unfolding route can also be addressed experimentally. Recently, a time-resolved diffusion study suggested that the N-terminal region, including Asp20, loses α-helical content after the proton transfer (35). Varying the ionic strength of the environment of PYP has a profound effect on the formation of pB, as shown by time-resolved absorption and fluorescence spectroscopy (36). These observations agree well with our findings that the favored unfolding pathway starts with the disruption of the Asp20-Lys55 ionic bond. Furthermore, future mutagenesis experiments altering the properties of this salt bridge could test our predictions. Changing Asp20 and Lys55 to alanine could lead to an accelerated photocycle, although we believe this effect to be minor, because other residues can form a similar ionic linkage (36). A promising experiment would be to modify the ionic bond to a disulphide bridge, by mutating Asp20 and Lys55 into cysteine. This would lead to less light-induced unfolding and significant retardation of the photocycle.

In addition to the experiments, future simulation studies might focus on computing the rate constant by for instance transition interface sampling (37) or milestoning (38). Also, the detection of important transitions might be automated, e.g., by means of applying Markov State Model approaches (39).

Results and Discussion

TPS Simulations.

Previous REMD simulations showed that the light-induced conformational change of PYP involves the unfolding of helix α3 (region 43–51), followed by the solvent exposure of pCA and Glu46. Also, free-energy profiles from these simulations suggested the presence of metastable states occurring during the formation of pB (19). Fig. 1 B displays such a free-energy profile as a function of the distance dXE, between pCA (phenolic oxygen O4′) and Glu46 (atom CD) and rmsd _α, the RMSD of helix α3, with respect to the conformation in the NMR structure (19). The figure shows several minima that represent the various (intermediate) states visited by the protein during the unfolding process. The label pB ^′ indicates the fully folded state; I _α indicates a state in which the helical conformation of helix α3 has partially disappeared. U _α denotes a state in which this region is completely unfolded, while Glu46 and pCA are still inside the protein. The labels S _E and S _X correspond to states with a solvent exposed Glu46 and pCA, respectively. Finally, pB indicates the signaling state, with both pCA and Glu46 exposed to solvent. The REMD simulations provided the stable state definitions (see Table S2).

Our first attempt to sample the transition from pB ^′ to pB directly with TPS was severely hampered by the presence of the metastable intermediate states I _α, U _α, S _E, and S _X, which caused very long trajectories (i.e., much longer than 10 ns). Therefore, we split up the unfolding transition of pB ^′ to pB into four separate transitions. These processes are: 1) the loss of α-helical structure in helix α3 (pB ^′ - I _α); 2) solvent exposure of Glu46 (U _α - S _E); 3) solvent exposure of pCA (U _α - S _X); and 4) solvent exposure of pCA following Glu46 (S _E - pB). We refrained from performing a TPS simulation of the (S _X - pB) transition, as this route turned out to be not productive.

We performed TPS simulations of these four transitions, using the definitions for the initial and final states listed in Table S2 and taking initial trajectories from either REMD simulations (19) or high temperature MD trajectories. Table 1 lists the sampling statistics for the four TPS simulations. The average path length indicates that the molecular timescale for the transitions is on the order of ns. Note that the actual reaction times are much longer.

Table 1.

Statistics of the TPS ensembles. The average path length is a weighted average over the whole ensemble. Decorrelated pathways have lost the memory of the previous decorrelated pathway. The aggregate time is the ensemble aggregate length

	pB′ - Iα	Uα - SE	Uα - SX	SE - pB
acceptance	41%	25%	38%	44%
avg. path length	105 ps	1.8 ns	1.5 ns	1.7 ns
accepted paths	3847	305	584	311
decorr. paths	180	18	7	29
aggregate time (μs)	1.0	2.3	2.3	1.2

Unfolding of Helix α3.

An initial TPS simulation of the pB ^′ - U _α transition yielded very long pathways due to the presence of intermediate state I _α. Therefore, we performed a TPS simulation of the pB ^′ - I _α transition. Figs. 2 A and B show representative pathways, plotted onto the path density (see SI Text) from both the pB ^′ - U _α and the pB ^′ - I _α TPS simulations. Once the protein is in intermediate state I _α it relaxes within nanoseconds to the U _α state in which the helix is completely unfolded, indicating that the barrier separating I _α and U _α is lower than the barrier between pB ^′ and I _α.

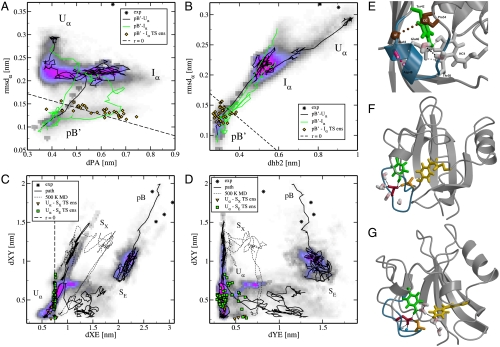
Fig. 2.

Path density plots and transition state estimates of the pB ^′ to pB transition. (A and B) Path density and representative pathways showing the unfolding of helix α3 in two representations, (A) the (dPA,rmsd _α) plane and (B) the (dhb2,rmsd _α) plane. The three pathways shown originate from the pB ^′ - U _α (black) and the pB ^′ - I _α (green) TPS simulations. The pathways are plotted onto the path density (see SI Text) from both TPS simulations. Yellow diamonds indicate the transition state ensemble. (C and D) Path density and representative pathways showing the solvent exposure of Glu46 and pCA in (C) the (dXE,dXY) plane and (D) the (dYE,dXY) plane. The dashed path is taken from a high temperature MD simulation of the S _X state at 500 K. The yellow triangles and the green squares indicate the transition state ensembles for U _α - S _X and U _α - S _E, respectively. The path density ranges from white (no paths) to magenta (many paths) via gray and blue. The labels indicate the different states. Experimental data is shown as stars. The dashed line shows the predicted dividing surface r = 0. (E) TS estimate of the pB ^′ - I _α transition. Helix α3 is shown in blue, hydrogen bond 2 is depicted as a pink stick model. Atoms of Pro-54 and Ala-44 used for the calculation of dPA are shown as brown spheres. Other residues making up the chromophore binding pocket are shown as light gray sticks. (F and G) TS estimates of solvent exposure of (F) Glu46 and (G) pCA. Representation is as described in Fig. 1. In (G) two backbone N-H groups are also shown as blue-white stick models.

For PYP, we have identified, based on visual inspection of the pathways and on chemical intuition, about 75 order parameters that could be involved in the signaling state formation (see Table S1). Only a fraction of these are used for the stable state definitions (see Table S2). We computed these order parameters for the entire shooting point ensemble of the pB ^′ - I _α TPS simulation. Application of the LM analysis yielded the linear combination of up to three order parameters that best describe the RC (see Table 2). When considering only single order parameters for the pB ^′ - I _α transition the best model for the RC is rmsd _α. Adding more order parameters to the RC model is significant only if the log-likelihood (ln L) increases by at least 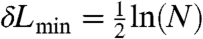(28), with N the number of shooting points. For this simulation N = 4149 and hence, δL _min = 4.17. Including the number of water molecules around Tyr42, nw _Y improves ln L by a value of δL = 19. Using three order parameters, ln L improves significantly by δL = 13 when nw _Y is replaced by dhb2 and dPA, respectively the length of the backbone hydrogen bond between Ala44 and Asp48 and the distance between Pro54 and Ala44. Application of the Bayesian path statistical analysis (26) confirms these findings (see Figs. S1 and S2).

Table 2.

LM analysis of the TPS ensembles sampled in three TPS simulations. The minimal improvement of likelihood required to accept an additional order parameter in the RC is indicated for each analysis as δL _min. All distances are given in nm.

n	ln L	reaction coordinate
pB′ - Iα transition δLmin = 4.17
1	−2117	3.89–29.10 × rmsdα
2	−2098	3.88–26.35 × rmsdα - 0.19 × nwY42
3	−2085	5.11–16.81 × rmsdα - 4.68 × dhb2 - 2.55 × dPA*
Uα - SE transition δLmin = 3.06
1	−280	-2.03 + 2.70 × dXE*
2	−277	-3.94 + 2.88 × dXE + 1.50 × dEK
3	−275	-4.00 + 2.81 × dXE + 1.55 × dEK + 0.40 × cos(ϕ45)
Uα - SX transition δLmin = 3.33
1	−396	-6.40 + 6.92 × dXYcom
2	−388	-5.92 + 4.25 × dXYcom + 3.01 × dXE
3	−383	-5.05 + 5.02 × dXYcom - 2.51 × dXEcom + 4.30 × dXE*

^*RC used to model the committor.

The description for the optimal RC obtained with the LM analysis agrees with visual inspection of the pB ^′ - I _α pathways. In pB ^′ Tyr42 is completely shielded from bulk water by Ala44 and Pro54. During the unfolding of helix α3, water molecules form hydrogen bonds to Tyr42, facilitated by Ala44 and Pro54 moving away from each other. This hydration is transient, as dPA decreases again when helix α3 is completely unfolded (see Fig. 2 A). dPA is not the only relevant order parameter, because the LM analysis also identified the dhb2 as an important contribution to the RC. Interestingly, including the helical hydrogen bonds between Asn43 and Gly47 (dhb1), and between Ala45 and Ile49 (dhb3) also increased the ln L significantly but not as much as the Ala44-Asp48 hydrogen bond. These three hydrogen bonds are located at the solvent accessible side of helix α3. The remaining two helical hydrogen bonds, located at the protein side of helix α3, do not contribute at all to the RC.

The LM analysis predicts that structures with r = 0 are transition states. From the pB ^′ - I _α path ensemble we extracted the conformations with the 3-variable RC (see Table 2) within the interval r∈[-0.05,0.05]. This TS ensemble is also plotted in Fig. 2 A and B, together with the predicted r = 0 dividing surface. Visual inspection suggested that this ensemble is quite uniform. Fig. 2 E displays a typical configuration from this predicted TS ensemble. The relevant order parameters that contributed most to the RC are highlighted. Helix α3 is clearly still in a helical conformation, indicating that the TS is very close to the folded state. We explicitly computed the committors of the predicted r = 0 structures (see SI Text), and confirmed that 30% of the predicted structures are true transition states (with committor values between 0.3–0.7). The other conformations had committors close to either zero or unity. We refrained from performing a full committor analysis due to excessive computational costs. The TS ensemble for the pB ^′ - I _α transition is thus very sensitive to small changes in the protein conformation, indicating it involves a relatively narrow barrier.

Solvent Exposure of Glu46 and pCA.

Once the helix is unfolded and the protein is in the U _α state, the solvent exposure of both Glu46 and pCA constitutes the next step in the formation of pB. Trajectories from the REMD simulations (19) showed the solvent exposure of either Glu46 or pCA only, subsequently followed by the solvent exposure of the other residue. Using REMD trajectories as initial pathways, we performed two TPS simulations, one for the solvent exposure of Glu46 (U _α - S _E) and one for the exposure of pCA (U _α - S _X). Definitions of the initial and final states are listed in Table S2. Both transitions proved difficult to sample, as the processes of exposing pCA or Glu46 involve long and diffusive paths. Figs. 2 C and D show representative, uncorrelated pathways for the U _α - S _E and the U _α - S _X transitions, plotted onto the path density. Note that these room temperature pathways are fully decorrelated from the initial REMD trajectories.

The U _α - S _E transition.

LM analysis of the U _α - S _E shooting point ensemble reveals that the best RC for the exposure of Glu46 to the solvent is dXE, the distance between Glu46 and pCA (see Table 2). As pCA is an important hydrogen bond donor, this distance parameter indicates that disruption of the hydrogen bond network around Glu46 inside the protein leads to Glu46’s solvent exposure. Adding more order parameters does not significantly improve ln L, although adding the backbone torsions of Ala45 and the distance between Glu9 and Lys110 almost reached the threshold. The latter parameter is a salt bridge that is involved in the formation of pB (36). For the best RC model r = dXE, the TS ensemble is plotted as squares in Fig. 2 C and D. Fig. 2 F shows one of these transition states. This prediction agrees with visual inspection of the pathways, suggesting that the main characteristic of the transition is the shift in the hydrogen bond network of the acidic side-chain of Glu46. Here, the water molecules do not enter the protein, but rather Glu46 moves to the solvent. On the U _α side of the barrier Glu46 interacts with Tyr42, Thr50, and the protein backbone. On the S _E side water molecules provide stabilization for Glu46. The TS conformation in Fig. 2 F shows a balance between these two hydrogen bonds networks, in which pCA does not participate.

The U _α - S _X transition.

LM analysis of the U _α - S _X simulation shows that dXY ^com, the distance between Tyr42 and pCA, is the single order parameter with the highest ln L. This RC indicates that the strength of the hydrogen bond between pCA and Tyr42 governs the solvent exposure of pCA. Allowing for multiple order parameters in the LM analysis reveals that including dXE significantly improves the log-likelihood. Subsequently adding dXE ^com, the center of mass distance between pCA and Glu46 to the RC is barely deemed significant (see Table 2). The transition state ensemble is plotted as triangles in Fig. 2 C and D and in Fig. S3. Fig. 2 G displays one of the predicted conformations of the TS ensemble for the pCA solvent exposure, showing a partially solvated pCA with a water-mediated hydrogen bond between Tyr42 and pCA. Glu46 is still located inside the protein and does not interact with water molecules at all but instead forms hydrogen bonds to N-H groups in the protein backbone to stabilize its negative charge. Visual inspection of the U _α - S _X TPS trajectories show Tyr42 and Glu46 interacting, while pCA detaches from this hydrogen bond network and becomes (partially) solvated.

Final Unfolding Step Toward pB.

Our results so far seem to suggest the existence of two possible pathways, both leading from the U _α state to the unfolded signaling state pB, each with its own intermediate state, S _E and S _X. However, the final state pB has both Glu46 and pCA solvent exposed. To test how accessible pB is from the intermediates, S _E and S _X, we performed 10 ns of conventional MD starting from conformations from both S _E and S _X at ambient and elevated temperatures. At 300 K no additional solvent exposure events occur, indicating that both S _E and S _X are sufficiently metastable to prevent a fast escape from these states. To reach pB thus involves crossing another barrier. We performed MD simulations starting from the same conformations at higher temperatures (425, 450, 475, and 500 K). One 500 K simulation samples the solvent exposure of Glu46 from the S _X state (indicated as a dashed curve in Fig. 2 C D), but instead of reaching pB, pCA goes back into the protein, followed by solvent exposure of Glu46. Because we do not observe the S _X - pB transition even at high temperature we label S _X a “dead end.” In contrast, starting from the S _E state, solvent exposure of pCA occurs already at 425 K. Thus, it is easier for pCA to leave the protein once Glu46 is already solvent exposed than vice versa. Using this unfolding MD trajectory as an initial path, we performed a TPS simulation of the S _E - pB transition (see Table 1). This transition proved to be less difficult to sample than the U _α - S _X transition. The representative S _E - pB pathway plotted in Figs. 2 C and D indeed reaches pB and the end point overlaps well with the experimental data (plotted as stars) (13). Examination of the pathways reveals that in the barrier region pCA is hydrated and still inside the protein. The chromophore also forms hydrogen bonds with the side chains of Asp97 and Arg52. Experimental studies have indicated that Arg52 and Tyr98 may act as gating residues, facilitating hydration of the chromophore binding pocket (40).

The Most Likely Pathway is Correlated with a Salt Bridge.

We have shown that when Glu46 exposes to the solvent first, formation of the signaling state will follow, whereas if pCA goes out first, the protein enters a dead-end route. What triggers the protein to choose either the successful or the unproductive pathway? Comparison of the two TS estimates for U _α - S _E and U _α - S _X (Figs. 2 F and G) reveals that the region 43–51 has a different conformation depending on whether Glu46 is exposed. Searching for interactions that may influence the conformation of the α3 region, we found a salt bridge between Asp20 and Lys55, which also exists in the pB ^′ and receptor states. This ionic bond is absent in the U _α - S _E TS but is present in the U _α - S _X TS. To find out whether this salt bridge is broken in U _α we extended several of the TPS trajectories in the backward time direction. Starting from four U _α endpoints from U _α - S _E paths and four U _α endpoints from U _α - S _X trajectories, we performed 10 ns MD simulations, denoted toS _E and toS _X, respectively. Fig. 3 A shows a 2-D free-energy plot (negative logarithm of the probability) as a function of rmsd _α and dDK, the salt-bridge distance between CG of Asp20 and NZ of Lys55. While this plot does not represent a converged free-energy landscape, it clearly shows that U _α splits into two substates with different dDK distance. In the toS _X simulations, dDK = 0.5 nm, indicating that Asp20 and Lys55 have a strong electrostatic interaction. In contrast, dDK ranges from 0.9 nm to over 2.5 nm in the toS _E simulations, indicating that the salt bridge is broken and unlikely to reform. Figs. 3 C and D show configurations with an open and a closed salt bridge. These observations suggest that the absence of the DK salt bridge leads to the Glu46 exposure, while its presence results in solvent exposure of the pCA first. As Asp20 is located in the N-terminal domain of PYP, the conformation of this domain is correlated to the presence of the salt bridge, and thus to whether the protein will choose a dead end or a productive pathway.

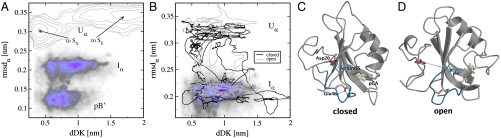
Fig. 3.

Characterization of the Asp20-Lys55 salt bridge. (A and B) Path density of the pB ^′ - I _α transition plotted in the (dDK,rmsd _α) plane. (A) The gray lines show a free-energy profile obtained from eight MD simulations of the U _α state at 300 K. (B) The black and gray lines show 100 ps smoothed MD trajectories initiated from the I _α state. (C and D) Structures from U _α with (C) a small and (D) a large value for dDK. Residues Asp20, Lys55, Glu46 and pCA are shown as stick models.

To determine when exactly the salt bridge breaks, we also plotted the TPS path density of the pB ^′ - I _α transition in Fig. 3 A. While the path density on the pB ^′ side shows already signs of two substates, the path density on the I _α end exhibits an even clearer picture, with peaks corresponding to a formed salt bridge at dDK = 0.6 nm and broken salt bridge with dDK = 9 nm and dDK = 1.1 nm. We performed 32 MD simulations of 15 ns at 300 K of the I _α state. Starting conformations were taken from end points in the pB ^′ - I _α TPS simulation. Half of these had a value below 0.6 nm for dDK (“closed”) and the other half had a value higher than 0.9 nm for dDK (“open”). Eight systems reached the U _α state within 15 ns, four of which started with an open salt bridge and four with a closed salt bridge. Fig. 3 B shows the (100 ps smoothed) trajectories of the simulations that crossed the low I _α - U _α barrier. All these simulations sample both open and closed conformations for the salt bridge, suggesting that fluctuations in U _α determine which unfolding pathway the protein will take.

Methods

Preparation of the system and all MD simulations were performed with the GROMACS 3.3.1 package (41), employing the Gromos96 43a1 force field (42, 43) in combination with the SPC water model (44). Transition path sampling (22, 23) carried out an unbiased sampling of MD trajectories that connect predefined initial and final ensembles of states, in the current case the different metastable states in PYP as derived from previous REMD simulations (19). TPS is a random walk through trajectory space, where new trajectories are generated from old trajectories by a shooting algorithm and accepted with a Metropolis rule (22, 23). Here, we use the one-way, flexible path length TPS algorithm as previously implemented and applied to protein systems (37). The likelihood maximization (LM) analysis (27, 28) screens many linear combinations of order parameters as candidate RCs and predicts the one that best describes the data. Required as input for this procedure is the ensemble of shooting point configurations belonging to accepted trajectories and the rejected shooting points. The Bayesian path statistical analysis (26) is used to confirm the predicted reaction coordinates. In addition, we computed the committor for certain configurations by starting many MD trajectories initialized with random momenta and measuring the fraction of paths that reaches the final state. Details on these methods can be found in SI Text.