Impact of spatial clustering on disease transmission and optimal control

Abstract

Spatial heterogeneities and spatial separation of hosts are often seen as key factors when developing accurate predictive models of the spread of pathogens. The question we address in this paper is how coarse the resolution of the spatial data can be for a model to be a useful tool for informing control policies. We examine this problem using the specific case of foot-and-mouth disease spreading between farms using the formulation developed during the 2001 epidemic in the United Kingdom. We show that, if our model is carefully parameterized to match epidemic behavior, then using aggregate county-scale data from the United States is sufficient to closely determine optimal control measures (specifically ring culling). This result also holds when the approach is extended to theoretical distributions of farms where the spatial clustering can be manipulated to extremes. We have therefore shown that, although spatial structure can be critically important in allowing us to predict the emergent population-scale behavior from a knowledge of the individual-level dynamics, for this specific applied question, such structure is mostly subsumed in the parameterization allowing us to make policy predictions in the absence of high-quality spatial information. We believe that this approach will be of considerable benefit across a range of disciplines where data are only available at intermediate spatial scales.

The spatial distribution of organisms is viewed as critically important for determining population dynamics. Numerous examples from the epidemiological and ecological literature have shown that spatial structure has a profound impact on how population-level dynamics emerge from individual-level behavior (1,2,3–4). For infectious diseases in particular, where transmission generally occurs over relatively short distances, spatial structure (and in particular the spatial distribution of sessile hosts) plays three roles: hosts that are far from sources of infection are at very little risk, local transmission and depletion of susceptible hosts can dramatically reduce the speed of epidemic growth, and local control measures can be applied using spatial proximity as a method of targeting at-risk hosts. These three elements are present for any spatial distribution of hosts, but are generally amplified by clustering. The impact of spatial structure on the spread of infectious disease has been examined for humans (5), wildlife (6, 7), and livestock (8, 9), but the ability to make useful quantitative predictions relies on the availability of good quality spatial and epidemic data. In recent years, considerable research has focused on the spread of livestock infections due to the extreme vulnerability of the livestock industry, the potential economic costs, the variety of strategies that can be used as control measures, and the costs associated with such measures.

The UK 2001 epidemic of foot-and-mouth disease (FMD) provides a prime example of what can be achieved when comprehensive spatial models, detailed host data, and detailed case data are brought together. This approach provided important insights and guidance during the 2001 epidemic (8, 9) and has been used retrospectively to investigate a range of alternative control strategies (10,11–12). Whilst the location of livestock holdings in the United Kingdom is known, the same is not true for many other countries. In particular, in the United States, although the US Department of Agriculture holds an agricultural census every 5 years, most of the census data that reside in the public domain are aggregated to county-scale, preserving the anonymity of farmers but losing valuable spatial information. From the 2007 census, we find that the US’s livestock industry is dominated by cattle, with 936,669 premises recorded as having cattle; 83,134 as having sheep; 75,442 as having pigs (or hogs); and 91,462 as having goats.

In the event of an outbreak of FMD (or other livestock disease) in the United States, it is likely that predictions from mathematical models would be an integral part of policy making and would help advise regarding optimal control strategies to limit the size and duration of the outbreak. The likelihood of a particular farm being infected with FMD is based upon many factors, including the type and size of the holding in question, but the proximity to other infectious farms has been consistently demonstrated to be the main contributing factor (13,14–15). It therefore seems vital to have complete information regarding the location and size of all farms in the region of an outbreak.

Given that information is only available at the county-scale in the United States, we consider the impact of making the naive assumption that farms are distributed randomly within each county. This assumption still allows us to implement spatial models, but loses any clustering that is present in the distribution of farms. In particular, we consider how a model using a random distribution of farms would be parameterized to match the temporal profile of an observed epidemic and show that this approach has strong applied benefits even in the absence of fine-scale positional data.

Model

The model used throughout this paper is an adaptation of the model developed by Keeling et al. (2001, 8) during the 2001 FMD epidemic and discussed in detail elsewhere (16). The rate at which an infectious farm i infects a susceptible farm j is given by

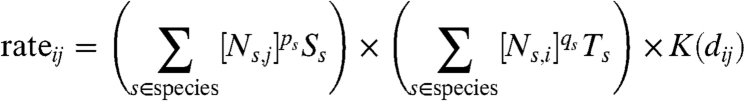[1]

N_s,i is the number of livestock species s recorded as being on farm i, S_s and T_s measure the species-specific susceptibility and transmissibility, d_ij is the distance between farms i and j, and K is the distance-dependent transmission kernel, estimated from contact tracing (8). Power law parameters p_s and q_s account for a nonlinear increase in susceptibility and transmissibility for species s as animal numbers on a farm increase (SI Text). This form of spatial transmission model has been shown to provide an accurate and robust description of the UK 2001 outbreak of foot-and-mouth, capturing national, regional, and individual-level patterns of infection (16,17–18). In keeping with observations from the UK 2001 epidemic, we assume that a farm acts as a single infectious unit, and once infected it enters the latent period (which lasts 5 days) before becoming infectious where it remains until its livestock are culled. We note that, although this assumption may be valid for regions of the United States with similar farming practices as the United Kingdom, very different behavior may occur in very large cattle farms (19). All parameters for the United Kingdom county models using the true farm locations take the same values as that obtained for the UK 2001 epidemic, as discussed in detail elsewhere (16).

During the UK foot-and-mouth outbreaks in 2001 and 2007, in addition to routine culling of infected premises (IPs), all “premises where animals have been in direct contact with infected animals or have, in any way, become exposed to infection” were defined by veterinary judgement as dangerous contacts (DCs) and were preemptively culled in an effort to control disease. In our model, DCs are identified based on their risk of infection from the infecting source, biased toward identifying farms that have actually been infected (11), assuming that veterinary judgement benefits from a range of detailed local knowledge. Here we assume that once identified all livestock on an infected premises are culled within 24 h and all associated preemptive culling is undertaken within 48 h; this is somewhat optimistic but was one of the principle aims during the 2001 epidemic.

Retrospective analysis of the 2001 epidemic has determined that a policy of IP and DC culling alone would have resulted in a much larger epidemic than actually occurred, implying that other culling strategies, including culling of contiguous premises and farms within 3 km of IPs, aided in disease control (12). With this in mind, we investigate the effectiveness of ring culling in addition to IP and DC culling. When an IP is reported, all farms within a particular radius of that IP will be targeted for culling. The radius of the ring is allowed to vary between simulations and we seek the radius which minimizes the “epidemic impact,” defined as the total number of farms with livestock culled (either as IPs, DCs, or ring-culled farms). The optimal ring size is clearly a tradeoff between too little culling, in which case the epidemic is not controlled, and too much culling, in which case an excessive number of farms lose their livestock.

Methodological Approach

Our goal is to test the accuracy of predictions made when detailed spatial data are not available and the only recourse is to randomly scatter farms across the landscape. As a first step, and focusing on regions where the location of farms (and their livestock composition) is known, we perform multiple simulations to determine the range of epidemics that can be expected. Using the same spatial data, we then conduct further simulations to determine the ring-cull radius (R_T) that minimizes the total number of farms losing livestock to either infection or control.

In the second step, we distribute the same farms randomly within the given region to simulate the effects of not having the precise spatial locations but knowing the heterogeneities in the number of livestock. At this stage, we could simulate epidemics on the random spatial dataset using the original UK parameters. However, it is naive to assume that the UK 2001 parameters could be used for a future epidemic in a different farm demography. We therefore choose instead to mimic what would happen during a real epidemic and estimate the parameters that allow us to accurately predict the epidemic behavior—in this case, matching the attack rates obtained using the randomly distributed farms to the attack rates obtained using the true spatial location of farms. This parameterization is achieved by fitting a two-parameter description of the transmission kernel (determining kernel width and height, K_w and K_h, respectively) and uses the same approach as outlined in Tildesley et al. (2008, 16): To provide a best fit, parameters are found that minimize the average difference on a daily basis between “simulated epidemics” from the random-location data to the “observed epidemic” simulated on the true spatial data for the cumulative number of farms reported and culled as well as the cumulative number of cattle and sheep on such farms (SI Text). Using this random distribution of farms, but with a refined parameterization, we determine the optimal ring-cull radius for the random-location reparameterized model (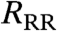). Comparison between R_T and 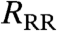, and the epidemic impact under both culling regimes, provides important insights into the necessity of detailed spatial data for informing policy. In all simulations, a single farm is randomly selected and seeded with infection. The onset of ring culling occurs 48 h after the first case is reported, with subsequent ring culling occurring 48 h after the reporting of the relevant IP. In essence, our approach is to use the first set of simulations (using the true spatial locations) as a surrogate for real epidemic data; this has the advantage that a variety of control options can be tested and compared using both true and randomized spatial data. We now examine how this approach can be applied to county-level data from the United Kingdom and the United States, as well as hypothetical data with arbitrary clustering.

County-Level Data

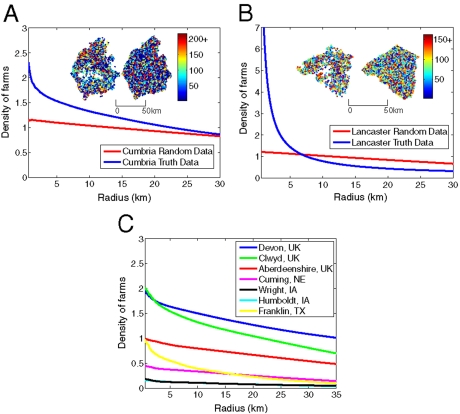
We begin by examining spatial location data for the county of Cumbria in the United Kingdom. Cumbria has a high density of large cattle farms and, as a consequence, was one of the worst affected areas in the UK 2001 outbreak. Comparing the true and randomized locations (Fig. 1A), we see significant local clustering as captured by the average density of farms around each farm. We note that the farm-centered density for randomized spatial locations is not constant (as theoretically expected) due to the finite scale of the region. For counties in the United States, although the true locations of farms are generally unknown, farms were geolocated for a handful of counties representing a diverse mixture of livestock operations within the United States. This spatial and heterogeneous farm information was generated using local and national agricultural, regulatory, farm subsidy, business, and tax assessor databases containing addresses or coordinates of farms. The locations of the farms were then georeferenced, visually checked, and modified if necessary with aerial imagery, Google Streetview, Google and Mapquest maps, and other ancillary data. In a few cases where available data sources were not able to locate the number of farms that were indicated by the agricultural census, probable farm locations were based on land parcels that were predominantly pasture, had farm buildings, and had access to a drinking water source. Fig. 1B shows example data from Lancaster County, PA, where we observe far stronger local clustering than in Cumbria despite a comparable density of farms. This pattern of local clustering of farms is consistent across other counties in the United Kingdom and the United States (Fig. 1C), although the strength of clustering and the overall density of farms differs considerably. We show later that these farm-centered density plots can be captured as the sum of exponentials. For the counties in the United States considered here, precise parameter values are unknown. Should UK parameters be applied to the United States, the lower overall farm density means that epidemics do not generally take off. Therefore, to provide epidemics of a sufficient size and duration for comparison with the random-location model, we scale the UK values of K_h and K_w for the clustered distribution of farms (“true data”) according to the relative densities of these counties in comparison to the United Kingdom, thus preserving the overall number of contacts between farms. It is not intended that the epidemic impacts given for the US counties should be in any way indicative of the actual epidemic impacts in the event of an epidemic—rather it is the level of agreement between the results for the true data and “random data” that is of importance for targeting of control in the event of future epidemics.

Fig. 1.

Graphs showing the average density of farms against radius around each farm as the radius varies for the true data (blue line) and random data (red line) in (A) Cumbria, UK and (B) Lancaster County, PA. Insets show farm locations for each respective county for the true data (left plot) and the random data (right plot). The color scale on the insets shows the number of cattle on each farm. (C) Average density of farms against radius around each farm for the true data for Devon, Aberdeenshire, and Clwyd in the United Kingdom and Cuming, Wright, Humboldt, and Franklin in the United States.

Epidemics simulated on the true Cumbrian data predict an average epidemic impact of 2,505 farms (31% of the population). In contrast, if the randomized data are used (with the same parameters), the average epidemic impact drops to 1,765 farms because the lack of spatial clustering means that it is more difficult for the epidemic to spread—in the clustered scenario, the minimum distance between farms is less and so the epidemic spreads more easily. However, we can reparameterize such that the random model gives comparable epidemic impacts to the fully clustered model. Table 1 gives a full list of epidemic impacts for all nine counties examined in Fig. 1 (note Wright and Humboldt counties border one another so the combined epidemic impact is given here); in all cases reparameterization for the random locations generates epidemic impacts that are in close agreement with predictions from the full spatial model; this is unsurprising because the results of the full spatial model are used for parameterization.

Table 1.

Mean epidemic impact for epidemics seeded within a given county for the true clustered location data (T) and for an equivalent dataset with random farm locations (R) within each county; epidemic impact is also given for random farm locations but with the model reparameterized to provide a best fit to epidemics simulated on the true location data (RR)

Region	Epidemic impact, T	Epidemic impact, R	Epidemic impact, RR
Cumbria, UK	2,505 (2,121–2,976)	1,765 (101–2,287)	2,429 (1,432–3,054)
Devon, UK	519 (27–1,998)	190 (31–561)	545 (34–981)
Clwyd, UK	679 (475–1,131)	388 (52–798)	641 (148–1,355)
Aberdeenshire, UK	80 (20–263)	25 (16–41)	76 (21–121)
Lancaster, PA	1,284 (954–1,634)	75 (20–216)	1,197 (576–1,545)
Cuming, NE	454 (443–461)	441 (423–453)	453 (437–463)
Wright/Humboldt, IA	134 (78–171)	121 (60–152)	133 (75–165)
Franklin, TX	244 (20–318)	118 (15–182)	220 (16–304)

Values in brackets give the 95% prediction intervals; all results are from 10,000 stochastic simulations.

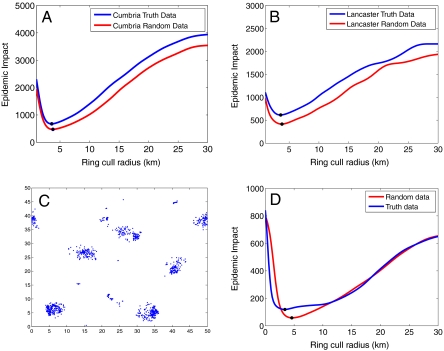
Although obtaining a good fit to the epidemic profile and hence being able to predict the likely extent of an epidemic are potentially informative, by far the most useful application of mathematical models is to inform the optimal policy for controlling an epidemic. As such, accurate mathematical models can be used to experimentally test a variety of control strategies to assess which is optimal, although it is the role of policy makers to decide which quantity needs to be optimized. Here we consider ring culling (in addition to IP and DC culling) and determine what size of ring minimizes the average epidemic impact. The simplest way to determine this value is through multiple simulations. We first adopt this approach using the true locations of farms in Cumbria and Lancaster counties (Fig. 2A and B, blue lines), which predict clear minima at the optimal radii (R_T) of approximately 3.6 km (2.24 miles) in both cases. A similar approach can be used to optimize other forms of control, such as vaccination under logistical constraints (11) or localized (contiguous) culling (12). However, the key question is whether we can perform the same meaningful calculation in the absence of detailed spatial location data. We therefore perform the same numerical experiment using the reparameterized model and the random farm locations (Fig. 2A and B, red lines) and observe that, although using random spatial locations leads us to overestimate the effect of control measures, the optimal ring-cull radius (R_RR) is close to the result from fully clustered spatial simulations. In fact, this level of agreement is so close that using the ring-cull radius R_RR in the fully clustered simulations only has a marginal effect on the average epidemic impact. For Lancaster County, using a ring-cull radius of R_RR = 3.8 km leads to an average epidemic impact of 678 farms, an increase of just three farms from the true optimal value at R_T = 3.6 km. Table 2 shows how this process holds across all nine counties discussed so far.

Fig. 2.

Epidemic impact against ring-cull radius for epidemics in (A) Cumbria and (B) Lancaster County. In both figures, the blue line shows the mean epidemic impact for simulations using the true location data while the red line shows the mean epidemic impact for the reparameterized random data. Both lines are calculated as locally smooth splines fit to 10,000 simulation results. (C) Farm network and (D) mean epidemic impact against ring-cull radius for the random data (red line) and the true data (blue line). For (C) and (D), S₀ = 4, N = 1,000, and B = 0.4. In (A), (B), and (D), the black dots show the minima of each line.

Table 2.

The optimal ring-cull radius in kilometers which minimizes the epidemic impact for both the true clustered location data (R_T) and the reparameterized random-location data (R_RR); also shown is the increase in epidemic impact if the optimal ring-cull radius for the reparameterized random data were implemented on the true location data, as opposed to the optimal ring-cull radius for the true data

Region	RT	RRR	Epidemic impact difference
Cumbria, UK	3.6 (3.5–3.8)	3.8 (3.6–4.0)	3 (0–11)
Devon, UK	2.8 (2.7–3.0)	2.8 (2.7–3.1)	0 (0–3)
Clwyd, UK	3.6 (3.5–3.7)	3.2 (3.1–3.4)	3 (1–7)
Aberdeenshire, UK	2.4 (2.3–2.7)	2.0 (1.9–2.2)	2 (1–3)
Lancaster, PA	3.6 (3.5–3.7)	3.8 (3.7–4.0)	2 (0–6)
Cuming, NE	0 (0–0)	0 (0–0)	0 (0–0)
Wright/Humboldt, IA	0 (0–0)	0 (0–0)	0 (0–0)
Franklin, TX	5.5 (5.4–5.6)	6.0 (5.8–6.1)	1 (0–3)

Values in brackets give the 95% confidence intervals for optimal ring-cull radii and epidemic impact difference; all results are for 10,000 stochastic simulations.

Although the optimal ring-cull radius is predicted to vary between counties, the increase in epidemic impact from the use of predictions made in the absence of spatial information is limited to no more than two or three farms in each case. This implies that, for the counties considered in this analysis, precise knowledge of farm location is not required to advise regarding optimal control strategies. It should be stressed that the reparameterization of the model is a crucial step in this process; should this be omitted from the procedure, models are unable to predict the true optimal radii with any accuracy. This effect is particularly noticeable in Lancaster County: In the absence of reparameterization, the random-location model predicts very low epidemic impacts and the optimal strategy is to employ no ring culling. After reparameterization, as discussed above, it is optimal to ring cull at ≈3.8 km.

Spatial Clustering

Although the nine counties considered so far imply that our results are general, to fully test this approach we generate alternative farm distributions based around a given average farm-centered density distribution 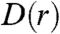. We define 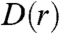as the number of farms per unit area at a distance r from an index farm, averaged over all possible index farms in the population. For highly clustered distributions, we expect D(r) to decrease nonlinearly with r as observed in Fig. 1. In practice, we find that 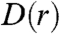can be fit by a sum of exponentials:

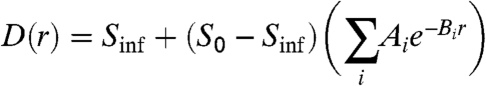[2]

where S_inf defines the long-distance asymptotic density, S₀ defines the average local density around a farm, and we insist that 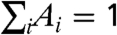. We find that a sum of three exponentials (and hence seven parameters) is sufficient to fully capture the observed density distributions from all nine counties (SI Text).

We now generate theoretical spatial distributions of farms to test the validity of our approach over a wider range of parameters. In particular, we distribute N = 1,000 farms in a 50 × 50 km area, according to a given density distribution. For each simulation, one farm is randomly seeded with infection. To simplify our analysis, we ignore heterogeneity in farm size and composition and use a reduced formulation for the density distribution; in particular, transmission of infection between infectious and susceptible farms is now a highly simplified version of Eq. 1, depending only on their separation (rate_ij = K(d_ij)), whereas the density distribution is defined in terms of a single exponential decay:

[3]

We fix the population size and area that we are going to study, which reduces our free parameters to the ratio S₀∶S_inf and the exponent B. Fig. 2C and D shows an example of applying our methodology to these theoretical spatial distributions (S₀∶S_inf = 10, B = 0.4, N = 1,000 such that S_inf = 0.4). This distribution is far more clustered than any of the previous real-world examples, and yet reparameterizing and determining the optimal ring-cull radius remains a valid approach. The estimated optimal radius R_RR is an overestimate of the true value, but culling in the highly clustered distribution with a radius of R_RR only increases the epidemic impact by three farms from the true optimal value of 152 farms. Here we find that our methodology benefits from a general principle that it is usually better to overtarget control (i.e., bias control more toward high-risk hosts than is strictly optimal) than to undertarget, hence it is better to ring cull using a radius that is slightly larger than optimal compared to one that is smaller than optimal.

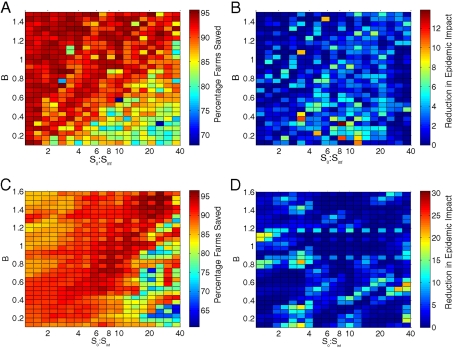
We can expand these theoretical spatial distributions to a range of clustering and repeat our basic analysis (Fig. 3); we allow our two fundamental parameters (S₀∶S_inf and B) to vary over a grid of values. For each clustered distribution, Fig. 3A shows the percentage reduction in the epidemic impact from the full clustered model (compared to IP and DC culling alone) by introducing ring culling at the optimal radius (R_RR) predicted from a random distribution of farms. This illustrates the substantial applied benefits that can be accrued from using well-parameterized mathematical models, even when some of the finer scale spatial information is missing. Localized ring culling is seen to have the greatest percentage impact as the ratio S₀∶S_inf decreases and as B increases; that is, a decrease in epidemic impact of approximately 90% is possible unless the spatial distribution is strongly clustered over relatively large spatial scales. However, it is important to understand whether better data would allow us to improve on these results; Fig. 3B shows the further reduction in epidemic impact to be gained by culling at the true optimal radius (R_T) rather than the radius (R_RR) predicted from a random distribution. We observe that, over the vast majority of spatial patterns considered, there is only a relatively small average improvement to be gained from using exact spatial knowledge.

Fig. 3.

Using the full clustered data, these graphs show the impact of ring culling at the true (R_T) and approximated (R_RR) optimal radius, as the distribution of farms controlled by the parameter B and the ratio S₀∶S_inf vary. In (A) and (B), the random-location model is fitted to the entire epidemic derived from a simulation using the spatially clustered location data, while in (C) and (D), only the first 14 days of the epidemic are used to fit the random-location model. In (A) and (C), the color scale gives the percentage of farms that would be saved by additional ring culling at radius R_RR compared with IP and DC culling alone. In (B) and (D), the color scale gives the additional saving in the epidemic impact when ring culling at the true optimal radius (R_T) is compared with at R_RR.

For models such as these to be used prospectively in the event of an epidemic of FMD, the approach described above could not be adopted in the same way. The results so far all use the entire epidemic on the clustered location data to reparameterize a random-location model before the development of preferred ring-cull strategies. For such a model to be used during an outbreak, as soon as an epidemic is reported, the early pattern of cases must be used to fit a model thus allowing an early investigation of intervention strategies. We therefore repeat the process described above, but this time use only the first 2 weeks of the epidemic from the true spatial model to fit the kernel parameters for the random-location model. In the absence of ring culling, epidemics on the true spatial distribution of farms last for typically 100–120 days, so the first 14 days of the epidemic represent the early growth phase. The fitting process is identical to that described above: Kernel parameters are determined that generate a best fit to the first two weeks of data; we find the optimal cull radius as suggested by these parameters and the random-location model; and finally we determine the effects of culling at this radius in the true model which contains the clustered locations of farms. The results are summarized in Fig. 3C and D. If ring culling at R_RR were implemented within the model, using the true clustered locations of farms, then the percentage reduction in the epidemic compared with IP and DC culling alone is still around 90% for most of the parameter space with a reduction to around 65–70% if farms are clustered over large spatial scales (Fig. 3C), mirroring the results seen when we fit to the entire epidemic. From Fig. 3D, we see that there is a further reduction in epidemic impact when culling at the true optimal radius R_T, but this improvement, though slightly higher than when we fit to the entire epidemic, is still relatively small. This result highlights that, during the early stages of an outbreak, epidemic data could be used to fit a random-location model which could then be used to predict preferred strategies for targeted interventions.

Discussion

Spatial clustering of individuals plays a highly significant role in ecological dynamics (1, 2, 20, 21) and in the spread of infectious disease (22,23–24). Therefore, when precise demographic data are unavailable, alternate methods need to be adopted for mathematical modelers to predict the best control policy to combat an epidemic and therefore provide useful policy advice. In the context of livestock diseases, in the event of an animal movement ban, the location of individual livestock is fixed, with infection between farms only occurring via movement of people, machinery, and other forms of local transmission. This epidemiological situation has been investigated in detail for the United Kingdom, Denmark, Australia, and New Zealand (25, 26) where detailed spatial location data are recorded and available, but not for the United States where only data aggregated at the county-scale are released.

This paper investigates the effect of assuming that farms are randomly located within a county (or given area), ignoring the spatial clustering that is known to exist; it is also assumed throughout that numbers of cases are also only available at this aggregated scale. The first observation is that using the same basic model parameters (i.e., identical K_w and K_h), but ignoring spatial clustering, leads to far smaller epidemics which underestimate the true level of optimal control. However, when the models using random spatial locations are reparameterized to match epidemics (either from real or surrogate sources), they can still be used to provide meaningful predictions for control. In this paper, we have focused on optimal control by localized ring culling, although alternative measures such as ring vaccination or stringent quarantine (27) could be investigated in the same way. The optimal ring size predicted from random spatial locations (but a reparameterized model) is, in general, a slight overestimate of the true optimal radius; using this overestimate still leads to a substantial improvement in the predicted epidemic impact and is only slightly worse than using the true value optimized to account for spatial structure in the distribution of farms.

We therefore find that recognizing that these epidemics take place in a spatial landscape is vital (measures such as ring culling cannot be applied in a nonspatial environment), but once a model has been parameterized to match the epidemic data, much of the spatial structure is subsumed into the reparameterization. As such, aggregate data and aggregate case reports can be used to derive predictions for control of epidemics with spatially localized transmission. Although we have focused on the spread of FMD between livestock on farms, many other examples of localized transmission of infection occur that could be considered with a similar methodology, including plant and crop diseases (28), wildlife diseases (29), human infections (30, 31), and other livestock diseases (32).

In the United States, where precise knowledge of farm location is unknown but aggregate farm statistics are available, this work provides an insight into the role that mathematical modeling can still play in informing disease control policy. However, several further points are worth considering. First, this methodology relies on the availability of epidemic data and can therefore only be used once an epidemic is in progress; it cannot be used to inform policy before an epidemic arises because case report data are vital if the model is to be reparameterized to capture the effects of spatial structure. For detailed predictive models to be available before an epidemic occurs would either require a vast change to the way information on farms is handled and distributed, or would require ground-truthed synthetic maps based on topological and geographical features. As an extension to this work, alternate maps could be developed for regions with known farm locations such as the United Kingdom, using these known geographical features to eliminate regions such as mountains and lakes which are not suitable for farming. This would affect the spatial clustering of farms and potentially the subsequent disease dynamics. Using the same approach as adopted in this paper, this work would provide strong support for the development of ground-truthed synthetic maps, such as those for the five counties in the United States investigated in this paper. However, even when such spatial information is available, the different farming and management practices in different regions of the country make it difficult to utilize a universal model of transmission. Our approach can only be used reactively; therefore, it is vitally important that case report data are available in real time and parameterization is performed using state-of-the-art methodology, so that timely policy advice can be given during the early stages of the epidemic when it will have the greatest effect. However, given the simplicity and parsimony of our approach, it is likely that it can be used robustly in many situations, providing rapid policy advice that could minimize potential losses.