Intrinsic Regression Models for Positive-Definite Matrices With Applications to Diffusion Tensor Imaging

Abstract

The aim of this paper is to develop an intrinsic regression model for the analysis of positive-definite matrices as responses in a Riemannian manifold and their association with a set of covariates, such as age and gender, in a Euclidean space. The primary motivation and application of the proposed methodology is in medical imaging. Because the set of positive-definite matrices do not form a vector space, directly applying classical multivariate regression may be inadequate in establishing the relationship between positive-definite matrices and covariates of interest, such as age and gender, in real applications. Our intrinsic regression model, which is a semiparametric model, uses a link function to map from the Euclidean space of covariates to the Riemannian manifold of positive-definite matrices. We develop an estimation procedure to calculate parameter estimates and establish their limiting distributions. We develop score statistics to test linear hypotheses on unknown parameters and develop a test procedure based on a resampling method to simultaneously assess the statistical significance of linear hypotheses across a large region of interest. Simulation studies are used to demonstrate the methodology and examine the finite sample performance of the test procedure for controlling the family-wise error rate. We apply our methods to the detection of statistical significance of diagnostic effects on the integrity of white matter in a diffusion tensor study of human immunodeficiency virus. Supplemental materials for this article are available online.

1. INTRODUCTION

Symmetric positive-definite matrices (SPD) arise in many applications including diffusion tensor imaging (DTI), computational anatomy, and statistics. For instance, DTI, which tracks the effective diffusion of water molecules in the human brain in vivo, contains a 3 × 3 positive-definite matrix D, called a diffusion tensor, at each voxel (three-dimensional pixel) of an imaging space. Because water molecules tend to diffuse along the pathways of white matter fibers, tracking their diffusion with DTI allows investigators to map the microstructure and organization of those pathways. Specifically, the three eigenvalue-eigenvector pairs {(λ_i, v_i) : i = 1, 2, 3} of D (λ₁ ≥ λ₂ ≥ λ₃) can quantify the degree and direction, respectively, of diffusivity and the principal directions (v₁) of the diffusion tensors (DTs) have been widely used to reconstruct the white matter fiber tracts (Basser, Mattiello, and LeBihan 1994a, 1994b; Zhu et al. 2007). Statistical analysis of DTI measures (e.g., eigenvalues and eigenvectors), diffusion tensors, and fiber tracts can reveal disruptions in structural organization and the neuronanatomical connectivity of the brains of persons with neurological and neuropsychiatric illnesses, and substance use disorders (Lim and Helpern 2002; Focke et al. 2008; Vernooij et al. 2008).

In computational anatomy, a symmetric positive-definite deformation tensor S = (JJ^T)^1/2 at each location of the image can capture the directional information of shape change decoded in the Jacobian matrices J (Grenander and Miller 1998; Lepore et al. 2008). The directional shape change information decoded in deformation tensors has been demonstrated to be more discriminative than the determinant of J in several structural MRI based studies of HIV/AIDS (Lepore et al. 2008). More generally, deformation tensors can be used to detect subtle changes of brain structures across groups and along time. An appropriate statistical analysis of deformation tensors is important for understanding normal brain development, the neural bases of neuropsychiatric disorders, and the joint effects of environmental and genetic factors on brain structure and function. A fundamental issue in many applications is modeling covariance matrices for multivariate data, longitudinal data, spatial data, and time series data (Chiu, Leonard, and Tsui 1996; Pourahmadi 1999, 2000; Anderson 2003).

Despite the extensive use of SPD matrices, a formal statistical framework for using a set of covariates in a Euclidean space to predict SPD matrices as responses has not yet been developed. One may ignore the fact that SPD matrices are in a nonlinear space and then directly apply classical multivariate regression to studying the association between SPD matrices and covariates. However, this method is not adequate in many applications. As an illustration, we consider the “mean” of SPD matrices. In Euclidean space, the mean of SPD matrices is just the empirical average of SPD matrices, which can lead to a swelling effect in imaging processing (Chefdhotel et al. 2004). In contrast, if one regards SPD matrices as points in Riemannian manifold and calculates their Frechét mean (Frechét 1948; Karcher 1977), then the swelling effect completely disappears (Pennec, Fillard, and Ayache 2006). Moreover, even when SPD matrices are regarded as random elements in Riemannian manifold, the existing statistical methods can only compare differences between the means of the two (or multiple) groups of SPD matrices, which is equivalent to modeling SPD matrices with a single categorical variable (Bhattacharya and Patrangenaru 2003, 2005; Schwartzman 2006; Whitcher et al. 2007). For instance, Schwartzman (2006) has developed several parametric models for SPD matrices and derived distributions of several test statistics for testing differences in two groups of SPD matrices. However, the use of parametric models to characterize SPD matrices in real applications requires further research. Recently, Kim and Richards (2008) have studied the problem of deconvolution density estimation on the space of SPD matrices. Although much effort has been devoted to appropriately modeling covariance matrices in longitudinal data and time series settings (Pourahmadi 1999, 2000), these covariance matrices are not response variables as is the case in medical imaging.

To the best of our knowledge, this is the very first paper that develops a semiparametric regression model with SPD matrices as responses in a Remannian manifold and covariates in Euclidean space. Compared with the existing literature, we extend the two-group model studied by Schwartzman (2006) to allow for general covariates and generalize the normal distributional modeling in Schwartzman (2006) by assuming only that certain appropriately defined residuals have mean zero. Our regression model is semiparametric, and thus it avoids specifying parametric distributions for random SPD matrices. We propose an inference procedure to estimate the regression coefficients in this semiparametric model. We establish asymptotic properties, including consistency and asymptotic normality, of the estimates of the regression coefficients. We develop score statistics to test linear hypotheses on unknown parameters. Finally, we develop a test procedure based on a resampling method to simultaneously assess the statistical significance of linear hypotheses across a large region of interest.

The rest of this paper is organized as follows. We will first review some basic results about the Riemannian geometrical structure for the space of SPD matrices. We will next present the semiparametric regression model and estimation methods for estimating the regression coefficients. Then we will develop score statistics to carry out hypothesis testing and develop a test procedure for correcting for multiple comparisons. Simulation studies will assess the empirical performance of the estimation algorithms and test statistics. Finally, we will analyze a neuroimaging dataset to illustrate an application of these methods, before offering some concluding remarks.

2. THEORY

In this section, we formally introduce a semiparametric regression model for a SPD matrix response, develop an estimation algorithm for estimating regression coefficients, and develop a score statistic for testing linear hypotheses of the regression coefficients. We then present a test procedure based on a resampling method for correcting multiple statistical comparisons.

2.1 Model Formulation

We develop a formal regression model for SPD matrices. Suppose we observe a m × m SPD matrix S_i and a k × 1 covariate vector x_i, such as diagnostic status and age, for i = 1,…, n. Let Sym⁺(m) be the set of m × m SPD matrices, β be a p × 1 vector of regression coefficients in R^p and Σ(·,·) be a map from R^k × R^p to Sym⁺(m). The regression model is obtained by modeling the “conditional mean” of S_i given x_i, denoted by Σ_i(β) = Σ(x_i, β) ∈ Sym⁺(m). Note that we just borrow the term “conditional mean” from Euclidean space, but we will formalize the notion of a “conditional mean” explicitly below.

Following Pourahmadi (2000), we consider a general specification of Σ(x, β) using the Cholesky decomposition of Σ(x, β). For the ith observation, through a lower triangular matrix C_i(β) = C(x_i, β) = (c_jk(x_i, β)) (Pourahmadi 2000), the Cholesky decomposition of Σ(x_i, β) is given by

$${\displaystyle \mathrm{\Sigma }({\mathbf{x}}_i,\mathit{\beta })={\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}={\mathbf{C}}_i(\mathit{\beta }){\mathbf{C}}_i{(\mathit{\beta })}^T.}$$ (1)

The specification in (1) has been widely used due to computational simplicity (Pourahmadi 1999, 2000). Now we need to specify the explicit forms of c_jk(x_i, β) for all j ≥ k in order to determine all entries in Σ_i(β). These functions c_jk(x_i, β) in C_i(β) can be regarded as link functions in generalized linear models (McCullagh and Nelder 1989). For instance, for m = 2, we may choose

$${\mathbf{C}}_i(\mathit{\beta })=\left(\begin{array}{cc}{\mathbf{z}}_i^T{\mathit{\beta }}_{(1)}& 0\\ {\mathbf{z}}_i^T{\mathit{\beta }}_{(2)}& {\mathbf{z}}_i^T{\mathit{\beta }}_{(3)}\end{array}\right),$$ (2)

where ${\mathbf{z}}_i=(1,{\mathbf{x}}_i^T{)}^T$ and β_(j) for j = 1, 2, 3 are subvectors of β. To ensure the uniqueness of the Cholesky decomposition, we may impose additional constraints that c_jj(x_i, β) > 0 for all j = 1, … ,m. For instance, we may assume that C_i(β) takes the form

$$\begin{array}{l}\left(\begin{array}{cc}{({\mathbf{z}}_i^T{\mathit{\beta }}_{(1)})}^2& 0\\ {\mathbf{z}}_i^T{\mathit{\beta }}_{(2)}& {({\mathbf{z}}_i^T{\mathit{\beta }}_{(3)})}^2\end{array}\right)\text{\hspace{1em}or}\\ \left(\begin{array}{cc}\text{exp}({\mathbf{z}}_i^T{\mathit{\beta }}_{(1)})& 0\\ {\mathbf{z}}_i^T{\mathit{\beta }}_{(2)}& \text{exp}({\mathbf{z}}_i^T{\mathit{\beta }}_{(3)})\end{array}\right).\end{array}$$ (3)

Compared with (3), the link function in (2) leads to a simpler computation. However, there is an ambiguous sign problem associated with (2), since Σ_i(β) = C_i(β)PP^TC_i(β)^T, where P = diag(±1, …,±1). In practice, we can standardize all covariates and impose additional sign constraints on the intercept terms of β₍₁₎ and β₍₃₎ to remove this ambiguity. The link functions in (2) and (3) can be easily generalized to m ≥ 3. When x_i = 0, Σ(0, β) = C(0, β)C(0, β)^T represents an intercept matrix, which is similar to the intercept in a linear model.

We may consider two direct reparametrizations of Σ_i(β). The first is a matrix-logarithmic model. If we consider the spectral decomposition of Σ ∈ Sym⁺(m) given by OVO^T, where O is a m × m orthonormal matrix and V is a m × m diagonal matrix with positive entries, then the matrix logarithm of Σ is log(Σ) = log(OVO^T) = O log(V)O^T, where log(V) ∈ diag(m) with diagonal elements equal the logarithm of the diagonal entries of V. Let vecs(U) represent (U₁₁, …, U_1m, U₂₂, …, U_2m, …, U_mm)^T for any m × m symmetric matrix U = (U_ij) and let l(x, β) be a map from R^k × R^p to R^m(m+1)/2. The matrix-logarithmic model assumes that the matrix logarithm of Σ_i(β) can be written as

$$\text{vecs}[\log ({\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })})]=\mathbf{l}({\mathbf{x}}_i,\mathit{\beta }).$$ (4)

A graphical illustration is given in Figure 1. For instance, let B be an m(m + 1)/2 × (k + 1) matrix. If we set l(x_i, β) = Bz_i and β contains all unknown parameters in B, then we obtain the matrix-logarithmic model for the covariance matrix in Chiu, Leonard, and Tsui (1996). For m = 1, we have $\mathbf{l}({\mathbf{x}}_i,\mathit{\beta })=({\mathbf{z}}_i^T{\mathit{\beta }}_{(1)})\text{and}{\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}=\text{exp}({\mathbf{z}}_i^T{\mathit{\beta }}_{(1)})=\text{exp}({\mathit{\beta }}_{1,1}+{\mathbf{x}}_i^T{\mathit{\beta }}_{1,(2)}),\text{where}{\mathit{\beta }}_{(1)}={({\mathit{\beta }}_{1,1},{\mathit{\beta }}_{1,(2)}^T)}^T$. Thus, exp(β_{1, 1}) can be represented as an intercept when x_i = 0, whereas β_{1, (2)} characterizes the “slope” vector.

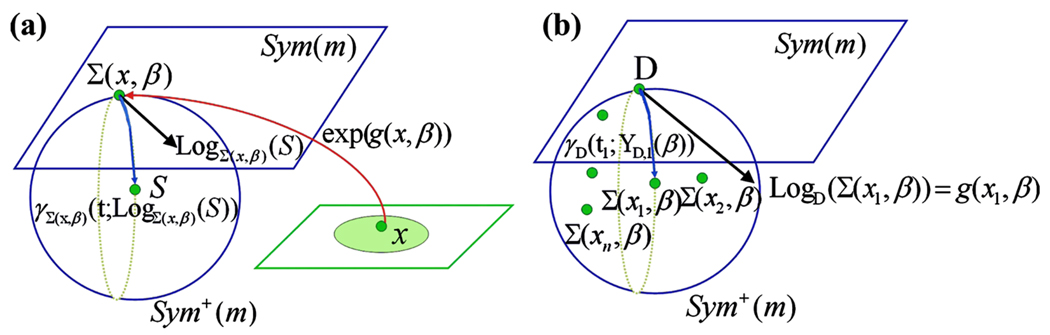
Figure 1.

Graphical illustration of two link functions in the (a) matrix-logarithmic and (b) geodesic models. In (a), the link function for the matrix-logarithmic model equals Σ(x, β) = exp(g(x, β)) or log(Σ(x, β)) = g(x, β). In (b), the link function for the geodesic model equals Log_D(Σ(x, β)) = g(x, β), where D is the intercept matrix.

The second is a “geodesic” model for Σ(x_i, β). Intuitively, a geodesic on the manifold Sym⁺(m) is a “straight line” on Sym⁺(m). Let GL(m) be the set of m × m matrices of nonzero determinant. For any C ∈ GL(m), we define the matrix exponential transformation of C, denoted by exp(C), as ${\displaystyle \text{exp}(\mathbf{C})={\sum }_{k=0}^{\infty }{\mathbf{C}}^k/k}$, where C⁰ = I_m is the m × m identity matrix and C^k is the ordinary matrix multiplication of C k times. We consider an intercept matrix D ∈ Sym⁺(m) and any square root of D, denoted by B, such that B ∈ GL(m) and Σ(0, β) = D = BB^T, when x_i = 0. Then, for a given l(x_i, β), we consider a “directional” matrix Y_D(x_i, β) = Y_D,i(β) in the space of m × m symmetric matrices, denoted by Sym(m), such that vecs(Y_D,i(β)) = l(x_i, β) and l(0, β) = 0. The geodesic model assumes that

$${\displaystyle \mathrm{\Sigma }({\mathbf{x}}_i,\mathit{\beta })={\mathbf{C}}_i(\mathit{\beta }){\mathbf{C}}_i{(\mathit{\beta })}^T=\mathbf{B}\text{exp}({\mathbf{B}}^{-1}{\mathbf{Y}}_{D,i}(\mathit{\beta }){\mathbf{B}}^{-T}){\mathbf{B}}^T}$$ (5)

for i = 1, …, n. As shown in proposition 2.2.7 of Schwartzman (2006), Σ(x_i, β) is closely related to the geodesic passing through D = BB^T in the direction of Y_D,i(β) and the specification of Σ(x_i, β) in (5) is unique. We will formalize the notions of “geodesic” and “direction” in Section 2.2. A graphical illustration is given in Figure 1(b). Because the specifications (4) and (5) involve the matrix exponential transformation, they can be much more computationally difficult than specifications (2) and (3).

We introduce a definition of “residual” to ensure that Σ_i(β) is the proper “conditional mean” of S_i given x_i. For instance, in the classical linear model, the response is the sum of a regression function and a residual term. Then, the regression function is the conditional mean of the response only when the conditional mean of the residual equals zero. Given two points S_i and Σ_i(β) on the manifold Sym⁺(m), we need to define the residual or “difference” between S_i and Σ_i(β). At Σ_i(β), we have a tangent space of the manifold Sym⁺(m), denoted by T_Σi(β) Sym⁺(m), which is a Euclidean space representing a first-order approximation of the manifold Sym⁺(m) near Σ_i(β). Then, we calculate the projection of S_i onto T_Σi(β) Sym⁺(m), denoted by Log_Σi(β)(S_i), which is given by

$${\text{Log}}_{{\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}}({\mathbf{S}}_i)={\mathbf{C}}_i(\mathit{\beta })\text{log}({\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\mathbf{S}}_i{\mathbf{C}}_i{(\mathit{\beta })}^{-T}){\mathbf{C}}_i{(\mathit{\beta })}^T.$$ (6)

Thus, Log_Σi(β)(S_i) on T_Σi(β) Sym⁺(m) can be regarded as the difference between S_i and Σ_i(β) for i = 1, …, n. Since Log_Σi(β)(S_i) for different i are in different tangent spaces (or Euclidean spaces), we must translate them back to the same tangent space, such as the tangent space at the identity matrix I_m, denoted by T_Im Sym⁺(m) (Schwartzman 2006). This translation can be done using the group action of GL(m) introduced in Section 2.2. Specifically, to translate Log_Σi(β)(S_i) ∈ T_Σi(β) Sym⁺(m) into T_Im Sym⁺(m), we follow Schwartzman (2006) to define the residual of S_i with respect to Σ_i(β) as

$$\begin{array}{cc}{\epsilon }_i(\mathit{\beta })\hfill & ={\epsilon }_{{\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}}({\mathbf{S}}_i)={\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\text{Log}}_{{\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}}({\mathbf{S}}_i){\mathbf{C}}_i{(\mathit{\beta })}^{-T}\hfill \\ \hfill & =\text{log}({\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\mathbf{S}}_i{\mathbf{C}}_i{(\mathit{\beta })}^{-T}),\hfill \end{array}$$ (7)

for i = 1, …, n. The ε_i(β) are uniquely defined, because the Cholesky decomposition is unique and Log_Σi(β)(S_i) is independent of the choice of the square root of Σ_i(β). Moreover, because all ε_i(β) are in the same tangent space T_Im Sym⁺(m) and T_Im Sym⁺(m) is a Euclidean space, we can apply classical multivariate analysis techniques in Euclidean space to the analysis of ε_Σi(β)(S_i) (Anderson 2003).

The intrinsic regression model for SPD matrices is then defined by

$$E[{\epsilon }_i(\mathit{\beta })|{\mathbf{x}}_i]=\mathbf{0}\text{\hspace{1em}or\hspace{1em}}E[{\text{Log}}_{{\displaystyle {\mathrm{\Sigma }}_i(\mathit{\beta })}}({\mathbf{S}}_i)|{\mathbf{x}}_i]=\mathbf{0},$$ (8)

for i = 1, …, n, where the expectation is taken with respect to the conditional distribution of S_i given x_i. Model (8) does not assume any parametric distribution for S_i given x_i, and thus it allows for a large class of distributions. In contrast, let Ω be an m × m matrix in Sym⁺(m), Schwartzman (2006, p. 42) considered a symmetric matrix variate normal distribution of ε_i (Gupta and Nagar 2000), whose density is given by

$$p({\epsilon }_i;\mathbf{0},\mathrm{\Omega })=\frac{1}{{(2\pi )}^m|\mathrm{\Omega }{|}^2}\text{exp}\left(-\frac{1}{2}\text{tr}({\epsilon }_i{\mathrm{\Omega }}^{-1}{)}^2\right).$$ (9)

Then, using S_i = C_i(β) exp(ε_i)C_i(β)^T, the density of S_i, denoted by p(S_i; β), is

$$\begin{array}{c}\frac{J({\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\mathbf{S}}_i{\mathbf{C}}_i{(\mathit{\beta })}^{-T})|{\mathbf{C}}_i(\mathit{\beta }){\mathbf{C}}_i{(\mathit{\beta })}^T|2}{{(2\pi )}^{2m}|\mathrm{\Omega }{|}^2}\hfill \\ \hfill \times \text{exp}\left(-\frac{1}{2}\text{tr}(\text{log}({\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\mathbf{S}}_i{\mathbf{C}}_i{(\mathit{\beta })}^{-T}){\mathrm{\Omega }}^{-1}{)}^2\right),\end{array}$$ (10)

where J(C_i(β)⁻¹S_iC_i(β)^−T) is the Jacobian of the transformation ε_i = C_i(β)⁻¹S_iC_i(β)^−T. Because the true distribution of ε_i may deviate from the Gaussian distribution in (9), it can be very restrictive to assume a parametric distribution, such as (10), for S_i. In addition, our model (8) does not assume homogeneous variance across all i. This is also desirable for applications, such as the analysis of imaging data, including diffusion tensor data, because between-subject and between-voxel variability in the imaging measures (e.g., DT) can be substantial.

2.2 Geometrical Structure of Sym⁺(m)

We summarize some basic results from Schwartzman (2006) about the geometrical structure of Sym⁺(m) as a Riemannian manifold (Do Carmo 1992; Lang 1999). The space Sym⁺(m) is a submanifold of the Euclidean space Sym(m). Geometrically, the spaces Sym⁺(m) and Sym(m) are differentiable manifolds of m(m + 1)/2 dimensions and they are homeomorphically related by the matrix exponential transformation and logarithm.

We first introduce the tangent vector and tangent space at any D ∈ Sym⁺(m). For a small scalar δ > 0, let C(t) be a differentiable map from (−δ, δ) to Sym⁺(m) such that it passes through C(0) = D. The tangent vector at D is defined as the derivative of the smooth curve C(t) with respect to t at t = 0. The set of all tangent vectors at D forms the tangent space of Sym⁺(m) at D, denoted by T_D Sym⁺(m). As shown in proposition 2.2.3 of Schwartzman (2006), T_D Sym⁺(m) is identified with a copy of Sym(m). For instance, when D = I_m, we consider the curve C(t) = exp(tY) ∈ Sym⁺(m) satisfying C(0) = I_m for any Y ∈ Sym(m) and t ∈ (−δ, δ). Then, the derivative of C(t) at t = 0 is just Y and thus T_Im Sym⁺(m) = Sym(m). Second, we introduce an inner product of any two tangent vectors in the same tangent space, which varies smoothly along the manifold. We consider the scaled Frobenius inner product of any two tangent vectors Y_D and Z_D in T_D Sym⁺(m), which is defined by

$$《{\mathbf{Y}}_{\mathbf{D}},{\mathbf{Z}}_{\mathbf{D}}》={\text{tr}(\mathbf{Y}}_{\mathbf{D}}{\mathbf{D}}^{-1}{\mathbf{Z}}_{\mathbf{D}}{\mathbf{D}}^{-1}).$$ (11)

Let B ∈ GL(m) be any square root of D ∈ Sym⁺(m) such that D = BB^T and let γ_D(t; Y_D) be the geodesic on Sym⁺(m) passing through D in the direction of the tangent vector Y_D ∈ T_D Sym⁺(m). As shown in proposition 2.2.7 of Schwartzman (2006), γ_D(t; Y_D) is uniquely given by

$${\gamma }_{\mathbf{D}}(t;{\mathbf{Y}}_{\mathbf{D}})=\mathbf{B}{\text{exp}(t\mathbf{B}}^{-1}{\mathbf{Y}}_{\mathbf{D}}{\mathbf{B}}^{-T}){\mathbf{B}}^T\text{for all}t\in (-\infty ,\infty ).$$ (12)

Given the geodesic γ_D(t; Y_D), the Riemannian exponential map Exp_D(Y_D), which maps the tangent vector Y_D ∈ T_D Sym⁺(m) to a point X ∈ Sym⁺(m), is uniquely defined as

$$\mathbf{X}={\text{Exp}}_D({\mathbf{Y}}_{\mathbf{D}})={\gamma }_{\mathbf{D}}(1;{\mathbf{Y}}_{\mathbf{D}})=\mathbf{B}\text{exp}({\mathbf{B}}^{-1}{\mathbf{Y}}_{\mathbf{D}}{\mathbf{B}}^{-T}){\mathbf{B}}^T.$$ (13)

When D = I_m, Exp_D reduces to the matrix exponential exp(·). Recall that in the geodesic model, we assume that Σ(0, β) = D = BB^T and Σ(x_i, β) = γ_D(1; Y_D,i(β)), in which vecs(Y_D,i(β)) = l(x_i, β) and l(0, β) = 0.

The Riemannian logarithmic map at D, denoted by Log_D(·), maps X ∈ Sym⁺(m) onto the tangent vector Y_D in T_D Sym⁺(m). Specifically, Log_D : Sym⁺(m) → T_D Sym⁺(m) at D = BB^T ∈ Sym⁺(m) is uniquely defined as

$${\mathbf{Y}}_{\mathbf{D}}={\text{Log}}_{\mathbf{D}}(\mathbf{X})=\mathbf{B}\text{log}({\mathbf{B}}^{-1}{\mathbf{\text{XB}}}^{-T}){\mathbf{B}}^T.$$ (14)

The Riemannian exponential and logarithmic maps satisfy

$${\mathbf{Y}}_{\mathbf{D}}={\text{Log}}_{\mathbf{D}}({\text{Exp}}_{\mathbf{D}}({\mathbf{Y}}_{\mathbf{D}}))\text{\hspace{1em}and\hspace{1em}}\mathbf{X}={\text{Exp}}_{\mathbf{D}}({\text{Log}}_{\mathbf{D}}(\mathbf{X})).$$ (15)

Recall that in the definition of “conditional residual,” we have two points D = Σ(x_i, β) and X = S_i on Sym⁺(m) and then we define Log_{Σ(xi, β)}(S_i) on T_{Σ(xi, β)} Sym⁺(m). Because Log_{Σ(xi, β)} (S_i) is independent of the square root of Σ(x_i, β), we can choose the Cholesky decomposition of Σ(x_i, β) = C_i(β)C_i(β)^T in the definition of Log_{Σ(xi, β)} (S_i).

A nice property of Sym⁺(m) is that a group action of GL(m) on Sym⁺(m) can relate any two (X, D) ∈ Sym⁺(m) and the tangent spaces at X and D, respectively. Specifically, the group action of GL(m) on Sym⁺(m) consists of all transformations ϕ_B(X) = BXB^T for any B ∈ GL(m). For any (X, D) ∈ Sym⁺(m), there exists B ∈ GL(m) such that BXB^T = D. The group action of GL(m) on Sym⁺(m) induces a group action between T_X Sym⁺(m) and T_ϕB(X) Sym⁺(m). Explicitly, if Y ∈ T_X Sym⁺(m), then ϕ_B(Y) = BYB^T ∈ T_ϕB(X) Sym⁺(m). Particularly, we have applied the group action to translate Log_Σi(β) (S_i) ∈ T_Σi(β) Sym⁺(m) to C_i(β)⁻¹ Log_Σi(β) (S_i) × C_i(β)^−T ∈ T_{Ci(β)⁻¹ Σi(β)Ci(β)^−T} Sym⁺(m) = T_Im Sym⁺(m) for i = 1, …, n.

We consider the geodesic distance between any two points on Sym⁺(m). Let B ∈ GL(m) be any square root of D, the geodesic distance between D and X in Sym⁺(m) is uniquely given by

$$\begin{array}{ll}d(\mathbf{D},\mathbf{X})\hfill & =\sqrt{《{\text{Log}}_{\mathbf{D}}(\mathbf{X}),{\text{Log}}_{\mathbf{D}}(\mathbf{X})》}\hfill \\ \hfill & =\sqrt{{\text{tr}(\text{log}}^2({\mathbf{B}}^{-1}{\mathbf{\text{XB}}}^{-T})).}\hfill \end{array}$$ (16)

The geodesic distance has many nice properties. For instance, the geodesic distance is a proper metric satisfying positive definiteness, symmetry, and the triangle inequality. Specifically, d(D, X) = d(X, D). The geodesic distance is also invariant under group actions, that is, d(D, X) = d(BDB^T , BXB^T) for any B ∈ GL(m).

2.3 Estimation

We calculate an intrinsic least squares estimator (ILSE) of the parameter vector β, denoted by β̂, by minimizing the total residual sum of squares:

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }}{\text{argmin}}{G}_n(\mathit{\beta })=\underset{\mathit{\beta }}{\text{argmin}}{\displaystyle \sum _{i=1}^n\text{tr}({\epsilon }_i{(\mathit{\beta })}^2).}$$ (17)

Thus, β̂ solves the estimating equations given by

$$\begin{array}{ll}{\partial }_{\mathit{\beta }}{G}_n(\mathit{\beta })\hfill & ={\displaystyle \sum _{i=1}^n{\partial }_{\mathit{\beta }}\text{tr}({\epsilon }_i{(\mathit{\beta })}^2)}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n\text{tr}\left({\partial }_{\mathit{\beta }}{[\text{log}({\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\mathbf{S}}_i{\mathbf{C}}_i{(\mathit{\beta })}^{-T})]}^2\right)=\mathbf{0},}\hfill \end{array}$$ (18)

where ∂ denotes partial differentiation with respect to a parameter vector, such as β. The ILSE is closely related to the intrinsic mean Σ_IM of S₁, …, S_n ∈ Sym⁺(m), which is defined as

$${\widehat{\mathrm{\Sigma }}}_{\mathit{\text{IM}}}=\underset{\mathrm{\Sigma }}{\text{argmin}}{\displaystyle \sum _{i=1}^{n}d{(\mathrm{\Sigma },{\mathbf{S}}_i)}^2,}$$ (19)

where d(·, ·) has been defined in equation (16). In this case, both Σ_i and C_i(β) are independent of i and the covariates. Let β = (c₁₁, c₂₁, c₂₂, …, c_m1, …, c_mm) be the entries of the lower triangular portion of C(β) = (c_jk) such that Σ = C(β)C(β)^T. It follows from (16) that ${\displaystyle {\sum }_{i=1}^n\text{tr}({\epsilon }_i{(\mathit{\beta })}^2)=}{\displaystyle {\sum }_{i=1}^{n}d{(\mathrm{\Sigma },{\mathbf{S}}_i)}^2}$, which leads to Σ̂_IM = C(β̂ )C(β̂)^T.

We now develop an annealing optimization algorithm for obtaining β̂. Our annealing algorithm consists of five steps. In Step 1, we first calculate the Cholesky decompositions of all S_i, denoted by ${\mathbf{S}}_i={\tilde{\mathbf{C}}}_i{\tilde{\mathbf{C}}}_i^T$, and then we fit a multivariate linear regression model with the lower part of C̃_i as the response and the corresponding part of C_i(β) as the mean function, which yield the initial value β⁽⁰⁾. Then, starting from β⁽⁰⁾, we use the downhill simplex method to search for another initial value β⁽¹⁾ (Nelder and Mead 1965). In Step 2, starting from β^(k), we use the Gibbs sampler coupled with the Metropolis–Hasting algorithm to iteratively draw N₀ (say, 200) dependent observations {β^(k,l) : l = 1, … ,N₀} from exp(−G_n(β)/τ_k). Among the {β^(k,l) : l = 1, …, N₀}, we find the optimal β̃^(k) = argmin_β^(k,l) {G_n(β)}. In Step 3, we use the downhill simplex method with β̃^(k) as the starting point to search for β^(k+1). In Step 4, we iterate between Steps 2 and 3 for k = 1, …, M₀ (say, M₀ = 4) and increase τ_k at each iteration. We choose τ₁ to achieve an acceptance rate of the Metropolis–Hasting algorithm within the Gibbs sampler around 0.25 and then we slightly reduce the acceptance rate to around 0.15 as k increases. We save the optimal β^B, which minimizes G_n(β), among all β^(k,l) and β^(k) during the iterations. In Step 5, starting from β^B, we use the Newton–Raphson algorithm to calculate β̂ as described below. Compared with other optimization methods, such as the simulated annealing algorithm, we can efficiently find β̂ due to several nice features. According to our experience, β⁽¹⁾ is usually close to β̂, and we always use the downhill simplex method to search for a new optimal estimator after drawing a small number of Monte Carlo samples. Thus, we avoid using large values of N₀ and M₀.

Let ∂_βG_n(β^(t)) and ${\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$, respectively, denote the first and second-order partial derivatives of G_n(β) with respect to β evaluated at β^(t). The Newton–Raphson algorithm yields

$${\mathit{\beta }}^{(t+1)}={\mathit{\beta }}^{(t)}+\rho {\left\{-{\partial }_{\mathit{\beta }}^2{G}_n\left({\mathit{\beta }}^{(t)}\right)\right\}}^{-1}{\partial }_{\mathit{\beta }}{G}_n\left({\mathit{\beta }}^{(t)}\right).$$ (20)

In addition, we choose 0 < ρ = 1/2^k₀ ≤ 1 for some k₀ ≥ 0 such that G_n(β^(t+1)) ≤ G_n(β^(t)). The Newton–Raphson algorithm stops when the absolute difference between consecutive β^(t)’s is smaller than a predefined small number, say 10⁻⁴. At the final iteration, we set β̂ = β^(t). In addition, because $-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$ may not be positive definite, we approximate $-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$ in order to stabilize the Newton–Raphson algorithm. Details regarding ∂_βG_n(β^(t)), and ${\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$ and its approximation are given in lemma 1 of the supplemental document.

2.4 Asymptotic Properties

We first introduce some notation to describe the limiting behavior of the ILSE for SPDs. Let β_* be the true value of β such that (8) holds at β_*. Let C_i* denote C_i(β_*) and ${\mathrm{\Sigma }}_{i*}={\mathrm{\Sigma }}_i({\mathit{\beta }}_{*})={\mathbf{C}}_{i*}{\mathbf{C}}_{i*}^T$; ℬ denotes the parameter space for β; ‖ · ‖ denotes the Euclidean norm of a vector or a matrix; a^⊗2 = aa^T for any vector a; and →^L denotes convergence in distribution.

We establish consistency and asymptotically normality of β̂. We obtain the following theorems, whose detailed assumptions and proofs can be found in the supplemental document.

Theorem 1

(a) For model (8), if assumptions (C1), (C2), and (C3) in the supplemental document are true, then β̂ converges to β_* in probability.

(b) For model (8), under assumptions (C1)–(C4), we have

$$\begin{array}{ll}{\left\{{\displaystyle \sum _{i=1}^n{\left[{\partial }_{\mathit{\beta }}\text{tr}({\epsilon }_i(\widehat{\mathit{\beta }}{)}^2)\right]}^{\otimes 2}}\right\}}^{-1/2}\hfill & [-{\partial }_{\mathit{\beta }}^2{G}_n(\widehat{\mathit{\beta }})](\widehat{\mathit{\beta }}-{\mathit{\beta }}_{*})\hfill \\ \hfill & \hfill {\to }^L\mathrm{N}(0,{\mathbf{I}}_p)\end{array}$$ (21)

as n → ∞.

Theorem 1 has several important applications. Theorem 1(a) establishes weak convergence of β̂. According to Theorem 1(b), the covariance matrix of β̂ under model (8) can be consistently estimated by

$${[-{\partial }_{\mathit{\beta }}^2{G}_n(\widehat{\mathit{\beta }})]}^{-1}\left\{{{\displaystyle \sum _{i=1}^n\left[{\partial }_{\mathit{\beta }}\text{tr}({\epsilon }_i(\widehat{\mathit{\beta }}{)}^2)\right]}}^{\otimes 2}\right\}{[-{\partial }_{\mathit{\beta }}^2{G}_n(\widehat{\mathit{\beta }})]}^{-1}.$$ (22)

Moreover, we can use Theorem 1(b) to construct confidence cones of β and its functions. Since Theorem 1 only establishes the asymptotic properties of β̂ when the sample size is large, these properties may be inadequate to characterize the finite sample behavior of β̂ for relatively small sample sizes. In the case of small and moderate sample sizes, we may have to resort to higher-order approximations, such as saddlepoint approximations and bootstrap methods (Davison and Hinkley 1997; Butler 2007).

2.5 Testing Linear Hypotheses

Our choice of hypotheses to test is motivated by scientific questions, which involve a comparison of SPDs across diagnostic groups or detecting change in SPDs across time (Schwartzman 2006; Whitcher et al. 2007; Lepore et al. 2008). These questions usually can be formulated as testing linear hypotheses of β as follows:

$$H_0:\mathbf{R}\mathit{\beta }={\mathbf{b}}_0\text{\hspace{1em}vs.\hspace{1em}}{H}_1:\mathbf{R}\mathit{\beta }\ne {\mathbf{b}}_0,$$ (23)

where R is an r × p matrix of full row rank and b₀ is an r × 1 specified vector. We test the null hypothesis H₀ : Rβ = b₀ using a score test statistic W_n defined by

$$W_n={\mathbf{L}}_{n,\mathit{\mu }}^T{\widehat{\mathbf{I}}}_{\mathit{\mu }\mathit{\mu }}^{-1}{\mathbf{L}}_{n,\mathit{\mu }},$$ (24)

where μ = Rβ, ${\mathbf{L}}_{n,\mathit{\mu }}=n^{-1/2}{\displaystyle {\sum }_{i=1}^n{\widehat{\mathbf{U}}}_{i,\mathit{\mu }}(\tilde{\mathit{\beta }}),}\text{and}{\widehat{\mathbf{I}}}_{\mathit{\mu }\mathit{\mu }}=n^{-1}{\displaystyle {\sum }_{i=1}^n{\widehat{\mathbf{U}}}_{i,\mathit{\mu }}}(\tilde{\mathit{\beta }}){\widehat{\mathbf{U}}}_{i,\mathit{\mu }}{(\tilde{\mathit{\beta }})}^T$, in which β̃ denotes the estimate of β under H₀ and the explicit expressions of Û_{i, μ} (β̃) and L_{n, μ} are given in the supplemental document (Rotnitzky and Jewell 1990).

Theorem 2

For model (8), if assumptions (C1)–(C4) in the supplemental document are true, then the statistic W_n is asymptotically distributed as χ²(r), a chi-square distribution with r degrees of freedom, under the null hypothesis H₀.

An asymptotically valid test can be obtained by comparing sample values of the test statistic with the critical value of the right-hand tail of the χ²(r) distribution at a prespecified significance level α. That is, we reject H₀ if $W_n\ge {\chi }_{\alpha }^2(r)$, and do not reject H₀ otherwise, where ${\chi }_{\alpha }^2(r)$ is the upper α-percentile of the χ²(r) distribution.

2.6 Multiple Hypotheses

In imaging applications, we need to test the hypotheses H₀ against H₁ across multiple brain regions or across the many voxels of the imaging volume. Thus, the next step entails using statistical methods (e.g., random field theory, false discovery rates, permutation methods) to adjust p-values for these multiple statistical tests. To test H₀ in all voxels of the region under study, we consider the maximum of the score test statistics given by

$$W_{n,𝒟}=\underset{d\in 𝒟}{\text{max}}{W}_n(d),$$ (25)

where W_n(d) denotes the score test statistic at voxel d and 𝒟 denotes the brain region. The maximum statistic W_{n, 𝒟} plays a crucial role in controlling the family-wise error rate.

We propose to use a test procedure that is based on a resampling method to approximate the null distribution of W_n,𝒟 (Kosorok 2003; Lin 2005). The test procedure is implemented as follows:

• Step 1. We calculate the score test statistic W_n(d) at each voxel d, and then we compute W_n,𝒟 = max_d∈𝒟 W_n(d).

• Step 2. Generate n realizations of ε denoted by $\{{\epsilon }_i^{(k)}:i=1,\dots ,n\}$, where ε equals ±1 with equal probability.

• Step 3. Calculate W_n(d)^(k) = L_{n, μ}(d)^(k)T [Î_μμ(d)]⁻¹ × L_{n, μ}(d)^(k), and then compute $W_{n,𝒟}^{(k)}={\text{max}}_{d\in 𝒟}{W}_n{(d)}^{(k)}$, where ${\mathbf{L}}_{n,\mathit{\mu }}{(d)}^{(k)}=n^{-1/2}{\displaystyle {\sum }_{i=1}^n{\widehat{\mathbf{U}}}_{i,\mathit{\mu }}(\tilde{\mathit{\beta }},d){\epsilon }_i^{(k)}}$.

• Step 4. Repeat Steps 2–3 K₀ times and calculate $\{W_{n,𝒟}^{(k)}:k=1,\dots ,K_0\}$. Finally, the p-value of W_n,𝒟 is approximated by $p_{\mu ,𝒟}=K_0^{-1}{\displaystyle {\sum }_{k=1}^{K_0}I(W_{n,𝒟}^{(k)}\ge W_{n,𝒟})}$. We reject the null hypothesis H₀ : Rβ = b₀ across all voxels of the region when p_μ,𝒟 is smaller than a prespecified value α, say 0.05.

• Step 5. Calculate the adjusted p-value of W_n(d) at each voxel d of the region according to $p_D(d)\approx K_0^{-1}\times {\displaystyle {\sum }_{k=1}^{K_0}I(W_{n,𝒟}^{(k)}\ge W_n(d))}$.

There are several advantages of using the resampling method in the above test procedure. The above procedure needs to compute Û_i,μ(β̃, d) and Ĩ_μμ only once. It also avoids repeated analyses of permuted datasets in the permutation methods, because fitting the regression models for SPD matrices across all voxels of an imaging volume can take up to more than 20 hours for each permuted dataset. In contrast, the proposed resampling method takes less than 5 minutes for K₀ = 1,000.

3. SIMULATION STUDIES

We conducted three sets of Monte Carlo simulations. All computations for these simulation studies were done in C++ on an IBM ThinkCentre M50 workstation. The first set of simulations was to evaluate the accuracy of the parameter estimates and their associated variance estimates for the proposed intrinsic regression model. We set m = 3 and generated the simulated data as follows. We considered the Cholesky decomposition (1) of Σ(x_i, β) with $\text{vecs}({\mathbf{C}}_i{(\mathit{\beta })}^T)={({\mathbf{z}}_i^T{\mathit{\beta }}_1,{\mathbf{z}}_i^T{\mathit{\beta }}_2,{\mathbf{z}}_i^T{\mathit{\beta }}_3,{\mathbf{z}}_i^T{\mathit{\beta }}_4,{\mathbf{z}}_i^T{\mathit{\beta }}_5,{\mathbf{z}}_i^T{\mathit{\beta }}_6)}^T$, in which z_i = (1, x_i1)^T was a 2 × 1 vector of covariates of interest, for i = 1, …, n. We generated x_i1 independently from a Gaussian generator with zero mean and unit variance. Thus, $\mathit{\beta }=({\mathit{\beta }}_1^T,\dots ,{\mathit{\beta }}_6^T{)}^T$ is a 12 × 1 vector. Then, we simulated ε_i from a N(0, Ω) distribution and calculated C_i(β_*) exp(ε_i)C_i(β_*)^T, in which we set ${\mathit{\beta }}_{k*}=[1+0.1\times (k-1)]{\mathbf{1}}_2^T$ for k = 1, …, 6. We chose two different Ω’s as follows: Ω₁ = 0.6I₃ and ${\mathrm{\Omega }}_2=0.3{\mathbf{I}}_3+{0.3\mathbf{1}}_3{\mathbf{1}}_3^T$, where 1₃ = (1, 1, 1)^T. For each Ω, we set n = 20 and 80 and then simulated 500 data sets for each case. For each simulated dataset, we applied the annealing optimization algorithm with N₀ = 200 and M₀ = 4, which took an average CPU time of about 30 seconds to obtain β̂ and Cov(β̂) in (22).

Based on 500 parameter estimates, we calculated the bias, the mean of the estimated standard error estimates (SE), the standard deviation of the estimated standard error estimates (SD–SE) and the root-mean-square error (RMS) (Table 1). All relative efficiencies (the ratio of the mean of the standard deviation estimates to the root mean-square error) are close to 1.0, indicating that matrix (22) is an accurate estimate of diag(Cov(β̂)). As expected, the root mean-square error decreases as the sample size increases. Moreover, comparing the results from Ω₁ and Ω₂, we note that increasing the correlation in Ω only slightly decreases the bias and SD of β̂.

Table 1.

Bias (×10⁻²), RMS (×10⁻²), SE (×10⁻²), SD–SE (×10⁻²), and RS of all 12 parameters under Ω₁ and Ω₂. BIAS denotes the bias of the mean of the ILSE estimates; RMS denotes the root-mean-square error; SE denotes the mean of the standard deviation estimates; SD–SE denotes the standard deviation of the standard deviation estimates; RS denotes the ratio of RMS over SD. Two different sample sizes {20, 80} and 500 simulated datasets were used for each case

	n = 20					n = 80
	BIAS	RMS	SE	SD–SE	RS	BIAS	RMS	SE	SD–SE	RS
Ω1
β1	2.60	6.10	6.73	2.20	1.10	0.58	3.59	3.37	0.68	0.94
β2	1.78	6.10	6.61	1.72	1.08	0.06	3.90	3.61	0.55	0.92
β3	1.88	7.06	6.96	1.32	0.98	0.69	3.91	3.56	0.35	0.91
β4	1.15	6.86	6.89	1.30	1.01	0.35	3.83	3.51	0.33	0.92
β5	3.83	15.34	17.24	4.22	1.12	1.08	8.35	8.58	1.20	1.02
β6	2.83	15.07	16.97	3.76	1.12	0.54	8.45	8.46	0.95	1.01
β7	1.43	8.75	8.07	1.42	0.92	−0.37	4.19	4.10	0.39	0.98
β8	0.48	8.32	7.98	1.40	0.96	−0.44	4.12	4.06	0.38	0.98
β9	5.14	29.38	32.06	7.57	1.09	1.6	14.84	16.07	2.23	1.08
β10	3.97	28.88	31.59	7.14	1.09	1.05	14.84	15.85	1.77	1.07
β11	3.62	20.32	19.91	3.87	0.98	1.00	10.63	10.15	0.85	0.96
β12	2.69	20.11	19.68	3.83	0.98	0.53	10.48	10.03	0.84	0.96
Ω2
β1	2.76	6.87	6.73	2.21	0.97	0.59	4.00	3.7	0.57	0.93
β2	1.81	6.72	6.61	1.63	0.98	0.46	3.97	3.7	0.53	0.93
β3	1.96	7.74	7.23	1.27	0.93	0.23	3.72	3.54	0.36	0.95
β4	1.24	7.43	7.15	1.26	0.96	0.03	3.67	3.5	0.36	0.95
β5	3.08	11.63	12.61	2.85	1.08	1.02	6.87	6.33	0.73	0.92
β6	1.87	11.78	12.41	2.31	1.05	0.86	6.9	6.3	0.7	0.91
β7	1.56	8.44	8.26	1.46	0.98	0.11	4.5	4.2	0.34	0.93
β8	0.62	8.09	8.17	1.44	1.01	0.04	4.5	4.1	0.34	0.91
β9	2.75	18.90	19.75	4.14	1.04	1.06	10.74	9.93	1.09	0.93
β10	1.33	18.84	19.46	3.68	1.03	0.86	10.79	9.82	0.93	0.91
β11	3.87	16.68	15.49	2.54	0.93	−0.58	7.45	7.44	0.66	0.99
β12	2.88	16.46	15.31	2.51	0.94	−0.91	7.22	7.37	0.65	1.02

The second set of simulations examined the finite sample performance of the score statistic W_n. We used the same setup as the first set of simulations except that we set β = 0, and then varied the second component of β_j = (β_j,1, β_j,2)′ for j = 1, …, 6. We were interested in testing whether the effect of the covariate xi1 is significant. Letting β_·,2 = (β_1,2, … , β_6,2)^T, we tested the following hypotheses:

$$H_0:{\mathit{\beta }}_{·,2}=\mathbf{0}\text{\hspace{1em}and\hspace{1em}}{H}_1:{\mathit{\beta }}_{·,2}\ne \mathbf{0}.$$

To assess the type I and II error rates for W_n, we chose four different values for β_·,2: 0 × 1₆, 0.2 × 1₆, 0.4 × 1₆, and 0.6 × 1₆, and chose Ω₁ and Ω₂. For each Ω, we set n = 20, 40, and 80 and then simulated 1,000 datasets for each case.

The score statistic W_n performs reasonably well for relatively small sample sizes (Table 2). The type I error rates were not excessive even for both the 5% and 1% significance levels at n = 40. Increasing the sample size can increase the power of rejecting the null hypothesis. Comparing the results from Ω₁ and Ω₂, we note that increasing the correlation in Ω only slightly influences the finite sample performance of W_n.

Table 2.

Comparisons of the rejection rates for score test statistics under Ω₁ and Ω₂. Three differing sample sizes {20, 40, 80} and 1,000 simulated datasets were used for each case and two significance levels, 5% and 1%, were considered. The null and alternative hypotheses were, respectively, given by H₀ : β_·,2 = 0 and H₁ : β_·,2 ≠ 0. Two methods including the resampling method (RE) and χ² distribution [χ²(6)] were used to calculate the rejection rates

	n = 20				n = 40				n = 80
	5%		1%		5%		1%		5%		1%
β·,2	RE	χ2(6)	RE	χ2(6)	RE	χ2(6)	RE	χ2(6)	RE	χ2(6)	RE	χ2(6)
Ω1
0 × 16	0.143	0.031	0.037	0	0.067	0.043	0.026	0.007	0.067	0.037	0.017	0.003
0.2 × 16	0.513	0.177	0.253	0.011	0.957	0.883	0.796	0.461	1	1	0.991	0.971
0.4 × 16	0.597	0.213	0.293	0.022	0.993	0.951	0.832	0.481	1	1	1	1
0.6 × 16	0.773	0.442	0.520	0.042	1	1	1	0.983	1	1	1	1
Ω2
0 × 16	0.126	0.023	0.037	0	0.063	0.037	0.017	0.003	0.061	0.033	0.013	0.003
0.2 × 16	0.581	0.221	0.302	0.010	0.977	0.953	0.851	0.491	1	1	0.991	0.991
0.4 × 16	0.602	0.227	0.321	0.032	0.991	0.981	0.871	0.562	1	1	1	1
0.6 × 16	0.903	0.51	0.611	0.051	1	1	1	0.981	1	1	1	1

In the third set of simulations, we examined the finite sample performance of W_n,𝒟. We generated 3 × 3 SPDs at all 2,500 pixels of a 50 by 50 image slice for each of all n subjects. We used the same setup as the first set of simulations with an exception. We only consider Ω₁, the variance of ε_i(d), at each pixel and for any two pixels d and d′, the correlation of ε_i,k(d) and ε_i,k(d′) equals ρ^{‖d−d′‖}, where ρ ∈ [0, 1]. We tested the null hypothesis H₀ : β_·,2(d) = 0 at all pixels on the slice. We set n = 40 and 80. We first assumed β_·,2(d) = 0 at all pixels on the slice to assess the family-wise error rate. To assess the power, we selected a region-of-interest (ROI) with 40 pixels on the reference slice and set β_·,2(d) at 0.3 × 1₆, 0.6 × 1₆, and 0.9 × 1₆ for any point d in the ROI. For each simulated dataset, we applied the annealing optimization algorithm with N₀ = 200 and M₀ = 5 to the simulated data at each pixel and the test procedure to all 2,500 pixels, which took an average CPU time of about 8 hours.

We used the family-wise error rate as the type I error rate and estimated it based on 100 replications with significance level α = 5%. We also calculated the average of the probabilities of rejecting each of the 40 pixels in the ROI as an estimate of the average power using 100 replications and a significance level of α = 5%.

For the test statistic W_n,𝒟, our test procedure worked reasonably well for relatively small sample sizes (Table 3). The family-wise error rates for our test procedure were not particularly accurate for n = 40 when the correlation is zero; in contrast, they improved at n = 40 and ρ = 0.5. Thus, the sample size could somewhat influence the finite sample performance of our test procedure, particularly when the sample sizes are small.

Table 3.

Comparisons of the family-wise error rates and average powers for the test procedure under two different correlations ρ = 0.0 and 0.5. We considered two different sample sizes {40, 80} and 100 simulated datasets for each case at the 5% significance level. In all voxels, the null and alternative hypotheses were, respectively, given by H₀ : β_·,2(d) = 0₆ and H₁ : β_·,2 (d) ≠ 0₆. We considered four different β_·,2(d) {0.0 × 1₆, 0.3 × 1₆, 0.6 × 1₆, 0.9 × 1₆} for all voxels within the region of interest, whereas we set β_·,2(d) = 0₆ for all voxels outside the region of interest. FWR denotes the family wise error rate and Apower denotes the average rejection rate for voxels inside the region of interest

	n = 40				n = 80
	ρ = 0.0		ρ = 0.5		ρ = 0.0		ρ = 0.5
β·,2(d)	FWR	Apower	FWR	Apower	FWR	Apower	FWR	Apower
0.0 × 16	0.12	0.00	0.06	0.00	0.08	0.00	0.07	0.00
0.3 × 16	0.18	0.10	0.12	0.10	0.06	0.56	0.06	0.57
0.6 × 16	0.14	0.67	0.06	0.68	0.02	1.00	0.03	1.00
0.9 × 16	0.12	0.83	0.10	0.85	0.08	1.00	0.06	1.00

4. HIV IMAGING DATA

We assess the integrity of white matter in human immunodeficiency virus (HIV). White matter is one of the three main solid components of the central nervous system (CNS) and is composed of bundles of myelinated nerve cell processes (or axons), which connect various gray matter areas (the locations of nerve cell bodies) of the brain to each other, and carry nerve impulses between neurons. The white matter is important for passing messages between different areas of gray matter within the CNS. After initial HIV infection, the virus is detectable in the CNS before antibodies are detectable in the blood and HIV could be cultured from brain tissue as early as 15 days (Davis et al. 1992; Rausch and Davis 2001). Since DTI can detect the subtle disruption of white matter structural integrity by assessing the degree to which fiber tracts within the white matter have lost their directional organization (Basser, Mattiello, and LeBihan 1994a, 1994b; Lim and Helpern 2002; Focke et al. 2008; Vernooij et al. 2008), DTI may be an important tool for detecting the early CNS HIV involvement.

We considered 47 subjects, in which 29 were HIV+ subjects (21 males and 8 females) and 18 were healthy (9 males and 9 females) controls from a cross-sectional study. The ages of the HIV+ subjects ranged from 30 to 52 years (mean: 40.0, SD: 5.6 years) and those of healthy controls ranged from 27 to 54 years (mean: 41.2, SD: 7.4 years). For each subject, both diffusion-weighted images and T1 weighted images were acquired. Diffusion gradients with a b-value of 1,000 s/mm² were applied in six noncollinear directions, (1, 0, 1), (−1, 0, 1), (0, 1, 1), (0, 1, −1), (1, 1, 0), and (−1, 1, 0). A b = 0 reference scan was also obtained for diffusion tensor matrix calculations. Forty-six contiguous slices with a slice thickness of 2 mm covered a field of view (FOV) of 256 × 256 mm² with an isotropic voxel size of 2 × 2 × 2 mm³. Eighteen acquisitions were used to improve the signal-to-noise ratio (SNR) in the images. High resolution T1 weighted (T1W) images were acquired using a 3D MP-RAGE sequence. Then, a weighted least squares estimation method was used to construct the diffusion tensors (Basser, Mattiello, and LeBihan 1994b; Zhu et al. 2007).

All images were visually inspected before analysis to ensure no bulk motion. A two-step image registration approach was utilized to spatially normalize the DTI parameters. The first step used a B-spline model based on a bidirectional elastic registration method to align the T1 weighted images of all subjects including both normal controls and HIV+ subjects to the T1 weighted images (template) of an arbitrarily chosen 41-year-old female healthy subject. In order to minimize biases induced by the choice of the template, the symmetry between the image pair to be coregistered was ensured through enforcing the consistency between the forward (e.g., from subject X to the template) and backward (from the template to subject X) transformations. The second step was to align each subject’s DTI images to his/her own anatomical T1 weighted images with a 12-parameter affine registration tool in FSL 3.2 (Analysis Group, FMRIB, Oxford, U.K.), so that DTI results can be spatially normalized through the spatial transformation obtained from high resolution T1 elastic registration. The tensor reorientation matrix at each voxel was derived as a rotation matrix approximating the transformation matrix (from T1 registration) through a singular value decomposition (SVD) (Alexander et al. 2001; Xu et al. 2003).

To control for the effects of covariates (diagnosis, age, and gender), we considered model (2) for C_i(β) for diffusion tensors at each voxel. The z_i = (1, x_1i, x_2i, x_3i)^T is a 4 × 1 vector, in which x_1i is Age/10, x_2i is gender, and x_3i denotes the diagnosis (1 HIV+ and 0 Healthy control). Moreover, we limited the statistical analysis within the major white matter regions which contains 17,444 voxels with mean fractional anisotropy (FA) value in normal volunteers greater than 0.4. We applied the annealing optimization algorithm with N₀ = 200 and M₀ = 4, which took an average CPU time of approximately 80 hours to carry out the statistical analysis.

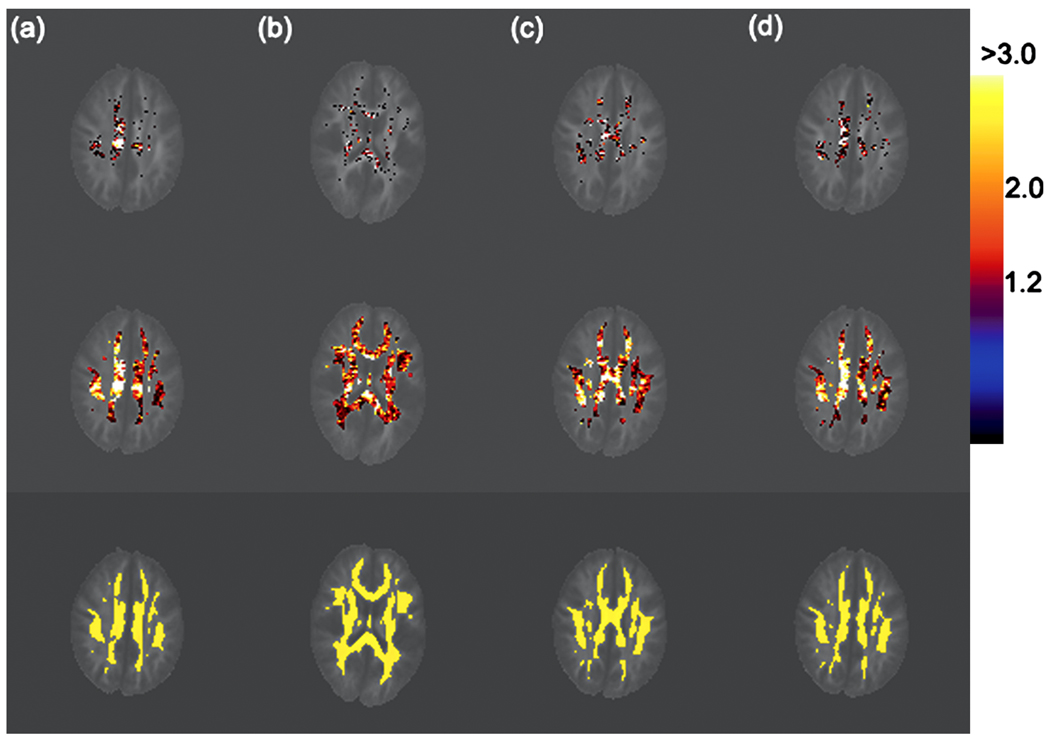
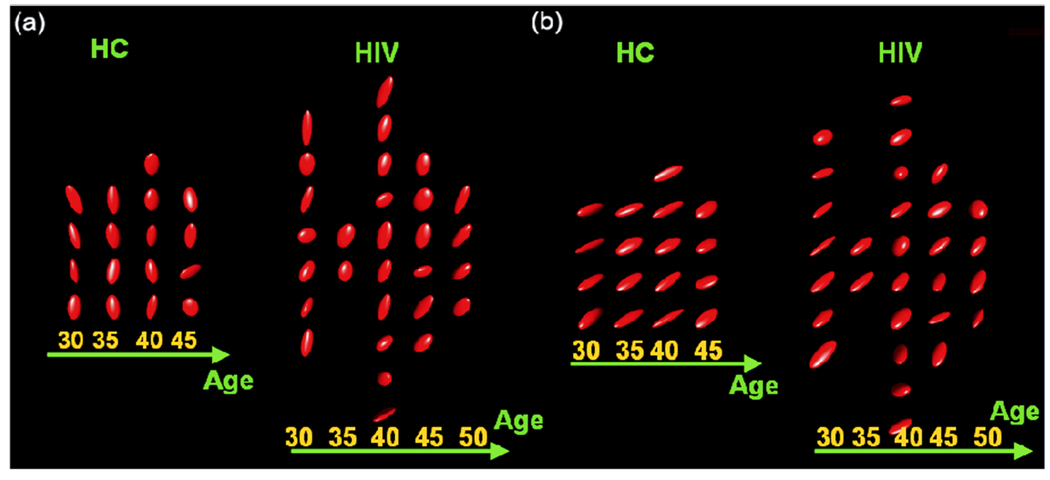
We detected the statistical significance of diagnosis (or age) on the integrity of white matter at all voxels with FA value greater than 0.4. Here, R is a 6 × 24 matrix and b₀ = (0, 0, 0, 0, 0, 0)^T for the hypotheses on either diagnosis or age. The uncorrected p-values based on the score statistics were color coded at each voxel in the selected regions of the reference brain (Figure 2). To correct for multiple comparisons, we applied our test procedure to calculate the adjusted p-value p_D(d) at each voxel in the selected regions of the reference brain (Figure 2). Color-coded maps of p-values using either the uncorrected p(d) alone or the corrected p_D(d) indicated several large-scale diagnosis and age effects for white matter integrity. The test procedure for correcting for multiple hypotheses, however, captured far fewer points of differences in the selected regions of the reference brain (Figure 2). As previously reported in studies of HIV (Kure et al. 1990; Pomara et al. 2001), the patients with HIV+ exhibited the subtle disruption of white matter structural integrity in the internal capsule and inferior longitudinal fasciculus. Our studies based on diffusion tensors thus seem to confirm these earlier results obtained with FA values (Pomara et al. 2001). We also picked two voxels and presented their diffusion tensors using an ellipsoid representation (Figure 3). We observed significant differences between HIV+ subjects and healthy controls (Figure 3a) and observed different age trends between HIV+ subjects and healthy controls (Figure 3b).

Figure 2.

Significance testing of diagnosis effect: color-coded maps of raw and adjusted p-values in four selected ROIs of the reference brain. The color scale reflects the magnitude of the values of −log₁₀(P), with black to blue representing smaller values (0–1) and red to white representing larger values (1.88–3). Row 1: adjusted −log₁₀(P) values of the score statistics based on our test procedure for the correction of multiple comparisons. Row 2: raw −log₁₀(P) values of the score statistics based on a χ² distribution. Row 3: selected ROIs with FA values greater than 0.4. After correcting for multiple comparisons, statistically significant diagnosis effects remain in the superior internal capsule area.

Figure 3.

Ellipsoid representation of diffusion tensors from two voxels to illustrate significant effects of diagnosis and age. Panel (a): testing diagnosis effect. Panel (b): testing age effect.

5. DISCUSSION

We have developed a general statistical framework for an intrinsic regression model of positive-definite matrices as responses in a Riemannian manifold and their association with a set of covariates, such as age and gender, in Euclidean space. The intrinsic regression model is based on the first moment of imaging measures and therefore it avoids any parametric assumptions regarding SPD matrices. We have proposed several link functions to map covariates in Euclidean space to positive-definite matrices in the Riemannian manifold Sym⁺(m). We have developed an annealing optimization algorithm to search for the ILSE of β. The test procedure based on the resampling method not only accounts for multiple comparisons across the entire region of interest under investigation, but it also asymptotically preserves the dependence structure among the test statistics. Our simulation studies have demonstrated that the methodology developed here provides relatively accurate control of the family-wise error rate.

We also note several limitations of our procedures. There is a computational issue with the estimation procedure for computing β̂. Since G_n(β) is generally not concave and can have many local minima, the annealing optimization algorithm proposed here cannot guarantee to locating the global minimum β̂ of G_n(β) for arbitrary link function. More advanced optimization algorithms are needed for more complex link functions. Our test procedure based on W_n,𝒟 and the resampling method performs reasonably well for relatively larger sample sizes, say 100. However, further improvement on controlling the family-wise error rates is needed. We may either use other computationally extensive methods, such as permutation method, in order to achieve better control of the family-wise error rates, or use other multiple comparison procedures, such as the false discovery rate.

Many issues still merit further research. One major issue is to develop diagnostic measures for assessing the influence of individual observations in semiparametric regression for SPD matrices. Another major issue is to construct goodness-of-fit statistics for testing possible misspecification in (7). Moreover, it is of interest to develop nonparametric regression methods for SPD matrices (Fan and Gijbels 1996). We will study these issues in our future work.