Mating-System Variation, Demographic History and Patterns of Nucleotide Diversity in the Tristylous Plant Eichhornia paniculata

Abstract

Inbreeding in highly selfing populations reduces effective size and, combined with demographic conditions associated with selfing, this can erode genetic diversity and increase population differentiation. Here we investigate the role that variation in mating patterns and demographic history play in shaping the distribution of nucleotide variation within and among populations of the annual neotropical colonizing plant Eichhornia paniculata, a species with wide variation in selfing rates. We sequenced 10 EST-derived nuclear loci in 225 individuals from 25 populations sampled from much of the geographic range and used coalescent simulations to investigate demographic history. Highly selfing populations exhibited moderate reductions in diversity but there was no significant difference in variation between outcrossing and mixed mating populations. Population size interacted strongly with mating system and explained more of the variation in diversity within populations. Bayesian structure analysis revealed strong regional clustering and selfing populations were highly differentiated on the basis of an analysis of F_st. There was no evidence for a significant loss of within-locus linkage disequilibrium within populations, but regional samples revealed greater breakdown in Brazil than in selfing populations from the Caribbean. Coalescent simulations indicate a moderate bottleneck associated with colonization of the Caribbean from Brazil ∼125,000 years before the present. Our results suggest that the recent multiple origins of selfing in E. paniculata from diverse outcrossing populations result in higher diversity than expected under long-term equilibrium.

THE rate of self-fertilization in hermaphrodite organisms is expected to affect a number of important features of population genetic structure and diversity. Most directly, homozygosity increases as a function of the selfing rate and thus reduces the effective population size (N_e), up to twofold with complete selfing (Pollak 1987; Charlesworth et al. 1993; Nordborg 2000). Further, because of increased homozygosity, crossing over rarely occurs between heterozygous sites, thus increasing linkage disequilibrium (LD). Higher LD causes stronger hitchhiking effects such as selective sweeps, background selection, and Hill–Robertson interference, all of which are expected to further reduce the amount of neutral genetic variation within populations (reviewed in Charlesworth and Wright 2001).

Population genetic processes resulting from inbreeding may be further augmented by demographic and life-history characteristics associated with the selfing habit. In particular, selfing populations can be founded by single individuals, resulting in striking reductions in diversity as a result of genetic bottlenecks and reproductive isolation. The capacity for uniparental reproduction gives many selfers prolific colonizing ability and the capacity to establish after long-distance dispersal, especially in comparison with obligate outcrossers (Baker 1955; Pannell and Barrett 1998). The colonization–extinction dynamics typical of many selfing species and limited pollen-mediated gene flow also increase differentiation among populations, resulting in considerable population subdivision (Hamrick and Godt 1990, 1996; Schoen and Brown 1991). Although the total amounts of among-population variation may be less affected by these processes (Pannell and Charlesworth 1999; Ingvarsson 2002), the demographic and life-history characteristics of many selfing species are likely to result in nonequilibrium conditions occurring in selfing populations.

In many taxa where selfing has evolved it may be of relatively recent origin (Schoen et al. 1997; Takebayashi and Morrell 2001; Foxe et al. 2009; Guo et al. 2009). Where selfing has recently established, demographic forces associated with colonization may be as important as the mating system per se in structuring patterns of diversity. For example, if selfing originates through the establishment of a small number of founders, we would expect a sharp reduction in diversity relative to the outcrossing progenitor and a strong signature of a genetic bottleneck. In contrast, if selfing has evolved recently through the spread of genetic modifiers of small effect, newly established populations may retain significant amounts of ancestral polymorphism from their outcrossing progenitors. In this latter case populations may retain considerably more variation than expected under long-term equilibrium predictions.

Molecular evidence for reduced nucleotide diversity and greater differentiation among populations of selfing taxa compared to populations of related outcrossing taxa has been reported from Leavenworthia (Liu et al. 1998, 1999), Arabidopsis (Savolainen et al. 2000; Wright et al. 2002), Solanum (Baudry et al. 2001), Mimulus (Sweigart and Willis 2003), Amsinckia (Perusse and Schoen 2004), and Caenorhabditis (Graustein et al. 2002; Cutter et al. 2006; Cutter 2008). In each case the reduction in diversity was more severe than the twofold reduction predicted for selfing populations at equilibrium. This indicates that factors in addition to the mating system are reducing diversity, but it has been difficult to uncouple the relative importance of genetic hitchhiking from the ecology and demographic history of selfing taxa. This challenge parallels similar difficulties in efforts to distinguish selective from demographic explanations in population genetic studies of Drosophila (Haddrill et al. 2005; Ometto et al. 2005; Thornton and Andolfatto 2006; Jensen et al. 2008). However, in many plant populations, especially those with annual life histories and small structured populations, demographic processes may play a more prominent role in causing reduced diversity than increased hitchhiking associated with selfing.

Molecular population genetic studies of selfing in plants have generally focused on either small samples from a large number of populations (e.g., Sweigart and Willis 2003; Nordborg et al. 2005) or relatively large within-population samples from a small number of populations (e.g., Baudry et al. 2001). Ideally, a deeper sampling both within and among populations combined with independent ecological and historical information is required to improve understanding of the interplay of demographic and selective factors. Here we address these issues by examining patterns of nucleotide diversity within a large sample of populations of Eichhornia paniculata (Pontederiaceae), an annual species for which there is considerable ecological and demographic information (reviewed in Barrett and Husband 1997).

E. paniculata occurs primarily in northeastern (N.E.) Brazil and the Caribbean islands of Cuba and Jamaica. Various lines of evidence suggest that Brazil is the original source region for Caribbean populations (reviewed in Barrett et al. 2009). Populations of E. paniculata exhibit striking mating-system diversity, ranging from predominantly outcrossing to those that are highly selfing (outcrossing rate, t = 0.002–0.96; n = 54 populations) (Barrett and Husband 1990; Barrett et al. 1992). Variation in mating system is associated with the evolutionary breakdown of the species' tristylous genetic polymorphism and the spread and fixation of selfing variants capable of autonomous self-pollination (Barrett et al. 1989). Populations of E. paniculata are characterized by three morph structures: trimorphic with long-, mid-, and short-styled morphs (hereafter L-, M-, and S-morphs); dimorphic, with two floral morphs, most commonly the L- and M-morphs; and monomorphic, primarily composed of selfing variants of the M-morph. The morph structure and presence of selfing variants within populations explain ∼60% of the variation in outcrossing rates among populations (Barrett and Husband 1990). Trimorphic populations are largely outcrossing, dimorphic populations display mixed mating, and monomorphic populations are highly selfing. Patterns of allozyme variation indicate a reduction in diversity with increased selfing rates and greater among-population differentiation (Glover and Barrett 1987; Barrett and Husband 1990; Husband and Barrett 1993). Finally, studies of the inheritance of mating-system modifiers (Fenster and Barrett 1994; Vallejo-Marín and Barrett 2009) in combination with allozyme (Husband and Barrett 1993) and molecular evidence (Barrett et al. 2009) indicate that the transition from outcrossing to selfing in E. paniculata has occurred on multiple occasions.

The goal of our study was to investigate the relation between mating-system variation and neutral molecular diversity for a large sample of E. paniculata populations encompassing most of the geographical range. This was accomplished by collecting multilocus nucleotide sequence data from 225 individuals sampled from 25 populations including trimorphic, dimorphic, and monomorphic populations. Because it has been previously demonstrated that this sequence of morph structures is strongly associated with increasing rates of self-fertilization (see Barrett and Husband 1990), we predicted a decrease in neutral diversity and increases in F_st and linkage disequilibrium from floral trimorphism to monomorphism. This extensive population-level sampling across a wide range of selfing rates allowed us to investigate the relative importance of mating system, geography, and current population size in structuring genetic variation. We also applied the approaches of Bayesian clustering (Pritchard et al. 2000; Falush et al. 2003; Gao et al. 2007) and divergence population genetics (Wakeley and Hey 1997; Hey and Nielsen 2004; Becquet and Przeworski 2007) to investigate the demographic history of E. paniculata and to provide a framework for understanding island colonization and the transition from outcrossing to selfing.

MATERIALS AND METHODS

Population sampling:

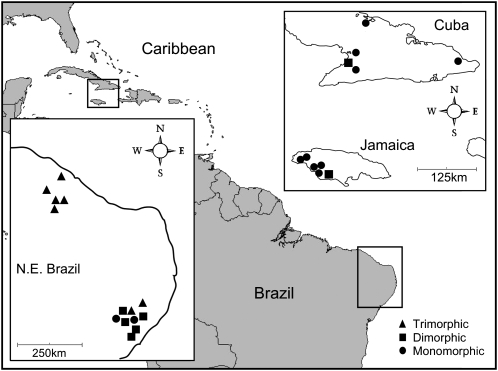
We sampled open-pollinated maternal seed families from E. paniculata populations occurring in N.E. Brazil (May 2005), Jamaica (January 2006), and Cuba (March 2008). Because of a significant break in the distribution of E. paniculata in N.E. Brazil, corresponding to an arid zone inimical for aquatic plant growth, we distinguish a northern (Ceara) and a southern (Pernambuco, Alagoas) portion of the Brazilian range. This is evident in Figure 1, which maps the location of all populations used in this study. Information on morph structure, morph diversity, the frequency of selfing variants within populations, and current population size is provided for each population in Table 1. Details of the methods we used to sample population size and morph diversity can be found in Barrett et al. (1989). We germinated seeds and grew plants for DNA extraction in a glasshouse at the University of Toronto. We used a single individual from each maternal family to minimize the number of closely related individuals and to provide the best estimate of population-level diversity. Sample sizes for the number of individuals sequenced in each population are provided in Table 1 (mean number of individuals per population = 9, range = 4–12).

Figure 1.—

Eichhornia paniculata populations sampled for this study. Inset maps show locations of populations from N.E. Brazil, Cuba, and Jamaica.

TABLE 1.

Populations samples and details of Eichhornia paniculata used in this study

Pop. codea	Nearest cityb	Morph structurec	Pop. sized	No. of sequencese	Freq. of selferf	Morph diversityg
B177	Anadia, Alagoas, Brazil	Dimorphic	500	12	0.256	0.743
B180	Vicosa, Alagoas, Brazil	Dimorphic	100	6	0.095	0.735
B182	Brejao, Pernambuco, Brazil	Monomorphic	500	12	1.000	0.000
B183	Corrente, Pernambuco, Brazil	Monomorphic	100	12	1.000	0.000
B184	Corrente, Pernambuco, Brazil	Dimorphic	500	12	0.268	0.535
B185	Sao Jose da Laje, Alagoas, Brazil	Dimorphic	750	6	0.130	0.737
B186	Garanhuns, Pernambuco, Brazil	Dimorphic	750	12	0.221	0.740
B187	Garanhuns, Pernambuco, Brazil	Trimorphic	1750	8	0.000	0.973
B192	Cupira, Pernambuco, Brazil	Trimorphic	8000	12	0.118	0.816
B202	Quixada, Ceara, Brazil	Trimorphic	1500	6	0.000	0.903
B206	Pirajana, Ceara, Brazil	Trimorphic	1500	6	0.000	0.899
B207	Choro, Ceara, Brazil	Trimorphic	2500	12	0.000	0.997
B210	Caninde, Ceara, Brazil	Trimorphic	3000	12	0.000	0.959
B211	Forteleza, Ceara, Brazil	Trimorphic	700	12	0.000	0.960
C1	Yara, Granma, Cuba	Monomorphic	500	5	1.000	0.000
C2	Manzanillo, Granma, Cuba	Dimorphic	800	11	0.850	0.382
C3	Chorerra, Granma, Cuba	Monomorphic	120	7	1.000	0.000
C4	Baracoa, Guantánamo, Cuba	Monomorphic	10	4	1.000	0.000
C5	Camalote, Camagüey, Cuba	Monomorphic	600	12	1.000	0.000
J28	Treasure Beach, St. Elizabeth, Jamaica	Dimorphic	200	10	0.970	0.087
J29	Fullerswood, St. Elizabeth, Jamaica	Monomorphic	28	12	1.000	0.000
J30	Cataboo, St. Elizabeth, Jamaica	Monomorphic	20	4	1.000	0.000
J31	Slipe, St. Elizabeth, Jamaica	Monomorphic	4	4	1.000	0.000
J32	Little London, Westmoreland, Jamaica	Monomorphic	25	10	1.000	0.000
J33	Georges Plain, Westmoreland, Jamaica	Monomorphic	Unknown	6	1.000	0.000

^aCode used throughout this article to identify collection locations.

^bCity nearest to the population.

^cDimorphic populations contain selfing variants of the M-morph in varying frequencies; monomorphic populations are composed exclusively of this form.

^dEstimate of the census size of populations at time of collection.

^eNumber of individuals that were sequenced for this study.

^fFrequency of the modified selfing variant in populations.

^gA measure of evenness of the three floral morphs normalized to one. Populations with even ratios of all three morphs have a diversity of one, and monomorphic populations have a diversity of zero (see Barrett et al. 1989 for further details).

Marker development:

We developed nuclear DNA primers on the basis of EST sequences collected from a cDNA library from leaf tissue of a single plant. We purified polyadenylated RNA from total RNA using the Ambion Micro Poly(A) Purist kit and reverse transcribed the mRNA using the InVitrogen (Carlsbad, CA) Superscript cDNA synthesis kit. We cloned cDNA into Escherichia coli and sequenced ∼480 clones.

From these clones, we selected sequences that aligned to well-annotated nuclear sequences from other plants and designed primers to amplify both coding regions and intron sequence where possible. We initially tested the primers by sequencing the loci in four inbred lines derived from selfing populations, our rationale being that there should be few heterozygous sites and any loci with these could be excluded as likely paralogs. From this screening we chose 10 EST-derived nuclear markers (see supporting information, Table S1) that were then amplified and sequenced in all individuals. Open reading frames in coding loci were identified and annotated using a combination of BLASTx, the original EST sequence, and the ORF prediction software GeneMark-E* (Lomsadze et al. 2005).

Amplification and sequencing:

We extracted DNA from all 225 individuals and this was used to PCR amplify the 10 loci in each individual. We sequenced both forward and reverse strands with an ABI 3730XL fluorescent-based capillary sequencer at the Centre for Applied Genomics facility at Sick Kids Hospital, Toronto, Ontario, Canada. We assembled and aligned sequences using Sequencher 4.7 and edited chromatographs and alignments manually to ensure that all base calls and polymorphisms including heterozygotes were reliably scored.

Polymorphism:

Of the analyses described below, both InStruct and analyses of LD include all sites while the remaining analyses used only silent sites (synonymous and noncoding). We calculated both silent and nonsynonymous polymorphism statistics including θ_W (Watterson 1975) and θ_π (Tajima 1983) for all loci and populations, using the program SITES (Hey and Wakeley 1997). We calculated Tajima's D (Tajima 1989) at silent sites with the program SITES and compared each locus in each population to simulation results to detect significant deviations from neutrality, using the program HKA (Hey and Wakeley 1997). In addition, we calculated multilocus estimates of nucleotide polymorphism (θ_W), using a maximum-likelihood method based on the number of segregating sites as implemented by Wright et al. (2003) to test for significant differences in polymorphism between Caribbean and Brazilian regions. Significant differences in θ_W were assessed using twice the relative ln likelihood following the χ² approximation. We also calculated the same maximum-likelihood estimate of θ_W for each population. However, for analyses of polymorphism at the population level we discuss only silent θ_π (see Table S2 for θ_W) because the patterns and significance attained are equivalent using both measures of genetic variation.

Correlates of nucleotide diversity:

To understand the factors influencing genetic variation we investigated the relation between nucleotide diversity (θ_π) and five population-level variables: population size, morph diversity, frequency of selfing variant, morph structure (tri-, di-, or monomorphic), and region (Caribbean or Brazil). Values for the variables are presented in Table 1. Morph diversity and the frequency of the selfing variant were highly correlated (Kendall's τ = 0.900). We therefore report results for analyses with the frequency of the selfing variant only, as results were similar using morph diversity. We tested for associations among population size, frequency of the selfing variant, morph diversity, and θ_π using Kendall's rank correlations. We also calculated Kendall's rank partial correlations (Kendall 1942) for each pairing of these variables to examine their associations in the absence of correlated effects from the third variable. Because region and morph structure were nominal variables, we compared mean nucleotide diversity within populations to these variables using a Kruskal–Wallis test and compared means between pairs of populations with the Tukey–Kramer honestly significant differences (HSD) test.

Population genetic structure:

To investigate the genetic structure of populations we used the Bayesian clustering program InStruct (Gao et al. 2007). The program is similar to the algorithm STRUCTURE developed by Pritchard et al. (2000), but allows for varying levels of inbreeding within subpopulations. We removed singletons from all alignments and sequences were converted to haplotypes and the phase of heterozygous sites was inferred using the program PHASE v2.1 (Stephens et al. 2001; Stephens and Scheet 2005). Simulations were conducted using InStruct version 2 to estimate structure with both admixture and selfing. We assumed all 10 loci are unlinked, which is supported by analyses of linkage disequilibrium among loci. We simulated 10⁶ iterations with a burn-in length of 10⁵ steps. This was repeated over cluster number (K) from one to the number of sampled populations (K = 1 to K = 25) and each simulation was run three times with the optimal number of clusters determined by the software using the deviance information criteria.

We calculated mean F_ST (Wright 1931) for silent sites within regions using the program SITES (Hey and Wakeley 1997) and averaged pairwise F_ST estimates for each population across all populations within its own region (Table 1). We also conducted an analysis of molecular variance (AMOVA) to investigate the partitioning of variation among and within populations and regions, using the program GenAlex 6 (Peakall and Smouse 2006).

Linkage disequilibrium:

We calculated all within-population and within-region pairwise associations (R²) between single-nucleotide polymorphisms (SNPs). For regional samples we present results for a “scattered sample” that includes one individual per population. This sampling strategy has been shown to most accurately reflect the deeper coalescent history of structured populations (Wakeley and Lessard 2003; Städler et al. 2009), which is likely in E. paniculata (see Husband and Barrett 1998), with minimal effects of population subdivision in generating excess LD. We estimated the expected decay in LD with distance within loci using the method of Cutter et al. (2006) and Equation 3 from Weir and Hill (1986),

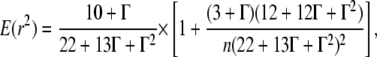where Γ is the product of the recombination rate (ρ = 4N_er) and distance in base pairs. We fitted this equation to our data, using values of associations between pairs of SNPs (R²) estimated with Weir's (1996) algorithm for unphased data as implemented by Macdonald et al. (2005). Values for R² were calculated only for pairs of SNPs within loci; however, we pooled values across all loci to estimate the decay in LD with distance. We complemented this method by using Hudson's (2001) estimator of the population recombination parameter ρ, which employs a composite-likelihood approach based on pairwise disequilibrium between pairs of SNPs within loci. We excluded loci with fewer than five SNPs in this analysis because this method does not accurately estimate ρ when there are few variable sites.

Demographic history:

We conducted coalescent simulations of the divergence between Caribbean and Brazilian populations of E. paniculata, using the isolation–migration software MIMAR (Becquet and Przeworski 2007). We chose MIMAR over other available methods because it allows for intralocus recombination, which we observed in the Brazilian and Caribbean regions. In MIMAR we simulated a single ancestral population that instantaneously split into two derived populations (Brazil and Caribbean) at some time (T) in the past. All populations were assumed to be at a constant size and to be linked by gene flow. Because we did not have a close outgroup sequence to reliably reconstruct ancestral states for SNPs, we used a modified version of MIMAR as implemented by Foxe et al. (2009), which does not assume knowledge of the ancestral state of polymorphic sites. We included silent-site variation from all 10 loci in our input, excluding positions with three or more variants. We allowed for locus-specific mutation rates by dividing θ_SIL from each locus by the mean θ_SIL.

We initially used wide prior limits for simulations to determine better priors for later runs. All θ priors had a uniform distribution and individual populations had prior probabilities of θ_CRB = 0.0005–0.002, θ_BRA = 0.0018–0.006, and θ_ANC = 0.0075–0.018 for the Caribbean, Brazilian, and ancestral populations, respectively. We also conducted simulations where θ_BRA = θ_ANC; however, this model did not influence the general results of the analysis and is not included. Simulation runs that included migration indicated a mode at zero and little effect on other parameters, and we therefore report only runs assuming no gene flow. The time of the split between contemporary Brazilian populations and the Caribbean was bounded between 10,000 and 175,000 years ago with a uniform distribution. The mutation rate for E. paniculata, a monocot, is unknown; therefore, to estimate time in generations and the effective population size, we used the mean synonymous-site mutation rate from the grass ADH sequence, which is μ = 6.5 × 10⁻⁹ substitutions per site per generation (Gaut et al. 1996). We ran simulations for 20,160 min (2 weeks). This allowed for ∼1.61 × 10⁶ iterations with a burn-in of 100,000 steps. Marginal posterior probabilities for all parameters were generated in R v2.8.1 (R Development Core Team 2008). To estimate the portion of the posterior distribution that encompasses 90% of the simulated values and describe confidence limits around point estimates of each parameter, we calculated the 90% highest probability density (90% HPD) for each parameter, using the boa package for R (Smith 2007).

RESULTS

Polymorphism:

Specieswide estimates of silent nucleotide variation in E. paniculata were θ_W = 0.0101 and θ_π = 0.0064. The ratio of replacement to silent segregating sites in all of the coding regions is consistent with purifying selection constraining changes in coding sites (see Table S1). Neutral genetic diversity was distributed unevenly within and among populations and the mean within-population diversity (θ_W = 0.0034, θ_π = 0.0020) was substantially lower than specieswide estimates. An AMOVA of all populations revealed that 64.3% of the molecular variation was partitioned within populations with the remaining 35.7% distributed among populations.

Correlates of nucleotide diversity:

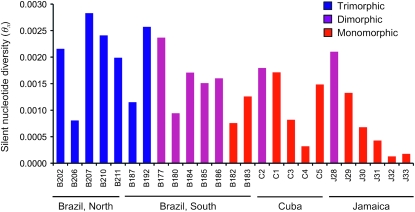
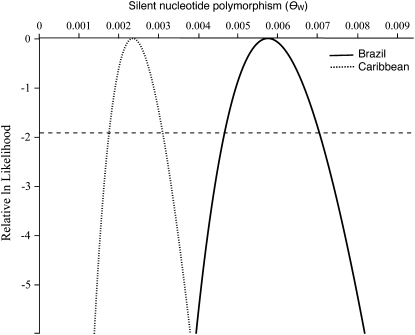
There was striking variation in silent nucleotide diversity among regions and populations within each floral morph structure (Figures 2 and 3). However, as predicted, monomorphic populations maintained significantly less variation than trimorphic or dimorphic populations (θ_{π,monomorphic} = 0.00083, θ_{π,trimorphic} = 0.001989, θ_π,dimorphic = 0.001719, Kruskal–Wallis test, χ² = 11.45, P < 0.01). To examine whether this difference in θ_π was significantly distinguishable from the twofold reduction in diversity predicted in selfing populations, we doubled the mean of θ_π in monomorphic populations and repeated the test. There was no longer a significant effect of morph structure on diversity, a result consistent with theoretical predictions of a 50% reduction due to selfing (Kruskal–Wallis test, χ² = 0.837, P = 0.658). There was no significant difference in the amount of nucleotide diversity within trimorphic vs. dimorphic populations (Tukey–Kramer test, P = 0.78). On the basis of measures of θ_π, a Kruskal–Wallis test revealed that the region of origin had a significant effect on within-population diversity (θ_π,Caribbean = 0.0009, θ_π,Brazil = 0.00172, χ² > 4.795, P < 0.05). Additionally, using the joint maximum-likelihood estimate of θ_W, the Caribbean sample treated as a single population was significantly less diverse than the total Brazilian sample (Figure 3; θ_W,Brazil = 0.0068, θ_W,Caribbean = 0.0023, χ² ≅ 20.55, P < 0.0001).

Figure 2.—

Estimates of within-population nucleotide diversity (θ_π) for 25 populations of Eichhornia paniculata based on the mean diversity of all 10 EST-derived nuclear loci.

Figure 3.—

Joint maximum-likelihood surface for nucleotide polymorphism (θ_W) for combined Caribbean and Brazilian populations. The reference line at relative ln likelihood = 1.92 represents the credibility interval that determines significantly different estimates on the basis of the χ²-approximation.

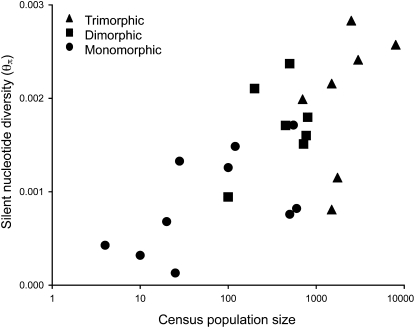
Nucleotide diversity was strongly associated with estimates of population census size and the frequency of the selfing variant within populations (Table 2). Population size was highly correlated with θ_π (Figure 4; Kendall's τ = 0.512, P < 0.001) but retained a lower partial correlation (0.105) after controlling for variation in the frequency of the selfing variant. However, while the frequency of the selfing variant correlated strongly with θ_π (Kendall's τ = −0.449, P < 0.005), it retained very little partial correlation (0.032) after we controlled for the influence of population size. However, neither of these partial correlations was significant because population size and the frequency of the selfing variant were so highly correlated (Kendall's τ = 0.629, P < 0.0001).

TABLE 2.

The statistical relations between population size, the frequency of selfing variants, and nucleotide diversity (θπ) in 25 populations of Eichhornia paniculata sampled from Brazil and the Caribbean

	Population size	Selfing variant frequency	Nucleotide diversity (θπ)
Population size	—	−0.520	0.105
Selfing variant frequency	***0.629	—	0.033
Nucleotide diversity (θπ)	**0.512	*0.449	—

Above the diagonal are Kendall's partial rank correlation coefficients and below are Kendall's τ estimates. Significant correlations are indicated with asterisks: *P < 0.005, **P < 0.001, and ***P < 0.0001.

Figure 4.—

Relation between census population size and nucleotide diversity in 25 populations of E. paniculata from Brazil and the Caribbean (Kendall's τ = 0.512, P < 0.001). Population size is plotted on a log scale.

Multilocus estimates of Tajima's D revealed that 40% of the populations sampled exhibited significantly negative average multilocus values (see Table S2). This pattern varied among regions. For example, within the southern portion of the Brazilian range, six of nine populations had significantly negative values (mean within-population D = −0.57, SE = 0.075), whereas one of five populations from the northern portion of the Brazilian range showed a significant negative Tajima's D and another population showed a significant positive value. When considered regionally, southern Brazil showed a highly significant negative Tajima's D (D = −1.159), while populations sampled from northern Brazil did not differ from neutrality (D = −0.134). Only two of five Jamaican populations and no Cuban populations had significantly negative values of Tajima's D. However, when Cuban and Jamaican populations were pooled, they showed a significant excess of rare variants (D = −0.59). It should be noted that the coalescent simulations as implemented in the HKA program assume no recombination, and thus this test should be conservative with respect to inferring departures from neutral equilibrium.

Population structure:

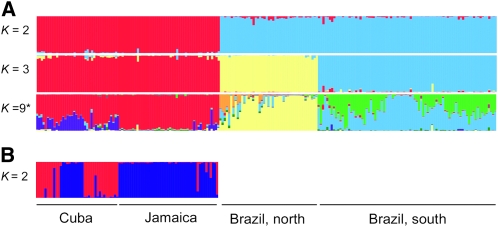
Using InStruct, we explored the genetic structure of E. paniculata across its geographical range. At K = 2, the clusters reflected the large geographic divide between populations sampled from Brazil and the Caribbean (Figure 5). At K = 3, the clusters corresponded to geographical subdivision within Brazil, plus individuals from the Caribbean populations. As the number of clusters increased, each larger region became subdivided into groups that did not correspond to the geographic locations of populations. The optimal number of clusters, as determined by the deviance information criterion, was K = 9. At this K-value there was still little change to the clusters from the three major regions as defined by K = 3. Individuals from Caribbean and Brazilian populations from the northern portion of the range were largely composed of single clusters, while individuals from the southern portion of the Brazilian range were mostly composed of an admixture of two different clusters. To further explore genetic structure, we also conducted separate runs of InStruct for each region separately. For Brazilian populations these analyses provide no additional insight; however, within the Caribbean individuals from a single population from Cuba (C5) clustered with Jamaican populations (Figure 5).

Figure 5.—

(A) Rangewide genetic structure of Eichhornia paniculata based on analyses conducted using InStruct with different numbers of clusters (K = 2, 3, 9). (B) Results for the Caribbean sample of populations from Jamaica and Cuba run separately (K = 2). Each thin bar represents a single individual, which may be partitioned into K colors depending on the estimated multilocus membership in each of K clusters, where each color represents the posterior probability of that individual belonging to a cluster. The best-fitting model K = 9 is indicated with an asterisk.

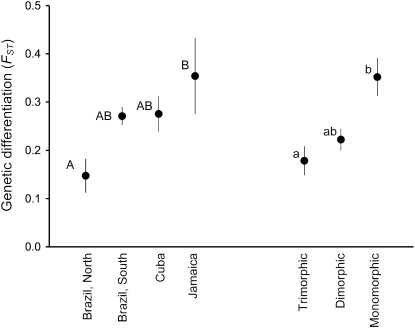
Our analyses of population differentiation using F_st corresponded with patterns obtained from InStruct. Pairwise F_st values, in which members of a pair are populations from different regions, were substantially higher than when both populations were sampled from a single region (data not shown). When pairs are restricted to comparisons within regions, mean pairwise F_st values were highest among Caribbean populations and lowest among trimorphic populations from northern Brazil (Figure 6; Tukey–Kramer test, q* = 2.512, P < 0.05). Populations representing all three morph structures are represented in the southern portion of the Brazilian range. This region had intermediate F_st values compared with the exclusively trimorphic populations from the northern portion of the Brazilian range and Caribbean populations. Population morph structure had a significant effect on F_st values within regions defined by InStruct at K = 3 (Kruskal–Wallis test, χ² = 8.4295, P < 0.05). Monomorphic populations exhibited significantly higher levels of differentiation than either dimorphic or trimorphic populations, which did not differ significantly from one another (Tukey–Kramer test, q* = 2.512, P < 0.05).

Figure 6.—

Mean F_st for pairwise population comparisons of Eichhornia paniculata within geographical regions. The values were averaged across populations within each of the four regions and also for trimorphic, dimorphic, and monomorphic populations. Letters indicate significant differences using the Tukey–Kramer HSD test. Error bars represent ±1 SE.

Linkage disequilibrium:

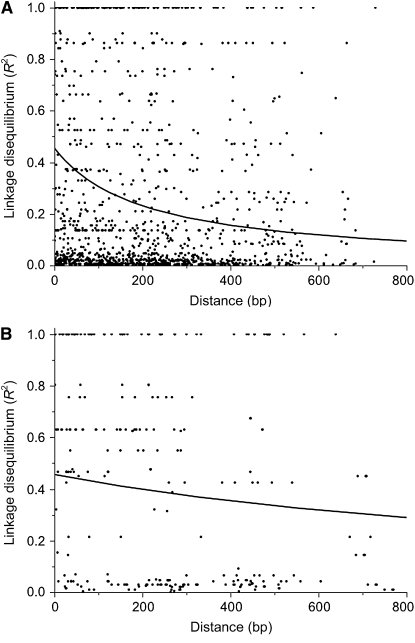
Using the method of Cutter et al. (2006) with a scattered sample we found evidence for reduced effective recombination (ρ = 4N_er) within loci from Caribbean vs. Brazilian populations (Figure 7; ρ_BRAZIL = 0.0100, ρ_CARIBBEAN = 0.0014). Moreover, when ρ was estimated using Hudson's coalescent-based approach, the breakdown of LD averaged across all loci was also moderately higher for Brazil than for the Caribbean (ρ_BRAZIL = 0.0160, ρ_CARIBBEAN = 0.0121). However, there was no evidence for recombination within any locus in populations of E. paniculata using either method. Estimates of ρ = 4N_er were zero for all sampled populations. In many cases there were not enough SNPs at a given locus to use Hudson's ρ-estimator. Mean LD among loci within populations was much lower than intralocus LD (R²_total = 0.140) and slightly lower in Brazil than in the Caribbean (R²_Brazil = 0.062, R²_Caribbean = 0.115).

Figure 7.—

Decay of linkage disequilibrium (R²) with distance (bp) in a scattered sample of Eichhornia paniculata from (A) Brazil and (B) Cuba and Jamaica combined. The line on each plot is fit to Weir and Hill's (1986) equation for the expected decay of LD with distance to infer the effective recombination rate, ρ = 4N_er (ρ_BRAZIL = 0.0100, ρ_CARIBBEAN = 0.0014).

Coalescent simulations:

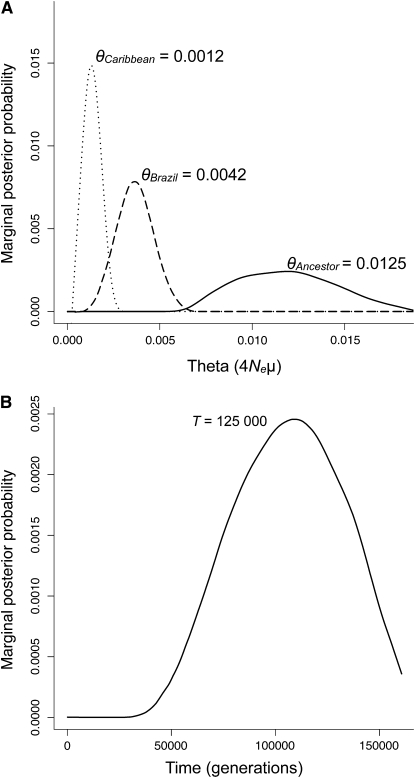
Our simulation results indicate that Caribbean populations exhibit lower effective population size than Brazilian populations (Figure 8A). The mode of the marginal posterior probability for θ_CRB = 0.0012 (90% HPD = 0.0008–0.0018) was lower than that for Brazil, θ_BRA = 0.0042 (90% HPD = 0.0019–0.0049). These model-based estimates were both substantially lower than the estimated diversity of the ancestral population, θ_ANC = 0.0125 (90% HPD = 0.0082–0.0154). This suggests that both regions have experienced a population bottleneck, with the Caribbean experiencing a more extreme reduction in effective population size. Using estimates of the mutation rate from grasses, these values provide estimates of effective population sizes for the three populations of N_CRB = 46,200, N_BRA = 161,500, and N_ANC = 481,000. The model-based estimate of diversity in the Caribbean was marginally lower than the estimate made directly from our sequence data (θ_π,Caribbean = 0.0019, SE = 0.0007), suggesting that the retention of ancestral polymorphism is inflating estimates of diversity in the Caribbean. Estimates of diversity from simulations and empirical estimates were similar for Brazilian populations (θ_π,_Brazil = 0.0039). Using the mode as a point estimate of the time since divergence between Caribbean and Brazilian populations gave a colonization time for the Caribbean of 125,000 generations before the present (90% HPD = 66,449–146,232; Figure 8B).

Figure 8.—

Marginal posterior probability distributions from coalescent simulations of the demographic history of Eichhornia paniculata. (A) Simulated estimates of diversity (θ = 4N_eμ) in populations from Brazil, the Caribbean, and their common ancestor represented by dotted, dashed, and solid lines, respectively. (B) Time (in annual generations) since divergence between Brazilian and Caribbean populations estimated using the average mutation rate of grass ADH sequences μ = 6.5 × 10⁻⁹. All curves were estimated using the program MIMAR (Becquet and Przeworski 2007), which implements coalescent simulations in a Bayesian framework. The mode for each distribution is labeled above each curve.

DISCUSSION

Highly selfing populations should have an effective size 50% that of equivalent outcrossing populations under neutral and equilibrium expectations (Charlesworth et al. 1993; Nordborg 2000). However, most interspecific comparisons of nucleotide diversity in outcrossing vs. selfing species indicate that selfing populations maintain considerably lower values than this prediction. This suggests that genetic hitchhiking and demographic differences between species are reducing diversity beyond the standard neutral expectations. In contrast, a major finding of our study was that the average neutral diversity of highly selfing monomorphic populations of E. paniculata showed a roughly twofold reduction relative to polymorphic populations. Hence, it is unnecessary to invoke genetic hitchhiking to explain differences in diversity among populations. Significantly, the census population size was a strong predictor of the amount of nucleotide diversity in populations, indicating an important role of demography in shaping patterns of diversity. Levels of population differentiation showed the expected increase for regions with higher selfing rates, and there was some evidence for higher levels of intralocus linkage disequilibrium in the Caribbean, where selfing rates are the highest. We now consider how colonization processes and the demographic origins of populations are likely to play a role in structuring regional patterns of nucleotide polymorphism.

Population size, morph structure, and nucleotide polymorphism:

Our results demonstrate that in E. paniculata population size and its association with morph structure are a stronger predictor of silent nucleotide diversity than mating patterns alone. Monomorphic, highly selfing populations were considerably smaller in size, consistent with higher population turnover and frequent founder events. Partial correlations indicated that morph diversity had little residual effect on within-population diversity levels once we controlled for census size. This suggests that the effect of mating system on variation within populations is primarily via its interaction with differences in colonization and/or persistence of selfing vs. outcrossing populations. Although the effects of population size on diversity are largely driven by the lowest population size classes, the majority of monomorphic populations fall within this range, highlighting the important interaction between selfing and population size on genetic diversity. Among the populations we sampled there are orders of magnitude differences in census population size (Table 1), while neutral models predict only twofold effects of the mating system. Therefore, it is perhaps not surprising that there is a strong signature of the influence of census size on nucleotide diversity in our study.

Diversity estimates among populations within each of the morph structures varied considerably, and this heterogeneity was not fully explainable by morph structure or population size. For example, although on average trimorphic populations maintained significantly more nucleotide diversity than monomorphic populations, two large trimorphic populations (B187 and B206) contained less variation than occurred in several of the most diverse monomorphic populations from Jamaica (J29) and Cuba (C1 and C5). The heterogeneity in estimates of neutral diversity within each of the morph structure classes probably results from multiple causes. First, it is important to emphasize that direct marker-based mating-system estimates were not obtained from the populations used in our sample. Although our previous work indicates that style-morph structure provides a reasonable predictor of mating patterns in E. paniculata, variation in outcrossing rate among populations occurs within each of the morph structure classes (see, for example, Figure 9.1 in Barrett et al. 1992). Second, as discussed above, aspects of demographic history associated with the species' annual life history also likely play a role in affecting diversity. Large-scale censuses of population size have demonstrated dramatic fluctuations from year to year and a turnover of populations consistent with frequent colonizing episodes and metapopulation dynamics (Husband and Barrett 1998). These local ecological processes are likely to have an important influence on levels of genetic diversity. Finally, nucleotide variation within populations of a particular morph structure also will be affected by regional patterns of diversity and colonization history. The fragmentation of the Brazilian range and colonization of the Caribbean from South America have both likely affected the pool of diversity available in any given region (and see below).

We detected no significant difference in nucleotide diversity between trimorphic and dimorphic populations of E. paniculata. Several features of dimorphic populations led us to predict reduced diversity compared to trimorphic populations. The vast majority of dimorphic populations of E. paniculata are missing the S-morph, including the seven populations sampled in this study. Theoretical and empirical evidence indicates that genetic drift and founder events play a prominent role in the origins of dimorphic populations (Barrett et al. 1989; Husband and Barrett 1992a,b). These stochastic processes could potentially erode diversity and, indeed, comparisons of allozyme variation between trimorphic and dimorphic populations support this prediction (Husband and Barrett 1993). In addition, dimorphic populations possess mixed mating because of the occurrence of self-pollinating variants of the M-morph. Estimated selfing rates from dimorphic populations are variable but in some cases can be considerable. These considerations led us to predict that dimorphic populations should have lower diversity than the more outcrossing trimorphic populations.

Why did we not observe the severe loss of diversity within our selfing and partially selfing populations seen in interspecific comparisons? If there was insufficient time to recover equilibrium since the evolution of dimorphism and monomorphism, many of the genetic consequences of selfing (such as reduced N_e, increased LD, or reduced efficacy of selection) would be less apparent. For example, selfing populations that evolved less than 4N generations ago can still retain ancestral variation and ancient, short-range linkage disequilibrium may be unexpectedly low in such selfing populations (Tang et al. 2007). Additionally, there may have been insufficient time for positive and negative selection to erode diversity through genetic hitchhiking. Thus the origin of stylar dimorphism and monomorphism less than 4N generations ago from diverse ancestral source populations probably explains the retention of significant amounts of ancestral polymorphism. Our coalescent simulation results are consistent with Caribbean populations having diverged from Brazilian populations less than 4N generations ago (see below).

Dimorphic and monomorphic populations in N.E. Brazil maintained large to moderate amounts of the polymorphism found in trimorphic populations. In the case of the two monomorphic populations in our Brazilian sample this amounted to 35.7% of the diversity found in the southern portion of the range. The maintenance of this diversity suggests that the spread of selfing in Brazilian dimorphic and monomorphic populations may have been sufficiently gradual to allow recombination and segregation to capture a significant portion of the neutral diversity of progenitor populations than would be expected if selfing evolved by a founder event or through a very rapid selective sweep.

Timescales and demographic history:

Previous studies of allozyme variation in E. paniculata suggested that Jamaican populations likely arose from at least two long-distance dispersal events (Husband and Barrett 1991). More recent molecular analyses of the Cuban populations investigated here (Barrett et al. 2009), in concert with the InStruct analysis presented here (Figure 5), indicate that they share a significant proportion of their nucleotide variation with Jamaica and may have descended from the same colonization event(s) from mainland South America, most likely Brazil. Interpreting these patterns of molecular variation can be assisted by the application of models of demographic history (e.g., Haddrill et al. 2005; Ometto et al. 2005; Wright et al. 2005; Ross-Ibarra et al. 2008; Nielsen et al. 2009). Our own coalescent simulations indicated that the time since colonization of the Caribbean by E. paniculata likely occurred ∼125,000 years before the present. This estimate is of significance because E. paniculata is a weed of rice fields in Cuba and Jamaica, raising the possibility that migration to the Caribbean from South America occurred in historic times through human introduction, as appears to be the case for the related E. crassipes (water hyacinth) also native to Brazil (Barrett and Forno 1982). However, our estimate of the date of Caribbean colonization casts serious doubt on this hypothesis. Instead, this analysis suggests that establishment in the Caribbean occurred much earlier, probably the result of natural long-distance dispersal events, presumably by birds. The predominance of selfing variants of the M-morph in Cuba and Jamaica, as well as the absence of the S-morph in this region, is generally consistent with the hypothesis that the facility for autonomous self-pollination in selfing variants enabled establishment following long-distance dispersal.

The estimate of divergence of Brazilian and Caribbean populations should be treated cautiously, because it is based on using the mean mutation rate from grasses (6.5 × 10⁻⁹ mutations per site per generation) and mutation rates in plants can vary by orders of magnitude (Gaut et al. 1996; Koch et al. 2000). Unfortunately, mutation rates are difficult to obtain and no estimates are available for species more closely related to E. paniculata. With these caveats in mind, we calculate that ∼2.6 N generations have elapsed since the colonization of the Caribbean islands, on the basis of the observed level of diversity and the time since divergence estimated from coalescent simulations. Standard neutral theory predicts that on average 4N generations is required for all individuals in a sample to coalesce and recover equilibrium (Kimura and Ohta 1969). This highlights the potential significance of the retention of ancestral diversity and recombination events in maintaining variation within and among monomorphic Caribbean populations.

Our MIMAR results indicate a 3- to 4-fold lower N_e for populations from the Caribbean islands compared with Brazil and a 10-fold reduction in effective size relative to the ancestral population. This result suggests that, although the effective size of Caribbean populations is lower than that from Brazil, they do not appear to have been derived from a single colonizer, a result consistent with Husband and Barrett's (1991) allozyme study. If this were the case, a much stronger signal of a genetic bottleneck would be evident in our data, as was observed, for example, to be associated with the evolution of selfing in Capsella (Foxe et al. 2009; Guo et al. 2009). This finding is more consistent with multiple colonization events or multiple colonizers allowing for the maintenance of a larger fraction of the diversity from founding populations.

Caribbean populations of E. paniculata as a whole may have not yet recovered equilibrium, but may be close to approaching this point. Evidence for the recovery of neutral diversity in Caribbean populations is that a substantial fraction of polymorphism (22.4%) is unique to populations from this region. Three Jamaican populations and the Caribbean as a whole show a significantly negative Tajima's D, and the remaining populations generally show a trend toward a negative Tajima's D. This suggests ongoing population expansion after colonization, perhaps associated with the species' weedy habit.

MIMAR simulations also implicate a threefold reduction in effective size in the Brazilian populations relative to the ancestor. It is possible that this result is an artifact of population subdivision in the ancestral population (Becquet and Przeworski 2009). However, this could also result from range fragmentation in Brazil with an historical bottleneck contributing to an erosion of diversity in outcrossing Brazilian populations. It is noteworthy that populations from Brazil, particularly in the southern portion of the range, show a significant negative Tajima's D, consistent with population expansion during recovery from a bottleneck.

Comparing diversity in outcrossing and selfing populations:

The retention of a moderate fraction of ancestral polymorphism in selfing populations of E. paniculata contrasts with several recent interspecific studies comparing molecular diversity in related selfing and outcrossing species. For example, in Solanum self-compatible species have between 4 and 40 times less variation than the least variable self-incompatible species (Baudry et al. 2001), selfing Mimulus nasutus has ∼7-fold less variation compared with its outcrossing relative M. guttatus (Sweigart and Willis 2003), and Capsella rubella has 100- to 1500-fold reduction in effective population size compared with C. grandiflora (Foxe et al. 2009). In this latter case it has been proposed that a speciation event was associated with the transition from outcrossing in C. grandiflora to selfing in C. rubella. This may have resulted from a rapid breakdown in self-incompatibility (Foxe et al. 2009; Guo et al. 2009). The transition to selfing in Arabidopsis thaliana appears to have been more complex with multiple independent losses of self-incompatibility (Boggs et al. 2009) and an ∼4-fold reduction in diversity relative to its closest self-incompatible relative A. lyrata (Ramos-Onsins et al. 2004; Nordborg et al. 2005). However, these two Arabidopsis species are believed to have been diverging for ∼5 million years (Koch et al. 2000) and demographic bottlenecks in A. lyrata complicate the use of these two species for understanding the influence of mating system on molecular diversity.

Our studies of intraspecific variation in mating system in E. paniculata allow for molecular population genetic comparisons with fewer confounding effects introduced by independent evolutionary histories and ecological and life-history differences between species. Nevertheless, in wide-ranging species capable of long-distance dispersal, such as E. paniculata, evolutionary history and the demographic origins of selfing populations also play an important role in determining patterns of regional diversity and these need to be taken into account when considering the influence of mating patterns on genetic diversity.