Gene Genealogies Strongly Distorted by Weakly Interfering Mutations in Constant Environments

Abstract

Neutral nucleotide diversity does not scale with population size as expected, and this “paradox of variation” is especially severe for animal mitochondria. Adaptive selective sweeps are often proposed as a major cause, but a plausible alternative is selection against large numbers of weakly deleterious mutations subject to Hill–Robertson interference. The mitochondrial genealogies of several species of whale lice (Amphipoda: Cyamus) are consistently too short relative to neutral-theory expectations, and they are also distorted in shape (branch-length proportions) and topology (relative sister-clade sizes). This pattern is not easily explained by adaptive sweeps or demographic history, but it can be reproduced in models of interference among forward and back mutations at large numbers of sites on a nonrecombining chromosome. A coalescent simulation algorithm was used to study this model over a wide range of parameter values. The genealogical distortions are all maximized when the selection coefficients are of critical intermediate sizes, such that Muller's ratchet begins to turn. In this regime, linked neutral nucleotide diversity becomes nearly insensitive to N. Mutations of this size dominate the dynamics even if there are also large numbers of more strongly and more weakly selected sites in the genome. A genealogical perspective on Hill–Robertson interference leads directly to a generalized background-selection model in which the effective population size is progressively reduced going back in time from the present.

OBSERVED levels of apparently neutral nucleotide diversity (π_n) are typically lower than expected under the assumptions of standard equilibrium theories, and they vary much less among species than do estimates of long-term effective population sizes (Nei and Grauer 1984; Bazin et al. 2006; Nabholz et al. 2008). Many explanations have been proposed for the apparent shortfalls and the lack of proportionality with population size, including (1) complex demographic histories (e.g., recurring population bottlenecks), (2) adaptive selective sweeps (Maynard Smith and Haigh 1974; Gillespie 1999), and (3) selection against deleterious mutations (Charlesworth et al. 1993, 1995; McVean and Charlesworth 2000; Comeron et al. 2008). Of these three possibilities, bottlenecks and sweeps are by far the most frequently mentioned, even though deleterious mutations occur at high rates in all species, regardless of ecological circumstances (Eyre-Walker and Keightley 2007). Here we show that weakly deleterious mutations can distort genealogies in three different ways and dramatically reduce nucleotide diversities in large populations of nonrecombining chromosomes. The mitochondrial genealogies of several species of whale lice (Kaliszewska et al. 2005) are distorted in exactly these ways, and several lines of evidence suggest that bottlenecks and adaptive sweeps are not likely to be the primary causes.

Mitochondria have been proposed to be especially sensitive to selective sweeps. Animal mitochondrial genomes contain more than three dozen essential protein and structural RNA genes, so they are large targets for both mutation and selection (Ballard and Whitlock 2004). They do not undergo sexual recombination, so every advantageous mutation that fixes will reduce variation throughout the genome. Mitochondrial nucleotide diversity therefore could depend strongly on rates of environmental change, which could be similar for species with very different population sizes. Indeed, if rates of mitochondrial adaptation were mutation limited, then larger populations might actually experience higher rates of adaptive substitution and as a result show lower average levels of neutral diversity than smaller populations (Gillespie 2000, 2001). This idea was recently invoked to explain the remarkable similarity of average levels of mitochondrial nucleotide diversity among the major animal classes which appear to have very different average population sizes and substantially different average levels of nuclear nucleotide and amino acid diversity (Bazin et al. 2006).

Unconditionally deleterious mutations can also depress linked neutral diversity by reducing the effective population size either through (1) background selection against relatively strongly selected mutations (Charlesworth et al. 1993, 1995) or (2) Hill–Robertson interference (Hill and Robertson 1966) among large numbers of relatively weakly selected mutations (reviewed by Comeron et al. 2008). The second of these processes, called “weak-selection Hill–Robertson interference” (wsHRi) by McVean and Charlesworth (2000) and “interference selection” (IS) by Comeron and Kreitman (2002), can shorten genealogies, give them strongly nonneutral branch-length proportions, and skew their topologies (Higgs and Woodcock 1995; Maia et al. 2004).

To date, weak interference has mainly been studied by forward simulation, with the aim of assessing its possible effects on patterns of optimal synonymous codon use within eukaryotic nuclear genes and genomes, in the presence of recombination (Comeron and Guthrie 2005; Loewe and Charlesworth 2007; Comeron et al. 2008). In an attempt to understand the striking genealogical distortions seen in whale-louse mitochondria (Kaliszewska et al. 2005), we have developed a structured-coalescent algorithm that accurately models selection of arbitrary strength on a nonrecombining chromosome of finite length. All of the distortions seen in the whale-louse mitochondria are replicated under parameters that might plausibly apply to whale lice and many other animal species, and these distortions scale only weakly with population size.

Whale lice are permanent, obligate ectoparasites of cetaceans. They feed on the dead outer surface of their host's skin, and they appear to be harmless. They are amphipod Crustacea comprising a monophyletic family, Cyamidae, with ∼50 described species in several genera. Three of these species (Cyamus ovalis, C. gracilis, and C. erraticus) occur on right whales (Eubalaena spp.) but not regularly on any other hosts. Most adult right whales carry large populations of all three species.

Right whales in the North Pacific, the North Atlantic, and the southern hemisphere have been separated for ∼5 million years, and so have their cyamids (Rosenbaum et al. 2000; Gaines et al. 2005; Kaliszewska et al. 2005). For this reason the right whales in different ocean systems are now considered distinct species (Eubalaena japonica, E. glacialis, and E. australis), and we refer to their cyamids as North Pacific C. ovalis, North Atlantic C. ovalis, southern C. ovalis, and so on, in anticipation that a future revision of the genus Cyamus will recognize them as “triplet” sibling species (3 × 3 = 9 species in all). We studied their mitochondrial population genetics with the initial aim of quantifying patterns of genetic differentiation among the cyamid populations on individual whales within local populations (Kaliszewska et al. 2005).

We had reasoned (incorrectly) that the pattern of differentiation among whales might say something about their social interactions, since cyamids can transfer only between whales that are in direct physical contact with each other. We found very low levels of differentiation among whales and to our surprise literally no differentiation among the major southern hemisphere breeding aggregations that calve off the coasts of South America, South Africa, Australia, and New Zealand (Kaliszewska et al. 2005). This absence of population structure seems remarkable by terrestrial standards but is easily explained by modest rates of cyamid exchange among whales within local populations and between the major breeding aggregations, given the enormous sizes of cyamid populations. Right whales are highly gregarious (spending hours per day in social interactions), mobile (traveling thousands of kilometers per year on annual foraging migrations), and mortal (carrying their cyamid populations to the sea floor when they die). Thus cyamids have many opportunities to transfer between whales, and they might be expected to have evolved an inclination to do so when the opportunity presents itself (Hamilton and May 1977).

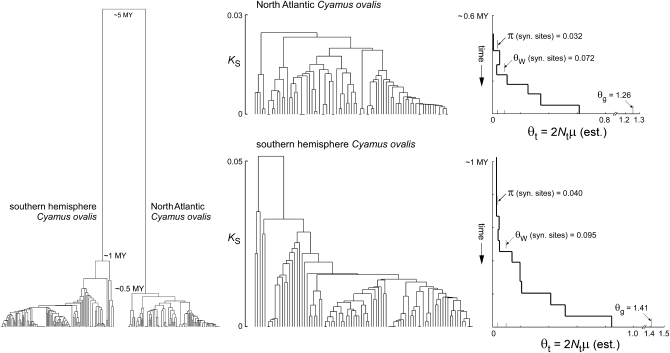
The well-defined ecology of right-whale cyamids allows their population sizes to be estimated directly. The number of adult cyamids per whale (∼500–10,000, varying by species) times the number of whales per ocean (∼50,000–200,000, prior to human exploitation) equals the number of cyamids per species (Kaliszewska et al. 2005). Thus for all three nominal species of right-whale cyamids, long-term census population sizes are expected to have been in the range 2.5 × 10⁷–2 × 10⁹. Given conservative estimates of the per-generation mitochondrial mutation rate, even the lower end of this range predicts levels of synonymous nucleotide diversity at least an order of magnitude larger than those actually seen in the cyamids, which are consistently modest and similar to those seen in typical terrestrial arthropods (Kaliszewska et al. 2005). The three North Atlantic and southern hemisphere sibling-species pairs are strongly reciprocally monophyletic, as illustrated for C. ovalis in Figure 1. This is not expected at mutation–drift equilibrium, given their very large population sizes.

Figure 1.—

Mitochondrial gene genealogies for North Atlantic and southern hemisphere Cyamus ovalis, estimated by UPGMA from partial COI sequences. Left: The intraspecific genealogies coalesce globally at ∼0.5 and 1 MY and share an ancestor at ∼5 MY (Kaliszewska et al. 2005). Center and right: Each intraspecific genealogy is aligned with a generalized skyline plot (Strimmer and Pybus 2001) showing estimates of θ at different times in the past under a piecewise constant model of population size change fit by GENIE 3.0 (Pybus and Rambaut 2002). Three different point estimates of present-day θ are also indicated on the plots (synonymous-site nucleotide diversity π, Watterson's θ estimated from synonymous sites, and θ estimated jointly with the apparent exponential growth rate by the MCMC coalescent algorithm in LAMARC). Values of Tajima's D are lower (−1.5 to −1.6) when estimated from the sequences than when estimated from the branch lengths of the trees (−2.1 to −2.4), as expected because multiple substitutions occur at some sites. Similar values of D_T (−2.3 for both species) were obtained from the highest-likelihood trees found by BEAST with a fully parameterized GTR substitution model and a coalescent prior. Those trees have standardized imbalance statistics (−I_S) of −3.7 (southern hemisphere C. ovalis) and −2.2 (North Atlantic C. ovalis). The trees shown here have more extreme values of −I_S (−5.5 and −4.0, respectively), probably as a consequence of artificially pectinate branching orders induced by UPGMA among sets of identical sequences. Slightly different sets of sequences were used to make the two-species genealogy on the left and the single-species genealogies in the center. The long interspecific branches in the two-species tree are based on a multispecies maximum-likelihood analysis involving smaller numbers of much longer (4.1 kb) sequences (Kaliszewskaet al. 2005, Figure 3).

These dramatic deficits of variation are not easily explained by population bottlenecks or adaptive selective sweeps. The bottleneck hypothesis is especially problematic because it requires the long-term near extinction of right whales in all three ocean systems. (Short bottlenecks such as those caused by human exploitation of right whales are not expected to have a noticeable effect on cyamid genetic diversity because cyamid populations remain large, and rates of genetic drift low, even when there are few whales.) That all three right whales have survived for millions of years suggests that they have maintained reasonably large population sizes, and the mitochondrial nucleotide diversity of southern right whales is consistent with this assumption (Kaliszewska et al. 2005), as is the nucleotide diversity of a cyamid nuclear gene (described below). Right whales eat copepods and krill, which are relatively close to the base of marine food webs, and right-whale populations are thought to be food limited. Thus a long-term, severe depression of their numbers would also seem to imply a collapse of marine ecosystems worldwide, for which there is no evidence.

Several features of cyamid mitochondrial nucleotide diversity are also inconsistent with the bottleneck model and with adaptive sweeps as well. The most obvious of these features is the uniformity of cyamid mitochondrial diversity among species (π = 0.007–0.015 for COI sequences in the seven species surveyed by Kaliszewska et al. 2005). Gene genealogies estimated from these sequences also seem remarkably uniform in total depth, with last common ancestors differing in age by only a factor of 3 and in six of the seven species by less than a factor of 2 (see Kaliszewska et al. 2005, Figure 4). Adaptive sweeps might be expected to occur at roughly random intervals and not to be well coordinated in time among seven species in three different ocean systems. Interspecific coordination of such sweeps (over the whole globe) would seem to be required if they were to be a plausible primary cause of the genealogical shortening.

Figure 4.—

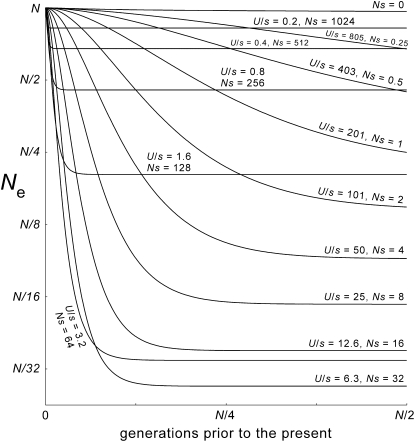
Apparent average effective sizes of ancestral populations, for models with different values of s. Values of N_e are given on the vertical axis (logarithmically scaled). They are estimated from the variance of expected contributions to the present, for the adults of any given generation. The parameters are those of Figure 2 (N = 65,536 = “64k,” μ = 1.5 × 10⁻⁶, L_s = 2048, U = 0.0031). In theory the curve for s = 0 should be perfectly horizontal. The discrepancy appears to be caused by subtle flaws in the shape of the very broad “idealized” simulated distribution that was used in this calculation. The curves for strong-selection cases are perfectly horizontal at times beyond a few thousand generations because the mutation-number distributions are compact, with little stochastic variation. The two lowest curves are those for the selection coefficients (s = 2⁻¹⁰, U/s = 3.2, and s = 2⁻¹¹, U/s = 6.3) that produce the most extreme values of the polymorphism and tree-shape statistics, given the other parameters (Figure 2).

In addition to showing too little nucleotide variation, the cyamid mitochondrial genomes show strong and consistent excesses of rare nucleotide states, reflecting the “comb-like” or “star-like” shapes of the genealogies, in which deeper branches tend to be much too short relative to terminal branches (as if the trees had been “squished” from behind). This kind of distortion causes negative values of Tajima's (1989) D and related statistics. It can be caused by population expansion from a bottleneck or by lineage expansion under positive selection (Kaplan et al. 1989; Slatkin and Hudson 1991; Rogers and Harpending 1992; Bamshad and Wooding 2003). However, the form of branch-length distortion seen in the cyamid genealogies suggests a slow, steady, roughly exponential form of population or lineage growth, not the relatively sudden increases suggested by the bottleneck and selective-sweep hypotheses. Generalized skyline plots (Strimmer and Pybus 2001) describing the histories of population size implied by the shapes of the northern and southern C. ovalis gene genealogies are shown in Figure 1. They are remarkably similar, as are the growth rates and estimates of present-day θ (= 2N_fμ_n) obtained by fitting exponential growth models using the coalescent algorithms in LAMARC (Kuhner et al. 1998, 2004) or BEAST (Drummond and Rambaut 2007).

Cyamid populations cannot have grown in numbers as seemingly implied by these analyses. The number of cyamids on each whale appears to be set mainly by microhabitat limitations (e.g., by the area of rough callosity tissue on the head, where C. ovalis and C. gracilis live), and these features of their environment have hardly changed for millions of years, as demonstrated by the strong similarities of northern and southern right whales and their cyamids. Likewise, the numbers of right whales cannot have increased gradually from vanishingly small numbers over several hundred thousand years, for the reasons discussed above.

The genealogical signals of “growth” therefore seem likely to be caused by selection. Environmental change is the most obvious potential cause of selection, but the apparent rate of growth seen here is strangely slow—in fact, slower than glacial. The orbitally forced Plio-Pleistocene glacial climate cycles have a major period of ∼100,000 years (Lambert et al. 2008 and references therein), but all seven of the right-whale cyamids for which we have mitochondrial population samples appear to have been “expanding,” more or less continuously, through at least several such cycles. The seemingly fairly consistent rate of branch-length foreshortening seen in the genealogies therefore suggests the action of a process that is relatively homogeneous in time, in addition to being very slow overall.

The cyamid mitochondrial genealogies also appear to be topologically skewed, with sister clades too unequal in size, on average. In random bifurcating trees, the distribution of sister-clade sizes is uniform (Yule 1924; Heard 1992; Rogers 1994). Deviations from this null expectation can be quantified by statistics such as Colless's (1982) index of tree imbalance (Shao and Sokal 1990; Rogers 1996). Our estimates of the cyamid genealogies tend to be excessively imbalanced (Figure 1). Strong topological imbalance is not caused by classic adaptive sweeps or by population growth following a bottleneck, but previous theoretical work has indicated that it can be caused by selection (Higgs and Woodcock 1995; Maia et al. 2004).

To summarize, the cyamid mitochondrial genealogies are consistently much too short, too squished, and too skewed, relative to neutral-theory expectations. Owing to several special features of cyamid and right-whale biology, selection seems to be the only plausible explanation for this set of distortions, but conventional adaptive sweeps do not seem likely to be the primary cause. We therefore asked whether weakly deleterious mutations might be sufficient to generate the observed combination of patterns, in the absence of environmental change. Previous work (mentioned above) showed that interference among weak mutations at many sites can strongly affect linked neutral variation, but this work did not fully explore the parameter space relevant to our system or connect all the patterns in a genealogical setting.

To address this question we first carried out forward simulations of populations of nonrecombining chromosomes with large numbers of nucleotide positions subject to forward and back mutations with unconditional fitness effects of size s. Large numbers of linked neutral sites were used to estimate genealogies and to calculate population statistics of interest. We found that for a range of intermediate values of s, considerable fitness variation was maintained and all three of the genealogical distortions (and the signal of apparent exponential growth) seen in the cyamid genealogies reached impressively large maxima. However, the computational burden of full forward simulation prevented us from considering realistic parameter values (i.e., large N and small μ), and it was not obvious that extrapolations based on compound parameters (e.g., Nμ and Ns) would work as hoped in all respects (see Comeron et al. 2008). We developed an equivalent coalescent algorithm that accurately reproduces all results of the forward simulations and allows for realistic parameter values. Under parameters relevant to cyamid mitochondria, the distortions of genealogical depth, proportions, and topology can be even more extreme than those seen in the cyamids, and the mean pairwise coalescence times (and resulting neutral nucleotide diversities) associated with maximally distorting intermediate values of s (U_s/s ∼ 5, where U_s is the total genomic mutation rate at sites with selection coefficents of size s) depend only weakly on N.

All parameters of this model (including those of the environment) remain constant over time, yet in some respects it displays apparently nonequilibirum behavior. Under weak to intermediate selection (U_s/s > 10), the effective population size appears to become progressively smaller as time recedes into the past, giving rise to the illusion of growth. And in the maximally distorting range of intermediate selection coefficients, the distributions of deleterious mutation numbers and the shapes of genealogies show conspicuous dynamical instability of a form that could be taken to suggest “adaptive evolution” in response to episodes of environmental change. Adaptive mutations contribute importantly to this process, but they are reversions at some of the many sites previously mutated to mildly deleterious states. Subtle patterns of environmental change that converted previously optimal nucleotide states to slightly suboptimal states could give rise to a category of “virtual reversions” that would augment (or even outnumber) simple reversions, and the effects of such a process might well be consistent with the distortions seen in the cyamid mitochondrial genealogies. However, models with no environmental change of any kind appear to explain the observations surprisingly well.

MATERIALS AND METHODS

The models described here all assume unstructured populations of fixed size N with discrete, nonoverlapping generations. Individuals are haploid and chromosomes are nonrecombining, with L_s selected sites at which one of the four nucleotides confers higher fitness than the others and L_n neutral sites where s = 0. Individual (i.e., chromosomal) fitness is multiplicative: W = (1 − s)ⁱ, where i is the number of deleterious nucleotide states carried by a chromosome. Mutations strike all sites with probability μ per generation, changing the nucleotide at a mutated site to any of the other three with equal (Jukes–Cantor) probabilities, so back mutations to the fittest nucleotide state occur with probability μ/3.

The population mutation parameter θ is often defined as 4N_eμ at a diploid locus, where N_e is some measure of the effective population size. Here we treat N_e as an effect of selection, not a given parameter, and the unqualified θ refers to 2Nμ (because the models are haploid). Statistics that estimate the parameter θ have other names (e.g., π) or carry subscripts (e.g., θ_W, θ_g).

Forward simulations:

The model was first implemented as a full forward Monte Carlo simulation written in C and using various methods including integer operations wherever possible to achieve speeds that allow modestly large populations of long chromosomes to be followed for many generations. As a consequence of this “extreme-integer” strategy, most of the parameters except the mutation rate were scaled as integral powers of 2. This allowed random numbers to be used in their raw form (as unsigned integers) in most situations, simply by truncating them to the appropriate range by right shifting. Chromosome samples (n = 200) were collected and population statistics were reported every 25,000 generations for 5 × 10⁶ generations (a total of 201 samples and reports) following initial burn-in periods of 3 × 10⁶ generations. In all of the forward simulations described here, μ = 1.5 × 10⁻⁶/site/generation.

Two forms of the model were considered. In model I, all selected sites had the same value of s that was varied among runs, holding other parameters constant. The case studied most thoroughly had chromosomes with 2048 selected and 6144 neutral sites, N = 65,536 (“64k”), and s varying from 2⁻¹⁸ to 2⁻⁶ at selected sites. In model II, each chromosome had blocks of sites with different values of s that spanned most of this range. Here a chromosome's fitness can be expressed as 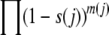, where m(j) is the number of deleterious nucleotide states in the block of sites with selection coefficient s(j), and the product is taken over all of the blocks. There was also a large block of neutral sites. The case described here had 11 selected blocks of 512 sites each, with s ranging from 2⁻¹⁷ to 2⁻⁷, and 2560 neutral sites. Runs were carried out at values of N from 2¹⁴ to 2¹⁷ (16,384 = “16k” to 131,072 = “128k”). Control runs were also carried out at the same values of N, but with selection turned off [s(j) = 0 in all blocks].

Coalescent simulations:

Building on a model of background selection described by Hudson and Kaplan (1994), Gordo et al. (2002) developed a structured coalescent algorithm to study Muller's (1964) ratchet. In this approach, all chromosomes carrying i deleterious mutations are treated as members of a randomly mating mutational class (analogous to a deme) within which a coalescence may occur with the usual per-generation hazard

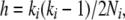(1)

where k_i is the number of lineages with i mutations in the sample at a given generation, and N_i is the size of mutational class i in the population as a whole. Mutations transfer chromosomes from class i to class i − 1 (going backward in time), but back mutations (to fitter states going forward or less fit states going backward) do not occur (i.e., the model assumes infinite sites). If the haploid genomic mutation rate U is low enough that a chromosome acquires at most one new mutation in any generation, then the probability that a chromosome with i mutations was derived from one that had i − 1 mutations in the previous generation can be expressed approximately as

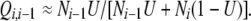(2)

These probabilities of “migration” from one mutational class to another are functions of U and of the current distribution of mutation numbers. Gordo et al. (2002) used the deterministic (infinite-N) distribution of mutation numbers under this model, which is the Poisson distribution with parameter λ = U(1 − s)/s ≈ U/s. Thus when U = s (so U/s = 1), the mean and variance of the mutation-number distribution is 1 and f(0) = f(1) = e⁻¹. As s declines relative to U, the mean of the distribution increases and the size of the unloaded chromosomal class decreases toward zero.

The resulting coalescent algorithm works well in regimes where selection is strong enough that the unloaded class is occupied (N₀ > 1), but its behavior begins to diverge from that of equivalent forward Monte Carlo simulations as selection becomes weak enough that all chromosomes carry at least one mutation and the ratchet begins to turn.

We generalized the approach of Gordo et al. (2002) to accommodate finite sites, four nucleotides, back mutations, and situations where all chromosomes may carry substantial numbers of deleterious mutations. At first we guessed that the problem might be solved by replacing the deterministic equilibrium distribution of mutation numbers with a distribution more appropriate to the finite-sites and finite-N assumptions of the model to be simulated (an idea inspired by the model of Rouzine et al. 2003, which works well for very weak selection). But we soon discovered that regimes involving intermediate values of s (those that give rise to the most extreme genealogical distortions) apparently cannot be modeled accurately with a fixed distribution of mutation numbers. We therefore resorted to simulating (in forward time) the full history of the mutation-number distribution which was then used (going backward) to guide the coalescent process. This hybrid approach is much more computationally intensive than classical coalescent simulation, but it is feasible for realistic parameter values and very accurate.

A simulation takes place in two phases, each carried out by a different program. First the forward program (WAVE) simulates a long history of the mutation-number distribution (the “wave” of Rouzine et al. 2003), by applying mutations to the current generation's distribution and then drawing a multinomial sample from it (weighted by relative fitness) to generate the next generation's distribution and so on for many generations. After the mutation–drift–selection process has reached steady state, a sequence of generations is saved to disk and then time reversed. These reversed-wave-history files can be huge (even using efficient schemes for representing each generation), depending on parameter values and the number of generations saved. The current implementation samples periodically from the mutation-number history rather than storing every generation to disk, because histories of ≥10⁸ generations are needed for realistic parameter values and the files would be unmanageable if not compressed in this way. A sampling interval of 100 generations was used for the cases with realistic parameter values described here (e.g., Figures 3, 5, 6, and 7).

Figure 3.—

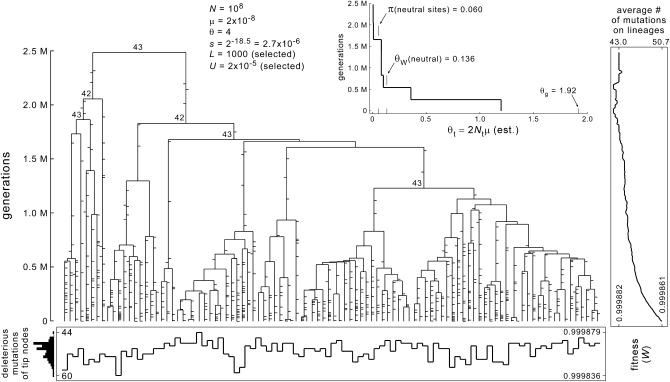
Genealogy simulated under model I with parameters that could be realistic for right-whale cyamids. Mutations are shown on the branches; ticks to the right are forward (deleterious) mutations, and ticks to the left are back mutations. The number of nucleotide positions in deleterious states is indicated for several of the deeper ancestral nodes. Mutation numbers and fitnesses for the tip nodes are shown graphically at the bottom. Average mutation numbers and fitnesses of ancestral lineages are shown graphically at the right. The inset shows a generalized skyline plot, in the format of those in Figure 1. In its size, shape, and topology, this tree appears to be quantitatively similar to real cyamid mitochondrial gene trees. Assuming four generations per year, the root would occur at an age of ∼0.6 MY. Branch-length foreshortening and topological skew are also both near the centers of the ranges typically estimated for cyamids (D_T = −2.5 and −I_S = −3.7). The selection coefficient (s = 2^−18.5) is near the center of the “intermediate-selection” regime, given the other parameters that seem reasonable for right-whale cyamids such as C. ovalis. Values of s in this range are expected to have the greatest influence on the sizes and shapes of genealogies (results; Figures 8 and 9). This particular tree was chosen for display because its statistics are typical of instances generated under these parameters.

Figure 5.—

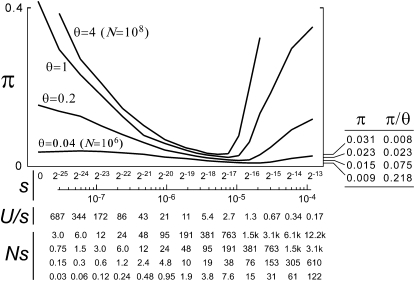
Average neutral nucleotide diversities (π_n) as functions of the selection coefficient (s) for models with a realistically low mutation rate (μ = 2 × 10⁻⁸), 2048 selected sites, and a range of realistically large population sizes. Four Ns scales are shown at the bottom, corresponding to the curves for N = 10⁸ (θ = 4) down to N = 10⁶ (θ = 0.04), respectively.

Figure 6.—

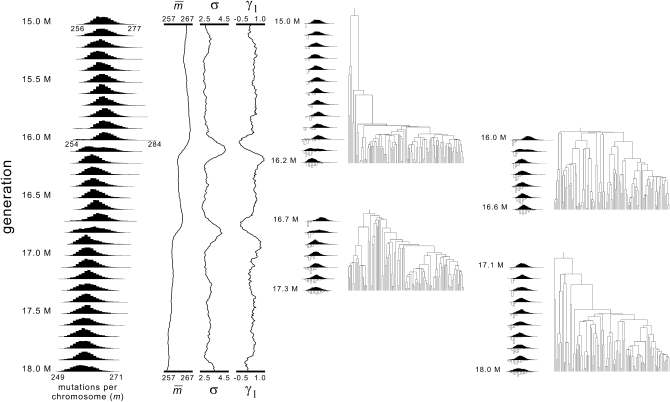
Mutation-number distributions and genealogies during pseudoadaptive sweeps. The history depicted covers 3 million generations (from 15 million to 18 million, from a total of 100 million) in a simulation where N = 2.5 × 10⁷, μ = 2 × 10⁻⁸, L_s = 2048, and s = 2⁻¹⁸ (one of the cases used to draw the curve for θ = 1 in Figure 4). The population's mutation-number distributions are shown on the left, at intervals of 0.1 million generations. Continuous histories of the mean, standard deviation, and skewness statistics are shown in the center. Genealogies sampled at generations 16.2, 16.6, 17.3, and 18 million are shown on the right, with miniaturized versions of the population's mutation-number distributions (solid histograms, above) and the sample's distributions (open histograms, below). The first of two “mini-pseudo-adaptive sweeps” begins at ∼15.9 million, continues through 16 and 16.1 million, and is finished by 16.2 million. The genealogy sampled at 16.2 million passes through it and shows highly accelerated rates of coalescence during the event. The genealogy sampled later (at 16.6 million) is cut off by the event, because all of the sample's lineages have reached the thin lower (left) tail of the population's mutation-number distribution by 16 million. The next genealogy (17.3 million) is shortened in a similar way by the second sweep that occurs at roughly 16.7–16.9 million. The fourth genealogy (18 million) is more typical of those that occur under these parameters (most take >1 million generations to coalesce globally). Conspicuous sweeps do not typically occur as often as illustrated here, under these parameters, but the genealogies are typical of ones sampled at these four times, from this particular history.

Figure 7.—

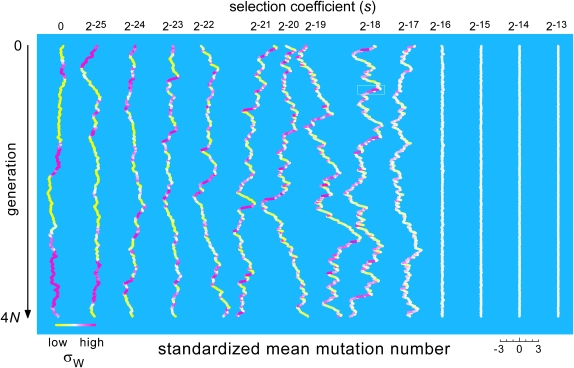
Dynamics of fitness as a function of s. Each trace shows the population's mean mutation number (as deviations from its long-term mean, in units of the average within-generation standard deviation) over all 100 million generations of the run that was used to generate a point on the curve for θ = 1 in Figure 4. The within-generation standard deviations decrease monotonically with s, from 15.4 for s = 0 and 10.0 for s = 2⁻²⁵ to 0.6 for s = 2⁻¹³. Thus the mean wanders much more widely, both absolutely and relatively, for cases in the intermediate-selection regime than for ones in the strong-selection regime, and it is also less stable (at least relatively) than for cases in the weak-selection regime. The traces are centered horizontally at intervals of six standard deviations; this scaling is shown explicitly for s = 2⁻¹⁴. The greatest range of relative mean mutation numbers (from −4.7 to +5.3 standard deviations) occurs where s = 2⁻¹⁹. Time flows from top to bottom. The mean mutation number is decreasing when a trace moves to the left and increasing when a trace moves to the right. Rapid, sustained decreases of the mean occur frequently in the intermediate-selection regime (s = 2⁻²¹–2⁻¹⁷), always in conjunction with an above-average variance of mutation number and hence of fitness. The color scale shows the population's current standard deviation of mutation number and fitness relative to its long-term mean; solid yellow indicates a standard deviation ≥37% below the long-term mean, and solid magenta indicates a standard deviation ≥58% above the mean. Figure 6 gives a high-resolution view of a small segment of the trace for s = 2⁻¹⁸ (boxed), during which fitness improves substantially, but at rates that also vary substantially.

The backward program (“dynamically restructured coalescent,” DRC) then reads the reversed-wave history and uses it to guide a series of coalescent simulations. First a sample of chromosomes is drawn from the mutation-number distribution of the current generation. Then lineages are advanced, generation by generation, allowing coalescence and mutation to occur as described above and elaborated below. Because the wave file records the mutation-number distribution only every 100 generations (or at some other specified interval), the distribution is smoothly “evolved” by linear interpolation between the previous distribution retrieved from the wave file and the next one, during the generations between values stored in the wave file.

When global coalescence occurs, DNA sequences are generated for each chromosome in the initial sample, statistics of interest are calculated from those sequences and from the genealogy itself, an approximate genealogy is estimated from the sequences (to mimic the estimation of genealogies in the forward simulations), and all of this information is written to report files. Time is then advanced over a large random number of generations in the reversed-wave file, and the process is repeated beginning with the sampling of chromosomes from the now-current generation. This goes on, sample after sample, until the end of the wave file is reached. If <100 samples have been simulated (because the average global coalescence time is large under the current parameters), then the wave file is reopened and advanced a large random number of generations, and the sampling process continues as before. Reusing the wave file in this way gives samples that are not fully independent of each other, but it yields better estimates of overall average statistics than would stopping with just a few samples. When ≥100 samples have been simulated, the averages and variances of various statistics are calculated and written to the relevant report files.

In the coalescent algorithm, expressions for the forward and backward mutational probabilities conditioned on the mutation-number distribution (Q_i,i−1 and P_i,i+1) are more complex than in the model of Gordo et al. (2002). The raw genomic mutation rates can be precalculated as lookup tables [forward rate U_f(i) = μ(L − i), backward rate U_b(i) = μi/3, where i is the genome's current deleterious mutation number]. However, the Q_i,i−1 and P_i,i+1 must be recalculated in every generation (or at least in every generation where the mutation-number distribution is updated by reading the wave file or by interpolation). Thus

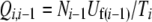(3)

and

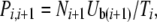(4)

where

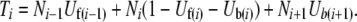(5)

Care must be taken with the treatment of boundary cases (where either N_i−1 or N_i+1 is zero) and with voids that can appear in the middle of the mutation-number distribution (where N_i goes from a finite number to zero while k_i is still greater than zero), but otherwise the underlying logic of the method follows directly from that of Gordo et al. (2002). Source code and documentation for all of the programs (forward and coalescent) can be obtained from J. Seger.

Cyamid DNA sequences:

The existing samples of mitochondrial COI sequences for North Atlantic and southern C. ovalis were increased to 128 and 105 individuals, respectively, by methods essentially identical to those previously described (Kaliszewska et al. 2005). The new sequences have been deposited in GenBank under accession nos. GU172208–GU172303.

Partial sequences of the nuclear EF-1α gene were obtained using “universal” arthropod primers and then extended by inverse PCR (Ochman et al. 1988, 1990). The gene has one small intron. A complete sequence from a North Atlantic C. ovalis individual (onVAsb04) is shown with its translation and heterozygosities in supporting information, Figure S1. Using this sequence, primers were designed to allow amplification and sequencing of most of the coding region and the intron (File S1). PCR products were sequenced directly on both strands for 7–15 individuals of North Atlantic and southern C. ovalis, C. gracilis, and C. erraticus. Heterozygous sites were identified by chromatogram traces showing well-defined peaks of approximately equal height for two different nucleotides at a given position. These are genuine allelic polymorphisms, as indicated by three facts: (1) almost all are synonymous, (2) almost all are close to Hardy–Weinberg genotype frequencies, and (3) some appear as shared polymorphisms between northern and southern hemisphere sibling species (Table 1 and Tables S1–S6). The sequences have been deposited in GenBank under accession nos. GU172304–GU172368.

TABLE 1.

Polymorphism and divergence of EF-1α in sibling species of cyamids on North Atlantic (NA) and southern hemisphere (SH) right whales (Eubalaena glacialis and E. australis)

Species	n	L (Lc)	S	π	θW	DT	Shared polymorphisms	Fixed differences (nearly)	FST
C. ovalis NA	26	1365	22	0.0035	0.0043	−0.66
C. ovalis SH	28	(1365)	26	0.0028	0.0049	−1.57	7	0 (5)	0.46
C. gracilis NA	30	1365	47	0.0050	0.0053	−0.24
C. gracilis SH	14	(1223)	23	0.0044	0.0046	−0.22	10	2 (5)	0.54
C. erraticus NA	14	1272	26	0.0062	0.0068	−0.38
C. erraticus SH	18	(1209)	33	0.0054	0.0075	−1.14	12	0 (1)	0.12

n, number of alleles sampled (twice the number of individuals); L, nominal (maximum) length of coding sequence determined for each allele (base pairs); L_c, length of shared homology for all alleles in sample (used to calculate π, θ_W, D_T, and F_ST); S, number of segregating (polymorphic) sites; π, nucleotide diversity (heterozygosity); θ_W, population mutation parameter estimated from segregating sites; D_T, Tajima's D; shared polymorphisms, sites where the same two nucleotides occur in both samples; fixed differences, sites fixed for different nucleotides in the two samples; (nearly), one sample is fixed for the nucleotide that is less frequent in the other sample, or the difference in nucleotide frequencies exceeds 0.75; F_ST, inbreeding (fixation) of subpopulations (hemispheres) relative to the total (nominal species), estimated by the method of Hudson et al. (1992).

Sequence analysis:

Mitochondrial genealogies for North Atlantic and southern C. ovalis were estimated as described previously (Kaliszewska et al. 2005) and also by BEAST (Drummond and Rambaut 2007). θ and the apparent exponential growth rate (r) were estimated by LAMARC (Kuhner et al. 1998). Topological skew was calculated as the negative of Colless's (1982) index after standardization by its expected standard deviation (Rogers 1994). This statistic (−I_S) can be viewed as an analog of Tajima's (1989) D (D_T), in that negative values indicate distortions of the kind expected under directional selection, and the units are standard deviations. Values were calculated by the program EIGENLAD (available from J. Seger), which also “eigenladderizes” trees for easier viewing (e.g., Figure 1). This way of rationally arranging the clades in a tree was developed by Gary Olsen (G. Olsen, personal communication) and used in a number of his articles (e.g., Olsen et al. 1994; Woese et al. 2000), but apparently it has never been described in print. Unaware of Olsen's work, we rediscovered the method and called it eigenladderization for reasons explained in File S1.

Introns were removed from the edited EF-1α sequences because some contain small indels that frustrate accurate determination of both alleles. We inferred haplotypes using PHASE 2.0 (Stephens and Donnelly 2003), but with little success because linkage disequilibrium within the gene is very low, as indicated by plots of diploid pairwise linkage disequilibrium (r²) against the distance between polymorphic sites (Figure S2) (Rogers and Huff 2009). Standard diversity and divergence statistics were estimated using DnaSP 4.10 (Rozas et al. 2003) and several programs written by us.

RESULTS

Distortions maximized at intermediate values of s:

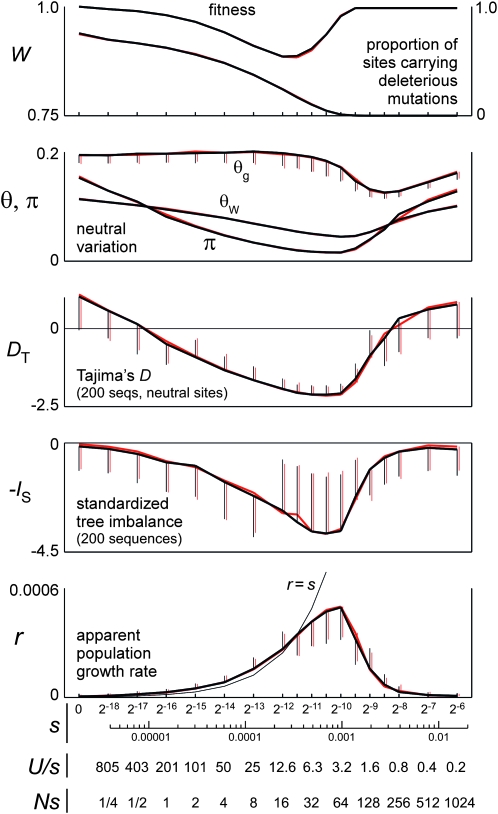
The sizes, shapes, and topologies of gene genealogies become substantially distorted as values of s decline from the “strong” end of the range (where U_s/s < 1 and most chromosomes are mutation free) and enter the “intermediate” range (where U_s/s is of order 5 and most chromosomes carry several mutations) (Figure 2). Mean values of π_n, D_T, and −I_S all reach well-defined minima at about the same intermediate value of s, and the apparent population growth rate r reaches a maximum value that is about half as large as s. As s decreases even more, toward the “weak” range where U_s/s > 10 and all chromosomes are substantially loaded, mean fitness reaches a minimum and then begins to recover, while π_n, D_T, and −I_S increase and the apparent population growth rate declines. In this weak-selection regime, r is slightly larger than s, and θ_g (the population mutation parameter estimated jointly with the growth rate r) is close to the true value of θ. In the strong-selection regime, θ_g underestimates θ by an amount very close to that predicted by the classic background-selection model (Charlesworth et al. 1993).

Figure 2.—

Polymorphism and tree-shape statistics for forward (black lines) and dynamically restructured coalescent simulations (red lines) of model I. Selection coefficients vary from weak (including s = 0) to strong along the horizontal axis. Other parameters are as described in the text (θ ≈ 0.2). Error bars are standard deviations of the statistics, over samples taken at regular intervals during a run; those from the coalescent simulations (red) are displaced slightly to the right so that their endpoints can be seen in cases where they are shorter than the error bar for the corresponding forward simulation.

The values of these statistics as observed in the forward and backward (coalescent) simulations are extremely similar over the full range of s (Figure 2); even their standard deviations (over samples) are nearly identical. Thus the dynamically restructured coalescent algorithm is quantitatively equivalent to an exact forward simulation, for all practical purposes.

A well-defined point of maximum genealogical distortion at intermediate s does not form unless Ns ≫ 1 (i.e., the effectiveness of selection is high) at that point. Thus at smaller population sizes, the point of maximum distortion may occur at larger values of s (and hence smaller values of the ratio U/s). Maximum reductions of the mean pairwise difference and tree length appear clearly in the studies of Gordo et al. (2002; Figures 1 and 3) and Williamson and Orive (2002; Table 4, Figures 3 and 4), but at values of U/s between 4 and 0.5, corresponding to values of Ns between 50 and 10, owing to the small population sizes modeled in those studies. This effect can also be seen in Figure 5 in this article, where the minimum neutral polymorphism occurs at a larger s for N = 10⁶ (Ns ≈ 20) than for N = 10⁸ (Ns ≈ 500).

Tajima's D becomes strikingly less variable in the zone of intermediate s (and maximum distortion) than it is at the strong-selection and weak-selection ends of the range. The standardized tree imbalance (−I_S) is more variable than D_T at all values of s, and it becomes more variable in the intermediate-selection zone, as does the apparent growth rate r.

All of the statistics shown in Figure 2 were estimated from neutral sequences linked to the selected sites, not from the genealogies themselves which are known without error only in the coalescent simulations. The coalescent results have been “dumbed down” to make them comparable to the forward simulations, for which the tree-based statistics −I_S and r must be calculated from trees estimated with error from sequences. Even so, in the coalescent simulations there is good agreement between the statistics as calculated from true and inferred genealogies.

Skew and growth caused by expansion of less-loaded clades:

A typical sample genealogy for apparently realistic N and μ, and 1000 selected sites at an intermediate value of s (U/s = 7.4), is shown in Figure 3, with its complete mutational history at selected sites marked by ticks on the branches. The root and several of the deeper branches have slightly fewer deleterious mutations than the best of the sequences in the contemporary sample, and an average contemporary sequence is worse than the oldest nodes in the tree by several mutational steps. The density of mutations is lower deep in the tree than near the present, and a larger fraction of the older mutations are back mutations that presumably helped to make their lineages among the best then present in the population. The least-loaded contemporary chromosomes have what appear to be improbably mutation-free histories (augmented in a few cases by back mutations), and they tend to have relatively large numbers of close relatives that themselves have lower than average numbers of deleterious mutations. Conversely, the most heavily loaded sequences and clades tend to be relatively isolated at the ends of longer branches, indicating that they have been declining for some time. These patterns all appear to be consistent with previous work on the ages of mutations (see Slatkin and Rannala 2000; Slatkin 2008).

The relative growth rates of two sister clades (at any level in the genealogy) will be influenced by selection (that is, by a difference in mean fitness, caused by a difference in mean mutation number) as well as by drift. Thus the expansion of less-loaded clades and the contraction of more-loaded clades will tend to increase the topological skew (Higgs and Woodcock 1995; Maia et al. 2004). This process also gives rise to the overall illusion of growth, because lineages that have been expanding for some time are usually larger those that have been contracting. Although extant lineages descend from ancestors that were among the least loaded of their generations, most will end up (in the future) more heavily loaded than average and doomed to displacement by lineages that appear to be almost miraculously mutation free, as they emerge from the endless flow of “allelic traffic” (Comeron and Kreitman 2002).

N_e not constant:

Going back in time, the ancestry of the current generation becomes progressively more restricted toward the high ends of the fitness distributions of earlier epochs (Figure 3). In the weak-selection regime, the apparent growth rate r is similar in value to the single-site selection coefficient s (Figure 2), but even here the apparent growth rate is not constant. This process can easily be modeled by projecting the distributions of parental mutation numbers backward in time, using the mutational probabilities conditioned on the distributions (Equations 3–5, above; see File S1 for additional details). This gives a sequence of probability density functions for the fitnesses of ancestors at any given time in the past (O'Fallon et al., in press). The apparent population size of a given generation t, with respect to the present, can then be estimated as 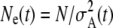, where 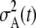is the variance of expected ancestry among the adults of that generation. In the generation immediately prior to the present, 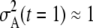(the Poisson variance when all parents have the same chance to be ancestors), but 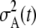increases with t as the distribution of ancestry becomes increasingly concentrated in the less-loaded (more fit) tails of the mutation-number distributions and the expected number of descendants at t = 0 for most members of the population declines toward zero. As a consequence, the apparent population size (as seen from the present) becomes smaller at times farther in the past (Figure 4).

In the strong-selection regime, the contraction proceeds quickly and then stops at a fixed N_e < N, as expected under classic background selection (Charlesworth et al. 1993, 1995). At smaller values of s (in the intermediate- and weak-selection regimes), there is a shift to slower rates of contraction that continue for many more generations before they finally level off, again at values of N_e that can be vastly smaller than N. In all regimes the rate of apparent contraction (going backward) or of growth (going forward) first increases and then declines (Figure S3). This happens relatively abruptly for strong selection, but gradually for weak selection, in which case the apparent population growth is roughly exponential (Figures 1, 3, and 4).

A progressive reduction of N_e explains much but not all of the phenomenology. We simulated neutral coalescents for populations that grow (literally) according to the models of N_e(t) depicted in Figure 4. Genealogies are shortened (having reduced mean values of π_n) and squished (with negative D_T) in ways quantitatively similar to those seen in the corresponding models of deleterious mutation (Figure 2). But as expected, there is no consistent pattern of topological skewing (−I_S ≈ 0). When θ is estimated from the genealogies, jointly with the apparent exponential growth rate r, the mean values of both estimates are similar to those from the corresponding models of selection, but the growth rates tend to be biased upward especially in the intermediate-selection regime (results not shown) (see Kuhner et al. 1998).

Levels of neutral variation nearly insensitive to N:

Most of the genealogical distortions depend only weakly on population size in the zone of intermediate s (where U_s/s ∼ 5). This is the regime in which Muller's ratchet would begin to turn, in the absence of back mutations (Gordo et al. 2002). Figure 5 shows nucleotide diversity at neutral sites (π_n) as a function of s, for four different population sizes spanning two orders of magnitude (N = 10⁶–10⁸, θ = 0.04–4). Minimum values of π_n at these four values of θ occur over a narrow range of values of s (U_s/s ∼ 1–5). All of these minimum values of π_n are much smaller than θ. For the largest population size that we considered (N = 10⁸, θ = 4), π_n < 1% of θ and absolutely less than the observed synonymous-site π for C. ovalis.

Models with different population sizes and mutation rates but the same values of θ (2Nμ) and L_s (the number of selected nucleotide positions) behave similarly, if the strength of selection is expressed in terms of the compound parameters Ns and U/s. Measures of neutral variation and tree shape take on nearly identical values, and the depression of mean fitness (mutational load) and apparent population growth rate are also very similar if expressed in units inversely proportional to N (Figure S4).

Dynamic instability maximized at intermediate s:

The transition from the “strong-selection” to the “intermediate-selection” regime occurs fairly suddenly, as s is decreased holding other parameters constant (Figures 2, 4, 5, and 7). At this transition, the size of the class of unloaded chromosomes falls to zero, which is to say, the least-loaded class becomes very rare and hence vulnerable to loss, no matter how large the population is (Gordo and Charlesworth 2000a,b, 2001; Rouzine et al. 2003). As mentioned above, this is the regime in which Muller's ratchet would turn in the absence of back mutations and in which the size of the subpopulation containing likely (future) last common ancestors becomes very small. The dynamics in this intermediate regime are strikingly different from those in the neighboring strong-selection regime, where the principal moments of the mutation-number distribution fluctuate very little. By contrast, even in the strong edge of the intermediate regime, the moments all make large, irregular excursions on a range of different timescales, and the shapes of gene trees may also vary dramatically (Figures 6 and 7).

The process giving rise to this dynamism is illustrated in Figure 6. When the least-loaded class is rare, the “even-less-loaded” class is empty but available to be repopulated by back mutation. Such mutations are advantageous in the classical sense, even though the environment has not changed. Of course in most cases they are lost simply because they are very rare. But occasionally one of them survives rarity and increases under positive selection, shifting the mutation-number distribution to a lower mean and thereby increasing the mean fitness. On even rarer occasions, two or three such “novel” back mutations will occur in the same lineage and escape immediate loss, leading to a relatively substantial and rapid increase of mean and maximum fitness. Two such events occur in the population history depicted in Figure 6, transiently changing the first three moments of the mutation-number distribution and strongly warping the shapes of genealogies that pass through these “mini-pseudo-adaptive sweeps.” The environment did not change, but the genealogies seem to suggest that it did.

These events tend to be most dramatic when s is as large as it can be while still being small enough that such events happen at all (because all chromosomes carry at least a few deleterious mutations, and “novel improvements” are therefore possible). The transition from the strong-selection-low-load regime to the intermediate-selection-high-load regime is a transition from quiet to noisy dynamics because at the strong/intermediate boundary, these “improvements” are rare but relatively dramatic. Figure 7 shows histories of the mean mutation number (equivalent to the mean fitness) for runs in which s takes values spanning the full range of relevant values. Each mutation-number history is plotted as the current deviation from the long-term mean, in units of the mean instantaneous standard deviation of mutation numbers. As s decreases from values in the strong range, the temporal variance of the standardized mean mutation number jumps from a very small value to something close to its maximum value, over just one halving of s.

Load and distortions caused mainly by sites with intermediate s:

The assumption that all selected sites have the same value of s is highly artificial. Real chromosomes (including mitochondrial chromosomes) must have sites with mutational effect sizes that vary more or less continuously over a very broad range. What happens when sites with different effect sizes exist together on the same asexual chromosome? To address this question we carried out forward simulations under model II, where each chromosome has a large number of sites with values of s that vary over several orders of magnitude from neutral and very weak through strong.

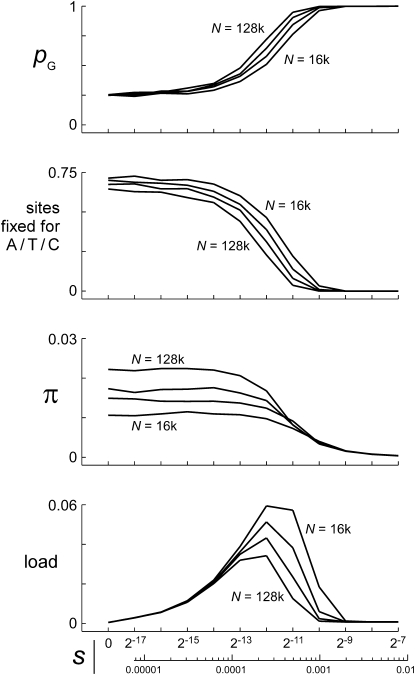
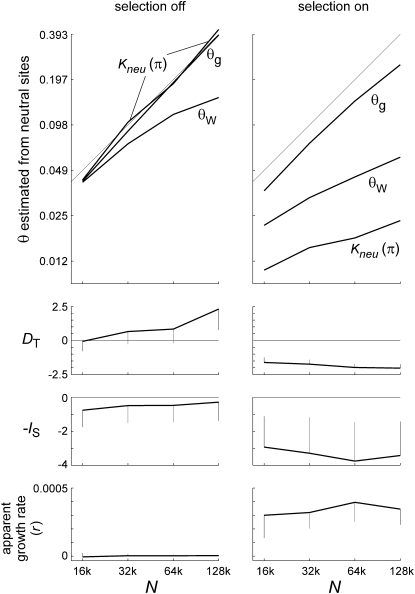
As expected, the favored nucleotide (arbitrarily defined as G) remained nearly fixed at strongly selected sites, regardless of population size, and the four nucleotides were equally frequent at neutral and very weakly selected sites (Figure 8). Nucleotide diversity at neutral and very weakly selected sites did vary with N, but only by a factor of slightly more than 2, for values of N that differed by a factor of 8. The genetic load was caused mainly by variation at sites with three intermediate values of s spanning just a factor of 4 (2⁻¹³ = 0.00012 to 2⁻¹¹ = 0.00049, U_s/s = 6.3–1.6), almost independent of N. The distortions of tree shape indicated by D_T and −I_S, and the signals of apparently exponential population growth (r), were remarkably similar at all four population sizes (Figure 9).

Figure 8.—

Statistics for chromosomal blocks with different values of s under model II. The chromosome has 11 blocks of 512 sites subject to mutations with effect sizes of s = 2⁻¹⁷–2⁻⁷ in a doubling series, plus a large number of neutral sites. The mutation rate is the same as in Figure 2, so U_s ≈ 0.0008 for each block. The model was run as a forward simulation for population sizes of N = 2¹⁴ (16k) through 2¹⁷ (128k) or θ = 0.05, 0.1, 0.2, and 0.4. Each panel displays curves for these four different population sizes. The top panel shows blockwise average frequencies of the fittest nucleotide state (arbitrarily defined as G for “good”), and the second panel shows average proportions of sites fixed for non-G. The third panel shows average nucleotide diversity in each block, and the bottom panel shows the contribution made by each block to the total mutational load. At all four population sizes, mutations of severity s = 2⁻¹² = 0.00024 (U_s/s = 3.15) make the largest contribution, and most of the load is generated by the blocks for which U_s/s = 1.6–12.6.

Figure 9.—

Estimates of θ and tree shape for model II. Panels on the left show control runs where s = 0 in all blocks; panels on the right show the experimental runs of Figure 8. Curves in the top panels show mean values of three estimators of θ (nucleotide diversity at neutral sites with correction for multiple substitutions, Watterson's θ at neutral sites, and θ_g from the tree-based exponential growth model) as functions of N. The 45° lines show true values of θ. Corrected π_n and θ_g both perform nearly perfectly with selection turned off, while θ_W increasingly underestimates θ as N increases, owing to multiple hits. With selection turned on, θ_g slightly underestimates θ, while Watterson's estimator and especially π_n severely underestimate θ. Both increase as N increases, but not proportionally. Tajima's D becomes strongly negative, with reduced variation (second panels from top), while −I_S becomes strongly negative with increased variation (third panels from top) when selection is turned on, and neither statistic is much affected by N. The apparent growth rate (bottom panels) is zero with selection turned off, but it averages 0.0003–4 with selection turned on, consistent with the intermediate values of s that contribute most to the load. Error bars are standard deviations of the statistics, over samples within a run.

These patterns indicate that sites with intermediate values of s will tend to dominate the dynamics, even where the genome contains equal or larger numbers of sites with stronger and weaker mutational effects. Selection coefficients at the sites contributing most to the load are similar to the apparent exponential growth rate of r ≈ 0.00035. θ estimated jointly with the apparent growth rate underestimates the true θ by 20–25%, as expected if N_e is reduced by background selection at the strongly selected sites (Charlesworth et al. 1993, 1995).

Cyamid nuclear polymorphism consistent with continuously large N:

If the reduced nucleotide diversity and strong reciprocal monophyly of cyamid mitochondrial genomes were caused by population bottlenecks that occurred after the separation of the northern and southern hemisphere sibling species, then nuclear genes should also show evidence of such events (e.g., Galtier et al. 2000). To look for such evidence we sequenced the nuclear EF-1α gene in samples of the three sibling species pairs. All three pairs show shared polymorphisms (at 7–12 sites, File S2 and Tables S1–S6), but they also show fixed or nearly fixed differences (at 1–7 sites) and modest values of F_ST (0.12–0.54, Table 1).

Such a pattern would be expected if the northern and southern hemisphere populations had been continuously large for the last 5 MY or so, with little or no gene flow during that time. The effective generation times of cyamids are not known but seem likely to be a few months. If there were four generations per year, then there would have been ∼2 × 10⁷ generations since separation. During this time, sibling species with effective population sizes of N_e ∼ 2.5 × 10⁷ would be expected to have accumulated only modest average levels of differentiation (F_ST ∼ 0.3) at neutral sites not strongly affected by directional selection at nearby loci, consistent with the retention of ancestral polymorphisms at many sites. However, the lack of ongoing gene flow would allow fixations to occur at other sites. No strong conclusions about the actual effective population sizes or levels of gene flow can be drawn from this small data set for just one locus, but similar patterns are seen in all three sibling species pairs, so these data appear to be inconsistent with models in which population bottlenecks play a major role.

DISCUSSION

Hitchhiking (Maynard Smith and Haigh 1974) has long been understood to strongly affect levels and configurations of linked neutral nucleotide diversity. Most theoretical and empirical effort to date has been aimed at understanding the effects of classic adaptive sweeps triggered by environmental change (Berry et al. 1991; Begun and Aquadro 1992; Gillespie 2000, 2001; Sabeti et al. 2006; Voight et al. 2006; Wang et al. 2006; Andolfatto 2007). Unconditionally deleterious mutations have received less attention in this context, but several studies have noted that deleterious mutations can reduce levels of neutral variation and distort the shapes and sizes of genealogies, especially in the absence of recombination (e.g., Kaplan et al. 1988; Hudson and Kaplan 1994, 1995; Charlesworth et al. 1995; Golding 1997; Nachman 1998; Rand and Kann 1998; Przeworski et al. 1999; McVean and Charlesworth 2000; Tachida 2000; Comeron and Kreitman 2002; Gordo et al. 2002; Williamson and Orive 2002; Barton and Etheridge 2004; Hughes 2005; Reed et al. 2005; Comeron et al. 2008). The present study shows that these effects can be dramatic for nonrecombining genomes with high mutation rates, many sites subject to mutations with suitably small values of s (U_s/s ∼ 5), and large population sizes (Ns ≫ 1). Distortions of genealogical size and shape similar to those seen in the mitochondria of right-whale cyamids can be produced by ∼1000 sites with s of order 3 × 10⁻⁶, given realistic values of N_e and μ (Figure 3).

However, the fact that unconditionally deleterious mutations and back mutations seem able to explain a set of observations does not imply that they are the sole or even the main cause of those observations. Right-whale cyamids may have unusually constant environments, and their mitochondria may be relatively well insulated from any ecological changes the cyamids experience on relevant timescales. But the world of the cyamids' mitochondrially encoded proteins and structural RNAs cannot simply be assumed to be nearly unchanging. Instead, this assumption must be tested. The models of greatest interest are therefore ones in which the genome includes environmentally sensitive sites (where the fittest nucleotide state occasionally changes) in addition to neutral and environmentally insensitive sites (like those modeled here, where one nucleotide state is always fittest) (e.g., Hahn 2008). We recently added a block of such sites to the coalescent algorithm so that it can be used to study how environmentally triggered adaptive evolution interacts with strictly purifying selection of the kind modeled here.

Although the form of selection modeled here is strictly “purifying,” the genealogical distortions that appear at intermediate values of s are caused by “directional” selective sweeps. As in classical sweeps, relatively fit alleles that are initially rare replace common, less fit alleles, causing a variety of effects including a dramatic shortening of the average pairwise coalescence time (e.g., Gillespie 2000, 2001). Here, however, the fitness differences among “alleles” arise from many mutations of individually small effect (mostly deleterious), rather than from one or a few mutations, each of relatively large effect (and advantageous). In the tree shown in Figure 3, representing a sample of 100 genomes at potentially realistic parameter values, there are 616 forward and 37 back mutations. The contemporary genomes carry loads of 44–60 sites in deleterious nucleotide states, from a total of 1000 selected sites. Ancestral fitnesses are generally higher, and relatively homogeneous, but the histories of sequential mutation along different lines of descent give rise to substantial heterogeneity within and between clades at all levels in the tree. Compared to a classic adaptive sweep, ones like this could be described as “diffuse” or even “futile,” in that the population's mean fitness is no higher (in typical instances) at the end of the sweep than at the beginning (reminiscent of the Red Queen process in a continually deteriorating environment). Given sufficiently large and well resolved genealogies (which could be generated for right-whale cyamid mitochondrial genomes), it might be possible to fit models that estimate the rates and effect sizes of mutations affecting the relative growth rates of lineages within the tree. An inferred mutational history like that of Figure 3 would then suggest a predominant role for “purifying sweeps” as opposed to “directional adaptive sweeps,” owing to the many mutations of small effect scattered throughout the tree that increase the variance of fitness especially toward the tips.

One implication is that a significant fraction of the total nucleotide variation could be weakly selected, especially in nonrecombining genomes with high mutation rates. This idea has been discussed as a potential explanation for the apparent time dependency of substitution rates (Ho et al. 2005, 2008) and the higher density of nonsynonymous substitutions near the tips of intraspecific mitochondrial genealogies (Kivisild et al. 2006). Site-frequency spectra and other statistics of weakly selected polymorphisms can differ substantially from those of neutral polymorphisms, potentially allowing their relative abundances and other parameters to be estimated even in nuclear genomes, given samples of sufficient size and quality (Messer 2009).

Previous studies have only rarely called attention to the dynamical liveliness associated with intermediate values of s (Comeron and Kreitman 2002; Comeron et al. 2008). The unsteadiness of the mutation-number distribution (Figures 6 and 7) appears to contribute to the pattern of genealogical distortion in at least two ways. First, it gives rise to the Hill–Robertson interference that shrinks the effective population size going back in time, thereby weakening the effect of selection and allowing mean mutation numbers to rise to levels far higher than would occur with recombination (Keightley and Otto 2006) or infinte N. The effects can be illustrated by repeating the coalescent simulations of Figure 2 using deterministic equilibrium mutation-number distributions for the same values of U and s. Such an experiment is shown (in the format of Figure 2) in Figure S5. In the strong-selection regime, and at the strong end of the intermediate regime, all of the statistics are indistinguishable from those under full stochastic dynamics. But mean fitness is not depressed in the intermediate- and weak-selection regimes. The other statistics (describing aspects of neutral polymorphism and tree shape) vary with s in patterns qualitatively similar to those for the full dynamics, but they differ quantitatively in many respects, especially at smaller values of s.

Second, generation-to-generation fluctuations of the mutation-number distribution also seem to matter, independent of the distribution's overall average shape, although these effects are relatively subtle. This can be demonstrated by repeating the simulations of Figure 2 with static idealized empirical distributions generated by averaging a modest number of typical distributions from the wave file for a given set of parameters. Such an experiment is also shown in Figure S5. To idealize the waves for different values of s, we calculated the first four moments of all the distributions in a history, then selected just a few hundred with moments most similar to the joint mean, and averaged them. The reduction of mean fitness in the intermediate-selection regime is then identical to that for the full dynamics, as expected, and the other statistics are generally more similar as well, compared to those obtained with deterministic equilibrium mutation-number distributions. But the means of the polymorphism and tree-shape statistics still differ noticeably from those obtained by forward simulation or the dynamically restructured coalescent algorithm, and not surprisingly they vary less (among instances) in the intermediate- and weak-selection regimes. Extreme variations such as the mini-pseudo-adaptive sweeps illustrated in Figure 6 can never occur under a static mutation-number distribution.

Despite these shortcomings, models based on static mutation-number distributions potentially offer many advantages, including that the coalescent simulation algorithm can be made simpler and faster than the one described here, and inference methods based on likelihood calculations become feasible. The challenge is to develop an adequate approximate model of the steady-state mutation-number (fitness) distribution. Such a model would need to work well in the intermediate-selection regime, which is likely to be of biological importance in systems with large population sizes, high mutation rates, and little recombination (e.g., animal mitochondria and many microbes and viruses), because in the absence of external environmental influences, sites belonging to this regime are expected to dominate the dynamics.

The depression of mean fitness and the genealogical distortions that occur in the intermediate-s regime are consequences of Hill–Robertson interference between linked beneficial and deleterious allelic states. The linkage disequilibrium giving rise to interference is relieved by even low levels of recombination (Felsenstein 1974; Keightley and Otto 2006; Gordo and Campos 2008). This suggests that the effects of symmetrical weak interference (as modeled here) might not be easy to detect in recombining nuclear genomes at distances greater than those of individual genes (Comeron and Guthrie 2005; Loewe and Charlesworth 2007) and that it might be especially difficult to distinguish such effects from those of asymmetrical interference (where conventional adaptive sweeps increase the frequencies of linked weakly deleterious alleles) (McVean and Charlesworth 2000; Comeron et al. 2008). In addition, animal nuclear genomes usually have mutation rates that are much lower than those of mitochondria, so intermediate mutational effect sizes will be smaller in the nucleus than in the mitochondrion, other things being equal.

In summary, the models described here show that interference among weakly selected, unconditionally deleterious mutations and back mutations can severely distort the genealogies of nonrecombining chromosomes with parameters plausibly like those of mitochondrial genomes in many animal species. One prediction is that levels of neutral polymorphism in mitochondrial genomes might depend only weakly on N, as seems to be the case (Bazin et al. 2006). We do not know to what extent these models explain the “paradox of variation” (Lewontin 1974) for mitochondria, but they seem likely to provide some part of the explanation because the necessary assumptions are all plausible. The mitochondrion is an ancient organelle serving a specific, highly conserved function. Its genome is compact, with a high mutation rate, and most of its amino acid polymorphisms appear to be young and mildly deleterious (Nachman 1998; Rand and Kann 1998; Weinreich and Rand 2000; Kivisild et al. 2006; Popadin et al. 2007). The question is, How deleterious are these segregating amino acid mutations, and how many additional synonymous and noncoding sites affect mitochondrial gene expression or other processes and also carry mutations of small effect? If the answer is many, and if nuclear genes are qualitatively similar in this respect, then very mildly deleterious mutations might indeed be, collectively, major contributors to fitness variation and to the average genetic loads of most species (Crow 1970, 1993, 1999; Kondrashov 1995; Eyre-Walker et al. 2002, 2006; Chamary et al. 2006; Loewe 2006; Ellegren 2009).