Regulatory Activity Revealed by Dynamic Correlations in Gene Expression Noise

Abstract

Gene regulatory interactions are context–dependent, active in some cellular states but not others. Stochastic fluctuations, or ‘noise,’ in gene expression propagate through active, but not inactive, regulatory links [1, 2]. Thus, correlations in gene expression noise could provide a non-invasive means to probe the activity states of regulatory links. However, global, ‘extrinsic’, noise sources generate correlations even without direct regulatory links. Here we show that single-cell time-lapse microscopy, by revealing time lags due to regulation, can discriminate between active regulatory connections and extrinsic noise. We demonstrate this principle mathematically, using stochastic modeling, and experimentally, using simple synthetic gene circuits. We then use this approach to analyze dynamic noise correlations in the galactose metabolism genes of E. coli. We find that the CRP-GalS-GalE feed-forward loop is inactive in standard conditions, but can become active in a GalR mutant. These results show how noise can help analyze the context-dependence of regulatory interactions in endogenous gene circuits.

Cells use circuits composed of interacting genes and proteins to implement diverse cellular and developmental programs. A major goal of systems biology is to connect the regulatory architectures of these circuits to the dynamic behavior of individual cells. However, several problems remain: Quantitative information about biochemical parameters is often minimal. In some cases, it may even be unclear in which direction regulation occurs (who regulates whom). And most critically here, regulatory links that are active in some cellular states may be inactive in the cell type or context being investigated. This can occur for several reasons: In the simplest case, the concentration of a regulatory factor may be outside its effective range (Fig. 1A). Transcription factors may also be inactive due to post-translational modification or the absence of necessary co-factors [3, 4]. Identifying the subset of regulatory links that are active in a given state would simplify analysis of the circuit as a whole [5].

Figure 1.

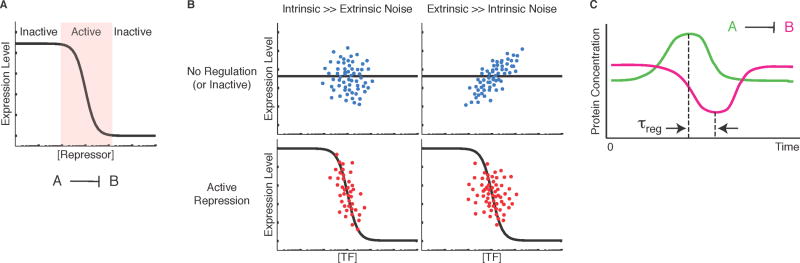
Using noise to analyze the activity of gene regulatory interactions. (A) Target gene expression versus repressor concentration (schematic). Regions where changes in repressor concentration cause changes in target gene expression are active. When repressor levels saturate (right) or are insufficient to repress (left), then the link is inactive. Regulatory links may be inactive for other reasons as well. (B) Noise can produce different types of static correlations between transcription factor (x-axis) and target gene expression (y-axis). In each plot, dots represent individual cells from a hypothetical population. Top plots show correlations without an active regulatory link, while the bottom shows correlations with active repression. The mean gene regulation function is shown as a black line [2]. We consider noise regimes in which either intrinsic (uncorrelated) or extrinsic (correlated) noise dominates. Active repression causes anti-correlation between the transcription factor and its target. Intrinsic noise decorrelates the two, and extrinsic noise causes positive correlations even without active regulation. Thus, correlations derived from static snapshots are ambiguous because high levels of extrinsic noise can conceal the anti-correlation expected from repression. (C) Temporal gene expression patterns (schematic) for a repressor, A, (green line) and its target, B, (magenta line), showing anti-correlations at a delay time denoted τ_reg.

Recent work has shown that gene expression is intrinsically ‘noisy’ – subject to stochastic fluctuations – causing substantial cell-cell variability [1, 2, 6–8]. Fluctuations in the concentration of a regulatory protein can cause corresponding fluctuations in the expression of a target only when the regulatory link is active [1, 2]. Thus, gene-gene correlations in expression could provide information about the activity state of regulatory connections without explicit perturbation of cellular components.

Such analysis is complicated, however, by the fact that gene expression correlations arise not only from regulation, but also from global variations, or ‘extrinsic noise,’ in the overall rate of expression of all genes [2, 6]. For example, fluctuating numbers of ribosomes, polymerase components, and cell size can affect the expression of many genes in a cell, positively correlating their expression. In practice, the definition of extrinsic noise depends on how the regulatory system is defined [9]. Here we assume extrinsic noise is global to all measured genes [2, 9, 10]. In addition, we assume that all genes also fluctuate independently due to ‘intrinsic noise’, or stochasticity, in their own expression. Fig. 1B illustrates how these opposing effects prevent discrimination between noise and regulation as a source of correlation in static measurements.

Gene regulation occurs with a delay; it takes time for protein concentrations to build up sufficiently to have a regulatory effect on the downstream genes they control (Fig. 1C) [11]. The sign of the delay between a fluctuation in regulator concentration and its effect on target protein levels provides information about the causal direction of the link. Note that no such delay occurs for global extrinsic noise, which affects all genes simultaneously. Thus, by following the expression of multiple genes over time in an individual cell, one can decouple extrinsic noise correlations from regulatory correlations. This effect can be analyzed using the temporal cross correlation function, which describes how well two signals are correlated when one of them is shifted in time relative to the other. Similar approaches have been used to infer connectivity of in vitro metabolic networks [12, 13]. Since experiments in these studies were not conducted in living cells they used a prescribed time-varying input to perturb the system and it was unnecessary to consider many of the details particular to actual cellular noise sources.

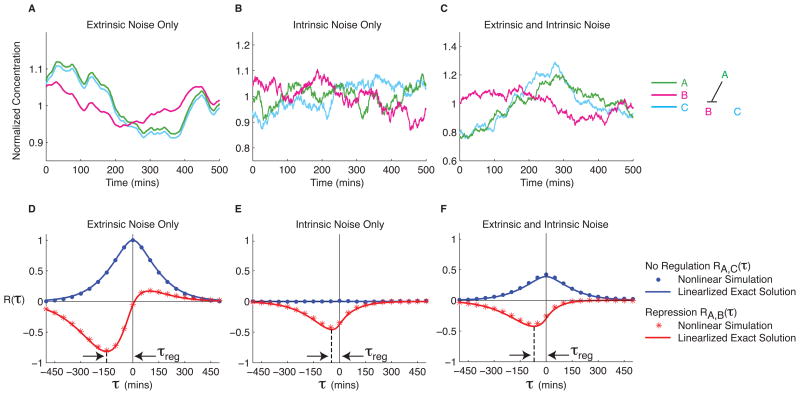
To further understand noise correlations, we implemented a stochastic model of gene regulation [14], incorporating values for biochemical and noise parameters from a previous study [2] (Methods). We simulated expression of a regulatory protein, A, which represses a target gene, B, and an additional unregulated gene, C. With only extrinsic noise the three signals are positively correlated, though A also represses B with a delay (Fig. 2A–C). With only intrinsic noise, repression of B by A generates a delayed anti-correlation in the expression of these two genes. To analyze these simulated time-series data, we computed their cross correlation functions (Fig. 2D–F). In addition, we also developed a linearized model to calculate analytic solutions that approximate the full system well (Supplementary Text). The cross correlations show several features: (1) Repression appears as a dip at an effective regulation delay time, denoted τ_reg. (2) The direction of regulation is given by the sign of τ_reg. (3) Extrinsic noise causes a positive peak in the cross correlation function close to τ=0, both with and without regulation. (4) The relative balance of intrinsic and extrinsic noise affects the magnitude of τ_reg. We found that τ_reg is most sensitive to the protein degradation time, while the magnitude of the dip is determined primarily by how switch-like the gene regulation function is (Supplementary Text).

Figure 2.

Dynamic cross correlations in simulated regulatory interactions. (A–C) Protein A (green line) represses production of protein B (magenta line). Protein C (cyan line) is expressed constitutively. Data are normalized by mean concentration. Extrinsic noise positively correlates the time traces, while fluctuations in A (green curve) produce opposite fluctuations in B (magenta) at a delay (τ_reg). (A–C) Simulated time traces are shown for three noise regimes, as indicated. Note that the intrinsic noise time scale is much faster than that due to extrinsic noise. See Methods for detailed model and numerical parameters. (D–F) Mean cross correlation functions R_A,B(τ) and R_A,C(τ) are shown in red and blue, respectively. Dots represent simulated data, while solid lines plot analytic solutions for the linearized model. Note that active repression causes a dip at τ_reg, while extrinsic noise results in positive correlation near τ=0. See Methods for definition of cross correlation function.

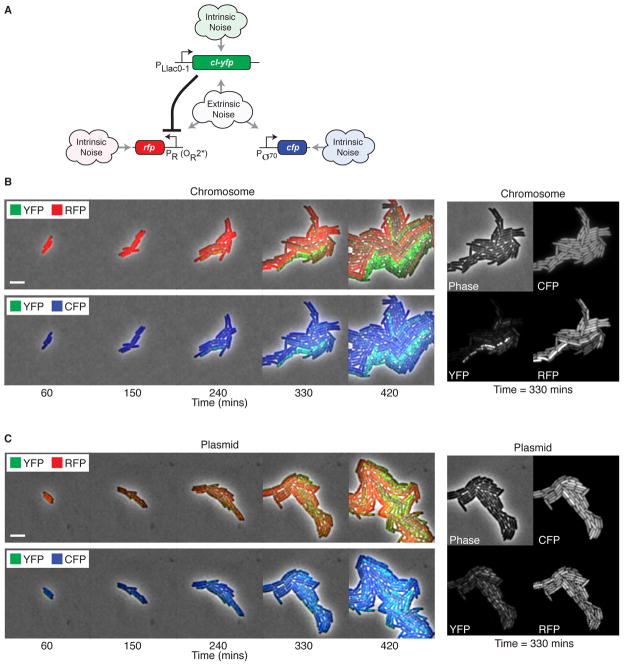
We tested this approach in vivo by measuring the cross-correlation functions of genes involved in active and inactive regulatory links in a well-controlled genetic circuit. We built a synthetic gene circuit, in which λ CI, fused to yellow fluorescent protein (YFP), termed CI-YFP, represses production of red fluorescent protein (RFP), expressed under the control of a variant of the λ P_R promoter[15]. On the same plasmid, cyan fluorescent protein (CFP) is controlled by a strong constitutive promoter, independent of CI-YFP (Methods). Thus, the circuit allows comparison of correlations generated by active regulation (CI-YFP and RFP) and no regulation (CI-YFP and CFP).

E. coli cells containing the circuit were grown and imaged in three colors using automated time-lapse fluorescence microscopy, as shown in Fig. 3B (Methods). Here, strong anti-correlation is visible between RFP and YFP, while CFP is expressed at a more homogeneous level across all cells. The appearance of spatially grouped sub-populations of cells that display similar fluorescence states occurs because τ_reg exceeds the cell cycle time, consistent with simulation predictions (Fig. 2) and previous measurements [10].

Figure 3.

Time-lapse movies of gene expression fluctuations in a synthetic genetic circuit. (A) Synthetic regulation system. LacI, produced constitutively from a chromosomal gene, regulates production of a YFP fusion to the λ CI repressor, which in turn represses production of RFP. cfp is expressed from a strong constitutive promoter. All three genes experience the same extrinsic noise, while intrinsic noise is different for each. (B) Filmstrip of cells with chromosomally integrated circuit. Cells are imaged in three colors; each filmstrip shows two colors at a time for clarity. Note strong anti-correlation between RFP (red) and YFP (green), and the reduced correlation between CFP (blue) and YFP. Scale bar, 5 μm. Supplementary Movies 1 and 2 show additional detail. Right panel shows individual colors and phase images at t = 330 mins. Note anti-correlation between RFP and YFP and the uniform expression of CFP. (C) Filmstrip of the same circuit on a low-copy plasmid reveals increased variability in all colors. The right panel shows the increased variability of CFP relative to the chromosomal case. Note that yellow pixels indicate equal levels of red and green.

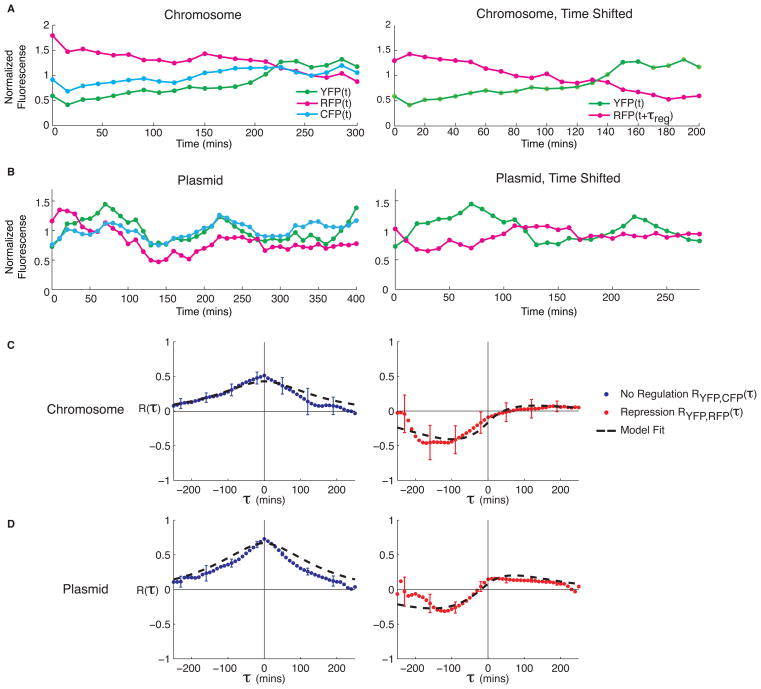
To analyze these data quantitatively, we used semi-automated image analysis software to extract fluorescence intensities for individual cells (Methods). A typical time trace of fluorescence data from a single cell lineage is shown in Fig. 4A. The same data shifted in time reveal the temporal anti-correlation between the CI-YFP and RFP signals. To properly handle the branching nature of the data, we introduced a modified formula for the cross correlation function (Methods). Fig. 4C shows the resulting cross correlations for cases of active repression (CI-YFP and RFP) and no regulation (CI-YFP and CFP). These functions displayed all features predicted by the model, including a strong dip at a negative lag time due to repression, and positive correlation at τ=0 due to global noise in the unregulated case.

Figure 4.

Experimental data and cross correlation analysis of regulated and unregulated target genes. (A) Typical lineage traces for the chromosomally integrated construct. RFP is shown unshifted (left) and shifted by τ_reg ≈ 100 mins (right) to reveal the delayed anti-correlation. Data are normalized by mean intensity. (B) The plasmid-based construct also shows delayed anti-correlation with τ_reg ≈ 120 mins. (C–D) Cross correlation functions R_CI-YFP,CFP(τ) (blue circles) and R_CI-YFP,RFP(τ) (red circles) and model fits (dashed black line) for the chromosomally integrated (C) and plasmid (D) construct. Data are averaged over n=5 independent movies (with 100–200 cells per microcolony upon movie completion) in the chromosomal circuit, and n=6 movies for plasmid circuit. Error bars show standard error of the mean. See methods for fit parameters.

We next asked how the relative amplitude of intrinsic and extrinsic noise affects cross-correlations. We constructed a plasmid-based variant of the synthetic circuit using the low-copy SC101 origin of replication (~10 copies per cell [16]). Copy number fluctuations on the plasmid-borne circuit increase the effective extrinsic noise level for genes in the circuit and reduce the relative importance of intrinsic noise, since gene expression fluctuations from each plasmid copy average out.

As expected, the circuit was more variable in fluorescence intensity on the plasmid than in the chromosome (Fig. 3C). Although anti-correlation is still visible between CI-YFP and RFP, certain cells are brighter than others in all colors, and more variability is seen in the time courses (Fig. 4B). Fig. 4D shows cross correlation functions calculated from this data. The amplitude at τ=0 is increased relative to the chromosomal construct in both the regulated and unregulated case, reflecting simultaneous correlations and confirming model predictions (Fig. 4C–D). These results show that regulation can be discriminated even when extrinsic noise amplitudes are large compared to intrinsic noise levels.

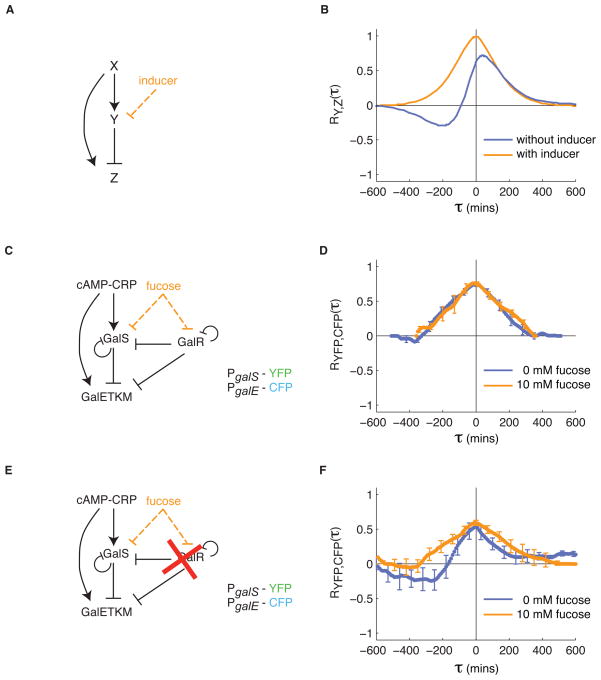
Do the methods demonstrated in the relatively well-controlled synthetic circuit apply to endogenous gene circuits? To address this, we considered the feed-forward loop network motif, which appears frequently in transcriptional gene circuits [17]. One fundamental question about specific natural instances of the feed-forward loop motif is whether they actively regulate their target genes in any given cellular state or context.

Mathematical modeling of the feed-forward loop (Fig. 5A) predicts that the cross correlation between Y and Z should appear similar to the cross correlation function one obtains with simple repression (Fig. 2), with an additional source of symmetric correlation due to X. Inducers that inactivate Y cause a loss of the anti-correlated features (Fig. 5B). Thus, the cross-correlation function between Y and Z appears qualitatively different when Y is actively repressing Z versus when the regulation is inactive.

Figure 5.

Regulatory interactions in the endogenous gal feed-forward loop are cell state-dependent. (A–B) In a model feed-forward loop, the cross correlation between Y and Z exhibits a positive peak at τ=0 due to their shared regulator, X, and due to extrinsic noise. In addition, repression of Z by Y produces a negative dip in the cross correlation function at τ_reg < 0. When repression by Y is inhibited by inducer (A, orange), the cross correlation function exhibits only the positive correlations at τ=0 (B, orange line). (C–D) The galactose metabolism operon galETKM is controlled by a feed-forward loop similar to that in (A), and through additional regulation by GalR, which is not regulated by CRP [20]. (D) Cross correlation functions between P_galS-YFP and P_galE-CFP, with and without fucose, show similar features (n=15 movies without fucose, n=8 movies with fucose). In particular, only positive correlations without a time delay are observed. (E) When galR is deleted, galE is only controlled by a feed-forward loop. (F) As a result, cross correlation functions between P_galS-YFP and P_galE-CFP without fucose show delayed anti-correlation between galS and galE, consistent with the model (A–B). When fucose is added, this anti-correlation is eliminated, as expected. These results are based on n=9 movies with and without fucose. Note that the peak of the cross correlation function is reduced from the galR deletion strain, suggesting that noise in GalR positively correlates GalS and GalE.

One of the best-studied feed-forward loops occurs in E. coli galactose metabolism (Fig. 5C) [18, 19]. The repressor GalS is activated by CRP in response to cyclic AMP. GalS in turn represses the galE operon, as well as itself. Finally, CRP also activates the galE promoter. Compared to the basic feed-forward loop model, this system is complicated by additional regulatory inputs from the GalR repressor. Repression by GalS and GalR is inhibited by galactose, or its non-metabolizable analog, fucose [20]. Glucose depletion was shown to produce a pulse of galE expression due to CRP-GalS-GalE feed-forward loop [18]. If the feed-forward loop is actively regulating expression of galE there should be a qualitative difference between the cross correlation functions with and without fucose.

We constructed strains in which the P_galE promoter controlled expression of cfp and the P_galS promoter controlled expression of yfp. Both reporter genes were integrated in the chromosome as transcriptional reporters (promoter fusions) rather than protein fusions. This more general strategy reduces perturbation of endogenous circuit function, and allows for signal amplification using strong ribosome-binding sites for reporter gene expression.

We used this strain to analyze gene expression noise in the wild type galactose metabolism network (Fig. 5C). Unexpectedly, we found that the cross correlation functions were similar both with and without fucose (Fig. 5D), showing a symmetric peak at τ=0. These results suggest that GalS does not play an active role in regulating GalE in this cellular context. However, the galE operon is also regulated by, GalR, which inhibits transcription through loop formation in the promoter [20]. We reasoned that dominant repression by GalR could explain the lack of feed-forward loop behavior. To test this hypothesis, we deleted galR (Methods) and repeated the measurements (Fig. 5E). In this strain, the cross correlation function without fucose showed a signature of repression with a dip at τ<0 and peak near τ=0 (Fig. 5F). Addition of fucose to the ΔgalR strain caused the cross correlation function to become symmetric, with a postive peak at τ=0, consistent with inhibition of GalS by the inducer. Together, these results reveal that the activity of the GalS-mediated feed-forward loop is cell state-dependent: inactive under the standard media conditions used here, but capable of functioning when GalR is disrupted. It may also be active under other environmental conditions, including transient stimuli (like glucose depletion, as in [18]).

An interesting aspect of gene expression in individual cells is the combination of correlated (extrinsic) and uncorrelated (intrinsic) noise sources. As described above, active regulatory links introduce characteristic features in the cross correlation function between genes. However, the converse is not true: the presence of time lags can in principle occur without direct regulation in complex gene networks. Certain network architectures can produce qualitatively similar cross correlation functions (Supplementary Material) [21]. As shown in the galactose feed-forward loop example, the use of dynamic noise correlations to measure potential regulatory links provides a powerful clue to the effective activity states of regulatory links.

The conflicting effects of intrinsic and extrinsic noise analyzed above constrain the design of cellular regulatory systems that suppress or exploit variability. Recent work has shown that noise provides an essential source of variation in differentiation [22, 23] and phenotypic switching [24, 25]. Our results now suggest that noise can be used to analyze context- or cell state-dependent regulatory interactions without explicit perturbations. This approach requires monitoring multiple gene expression levels over time in individual cells, something that has become increasingly feasible in diverse biological systems [26]. Our results underscore a basic principle of genetic circuit operation: not all regulatory interactions are active all of the time. More importantly, they provide a general framework for inferring regulatory activity states in natural genetic circuits with minimal perturbations.

Methods

Plasmids and Cells

The plasmid pNS2-σVL (Fig. S1) was constructed by synthesizing a region starting with the kanamycin promoter and ending just before CI-YFP (synthesis by Blue Heron). The sequences for CFP and the red fluorescent protein mCherry were codon-optimized for E. coli. The synthesized construct was cloned into the plasmid pZS21-cIYFP [2], replacing its TetR-regulated promoter. The resulting plasmid was transformed into MG1655Z1, a derivative of MG1655 that over-expresses LacI, for experiments.

To integrate the construct onto the chromosome, the region from the kanamycin resistance marker through the end of CI-YFP was amplified by PCR and integrated into the galK region of MG1655Z1, using recombineering techniques [27]. Insertion was verified with colony PCR and sequencing.

Promoter regions for galS and galE were taken from the reporter library in [28]. Promoter-fluorescent protein reporters were made with fusion PCR and verified with sequencing. The fusion PCR product was cloned into a vector with the kanamycin resistance marker and SC101 origin of replication. A region including kanamycin and both promoter-reporter fusions was amplified using PCR with homology arms for intC and integrated into the chromosome of MG1655 by recombineering, as described [27]. Integration was verified by colony PCR and sequencing.

galR was deleted from the MG1655 strain with chromosomally integrated P_galS-YFP/P_galE-CFP. The chloramphenicol resistance gene from pKD3 was amplified using the PCR primers described in [29] with the homology arms for GalR deletion from [30].

Time-Lapse Microscopy

Synthetic Circuit

Single colonies were inoculated in selective LB media and grown overnight. This culture was diluted back 1:100 into 1:4 dilution of LB containing 30 μg/ml kanamycin and 10–15 μM IPTG (varies for different movies). IPTG concentration was adjusted to maintain the mean CI-YFP concentration in the active regulatory range. The cells were then grown to OD 0.1–0.2 and diluted back 1:100 in M9 minimal media containing 0.2% glycerol, 0.01% Casamino Acids, 0.15 μg/ml biotin, and 1.5 μM thiamine (we denote this media MGC). Cells were placed on 1.5% MGC low melting temperature agarose pads containing 10–15 μM IPTG and grown at 37°C for 3 hours to equilibrate to the inducer conditions on the pad. The pad was then placed in 200 μl of MGC and shaken to release the cells. These equilibrated cells were placed on a fresh pad for time-lapse imaging. The temperature of the microscope chamber was kept at 32°C for the duration of the movie. Images were acquired every 10 minutes in phase and each of the three fluorescent color channels.

Galactose Network

Reporter strains were grown overnight in MO (M9 salts supplemented with 1 mM MgS0₄, 0.1 mM MgCl₂, and 30 μg/ml kanamycin) supplemented with 0.4% (w/v) glucose, 0.5% (v/v) glycerol, and 0.1% (w/v) Casamino acids (MON in [18]). Cultures were diluted back 1:50 in MO + 0.8% mannose (and 10 mM D-fucose, where applicable). After reaching OD 0.1–0.2, cells were further diluted and placed on a pad made of the same MO + mannose (and fucose) media as the original dilution. Cells were grown and imaged at 37°C.

Fluorescence analysis of cell lineages was done with custom MATLAB software, which has three stages: First, images are segmented to select all individual cells. Next, cells are tracked between frames to establish the cell lineage tree. Finally, fluorescence intensities for each cell lineage are compiled.

Stochastic Simulations

The circuit shown in Fig. 2A (right) was modeled as modeled as follows, with A, B, and C representing the three indicated protein concentrations:

$$\begin{array}{l}\stackrel{\cdot }{A}={\alpha }_A+E+I_A-\beta A\\ \stackrel{\cdot }{B}=\frac{{\alpha }_B}{1+{(A/K)}^n}+E+I_B-\beta B\\ \stackrel{\cdot }{C}={\alpha }_C+E+I_C-\beta C\end{array}$$ (1)

These equations include terms for protein production (α_i), protein degradation and dilution (β), and the contributions of extrinsic and intrinsic noise sources (E and I_i, respectively). All noise and biochemical parameters are based on [2], or values measured directly from the present experimental data; all are listed below for completeness. E(t) represents extrinsic noise and is the same for the three proteins; I_i(t) for i={A,B,C} models intrinsic noise, which is distinct for each protein. Noise sources are modeled as zero-mean signals with finite correlation times using an Ornstein-Uhlenbeck process [14]. This extrinsic noise signal has a standard deviation of σ_ext=0.35, and a correlation time proportional to the cell cycle length: T_cc/log(2). Intrinsic noise has a standard deviation σ_int,i=(α_i)^1/2, and a correlation time of T_int/log(2). The cell cycle time is T_cc=60 mins and T_int=5 mins. The following parameters are used, unless otherwise indicated: n = 1.7, K = 120 nM, α_A = α_C = 1.39 mol/cell/min (chosen so that α_A/β = K), α_B = 4.5 mol/cell/min, and β = log(2)/T_cc.

Cross Correlations

The cross correlation between two discrete signals f(t) and g(t) is defined as

$$\begin{array}{ll}{S}_{f,g}(\tau )=\frac{1}{N-\mid \tau \mid }\sum _{n=0}^{N-\mid \tau \mid -1}\stackrel{\sim }{f}(n+\tau )\stackrel{\sim }{g}(n)\hfill & \tau \ge 0\hfill \\ S_{f,g}(\tau )=S_{g,f}(-\tau )\hfill & \tau <0.\hfill \end{array}$$

Here, $\stackrel{\sim }{f}=f-\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}}f(n)$ and N is the number of time points. This function is normalized to $R_{f,g}(\tau )=\frac{S_{f,g}(\tau )}{\sqrt{S_{f,f}(0)S_{g,g}(0)}}$. This function is also known as cross covariance.

We adapted this standard formula to accommodate tree-structured (branching) data. First, we take each cell lineage, identified by a cell on the final frame of the movie, separately, and calculate the R_f,g(τ). However, because all cell lineages originate from a single cell, many pairs of points are counted multiple times. Therefore, we subtract off the extra contribution of such point pairs, so that each pair is counted only once in the overall sum. The following modified formula incorporates this correction:

$$\begin{array}{l}\begin{array}{ll}{S}_{f,g}(\tau )=\frac{1}{N-\mid \tau \mid }\frac{1}{N_{\mathit{cells}}}\left[\sum _{i=0}^{N_{\mathit{cells}}-1}\left(\sum _{n=0}^{N-\tau -1}{\stackrel{\sim }{f}}_i(n+\tau ){\stackrel{\sim }{g}}_i(n)\right)-\sum _{i=0}^{N_{\mathit{cells}}-2}\left(\sum _{n=0}^{k_i-\tau -1}{\stackrel{\sim }{f}}_i(n+\tau ){\stackrel{\sim }{g}}_i(n)\right)\right]\hfill & \tau \ge 0\hfill \\ S_{f,g}(\tau )=S_{g,f}(-\tau )\hfill & \tau <0.\hfill \end{array}\\ {\stackrel{\sim }{f}}_i=f_i-\frac{1}{N_{\mathit{cells}}}\sum _{i=0}^{N_{\mathit{cells}}-1}{f}_i.\end{array}$$

Here N_cells is the number of cells at the end of the movie and k_i is the branching point between f_i and f_i+1. Note that the first term is the original cross correlation function averaged over N_cells. The second term removes over-counted data.

As in the non-branched case, the function is normalized by

$$R_{f,g}(\tau )=\frac{S_{f,g}(\tau )}{\sqrt{S_{f,f}(0)S_{g,g}(0)}}.$$

Experimental cross correlation curves have been cropped at the ends to remove points that are generated by very small amounts of data.

Model Fits

Optimization software (MATLAB) was used to minimize the difference between experimental and simulated data, taking into account standard errors for experimental data points. Three parameters were fit: g, the derivative of the gene regulation function evaluated at the steady state repressor concentration (see Supplementary Text); W_E/W_I, the ratio of extrinsic to intrinsic noise; and α_B, the rate of protein production in steady-state. For the model fit to the chromosomal construct, local sensitivity g=−0.01, ratio of extrinsic to intrinsic noise W_E/W_I=4.5, and strength of target promoter, α_B=1.7 (Fig. 4C). All other parameters are listed in the stochastic modeling section above. For the plasmid-based construct g=−0.01, W_E/W_I=1.7, α_B=0.5 (Fig. 4D).

Feed Forward Loop Simulations

The cross correlation functions were calculated analytically using the methods described in the Supplementary Material. The following linearized equations were used to describe the system:

$$\begin{array}{l}\stackrel{\cdot }{x}=-\beta x+E+{\eta }_x\\ \stackrel{\cdot }{y}=-\beta y+g_{xy}x+E+{\eta }_y\\ \stackrel{\cdot }{z}=-\beta z+g_{xz}x+g_{yz}y+E+{\eta }_z,\end{array}$$

where the parameter values used in these calculations are g_xy = g, ${\text{g}}_{\underset{\_}{\text{xz}}}=\text{g}$, g_yz = −g, where g = 0.01, and the white noise power constants are W_x = W_y = W_z = 1 and W_e = 0.064 (Supplementary Note). Addition of fucose is modeled by setting g_yz = 0. Here, for simplicity, we model intrinsic noise as white noise. Extrinsic noise is modeled using an Ornstein-Uhlenbeck process, as described in the Supplementary Material.