Conformational Analysis of Stiff Chiral Polymers with End-Constraints

Abstract

We present a Lie-group-theoretic method for the kinematic and dynamic analysis of chiral semi-flexible polymers with end constraints. The first is to determine the minimum energy conformations of semi-flexible polymers with end constraints, and the second is to perform normal mode analysis based on the determined minimum energy conformations. In this paper, we use concepts from the theory of Lie groups and principles of variational calculus to model such polymers as inextensible or extensible chiral elastic rods with coupling between twisting and bending stiffnesses, and/or between twisting and extension stiffnesses. This method is general enough to include any stiffness and chirality parameters in the context of elastic filament models with the quadratic elastic potential energy function. As an application of this formulation, the analysis of DNA conformations is discussed. We demonstrate our method with examples of DNA conformations in which topological properties such as writhe, twist, and linking number are calculated from the results of the proposed method. Given these minimum energy conformations, we describe how to perform the normal mode analysis. The results presented here build both on recent experimental work in which DNA mechanical properties have been measured, and theoretical work in which the mechanics of non-chiral elastic rods has been studied.

1 Introduction

This paper presents Lie-group-theoretic descriptions of semiflexible chiral polymers. The subject presented in this paper represents the confluence of three research areas: (1) mechanics-based models of end-constrained elastic thin rods; (2) the theory of Lie groups and Lie algebras, (especially as it has been applied in geometric control theory); (3) experimentally motivated stiffness models used in modern statistical mechanics of semi-flexible polymers. In the subsections of this section a brief review of relevant literature is presented, and notation and terminology from the theory of Lie groups are reviewed. In subsequent sections we develop the following: a general model of chiral elastic filaments; a variational calculus formulation for deriving the filament shape under end constraints; a numerical procedure for solving these equations; normal mode analysis of a continuous rod model for semiflexible chiral polymers given minimum energy conformations. These techniques are demonstrated with numerical results.

1.1 Literature Review

A number of recent studies on chiral and uncoupled end-constrained elastic rod models of DNA with circular cross-section have been presented (1; 2; 3; 4). These models use classical elasticity theory of continuum filaments with or without self-contact constraints to model the stable conformations of DNA in plasmids, in chromosomes, and during transcription. That work is related to studies on DNA topology (5; 6; 7; 8; 9; 10; 11; 12) in the sense that the topological constraint of no self-interpenetration is enforced. In some works, Euler angles are used in parametrizing equations of the Kirchhoff thin elastic rod theory to obtain minimum energy conformations of DNA and determine its stability (13; 14; 15). Also, the worm-like chain model has been used to model the equilibrium behavior of DNA (16). More recent works involve the modeling of DNA as an anisotropic inextensible rod and also include the effect of electrostatic repulsion for describing the DNA loops bound to Lac repressor, etc. (17; 18). Another recent work includes sequence-dependent elastic properties of DNA (19). All of these aforementioned works are based on Kirchhoff’s thin elastic rod theory (20). This theory, as originally formulated, deals with non-chiral elastic rods with circular cross-section. Another example is the special Cosserat theory of rods (21), which can be viewed as an extension of Kirchhoff’s theory in that it includes extensible and shearable rods. Several researchers in elasticity have employed this rod theory to describe the static and dynamic characteristics of rods. For example, Simo and Vu-Quoc formulated a finite element method using rod theory (22). Dichmann et al. employed a Hamiltonian formulation using the special Cosserat theory of rods for the purpose of describing DNA (23). Coleman et al. reviewed dynamical equations in the theories of Kirchhoff and Clebsch (24). Steigmann and Faulkner derived the equations of classical rod theory using parameter-dependent variational approach (25). Recently, Gonzalez and Maddocks devised a method to extract sequence-dependent parameters for a rigid base-pair DNA model from molecular dynamics simulation (26). In their paper, they used a force moment balance equation from Kirchhoff’s rod theory to extract stiffness and inertia parameters. Another recent work includes the application of Kirchhoff rod theory to marine cable loop formation and DNA loop formation (27). In contrast to these uncoupled chiral models of DNA based on the elasticity of thin rod with isotropic or anisotropic cross-sectional properties, a number of stiffness models used in the statistical mechanics of semi-flexible polymers have been presented over the years (28; 29; 30; 31; 32). These models address the chirality, anisotropic elasticity, and coupling between stiffnesses in semi-flexible polymers like DNA, though end-constrained minimum energy conformations for such models have not been obtained previously. Other models based on DNA structure (29; 33; 34; 35; 36; 37; 38) and experimental measurements in which DNA is manipulated (39; 40; 41; 42) have also contributed to the development of anisotropic and coupled stiffness models of chiral macromolecules. Recently, Wiggins et al. developed a theory based on nonlinear elasticity, called kinkable wormlike chain model, for describing spontaneous kinking of polymers including DNA (43). Also there have been many studies on the extensible properties of DNA (8; 44; 45; 46; 47; 48; 49) including twist-stretch coupling factor.

Normal mode analysis has been a major tool for the study of large motions of biopolymers (see, e.g. (50; 51) and references therein). It has been mainly applied for the description of large motions of macromolecules such as proteins. It has also been shown that normal mode analysis can be used to determine statistical mechanical properties of DNA supercoiling such as free energy, enthalpy, entropy, and so on (52). In this work, DNA was modeled as an inextensible elastic rod with circular- shaped configuration. On the other hand, there have been another approaches to normal mode analysis of DNA. First, people have considered a DNA chain as a set of rigid plates each of which represents the base pair consisting of DNA (53; 54; 55). In this sort of study, there are six parameters to describe the motion of DNA: tilt, roll, twist, rise, shift, and slide. The first three are related to the orientation, and the latter three are to the relative rigid-body translation of each rigid base-pair plate. Secondly, one can consider full atoms in the chain and solvent such as in (56). This work is an example of how normal mode analysis can help to understand biological processes such as DNA-protein recognition.

In this paper, we propose a Lie-group-theoretic method to determine the minimum energy conformations of general elastic model of semiflexible polymers with appropriate end constraints, and describe how to perform normal mode analysis given the conformations determined by the proposed method. More specifically in this study, the theory of rotation and rigid-body motion groups is used. The main differences between previous works and our approach are: (1) unlike previous works on DNA modeling which are based on rod theory (i.e., rods with uncoupled/diagonal stiffness tensor in a local frame of reference with one axis tangent to the filament in the shearless case), our approach applies to the chiral, anisotropic and coupled case. That is, we consider the most general small-strain model either inextensible or extensible, which is also the most accurate reflection of recent experimental measurements; (2) Previous modeling works either use the balance equations for momentum and angular momentum from continuum mechanics and/or weak forms of these equations such as FEM/Galerkin methods. In contrast we use a Lie-group-based variational approach based on the Euler-Poincaré equation, which is different from previous works. With this approach, the number of resulting differential equations becomes smaller, which is easy to deal with. In subsequent sections of this paper a model of elastic filaments that incorporates these stiffness properties is presented in which the theory of rotation and motion groups is used. For this reason, the following subsection reviews mathematical notation and terminology that is necessary to understand the formulation of this paper. Ideas from the theory of Lie groups have been applied in recent years in the fields of mechanics (57; 58) and robotics/systems theory (59; 60; 61; 62; 63). The material in the following subsection is motivated by these previous works on applications of Lie theory, and is presented in a way so as to be directly applicable to the mechanics of end-constrained chiral and coupled rods.

1.2 Notation and Terminology

The terminology necessary to understand the formulation in subsequent sections is now reviewed. The focus here is Lie-group-theoretic notation for describing spatial rigid-body motions. For more detailed explanation, see (62; 64).

Translations (and positions) are described as vectors in three-dimensional Euclidean space: a ∈ ℝ³. Translational motions have the property of being commutative, a₁ + a₂ = a₂ + a₁. This is not a property that is generally shared by spatial rotations or full rigid-body motions. The general and rigorous definition of Lie groups can be found in many books on group theory. In this paper, we are especially interested in Lie groups which correspond to rotation and rigid-body motion in three-dimensional space, i.e., SO(3) and SE(3), respectively.

Orientations and rotational motions in three-dimensional space are described as elements of the rotation group, or “special orthogonal” group, SO(3). This is the set of 3 × 3 real matrices that satisfy the conditions A^T A = 𝕀 and det(A) = +1, where 𝕀 denotes an identity matrix. The group law is matrix multiplication. Rotations (or orientations) are often parameterized using ZXZ Euler angles:

$$A(\alpha ,\beta ,\gamma )=\text{ROT}[{\mathbf{e}}_3,\alpha ]\text{ROT}[{\mathbf{e}}_1,\beta ]\text{ROT}[{\mathbf{e}}_3,\gamma ],$$

where ROT[e_i, φ] denotes the rotation matrix describing counterclockwise rotation by φ about the natural basis vector e_i which has elements (e_i)_j = δ_ij. Each of these basic rotations can be written as the matrix exponential

$$\text{ROT}[{\mathbf{e}}_i,\phi ]=\text{exp}(\phi E_i)$$

where

$$E_1=\left(\begin{array}{ccc}\hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 1& \hfill 0\end{array}\right);E_2=\left(\begin{array}{ccc}\hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0\end{array}\right);E_3=\left(\begin{array}{ccc}\hfill 0& \hfill -1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0\end{array}\right).$$

Any 3 × 3 skew symmetric matrix can be written as a linear combination of these three basic matrices.

There is a close relationship between 3 × 3 skew symmetric matrices and the vector cross product. Namely, given a vector ω = [ω₁, ω₂, ω₃]^T ∈ ℝ³, then

$$({\omega }_1{E}_1+{\omega }_2{E}_2+{\omega }_3{E}_3)\mathbf{x}=\mathit{\omega }\times \mathbf{x}.$$

In this context we use the notation

$$\mathit{\omega }={\left({\displaystyle \sum _{i=1}^3{\omega }_i{E}_i}\right)}^{\vee }.$$ (1)

If one defines the following inner product on the vector space formed by all 3 × 3 skew-symmetric matrices,

$$(V,W)=\frac{1}{2}\text{tr}({\mathit{\text{VW}}}^T),$$ (2)

where tr(·) denotes the trace of a matrix, then it is clear that (E_i,E_j) = δ_ij and

$$\mathbf{\omega }·{\mathbf{e}}_k=\left(E_k,{\displaystyle \sum _{i=1}^3{\omega }_i{E}_i}\right)={\omega }_k.$$

Similarly, one can define the matrix commutator as

$$[V,W]=\mathit{\text{VW}}-\mathit{\text{WV}}.$$ (3)

Whereas large rotations are elements of SO(3), small rotations can be associated with the set of 3 × 3 skew symmetric matrices. When endowed with the above inner product and commutator, this set of matrices is called so(3). Exponentiating any element of so(3) produces an element of SO(3), and every element of SO(3) can be viewed as the exponential of an element of so(3). Another important relationship between SO(3) and so(3) is that given A(t) ∈ SO(3) and $Ȧ\triangleq \frac{\mathit{\text{dA}}}{\mathit{\text{dt}}}$, the matrix products A^T Ȧ and ȦA^T are both elements of so(3). (A^T Ȧ)^∨ and (ȦA^T)^∨ have the meaning of angular velocity as seen in the body-fixed and space-fixed frames of reference, respectively. We will exclusively use the body-fixed perspective, in which

$$\mathit{\omega }={(A^TȦ)}^{\vee }$$ (4)

One observes that

$$[E_1,E_2]=E_3;[E_2,E_3]=E_1;[E_3,E_1]=E_2.$$

The above commutator relations are written all together as

$$[E_i,E_j]={\displaystyle \sum _{k=1}^3{C}_{\mathit{\text{ij}}}^k{E}_k}$$ (5)

where $C_{\mathit{\text{ij}}}^k$ are called the structure constants of the Lie algebra so(3). Note that most of the structure constants are equal to zero, with all the others equal to ±1. Since [E_i, E_j] = −[E_j, E_i] it must be the case that $C_{\mathit{\text{ij}}}^k=-C_{\mathit{\text{ji}}}^k$.

The Euclidean motion group (or “special Euclidean” group), SE(3), is the semidirect product of ℝ³ with the special orthogonal group, SO(3). Physically, it represents the rigid-body motion, or the rotation and the translation, in three-dimensional space. Knowing that rotation can be expressed with an element of SO(3), and translation with an element of ℝ³, we denote elements of SE(3) as g = (a, A) ∈ SE(3) where A ∈ SO(3) and a ∈ ℝ³. The group law is written as g₁ ◦ g₂ = (a₁ + A₁a₂,A₁A₂), and g⁻¹ = (−A^Ta, A^T). Any element of SE(3) can be written as the product of a pure translation and pure rotation as (a, A) = (a, 𝕀) ◦ (0, A).

One may represent any element of SE(3) as a 4 × 4 homogeneous transformation matrix of the form:

$$g=\left(\begin{array}{cc}\hfill A& \hfill \mathit{a}\\ \hfill {\mathbf{0}}^T& \hfill 1\end{array}\right)$$

Given a rigid-body motion g(t), the quantity

$$g^{-1}ġ=\left(\begin{array}{cc}{A}^TȦ\hfill & A^T\mathit{ȧ}\\ {\mathbf{0}}^T& 0\end{array}\right)$$ (6)

is a spatial velocity as seen in the body-fixed frame. It is also an element of the Lie algebra se(3) associated with SE(3). This velocity can be described with the six-dimensional vector

$$\mathbf{\xi }={(g^{-1}ġ)}^{\vee }=\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}{(A^TȦ)}^{\vee }\\ A^T\mathit{ȧ}\end{array}\end{array}\end{array}\right)=\left(\begin{array}{c}\mathit{\omega }\\ \mathit{\upsilon }\end{array}\right)$$ (7)

The vector ξ contains both the angular and translational velocity of the motion g(t) as seen in the body-fixed frame of reference. As similarly done for SO(3), this g⁻¹ġ can be expressed as a linear combination of the basis elements of se(3)

$$g^{-1}ġ={\displaystyle \sum _{i=1}^6{\xi }_i{Ẽ}_i}$$ (8)

where Ẽ_i denotes the basis element of se(3) defined as

$$\begin{array}{c}{\mathit{Ẽ}}_1=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\mathit{Ẽ}}_2=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\mathit{Ẽ}}_3=\left(\begin{array}{cccc}\hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);\hfill \\ {\mathit{Ẽ}}_4=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\mathit{Ẽ}}_5=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\mathit{Ẽ}}_6=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right).\hfill \end{array}$$

As similarly done with the case of SO(3), linear combination and exponentiation of these matrices produces elements of SE(3). The products of exponentials of elementary motions can be used to generate any rigid-body motion, much like the Euler angles do for pure rotation.

Finally, one can define the adjoint operator, for a given g = (a, A) ∈ SE(3), as

$$\text{Ad}(g)=\left(\begin{array}{cc}A& 0_{3\times 3}\\ \mathit{â}A& A\end{array}\right)$$

where â corresponds to the skew-symmetric matrix associated with a, i.e. (â)^∨ = a. This adjoint operator changes the view of a 6D rigid-body velocity or an element of se(3) from the body frame to the spatial frame of reference.

2 Elastic Energy of Chiral Rods

In this section we discuss an energy functional which, when subject to certain constraints, defines the minimum energy conformations of chiral elastic rods.

2.1 Inextensible Rods

A number of authors have derived potential energies of bending and/or twisting of a stiff inextensible chain that are of the form

$$E={\displaystyle {\int }_0^{L}U(\mathit{\omega }(s))\mathit{\text{ds}}}$$

where L is the length of the macromolecule and

$$U=\frac{1}{2}{\mathit{\omega }}^{T}B\mathit{\omega }-{\mathit{b}}^T\mathit{\omega }+{\beta }^{\prime }.$$ (9)

Here B = B^T ∈ ℝ^{3 × 3} is a positive semi-definite stiffness matrix, b ∈ ℝ³, and β′ ∈ ℝ. ω is the “angular velocity”(with arclength s replacing time) of a frame of reference (a(s), A(s)) which is affixed to the duplex-axis curve of the macromolecule at each value of arclength s. If there are no end-constraints, the minimal energy conformation is defined by ω(s) = B⁻¹b, which defines a helix (including straight lines and circles as degenerate cases).

As well-known examples of equation (9) from the polymer science literature, consider:

• The Kratky-Porod Model (29)

  $$B=\left(\begin{array}{ccc}{\alpha }_0& 0& 0\\ 0& {\alpha }_0& 0\\ 0& 0& 0\end{array}\right);\mathit{b}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right);{\beta }^{\prime }=0.$$
• The Yamakawa Model (32)

  $$B=\left(\begin{array}{ccc}{\alpha }_0& 0& 0\\ 0& {\alpha }_0& 0\\ 0& 0& {\beta }_0\end{array}\right);\mathit{b}=\left(\begin{array}{c}0\\ {\alpha }_0{\kappa }_0\\ {\beta }_0{\tau }_0\end{array}\right);{\beta }^{\prime }=\frac{1}{2}({\beta }_0{\tau }_0^2+{\alpha }_0{\kappa }_0^2).$$
• The Marko-Siggia DNA Model (38; 40)

  $$B=\left(\begin{array}{ccc}{a}_0+b_0^2/c_0& 0& b_0\\ 0& a_0& 0\\ b_0& 0& c_0\end{array}\right);\mathit{b}=\left(\begin{array}{c}{b}_0{\omega }_0\\ 0\\ c_0{\omega }_0\end{array}\right);{\beta }^{\prime }=\frac{1}{2}{c}_0{\omega }_0^2.$$

The Yamakawa and Kratky-Porod models can be viewed as special cases of classical rod theory, with the Kratky-Porod model being degenerate in the sense that it has no twist stiffness and no chirality. The most general model is, therefore, the Marko-Siggia model which includes anisotropy, chirality and twist-bend coupling. For this reason, we employ the Marko-Siggia model for the purpose of simulation, although our method described below can be applied to any of these three models.

Under the constraint that the molecule is inextensible, and all the frames of reference are attached to the backbone with their local z-axis pointing in the direction of the next frame, one observes

$$\mathit{a}(L)={\displaystyle {\int }_0^L\mathit{u}(s)}ds\text{\hspace{1em}and\hspace{1em}}\mathit{u}(s)=A(s){\mathit{e}}_3.$$ (10)

2.2 Extensible Rods

Experimental evidence suggests that DNA is an extensible chain (44) and there is coupling between torsional and extensional stiffnesses (45). The most general continuum elastic filament model that can capture this scenario is one in which equation (9) is replaced with

$$U=\frac{1}{2}{\mathit{\xi }}^{T}K\mathit{\xi }-{\mathit{k}}^T\mathit{\xi }+{\beta }^{\prime }.$$ (11)

where ξ = [ω^T, υ^T]^T is defined in equation (7). The minimum energy conformation of such a chain without end constraints or self-contact is defined by ξ(s) = K⁻¹k. As a defining equality for k one observes strictly from geometry that

$$K^{-1}\mathit{k}=\left(\begin{array}{c}2\pi n{\mathit{e}}_3\\ {\mathit{e}}_3\end{array}\right)$$

for DNA, where n is the number of revolutions per unit length of the double-helix. This defines a straight (as opposed to helical) backbone curve with a superimposed twist. A different definition for k can easily be substituted for helical wormlike chains.

The matrix K can be modelled in a number of ways, all of which will be of the form

$$K=\left(\begin{array}{cc}B& C\\ C^T& D\end{array}\right)$$

where B is the stiffness matrix discussed previously.

If one assumes that in addition to the couplings in the Marko-Siggia DNA model discussed in the previous section there is only twist-extension coupling then

$$C=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& \tau \end{array}\right)$$

(where τ is the twist-extension coupling stiffness parameter), and

$$D=\left(\begin{array}{ccc}{s}_1& 0& 0\\ 0& s_2& 0\\ 0& 0& d\end{array}\right)$$

where s₁ and s₂ describe the stiffness due to transverse shearing of the filament and d is the extensional (longitudinal) stiffness. Of course, if there is reason to include additional coupling parameters in either C or D this can be done easily.

Other than the increase in dimension of the stiffness matrix, and the use of SE(3) terminology rather than SO(3), a notable difference in the extensible case is that there is no need for an integral constraint equation analogous to equation (10).

3 Determination of Minimum Energy Conformations

In this section, we describe how to determine the minimum energy conformations of semiflexible chiral polymers with appropriate end constraints. More specifically, we apply variational calculus on Lie groups to obtain Euler-Poincaré equation. In appendix A is shown derivation of the equation in detail. This section writes equation (46) explicitly for the energy in equation (9) and (11), and describes a technique for solving these equations for given boundary conditions and other constraints.

3.1 Inextensible Rods

Considering the case of equation (9) with the kinematic constraint of inextensibility (10), one writes equation (46) with f = U for i = 1, 2, 3 together as the vector equation

$$B\frac{d\mathit{\omega }}{\mathit{\text{ds}}}+\mathit{\omega }\times (B\mathit{\omega }-\mathit{b})=\left(\begin{array}{c}-{\mathbf{\lambda }}^T{\mathit{\text{Ae}}}_2\\ {\mathbf{\lambda }}^T{\mathit{\text{Ae}}}_1\\ 0\end{array}\right)$$ (12)

where a dot represents differentiation with respect to arclength s, λ ∈ ℝ³ is the vector of Lagrange multipliers necessary to enforce the vector constraint in equation (10), and the right-hand-side of equation (12) results from the fact that

$$E_i^R({\mathbf{\lambda }}^{T}A{\mathit{e}}_3)=\frac{d}{\mathit{\text{dt}}}{\mathbf{\lambda }}^{T}A(𝕀+{\mathit{\text{tE}}}_i){\mathit{e}}_3{|}_{t=0}={\mathbf{\lambda }}^T{\mathit{\text{AE}}}_i{\mathit{e}}_3={\mathbf{\lambda }}^{T}A({\mathit{e}}_i\times {\mathit{e}}_3).$$

Equation (12) is solved iteratively subject to the initial conditions ω(0) = μ which are varied together with the Lagrange multipliers until a(L) and A(L) attain the desired values. A(s) is computed from ω(s) in equation (12) by integrating the matrix differential equation

$$\frac{\mathit{\text{dA}}}{\mathit{\text{ds}}}=A\left({\displaystyle \sum _{i=1}^3{\omega }_i(s)E_i}\right),$$

and a(L) is then obtained from equation (10).

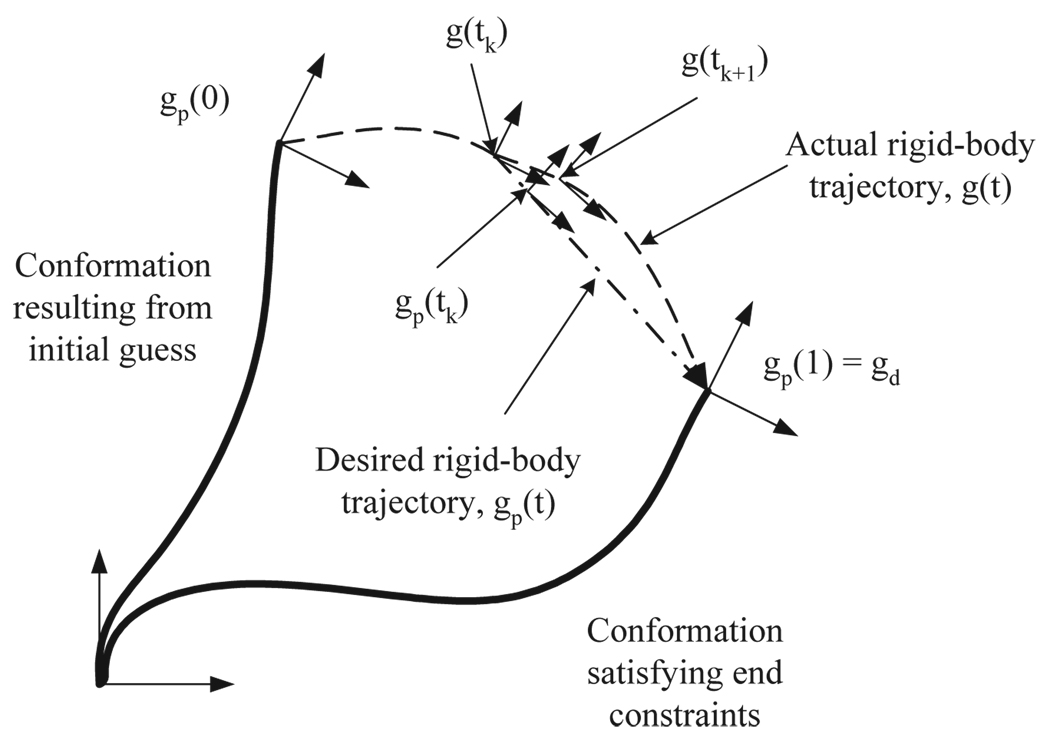
Let η = [μ^T, λ^T]^T ∈ ℝ⁶ be the vector of all the undetermined coefficients. Denote the distal frame of reference of the rod for a given value of η as g(η, L). Denote the desired position and orientation of the distal frame of reference as g_d. Let η₀ be an initial guess for the value of η and g₀ = g(η₀, L). Theoretically, One can drive the updates of η as follows. First define g_p(t) to be a rigid-body trajectory (or path) such that g_p(0) = g(η₀, L) and g_p(1) = g_d. See figure 1 for a pictorial explanation. Then by forcing η to update such that the reference frame of the distal end stays on the path, the velocity condition

$$\frac{{\mathit{\text{dg}}}_p}{\mathit{\text{dt}}}={\displaystyle \sum _{i=1}^6\frac{\partial g}{\partial {\eta }_i}}\frac{d{\eta }_i}{\mathit{\text{dt}}}$$

must hold in order for g_p(t) = g(η(t), L).

Figure 1.

Schematic diagram explaining the concept of rigid-body trajectory. g_p(0) is the position and orientation of the distal end in the conformation resulting from the initial guess, and g_p(1) should be the desired one of the distal end, i.e., g_p(1) = g_d. At time t_k, g_p(t) forms the geodesic from the current frame, g(t_k), to g_d.

We can write the velocity condition in the form

$${\left(g_p^{-1}\frac{{\mathit{\text{dg}}}_p}{\mathit{\text{dt}}}\right)}^{\vee }=J_R(\mathit{\eta })\frac{d\mathit{\eta }}{\mathit{\text{dt}}},$$ (13)

where

$$J_R(\mathit{\eta })=\left[(g^{-1}\frac{\partial g}{\partial {\eta }_1}{)}^{\vee },(g^{-1}\frac{\partial g}{\partial {\eta }_2}{)}^{\vee },\cdots ,(g^{-1}\frac{\partial g}{\partial {\eta }_6}{)}^{\vee }\right]$$

is a 6 × 6 matrix called the right Jacobian for SE(3) associated with the parameters η (64).

Equation (13) is a differential equation that defines η(t). This equation can be solved by inverting J_R at each time step and integrating numerically. This can be achieved only if we know the position and orientation of the distal end as an explicit function of η(t). However, since we do not know that function, direct numerical integration of equation (13) always contains numerical error, which leads to the failure of reaching the desired value because the error becomes larger as time increases. To circumvent this problem, we devise the following numerical algorithm.

First define an artificial rigid-body trajectory, g_p(t) which satisfy the conditions g_p(0) = g₀ and g_p(1) = g_d. Here g_p(t) is defined as

$$g_p(t)=(\mathit{a}(t\prime )+t({\mathit{a}}_d-\mathit{a}(t\prime )),A(t\prime )\text{exp}[t·\text{log}(A^T(t\prime )A_d)]),$$

where g(t′) = (a(t′), A(t′)) is the distal frame at time t′, and t′ = t, but when it comes to differentiation with respect to the artificial time parameter t, t′ is treated as a constant. Also g_d = (a_d, A_d) represents the desired position and orientation. The function g_p(t) generates a left-invariant geodesic in SE(3) which is formed from the current distal frame to the desired one, and pushes the distal end to the desired pose of the distal frame of reference.

At the kth step, we apply the velocity condition

$$\frac{d{\mathit{\eta }}_k}{\mathit{\text{dt}}}=J_R^{-1}\text{Ad}(g^{-1}{g}_p(t_k)){\left(g_p^{-1}(t_k)\frac{{\mathit{\text{dg}}}_p}{\mathit{\text{dt}}}(t_k)\right)}^{\vee }$$ (14)

to calculate the increment of η. In the above equation, Ad(g⁻¹g_p), including the one in the equation below, changes the view of a velocity or an element of se(3) so that it can be viewed from the current frame of reference (65). Since this relation only contains velocity tracking term, we need the position correction term defined as

$${\mathit{\eta }}_k^c=J_R^{-1}\text{Ad}(g^{-1}{g}_p(t_k))[\text{log}(g^{-1}(t_k)g_p(t_k)){]}^{\vee }.$$ (15)

Then we obtain η at the (k + 1)th step as

$${\mathit{\eta }}_{k+1}={\mathit{\eta }}_k+\mathrm{\Delta }t\frac{d{\mathit{\eta }}_k}{\mathit{\text{dt}}}+{\mathit{\eta }}_k^c.$$ (16)

In practice, the partial derivatives in the definition of J_R are computed approximately as

$$\frac{\partial g}{\partial {\eta }_i}\approx \frac{1}{\epsilon }[g(\mathit{\eta }+\epsilon {\mathit{e}}_i,L)-g(\mathit{\eta },L)]$$

for a small number ε such as ε = 10⁻¹⁰. Together with ε and Δt which are small enough, the feedback information of the current distal end frame included in the above scheme guarantees the convergence to the desired frame of reference.

3.2 Extensible Rods

From equation (46) and (11) one can obtain the following equation for the extensible case:

$$K\frac{d\mathit{\xi }}{\mathit{\text{ds}}}+(K\mathit{\xi }-\mathit{k})\wedge \mathit{\xi }=\mathbf{0}$$ (17)

where ∧ is the product of infinitesimal rigid-body motions defined by

$$\left(\begin{array}{c}{\mathit{\omega }}_1\\ {\mathit{\upsilon }}_1\end{array}\right)\wedge \left(\begin{array}{c}{\mathit{\omega }}_2\\ {\mathit{\upsilon }}_2\end{array}\right)=\left(\begin{array}{c}{\mathit{\omega }}_2\times {\mathit{\omega }}_1+{\mathit{\upsilon }}_2\times {\mathit{\upsilon }}_1\\ {\mathit{\omega }}_2\times {\mathit{\upsilon }}_1\end{array}\right).$$

This wedge operator is related to the “ad” operator as

$${\mathit{\xi }}_1\wedge {\mathit{\xi }}_2=-\text{ad}({\mathit{\xi }}_2{)}^T{\mathit{\xi }}_1$$ (18)

where ${\mathit{\xi }}_i={[{\mathit{\omega }}_i^T,{\mathit{\upsilon }}_i^T]}^T$, i = 1, 2 and the matrix of “ad” operator is defined as (66)

$$\text{ad}(\mathit{\xi })=\left(\begin{array}{cc}\widehat{\mathit{\omega }}& 0_{3\times 3}\\ \widehat{\mathit{\upsilon }}& \widehat{\mathit{\omega }}\end{array}\right).$$

Equation (17) is solved subject to the initial conditions ξ(0) = η ∈ ℝ⁶. This, together with the kinematic condition

$$\frac{\mathit{\text{dg}}}{ds}=g\left({\displaystyle \sum _{i=1}^6{\xi }_i{\mathit{Ẽ}}_i}\right),$$

is integrated for 0 ≤ s ≤ L to define g(ξ, L). From this point everything follows in exactly the same way as for the inextensible case.

It is worth noting that since in this case there is no integral constraint, there are no Lagrange multipliers on the right-hand-side of equation (17), but there are six rather than three initial conditions. This also means that s is no longer the arclength of the filament. Rather, s denotes what the arclength of the filament would be in its referential (undeformed conformation), but when the chain bends, twists, and extends, s deviates from being arclength.

4 Normal Mode Analysis

After one obtains the minimum energy conformations, one can perform normal mode analysis given those minimum energy conformations. Normal mode analysis has been widely used as a tool for describing thermal fluctuations. Thermodynamic and statistical mechanical properties related to thermal fluctuations can be expressed using normal modes and corresponding natural frequencies obtained by normal mode analysis (52; 53). In this section we formulate the method of normal mode analysis using the concept of Lie groups. Here we present normal mode analysis using the extensible rod model. The reason to employ the extensible rod model is that, first it is easy to implement than the inextensible-rod model due to the fact that there is no kinematic constraints in the extensible rod model, and secondly it can describe local deformations including extension during the fluctuation, as in normal mode analysis treating each base pair as a rigid plate. We note that we can obtain the same minimum energy conformations using both inextensible and extensible rod.

Let g_E(s) ∈ SE(3) denote an minimum energy conformation obtained by the aforementioned approach. Let also g_P (s, t) ∈ SE(3) represent conformations which are vibrating or fluctuating around the minimum energy conformation. Here s denotes the referential arclength. If we assume small fluctuation, then g_P (s, t) = g_E(s) (𝕀 + Σ(s, t)). Here

$$\mathrm{\Sigma }(s,t)=\left(\begin{array}{cccc}0& -{\omega }_3& {\omega }_2& {\upsilon }_1\\ {\omega }_3& 0& -{\omega }_1& {\upsilon }_2\\ -{\omega }_2& {\omega }_1& 0& {\upsilon }_3\\ 0& 0& 0& 0\end{array}\right)$$

is an element of se(3) representing small deviations or displacements from the minimum energy conformation. It can be related to a 6 × 1 vector σ = [ω^T, υ^T]^T where ω = [ω₁, ω₂, ω₃]^T and υ = [υ₁, υ₂, υ₃]^T, with (Σ)^∨ = σ. Now let us assume

$$\begin{array}{cc}{\omega }_i(s,t)\hfill & ={\displaystyle \sum _{j=1}^n{a}_j^{(i)}(t){\mathrm{\Phi }}_j(s)}\hfill \\ {\upsilon }_i(s,t)\hfill & ={\displaystyle \sum _{j=1}^n{b}_j^{(i)}(t){\mathrm{\Phi }}_j(s)}\hfill \end{array}$$ (19)

where {Φ_j(s)} is a set of geometrically compatible functions which have the properties of completeness and orthogonality, and also satisfy the boundary conditions Φ_j(0) = Φ_j(L) = 0, where L denotes the total length of a polymer. In this work, we choose

$${\mathrm{\Phi }}_j(s)=\text{sin}\left(\frac{\pi \mathit{\text{js}}}{L}\right).$$

This approach is very similar to Rayleigh-Ritz approximation method (67).

The kinetic energy of a polymer has two parts. One is linear velocity part, and the other is rotational velocity part. The former is defined as $\frac{1}{2}{\rho }_0{\displaystyle {\int }_0^L\Vert \frac{\partial {\mathit{r}}_P}{\partial t}{\Vert }^2\mathit{\text{ds}}}$ if we assume the uniform mass density. Note that ρ₀ = ρS where S is the cross-sectional area of a rod and ρ is a uniform mass density. The latter part can be expressed, using moment of inertia I, as $\frac{1}{2}{\displaystyle {\int }_0^L{\mathit{\omega ̇}}^{T}I\mathit{\omega ̇}}$. In practice, in the thin elastic rod cases, we can only consider torsional term, which has the form of $\frac{1}{2}\rho I_{\mathit{\text{zz}}}{\displaystyle {\int }_0^L{\mathrm{\omega ̇}}_3^2\mathit{\text{ds}}}$, where I_zz denotes the area moment of cross section and for a circular cross-sectional rod case, $I_{\mathit{\text{zz}}}=\frac{\pi r^4}{4}$. Here r denotes the radius of a circular cross section. Hence the total kinetic energy can be expressed as

$$T=\frac{1}{2}{\rho }_0{\displaystyle {\int }_0^L\Vert \frac{\partial {\mathit{r}}_P}{\partial t}{\Vert }^2}\mathit{\text{ds}}+\frac{1}{2}\rho I_{\mathit{\text{zz}}}{\displaystyle {\int }_0^L(\frac{\partial {\omega }_3}{\partial t}{)}^2}\mathit{\text{ds}}.$$ (20)

Note that $g_P{\mathit{e}}_4={[{\mathit{r}}_P^T,1]}^T$. Then

$$\begin{array}{cc}\Vert \frac{\partial {\mathit{r}}_P}{\partial t}{\Vert }^2\hfill & =\Vert \frac{\partial g_P}{\partial t}{\mathit{e}}_4{\Vert }^2\hfill \\ \hfill & =\Vert g_E(s)\frac{\partial \mathrm{\Sigma }}{\partial t}{\mathit{e}}_4{\Vert }^2\hfill \\ \hfill & =\Vert \frac{\partial \mathit{\upsilon }}{\partial t}{\Vert }^2.\hfill \end{array}$$ (21)

Letting $\mathit{q}={[\cdots ,{\mathit{q}}_j^T,\cdots ]}^T\text{where}{\mathit{q}}_j={[a_j^{(3)},b_j^{(1)},b_j^{(2)},b_j^{(3)}]}^T$, the kinetic energy can be expressed in matrix form as

$$T=\frac{1}{2}{\mathit{q̇}}^{T}M\mathit{q̇}$$ (22)

where M is a block-diagonal matrix, expressed as M = diag(M_j), whose diagonal element M_j is defines as

$$M_j=\left(\begin{array}{cccc}\frac{\rho I_{\mathit{\text{zz}}}L}{2}& 0& 0& 0\\ 0& \frac{{\rho }_{0}L}{2}& 0& 0\\ 0& 0& \frac{{\rho }_{0}L}{2}& 0\\ 0& 0& 0& \frac{{\rho }_{0}L}{2}\end{array}\right).$$ (23)

Here we use the notation $\frac{\partial }{\partial t}(·)=\stackrel{·}{(·)}$.

Now let us consider the potential energy term. Note that we cannot consider Σ(s, t) as a small deformation which is denoted as ω in the definition of the potential energy. The small deformation or the “body-fixed velocity” ξ_P is defined as

$${\mathit{\xi }}_P={({\mathrm{\Xi }}_P)}^{\vee }={\left(g_P^{-1}\frac{\partial g_P}{\partial s}\right)}^{\vee }.$$ (24)

From this point of view, if we compute the small deformation or the “angular velocity” of a chain, then together with g_P = g_E(𝕀 + Σ), it becomes

$${\mathrm{\Xi }}_P=g_P^{-1}{g}_P^{\prime }={\mathrm{\Xi }}_E+[{\mathrm{\Xi }}_E,\mathrm{\Sigma }]+\mathrm{\Sigma }\prime$$ (25)

or in vector form as

$${\mathit{\xi }}_P={\mathit{\xi }}_E+\text{ad}({\mathit{\xi }}_E)\mathit{\sigma }+\mathit{\sigma }\prime$$ (26)

up to the first order. Here $\frac{d}{\mathit{\text{ds}}}(·)\text{or}\frac{\partial }{\partial s}(·)=(·)\prime \text{and}({\mathrm{\Xi }}_E{)}^{\vee }={\mathit{\xi }}_E=[{\mathit{\omega }}_E^T,{\mathit{\upsilon }}_E^T{]}^T$ denote the deformations or the “body-fixed velocity” of the minimum energy conformation. That is to say, the perturbed deformation is defined as δ = ξ_P − ξ_E = ad(ξ_E)σ + σ′, which leads to the following potential energy

$$V={\displaystyle {\int }_0^L\left(\frac{1}{2}{\mathit{\delta }}^{T}K\mathit{\delta }-{\mathit{k}}^T\mathit{\delta }\right)\mathit{\text{ds}}.}$$ (27)

Let $\mathit{\theta }=[\cdots ,{\mathit{\theta }}_j^T,\cdots {]}^T\text{where}{\mathit{\theta }}_j=[{\mathit{a}}_j^T,{\mathit{b}}_j^T{]}^T\text{wherein}{\mathit{b}}_j=[b_j^{(1)},b_j^{(2)},b_j^{(3)}{]}^T\text{and}{\mathit{a}}_j=[a_j^{(1)},a_j^{(2)},a_j^{(3)}{]}^T$. Then the potential energy is expressed as the following quadratic form

$$V=\frac{1}{2}{\mathit{\theta }}^T{K}_t\mathit{\theta }-{\mathit{k}}_t^T\mathit{\theta }.$$ (28)

Here the stiffness matrix is defines as

$$K_t=\left(\begin{array}{cccc}{K}_1& K_{1,2}& \cdots & K_{1,n}\\ K_{1,2}^T& K_2& \cdots & K_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ K_{1,n}^T& K_{2,n}^T& \cdots & K_n\end{array}\right)$$ (29)

where

$$\begin{array}{c}{K}_j=\frac{j^2{\pi }^2}{2L}K+{\displaystyle {\int }_0^L\left\{{\mathrm{\Phi }}_j^2{\text{ad}}^T({\mathit{\xi }}_E)K\text{ad}({\mathit{\xi }}_E)+\left({\text{ad}}^T({\mathit{\xi }}_E)K+K\text{ad}({\mathit{\xi }}_E)\right){\mathrm{\Phi }}_j^{\prime }{\mathrm{\Phi }}_j\right\}\mathit{\text{ds}}}\hfill \\ K_{j,k}={\displaystyle {\int }_0^L\left({\mathrm{\Phi }}_j{\mathrm{\Phi }}_k{\text{ad}}^T({\mathit{\xi }}_E)K\text{ad}({\mathit{\xi }}_E)+{\mathrm{\Phi }}_j{\mathrm{\Phi }}_k^{\prime }{\text{ad}}^T({\mathit{\xi }}_E)K+{\mathrm{\Phi }}_j^{\prime }{\mathrm{\Phi }}_{k}K\text{ad}({\mathit{\xi }}_E)\right)\mathit{\text{ds}}.}\hfill \end{array}$$ (30)

${\mathit{k}}_t^T$ is defined as

$${\mathit{k}}_t^T=\left[\cdots ,{\mathit{k}}^T{\displaystyle {\int }_0^L(\text{ad}({\mathit{\xi }}_E){\mathrm{\Phi }}_j+𝕀{\mathrm{\Phi }}_j^{\prime })\mathit{\text{ds}},\cdots }\right]$$ (31)

where 𝕀 denotes an 6 × 6 identity matrix. Note that, in (11), if we define ξ_a = ξ − K⁻¹k, then the potential energy has only quadratic term as $V=\frac{1}{2}{\displaystyle {\int }_0^L{\mathit{\xi }}_a^{T}K{\mathit{\xi }}_a\mathit{\text{ds}}}$, which eliminates k_t in the above equation.

Now we rearrange the parameters and the matrices. If we define $\mathit{u}=[{\mathit{q}}^T,{\mathit{q}}_r^T{]}^T\text{where}{\mathit{q}}_r=[\cdots ,a_j^{(1)},a_j^{(2)},\cdots {]}^T$ instead of θ, then we need to rearrange K_t. This can be done simply by changing the corresponding rows and columns in K_t and k_t. Now let K_t and k_t denote the stiffness matrix and the forcing vector of which rows and columns are changed appropriately. Then the Lagrangian ℒ = T − V becomes

$$ℒ=\frac{1}{2}{\mathit{u̇}}^T\left(\begin{array}{cc}M& 0_{4n\times 2n}\\ 0_{2n\times 4n}& 0_{2n\times 2n}\end{array}\right)\mathit{u̇}-\frac{1}{2}{\mathit{u}}^T\left(\begin{array}{cc}{K}_{11}& K_{12}\\ K_{12}^T& K_{22}\end{array}\right)\mathit{u}+{\mathit{k}}_t^T\mathit{u}.$$ (32)

Lagrangian equation gives the equation of motion as

$$\left(\begin{array}{cc}M& 0_{4n\times 2n}\\ 0_{2n\times 4n}& 0_{2n\times 2n}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\mathit{q̈}\\ {\mathit{q̈}}_r\end{array}\end{array}\right)+\left(\begin{array}{cc}{K}_{11}& K_{12}\\ K_{12}^T& K_{22}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\mathit{q}\\ {\mathit{q}}_r\end{array}\end{array}\right)={\mathit{k}}_t.$$ (33)

The main issue now is to solve the eigenproblem

$$\left(\begin{array}{cc}M& 0_{4n\times 2n}\\ 0_{2n\times 4n}& 0_{2n\times 2n}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\mathit{q̈}\\ {\mathit{q̈}}_r\end{array}\end{array}\right)+\left(\begin{array}{cc}{K}_{11}& K_{12}\\ K_{12}^T& K_{22}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}\mathit{q}\\ {\mathit{q}}_r\end{array}\end{array}\right)=0.$$ (34)

This can be divided into two matrix equations as

$$M\mathit{q̈}+K_{11}\mathit{q}+K_{12}{\mathit{q}}_r=\mathbf{0}$$ (35)

and

$$K_{12}^T\mathit{q}+K_{22}{\mathit{q}}_r=\mathbf{0}.$$ (36)

The second one defines the angular (or bending) deformation. Substituting the lower equation into the upper one gives

$$M\mathit{q̈}+(K_{11}-K_{12}{K}_{22}^{-1}{K}_{12}^T)\mathit{q}=\mathbf{0}.$$ (37)

Solving this eigenvalue problem gives the normal modes of interest.

5 Numerical Results

In this section, we present numerical examples to apply our method. Specifically, we generate conformations of DNA in which one segment binds to the cylindrical histone protein and the other is a free segment. We use the basic physical data from the work of Swigon, et al. (2). First we demonstrate how to determine the minimum energy conformations, and then select one exemplary case to demonstrate normal mode analysis. As for the minimum energy conformations, since parameters regarding inextensible rod model are available, we present the results from the inextensible rod modeling, though we can do the same with the extensible rod model.

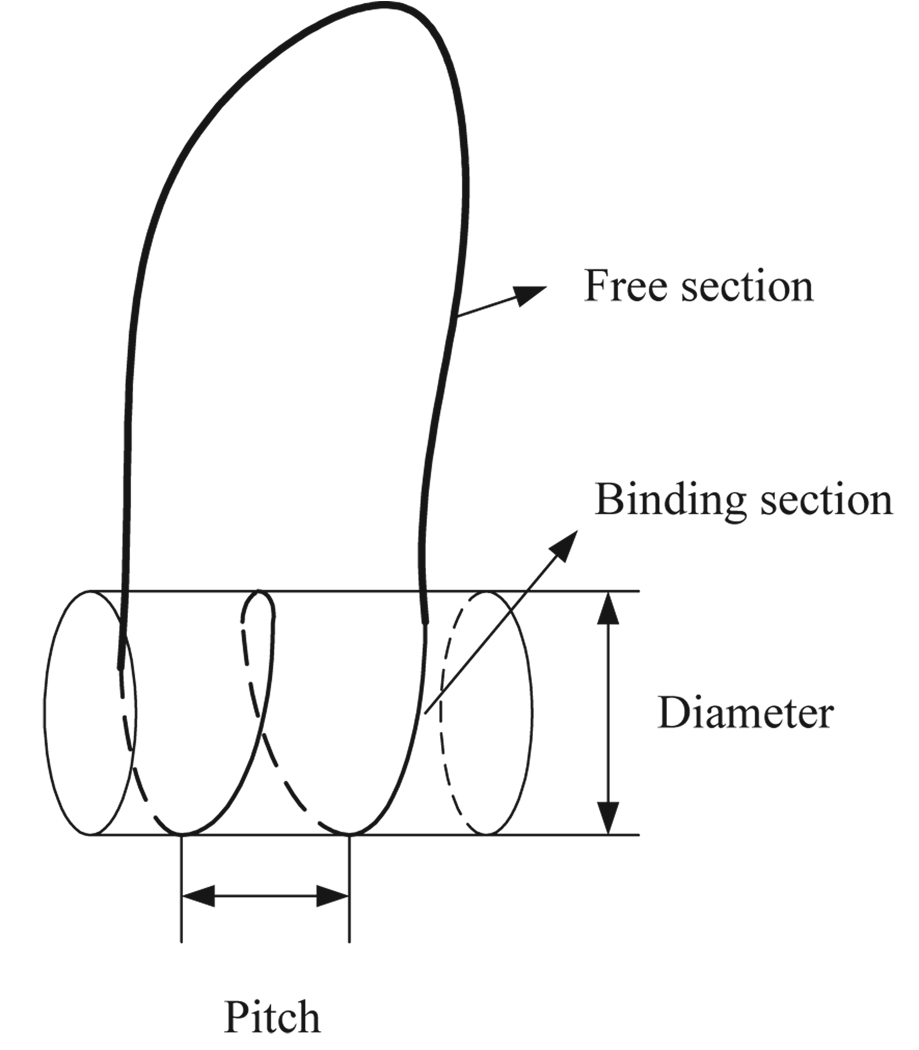
The schematic picture is depicted in figure 2. As for the physical model of DNA, we employ the Marko-Siggia DNA model. The physical parameters used in this example are shown in table 1. In the first example, we set b₀ = 0. The fact that b₀ = 0 means that we treat DNA as an isotropic elastic filament. In order to determine the minimum energy conformation of a free section, we need to know: (1) the number of base pairs in the entire DNA section, which we call N, (2) the number of wraps, w, of DNA around the cylindrical histone molecule, (3) the end constraints, which can be obtained from the information of the the DNA section which binds to the histone. Basically if we have exact data for the bound part, for example those from the Protein Data bank (PDB), then the end constraints may easily be determined. Since precise experimentally determined end constraints appear to be unavailable at the current time, we need to assume the appropriate end constraints for the demonstration of our method. We therefore treat the backbone curve of the bound segment as a helix, which means that we can obtain the conformation of that backbone curve simply from the geometric parameters such as pitch, and diameter of the cylinder, which are shown in figure 2. Here, we use the pitch value of 2.7 nm, and a diameter of 8.6 nm (2). As for the twist density of the bound section, it is experimentally shown that the helical repeat length(HRL) of the bound section has three different values (68). Two outer segments have 10.0 bp/turn as a HRL, and the middle one has a HRL of 10.4 ~ 10.7 bp/turn. For this reason, it seems that Swigon, et al made an assumption that the length of a middle segment corresponds to w = 1.45, and when w = 1.70 the remaining parts form the two outer segments (2). We employ their aforementioned assumption in our paper to determine the length of each segment of the bound section. Moreover, in each of the segments, the twist density can be expressed as

$${\omega }_b=\frac{2\pi }{0.34h_b},$$

where, h_b = 10.40 bp/turn for the middle segment (2), and h_b = 10.0 bp/turn for two outer segments (68). Given the appropriate end constraints and the above parameters, we can determine the minimum energy conformations of the DNA by the proposed method. After that, we can calculate the topological values such as the writhe W_r, twist T_w, and the linking number L_k of the entire DNA segment. Elastic energy also can be calculated. Let x(s) be the coordinates of the DNA backbone curve. Then the writhe is defined by the Gaussian integral as (64)

$$W_r=\frac{1}{4\pi }{\displaystyle \oint {\mathit{\text{ds}}}_1}{\displaystyle \oint {\mathit{\text{ds}}}_2[\mathbf{ẋ}(s_1)\times \mathbf{ẋ}(s_2)]·\frac{\mathbf{x}(s_1)-\mathbf{x}(s_2)}{\Vert \mathbf{x}(s_1)-\mathbf{x}(s_2){\Vert }^3}.}$$

Figure 2.

Schematic diagram of DNA in the example. Free section and the section which binds to the cylindrical histone are shown. In this geometry, we use a value of pitch of 2.7 nm and a value of diameter of 8.6 nm.

Table 1.

The physical parameters for the Marko-Siggia model. Here, a₀ is related to the bending stiffness of DNA, b₀ is the bending-twisting coupling factor, c₀ is related to the torsional stiffness, and ω₀ is the intrinsic twist density of a straight DNA. b₀ = 0 means that we treat DNA as an isotropic rod.

a0 [pN · nm2]	b0 [pN · nm2]	c0 [pN · nm2]	ω0 [nm−1]
205.72	0 or 2.4c0	1.4a0	1.85

The twist is defined similarly as

$$T_w=\frac{1}{2\pi }{\displaystyle \oint {\omega }_3(s)\mathit{\text{ds}}.}$$

Then the linking number is calculated as

$$L_k=W_r+T_w.$$

Another important issue before the discussion of the resulting minimum energy conformations is how to obtain multiple solutions. As one can imagine, there can be a great number of conformations which meet the given end constraints. Amongst various possible methods for obtaining these conformations, we utilize the following method. First we assume eight different initial guesses. Our goal is to obtain the minimum energy conformations of which the twist density is close to the intrinsic twist density of DNA, called ω₀. This leads to the assumption that the initial angular velocity should be [0, 0, ω₀]^T. As for the Lagrange multiplier, we assume the eight different values such as [0.1, 0, 0]^T, [0, 0.1, 0]^T, [0.1, 0.1, 0]^T, [−0.1, 0, 0]^T, [0,−0.1, 0]^T, [−0.1,−0.1, 0]^T, [0.1,−0.1, 0]^T, [−0.1, 0.1, 0]^T. Since the physical meaning of Lagrange multiplier is the force acting on the distal end to keep the geometric constraint, the above assumption gives the initial conformations which has the intrinsic twist density along the backbone curve and are slightly bent to eight different directions. Some initial guesses can return the same resulting conformations and others can return highly twisted conformations which we exclude from our paper. We have verified that the above method can generate the minimum energy conformations that we want. We show the values of those topological parameters and the elastic energy of the free section based on our calculation in table 2 and each conformation of DNA is depicted in figure 3 as a light curve. These results coincide well with those of Swigon, et al. (2). One can see that there is no self-contact in those conformations.

Table 2.

Calculated physical values when b₀ = 0. In this table, N represents the number of base pairs in the DNA, w is the number of times DNA wraps around the cylindrical histone, L_k is the linking number of the entire DNA, and E is the elastic energy of the free section.

N [bp]	w	Lk	Wr	E [kcal/mol]
341	1.45	31	−1.1631	6.7813
341	1.45	32	−0.8127	6.5656
341	1.70	31	−1.5440	6.5349
341	1.70	32	−0.7031	10.9133
359	1.45	33	−1.0524	4.9821
359	1.45	34	−0.6050	8.1118
359	1.70	33	−1.4462	6.5069
359	1.70	32	−1.9324	9.1095

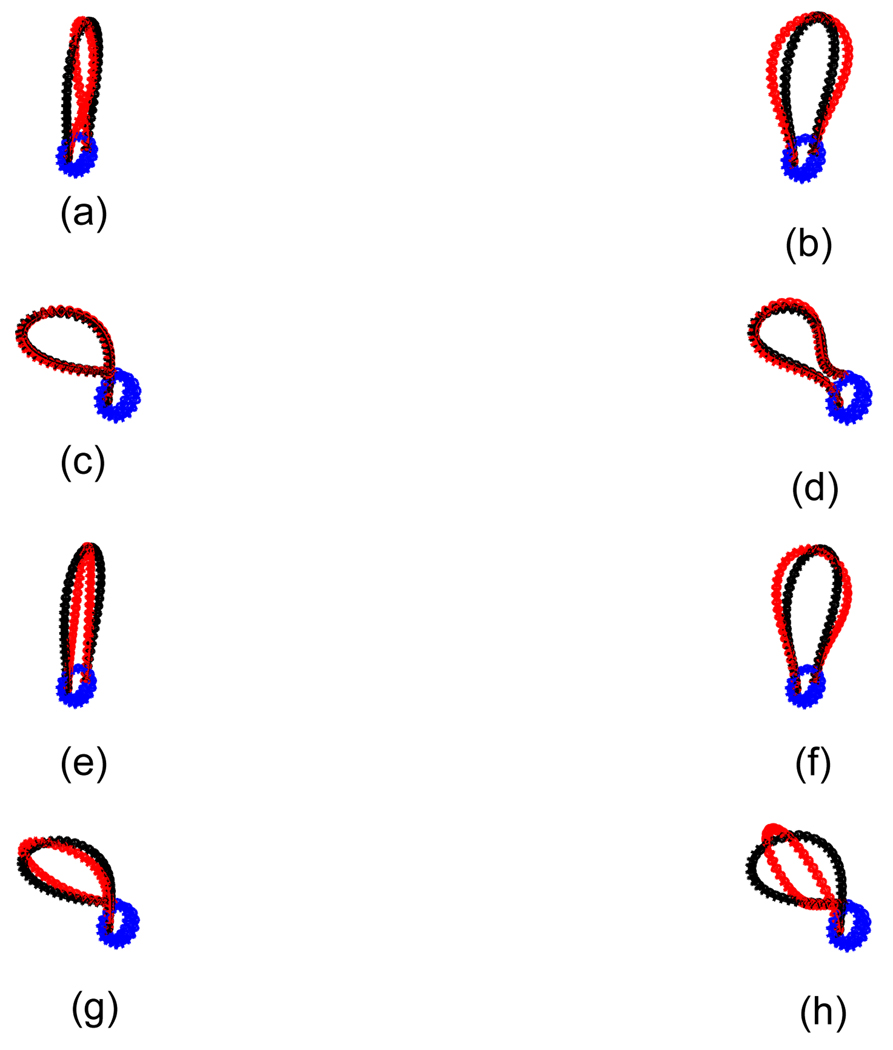
Figure 3.

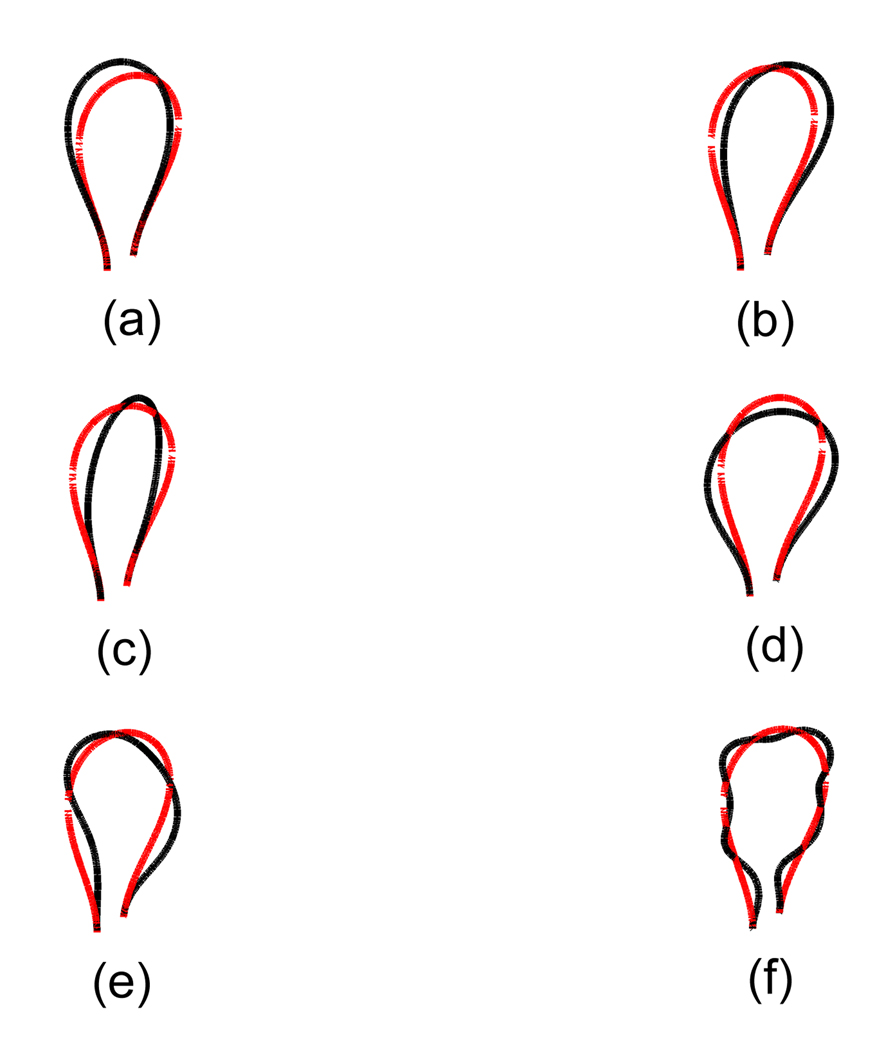
The superimposed conformations for different b₀’s. We show duplex-axis curve and double helix around the duplex-axis curve together in this figure. The light line corresponds to the case when b₀ = 0, and the heavy black line to the case when b₀ = 2.4c₀. Below, N is the number of base pairs in the DNA, w is the number of wraps of DNA around the cylindrical histone, and L_k is the linking number of the DNA. (a) N = 341, w = 1.45, L_k = 31. (b) N = 341, w = 1.45, L_k = 32. (c) N = 341, w = 1.70, L_k = 31. (d) N = 341, w = 1.70, L_k = 32. (e) N = 359, w = 1.45, L_k = 33. (f) N = 359, w = 1.45, L_k = 34. (g) N = 359, w = 1.70, L_k = 33. (h) N = 359, w = 1.70, L_k = 32. Except (c) and (d), the loop region, i.e., the free section of the DNA for each conformation when b₀ = 2.4c₀ does vary compared with the case when b₀ = 0.

As for the next numerical example, let us consider the case when b₀ is not zero. One can find the twist-bend coupling factor b₀ to have the value such that b₀ = 2.4c₀ (40). In this case the DNA is treated as an elastic rod with anisotropic and coupled stiffnesses. In such a case, unlike the isotropic rod case, the twist density along the backbone curve is not constant any more. Hence one should include this anisotropy in the determination of the free section conformation. We employ the same end constraints as described in the above isotropic cases. Then we apply our method to describe the conformations of the free section with nonzero b₀. As a result, we have generated a set of ten different conformations, including eight different ones which have the same linking numbers as in the isotropic cases. We have shown the calculated physical parameters in table 3. In figure 3 we show the conformations in both the cases when b₀ = 0 or 2.4c₀ are superimposed for eight overlapping situations. Since we include the effect of anisotropy, one can imagine that the resulting minimum energy conformations should be different from those for an isotropic case, which can be verified in figure 3, except the cases when the number of base pairs is 341 and the number of wraps is 1.70 for which isotropic and anisotropic conformations are very similar. Looking at others, one can see that the orientation of each loop is much different from the isotropic case. Hence these may explain the effect of anisotropy, which cause the difference of the resulting loop conformations between the isotropic and the anisotropic case when those loops share the same end constraints. In any case, our results together with isotropic and anisotropic cases explain the experiments that linking number 32 and 31 are dominant when the number of base pairs is 341, and 33 is dominant when the number of base pairs is 359 as the work of Swigon, et al did (2; 69).

Table 3.

Calculated physical values for b₀ = 2.4c₀. In this table, all the symbols have the same meaning as in the previous table.

N [bp]	w	Lk	Wr	E [kcal/mol]
341	1.45	31	−1.0037	5.1342
341	1.45	32	−0.9519	5.2822
341	1.70	31	−1.5268	6.5340
341	1.70	32	−0.5968	10.9784
359	1.45	33	−0.9881	4.6762
359	1.45	34	−0.9330	5.3949
359	1.70	33	−1.5257	6.1629
359	1.70	32	−1.5796	6.4107
341	1.45	33	−0.1302	10.9081
359	1.70	34	−1.4618	8.1228

Recent experimental data has been published on conformations of DNA-Histone complexes (70). In that work experiments for 11 different DNA’s were studied with lengths from 351 base pairs to 366 base pairs and wrapping numbers of either 1.40 or 1.75. The results from two relaxation experiments show that the linking number for all 11 is dominant in the range from 32 to 34. As another application of our method, we present the corresponding computational results. All assumptions, such as the HRL of the bound part and geometrical parameters, are the same as in the previous example. One difference between these simulations and the previous ones is that the numbers of wraps are now w = 1.40 and 1.75 rather than the old values of w = 1.45 and 1.70. We use these numbers because they are consistent with the most recent experimental data (70). The resulting conformations are depicted in figure 4, in which we show the superimposed conformations for the cases when b₀ = 0 and 2.4c₀ in eight different situations selected from the entire results, of which the calculated parameters such as linking number and elastic energy of the loop are shown in table 4 for the isotropic case and in table 5 for the anisotropic case. Our results show that from the minimum-energy viewpoint, in both the isotropic and anisoptropic/coupled cases, the linking numbers of 32 and 33 are dominant when the number of base pair is around 350 ~ 360 and that of 33 and 34 are dominant over 360, which is the same as the experimental results. However, as can be seen, the corresponding minimum energy conformations predicted in the isotropic case and those in the anisotropic/coupled case can be quite different.

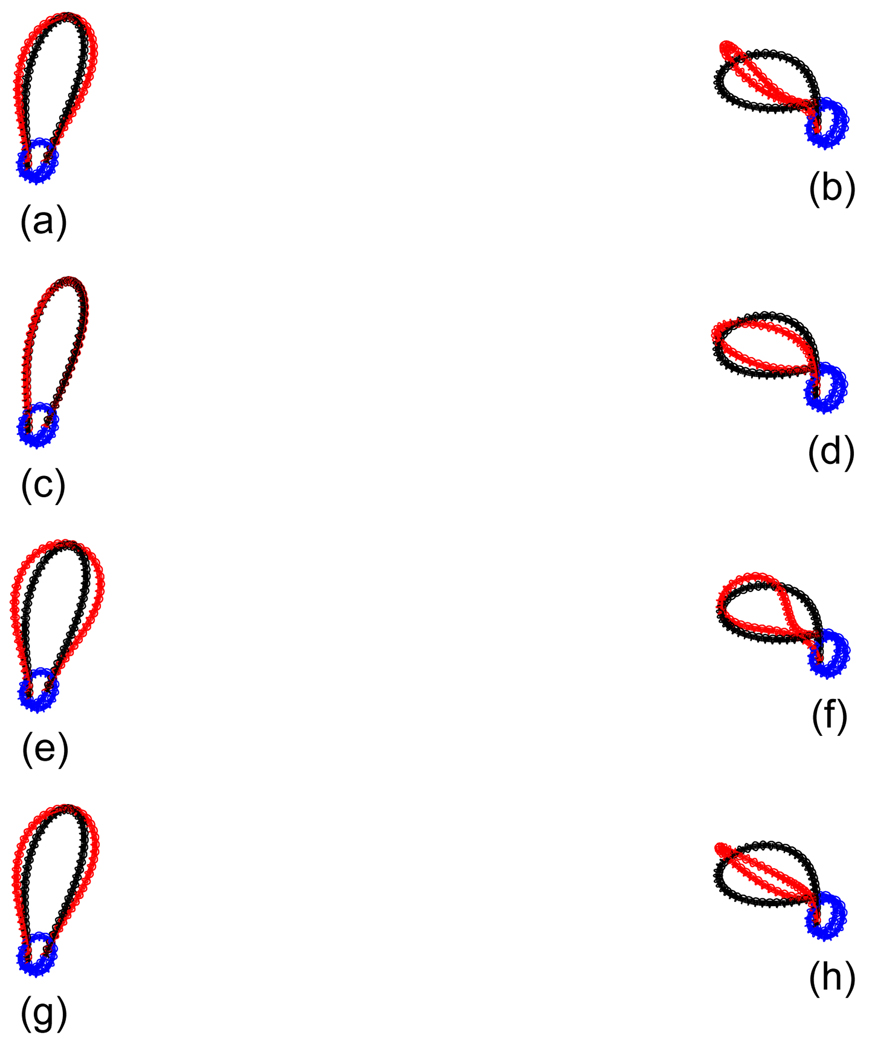
Figure 4.

The superimposed conformations for different b₀’s for the new experimental data. We show duplex-axis curve and double helix around the duplex-axis curve together in this figure. The light line corresponds to the case when b₀ = 0, and the black line to the case when b₀ = 2.4c₀. The symbols have the same meaning as in previous figures. (a) N = 353, w = 1.40, L_k = 33. (b) N = 354, w = 1.75, L_k = 33. (c) N = 356, w = 1.40, L_k = 33. (d) N = 358, w = 1.75, L_k = 33. (e) N = 361, w = 1.40, L_k = 34. (f) N = 362, w = 1.75, L_k = 34. (g) N = 363, w = 1.40, L_k = 34. (h) N = 366, w = 1.75, L_k = 34. Except (c), the loop region, i.e., the free section of the DNA for each conformation when b₀ = 2.4c₀ does vary compared with the case when b₀ = 0.

Table 4.

Calculated physical values for b₀ = 0 for the new configuration. In this table, all the symbols have the same meaning as in the previous table. We only show eight different configurations.

N [bp]	w	Lk	Wr	E [kcal/mol]
353	1.40	33	−0.8729	5.2214
354	1.75	33	−1.2559	10.4960
356	1.40	33	−0.9422	4.4306
358	1.75	33	−1.4987	7.2721
361	1.40	34	−0.7874	6.5229
362	1.75	34	−0.6601	11.5992
363	1.40	34	−0.8549	5.2834
366	1.75	34	−1.3865	8.8330

Table 5.

Calculated physical values for b₀ = 2.4c₀ for the new configuration. In this table, all the symbols have the same meaning as in the previous table. Only eight different configurations are shown.

N [bp]	w	Lk	Wr	E [kcal/mol]
353	1.40	33	−0.9381	4.6305
354	1.75	33	−1.5655	7.0435
356	1.40	33	−0.9466	4.4347
358	1.75	33	−1.5829	6.3217
361	1.40	34	−0.9289	4.7634
362	1.75	34	−1.5601	7.3264
363	1.40	34	−0.9348	4.5247
366	1.75	34	−1.5775	6.4216

Now we demonstrate how to perform normal mode analysis with one exemplary case: the case of N = 341, w = 1.45, L_k = 32 in the first numerical example. In order to perform normal mode analysis explained in Section 4, we need physical parameters related to the extensibility, as well as those used in inextensible rod model. As for the stretching stiffness and stretch-twist coupling factor, there is still some variability though one can see that those are roughly in good agreements. For the purpose of simulation, in this paper, we adopt the values published in (46) or (47) such that the extension stiffness d = 1100 [pN] and the stretch-twist coupling factor τ = 22k_BT. However, there have been no studies on determining the values of shear stiffnesses of DNA molecules. For this reason, since we model DNA as a thin elastic rod with circular cross section, we assume that the rod has 0.3 as Poisson’s ratio though this assumption is not true. Then we obtain $s_1\text{or}{s}_2=\frac{d}{2(1+\nu )}$, where ν denotes assumed Poisson’s ratio. We use the same values in the previous examples for the bending stiffness, torsional stiffness, and bending-twist coupling factor as in table 1. Another parameters necessary for this simulation is geometrical information on the circular rod. As is well known, the radius of circular cross section of DNA is 1 nm. From this, we can compute the circular cross-sectional area S = πr² and the area moment of inertia $I_{\mathit{\text{zz}}}=\frac{\pi r^4}{4}$. The last important parameter is mass density of a DNA chain. We employ data shown in (52). More specifically, total weights of all the atoms in the cylindrical section whose volume is πr²δ_s, where the spacing between adjacent base pairs δ_s = 0.34 [nm], is 1.0960 × 10⁻²⁴ [kg]. This enables us to compute uniform mass density of a DNA rod.

There is one practical issue for normal mode analysis of a DNA chain molecule. Even if we approximate a DNA molecule with a elastic rod, there should be a practical limit on the normal modes. That is to say, the smallest wavelength, equivalently the wavelength of the highest normal mode, should not be smaller than double the spacing between adjacent base pairs, 2 × δ_s. Let n_lim denotes the maximum limit of n. From our formulation, we can get 4n normal modes. Since we assume sine functions, the relation for determining n_lim should be

$$n_{\mathit{\text{lim}}}<\frac{L}{4{\delta }_s}$$

where L denotes the total length of DNA in a free section.

Since we only have minimum energy conformations by means of inextensible rod modeling, what we have is information on the angular velocity ω_E(s) along a curve. In order to apply normal mode analysis to this inextensible rod model, we assume that ${\mathit{\xi }}_E(s)=[{\mathit{\omega }}_E^T(s),0,0,1{]}^T$, because the tangent vector along a curve should be [0, 0, 1]^T due to the inextensibility. Note that we could generate very similar minimum energy conformations with extensible rod modeling. However, the fact is that ξ_E from the extensible rod model does not match exactly with $[{\mathit{\omega }}_E^T,0,0,1{]}^T$ from the inextensible rod model. Also when it comes to normal mode analysis, the knowledge of stiffness parameters may affect the determination of each mode. All these together may lead to different mode shapes and frequencies. We believe that after possessing accurate stiffness parameters regarding extensibility, we can evaluate normal modes more accurately. For now, we utilize minimum energy conformations from inextensible rod modeling. Another advantage of using the extensible rod model is that it can incorporate the sequence-dependent elastic properties by treating these stiffnesses as functions of arclength to analyze the deformation such as rise, slide, and shift as done in (53; 54; 55).

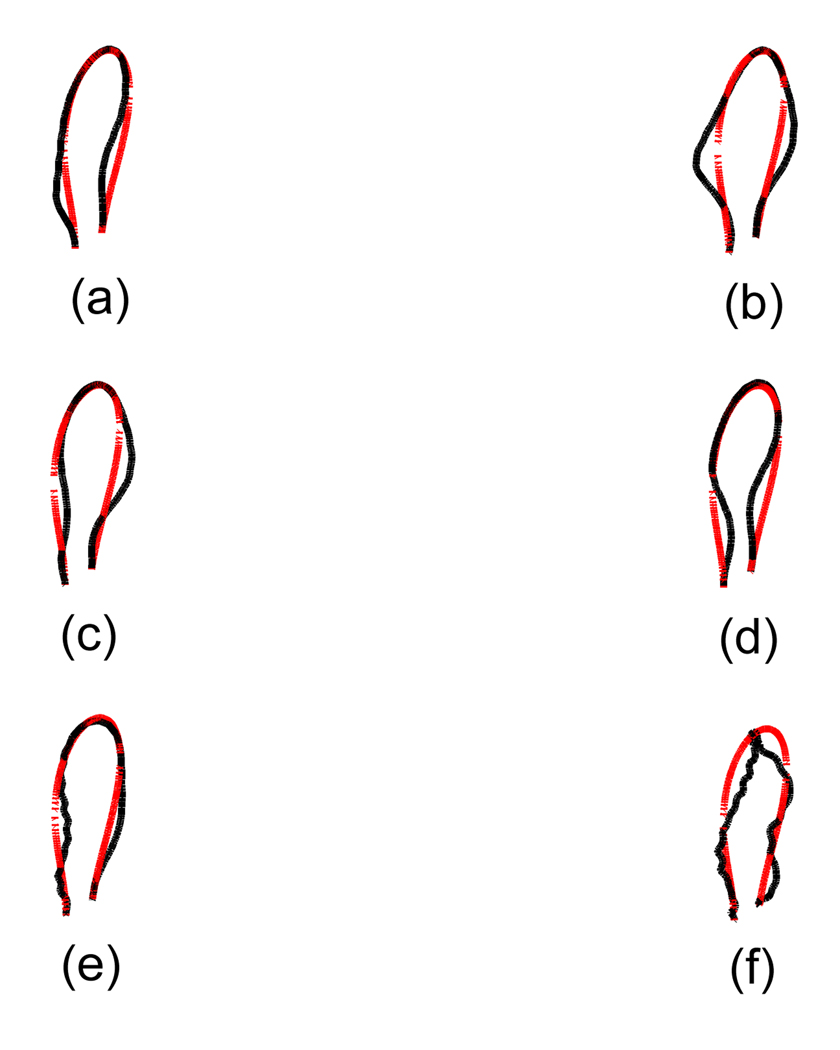
In figure 5 and 6 we show some of exaggerated normal modes in the case of isotropic and anisotropic rod modeling, respectively. Generally one can see the expected normal modes that can be inferred from non-chiral elastic rod cases, such as bending modes. However, those two cases show some differences in each normal mode shapes. First, looking at the lowest modes, the isotropic rod case has more global motions than the anisotropic rod case. A few lowest modes in the isotropic rod case are similar to swinging of a loop, whereas that in the anisotropic rod case is not. Secondly, the normal modes of an anisotropic rod exhibit more coupling between bending and twisting modes. Comparing two figures, one can see that the seventh mode of an isotropic rod is similar to the first mode of an anisotropic rod, which means that the anisotropic rod is dynamically stiffer than the isotropic rod. These are possibly due to the effect of twist-bending coupling. From this, we can infer that twist-bending coupling has an influence on the dynamical properties which shows the possibility of its existence. A better knowledge of stiffness parameters may help to reveal more accurate dynamical phenomena of chiral polymer structures.

Figure 5.

Some of exaggerated normal mode shapes when DNA is treated as an isotropic rod. (a) The first mode shape. (b) The second mode shape. (c) The third mode shape. (d) The fourth mode shape. (e) The seventh mode shape. (f) The fifteenth mode shape. The light line corresponds to the minimum energy conformation and the black line to each mode shape. We show only duplex-axis curve here.

Figure 6.

Some of exaggerated normal mode shapes when DNA is treated as an anisotropic rod. (a) The first mode shape. (b) The second mode shape. (c) The third mode shape. (d) The fourth mode shape. (e) The seventh mode shape. (f) The fifteenth mode shape. The light line corresponds to the minimum energy conformation and the black line to each mode shape. We show only duplex-axis curve here.

It is worth noting that we can make use of normal mode analysis as a criterion of whether the minimum energy conformation is truly energy-minimal one. Specifically, if some of eigenvalues are complex, then one can say that the corresponding minimum energy conformation is not a truly stable or energy-minimized one.

6 Conclusions

A method for obtaining the minimal energy conformations of semi-flexible polymers with end constraints has been presented in this paper. This method is general enough to include any stiffness and chirality parameters in the context of elastic filament models either inextensible or extensible/shearable. A variational calculus formulation is used in conjunction with concepts from the the theory of Lie groups and Lie algebras. Differential equations that describe the shapes of end-constrained polymers are derived. These equations evolve on the group of rotations and rigid-body motions. A general solution technique has also been presented, including a new “inverse kinematics” procedure for enforcing end constraints. With the minimum energy conformations determined by the aforementioned method, we have described how to perform normal mode analysis. The extensible rod model has been used for normal mode analysis. We have verified our method with appropriate numerical examples by reproducing results of others for the case of isotropic bending stiffness and no twist-bending coupling. We have also demonstrated that our method can be applied to the anisotropic model with finite twist-bending coupling. By comparing the results of anisotropic case with those of isotropic cases, we have shown that the anisotropic DNA stiffness model with twist-bending coupling may generate conformations which are different from the isotropic case. With our method, we also verified the other experimental results published. If one wants to find the equilibrium or average conformation over the entire of all possible conformations, then one could apply the methods in this paper to multiple solutions of the Euler-Poincaré equation, perform normal mode analysis on each, and weight results by an appropriate Boltzmann factor. We have also performed normal mode analysis with a specific example. We have shown that in case of treating DNA as an anisotropic chiral rod, bending modes mostly tend to be coupled with torsional modes given end constraints possibly due to the influence of twist-bending coupling. By comparing the resulting normal modes of two different cases, we have suggested that first the anisotropy of DNA structure makes its structure dynamically stiff, and there might exist twist-bending coupling in DNA structure, which has not been able to be detected experimentally. Future work includes the determination of stiffness parameters related to the extensibility, and performing normal mode analysis with minimum energy conformations describe as an extensible rod, incorporating sequence-dependent properties into the extensible rod model, etc.

A Variational Calculus on Lie Groups

The Calculus of Variations is a method that is commonly used in classical mechanics to find paths which extremize functionals subject to boundary and other conditions. In the current context the functional of interest is equation (9) for inextensible rods and equation (11) for extensible rods. If one parameterizes rotations using Euler angles, then both of these energy functions become functions of Euler angles and their rates, and classical variational calculus can be used to obtain the necessary conditions for minimum energy conformations (without accounting for contact) (71). However, the Euler angles (as well as every other three-parameter description of orientation) artificially introduce singularities in the problem. For this reason we use a coordinate-free group-theoretic modification of variational calculus. This formulation is particularly natural in the current context because the conformation of an inextensible elastic rod bears a one-to-one correspondence with a path in the rotation group SO(3), and that of an extensible elastic rod with a path in the rigid-body motion group SE(3).

The elastic energy in equation (9) is an example of a more general functional of the form

$$J={\displaystyle {\int }_{t_1}^{t_2}f(g;g^{-1}ġ;t)\mathit{\text{dt}}}$$ (38)

where g(t) is an element of a matrix Lie group G (see (64) for definition). In particular, we assume g ∈ ℝ^{N × N} and it has n generators (i.e., it is an element of an n-dimensional group represented as an N × N matrix). The identity element is the N × N identity matrix, 𝕀, and any small motion around the identity can be expressed as

$$g_{\mathit{\text{small}}}=𝕀+{\displaystyle \sum _{i=1}^n{\gamma }_i{E}_i}$$ (39)

where |γ_i| << 1 and E_i is a unit basis element of the Lie algebra 𝒢, which is also represented as an N × N matrix. For small deviations from the identity, $g_{\mathit{\text{small}}}^{-1}\approx 𝕀-{\displaystyle {\sum }_{i=1}^n{\gamma }_i{E}_i}$. Furthermore, exponentiation of any linear combination of Lie algebra basis elements results in an element of the Lie group G, and equation (39) can be viewed as the truncated version of this exponential for small values of γ_i.

Given a functional of the form equation (38), and constraint equations of the form

$${\displaystyle {\int }_{t_1}^{t_2}{h}_k(g)\mathit{\text{dt}}=C_k}$$ (40)

one can use the structure of the Lie group G and Lie algebra 𝒢 to find a natural analogue of the Euler-Lagrange equations. Only in this context, the concept of addition (which was used heavily in the previous subsection) is replaced by the group law and certain operations in the Lie algebra. In particular, the analogue of x_i → x_i + α_iε_i for i = 1, …, n in the classical variational calculus is

$$g\to g\circ \text{exp}\left({\displaystyle \sum _{i=1}^n{\alpha }_i{\epsilon }_i{E}_i}\right)\approx g\circ (𝕀+{\displaystyle \sum _{i=1}^n{\alpha }_i{\epsilon }_i{E}_i})$$

where exp(·) is the matrix exponential and g₁ ∘ g₂ is simply matrix multiplication(which will be written as g₁g₂ henceforth). The product rule of elementary Calculus then dictates that

$$ġ\to \frac{d}{\mathit{\text{dt}}}\left(g(𝕀+{\displaystyle \sum _{i=1}^n{\alpha }_i{\epsilon }_i{E}_i)}\right)=ġ(𝕀+{\displaystyle \sum _{i=1}^n{\alpha }_i{\epsilon }_i{E}_i)+g}{\displaystyle \sum _{i=1}^n{\alpha }_i{\mathrm{\epsilon ̇}}_i{E}_i.}$$

Substituting these into the functional (38) and incorporating the constraint (40) using Lagrange multipliers, the goal becomes the minimization of

$$\begin{array}{c}J\prime ({\alpha }_1,\dots ,{\alpha }_n;{\lambda }_1,\dots ,{\lambda }_m)=\\ {\displaystyle {\int }_{t_1}^{t_2}f(g(𝕀+{\displaystyle {\sum }_{i=1}^n{\alpha }_i{\epsilon }_i{E}_i});(𝕀-{\displaystyle {\sum }_{i=1}^n{\alpha }_i{\epsilon }_i{E}_i})g^{-1}(ġ+{\displaystyle {\sum }_{i=1}^n{\alpha }_i\{{\epsilon }_iġ+{\mathrm{\epsilon ̇}}_{i}g\}{E}_i});t)\mathit{\text{dt}}}\\ +{\displaystyle {\sum }_{k=1}^m{\mathrm{\lambda }}_k\left({\displaystyle {\int }_{t_1}^{t_2}{h}_k}(g(𝕀+{\displaystyle {\sum }_{i=1}^n{\alpha }_i{\epsilon }_i{E}_i});t)\mathit{\text{dt}}-C_k\right)}\end{array}$$ (41)

In analogy with classical variational calculus, we compute

$$\frac{\partial J\prime }{\partial {\alpha }_i}{|}_{{\alpha }_i=0}=0$$ (42)

and

$$\frac{\partial J\prime }{\partial {\mathrm{\lambda }}_j}=0$$ (43)

for i = 1, …, n and j = 1, …, m. Equation (43) is nothing more than equation (40).

By defining f′ = f + Σ_k λ_kh_k, one finds that the integration by parts and using the localization argument on equation (42) produces the following ordinary differential equations:

$$E_i^{R}f\prime +\left({\nabla }_{g^{-1}ġ}f\prime ,[g^{-1}ġ,E_i]\right)-\frac{d}{\mathit{\text{dt}}}\left({\nabla }_{g^{-1}ġ}f\prime ,E_i\right)=0$$ (44)

where for any function F ∈ C^∞(G)

$$E_i^{R}F(g)\triangleq \frac{d}{\mathit{\text{dt}}}F(g\circ \text{exp}({\mathit{\text{tE}}}_i)){|}_{t=0}$$ (45)

is the ‘right’ derivative of F with respect to the i^th Lie algebra basis element. [·, ·] is the Lie bracket (which in this case is the matrix commutator [A, B] = AB − BA). ∇_X is a directional derivative in the Lie algebra in the direction X ∈ 𝒢. And (·, ·) is the inner product for the Lie algebra 𝒢 such that (E_i, E_j) = δ_ij.

By observing that for any Lie group (not only SO(3) or SE(3)) we can define ξ = (g⁻¹ġ)^∨, then

$$\begin{array}{c}[g^{-1}ġ,E_i]=\left[{\displaystyle \sum _{j=1}^n{\xi }_j{E}_j,E_i}\right]={\displaystyle \sum _{j=1}^n{\xi }_j[E_j,E_i]=}{\displaystyle \sum _{j=1}^n{\xi }_j\left(-{\displaystyle \sum _{k=1}^n{C}_{\mathit{\text{ij}}}^k{E}_k}\right),}\\ ({\nabla }_{g^{-1}ġ}f,E_i)=\left({\displaystyle \sum _{j=1}^n\frac{\partial f}{\partial {\xi }_j}{E}_j,E_i}\right)={\displaystyle \sum _{j=1}^n\frac{\partial f}{\partial {\xi }_j}(E_j,E_i})=\frac{\partial f}{\partial {\xi }_i},\end{array}$$

and

$$\begin{array}{cc}({\nabla }_{g^{-1}ġ}f,[g^{-1}ġ,E_i])\hfill & =\left({\displaystyle \sum _{l=1}^n\frac{\partial f}{\partial {\xi }_l}{E}_l,-}{\displaystyle \sum _{j,k=1}^n{\xi }_j{C}_{\mathit{\text{ij}}}^k{E}_k}\right)\hfill \\ \hfill & =-{\displaystyle \sum _{j,k,l=1}^n\frac{\partial f}{\partial {\xi }_l}{C}_{\mathit{\text{ij}}}^k{\xi }_j(E_l,E_k)}\hfill \\ \hfill & =-{\displaystyle \sum _{j,k=1}^n\frac{\partial f}{\partial {\xi }_k}{C}_{\mathit{\text{ij}}}^k{\xi }_j.}\hfill \end{array}$$

Equation (44) can then be written in terms of the functions f and h_k as

$$\frac{d}{\mathit{\text{dt}}}(\frac{\partial f}{\partial {\xi }_i})+{\displaystyle \sum _{j,k=1}^n\frac{\partial f}{\partial {\xi }_k}{C}_{\mathit{\text{ij}}}^k{\xi }_j=E_i^R(f+{\displaystyle \sum _{l=1}^m{\mathrm{\lambda }}_l{h}_l})}$$ (46)

This is a modified version of the Euler-Poincaré equation (57; 58; 72; 73; 74).