Abstract
Homeostatic mechanisms are essential for the protection and adaptation of organisms in a changing and challenging environment. Previously, we have described molecular mechanisms that lead to robust homeostasis/adaptation under inflow or outflow perturbations. Here we report that harmonic oscillations occur in models of such homeostatic controllers and that a close relationship exists between the control of the p53/Mdm2 system and that of a homeostatic inflow controller. This homeostatic control model of the p53 system provides an explanation why large fluctuations in the amplitude of p53/Mdm2 oscillations may arise as part of the homeostatic regulation of p53 by Mdm2 under DNA-damaging conditions. In the presence of DNA damage p53 is upregulated, but is subject to a tight control by Mdm2 and other factors to avoid a premature apoptotic response of the cell at low DNA damage levels. One of the regulatory steps is the Mdm2-mediated degradation of p53 by the proteasome. Oscillations in the p53/Mdm2 system are considered to be part of a mechanism by which a cell decides between cell cycle arrest/DNA repair and apoptosis. In the homeostatic inflow control model, harmonic oscillations in p53/Mdm2 levels arise when the binding strength of p53 to degradation complexes increases. Due to the harmonic character of the oscillations rapid fluctuating noise can lead, as experimentally observed, to large variations in the amplitude of the oscillation but not in their period, a behavior which has been difficult to simulate by deterministic limit-cycle models. In conclusion, the oscillatory response of homeostatic controllers may provide new insights into the origin and role of oscillations observed in homeostatically controlled molecular networks.
Introduction
Mechanisms that maintain robust homeostasis in genetic and biochemical networks are essential for the fitness of organisms in a changing and challenging environment (1). Many physiologically important variables are under tight homeostatic control, where internal concentrations or fluxes are maintained at well-defined levels despite environmental perturbations. Such perfect adaptation/homeostasis (2) has been found, for example, in bacterial chemotaxis (3–6), photoreceptor responses (7), and MAP-kinase regulation (8–10). Drengstig et al. (11) have recently shown how perfect adaptation motifs may be identified in reaction kinetic networks.
Although perfect homeostasis can be related to the control-theoretic concepts of integral feedback or integral control (12,13), it has recently been shown that, in reaction kinetic terms, perfect homeostasis is closely connected to the presence of a zero-order flux (14), which controls another controlling agent (i.e., control of the controller). The latter is responsible for the removal or synthesis of a homeostatically regulated intermediate. Fig. 1 shows two controller motifs from Ni et al. (14), in which intermediate A is homeostatically regulated. Fig. 1 a presents an inflow controller, where the control mechanism can compensate for large in-flow perturbations of A, and Fig. 1 b presents an outflow-controller, where A shows homeostasis when A is subject to large fluctuations in its removal. It should be noted that these control schemes will generally fail, when large outflows occur in inflow controllers or large inflows occur in outflow controllers (14).
Figure 1.

Schemes of inflow (a) and outflow (b) homeostatic controllers in which component A shows robust homeostasis against environmentally uncontrolled perturbations in the inflow and outflow of A (14). Eadapt represents an enzyme important in the adaptation/homeostasis of A, Etr represents one or several enzymes important in transforming/removing A, and ksynth is a rate constant associated with the synthesis of A. Thick solid arrows with kpert indicate where in the controller inflow or outflow perturbations occur. For a more detailed discussion of these schemes, see Ni et al. (14).
Here, we demonstrate that the two homeostatic controllers in Fig. 1 can show damped or practically undamped large amplitude harmonic oscillations. The degree of damping depends on the binding characteristics between the controller Eadapt and A, as well as on the synthesis and removal of the homeostatically controlled intermediate A. To our knowledge, this is the first example that describes large amplitude harmonic oscillations in a biochemical oscillator model (see the recent review on design principles of biochemical oscillators (15)).
Interestingly, the controller in Fig. 1 a shows high similarity to the feedback control of p53 by Mdm2, when A is taken as p53, Eadapt as Mdm2, and Etr as the class of Mdm2-independent proteasomal degradation reactions of p53 (16–21). In the presence of DNA damage, p53 is upregulated by slowing down its various degradation reactions, but still requires a tight control to avoid premature apoptosis by high levels of p53 (22,23). We propose the idea that this control is mediated by Mdm2 and related factors by means of a homeostatic inflow mechanism, which maintains a level of p53 in a state of indecisiveness, until a final decision between cell cycle arrest/DNA repair and apoptosis is made (24). Oscillations in p53/Mdm2 (25,26) may participate in making this decision. In the proposed inflow model, harmonic oscillations in p53 and Mdm2 can occur when p53 binds strongly to the Mdm2-induced degradation machinery, where p53 oscillates around the level defined by the homeostatic controller. Due to the harmonic character of the oscillation, rapid molecular noise leads to large variations in the p53/Mdm2 amplitude whereas the period is only little affected—a behavior that has been experimentally observed (27) but which is difficult to reproduce by deterministic limit-cycle models (27,28). Large fluctuating amplitudes in the p53/Mdm2 oscillations seem to be of importance in determining cell fate (26,27), as will be discussed in more detail below. Thus, a homeostatic inflow model provides an integrative view on the negative feedback regulation of p53 and the appearance of oscillations. Such a view may also provide new insights into the origin and role of oscillations observed in homeostatically controlled molecular networks.
Harmonic oscillations in perfect controllers
A possible kinetic representation for the inflow-controller scheme of Fig. 1 a can be given by
| (1) |
| (2) |
where with and Eitot is the turnover number and total concentration of enzyme species i, respectively. The n is the reaction order with respect to A in the removal of A by Eadapt. With respect to the discussion that will follow below, it may be noted that zero-order kinetics with respect to A (n = 0 in Eq. 1) may be obtained by
| (3) |
when . In terms of a rapid equilibrium model of the Michaelis-Menten equation, small values can be interpreted as a strong affinity between substrate A and Eadapt.
The set-point for homeostatic regulation in A is determined by setting Eq. 2 to zero and demanding that the controller Eadapt is removed by another control species (Eset) under zero-order conditions. This requires that , which gives the homeostatic set-point Aset for A at steady-state conditions (14):
| (4) |
A is robustly regulated as long as the right-hand term of Eq. 4 remains practically constant and as long the degradation in A is not dominating with respect to the influxes kpert and ksynth. In Eq. 2, the removal of Eadapt by Eset using Michaelis-Menten kinetics also ensures that, even at low values, Eadapt does not become negative, as it sometimes would if the Aset term were to be replaced by a true constant (14).
An interesting aspect is that oscillations emerge in the controller when the reaction order becomes zero with respect to A. Fig. 2 illustrates this behavior by applying a stepwise change in kpert (from 1.0 to 2.0) when the system is initially at a steady state at first and zero reaction orders with respect to A. By using the rate constant values described in Fig. 2 such that the term in Eq. 1 can be neglected and assuming zero-order kinetics with respect to A, we can approximate Eqs. 1 and 2 by Eq. 5,
| (5) |
which leads to undamped harmonic oscillations in A and Eadapt with a period length P = 2π/(k · kadapt).
Figure 2.

Generation of harmonic oscillations for the homeostatic controller in Fig. 1a by decreasing reaction order n with respect to A. Rate constant values are kpert = 1.0, kadapt = 3.0, , , , , and with Aset = 1.0. The reaction orders n with respect to A are (a) 1.0; (b) 1 × 10−1; (c) 1 × 10−2; and (d) 0.0. At time t = 10.0 a.u., kpert is increased from 1.0 to 2.0 and the system approaches a new steady state. Note that A shows robust homeostasis with Aset = 1.0. With decreasing n values harmonic oscillations are emerging where A oscillates around Aset with a peak amplitude approaching Aset as n approaches zero.
A kinetic representation of the outflow control scheme of Fig. 1 b can be described as
| (6) |
| (7) |
In this formulation, the controller shows an oscillatory response in A and Eadapt for moderate ksynth values and for low values in and , i.e., having a zero-order degradation of A in Eq. 6 and a first-order degradation rate of Eadapt with respect to A in Eq. 7. In the following we will focus on the inflow controller scheme of Fig. 1 a as a simple model for the p53 regulatory system and its oscillatory behavior.
Regulation of p53
The p53 system is one of the most complex regulatory networks known (22,24,29–35). It is involved in the control of cell cycle, senescence, DNA repair, apoptosis, and the prevention of tumor development. More than half of all human tumors contain mutations of the p53 gene and in almost all tumors the p53 regulatory circuit is nonfunctional (31,32). Normally (i.e., in the absence of DNA damaging conditions), p53 levels are low due to a rapid degradation by ubiquitin-dependent and ubiquitin-independent pathways with an approximate p53 half-life between 6 and 30 min (16–21,36,37). An important regulator of p53 is Mdm2, an E3 (ubiquitin) ligase for p53 and other tumor suppressors (38,39). p53 activates the transcription of Mdm2, which binds p53 (40), ubiquitinates it, and thus initiates the proteasomal degradation of p53 both in the nucleus and cytosol (41). This is the central autoregulatory (negative) feedback loop of p53 (29,32). In the presence of DNA damage or oxidative stress, p53 is upregulated by several mechanisms that inhibit Mdm2 activity (42), increase Mdm2 autodegradation (43), and inhibit p53 degradation (44,45). This leads either to cell cycle arrest and DNA repair at lower DNA damage, or to the induction of programmed cell death (apoptosis) at higher DNA damage (24,46,47).
Interestingly, in the presence of high DNA damage, p53 and Mdm2 have been found to oscillate (25–27,48–50). The origin and purpose of these oscillations is little understood, but may be of considerable interest (26,50,51).
We became interested in the feedback regulation of the p53/Mdm2 system and its oscillatory response because it shows a close analogy to the inflow homeostatic control scheme shown in Fig. 1 a with A ≡ p53 and Eadapt ≡ Mdm2. The control scheme suggests that, under DNA-damaging conditions, p53 is homeostatically regulated to a certain upper level defined by Mdm2 (and other factors), at which it decides on the essential cellular functions mentioned above. This view is supported by the fact that transgenic mice, which lack both Mdm2 and p53, grow up normally, whereas mice lacking only Mdm2 die as embryos, possibly due to the uncontrolled apoptotic activity of p53 (22,23).
Once p53 is regulated to a high level, harmonic oscillations can occur when p53 binds strongly to ternary or multiprotein complexes/scaffolds containing Mdm2 (52–54), which are involved in the (proteasomal) degradation of p53. In the presence of rapidly fluctuating molecular noise, the harmonic character of the p53/Mdm2 oscillations leads to a large variability in their amplitudes but not in their frequency, as will be shown below. This property is difficult to simulate by limit cycle models (28). At normal conditions, i.e., in the absence of DNA damage, p53 is rapidly degraded by ubiquitin-dependent and ubiquitin-independent processes, keeping p53 levels well below its upper limits.
Fig. 3 a shows an outline of a simple inflow regulatory circuit for the p53-Mdm2 system. A kinetic representation of this model can be given by the following equations:
| (8) |
| (9) |
| (10) |
| (11) |
Figure 3.

(a) The p53-Mdm2 negative feedback system as a homeostatic inflow control model. Reactions outlined in black occur in the absence of DNA damage. Under latter conditions, p53 is considered to be rapidly removed through Mdm2 and through Mdm2-independent proteasomal degradation. The Mdm2-independent degradation processes are represented in the model by Ed with Michaelis-Menten parameters and . EsetMdm2 is an enzyme or a class of enzymes involved in the degradation of Mdm2. When this degradation becomes zero-order with respect to Mdm2, then p53 shows robust homeostatic regulation to the set-point p53set = . However, due to rapid p53 degradation at normal conditions, p53 levels are well below p53set. In the presence of DNA damage the degradation of p53 is slowed down and p53 is stabilized. One of the stabilizing mechanisms involve upregulation of NQO1 (16,19,20). Due to the zero-order degradation of Mdm2 by EsetMdm2, p53 levels are limited by the set-value p53set (see Fig. 4, a and b). When the removal of p53 induced by Mdm2 becomes zero-order with respect to p53, harmonic oscillations in p53 and Mdm2 are generated (see Fig. 4, c and d). p53∗ and Mdm2∗ represent posttranslational modification species of p53 and Mdm2, respectively. There is evidence that the modified forms p53∗ and Mdm2∗ do interact much less (30,35). In the model, p53∗ and Mdm2∗ are assumed to be in rapid equilibrium with p53 and Mdm2, respectively. (b) Molecular mechanism in the Mdm2-mediated degradation which can lead to zero-order kinetics with respect to p53 and first-order kinetics with respect to Mdm2. p53 and Mdm2 bind to a protein complex/scaffold C, which leads to the ubiquitination and degradation in p53. A strong binding of p53 to the complex (small KA and KBA values) lead to zero-order kinetics with respect to p53, whereas a relative weak binding of Mdm2 lead to first-order kinetics with respect to Mdm2. For details, see main text and the Supporting Material.
The Mdm2-mediated degradation term in Eq. 8 is based on a rapid equilibrium among p53, Mdm2, and a protein complex/scaffold C as illustrated in Fig. 3 b (and described in more detail in the Supporting Material). C0 denotes the total concentration of C, and KA, KB, KAB, and KBA are dissociation (KM) constants. Due to the “Principle of Detailed Balance” (55), we have KA · KAB = KB · KBA. Low values in the Ki values indicate strong binding and stable complexes. Zero-order kinetics in p53 can be achieved by low KA and KBA values, whereas first-order kinetics with respect to Mdm2 is obtained for relative large KAB values. Applying these conditions, we get
| (12) |
In Fig. 3 a, the outline in black shows the functioning of the system in the absence of DNA damage. p53 is held at low levels due to degradation through a Mdm2-mediated ubiquitin-dependence and Mdm2-independent proteasomal degradations (16–20,36,37).
Under DNA-damaging conditions, p53 is upregulated and posttranslationally modified. One of the processes that lead to an increase in p53 is the Mdm2-independent upregulation of NADH quinone oxidoreductase 1 (NQO1) (16). NQO1 binds to p53 and thereby stabilizes it (56). Both p53 and Mdm2 undergo posttranslational modifications (22,57), where phosphorylated and acetylated forms are indicated in the model by p53∗ and Mdm2∗. These forms interact much less than unmodified forms of Mdm2 and p53 and thus cause a stabilization of p53. Due to the decrease in the Mdm2-independent degradation of p53 under DNA damaging conditions but due to the presence of the (still operative) zero-order kinetic degradation of unmodified p53 by unmodified Mdm2, harmonic oscillations of p53 and Mdm2 are initiated, and subsequently propagated to the posttranslationally modified forms p53∗ and Mdm2∗. In addition, MdmX has been shown to bind to both Mdm2 and p53, which stabilizes each of these species (58). In our model, the stabilization of Mdm2 and p53 by MdmX is lumped together with the formation of the Mdm2∗ and p53∗ species. However, it should be noted that MdmX is also present in undamaged cells and considered to maintain transcriptionally inactive p53 in the nucleus of these cells (58).
Fig. 4 shows concentration profiles for p53 and Mdm2 using the model Eqs. 8–11 with decreasing rates in the ubiquitin-independent degradation of p53 when the Mdm2-mediated degradation of p53 is zero-order with respect to p53. Large degradation rates in p53 through Ed lead to p53 levels well below p53set (Fig. 4 a),
| (13) |
whereas p53 levels become homeostatically regulated when the Ed-induced degradation becomes sufficiently low (Fig. 4 b). At even lower Ed-mediated degradation of p53, damped oscillations appear (Fig. 4 c), where p53 oscillates around p53set with a peak amplitude, which (in the absence of noise) cannot exceed p53set (Fig. 4 d).
Figure 4.
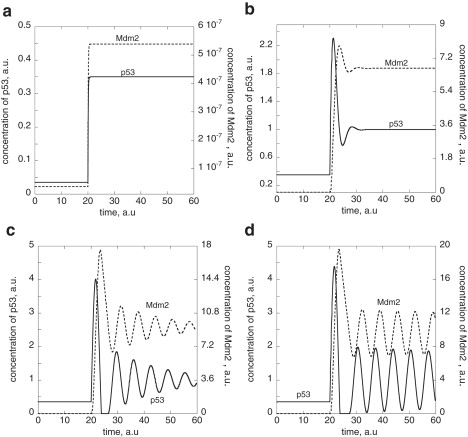
Generation of harmonic oscillations for the homeostatic inflow controller of the p53-Mdm2 system by upregulating p53, i.e., by successively decreasing the value of the Mdm2-independent degradation of p53 (see Fig. 3 and Eqs. 8–11). Rate constant values (in a.u.) are as follows: ksp53 = 3.5, KA · KAB = 1.0 × 10−4, KAB = 1.0 × 102, KBA = 1.0 × 10−7, k′ · C0 = 40.0, ksMdm2 = 3.0, , , , krp53lowast; = 50.0, kdp53lowast; = 0.0, krMdm2lowast; = 1.0 × 102, kdMdm2lowast; = 0.0, Eset,totMdm2 = 5.0 × 10−7, Ed,tot = 0.1, and p53set = 1.0. (a) High values of lead to p53 steady-state values well below its homeostatic set-value p53set. At t = 20 time units is decreased from 1.0 × 107 to 1.0 × 106 with ksp53lowast; = ksMdm2lowast; = 0.0, which leads to an increase in the p53 and Mdm2 steady-state levels. (b) At t = 20 time units, is decreased from 1.0 × 106 to 1.0 × 105 with ksp53lowast; = ksMdm2lowast; = 0.1. Note that p53 attains now its homeostatic regulated set-value. (c) At t = 20 time units, is decreased from 1.0 × 106 to 1.0 × 104 with ksp53lowast; = ksMdm2lowast; = 0.5. Damped harmonic oscillations in p53 start to emerge around the homeostatic set-value. (d) At t = 20 time units, is decreased from 1.0 × 106 to 1.0 × 102 with ksp53lowast; = ksMdm2lowast; = 1.0. Much less damped harmonic oscillations in p53, p53∗, Mdm2, and Mdm2∗ are generated (data for p53∗ and Mdm2∗ not shown).
Amplitude/frequency behavior and influence of noise
The damping of the oscillations given by Eqs. 8–11 depends on several parameters. A strong damping or no oscillatory response is observed when p53 or the posttranslationally modified species Mdm2∗ or p53∗ are rapidly degraded, i.e., when rate constants , , or are large compared to the influx of p53. On the other hand, sustained oscillations are observed when , , or are much lower than the influx of p53 into the controller. When and are zero, the system oscillates with the period 2π/(k · ksMdm2). When , and are nonzero, sustained oscillations are also observed when and are zero and a rapid equilibrium between p53∗ and p53 as well as Mdm2∗ and Mdm2 is established. The period increases as the rapid equilibrium is shifted more to the p53∗ and/or Mdm2∗ side. If the equilibrium between posttranslationally modified p53∗/Mdm2∗ and unmodified p53/Mdm2 is slow compared with the influx of p53, oscillations become damped.
Fig. 5 shows trajectories of (practically) undamped oscillations in the p53-Mdm2 phase plane with different initial concentrations. Because the system is harmonic (conservative), no limit cycle is observed, but parallel trajectories emerge. In the case in which the trajectories reach the ordinate (Mdm2 axis when p53 = 0), Mdm2 concentrations decrease until an oscillator with maximum peak amplitude equal to the p53 set-value emerges (trajectory 5 in Fig. 5). One may consider such a behavior as a filtering of large excursions in p53 down to a maximum peak level determined by p53set.
Figure 5.
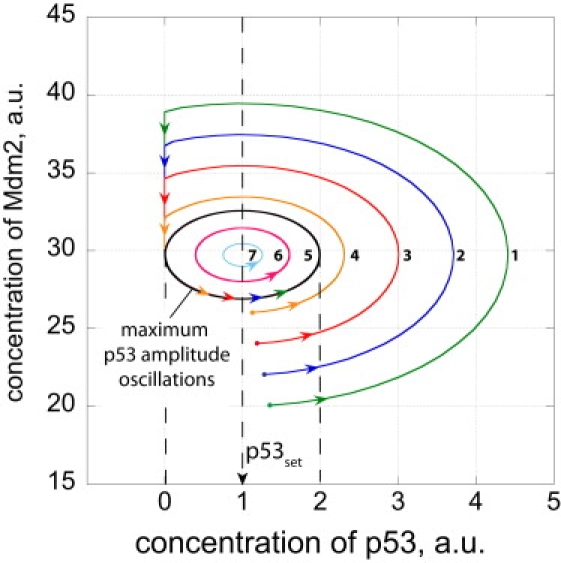
Phase plane trajectories of p53-Mdm2 harmonic oscillations going through three cycles. Rate constants as described in the legend of Fig. 4. To illustrate that ksp53 can be chosen without affecting the p53 oscillations around p53set, ksp53 was set to 11.0, and . For the sake of simplicity, all ks,r,dp53lowast; and ks,r,dMdm2lowast; rate constants are set to zero. Dots show different p53 and Mdm2 start concentrations. Because the system is conservative, parallel trajectories 1–7 emerge from each of the starting points. Trajectories 1–4 which lie outside of trajectory 5 (which is tangenting the ordinate at p53 = 0) will hit the ordinate at low p53 levels and Mdm2 concentrations will decrease until the system emerges as trajectory 5 oscillations, which have the largest peak amplitude equal to the p53 set-value. Trajectories 6 and 7 which start inside of trajectory 5 will not be altered, and the system oscillates with peak amplitudes lower than the p53 set-value.
The period is not affected by the remaining rate constants. Note that needs to be sufficiently small and needs to be sufficiently large to get oscillations, but the period of the oscillations is not dependent on those values.
Due to the large amplitude variations found for experimentally recorded p53/Mdm2 oscillations (27), we became interested in the effect of fluctuations on the model. For this purpose, rate parameters were allowed to vary randomly and rapidly within a certain range by using the Fortran routine RAN1 (59). Fig. 6, a and b, shows the variations in ksp53 and as a function of time (see Supporting Material for an overview of all rate parameter variations). Fig. 6 c shows the behavior of the model compared to experimental data (Fig. 6 d). The computations show, in agreement with the experimental observations, that the amplitude of the oscillations is subject to considerable variation, whereas the period and the phase relationship between p53 and Mdm2 are little affected. However, it should be noted that changes in the average values of k (Eq. 12) or ksMdm2 will lead to period changes, because these two parameters determine period length (compare with Eq. 5).
Figure 6.

Rapid fluctuations in rate parameters lead to variations in the amplitude of the p53/Mdm2 oscillations, but preserve their period. For the sake of simplicity, all ks, r,dp53lowast; and ks,r,dMdm2lowast; rate constants are set to zero. (a and b) Variations for ksp53 and , respectively; see also Supporting Material. (c) Resulting oscillations in p53 and Mdm2 levels when applying rapid fluctuations for all rate parameters within the ranges indicated by Table S1 in the Supporting Material. Rate constant values of k and ksMdm2 have been adjusted such that the period of the harmonic unperturbed oscillations is close to the experimental value of 5.5 h (27). (d) Observed p53 (solid line) and Mdm2 (dashed line) oscillations in single cells. (Replotted from upper left of Fig. 1B in Geva-Zatorsky et al. (27).)
Discussion
p53 regulation: comparison with experiments
The homeostatic inflow model suggests the need for p53-regulation to avoid unregulated large p53 levels that would lead to premature apoptosis. An intriguing aspect of the p53-Mdm2 regulatory system is the occurrence of oscillations. There are two major requirements to get oscillations in the homeostatic inflow model:
-
1.
The need for a relatively strong binding between p53 and the controller (Mdm2); and
-
2.
That the degradation of p53 by Mdm2-independent processes (represented in the model by the Ed degradation pathway) should be low compared to the removal of newly synthesized p53 by Mdm2 (Eq. 8).
With respect to the first requirement, binding studies have shown that Mdm2 and p53 can interact by their N-terminal domains or by Mdm2‘s acid domain and p53's core domain (40). The latter binding site appears to be essential for the ubiquitination of p53 and its degradation. Ma et al. (60) estimated the dissociation constant (Kd) of this binding site as well as the KM value of p53 from ubiquitination kinetics. They concluded that there is a relative high affinity (<1 μM) between Mdm2 and p53 for this binding site, supporting the requirement by the homeostatic inflow model. Ma et al. further conclude that although the individual peptides derived from the acidic and zinc-finger domain of Mdm2 show a weak affinity toward p53 (40), there may be multiple contacts to form a specific site with higher affinity in binding to p53 within the central domain of Mdm2. With respect to the model's second requirement, experiments have shown that p53 becomes stabilized by a decrease in the Mdm2 stability (43) and by inhibiting Mdm2-independent degradation pathways (16–21,36,37). Although in the model oscillations with little damping can be observed when is decreased to 102 a.u. (Fig. 4), can practically be set to zero without significantly altering the oscillations, as long as there is some synthesis in p53.
The other parameters can be varied within a wide range during which oscillations can still be observed, and rate constant values (with timescales in hours, Fig. 6, a–c) can reflect observed half-lives for p53 and Mdm2 (43,61).
For getting p53 to be homeostatically controlled, Mdm2 (or other p53-degrading factors which constitute a negative feedback loop with p53) need to be removed by zero-order kinetics, i.e., at the maximum enzymatic activity for Mdm2 removal (14). It may be that accelerated MDM2 autodegradation (43) is a mechanism to reach maximum (zero-order) Mdm2 degradation and thus p53 homeostasis.
Due to the harmonic character of the model's oscillations, the phase difference between p53 and Mdm2 is given by the relationship π/2: 2π = ϕ: P, where P is the period of the harmonic oscillator in the absence of posttranslational modifications. With an average experimental period of ∼6 h (27), the calculated phase difference is ∼1.5 h, which is in good agreement with the experimentally determined value of 2h ± 0.5h (27). The period length P is dependent on two rate constants by P = 2π/(k · kadapt). This relationship is a good approximation. In the presence of posttranslational modifications of p53 and Mdm2, the period increases with increasing amounts of p53∗ and Mdm2∗. Assuming rapid equilibria between p53∗/Mdm2∗ and the respective unmodified forms p53/Mdm2, in the harmonic limit kadapt is multiplied by a factor , with , whereas k is multiplied with a corresponding factor with . Thus, in this representation of the p53 regulation the period of the oscillations should change when the ratio between posttranslationally modified p53/Mdm2 is altered. The model also implies that the source of oscillations is the presence of unmodified p53 and Mdm2, probably due to an undisturbed synthesis (22).
Geva-Zatorsky et al. (27) reported that not all cells show oscillations but that the fraction of oscillatory cells increase as the dose of the γ-irradiation increases. Our model suggests that with increasing dose of γ-irradiation and the subsequent lowering of the Mdm2-independent degradation of p53, oscillations appear when the Mdm2-induced removal of p53 is zero-order, with respect to p53. The damping of the oscillations is determined by several factors including the strength of p53-binding to the p53-degrading protein-complexes or scaffolds. When this binding is weak, our model predicts strong damping in the p53/Mdm2 oscillations, whereas the oscillations should become less damped when the binding to the p53-degrading protein complexes is strong. Other factors leading to damping or loss of the oscillations is a high (Mdm2-independent) p53 degradation rate and the accumulation of excess posttranslationally modified p53.
Significance of zero-order kinetics
Zero-order kinetics appear to be significant in several respects. In robust homeostatic controllers, zero-order fluxes define the set-values of (homeostatically) controlled variables (14), i.e., define the integral feedback (13) necessary for robust control. In the model presented here, zero-order flux in the degradation of Mdm2 suggests that p53 may be subject to robust control, such that its concentration is not able to exceed an upper boundary limit. This limit (p53set, Eq. 13) is reached in the presence of DNA damage when the Mdm2-independent degradation reaction of p53 (16–21) is inhibited or slowed down by mechanisms still not well understood (Fig. 3). When, in addition to this upregulation of p53, the p53 reaction order in the Mdm2-mediated removal of p53 is zero due to a strong binding of p53 to its degradation complex, harmonic oscillations appear, whose peak amplitude is determined by p53set (Fig. 5). Due to the harmonic character of the oscillations, the amplitude of the p53/Mdm2 oscillations is quite sensitive to rapid perturbations/fluctuations similar to experimental observations (Fig. 6).
Biological significance
Do the oscillations and the large variability in the p53/Mdm2 amplitudes serve a purpose? One possibility may be that the oscillations represent a counting mechanism by which decisions are made whether DNA repair should be enhanced or apoptosis should be initiated (62). A higher number of cycles would favor apoptosis because higher p53 activity/concentration activates pro-apoptotic genes (63). A periodic activation of these genes may have the advantage of lowering inhibition actions at the promoter site or elsewhere—compared to continuous activation (64). This can be associated with a significant decrease in the threshold level of radiation at which the decision from pro-survival to pro-apoptotic state occurs (51). To make such a decision as unbiased as possible, the large variability in the p53 amplitudes seem to indicate that such fluctuations play a role in the p53 decision between “life and death” (46). Another possibility discussed for the role of oscillations is a longer maintenance of indecisiveness for a better evaluation of the pros and cons of a decision (26).
Besides defining the set-values of homeostatically controlled variables (14), zero-order reactions are also key elements in ultrasensitive switches (65–67). Although we have not considered such switches explicitly here, it is intriguing that zero-order kinetics can lead to such diverse behaviors ranging from ultrasensitive switches, relating homeostatic threshold values to oscillatory responses. It will be interesting to combine such regulatory motifs in regulatory models of biological networks.
Comparison with other models
Due to the importance of p53 in the control of DNA integrity, cell cycle arrest, and apoptosis, as well as its relevance for cancer research (48,49), a variety of models for the negative feedback control of p53 by Mdm2 and its oscillatory responses have been proposed (27,68–75). In contrast to the model presented here which shows harmonic oscillations, other models (27,68,70–74) are based on deterministic limit cycle oscillations. Several additional oscillator classes have recently been analyzed by Geva-Zatorsky et al. (27) and Zhang et al. (70). The model presented here is based on a homeostatic inflow control mechanism (14) when p53 becomes upregulated. This inflow controller can show harmonic oscillations, which are suppressed when p53 is normally at low levels due to several degradation mechanisms (16–21,36,37). Concerning the observed oscillations in the inflow controller, we are not aware of any molecular mechanism that has been shown to exhibit large amplitude harmonic oscillations. It may also be noted that the rapidly fluctuating molecular noise applied on rate parameters by RAN1 (Fig. 6, a and b, and Supporting Material) has practically an infinite period (59) and leads to large variations in the amplitude of the p53/Mdm2 oscillation (Fig. 6 c) in close agreement to experimental data (Fig. 6 d). With the exception of recent stochastic approaches (28,69,75) none of the deterministic models have presently been able to model the large variability in amplitude in the presence of rapid molecular fluctuations.
Since the pioneering work of Goodwin (76), many studies have shown that negative feedback regulation can lead to oscillations. The Goodwin equations (76) have been applied to circadian (77) as well as ultradian rhythms (73). In transcriptional-translational negative feedback regulators the intermediate mRNA species have been recognized to induce transcriptional time delays, which are important to generate these oscillations (73). In addition, protein (or mRNA) stabilities are important determinants for period length (78,79).
In this model the negative feedback involving the transcriptional and translational processes induced by p53 have been fused into the single first-order term ksMdm2 · p53 (Eq. 9). This first-order term suggests that binding of p53 at the Mdm2 promoter is relatively weak, where ksMdm2 describes the overall expression of Mdm2 under such conditions (see Supporting Material).
The occurrence of large amplitude harmonic oscillations in cell regulatory networks, such as the oscillations in the core regulatory unit of the p53/Mdm2 system, appears intriguing. Similar highly variable amplitude oscillations with a relatively fixed frequency have been reported in the SOS DNA-damage response of Escherichia coli (80) and in the NF-κB system (81–83). Both NF-κB and the SOS regulation in E. coli are based on negative feedback regulation similar to the p53/Mdm2 system. Whether the variability in amplitude in the SOS or in NF-κB system can be based on similar oscillatory dynamics as found for homeostatic controllers (14) and considered here for the p53/Mdm2 system will be the subject of further investigations.
Supporting Material
Description of computational methods, kinetics of scaffold-supported p53 and Mdm2 degradation, kinetics of p53 induced Mdm2 synthesis, and random variation of rate constants are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01740-8.
Supporting Material
Acknowledgments
P.R. thanks Jay Dunlap for hospitality while a revised version of the manuscript was prepared.
This research was supported in part by the Norwegian Research Council under grant No. 167087/V40 (to I.W.J.) and FUGE Systems Biology (SysMO) grant No. 183085/S10 (to X.Y.N.).
References
- 1.Stelling J., Sauer U., Doyle J. Robustness of cellular functions. Cell. 2004;118:675–685. doi: 10.1016/j.cell.2004.09.008. [DOI] [PubMed] [Google Scholar]
- 2.Asthagiri A.R., Lauffenburger D.A. Bioengineering models of cell signaling. Annu. Rev. Biomed. Eng. 2000;2:31–53. doi: 10.1146/annurev.bioeng.2.1.31. [DOI] [PubMed] [Google Scholar]
- 3.Berg H.C., Tedesco P.M. Transient response to chemotactic stimuli in Escherichia coli. Proc. Natl. Acad. Sci. USA. 1975;72:3235–3239. doi: 10.1073/pnas.72.8.3235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barkai N., Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 5.Alon U., Surette M.G., Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
- 6.Hansen C.H., Endres R.G., Wingreen N.S. Chemotaxis in Escherichia coli: a molecular model for robust precise adaptation. PLoS Comput. Biol. 2008;4:0014–0027. doi: 10.1371/journal.pcbi.0040001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ratliff F., Hartline H.K., Miller W.H. Spatial and temporal aspects of retinal inhibitory interaction. J. Opt. Soc. Am. 1963;53:110–120. doi: 10.1364/josa.53.000110. [DOI] [PubMed] [Google Scholar]
- 8.Asthagiri A.R., Nelson C.M., Lauffenburger D.A. Quantitative relationship among integrin-ligand binding, adhesion, and signaling via focal adhesion kinase and extracellular signal-regulated kinase 2. J. Biol. Chem. 1999;274:27119–27127. doi: 10.1074/jbc.274.38.27119. [DOI] [PubMed] [Google Scholar]
- 9.Hao N., Behar M., Dohlman H.G. Systems biology analysis of G protein and MAP kinase signaling in yeast. Oncogene. 2007;26:3254–3266. doi: 10.1038/sj.onc.1210416. [DOI] [PubMed] [Google Scholar]
- 10.Mettetal J.T., Muzzey D., van Oudenaarden A. The frequency dependence of osmo-adaptation in Saccharomyces cerevisiae. Science. 2008;319:482–484. doi: 10.1126/science.1151582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Drengstig T., Ueda H.R., Ruoff P. Predicting perfect adaptation motifs in reaction kinetic networks. J. Phys. Chem. B. 2008;112:16752–16758. doi: 10.1021/jp806818c. [DOI] [PubMed] [Google Scholar]
- 12.Wilkie J., Johnson M., Reza K. Palgrave; New York: 2002. Control Engineering. An Introductory Course. [Google Scholar]
- 13.Yi T.M., Huang Y., Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ni X.Y., Drengstig T., Ruoff P. The control of the controller: molecular mechanisms for robust perfect adaptation and temperature compensation. Biophys. J. 2009;97:1244–1253. doi: 10.1016/j.bpj.2009.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Novák B., Tyson J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008;9:981–991. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Asher G., Lotem J., Shaul Y. Regulation of p53 stability and p53-dependent apoptosis by NADH quinone oxidoreductase 1. Proc. Natl. Acad. Sci. USA. 2001;98:1188–1193. doi: 10.1073/pnas.021558898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Leng R.P., Lin Y., Benchimol S. Pirh2, a p53-induced ubiquitin-protein ligase, promotes p53 degradation. Cell. 2003;112:779–791. doi: 10.1016/s0092-8674(03)00193-4. [DOI] [PubMed] [Google Scholar]
- 18.Dornan D., Wertz I., Dixit V.M. The ubiquitin ligase COP1 is a critical negative regulator of p53. Nature. 2004;429:86–92. doi: 10.1038/nature02514. [DOI] [PubMed] [Google Scholar]
- 19.Asher G., Shaul Y. p53 proteasomal degradation: poly-ubiquitination is not the whole story. Cell Cycle. 2005;4:1015–1018. doi: 10.4161/cc.4.8.1900. [DOI] [PubMed] [Google Scholar]
- 20.Asher G., Shaul Y. Ubiquitin-independent degradation: lessons from the p53 model. Isr. Med. Assoc. J. 2006;8:229–232. [PubMed] [Google Scholar]
- 21.Yang W., Rozan L.M., El-Deiry W.S. CARPs are ubiquitin ligases that promote MDM2-independent p53 and phospho-p53Ser20 degradation. J. Biol. Chem. 2007;282:3273–3281. doi: 10.1074/jbc.M610793200. [DOI] [PubMed] [Google Scholar]
- 22.Vogelstein B., Lane D., Levine A.J. Surfing the p53 network. Nature. 2000;408:307–310. doi: 10.1038/35042675. [DOI] [PubMed] [Google Scholar]
- 23.Carr A.M. Cell cycle. Piecing together the p53 puzzle. Science. 2000;287:1765–1766. doi: 10.1126/science.287.5459.1765. [DOI] [PubMed] [Google Scholar]
- 24.Vousden K.H., Lu X. Live or let die: the cell's response to p53. Nat. Rev. Cancer. 2002;2:594–604. doi: 10.1038/nrc864. [DOI] [PubMed] [Google Scholar]
- 25.Lev Bar-Or R., Maya R., Oren M. Generation of oscillations by the p53-Mdm2 feedback loop: a theoretical and experimental study. Proc. Natl. Acad. Sci. USA. 2000;97:11250–11255. doi: 10.1073/pnas.210171597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lahav G., Rosenfeld N., Alon U. Dynamics of the p53-Mdm2 feedback loop in individual cells. Nat. Genet. 2004;36:147–150. doi: 10.1038/ng1293. [DOI] [PubMed] [Google Scholar]
- 27.Geva-Zatorsky N., Rosenfeld N., Alon U. Oscillations and variability in the p53 system. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100068. 2006-0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wilkinson D.J. Stochastic modeling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 2009;10:122–133. doi: 10.1038/nrg2509. [DOI] [PubMed] [Google Scholar]
- 29.Wu X., Bayle J.H., Levine A.J. The p53-mdm-2 autoregulatory feedback loop. Genes Dev. 1993;7(7A):1126–1132. doi: 10.1101/gad.7.7a.1126. [DOI] [PubMed] [Google Scholar]
- 30.Kubbutat M.H., Jones S.N., Vousden K.H. Regulation of p53 stability by Mdm2. Nature. 1997;387:299–303. doi: 10.1038/387299a0. [DOI] [PubMed] [Google Scholar]
- 31.Levine A.J. p53, the cellular gatekeeper for growth and division. Cell. 1997;88:323–331. doi: 10.1016/s0092-8674(00)81871-1. [DOI] [PubMed] [Google Scholar]
- 32.Jin S., Levine A.J. The p53 functional circuit. J. Cell Sci. 2001;114:4139–4140. doi: 10.1242/jcs.114.23.4139. [DOI] [PubMed] [Google Scholar]
- 33.Brooks C.L., Gu W. Dynamics in the p53-Mdm2 ubiquitination pathway. Cell Cycle. 2004;3:895–899. [PubMed] [Google Scholar]
- 34.Candeias M.M., Malbert-Colas L., Fåhraeus R. P53 mRNA controls p53 activity by managing Mdm2 functions. Nat. Cell Biol. 2008;10:1098–1105. doi: 10.1038/ncb1770. [DOI] [PubMed] [Google Scholar]
- 35.Kruse J.P., Gu W. Modes of p53 regulation. Cell. 2009;137:609–622. doi: 10.1016/j.cell.2009.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tai E., Benchimol S. TRIMming p53 for ubiquitination. Proc. Natl. Acad. Sci. USA. 2009;106:11431–11432. doi: 10.1073/pnas.0905997106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Allton K., Jain A.K., Barton M.C. Trim24 targets endogenous p53 for degradation. Proc. Natl. Acad. Sci. USA. 2009;106:11612–11616. doi: 10.1073/pnas.0813177106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Momand J., Wu H.H., Dasgupta G. MDM2—master regulator of the p53 tumor suppressor protein. Gene. 2000;242:15–29. doi: 10.1016/s0378-1119(99)00487-4. [DOI] [PubMed] [Google Scholar]
- 39.Fu W., Ma Q., Bai W. MDM2 acts downstream of p53 as an E3 ligase to promote FOXO ubiquitination and degradation. J. Biol. Chem. 2009;284:13987–14000. doi: 10.1074/jbc.M901758200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yu G.W., Rudiger S., Fersht A.R. The central region of HDM2 provides a second binding site for p53. Proc. Natl. Acad. Sci. USA. 2006;103:1227–1232. doi: 10.1073/pnas.0510343103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shirangi T.R., Zaika A., Moll U.M. Nuclear degradation of p53 occurs during down-regulation of the p53 response after DNA damage. FASEB J. 2002;16:420–422. doi: 10.1096/fj.01-0617fje. [DOI] [PubMed] [Google Scholar]
- 42.Michael D., Oren M. The p53-Mdm2 module and the ubiquitin system. Semin. Cancer Biol. 2003;13:49–58. doi: 10.1016/s1044-579x(02)00099-8. [DOI] [PubMed] [Google Scholar]
- 43.Stommel J.M., Wahl G.M. Accelerated MDM2 auto-degradation induced by DNA-damage kinases is required for p53 activation. EMBO J. 2004;23:1547–1556. doi: 10.1038/sj.emboj.7600145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Asher G., Lotem J., Shaul Y. NQO1 stabilizes p53 through a distinct pathway. Proc. Natl. Acad. Sci. USA. 2002;99:3099–3104. doi: 10.1073/pnas.052706799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Asher G., Lotem J., Shaul Y. Mdm-2 and ubiquitin-independent p53 proteasomal degradation regulated by NQO1. Proc. Natl. Acad. Sci. USA. 2002;99:13125–13130. doi: 10.1073/pnas.202480499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Das S., Boswell S.A., Lee S.W. P53 promoter selection: choosing between life and death. Cell Cycle. 2008;7:154–157. doi: 10.4161/cc.7.2.5236. [DOI] [PubMed] [Google Scholar]
- 47.Pietsch E.C., Sykes S.M., Murphy M.E. The p53 family and programmed cell death. Oncogene. 2008;27:6507–6521. doi: 10.1038/onc.2008.315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tyson J.J. Monitoring p53's pulse. Nat. Genet. 2004;36:113–114. doi: 10.1038/ng0204-113. [DOI] [PubMed] [Google Scholar]
- 49.Tyson J.J. Another turn for p53. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100060. 2006 -0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lahav G. Oscillations by the p53-Mdm2 feedback loop. In: Maroto M., Monk N.A.M., editors. Cellular Oscillatory Mechanisms. Landes Bioscience and Springer Science & Business Media; Austin, TX: 2008. [Google Scholar]
- 51.Wee K.B., Surana U., Aguda B.D. Oscillations of the p53-Akt network: implications on cell survival and death. PLoS One. 2009;4:e4407. doi: 10.1371/journal.pone.0004407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kamijo T., Weber J.D., Sherr C.J. Functional and physical interactions of the ARF tumor suppressor with p53 and Mdm2. Proc. Natl. Acad. Sci. USA. 1998;95:8292–8297. doi: 10.1073/pnas.95.14.8292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Borden K.L. RING domains: master builders of molecular scaffolds? J. Mol. Biol. 2000;295:1103–1112. doi: 10.1006/jmbi.1999.3429. [DOI] [PubMed] [Google Scholar]
- 54.Savchenko A., Yurchenko M., Kashuba E. Study on the spatial architecture of p53, MDM2, and p14ARF containing complexes. Mol. Biotechnol. 2009;41:270–277. doi: 10.1007/s12033-008-9116-x. [DOI] [PubMed] [Google Scholar]
- 55.Moore J.W., Pearson R.G. 3rd Ed. John Wiley & Sons; New York: 1981. Kinetics and Mechanism. [Google Scholar]
- 56.Asher G., Lotem J., Shaul Y. P53 hot-spot mutants are resistant to ubiquitin-independent degradation by increased binding to NAD(P)H:quinone oxidoreductase 1. Proc. Natl. Acad. Sci. USA. 2003;100:15065–15070. doi: 10.1073/pnas.2436329100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gu W., Luo J., Brooks C.L., Nikolaev A.Y., Li M. Dynamics of the p53 acetylation pathway. Novartis Found. Symp. 2004;259 197–207, 223–225. [PubMed] [Google Scholar]
- 58.Jackson M.W., Berberich S.J. MdmX protects p53 from Mdm2-mediated degradation. Mol. Cell. Biol. 2000;20:1001–1007. doi: 10.1128/mcb.20.3.1001-1007.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Press W.H., Flannery B.P., Vetterling W.T. The Art of Scientific Computing (Fortran Version) Cambridge University Press; New York: 1989. Numerical recipes. [Google Scholar]
- 60.Ma J., Martin J.D., Lai Z. A second p53 binding site in the central domain of Mdm2 is essential for p53 ubiquitination. Biochemistry. 2006;45:9238–9245. doi: 10.1021/bi060661u. [DOI] [PubMed] [Google Scholar]
- 61.Joseph T.W., Zaika A., Moll U.M. Nuclear and cytoplasmic degradation of endogenous p53 and HDM2 occurs during down-regulation of the p53 response after multiple types of DNA damage. FASEB J. 2003;17:1622–1630. doi: 10.1096/fj.02-0931com. [DOI] [PubMed] [Google Scholar]
- 62.Ma L., Wagner J., Stolovitzky G.A. A plausible model for the digital response of p53 to DNA damage. Proc. Natl. Acad. Sci. USA. 2005;102:14266–14271. doi: 10.1073/pnas.0501352102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sionov R.V., Haupt Y. The cellular response to p53: the decision between life and death. Oncogene. 1999;18:6145–6157. doi: 10.1038/sj.onc.1203130. [DOI] [PubMed] [Google Scholar]
- 64.Waxmann D. Growth hormone pulse-activated STATS signaling: a unique regulatory mechanism governing sexual dimorphism of liver gene expression. Mechanisms and biological significance of pulsatile hormone secretion. Novartis Found. Symp. 2000;227:61–81. doi: 10.1002/0470870796.ch5. [DOI] [PubMed] [Google Scholar]
- 65.Goldbeter A., Koshland D.E. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA. 1981;78:6840–6844. doi: 10.1073/pnas.78.11.6840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Goldbeter A. Zero-order switches and developmental thresholds. Mol. Syst. Biol. 2005;1 doi: 10.1038/msb4100042. 2005-0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Soyer O.S., Kuwahara H., Csikász-Nagy A. Regulating the total level of a signaling protein can vary its dynamics in a range from switch like ultrasensitivity to adaptive responses. FEBS J. 2009;276:3290–3298. doi: 10.1111/j.1742-4658.2009.07054.x. [DOI] [PubMed] [Google Scholar]
- 68.Sun T., Chen C., Shen P. Modeling the role of p53 pulses in DNA damage- induced cell death decision. BMC Bioinformatics. 2009;10:190. doi: 10.1186/1471-2105-10-190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Proctor C.J., Gray D.A. Explaining oscillations and variability in the p53-Mdm2 system. BMC Syst. Biol. 2008;2:75. doi: 10.1186/1752-0509-2-75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zhang T., Brazhnik P., Tyson J.J. Exploring mechanisms of the DNA-damage response: p53 pulses and their possible relevance to apoptosis. Cell Cycle. 2007;6:85–94. doi: 10.4161/cc.6.1.3705. [DOI] [PubMed] [Google Scholar]
- 71.Ciliberto A., Novak B., Tyson J.J. Steady states and oscillations in the p53/Mdm2 network. Cell Cycle. 2005;4:488–493. doi: 10.4161/cc.4.3.1548. [DOI] [PubMed] [Google Scholar]
- 72.Wagner J., Ma L., Stolovitzky G.A. p53-Mdm2 loop controlled by a balance of its feedback strength and effective dampening using ATM and delayed feedback. Syst. Biol. (Stevenage) 2005;152:109–118. doi: 10.1049/ip-syb:20050025. [DOI] [PubMed] [Google Scholar]
- 73.Monk N.A. Oscillatory expression of Hes1, p53, and NF-κB driven by transcriptional time delays. Curr. Biol. 2003;13:1409–1413. doi: 10.1016/s0960-9822(03)00494-9. [DOI] [PubMed] [Google Scholar]
- 74.Qi J.P., Shao S.H., Zhu Y. A mathematical model of P53 gene regulatory networks under radiotherapy. Biosystems. 2007;90:698–706. doi: 10.1016/j.biosystems.2007.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cai X., Yuan Z.M. Stochastic modeling and simulation of the p53-MDM2/MDMX loop. J. Comput. Biol. 2009;16:917–933. doi: 10.1089/cmb.2008.0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Goodwin B.C. Oscillatory behavior in enzymatic control processes. In: Weber G., editor. Advances in Enzyme Regulation. Vol. 3. Pergamon Press; Oxford, UK: 1965. [DOI] [PubMed] [Google Scholar]
- 77.Ruoff P., Rensing L. The temperature-compensated Goodwin oscillator simulates many circadian clock properties. J. Theor. Biol. 1996;179:275–285. [Google Scholar]
- 78.Ruoff P., Loros J.J., Dunlap J.C. The relationship between FRQ-protein stability and temperature compensation in the Neurospora circadian clock. Proc. Natl. Acad. Sci. USA. 2005;102:17681–17686. doi: 10.1073/pnas.0505137102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ruoff, P. 2003. Modeling circadian clocks and temperature compensation. http://online.kitp.ucsb.edu/online/bionet03/ruoff/oh/47.html.
- 80.Friedman N., Vardi S., Stavans J. Precise temporal modulation in the response of the SOS DNA repair network in individual bacteria. PLoS Biol. 2005;3:e238. doi: 10.1371/journal.pbio.0030238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hoffmann A., Levchenko A., Baltimore D. The IκB-NF-κB signaling module: temporal control and selective gene activation. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- 82.Nelson D.E., Ihekwaba A.E., White M.R. Oscillations in NF-κB signaling control the dynamics of gene expression. Science. 2004;306:704–708. doi: 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
- 83.Ashall L., Horton C.A., White M.R. Pulsatile stimulation determines timing and specificity of NF-κB-dependent transcription. Science. 2009;324:242–246. doi: 10.1126/science.1164860. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


