Abstract
This paper summarizes the newly developed immersed finite element method (IFEM) and its applications to the modeling of biological systems. This work was inspired by the pioneering work of Professor T.J.R. Hughes in solving fluid–structure interaction problems. In IFEM, a Lagrangian solid mesh moves on top of a background Eulerian fluid mesh which spans the entire computational domain. Hence, mesh generation is greatly simplified. Moreover, both fluid and solid domains are modeled with the finite element method and the continuity between the fluid and solid subdomains is enforced via the interpolation of the velocities and the distribution of the forces with the reproducing Kernel particle method (RKPM) delta function. The proposed method is used to study the fluid–structure interaction problems encountered in human cardiovascular systems. Currently, the heart modeling is being constructed and the deployment process of an angioplasty stent has been simulated. Some preliminary results on monocyte and platelet deposition are presented. Blood rheology, in particular, the shear-rate dependent de-aggregation of red blood cell (RBC) clusters and the transport of deformable cells, are modeled. Furthermore, IFEM is combined with electrokinetics to study the mechanisms of nano/bio filament assembly for the understanding of cell motility.
Keywords: Immersed finite element method, Reproducing Kernel particle method, Fluid–structure interaction, Cytoskeletal dynamics, Red blood cell, Aggregation, Thrombosis, Cardiovascular system, Micro-circulation, Nano-electro-mechanical-sensors, Cell motility, Surgical corrective procedures
1. Introduction
For the past few decades, tremendous research efforts have been directed to the development of modeling and simulation approaches for fluid–structure interaction problems. Methods developed by Tezduyar and his coworkers are widely used in the simulation of fluid–particle (rigid) and fluid–structure interactions [1,2]. To accommodate the complicated motion of fluid–structure boundaries, we often use adaptive meshing or the arbitrary Lagrangian Eulerian (ALE) techniques [3-9]. Recently, such approaches have also been adopted by Hu et al. in the modeling of fluid–particle (rigid) systems [10]. Nevertheless, mesh update or remeshing algorithms can be time consuming and expensive. A detailed discussion on this issue is presented in Ref. [11].
In the 1970s, Peskin developed the immersed boundary (IB) method [12] to study flow patterns around heart valves [13-15]. The mathematical formulation of the IB method employs a mixture of Eulerian and Lagrangian descriptions for fluid and solid domains. In particular, the entire fluid domain is represented by a uniform background grid, which can be solved by finite difference methods with periodic boundary conditions; whereas the submerged structure is represented by a fiber network. The interaction between fluid and structure is accomplished by distributing the nodal forces and interpolating the velocities between the Eulerian and Lagrangian domains through a smoothed approximation of the Dirac delta function. The advantage of the IB method is that the fluid–structure interface is tracked automatically, which circumvents one of the most costly computations, namely mesh update algorithms.
Nevertheless, one major disadvantage of the IB method is the assumption of a fiber-like one-dimensional immersed structure, which may carry mass, but occupies no volume in the fluid domain. This assumption also limits accurate representation of immersed flexible solids which may occupy finite volumes within the fluid domain. Furthermore, uniform fluid grids also set limitations in resolving fluid domains with complex shapes and boundary conditions.
Recently, following the pioneering work of Peskin and co-workers on the IB method, an alternative approach, the immersed finite element method (IFEM) was developed by Zhang et al. [16]. This method is able to eliminate the aforementioned drawbacks of the IB method by adopting parts of the work on the Extended Immersed Boundary Method (EIBM) developed by Wang and Liu [17]. With finite element formulations for both fluid and solid domains, the submerged structure is solved more realistically and accurately in comparison with the corresponding fiber network representation. The fluid solver is based on a stabilized equal-order finite element formulation applicable to problems involving moving boundaries [1,2,18], one of Professor T.J.R. Hughes' many important contributions to the field of computational mechanics. This stabilized formulation prevents numerical oscillations without introducing excessive numerical dissipation. Moreover, in the proposed IFEM, the background fluid mesh does not have to follow the motion of the flexible fluid–structure interfaces and thus it is possible to assign a sufficiently refined fluid mesh within the region around the immersed, moving, deformable structures.
Unlike the Dirac delta functions in the IB method which yield C1 continuity [19,20], the discretized delta function in IFEM is the Cn shape function often employed in the meshfree reproducing Kernel particle method (RKPM) [21-24]. Because of the higher order smoothness in the RKPM delta function, the accuracy is increased in the coupling procedures between fluid and solid domains [17]. Furthermore, the RKPM shape function is also capable of handling non-uniform fluid grids.
The outline of this paper is as follows. We first give a review of the IFEM formulations and algorithm in Section 2. Application of IFEM to the modeling of human blood circulation systems is given in Section 3, where a heart model, angioplasty stent deployment, monocyte and platelet deposition, and RBC aggregation problems are studied. In Section 4, we summarize the IFEM concept, its attributes and future applications.
2. Review of immersed finite element method
2.1. Formulations of IFEM
The IFEM was recently developed by Zhang et al. [16] to solve complex fluid and deformable structure interaction problems. Because much of the following has already been derived in detail in Zhang et al. [16], we refer the interested reader to those works for further details.
Let us consider an incompressible three-dimensional deformable structure in Ωs completely immersed in an incompressible fluid domain Ωf. Together, the fluid and the solid occupy a domain Ω, but they do not intersect:
| (1a) |
| (1b) |
In contrast to the IB formulation, the solid domain can occupy a finite volume in the fluid domain. Since we assume both fluid and solid to be incompressible, the union of two domains can be treated as one incompressible continuum with a continuous velocity field. In the computation, the fluid spans the entire domain Ω, thus an Eulerian fluid mesh is adopted; whereas a Lagrangian solid mesh is constructed on top of the Eulerian fluid mesh. The coexistence of fluid and solid in Ωs requires some considerations when developing the momentum and continuity equations.
In the computational fluid domain Ω, the fluid grid is represented by the time-invariant position vector x; while the material points of the structure in the initial solid domain and the current solid domain Ωs are represented by Xs and xs(Xs, t), respectively. The superscript s is used in the solid variables to distinguish the fluid and solid domains.
In the fluid calculations, the velocity v and the pressure p are the unknown fluid field variables; whereas the solid domain involves the calculation of the nodal displacement us, which is defined as the difference of the current and the initial coordinates: us = xs − Xs. The velocity vs is the material derivative of the displacement dus/dt.
As in Refs. [16,17], we define the fluid–structure interaction force within the domain Ωs as , where FSI stands for fluid–structure interaction:
| (2) |
Naturally, the interaction force in Eq. (2) is calculated with the Lagrangian description. Moreover, a Dirac delta function δ is used to distribute the interaction force from the solid domain onto the computational fluid domain:
| (3) |
Hence, the governing equation for the fluid can be derived by combining the fluid terms and the interaction force as
| (4) |
Since we consider the entire domain Ω to be incompressible, we only need to apply the incompressibility constraint once in the entire domain Ω:
| (5) |
To delineate the Lagrangian description for the solid and the Eulerian description for the fluid, we introduce different velocity field variables and vi to represent the motions of the solid in the domain Ωs and the fluid within the entire domain Ω. The coupling of both velocity fields is accomplished with the Dirac delta function:
| (6) |
Let us assume that there is no traction applied on the fluid boundary, i.e. ∫Γhi δvihidΓ = 0, applying integration by parts and the divergence theorem, we can get the final weak form (with stabilization terms):
| (7) |
The non-linear systems are solved with the Newton–Raphson method. Moreover, to improve computational efficiency, we also employ the GMRES iterative algorithm and compute the residuals based on matrix-free techniques [25,26].
The transformation of the weak form from the updated Lagrangian to the total Lagrangian description is to change the integration domain from Ωs to . Since we consider an incompressible fluid and solid, and the Jacobian determinant is 1 in the solid domain, the transformation of the weak form to total Lagrangian description yields
| (8) |
where the first Piola–Kirchhoff stress Pij is defined as and the deformation gradient Fij as .
Using integration by parts and the divergence theorem, we can rewrite Eq. (8) as
| (9) |
Note again that the boundary integral terms on the fluid–structure interface for both fluid and solid domains will cancel each other and for brevity are not included in the corresponding weak forms.
For structures with large displacements and deformations, the second Piola–Kirchhoff stress Sij and the Green–Lagrangian strain Eij are used in the total Lagrangian formulation:
| (10) |
where the first Piola–Kirchhoff stress Pij can be obtained from the second Piola–Kirchhoff stress as Pij = SikFjk.
Finally, in the interpolation process from the fluid onto the solid grid, the discretized form of Eq. (6) can be written as
| (11) |
Here, the solid velocity at node I can be calculated by gathering the velocities at fluid nodes within the influence domain ΩϕI. A dual procedure takes place in the distribution process from the solid onto the fluid grid. The discretized form of Eq. (3) is expressed as
| (12) |
By interpolating the fluid velocities onto the solid particles in Eq. (11), the fluid within the solid domain is bounded to solid material points. This ensures not only the no-slip boundary condition on the surface of the solid, but also automatically stops the fluid from penetrating the solid, provided the solid mesh is at least twice as dense as the surrounding fluid mesh. This heuristic criterion is based on the numerical evidence and needs further investigation.
2.2. Computational algorithm of IFEM
The governing equations of IFEM in discretized form (except the Navier–Stokes equations, for convenience) are summarized as follows:
| (13a) |
| (13b) |
| (13c) |
| (13d) |
| (13e) |
An outline of IFEM algorithm with a semi-explicit time integration is illustrated as follows:
Given the structure configuration xs,n and the fluid velocity vn at time step n.
Evaluate the nodal interaction forces fFSI,s,n for solid material points, using Eq. (13a).
Distribute the material nodal force onto the fluid mesh, from fFSI,s,n to fFSI,n, using the delta function as in Eq. (13b).
Solve for the fluid velocities vn+1 and the pressure pn+1 implicitly using Eqs. (13c) and (13d).
Interpolate the velocities in the fluid domain onto the material points, i.e. from vn+1 to vs,n+1 as in Eq. (13e), and
Update the positions of the structure using us,n+1 = vs,n+1 Δt and go back to step 1.
Note that even though the fluid is solved fully implicitly, the coupling between fluid and solid is explicit. If we rewrite the fluid momentum equation (for clarity only discretized in time), we have
| (14) |
It is clear that the interaction force is not updated during the iteration, i.e. the solid equations are calculated with values from the previous time step. For a fully implicit coupling, this force must be a function of the current fluid velocity and the term should be included into the linearization of the fluid equations.
2.3. Electrohydrodynamic coupling through IFEM formulation
An electric field is widely used to manipulate biological objects such as cells or biofibros. It is important to incorporate the electric field into the fluid–structure interaction problem, thus solving an electrohydrodynamic problem.
The factors involved in electro-manipulation and their applicable conditions are summarized in Table 1. Electrophoresis is usually used in the manipulation of charged particles. For a particle with fixed charge density q, the electrostatic force is defined as
| (15) |
where E is the electric field intensity.
Table 1.
Electro-mechanics involved in electro-manipulation
| Mechanisms | Applicable condition |
|---|---|
| Electrophoresis (EP) | DC or low freq AC |
| Dielectrophoresis (DEP) | AC |
| Electroosmosis flow | DC or low freq AC |
| Drag force | Viscous fluid |
| Brownian motion | Nano/micro-scale particles |
Dielectrophoresis force results from an induced dipole moment under a non-uniform electric field. A dipole moment is induced when a polarizable object is put into an electric field. If the electric field is inhomogeneous, the field strength and thus the force acting on each part of the object is different, leading to relative motion of the object to the medium. The force exerted by an electric field E on a dipole with dipole moment p is given by F =(p·∇)E. A widely used expression for the time-averaged DEP force on a particle is given as [27]:
| (16) |
where Γ is a parameter that depends on the particle shape and size; ε1 is the real part of the permittivity of the medium; Kf is a factor that depends on the complex permittivities of both the particle and the medium; and ∇|E|2 is the gradient of the energy density of the electric field. For a sphere with a radius a, Γ=2πa3, (called the Clausius–Mossotti factor). For a cylinder with a diameter r and a length l, Γ = πr2l/6, . The frequency dependent complex permittivities shown with the asterisk are expressed by the complex combination of conductivity σ, permittivity ε, and electric field frequency ω as: , and , where and the indices 1 and 2 refer to the medium and the particle, respectively.
The electroosmotic flow is treated as a slip boundary condition for the fluid. Also, since the Debye layer (the layer close to the wall where the velocity is varying) is only a few nano-meters, only the steady velocity is taken into account [28]:
| (17) |
where ψ0 is the zeta potential (the electric potential at the slipping plane close to the solid surface), μ and ε are the viscosity and permittivity of the medium, respectively.
The Brownian force induced by thermal fluctuations will influence the motion of nano-scale particles. We will adopt the approach described in Sharma et al.'s work on Brownian motion of rigid particles [29], which is able to capture the thermal motion of complex shaped objects without using approximations for the viscous drag on these objects.
The coupled electrohydrodynamic equation of motion is written in the context of IFEM formulation by revising Eq. (2) and Eq. (4) to Fluid equation with fluid–structure interaction force
| (18) |
Solid equation
| (19) |
where fext, fDEP, fe are the external force, dielectrophoresis force, and electrostatic force, respectively. The external force is usually the gravity force. The expressions for the electrostatic force and dielectrophoresis force are given in Eqs. (16) and (15). The other variables have been defined in Section 2.1.
In this way, the solid, fluid, and electrokinetic equations are coupled together. In the current simulations, the electrokinetic equation and solid/fluid motion equation are solved iteratively, thus a semi-static approach. Since the transition time of the electric field is much shorter than the characteristic time of the solid/fluid motion, this iterative approach is reasonable.
3. Application to biological systems
There are various scales involved in a biological system [30]. Fig. 1 depicts the multiple scale phenomena in the cardiovascular system to which we are applying multiscale analysis. The objective is to predict blood flow, its effect on the blood vessels and in turn the effect on the blood cells, which are interrelated. The far left shows a model of the heart which includes interaction with blood flow (developed in collaboration with Professors T.J.R. Hughes and Bajaj of the Texas Institute for Computational and Applied Mathematics). The next bar to the right of the heart shows models of the blood vessels, where the properties of the vessel wall and thrombus deposition on the wall are the interactions of interest. The third scale is the cellular scale, where blood components such as red blood cells, white blood cells, platelets, as well as their interactions are considered. The next two scales are the sub-cellular and molecular scales. Our modeling efforts at these scales are focused on understanding how a cell migrates. Understanding and modeling the mechanics of the cell is one of the major challenges of the next few decades. A model of cell motility (migration) can provide the information for possible treatments such as the obstruction of cancer metastasis and an understanding of critical cell functions such as neuronal development and embryonic morphogenesis.
Fig. 1.
Modeling of biological processes using a 3D multiscale technique.
The ultimate goal of the three-dimensional (3D) multiple scale modeling is to better understand biological phenomena that span the five scales depicted in Fig. 1. This multiscale model will help understand diseases, such as vascular atherogenesis, a disease which affects a large portion of the elderly population. They can also potentially be used to design surgical corrective procedures, such as angioplasty. We are currently using the same simulation-based software to design and fabricate a novel nano-electromechanical sensor for cellular force measurements. The measurements of traction forces and the simultaneous imaging of the fibrous structure of the cell will provide critical input to the simulation of cell motility.
The following will summarize the application of IFEM on the various scales of the human blood circulation system, from the organ level to the molecular level.
3.1. Heart model
In collaboration with Professors Hughes and Bajaj of the Texas Institute for Computational and Applied Mathematics, the multiple scale mechanical model of the human heart was constructed. The heart and its associated arteries, veins, valves and blood represents the largest scale at which continuum solid and fluid mechanics can be utilized. At this macroscopic scale, the heart is modeled as an elastic body. The tetrahedral heart mesh was constructed from volumetric data using an extended dual contouring method [31]. All fourteen inlet/outlet meshes of the heart were extended to the surface of the surrounding fluid domain in order to apply periodic pressure boundary conditions. The heart model includes essential features such as the aorta, pulmonary artery, inferior vena cava, superior vena cava pulmonary vein, four chambers (left/right atriums and ventricles), heart valves (tricuspid valve, pulmonary valve, aortic valve, and left ventricle valve) and muscles. Fig. 2(a) shows the heart mesh with extended vessels immersed in the fluid mesh. Fig. 2(b) shows an aortic valve. The dynamic process of heart beating and the blood flow pattern inside the heart will be modeled through IFEM in the future.
Fig. 2.
The heart model [31]: (a) heart model immersed in the fluid mesh, (b) aortic valve.
3.2. Flexible valve–viscous fluid interaction
In order to validate the IFEM, results from a simple flexible valve–viscous fluid interaction analysis are compared with experiments performed recently at ABIOMED, a leading company in the manufacture of artificial hearts. As shown in Fig. 3, water was pulsed through a column with a square cross-section (5 × 5 cm) at a frequency of 1 Hz. A rubber sheet was located inside this column. Analysis of Fig. 3 reveals excellent correlation between experimental observations of structural displacement and the simulation.
Fig. 3.
Comparison of experimental observation and simulation result of a rubber sheet deflecting in a column of water. Pulsatile flow through the column (square cross-section) is from left to right at a frequency of 1 Hz. Velocity vectors and beam stress concentration can be seen in the simulation: (a) experiment, (b) simulation.
3.3. Angioplasty stent
Coronary stents physically open the channel of constricted arterial segments by fatty deposits or calcium accumulations. During stenting, a balloon deploys the stent which is kept inflated for 30 s and then is deflated. At the end of the process, the expanded stent is embedded into the wall of the diseased artery and holds it open. The objective of our research is to study the mechanical behavior of angioplasty stents during implantation using the fluid–structure interaction computational technique. The deployment of a balloon expandable stent is simulated using the immersed finite element method (IFEM) [32].
Using this method, we model a stainless steel stent in a blood vessel. A balloon is deployed to assist the expansion of the stent which is to be plastically deformed. A balloon is designed in its initial undeformed configuration with deflated tips at the two ends. The balloons used for stenting are made of very stiff polyamide (nylon) material, which is modeled as a hyperelastic material in the simulation. A stent is a cylindrical, symmetrical assembly of inter-connected diamond-shaped members. Our studies focus on the Medtronic AVE Modular stents S7. Each of the sixteen structural members has a length of 8 mm. The cross-section of the wire has a width of 0.08 mm before expansion. Stents are made from materials like stainless steel 316L, which can be plastically deformed through the inflation of a balloon. Finally, the stent is mounted around the balloon as shown in Fig. 4.
Fig. 4.
Design of the catheter, balloon and stent before inflation.
The expansion mechanism is modeled as a uniform radial internal pressure. This pressure difference is applied from the centerline towards the outer diameter of the balloon and the artery wall and is an intrinsic property of the balloon and stent. Fig. 5 shows the deployment of the stent through the expansion of the balloon at different time steps.
Fig. 5.
Deployment of the stent through the inflation of the balloon at different time steps.
During the deployment, the diameter of the stent increases from 1.64 mm to 2.82 mm. As expected the stent deforms uniformly in its radial direction and expands to 1.7 times its initial diameter for our given material.
By using the IFEM method, we were able to study the flow pattern during the deployment of a stent, its deformation and stress distribution. The results show that this computational method provides a useful tool for future stent designs.
3.4. Monocyte deposition
Fig. 6 illustrates some preliminary results of a study of the deposition of monocytes (white blood cells) near the expansion of a large blood vessel, a condition which may be the result of a poorly matched vascular graft. The vessel section upstream of the graft may differ in size, creating a geometry similar to a diverging duct. This geometry results in a classical flow recirculation region into which particles suspended in the bulk fluid may become entrained. This recirculation region allows the cells to approach and deposit on the vessel wall due to the interaction of the proteins present on the monocyte surface and endothelium. We use tools previously developed in Ref. [33] to model the interactions of monocytes suspended in a fluid, extended to include cell-vessel wall attraction/repulsion via a similar potential approach. The eventual goal of the study is the development of a predictive tool which would be of use during the design and evaluation of engineered grafts, stents, etc. and to provide a model beyond the typical continuum formulation with growth prediction model.
Fig. 6.
Preliminary result of monocyte deposition in idealized blood vessel: (a) before sticking, (b) sticking.
3.5. Platelet adhesion and blood clotting
The repair of capillary blood vessels and the mediation of hemostasis involve the adhesion and aggregation of platelets to certain portions of the vessel wall. Platelets are initially non-adhesive; however, if in contact with the adhesive wounded region of the vessel wall or activated by the above threshold concentration of adenosine diphosphate (ADP), platelets will become adhesive, glue together, and eventually form aggregates to block the blood flow. Such aggregation process was first studied mathematically by Fogelson et al. [34,35]. Here, we used a more simplified model to demonstrate the capabilities of our proposed IFEM method.
Using the IFEM formulation, we study a simple case of blood flow through a capillary vessel, where the middle quarter of the vessel is designated to be injured and capable of activating platelets. The capillary vessel has a diameter of 50 μm and a length of 100 μm. The adhesion between the platelet and injured vessel wall is described by an attractive force combined with an elastic link which provides the resistance of the platelet to shear after bonding to the blood vessel. The activation of the platelet is described by dynamically updating the array which stores information for the activated platelet. Due to the small scale of the platelet (the diameter is around 2 μm), it is treated as a rigid particle immersed in plasma. The density of the platelet is very close to that of the plasma, thus ρs = ρf.
Using the method described above, we modeled the platelet aggregation process. The potential energy is chosen to be a Leonard-Jones type potential between activated platelets: ϕpp(r)= 4∈[(σ/r)12 − (σ/r)6], where r is the distance between two platelets, ∈ is the interaction strengths, and σ is the equilibrium distance. Also, a spring potential between platelets and the injured wall with a spring constant k and equilibrium length λ: ϕpw(r) = k(r − λ)2/2. The total potential energy is ϕ = ϕpp + ϕpw. The forces induced by these potentials are integrated into the IFEM formulation as extra terms in as defined in Eq. (2), thus fFSI,si = −∂ϕ/∂Xi. Our preliminary results are shown in Fig. 7 (simulation time is normalized to the time when steady state flow is reached): At t = 0.0, the initial stage, the platelets are positioned uniformly. A pseudo-periodic boundary condition is used where the platelets leave the right boundary will reenter the left boundary in a random position. At t = 0.33, the first layer of platelets form bonds with the injured vessel wall and become activated as well. More platelets stick to either activated platelets or the injured vessel wall. At t = 0.66, an aggregate of platelets is formed and accumulates, and at t = 1.0, a steady form of platelet clot is formed.
Fig. 7.
Preliminary result of platelets adhesion and aggregation simulation. The streamline of the flow is plotted: (a) t = 0.0, (b) t = 0.33, (c) t = 0.66, (d) t = 1.0.
It should be noticed that red blood cells (RBC) are not included in this model. Actually, RBC also plays an important role in blood clotting: RBCs' dense packing and tumbling will push platelets to be in contact with the injured vessel wall, thus accelerate the aggregation process; secondly, with its large size compared to a platelet, RBC can block the blood flow more efficiently. The coexistence of the RBCs and platelets can be easily achieved in our model. The interaction between activated platelet and RBC is simplified into a spring model and the RBC is assumed to be rigid here. Our preliminary results are shown in Fig. 8. It can be observed that platelets adhere and cover the RBC surface. The collisions between the RBCs and platelets push platelets toward the wound site, and thus help platelets adhere. In the future, the RBC–RBC interaction, RBC–platelet interaction, and platelet–platelet interaction will be combined in a uniform way for the description of the blood clotting and wound healing process.
Fig. 8.
Preliminary result of platelets adhesion in blood flow: (a) t = 0, (b) t = 0.33, (c) t = 0.66, (d) t = 1.0.
3.6. RBC aggregation and blood rheology
The human blood circulatory system has evolved to supply nutrients and oxygen to and carry the waste away from the cells of multicellular organisms through the transport of blood, a complex fluid composed of deformable cells, proteins, platelets, and plasma. Overviews of recent numerical procedures for the modeling of macro-scale cardiovascular flows are available in Ref. [36]. While theories of suspension rheology generally focus on homogeneous flows in infinite domains, the important phenomena of blood flows in micro-circulation depend on the combined effects of vessel geometry, cell deformability, wall compliance, flow shear rates, and many micro-scale chemical, physiological, and biological factors [37]. There have been past studies on shear flow effects on one or two cells, leukocyte adhesion to vascular endothelium, and particulate flow based on continuum enrichment methods [9]. However, no mature theory is yet available for the prediction of blood rheology and blood perfusion through micro-vessels and capillary networks. The different time and length scales as well as large motions and deformations of immersed solids pose tremendous challenges to the mathematical modeling of blood flow at that level.
In this section, we present simulations of biological fluid flow problems with deformable cells using a newly developed modeling technique by Liu et al. [33] with a combination of IFEM [16] and protein molecular dynamics. The effects of cell–cell interaction (adhesive/repulsive) and hydrodynamic forces on RBC aggregates are studied by introducing equivalent protein molecular potentials into the IFEM. For a detailed description of the IFEM coupled with cell interactions and its applications to hemodynamics, we refer the readers to Liu et al. [33]. Here, we concentrate on the rheological aspects of flow systems of arterioles, capillaries, and venules which involve deformable cells, cell–cell interactions, and various vessels. The demonstrated problems are: shear of a cluster of deformable RBCs, normal and sickle RBCs passing through capillary vessels, and finally a single cell squeezing through a micro-vessel constriction.
3.6.1. Discrete RBC model
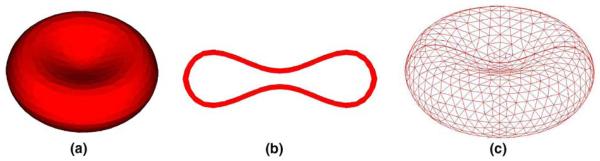
The RBC is modeled as a flexible membrane enclosing an imcompressible fluid. As shown in Fig. 9, to account for both bending and membrane rigidities, the RBC membrane is modeled with a three-dimensional finite element formulation using the Lagrangian description. In this work, a typical membrane is discretized with 1043 nodes and 4567 elements. The static shape of a normal RBC is a biconcave discoid. The material behavior of the RBC membrane is depicted by the Neo-Hookean strain energy function.
Fig. 9.
A three-dimensional finite element mesh of a single RBC model: (a) 3D RBC model, (b) RBC cross-section, (c) RBC mesh.
3.6.2. RBC aggregation
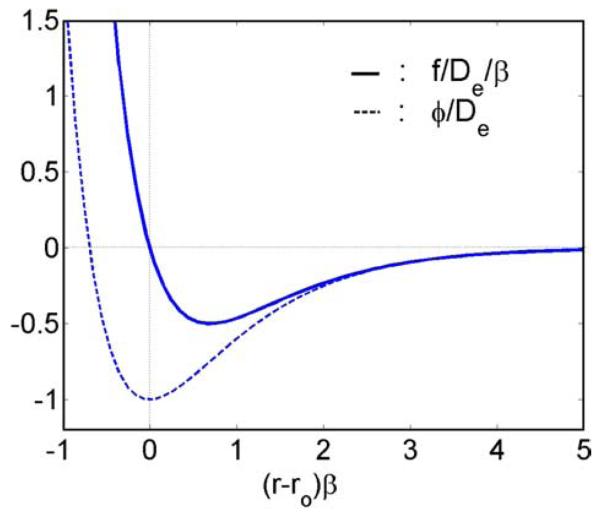
Cell–cell adhesion plays an important role in various physiological phenomena including the recognition of foreign cells. Although the exact physiological mechanisms of RBC coagulation and aggregation are still ambiguous, it has been found that both the RBC surface structure and membrane proteins are key factors in producing adhesive/repulsive forces. The proposed explanations in general fall into two categories: the bridging and adsorption models with adsorption and exclusion of the plasmatic macro-molecules at RBC surfaces, respectively. The primary macro-molecules that cause RBC aggregation are fibrinogen. The depletion layer results in a reduction of osmotic pressure in the gap between nearby RBCs, which consequently produces an attractive force. The repulsive forces include the steric forces due to the glycocalyx and the electrostatic repulsive force induced from the same negative fixed charges at RBC surfaces. Recently, Neu and Meiselman [38] proposed a theoretical model for depletion-mediated RBC aggregation in polymer solutions. The basic behavior of the interaction forces between two RBCs is simply illustrated as the weak attractive and strong repulsive forces at far and near distances. Due to the complexity of the aggregation process, we accumulate the intermolecular force, electrostatic force, and protein dynamics into a potential function, similar to an intermolecular potential. Here we adopt the Morse potential (Fig. 10), found to be capable of generating similar interactional energy versus RBC–RBC separation distance plot given in [38]. As shall be seen later, the aggregation behaviors simulated by this potential qualitatively agree with experimental observations:
| (20) |
| (21) |
where r0 and De are the zero force length and surface energy, respectively, and β is a scaling factor.
Fig. 10.
Non-dimensionalized Morse potential and force.
After the finite element discretization of the solid domain, a sphere with the diameter of the cut-off length is used to identify the cell surface Yc within the influencing domain around the cell surface Xc. Hence, a typical cell–cell interaction force can be denoted as , where r = Xc − Yc, r = ∥Xc − Yc∥, and Γ(Yc) represents the cell surface area within the influencing domain surrounding surface Xc.
To incorporate IFEM with protein molecular dynamics, the cell–cell interaction force is applied on the surfaces of cells:
| (22) |
3.6.3. Blood viscoelasticity
Blood plasma can be accurately modeled with a Newtonian fluid model, yet blood flows do exhibit non-Newtonian or viscoelastic behaviors, in particular under low Reynolds numbers. In a typical blood viscoelasticity test, as the shear rate increases, the blood viscosity decreases initially and eventually reaches a plateau marking the plasma viscosity, and the blood elasticity continues to decrease.
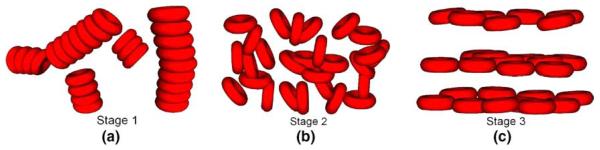
On the microscopic level, RBCs play an important role in the viscoelastic behavior of blood [30]. In the quiescent state, normal RBCs tend to aggregate. Under low shear rate, aggregates are mainly influenced by cell–cell interaction forces; in the mid-shear rate region, RBC aggregates start to disintegrate and the influence of the deformability gradually increases; and under high shear rate, RBCs tend to stretch, align with the flow, and form layers. The illustration of these three different stages is shown in Fig. 11.
Fig. 11.
Blood microscopic changes under different shear rates: (a) low shear region, (b) mid shear region, (c) high shear region.
3.6.4. Cell–cell interaction and shear rate effects
RBC aggregation is one of the main causes of the non-Newtonian behaviors of blood flows. Due to the presence of the cross-linking proteins fibrinogen on cell membranes and globulin in the plasma, RBCs tend to form aggregates called rouleaus, in which RBCs adhere loosely like a stack of coins. The presence of massive rouleaus can impair blood flow through micro- and capillary vessels and cause fatigue and shortness of breath. The variation in the level of RBC aggregation may be an indication of thrombotic disease. In general, cell–cell interaction forces are not sufficient to deform cell membranes. However, the ensuing aggregate could alter the surrounding fluid significantly.
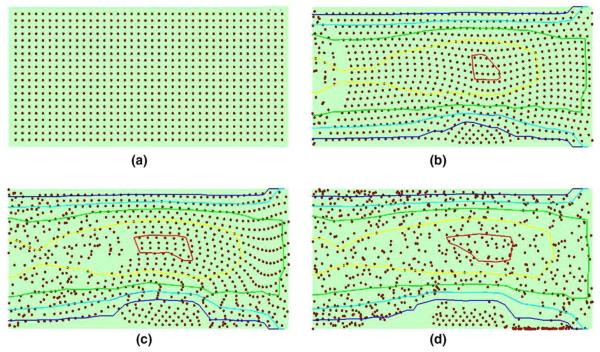
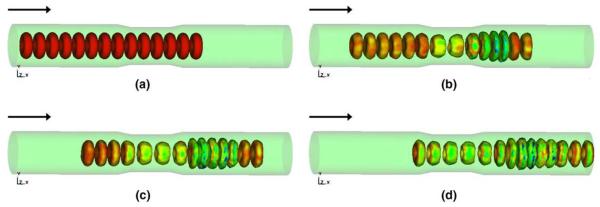
In a set of numerical experiments, we subject the RBC aggregate to low shear rates and observe that RBC aggregate rotates as a bulk, as shown in Fig. 12. With an intermediate shear rate, our numerical simulation demonstrates that after the initial rotations the RBC aggregate aligns with the shear direction and then disaggregates. At higher shear rate, the RBC aggregate completely disintegrates and the cells begin to orient themselves into parallel layers. The disintegration of RBC aggregates with the increase of the shear rate is an indication of the decrease of the macroscopic viscosity, which is consistent with the experimental observation.
Fig. 12.
The shear of a four-RBC cluster at the shear rate of 0.25, 0.5, and 3.0 s−1, respectively. The vectors represent the fluid velocity field.
3.6.5. Shear-rate dependent viscosity
The effective viscosity of the blood is calculated from our simulation by measuring the shear force exerted by the plasma onto the shear velocity boundary. A shear velocity of −U0 and +U0 are applied on the top and bottom boundaries, respectively. The fluid domain has a height of 2H and a length of L. Periodic boundary conditions are used for the left and right boundaries (i.e. the RBCs nodes that move out off the left boundary re-enter through the right boundary).
Without suspended RBCs, the flow velocity in the x-direction is given by u = U0y/H and the shear force on the top and bottom walls are given by F = μLU0/H. With suspended RBCs, the effective viscosity of the blood is defined as
| (23) |
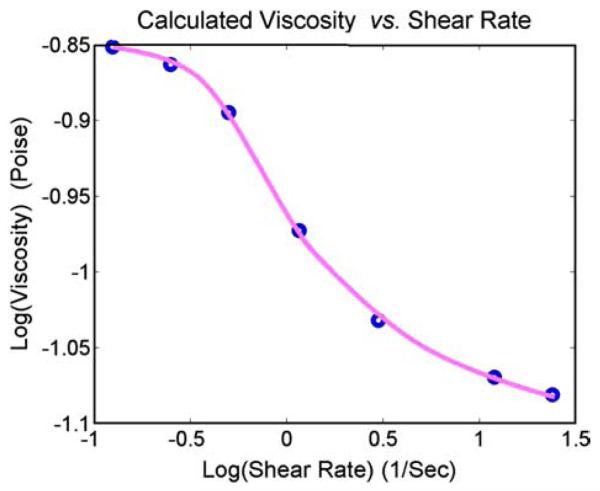
The effective viscosities of the blood at shear rates between 0.125 s−1 and 24 s−1 are plotted in Fig. 13. There is a large drop in the viscosity between the shear rates of 0.5 s−1 and 3.0 s−1, indicating the dispersion of RBC rouleaus. The effective viscosity changes very slowly for shear rate below 0.125 s−1 or above 24 s−1, indicating the massive aggregation of RBCs and partial parallel dispersion of RBCs separately. For a precise comparison to the experimental results, more RBCs have to be used in the simulation, which is too computationally expensive at the current stage. However, to our knowledge, this is the first attempt that links the microscopic mechanism of RBC aggregation to the macroscopic blood viscosity.
Fig. 13.
The calculated effective viscosities of the blood at different shear rate.
3.6.6. Micro- and capillary vessels
Red blood cells are important for blood flows in micro-circulation. The typical diameter of a micro-vessel is 1.5–3 times larger than that of a cell. On the other hand, a capillary vessel diameter is about 2–4 μm, which is significantly smaller. The pressure gradient which drives the flow is usually around 3.2–3.5 kPa. For the chosen diameter and pressure, the Reynolds number in a typical capillary is around 0.01. In fact, in the process of squeezing through capillaries, large deformations of red blood cells not only slow down the blood flow, but also enable the exchange of oxygen through capillary vessel walls.
Sickle cell anemia occurs from genetic abnormalities in hemoglobin. When sickle hemoglobin loses oxygen, the deoxygenated molecules form rigid rods which distort the cell membrane into a sickle or crescent shape. The sickle-shaped cells are both rigid and sticky and tend to block capillary vessels and cause blood flow blockage to the surrounding tissues and organs. To relate blood rheology to sickle cell anemia, we consider the normal and sickle RBCs passing through a micro-vessel contraction. The strong viscous shear introduced by such a flow contraction leads to some interesting phenomena of the RBC aggregation with respect to cell–cell interaction forces and cell deformability. Furthermore, the modeling of this complex fluid–solid system also demonstrates the capability of the coupling of the Navier–Stokes equations with protein molecular dynamics.
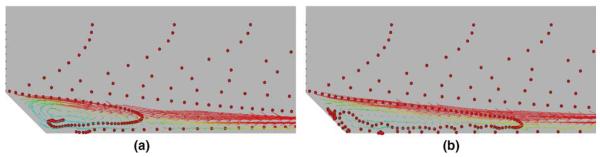
It is shown in Fig. 14, as RBCs pass the diffuser stage of the contraction, the deceleration of the RBCs forms a blockage for the incoming RBCs. Therefore, dilation of RBCs is coupled with the pile-up of RBCs at the outlet of the vessel constriction. Also confirmed in Fig. 15, under the similar flow conditions, rigid and sticky sickle cells eventually block the micro-vessel entrance which will certainly result in de-oxygenation of surrounding tissues.
Fig. 14.
Normal red blood cell flow with inlet velocity of 10 μm/s at different time steps: (a) t = 0, (b) t = 2.3, (c) t = 4.6, (d) t = 6.9.
Fig. 15.
The sickle cell flow with the inlet velocity of 10 μm/s at different time steps: (a) t = 0, (b) t = 2.3, (c) t = 4.6, (d) t = 6.9.
To demonstrate the effect of vessel constriction more clearly, we present a three-dimensional simulation of a single red blood cell squeezing through a capillary vessel. The RBC diameter is 1.2 times larger than that of the capillary vessel, which leads to the divergence of the cytoplasm (internal liquid) to the two ends of the capsule by deforming into a slug during the squeezing process. During the exiting process, there is a radial expansion of the slug due to the convergence of the cytoplasm, which deforms the capsule into an acaleph (or jellyfish) shape. In Fig. 16, four snapshots illustrate various stages of the red blood cell with respect to the capillary vessel. The pressure drop within the capillary vessel is also presented in Fig. 17. The driving pressure here is defined as the average pressure difference between the inlet and outlet of the flow. It is clear that driving pressure level corresponds to the plugged flow which is before the entrance and exit of the deformable cell to the capillary vessel. The increase in pressure for cell to squeeze through capillary with diameter smaller than its size directly leads to an increase in blood's apparent viscosity, a phenomenon called the reverse Fahraeus–Lindqvist effect.
Fig. 16.
Three-dimensional simulation of a single red blood cell (essentially a hollow sphere for simplicity) squeezing through a capillary vessel: (a) t = 0.01, (b) t = 0.49, (c) t = 0.97, (d) t = 1.45.
Fig. 17.
The history of the driven pressure during the squeezing process.
3.7. Cell migration and cell–substrate adhesion
According to their motility, cells can roughly be divided into two categories: passive cells such as RBCs, and active cells such as cancer cells, activated WBCs, and fibroblasts. The deformation of simple passive cells such as red blood cells can be studied by continuum models. However, motility models of most living cells require the detailed accounts of internal structure, spatial granularity, heterogeneity and the active features unique to active cells. We consider a general momentum equation for the effective behavior of the cell material:
| (24) |
where ρ is the material density, v is the velocity field, σpass is the passive stress in the material, and σact is the active stress generated by cytoskeleton filament polymerization or molecular motor induced contraction. A simplistic view is that the passive stress is the response of the material to the imposed flow, e.g. shearing. The passive stress directly depends on the material properties of the fluid and the filaments inside the cell and the structure of the filaments. It is expected to be a viscoelastic response. The filament structure in turn depends on various factors, importantly on the active processes (e.g. polymerization and motors) among others. Thus, the active processes affect the passive stress primarily through the filament structure, i.e. indirectly. The active stress directly depends on the active processes.
Movement of ameboid cells involves at least four stages: protrusion, attachment to the substrate, translocation of the cell body, and detachment of the rear [42-47]. Protrusion of the cell front involves the dynamic assembly/disassembly of actin filaments, as shown in Fig. 18. Protrusions are stabilized by adhesive complexes. Actomyosin filaments contract at the rear and the cytoplasm is squeezed forward. Finally, cells detach the adhesive sites at the rear, allowing the tail of the cell to follow the main cell body. The actin filaments are usually accumulated at the cell–substrate anchoring sites. Cell–substrate adhesion dynamics can usually be tracked through the dynamic changes of the actin filament concentration, which is shown in Fig. 19. We will modulate the continuum simulations to match detailed experiments to be conducted by our collaborators. The experiments will be based on a novel nano-electro-mechanical-system (NEMS) device that can measure the cell–substrate traction force with good sensitivity and spatial resolution. The substrate can be patterned differently with ligands so that the corresponding changes in the cell substrate traction and the cell motion can be quantified. Simultaneous imaging of the cytoskeletal structure will be conducted and compared with the structures from bio fiber suspension simulations to obtain clues regarding the underlying active processes. Continuum simulations of cell migration will be conducted by solving equations of motion together with the conservation equations, e.g. filament and motor concentrations. Appropriate boundary conditions will be used. The cell membrane can be modeled as an elastic material enclosing the cell interior. We are particularly interested in performing simulations that reproduce the cellular motion observed in experiments. To that end, we will use cell–substrate traction forces measured from the experiments as boundary conditions in the continuum simulations discussed below. We will assume a rheological model for the passive stress. The active force distribution will be regarded as the unknown. We will then consider various active force distributions that most closely reproduce the cell motion observed in experiments.
Fig. 18.
Dynamic assembly/disassembly of actin during movement of Dictyostelium amoeba, a representative amoeboid cell. Rhodamine-actin was micro-injected with a volume marker fluorescein-BSA and the signal was rationed such that the intensity represents relative concentration of actin. The panel shows the dynamic change of actin assembly every 30 s. Pixel intensity was converted into color using an algorithm as shown by the color bar [39].
Fig. 19.
F-actin accumulation into cell–substrate anchoring structure. F-actin was visualized by expressing GFP-coronin, an actin-binding protein and imaged by spinning-disk laser confocal microscope at video rate. Pixel intensity was exhibited on the z-axis and then converted into color using an algorithm as shown by the color bar. The image sequence represents the F-actin dynamic every 30 s [40].
As a test case for 3D cell migration simulation, we have used a simple model in which fpass(x) is an elastic stress while fact(x) was prescribed such that realistic cell motion was reproduced. The cell is simply modeled as an elastic material. A non-slip boundary condition is applied at the substrate surface. A dynamically prescribed non-uniform active force is exerted onto the cell body at different migration stages: at the protrusion stage, a pulling force is applied onto the leading edge, representing the force induced by the actin polymerization; at the contraction stage, a contactile force is applied onto the rear part, representing the contactile force induced by the actomyosin filaments; at the translocation stage, no active force is applied. Our preliminary results obtained through the simplified approach described above are shown in Fig. 20.
Fig. 20.
Continuum scale 3D simulation of cell migration. Stages of cell migration—protrusion, contraction, translocation—are shown. Colors indicate the stress inside the cell; the velocity vectors in the surrounding gel are also shown. The traction force vectors on the bottom of the cell are shown on the right. This force field can be measured by some novel nano-electro-mechanical-system (NEMS) devices [41].
Cell adhesion is an important issue in the above simulations. When the cell adheres to the substrate, receptors on the cell membrane bond with ligands on the substrate, forming so-called focal adhesion complexes. Dembo et al. [49] proposed a reaction model (also called an adhesion kinetic equation), where the bond density Nb is calculated as (see Fig. 21).
| (25) |
where Nl and Nr are the ligand and receptor densities, respectively, and kr and kf are the reverse and forward reaction rates, respectively. This reaction model represents a conservation equation of the different species (ligands, receptors, and bonds). The receptor-ligand bonds are modeled as springs with spring constant σ and equilibrium length λ, thus the bond forces are described as a function of bond length L as
| (26) |
In this model, bonds form and break according to some empirical statistical law: Pf = 1 − exp(−konΔt), Pr = 1 − exp(−koffΔt), where Pf is the forward (bond formation) probability and Pr is the bond breaking probability, kon and koff are functions of bond length and temperature. The ligand–receptor bond forces can then be accumulated on the FEM element surface through an integration over the cell surface: σs · n = ∫ΓfL(Xc)dΓ. This adhesion force will be equivalent to a surface traction on the cell membrane. Such an approach has been used by Chang et al. [48] and Dong et al. [50] in the study of white blood cell (WBC) rolling. As a test of this adhesion model, we simulate the steady state rolling speed of a white blood cell (WBC) on a capillary wall (inflow velocity = 40 μm/s). The rolling speed of the WBC without ligand–receptor binding was found to be 7.46 μm/s, while that with a ligand–receptor binding density of 1010 sites/cm2 was 6.55 μm/s. This approach can be applied to model the rolling of multiple deformable WBCs and cell-extracellular-matrix (cell-ECM) adhesion in the future.
Fig. 21.
A schematic figure of the ligand–receptor binding model for cell–substrate interaction. The bonds are modeled as springs. Reproduced from [48].
The contractile force generation inside actomyosin filaments is important to understand contraction during cell migration. The proteins that are capable of transducing chemical energy of ATP to mechanical energy are called molecular motors. The principal molecular motor associated with actin are myosin-I and myosin-II. Myosin-I has a single globular head containing the actin-binding site, while myosin-II is a dimmer with two actin-binding heads attached to a flexible tail. Each actin filament has a specific polarity, pointing from its fast-growing, barbed end to slow-growing, pointed end. Two aligned actin filaments with the same polarity are referred to parallel actin filaments, while the ones with opposite polarities are referred to antiparallel actin filaments. The contactile forces are generated by myosin-II motor mediated sliding of antiparallel actin filaments. Despite the extensive study on how double headed myosin-II motors can induce sliding movements along actin filaments, it is yet to be investigated how tension is generated between focal adhesions that are interconnected by actin filament bundles. The force generated by a single myosin motor has been measured to be around 1 pN by the hydrolysis of an ATP [51]. The myosin-II motor can bind or unbind onto an actin filament at a rate of about 10 times every second. A bound myosin can travel toward the plus end of the actin filament it binds to, at about 1 μm/s. However, when a double headed myosin-II motor binds simultaneously onto two antiparallel actin filaments, it generates two forces of 1 pN per step at its binding sites in two opposite directions, leading to the contactile sliding of the two actin filaments. The unbound motors can diffuse freely in the cytoplasma, described as: 〈(Δx)2〉 = 6Dt, where t is the current time, D is the diffusion coefficient, given as D = kBT/f, and f = 6πηa for a sphere with diameter a in a fluid with the viscosity of η, T is the temperature, and kB is the Boltzman constant. Since only translocation is involved in actin filament sliding, the motion of an actin filament can be described by the standard Lange-vin equation as
| (27) |
where mi is the mass of the ith actin filament, vi is the velocity, fi,m is the force applied by the myosin motors, γ is the drag coefficient, and R is a random term.
It can be expected that the contraction rate of an actomyosin bundle depends on the concentration of myosin motors. For modeling, we assume that an actin filament bundle is made of 60 filaments with an average length and spacing of 1 μm and 15 nm, respectively, and they are composed into a simulation box of 60 μm by 2 μm. The initial configuration is shown in Fig. 22. It is expected that with random polarity and a myosin concentration of 5 μM(1 μM = 10−21 mol/μm3), the average contraction of the actin bundles is around two thirds of their original length. Using this model, we will study the contraction or elongation of actomyosin bundles under various myosin concentrations and actin filament polarity distributions. Such a microscopic simulation will help reveal the contractile force generation mechanism of actin-based cytoskeleton such as stress fibers, which is believed to play significant role in cell migration.
Fig. 22.
A schematic figure of the actomyosin contraction model. Each actin filament is illustrated as an arrow and its polarity is indicated. The double headed myosin-II motors are assumed to be distributed randomly inside the domain.
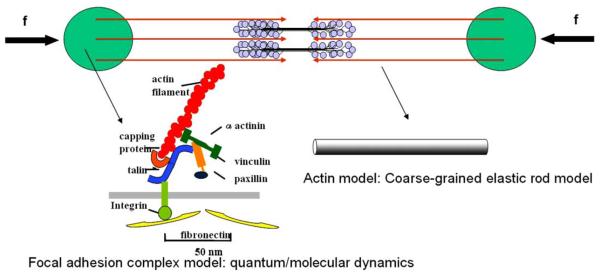
Focal adhesions (FAs) form during spreading or migration of a cell on a substrate coated with ECM components. The assembly of FAs starts from focal adhesion complex that forms at the periphery of a spreading cell or at the leading edge of a migrating cell. The focal adhesion complex is not strong enough to form a firm adhesion and has to be stabilized by assembling together with cytoskeleton structures, such as the formation of stress fibers. Focal adhesion complex matures into FAs when tension induced by the stress fibers or external forces are applied onto the FAs sites. The assembly of FAs involves cross-talk between integrin and other associated proteins. The clustering of integrin is associated with cytoskeletal and signaling networks that promotes actomyosin bundle formation. The formation of actomyosin bundles into stress fibers and the application of tension will, in turn, enhance integrin clustering and FAs development. The FAs development and contractile force generation is thus a positive feedback loop [52]. Combining adhesion and contraction together, we propose a multiscale model that includes a single stress fiber (an actomyosin bundle consisting of actin filaments and myosin motors) interconnecting two focal adhesion sites, as shown in Fig. 23. The positive feedback loop between the FAs and tension will be studied via novel quantum and molecular dynamics simulations of integrin–fibronectin binding, and the conformational transition of integrin associated proteins under mechanical force. The contractile force (tension) generated by the stress fiber will be applied onto the focal adhesion sites via other linking proteins. An actin filament will be modeled as a continuum elastic rod while the associated linking proteins will be modeled as atomistic structures. To achieve this, coupled continuum mechanics and quantum or molecular dynamics simulation [53] will be used.
Fig. 23.
A schematic figure of the actomyosin-focal adhesion model. Each actin filament is illustrated as an arrow and its polarity is indicated. The two circular areas represent the focal adhesion sites. The double headed myosin-II motors are assembled into bipolar ‘mini-filaments’ that connect actin-filaments of opposite polarities. The focal adhesion complex will be modeled by quantum or molecular dynamic simulations. The actin filaments will be modeled as coarse-grained elastic rods. The contractile force will be applied onto the focal adhesion complex via atomistic–continuum coupling methods.
The predictions of the model will be verified by experimental measurements of the cellular forces applied by a stress fiber onto the FAs sites. Such cellular forces will be measured through an elastic membrane supported by a bed of micro-needles, shown in Fig. 24. The elastic membrane will be coated with ligands (an ECM component), so that a cell will contact the membrane by the specific receptor-ligand binding mode. The traction forces will be calibrated by performing the topographic surface mapping of the membrane. Although innovative, this technique does not isolate traction forces from contractile forces and adhesive forces. To overcome this problem, we designed a novel NEMS device as shown in Fig. 25. This device is equipped with a channel filled with a gel to mimic natural ECM. Along the bottom of the device, nano-wires (e.g. carbon nano-tubes; CNTs) will be assembled into a parallel array. The nano-wire sensor will be coated with ligands. In this device, the deflections of the nano-wires can be measured by diffraction-limited microscopy and force patterns and magnitudes will be reconstructed by our simulation techniques. The calibrated traction force distribution pattern, when combined with the actomyosin contraction and focal adhesion models, should provide a valuable information to determine the mechanism of cell migration. The details of the model described here will be addressed separately.
Fig. 24.
An elastic silicone membrane supported by a bed of silicone micro-needles: (a) bed of micro-needles, (b) the membrane supported by the micro-needle bed. The membrane will be coated with ECM ligands such that cells are attached and migrate in a similar manner as they do in vivo. The cellular traction forces posed on every FA will be quantitated by defining the topographic map of the membrane. Image: Courtesy of Juhee Hong, Junghoon Lee, School of Mechanical and Aerospace Engineering, Seoul National University.
Fig. 25.
A schematic drawing of proposed NEMS device to be used to measure the cellular traction forces. The device will be fabricated using nano-wires: (a) side view, (b) top view.
3.8. CNT/DNA assembly simulation
The assembly of nano/bio materials is of great interest and demand since the development of scanning probe microscopes, specifically of atomic force microscope (AFM). Many unique methods have been proposed to immobilize those materials and accomplish an array format. Recently a more precise assembly method was proposed to assemble multi-walled carbon nano-tubes and DNAs by combining an AC with a DC electric field [54-56]. However, its fundamental mechanism was not fully understood due to the complexity of the deposition processes at a small scale, e.g. nano-scale. We are trying to understand the deposition process of nano/bio materials using electric fields through a multiscale/multiphysics modeling method [57].
To model the sorting and assembly of CNTs, the electric fields induced by parallel rectangular and semi-circular shaped electrodes are computed, the dielectrophoretic (DEP) force is evaluated and electroosmotic flow governed by the Navier–Stokes equation is calculated with a slip boundary condition, as described in Section 2.3. The dynamic process of the attraction, alignment, and deposition of CNTs between micro-electrodes is modeled by fully resolving the electrokinetics, drag force, and Brownian motion. Our simulations show that a pure AC field can lead to bundles due to the high electric field gradient near the deposited CNTs (Fig. 26(a)–(f)), and a pure DC field can lead to the deposition of the charged CNTs onto the electrode surface (Fig. 26(g)–(i)). It can be also shown that different electrode geometries can lead to different bundle patterns (Fig. 26(a)–(f)), i.e. parallel bundles for parallel rectangular shaped electrodes and cross-linked bundles for semi-circular shaped electrodes. In the future, we plan to extend this method to model the electrohydrodynamic assembly of flexible, arbitrary-shaped particles. The uniqueness of our proposed method is that we can use direct numerical simulation techniques (no assumptions of the drag force and fluid flow are used) to study the electrohydrodynamic motion of multiple, flexible, arbitrary-shaped nano/bio filaments in complex environments such as complex electrode geometries, composite DC/AC field, etc. All of our calculations are in 3D and are dynamic, thus enabling us to reproduce the assembly in a physical and precise way.
Fig. 26.
Simulation of the assembly of CNTs by the application of AC and DC fields. The first two sets of figures correspond to short CNTs assembling in AC field between semi-circular and parallel electrodes, respectively. The third set of figures is long CNTs alignment in DC field between semi-circular electrodes. All simulations are in 3D: (a) t = 0, (b) t = 0.5, (c) t = 1.0, (d) t = 0,(e) t = 0.5, (f) t = 1.0, (g) t = 0, (h) t = 0.5, (i) t = 1.0.
4. Conclusions
In this paper, we presented a numerical scheme, the immersed finite element method (IFEM), for solving complex fluid–structure interaction problems. In comparison with the IB method, this approach has the following advantages: the structural models in IFEM are not restricted to one-dimensional volumeless structures such as fibers; instead, they may occupy finite volumes in the fluid. Finite elements are used to discretize the submerged solid and as a consequence the calculated stress are more realistic and accurate. In addition, in IFEM, different material laws can be assigned to the submerged solid.
The higher ordered RKPM delta function has the ability to handle non-uniform grids and is particularly useful for fluid domains with arbitrary geometries and boundaries. Finally, unlike the periodic boundary conditions implemented in most IB applications, essential and natural boundary conditions in the context of finite element methods are relatively easy to implement in IFEM.
For the applications of IFEM to biological systems, we studied fluid–structure interaction problems encountered in the human blood circulation system. A heart model is being constructed from MRT data [31]. The deployment process of an angioplasty stent has been simulated. The preliminary results of monocyte and platelet deposition have been presented. Blood rheology, in particular, the shear-rate dependent de-aggregation of RBC clusters and the transport of deformable cells, has been modeled. Furthermore, the IFEM has been combined with electrokinetics to study the mechanisms of bio-NEMS devices. In these 3D dynamic simulations, the fluid flow and solid deformation/motion are reasonably captured.
In the near future, using recently developed novel NEMS devices, we will be able to simultaneously visualize the cellular scale structures and measure the cellular traction forces and cell-ECM adhesion forces. The research proposed in this paper should provide a powerful means to understand the structural and functional aspects of molecules, cells and tissues. Ultimately the outcome may have great impact in a broad range of medical sciences.
Acknowledgment
The support of this research by the National Science Foundation (NSF), the National Aeronautics and Space Administration (NASA), the NSF Summer Institute on Nano Mechanics and Materials, and NSF IGERT is gratefully acknowledged.
References
- 1.Tezduyar TE. Stabilized finite element formulations for incompressible-flow computations. Adv. Appl. Mech. 1992;28:1–44. [Google Scholar]
- 2.Tezduyar TE. Finite element methods for flow problems with moving boundaries and interfaces. Arch. Comput. Methods Engrg. 2001;8(2):83–130. [Google Scholar]
- 3.Huerta A, Liu WK. Viscous flow with large free surface motion. Comput. Methods Appl. Mech. Engrg. 1988;69:277–324. [Google Scholar]
- 4.Hughes TJR, Liu WK, Zimmerman TK. Lagrangian–Eulerian finite element formulations for incompressible viscous flows. Comput. Methods Appl. Mech. Engrg. 1981;29:329–349. [Google Scholar]
- 5.Liu WK. Finite element procedures for fluid–structure interactions and application to liquid storage tanks. Nucl. Engrg. Des. 1981;65:221–238. [Google Scholar]
- 6.Liu WK, Gvildys J. Fluid–structure interaction of tanks with an eccentric core barrel. Comput. Methods Appl. Mech. Engrg. 1986;58:51–77. [Google Scholar]
- 7.Liu WK, Ma DC. Computer implementation aspects for fluid–structure interaction problems. Comput. Methods Appl. Mech. Engrg. 1982;31:129–148. [Google Scholar]
- 8.Wagner GJ, Ghosal S, Liu WK. Particulate flow simulations using lubrication theory solution enrichment. Int. J. Numer. Methods Engrg. 2003;56(9):1261–1289. [Google Scholar]
- 9.Wagner GJ, Moës N, Liu WK, Belytschko TB. The extended finite element method for rigid particles in stokes flow. Int. J. Numer. Methods Engrg. 2001;51(3):293–313. [Google Scholar]
- 10.Hu HH, Patankar NA, Zhu MY. Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 2001;169:427–462. [Google Scholar]
- 11.Johnson A, Tezduyar TE. Advanced mesh generation and update methods for 3d flow simulations. Comput. Mech. 1999;23:130–143. [Google Scholar]
- 12.Peskin CS. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977;25:220–252. [Google Scholar]
- 13.Peskin CS, McQueen DM. A three-dimensional computational method for blood flow in the heart. I. Immersed elastic fibers in a viscous incompressible fluid. J. Comput. Phys. 1989;81(2):372–405. [Google Scholar]
- 14.Peskin CS, McQueen DM. Computational biofluid dynamics. Contemp. Math. 1993;141:161–186. [Google Scholar]
- 15.McQueen DM, Peskin CS. Shared-memory parallel vector implementation of the immersed boundary method for the computation of blood flow in the beating mammalian heart. J. Supercomput. 1997;11:213–236. [Google Scholar]
- 16.Zhang L, Gerstenberger A, Wang X, Liu WK. Immersed finite element method. Comput. Methods Appl. Mech. Engrg. 2004;193(21–22):2051–2067. [Google Scholar]
- 17.Wang X, Liu WK. Extended immersed boundary method using FEM and RKPM. Comput. Methods Appl. Mech. Engrg. 2004;193(12–14):1305–1321. [Google Scholar]
- 18.Hughes TJR, Franca LP, Balestra M. A new finite element formulation for computational fluid dynamics: V. Circumventing the Babus̆ka–Brezzi condition: a stable Petrov–Galerkin formulation of the Stokes problem accommodating equal-order interpolations. Comput. Methods Appl. Mech. Engrg. 1986;59:85–99. [Google Scholar]
- 19.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 20.Wang X. On the discretized delta function and force calculation in the immersed boundary method. In: Bathe KJ, editor. Computational Fluid and Solid Mechanics. Elsevier: 2003. pp. 2164–2169. [Google Scholar]
- 21.Liu WK, Jun S, Zhang YF. Reproducing Kernel particle methods. Int. J. Numer. Methods Fluids. 1995;20:1081–1106. [Google Scholar]
- 22.Liu WK, Chen Y, Uras RA, Chang CT. Generalized multiple scale reproducing Kernel particle methods. Comput. Methods Appl. Mech. Engrg. 1996;139:91–158. [Google Scholar]
- 23.Li S, Liu WK. Meshfree and particle methods and their applications. Appl. Mech. Rev. 2002;55:1–34. [Google Scholar]
- 24.Li S, Liu WK. Meshfree Particle Methods. Springer-Valerg; 2004. [Google Scholar]
- 25.Saad Y, Schultz MH. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986;7(3):856–869. [Google Scholar]
- 26.Zhang L, Wagner GJ, Liu WK. A parallelized meshfree method with boundary enrichment for large-scale CFD. J. Comput. Phys. 2002;176:483–506. [Google Scholar]
- 27.Jones TB. Electromechanics of Particles. Cambridge University Press; New York: 1995. [Google Scholar]
- 28.Solomentsev Y, Bohmer M, Anderson JL. Particle clustering and pattern formation during electrophoretic deposition: a hydrodynamic model. Langmuir. 1997;13:6058–6068. [Google Scholar]
- 29.Sharma N, Patankar N. Direct numerical simulation of the Brownian motion of particles by using fluctuating hydrodynamic equations. J. Comput. Phys. 2004;201(2):466–486. [Google Scholar]
- 30.Fung YC. Biomechanics: Circulation. Springer-Verlag; 1996. [Google Scholar]
- 31.Liu WK, Chen X, Wang X, Zhang Y, Bajaj C, Hughes T. A study of a three-dimensional heart model using immersed continuum method. ICES Technical Report. 2004 [Google Scholar]
- 32.Gay M, Zhang L, Liu WK. Stent deployment using immersed finite element method. Comput. Methods Appl. Mech. Engrg. 2005 accepted for publication. [Google Scholar]
- 33.Liu Y, Zhang L, Wang X, Liu WK. Coupling of Navier–Stokes equations with protein molecular dynamics and its application to hemodynamics. Int. J. Numer. Methods Fluids. 2004;46(1237–1252) [Google Scholar]
- 34.Fogelson A. A mathematical model and numerical method for studying platelet adhesion and aggregation during blood clotting. J. Comput. Phys. 1985;56:111–134. [Google Scholar]
- 35.Wang NT, Fogelson A. Computational methods for continuum models of platelet aggregation. J. Comput. Phys. 1999;151:649–675. [Google Scholar]
- 36.Taylor CA, Hughes TJR, Zarins CK. Finite element modeling of blood flow in arteries. Comput. Methods Appl. Mech. Engrg. 1998;158:155–196. [Google Scholar]
- 37.Diamond SL. Reaction complexity of flowing human blood. Biophys. J. 2001;80:1031–1032. doi: 10.1016/S0006-3495(01)76083-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Neu B, Meiselman HJ. Depletion-mediated red blood cell aggregation in polymer solutions. Biophys. J. 2002 November;83:2482–2490. doi: 10.1016/S0006-3495(02)75259-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yumura S, Fukui Y. Spatiotemporal dynamics of actin concentration during cytokinesis and locomotion in dictyostelium. J. Cell Sci. 1998;111:2097–2108. doi: 10.1242/jcs.111.15.2097. [DOI] [PubMed] [Google Scholar]
- 40.Fukui Y, de Hostos EL, Yumura S, Yumura TK, Inoue S. Architectural dynamics of eupodia suggest their role for invasive locomotion in dictyostelium. Exp. Cell Res. 1999;249:33–45. doi: 10.1006/excr.1999.4445. [DOI] [PubMed] [Google Scholar]
- 41.Liu Y, Hsu H, Patankar N, Liu WK. Three dimensional simulation of cell migration. in preparation. [Google Scholar]
- 42.Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophys. J. 1996;71(6):3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mitchison TJ, Cramer LP. Actin-based cell motility and cell locomotion. Cell. 1996;84(3):371–379. doi: 10.1016/s0092-8674(00)81281-7. [DOI] [PubMed] [Google Scholar]
- 44.Sheetz MP, Felsenfeld D, Galbraith CG, Choquet D. Cell migration as a five-step cycle. Cell Behav.: Control Mechanism Motility. 1999;65:233–243. [PubMed] [Google Scholar]
- 45.Gracheva ME, Othmer HG. A continuum model of motility in ameboid cells. Bull. Math. Biol. 2004;66(1):167–193. doi: 10.1016/j.bulm.2003.08.007. [DOI] [PubMed] [Google Scholar]
- 46.Stossel TP. On the crawling of animal cells. Science. 1993;260(5111):1086–1094. doi: 10.1126/science.8493552. [DOI] [PubMed] [Google Scholar]
- 47.Fukui Y. Toward a new concept of cell motility: cytoskeletal dynamics in amoeboid movement and cell division. Int. Rev. Cytol. 1993;144(85–127) doi: 10.1016/s0074-7696(08)61514-4. [DOI] [PubMed] [Google Scholar]
- 48.Chang KC, Tees DFJ, Hammer DA. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. USA. 2000;97(21):11262–11267. doi: 10.1073/pnas.200240897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dembo M, Torney DC, Saxman K, Hammer D. The reaction limited kinetics of membrane to surface adhesion and detachment. Proc. R. Soc. London. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 50.Dong C, Cao J, Struble EJ, Lipowsky HW. Mechanics of leukocyte deformation and adhesion to endothelium in shear flow. Ann. Biomed. Engrg. 1999;27(3):298–312. doi: 10.1114/1.143. [DOI] [PubMed] [Google Scholar]
- 51.Ishijima A, Doi T, Sakurada K, Yanagida T. Sub-piconewton force fluctuations of actomyosin in vitro. Nature. 1991;352(301–306) doi: 10.1038/352301a0. [DOI] [PubMed] [Google Scholar]
- 52.Sastry SK, Burridge K. Focal adhesions: a nexus for intracellular signaling and cytoskeletal dynamics. Exp. Cell Res. 2000;261:25–36. doi: 10.1006/excr.2000.5043. [DOI] [PubMed] [Google Scholar]
- 53.Liu WK, Karpov EG, Zhang S, Park HS. An introduction to computational nanomechanics and materials. Comput. Methods Appl. Mech. Engrg. 2004;193(17–20):1529–1578. [Google Scholar]
- 54.Chung JY, Lee KH, Lee JH, Ruoff RS. Toward large-scale integration of carbon nanotubes. Langmuir. 2004;20(8):3011–3017. doi: 10.1021/la035726y. [DOI] [PubMed] [Google Scholar]
- 55.Chung J, Lee J, Ruoff RS, Liu WK. Nanoscale gap fabrication and integration of carbon nanotubes by micromachining; Solid-State Sensor, Actuator, and Microsystems Workshop; Hilton Head, SC. June 2–6, 2002. [Google Scholar]
- 56.Chung J, Lee J, Ruoff RS, Liu WK. Integration of single multi-walled carbon nanotube on microsystems; ASME Conference, IMECE2002-33325; New Orleans, Louisiana. November 17–22, 2002. [Google Scholar]
- 57.Liu Y, Chung J, Liu WK, Ruoff RS. 3-Dimensional simulation and experiments on dielectrophoretic assembly of nanowires. 2005 in preparation. [Google Scholar]