Isotropic isotopy and symplectic null sets

Abstract

Capacity is an important numerical invariant of symplectic manifolds. This paper studies when a subset of a symplectic manifold is null, i.e., can be removed without affecting the ambient capacity. After examples of open null sets and codimension-2 non-null sets, geometric techniques are developed to perturb any isotopy of a loop to a hamiltonian flow; it follows that sets of dimension 0 and 1 are null. For isotropic sets of higher dimensions, obstructions to the perturbation are found in homotopy groups of the orthogonal groups.

Among all manifolds with geometric structures, symplectic manifolds are singled out by the property that every dynamics induced by a potential on them (hamiltonian dynamics) preserves both the level of the potential and the underlying structure. Symplectic capacity, defined in terms of hamiltonian dynamics, has been instrumental in the progress of several fields: its properties explain fundamental facts of symplectic topology (nonsqueezing, symplectic rigidity, etc.) as well as yield new qualitative information on hamiltonian systems (e.g., almost sure existence of a periodic orbit). But capacity is notoriously hard to compute. A natural approach to making it more computable is to study its behavior under various operations on symplectic manifolds. The present paper outlines results (Corollaries 7–9) in the simplest case: what subsets are null, i.e., can be removed from a manifold without affecting the ambient capacity?

Definitions

Let (M, ω) be a symplectic manifold. A function h on M generates a vector field X_h such that ι_Xhω = −dh. The flow ϕ^t of X_h is a hamiltonian flow, h is its hamiltonian. At each t a hamiltonian flow is a symplectomorphism, i.e., (ϕ^t)*ω = ω. A subset N of M is isotropic if ω|_N = 0 and dim N < ½dim M. If γ is a contractible loop in M bounding a 2-disk D, the area of γ is ∫_Dω. The area is independent of D mod π₂(M); whenever areas are mentioned, some choice of a class of D will be implicit. A canonical example of a symplectic manifold is ℝ^2m with coordinates p_i, q_i, and ω = ∑ dp_i ∧ dq_i. B(r) and Z(r) stand for the subsets defined, respectively, by ∑ p_i² + q_i² ≤ r² and p₁² + q₁² ≤ r².

Now we recall the definition of capacity (ref. 1). A hamiltonian h is admissible if h ≥ 0, h has compact support, h ≡ max h on some open U and h ≡ 0 on some open V ⊃ ∂ M, and X_h has no periodic orbit of period ≤1. The numerical invariant c(M, ω) = sup{max h | h is admissible} is called the capacity of (M, ω). We call a subset N of M null if c(M/N) = c(M).

Examples of Null Sets

Null sets come in many shapes and dimensions. Open sets may be null: Gromov’s nonsqueezing theorem (ref. 2) implies that every subset of Z(r)/B(r) is null in Z(r). Sets of codimension 2 need not be null: c(S²(ɛ) × ℝ^2m−2) = ∞, but if we remove N = pt × ℝ^2m−2, then c(S²(ɛ) × ℝ^2m−2/N) = 4πɛ². Every algebraic subvariety is null in ℂP^m; this follows from ref. 3.

Isotropic Isotopy and Obstructions

One method for proving a set null consists of using a hamiltonian flow to move the set into a region that goes unnoticed by capacity. The existence of such a region is guaranteed by the admissible type of hamiltonians whose heights approximate the capacity: their graphs have open zero-levels (V, above) that can accommodate the boundary resulting from the removal of the moved set.

Lemma 1. If N ⊂ M can be isotoped by a hamiltonian flow into an arbitrarily small ball or neighborhood of ∂M, then N is null.

In view of applying Lemma 1, we devise geometric tricks for extending an isotopy of a submanifold to an ambient hamiltonian flow.

Proposition 2. Let N_t be an isotopy of an isotropic submanifold N ⊂ M. It extends to an ambient hamiltonian flow on M if and only if: (i) N_t remains isotropic for all t; and (ii) the areas of cycles generating H₁(N_t) are constant.

An isotopy that satisfies Proposition 2, (i) and (ii), is called an isotropic isotopy. When dim N = 0 or 1, (i) is automatic. Item (ii) is controlled by

Theorem 3. When dim M ≥ 4, an isotopy between loops of equal area can always be perturbed so as to keep the area constant during the isotopy.

The proof is in two parts. First, the “relative Darboux theorem” (ref. 4) reduces the problem to perturbing a segment in ℝ^2m. Second, we perform the perturbation as depicted.

In (c), the segment has acquired the additional shaded area. By stacking enough such “wiggles” along the p₁-direction, we can compensate for any variation in area, while confining the perturbation inside a C⁰-small neighborhood.

When dim N ≥ 2, Proposition 2, (i), is no longer automatic. An inductive procedure for achieving Proposition 2, (i), reveals an obstruction that we now describe.

Let N₀, N₁ be isotropic submanifolds in the same isotopy class and with the same areas of 1-cycles. Take isotopic triangulations on them. Isotope the 1-skeleton of N₀ onto the 1-skeleton of N₁ and perturb it so that the isotopy extends to an ambient hamiltonian flow; along this flow, drag the rest of N₀. Now the inductive step takes the form

Problem 4. Given a pair of isotropic n-cells sharing an isotropic boundary (n − 1)-sphere, find an isotropic isotopy of one cell to the other relative to the boundary.

Problem 4, as well as the discussion below, are amenable to an h-principle as follows. Weinstein’s isotropic neighborhood theorem realizes near each cell L a symplectic copy of an open neighborhood U of the zero section of T*L. The problem then is to isotope the symplectic embeddings U → M. This is an exercise in ref. 5: “Prove the parametric h-principle for isometric embeddings … ” Although the answer is unwritten, it certainly seems well known to experts. Here, however, we adopt an elementary method.

For simplicity we proceed under the assumption that the cells lie within a chart symplectomorphic to a topological ball in ℝ^2m. The problem splits into the problem on the boundary jet and the homotopy problem for the interior of the cell.

Counting dimensions, we find that the first of these is solvable provided the dimension of the isotropic submanifold is moderately low. Let N ⊂ M be isotropic. A section X of T_NM is an isotropic normal field on N if it is everywhere independent of TN and ℝX + TN is isotropic.

Theorem 5. Let S ⊂ M be an isotropic (n − 1)-sphere, dim M = 2 m, and X₀, X₁ be isotropic normal fields on S. If n < 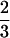(m+1), then X₀ and X₁ are homotopic through isotropic normal fields X_t.

This reduces Problem 4 to the case where the n-cells are the two hemispheres of an immersed n-sphere S′⊂ ℝ^2m folded along the equator. Let us denote by I(n, 2m) the space of all isotropic n-planes in ℝ^2m. The Gauss map g : S′ → I(n, 2m) associates to each x ∈ S′ the isotropic tangent plane of S′ at x. The obstruction to our problem lies in π_n[I(n, 2m)]. An explicit homotopy along a conic shows

Proposition 6. I(n, 2m) is homotopy-equivalent to U(m)/[O(n)× U(m − n)].

Since U(m)/U(m − n) is aspherical up to high enough dimensions, the obstructions in fact arise from π_n−1[O(n)].

Applications to Null Sets

Return to null sets. The tactics is always to reduce to the situation of Lemma 1.

Corollary 7. Every set that lies in a lagrangian disk is null.

Indeed, Proposition 2 applies to the retraction of the disk along itself to a point. A lagrangian disk is a disk of dimension =½dim M on which ω vanishes.

In particular, points and segments are null. Moreover, from Theorem 3 we deduce

Corollary 8. If dim M ≥ 4, then every loop contractible in M is null.

It suffices to note that an arbitrarily small ball can include a loop of any prescribed area: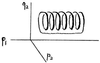

Remark.

The product of such a “spring” in ℝ⁴ with another copy is an isotropic 2-torus; forming the connect-sum of such tori, we can construct, inside an arbitrarily small ball, an isotropic 2-manifold of any genus and with any areas for its 1-cycles.

Corollary 9. If N ⊂ M is isotropic, lies in a chart symplectomorphic to a star-shaped subset of ℝ^2m, and H₁(N) = 0, then N is null.

In this case the homothetic retraction to the origin of the chart satisfies the conditions of Proposition 2.