Using stochastic models calibrated from nanosecond nonequilibrium simulations to approximate mesoscale information

Abstract

We demonstrate how the surrogate process approximation (SPA) method can be used to compute both the potential of mean force along a reaction coordinate and the associated diffusion coefficient using a relatively small number (10–20) of bidirectional nonequilibrium trajectories coming from a complex system. Our method provides confidence bands which take the variability of the initial configuration of the high-dimensional system, continuous nature of the work paths, and thermal fluctuations into account. Maximum-likelihood-type methods are used to estimate a stochastic differential equation (SDE) approximating the dynamics. For each observed time series, we estimate a new SDE resulting in a collection of SPA models. The physical significance of the collection of SPA models is discussed and methods for exploiting information in the population of estimated SPA models are demonstrated and suggested. Molecular dynamics simulations of potassium ion dynamics inside a gramicidin A channel are used to demonstrate the methodology, although SPA-type modeling has also proven useful in analyzing single-molecule experimental time series [J. Phys. Chem. B 113, 118 (2009)].

INTRODUCTION

Recent single-molecule studies^{1, 2, 3, 4, 5} have provided a new motivation for using time series of low-dimensional system observables to summarize the state of a complex atomistic system. In this work, we use data-driven models^{6, 7, 8} to approximate mesoscopic and macroscopic quantities associated with such observables. The methods utilize recent results in nonequilibrium statistical mechanics.^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18} The main interest is using nonequilibrium trajectories to extract both equilibrium quantities and kinetic parameters which are sometimes used to describe dynamics occurring over longer time scales than those explored in the simulation. The surrogate process approximation (SPA) method^{7, 8} is used to assist in these tasks. The SPA modeling ideas have also proven to be relevant to understanding dynamical information contained in experimental time series containing measurement noise.^{19, 20}

The SPA method uses recent time series techniques^{7, 19, 21, 22, 23, 24} to estimate a low-dimensional stochastic differential equation (SDE) approximating the dynamics of an observed signal coming from a computer simulation or experiment. In this article, we use such SDEs to approximate various statistical properties associated with steered molecular dynamics (SMD) simulations of ion transport across a channel protein. A new SPA model is estimated for each observed trajectory in a “pathwise,” or trajectorywise, fashion. This is different from what we refer to as “ensemble” approaches sometimes used in statistical physics.²⁵ Novel contributions of this work are associated with using this collection of SPA models to provide quantitative statistical information. For example, uncertainty quantification on point and function estimates are demonstrated and applied to potential of mean force (PMF) and diffusion coefficient estimates calibrated from nonequilibrium time series data. The uncertainty bands we construct for the PMF respect the temporal dependence (and continuity) of the nonequilibrium work paths²⁶ while at the same time accounting for the inherent variability induced by both the initial configuration and “standard” fast-scale thermal fluctuations.^{19, 27} The variability observed in the population of SPA models is partially due to degrees of freedom not explicitly modeled. Physical interpretations of the confidence bands are discussed and possible methods for exploiting information contained in the confidence bands are suggested. We demonstrate that by using a relatively small number (10–20) of 1 ns long nonequilibrium MD trajectories one can use the SPA models to make predictions comparable to established umbrella-sampling-type methods that aim at extracting the PMF^{16, 28, 29} and diffusion coefficient³⁰ in a complex system.³¹

In this paper we apply the SPA method to study potassium ion (K⁺) transport through an all-atom model of the gramicidin A (gA) ion channel. In particular, we use a small number of fast, nonequilibrium SMD pulling trajectories of K⁺ through the gA channel to reconstruct the corresponding PMF and to estimate the diffusion constant of the ion within the pore. Our study of this system was motivated by the fact that gA is a channel protein that has been extensively studied both experimentally and theoretically. The PMF of K⁺ along the axis of the gA channel was determined in several previous studies by means of equilibrium all-atom MD simulations by employing the widely used umbrella sampling method.^{28, 32, 33, 34, 35, 36} Recently, an attempt of reconstructing the PMF from unidirectional SMD pullings of K⁺ by employing the Jarzynski equality (JE) method failed.^{31, 37} This negative result prompted the authors to conclude that such nonequilibrium methods are not suitable for calculating PMFs in complex biomolecular systems. However, in a very recent publication,¹⁶ we have demonstrated that a small number of fast, bidirectional, i.e., forward (F) and time-reversed (R), SMD pulling trajectories can be efficiently used to compute the PMF of K⁺ in the gA channel, as well as in other nontrivial biomolecular systems. The JE method fails to reproduce a reasonable PMF because it grossly underestimates the mean dissipative work determined directly from the few unidirectional pulling trajectories.¹⁶ The FR method¹⁵ is based on Crooks’ fluctuation theorem,^{11, 38} which is more general than the JE. In Ref. 16 the FR method is applied to approximate the free energy differences and PMF associated with the steered reaction coordinate. Besides providing an efficient way for calculating PMFs, the FR method can also be used to approximate the position dependent diffusion coefficient of the ion within the channel. However, the FR method is exact only when the work distribution along the SMD paths is Gaussian. When this is not the case, the FR method may fail. In addition it is difficult to estimate the error for the predicted PMF. By contrast, the SPA method is not limited by the Gaussian distribution of the external work along the SMD pulling trajectories and is also capable of providing an error estimate for the computed PMF and diffusion coefficient. The SPA method can determine the local diffusion coefficient of K⁺ along the axis of the gA channel in both F and R pulls; the method can also be used to provide the FR method with new simulated data to estimate the diffusion coefficient and confidence bands on this estimate. In this work, we apply the SPA method to the same SMD simulations reported in Ref. 16. We use two recent bidirectional methods^{16, 17} to obtain the PMF using simulated data from a collection of SPA models calibrated from a small number of SMD trajectories and discuss two methods for estimating the diffusion coefficient using these data.

The article is organized as follows: Section 2 presents the theoretical background and outlines the methods used. Section 3 presents the results and discussion and Sec. 4 provides the conclusion.

THEORY AND METHODS

Time-dependent diffusion models

Diffusion models have been used in various models of complex systems.^{7, 8, 14, 19, 39, 40, 41, 42, 43} We attempt to fit a collection of nonlinear SDEs (Ref. ⁴⁴) given an ensemble of observed trajectories coming from SMD simulations.^{14, 15} The equations governing the dynamics are assumed to have the following form:

$$d{z}_t=\mu \left(z_t,t\right)dt+\sqrt{2}\sigma \left(z_t\right)d{B}_t,$$ (1)

where B_t represents the standard Brownian motion (or Wiener process), μ(⋅,⋅) is the time-dependent drift function, and σ²(⋅) represents the diffusion function associated with the SDE. In both cases we assume that for a given trajectory, these functions are deterministic and smooth differentiable functions. To avoid technical complications we will simply assume that the drift and diffusion functions are infinitely differentiable, but this assumption can be relaxed if needed.²³ Note that the diffusion function is different than the diffusion coefficient typically used in classical statistical mechanics;^{45, 46} we denote the latter quantity by $\tilde{D}$ throughout.

It is known that a Fokker–Planck-type, or a forward Kolmogorov, partial differential equation (PDE) is associated with the SDE above:⁴⁷

$$\frac{\partial }{\partial t}f\left(z,t\right)=-\frac{\partial }{\partial z}\left[\mu \left(z,t\right)f\left(z,t\right)\right]+\frac{{\partial }^2}{\partial z^2}\left[{\sigma }^2\left(z\right)f\left(z,t\right)\right],$$ (2)

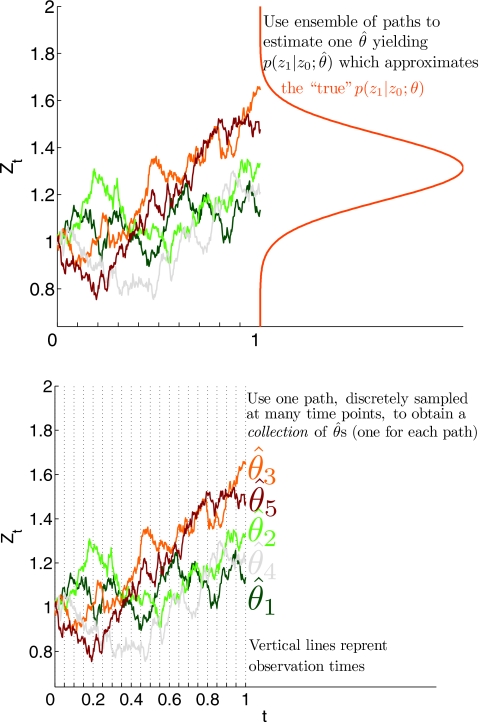
where f(z_i,t_i)≡p(z_i∣z_i−1) denotes the conditional probability density associated with observing the value of the reaction coordinate z_i at time t_i given the state value z_i−1 at time t_i−1 and the drift and diffusion functions. This PDE is often utilized in pathwise estimation (i.e., only one time series is used to determine the SDE) and also in ensemble based methods. These two different viewpoints are illustrated in Fig. 1 and a MATLAB script demonstrating a pathwise estimation procedure is provided in the supplementary materials;⁴⁸ details of the pathwise estimation procedure we use are discussed further in Sec. 2D.

Figure 1.

Illustration of ensemble (top) and pathwise (bottom) methods for estimating a SDE from observations. Five sample paths are shown each possessing a deterministic common initial condition (the two panels plot the same paths). An ensemble method would use the collection of paths at a fixed time and attempt to find the parameter “θ” yielding the best fit to the observed conditional density consistent with a Fokker–Planck equation [see Eqs. 1, 2]. The exact conditional density associated with the sample paths at “time 1” is plotted in red with z_t (y axis) vs p(z₁∣z₀) (x axis). The p(z₁∣z₀) units are omitted for clarity; note how the sample paths fall within a region associated with high probability in regards to p(z₁∣z₀). Examples of ensemble methods applied to atomistic data are discussed in Refs. ⁴², ⁴³. A pathwise method would use each observed time series to construct a new SDE. The estimated SDE function can be combined to provide one model if desired, but we stress in this paper that this can cause a loss in accuracy of PMF and diffusion coefficient estimates calibrated from these surrogates. In discrete time, this is often accomplished by solving/approximating the Fokker–Planck PDE for many different values of θ (Ref. ⁸²). A discrete maximum likelihood estimate would use the observed time series to find the $\widehat{\theta }$ maximizing the associated “log likelihood” ${\sum }_{i=0}^N\log \left[p\left(z_{i+1}\mid z_i;\theta \right)\right]$. In this example the initial condition does not contribute to the sum because it is assumed to be a fixed delta function distribution. Examples demonstrating this on time-dependent nonequilbrium trajectories can be found in Refs. ⁷, ⁸, ¹⁹, ²⁰.

Traditionally in statistical physics applications, one attempts to estimate a single coarse-grained SDE summarizing the system dynamics.^{10, 30, 43, 49} In contrast we estimate, for each observed time series, a new SDE resulting in a collection of SPA models. A collection of models may be needed to describe a complex (many-body) system for a variety of reasons. For example, at time scales typically accessible to simulations, it is known that artifacts of ignored degrees of freedom can make the validity of using a mesoscopic diffusive model calibrated from atomistic time series questionable.^{10, 27, 30, 39, 43, 49} In other words, measurable non-Markovian noise can result from not including certain important degrees of freedom in the diffusive model (e.g., particle momentum³⁹). Given sufficient time, some of these non-Markovian effects “average out.”^{27, 50, 51} All SPA models presented here passed the type of goodness-of-fit tests demonstrated in Refs. ^{19, 27}. The tests indicated that fast-scale non-Markovian noise sources, such as z momentum, were negligible. However, we should stress that each observed time series resulted in a different stochastic model. That is, the effective drift and diffusion functions estimated from different time series have statistically significant differences,^{8, 19} and hence we observe a collection of SPA models. The motivation for estimating a collection of SPA models from time series is discussed throughout.

Free energy and PMF computations

The free energy difference between two states and the PMF along a specified reaction coordinate are well-defined quantities in classical statistical mechanics and quantitative estimates of these equilibrium properties have several potential applications.^{13, 14} Denote the free energy difference between two states by ΔF. We are interested in computing ΔF between the channel entrance (z=15 Å) and channel center (z=0 Å) because it is needed to compute U(z) along the channel interior using the method of Ref. 17. Equilibrium methods for computing U(z) and ΔF often require a computationally expensive sampling of configurations from a stationary distribution. One appeal of using nonequilibrium methods to approximate these equilibrium quantities is the potential to avoid the cost of building multiple histograms summarizing the stationary distribution at different state points inherent to umbrella-sampling-type computations.^{28, 29}

When nonequilibrium data are used to approximate these quantities several complications can be encountered. For example, suppose a single nonequilibrium time series is used to estimate a SDE. If one attempts to directly relate the drift in Eq. 1 to the effective force, i.e., ∇U(z), this is likely to give inaccurate results.^{10, 14, 30, 43, 49} The problem typically encountered is poor sampling of the phase space, i.e., some configurations which provide significant weight to the stationary distribution cannot be accessed due to large kinetic barriers experienced on the time scale of the simulation. In this case one obtains a biased PMF, U(z;Γ) where Γ is used to denote that the estimate depends on the phase space path sampled in the simulation. Even if the calculated U(z;Γ) is close to the sought equilibrium U(z), one may encounter artifacts of approximating a high-dimensional system with a scalar SDE.^{33, 52}

In our particular SMD simulations, each of the nonequilibrium SMD simulations have initial conditions drawn randomly from an ensemble of configurations having a stationary distribution, and hence each starts at a different point on the effective free energy surface due to this random draw. We need to use such an ensemble of configurations in order utilize Crooks’ equality¹¹ to estimate the PMF (this is briefly reviewed below). By using a collection of SPA models, we are characterizing the stochastic dynamical responses associated with a given ensemble of initial configurations.⁵³ Using this collection of SPA models allows us to respect the variability induced by the significant time-scale separation inherent to our simulations, i.e., in our gA system, channel protein conformations are not “ergodically” sampled along a single trajectory in a 1 ns simulation. The collection of SPA models also lets us resolve different effective forces (drift) and diffusion functions depending on this initial configuration which do not average out due to kinetic barriers. We demonstrate how this collection of models can be used to identify such phenomenon and also use the models to obtain coarser system quantities, e.g., U(z).

We appeal to the recent nonequilibrium statistical mechanics theory to combine the nonequilibrium work values taken from different simulation to equilibrium quantities, namely, we use Crooks’ equality to estimate free energy differences:

$$\frac{p\left({\mathcal{W}}_F\right)}{p\left({\mathcal{W}}_R\right)}=\text{exp}\left(\beta \left({\mathcal{W}}_{\mathcal{F}}-\Delta F\right)\right),$$ (3)

where W_F (W_R) denotes a work valued observed in “forward” (“reverse”) direction and β≡1/k_BT represents the inverse of Boltzmann’s constant multiplied by the system temperature. The label forward corresponds to SMD simulations where we pull the ion from initial state A (z=15 Å) to B (z=0 Å). The control protocol λ is a deterministic function changing the state of the system from A to B within a fixed finite time T (note that in this article system temperature always appears with Boltzmann’s constant and T alone refers to time); the same protocol is used in all forward simulations. We specified a λ(⋅) changing from A to B at a constant rate (velocity) in all simulations. The reverse direction is similar, but we change from B to A and using a “time-reversed” protocol λ^R(t)≡λ(T−t). For the remainder of the article, we omit the superscript on the control protocol; the label F or R is used to determine the form of this function. Also, due to the channel’s symmetry we call simulations starting at z=−15 (0) Å and ending at z=0 (−15) Å forward (reverse) pulls. The probability density p(W_F) [p(W_R)] corresponds to the probability of observing the forward (reverse) work value under the nonequilibrium protocol determined by λ(⋅).^{9, 11, 14} The nonequilibrium forward work is defined as ${\mathcal{W}}_F={\int }_0^T{F}_{\mathrm{ext}}\left(z_t,t;\Gamma \right)v_{\text{pull}}^{F}dt$, where F_ext denotes the external force added into the system^{9, 11, 14} and v^F is the constant velocity specified.⁵⁴

The Bennett⁵⁵ and FR methods¹⁶ were used to estimate ΔF given the observations. We used a recent method¹⁷ to construct the corresponding PMF along the reaction coordinate in addition to the FR method’s approximation of this quantity. The methods used all rely on the validity of Crooks’ equality in addition to other various approximations. Approximations are needed in practice because only a finite number of trajectories are available to analyze.

The work and sample paths obtained from simulating a collection of estimated SPA models are subsequently used to (1) test implicit assumptions underlying various PMF methods (this article focuses on methods which assume a Gaussian limit of the work under certain conditions^{14, 15, 16, 56}), (2) generate confidence bands in the estimated quantities coming from nonequilibrium simulations without making overly restrictive assumptions on the nonequilibrium work distribution (given the time-dependent nature of the work trajectory²⁶ and potential long-time dependence on the random initial configuration,¹⁹ this is somewhat problematic in current formulations^{13, 17, 55, 56}), and (3) assist in determining if phase space has been sufficiently explored in a small collection of sample paths. Although we focus on estimating PMFs with a few selected computational methods, we would like to note that the main idea behind SPA modeling can, in principle, be used to assist any scheme only requiring sample paths of the reaction coordinate and nonequilibrium work distribution information. Our surrogate models are being used to assist in the computation of physical quantities in a spirit similar to the one reported in Ref. 10 except we are utilizing recent developments in time series statistical inference^{21, 22, 57, 58} and local polynomial models applied to time-dependent SDEs with a diffusion coefficient dependent on the state.^{7, 8, 19} Another unique feature of the SPA approach is the ability to use information contained in a collection of models to refine computations commonly carried out in chemical physics.

All of the items are demonstrated by examples. We focus on assessing approximations associated with the FR method^{15, 16} and the “stiff-spring approximation.”¹⁴ The FR method has shown to approximate free energy differences with a small number of nonequilibrium paths (in addition to computing other physically interesting quantities).^{15, 16} The validity of the FR method depends on the nonequilibrium work process having a Gaussian distribution at all times. With a small number of observations it is difficult to empirically test the Gaussian assumption by inspecting the SMD work alone. Analytic results exist that show that the Gaussian work assumption is valid if the stochastic dynamics of the complex system can be described by a single “overdamped” SDE and the spring constant used to add the external force is “large enough.”¹⁴ However, memory effects and slow configurational fluctuations can make the validity of using a single-overdamped model questionable at nanosecond (or shorter) time scales^{10, 30, 39, 43, 49, 59} even if one has knowledge of a “good” reaction coordinate.^{33, 52} In these situations, a collection of SPA models can often help in identifying this situation.^{8, 19, 27}

We demonstrate how the collection of SPA models can also be used to generate new data which helps quantify the uncertainty in the estimated PMF and $\tilde{D}$ (and this can vary with z). The uncertainty bands are constructed using model bootstrapping ideas discussed in Refs. ^{8, 19}. Uncertainty quantification in PMF computations is useful in comparing different methods for computing the equilibrium quantity and we present a method for constructing such confidence bands in a far from equilibrium situation attempting to construct the PMF. Recall that the confidence bands take temporal dependence, thermal fluctuations, and initial configuration variability into account. The last item is especially important if a single SPA model (using the reaction coordinates selected) does not adequately describe the stochastic dynamical responses observed. We discuss some limitations and potential other uses of the confidence bands we construct in Sec. 3.

Diffusion coefficient estimation

Techniques for reliably estimating the diffusion coefficient $\tilde{D}$ associated with a mesoscopic model from biased equilibrium simulations is still an area of active research.^{30, 43, 46, 60, 61} Methods for extracting this kinetic quantity in systems driven far from equilibrium have been developed to a lesser extent.^{16, 41} If a single reaction coordinate can be used to accurately describe the stochastic dynamics on the time scales observations are available at, then one would hope that the diffusion function σ²(⋅) of the SPA model calibrated from a single time series would be consistent with the diffusion coefficient $\tilde{D}(\cdot )$ typically used in statistical mechanics.^{30, 39, 43, 46, 60, 61} A diffusion coefficient obtained directly from the diffusion function of the SDE will be denoted by $\tilde{D}\left(z;\Gamma \right)={\left(\sigma \left(z;\Gamma \right)\right)}^2$. We label this technique for obtaining a diffusion coefficient from a single trajectory as “method 1” and use “Γ” to remind us that there may be lurking degrees of freedom causing systematic differences in the dynamics, e.g., the value may depend on unobserved slowly evolving degrees of freedom.^{8, 19, 27, 52, 60} Note that for method 1’s estimate to correspond to the standard effective mean square displacement diffusion coefficient typically used in the physical sciences,³⁹ one would need to have a substantial amount of temporal coarse graining already occur to have a single-overdamped SDE adequately describe the dynamics of all trajectories.^{10, 41} We have already mentioned that this is not likely the case in our nanosecond simulation data because the fluctuations induced by conformational degrees of freedom are not likely adequately sampled in such a short simulation. Some methods based on recent developments in statistics and SPA modeling ideas have been proposed for testing the various assumptions needed for this situation to occur.²⁷

In Refs. ^{10, 16}, the Einstein relation is appealed to and the nonequilibrium driving force in this relationship is assumed to come from taking the derivative of the dissipated work with respect to the reaction coordinate, i.e.,

$$\tilde{D}\left(z;\Gamma \right)\approx v_{\text{pull}}∕\left(\beta d⟨{\mathcal{W}}_d\left(z\right)⟩∕dz\right),$$ (4)

where W_d denotes the dissipated work (W_d≡W−ΔF) and angular brackets denote taking the ensemble averages. This heuristic method assumes that the work dissipation rate is linearly related to the velocity. It has the appealing feature of accounting for different conformational degrees of freedom because it depends on averaging results from multiple sample paths (method 1 uses only one path). We apply a minor variant of the method given in Ref. 16, namely, we use the observed work trajectory and subtract off U(z) and estimate the ensemble average ⟨W_d(z)⟩ with these data.⁶² Results assuming Gaussian work distributions can be obtained with explicit formulas depending only low-order moments of the work,¹⁶ but the method employed here does not require this distribution assumption. The technique for obtaining a diffusion coefficient using the dissipated work relation above will be referred to as “method 2.”

The diffusion coefficients estimated with methods 1 and 2 are significantly different in magnitude in the channel interior, but we show that they each correspond closely with other results obtained by different methods presented in earlier works studying K+dynamics in a gA channel.^{16, 30, 32} Both “diffusion coefficients” might by physically relevant depending on the system conditions and a physical interpretation of the difference is discussed at the end of Sec. 3.

Local maximum likelihood estimation

The functional form of an accurate global stochastic dynamical model describing the system is assumed to be unknown by a simple parametric model. In order to quantitatively summarize the dynamics in our signals in this situation, we use data-driven⁶³ modeling techniques which utilize local maximum likelihood methods.^{7, 8, 27, 64} More specifically, given a time series trajectory coming from a driven (or steered) complex system we estimate a sequence of simple diffusion models describing the dynamics in the signal. Here we focus exclusively on overdamped Langevin-type equations³⁹ using low-order polynomial functions for the drift and diffusion, but the methodology is not limited to this regime. For instance, in Ref. 6 we demonstrated how at high pulling velocities this overdamped Langevin approximation breaks down, but another SDE can still be used to satisfactorily describe the system dynamics. Note also that one is not limited to using just diffusion SDEs with the SPA modeling idea. The local SDE fit to an observed time series has the following structure:

$$\sigma \left(z\right)=\sqrt{\tilde{D}\left(z;\Gamma \right)}\approx \left(C+D\left(z-z_o\right)\right),$$

$$\mu \left(z,t\right)≔\beta \tilde{D}\left(z;\Gamma \right)F_{\text{net}}\left(z,t;\Gamma \right),$$

$${\mathcal{U}}_{\lambda }\left(z,t;\Gamma \right)≔\mathcal{U}\left(z;\Gamma \right)+\frac{1}{2}{k}_{\text{pull}}{\left(z-\lambda \left(t\right)\right)}^2,$$

$$F\left(z;\Gamma \right)≔-\frac{\partial }{\partial z}\mathcal{U}\left(z;\Gamma \right)\approx A+B\left(z-z_o\right),$$

$$F_{\text{net}}\left(z,t;\Gamma \right)≔-\frac{\partial }{\partial z}{\mathcal{U}}_{\lambda }\left(z,t;\Gamma \right)=F\left(z;\Gamma \right)-k_{\text{pull}}\left(z-\lambda \left(t\right)\right).$$

How close the manipulated ion is to the time-varying set point is dictated by the stiffness of the harmonic spring constant k_pull (a tunable parameter). In what follows, we assume that the drift is related to the gradient of an effective potential; however, note that this is not overly important to our SPA modeling procedure. U_λ(z,t;Γ) denotes the effective biased system potential and U(z;Γ) the effective unbiased potential. The effective potentials describing the dynamics may not necessarily correspond to U(z). $\tilde{D}\left(z;\Gamma \right)$ represents the diffusion coefficient (associated with one trajectory) and F(z,t;Γ) the effective internal force experienced by z as a result of the unbiased potential [F_net(z,t;Γ) denotes the net force experienced due to the biased potential]. F(z,t;Γ) and $\sqrt{\tilde{D}\left(z;\Gamma \right)}$ were approximated using local linear function approximations. The symbols not defined above were introduced in Sec. 2B.

The “overdamped Langevin” name stems from forcing the drift function to relate to the system force and diffusion coefficient via the relation defining μ(z,t) in the equations above. In other words we are assuming that the Einstein relation, $\tilde{D}\left(z;\Gamma \right)={\left(\gamma \left(z;\Gamma \right)\right)}^{-1}{k}_{B}T$, holds¹⁶ for each sample path, where γ(z;Γ) denotes the effective friction coefficient. In this model, the local parameter vector estimated is denoted by θ≡(A,B,C,D). The local models were selected so that the estimated parameters correspond to physically interpretable quantities.

Each different simulation trajectory possesses a substantially different Γ value. The only thing we manipulate in the nonequilibrium simulation is z; the time-dependent protocol we used to manipulate this coordinate does not allow Γ to change appreciably from its initial value. In this way Γ modulates the dynamical response. The variability observed in the estimated SDE models indirectly reflects the influence that the full state-space vector Γ has on the dynamics.

Maximum likelihood motivated approximations of Ref. 21 are used to obtain local parameter estimates. Given a time series ${\left\{z_i\right\}}_{i=1}^N$ entries we find the parameter vector $\widehat{\theta }$ which maximizes the probability density p(z₁,…,z_N;θ) of the normalized innovation sequence.²¹ Since a constant velocity protocol is used for λ(⋅), we set z^o to the average value in local time series windows. The windows were formed by dividing a single global time series into M=40 windows, each representing an equal temporal fraction of the total time series observed. The SPA models can yield a refined approximation of the nonequilibrium work distribution by model bootstrapping.^{7, 8, 19} The full numerical details of this model bootstrapping procedure are outlined in Ref. 19.

SMD simulation of gramicidin A

The SMD simulations used in this paper to study the transport of a K⁺ ion through the gA channel are the same as those reported in Ref. 16. The main benefit of using the same SMD simulations to evaluate the PMF of K⁺ in gA by two different methods, i.e., the FR method¹⁶ and the SPA method in the present work, is that it makes the comparison between these methods more objective. Here we present a brief description of the computer modeling of the gA system and the SMD protocol used (for further technical details see Ref. 16).

The computer model was built by inserting a high resolution NMR structure [Protein Data Bank code 1JNO (Ref. ⁶⁵)] of gA into a previously pre-equilibrated patch of POPE lipid bilayer by using the VMD (Ref. ⁶⁶) plugin Membrane. After removing the lipids within 0.55 Å of gA, the membrane-protein complex was solvated by adding two 13 Å thick layers of water to each side of the membrane using the VMD plugin Solvate. The final system comprised a total of 36 727 atoms, including 155 lipid molecules and 5700 water molecules, and had a size of approximately 70×70×67 ų.

All simulations were performed with NAMD 2.5 (Ref. ⁶⁷) and the CHARMM27 force field for proteins and lipids.^{68, 69} A cutoff of 12 Å (switching function starting at 10 Å) for van der Waals interactions was used. The SMD simulations were carried out at constant temperature (T=310 K) and normal pressure (1 atm) in the NpT ensemble⁷⁰ by employing periodic boundary conditions to minimize finite-size effects. Because our system size considerably exceeded the minimal one recommended in Ref. 71, our results should be in fact free of finite-size effects. The full long-range electrostatic interactions were treated using the particle mesh Ewald method,⁷² which has been shown to be important in simulating lipid bilayers.⁷³

After proper energy minimization and 0.5 ns long equilibration of the system, a K⁺ ion was added at the entrance of the channel. To preserve change neutrality a Cl⁻ counterion was also added to the solvent. This was followed by another 10 000 steps energy minimization and 0.5 ns equilibration with K⁺ placed in three different positions along the z axis of the channel, namely, at z∊{−15,0,15} Å. The origin of the z axis corresponded to the middle of gA. In order to prevent the pore from being dragged during the SMD pulls of the K⁺ ion, the backbone atoms of gA were restrained with an elastic force (k_bb=20 kcal∕mol∕Ų) along the z axis. However, the motion of these atoms in the xy plane (perpendicular to the axis of the channel) was unrestrained, thus leaving unaffected the flexibility of the channel that plays an important role in the ion transport through gA.²⁹

A total of ten F and ten R SMD pulls were performed along the z axis of gA on two segments: z∊[−15,0] Å and z∊[0,15] Å, respectively, corresponding to the two helical monomers. The pulling speed was v=15 Å∕ns, while the spring constant of the harmonic potential that guided K⁺ across the pore was k=20 kcal∕mol∕Ų. The pulls were performed by employing two different pulling protocols.¹⁶ First, the pulling force on K⁺ was applied along the z axis but there was no restrain on the cation’s motion in the xy plane. In the second set of SMD pullings, beside the elastic pulling force along the z axis, the potassium ion was constrained (by applying a harmonic potential, with k=20 kcal∕mol∕Ų in the xy plane) to move along the axis of the channel. By employing the FR method, both pulling protocols yielded essentially the same PMF inside the channel.¹⁶ In the present study we have only analyzed the F and R SMD trajectories obtained with the second pulling method, especially because during the first pulling protocol the potassium ion occasionally escaped between the two helices into the lipid bilayer. However, one should note that the profile of the PMF at the middle and the entrances into the channel are difficult to determine and the obtained result may depend considerably by the MD simulation method employed. This is a well known, still unsettled issue that has been pointed out in several previous publications.^{32, 33, 74, 75}

The SMD simulations of the reported system (36 727 atoms) were carried out on 36 central processing units (CPUs) of a cluster with Intel Xeon Core 2 Duo CPUs with a typical performance of 0.5 days∕ns. Thus, on the 36 CPUs, with pulling speed v=15 Å∕ns, one obtained two F or R trajectories per day.

RESULTS AND DISCUSSION

PMF computations

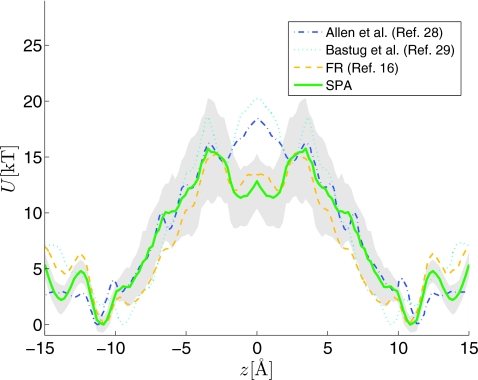
Figure 2 reports the PMF estimated using 20 FR paths from a SMD simulation (using ten paths from z∊[−15,0] and ten from z∊[0,15] Å). The solid line represents the average PMF obtained using the SPA models and the shaded region reports the pointwise 95% confidence band associated with the estimate. The “model bootstrapping” procedure (first presented in the Appendix of Ref. 19) was used to construct these quantities; the procedure is briefly outlined later for the reader’s convenience. The PMF estimate is compared to published equilibrium^{28, 29} and nonequilibrium¹⁶ methods describing the same system (though it should be mentioned that some of the underlying simulation details differ^{16, 28, 29}). A noteworthy feature is that the confidence bands constructed indicate that each PMF estimate is plausible in the interior of the channel (i.e., Å<∣z∣<11 Å) given the resolution available from our SMD measurements and SPA analysis. The FR method’s¹⁶ estimate is qualitatively similar to that of the SPA. This is not surprising due to the fact that both the SPA and FR methods used the same underlying SMD paths. However, the Gaussian assumption is not invoked in the SPA estimate and this explains the small differences between the SPA and FR methods. We return to this point when discussing Figs. 34.

Figure 2.

The PMF estimated using 20 FR (bidirectional) nonequilibrium work paths simulated using SPA models (Refs. ⁷, ⁸, ¹⁹) along with the estimator of Ref. 17. The shaded region contains reports the 95% confidence band of the estimate (obtained using the model bootstrapping discussed in Refs. ⁷, ¹⁹). The estimate is compared to published equilibrium (Refs. ²⁸, ²⁹) and nonequilibrium (Ref. ¹⁶) methods. In all cases, the PMF was shifted to have the binding pocket minimum near z≈11 Å correspond to zero energy level and symmetry of the PMF was enforced to facilitate comparison with previously published results.

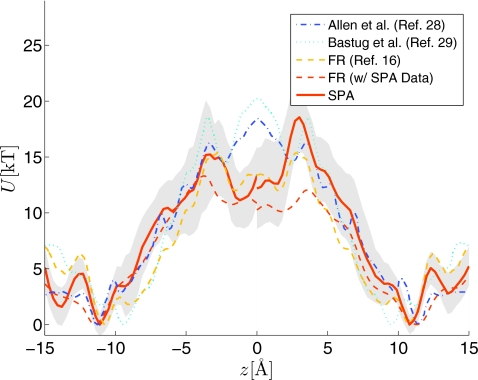
Figure 3.

The PMF estimated using ten FR (bidirectional) nonequilibrium work paths simulated using the SPA method (Refs. ⁷, ⁸, ¹⁹). The same data used in Fig. 2 underlie the estimates, but we partitioned the FR pulls into those coming from the “left,” z∊[−15,0], and “right” portions of the channel, z∊[0,15], and recomputed the PMF using the two sets of FR data. This was done to illustrate the asymmetry of the PMF estimated with finite collection of paths (in the large sample limit the PMFs would be identical in this dimer channel). The symmetrized reference data (Refs. ¹⁶, ²⁸, ²⁹) is also plotted.

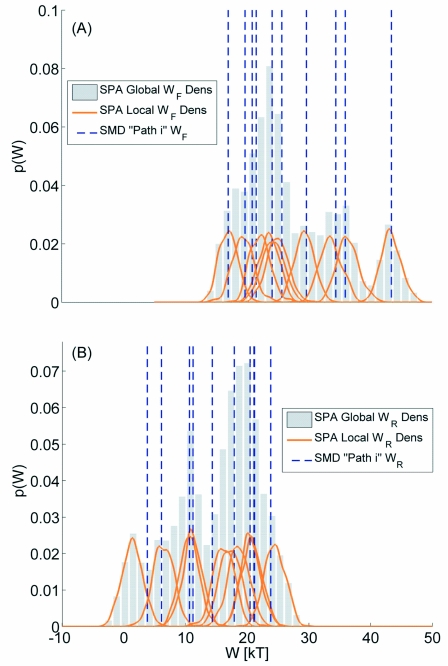
Figure 4.

The probability density of the nonequilibrium work estimated using the F direction [panel (a)] and the R direction [panel (b)] data for z∊[−15,0]. The vertical lines correspond to the work values observed in the SMD simulations. The normalized histogram bars correspond to combining 500 SPA work trajectories from ten different SPA models together to approximate the population nonequilibrium work distribution. The collection of ten curves in each plot represents the work densities associated with each of the ten SPA models (the population work distribution represented by the histogram bars can be thought of as a sum of these curves).

The largest difference between the PMFs estimated using nonequilibrium and equilibrium methods can be seen near the entrances and in the channel center. In both of these regions, the details of the umbrella sampling constraints and/or guiding potential can significantly influence the PMF because the particular biasing potential used can significantly influence the region of phase space are explored.^{32, 33, 74, 75} A more detailed discussion was presented in Sec. 2E. In the majority of the interior, the protein acts effectively as a cylindrical constraint^{74, 75} in the directions orthogonal to z. This feature facilitates making comparisons between different PMF estimates in this particular region of phase space and the SPA method’s PMF estimate is strikingly close to the equilibrium estimate of Ref. 28 in the interior region (2 Å<∣z∣<11 Å).

Before proceeding, we briefly summarize the basic ingredients of the model bootstrapping procedure¹⁹ to facilitate the discussion with the remaining results. We estimated 20×2 (factor of 2 due to the F and R data) different global SDEs using the observed SMD paths. The goodness of fit of the SPA proxy was tested using time series methods.^{19, 22, 27, 58} We then used the models, deemed acceptable proxies of the dynamics, to simulate 5000×20 work paths in both the F and R directions. From this total population of curves, 500 batches of F and R work paths were taken N at time (N is a sampling parameter we set in this article to be equal to the number of underlying SMD paths which varies between 10 and 20). The value 5000 corresponds to the sampling parameter K discussed in the Appendix of Ref. 19 and the value 500 corresponds to the number of “bootstrap” samples (i.e., number of times we repeated the procedure in order to obtain confidence bands); increasing these two sampling parameters had negligible effects on the reported confidence regions. For example, the pointwise confidence band plotted with the SPA PMF uses the 500 batches of SPA work paths, each containing NFR trajectories, and computes the PMF using a bidirectional method¹⁷ and then computes the empirical mean, $\widehat{\mu }\left(z\right)$, and standard deviation, $\widehat{\sigma }\left(z\right)$, of the 500 estimated U(z) at each z value and constructs the shaded region using $\widehat{\mu }\left(z\right)\pm 2\widehat{\sigma }\left(z\right)$. Other confidence bands/interval ideas could be entertained.⁷⁶

Using the collection of SPA models to assess PMF accuracy

Figure 3 plots results similar to Fig. 2, but there are important differences and these serve several purposes. We plot the PMF obtained using the same simulated SPA work paths as those used in Fig. 2, but in Fig. 3 we partition the simulated SPA work paths into two groups (one group corresponds to z∊[−15,0] and the other to z∊[0,15]) and change the SPA model bootstrap parameter to N=10. This was done to demonstrate the degree of asymmetry present in the PMF estimate and also to demonstrate the effect of sample size without adding new sources of variation. In the large sample limit, the PMF should be symmetric about z=0. With only ten pairs of underlying SMD bidirectional sample paths, we clearly do not have the average PMF exactly symmetric about z=0; however, the confidence bands (computed now with N=10) suggest that symmetry is plausible. However, the systematic difference in the mean value of the PMF computed in the two portions of the channel is most likely due to the different conformational degrees of freedom sampled in the initial condition.^{8, 19} In this plot we demonstrate another useful feature of the SPA method, namely, it can be used to quantify bias. With only ten pairs of FR trajectories it is hard to claim that the FR method is biased given than it falls within the confidence band of the method computed with the simulated SPA data and PMF using other methods¹⁷ for most values of z. To quantify potential bias of the FR method, we can apply it to the larger set of simulated SPA work data. The asymmetric FR data in Fig. 3 plot the average result of doing this procedure (using the same sample size as the case labeled “SPA”). It can be seen that the average appears to be systematically different than that obtained using the method in Ref. 17, although the difference is not particularly large relative to the size of the confidence bands.

Note also that the confidence band associated with batches using N=10 underlying SMD paths are similar in width to those associated with N=20. This is further evidence that conformational degrees of freedom that vary slowly relative to the time scale of the simulation are not fully sampled in only ten SMD trajectories. Once the number of underlying SMD paths is large enough to adequately sample portions of phase space making significant contributions to the PMF, then further increases in N would result in a shrinking confidence band. If increasing the number of SMD samples broadens the confidence band, this would suggest that a new path making an important contribution to Crooks’ equality was encountered and this “important rare event”^{8, 77} has not previously been represented in the finite-size path ensemble in hand. In the case where increasing the number of SMD paths results in effectively the same size of confidence band (our situation) this suggests that conformational space has crudely covered in the smaller sample and that the larger sample is more or less “filling in the gap.” The next set of results aims at clarifying the last statement with a more concrete example.

Recall that we analyzed ten FR SMD paths in each portion of the channel; in Fig. 4 we focus on the distribution of 5000 work paths (evaluated at T=1 ns) generated by the ten SPA models calibrated from SMD observations coming from the left portion of the channel; results for the right portion of the channel are similar and reported in the supplementary materials.⁴⁸ The probability density for each of the ten SPA models was empirically measured⁷⁸ and is represented as a solid line for both the F and R directions. The normalized histogram of 5000×10 work paths is represented by bars in the figure. There are several things worth noting in this plot (a discussion of each item follows this list):

• The “true” work value measured directly from the SMD path (denoted by a vertical line) falls within a region of high probability of the corresponding SPA model.

• The individual work probability densities associated with different SPA models predict regions of high probability that are different, i.e., the collection of work densities appears to be a mixture of different probability densities instead of samples coming from one common work distribution possessing a unimodal probability density.

• The pooled work histogram appears to be skewed and non-Gaussian in both the F and R directions (the same holds for the ten FR paths reported in the supplementary materials, Fig. 1⁴⁸).

• The pooled work distribution (as plotted) is multimodal, but the individual work densities making up the components of the mixture are all unimodal.

The first item gives evidence that the effective force and thermal fluctuations of our global SPA models can quantitatively approximate “fast-scale” randomness.¹⁹ The second item suggests the slowly evolving channel degrees of freedom, e.g., lipid bilayer undulations or the orientation of the monomers at the channel center,³⁶ are significantly different in each SMD path and this modulates the effective dynamics in a way that can be measured by the SPA models. Physically this suggests that a scalar diffusion model using z alone is not sufficient to summarize the phase space statistics at the length and time scales used in the simulation (we utilize this fact when discussing the third item). One might suggest using an additional reaction coordinate, but the approach we take uses a collection (or population) of SPA models instead. The results obtained for the PMF and diffusion coefficient suggest that our collection of SPA models can serve as an adequate proxy to represent the phase space statistics needed to approximate these physical quantities. The main motivation for this is due to the fact that in single-molecule experiments, one often has experimental access to systems observables which are “bad” reaction coordinates. Our methods aim at extracting/inferring useful information from such time series (discussed further in Sec. 4). Item 3 has been observed in other works studying different systems.^{8, 79, 80} Recall that if one has a good reaction coordinate and a single-overdamped diffusion model can be used to describe the dynamics, then it can be shown that if a sufficiently stiff spring is used in the SMD situations, the work distribution will be Gaussian for all time points.¹⁴ This property would make the FR method more attractive due to its validity requiring a Gaussian work distribution. However, we already discussed that we cannot use a single (scalar) overdamped diffusion model to describe the z dynamics of each SMD response. One advantage of the SPA method is that it can, with a fairly small sample size, determine if a Gaussian work distribution is plausible.^{8, 19} The ability to simulate new trajectories significantly facilitates this task (e.g., if only ten SMD work values were analyzed, it would be very hard to determine the work distribution shape¹⁹). The shape of the work distribution predicted using the SPA work paths explains the small systematic bias apparently committed by the FR method in Fig. 3. The last item is relevant to the filling in the gaps description used when discussing Fig. 3. In this system, the z coordinate is believed to be a fairly good (though not perfect) reaction coordinate in equilibrium situations.^{32, 37, 74, 75} Given this information, it would be somewhat surprising if the large sample work distribution of the nonequilibrium simulation was truly multimodal. It is possible that large barriers and the interaction of the effective free energy surface with different kinetic phenomena⁵² cause a large sample multimodal work distribution when the system is driven far from equilibrium by a time-dependent potential, but we do not believe that is the case we face. We believe that the mixture of distributions has simply not been adequately sampled with only ten trajectories. If we increase the number of SMD paths (and hence SPA models) and continually update the SPA work histogram, eventually the population of individual work densities would fill in the gaps and result in a unimodal work density. This hypothesis is supported by the plot shown here and in the supplementary materials, Fig. 1⁴⁸ (the work distribution in the other portion of the channel contains a slightly different mixture of work densities). This also explains why the confidence bands for 20 and 10 SMD paths did not change appreciably. The net work distribution did not appreciably change; it became smoother (less multimodal) when more samples were added and hence the tails of the work approximate distribution were effectively the same (this property dictates how well Crooks’ equality predicts the PMF^{11, 17}).

We would like to carefully point out that if rare events making important contributions to the histograms constructed using the bidirectional pullings have not been sampled in the SMD simulation and these events cannot be approximated using the SPA models in hand, then the PMF and confidence bands we construct are going to contain potentially large systematic biases. If slowly evolving conformational degrees of freedom are responsible for such rare events and these trajectories are not observed, then the SPA models would have a difficult time approximating this effect.^{7, 8} However, if such slowly evolving conformational degrees of freedom are sampled in the SMD data, our methods can be helpful in refining the work distribution associated with that portion of phase space because we can simulate many different trajectory realizations after observing only SMD path.⁸¹ In addition, if one observes a sudden increase in the confidence bands of a PMF when sample size is increased, this would suggest that such an event has been sampled in the augmented data set. Note also that the bidirectional (i.e., FR) pullings^{17, 77} are designed to help reduce the severity of the “rare event sampling problem” known to introduce bias in computations aiming to extract equilibrium information from finite time nonequilibrium data. With future developments and refinements in bidirectional sampling protocols, the caveats we presented here are likely to become less of a practical concern (e.g., algorithms that enhance sampling of the initial configuration⁴⁵ would be of particular help).

Diffusion coefficient estimation

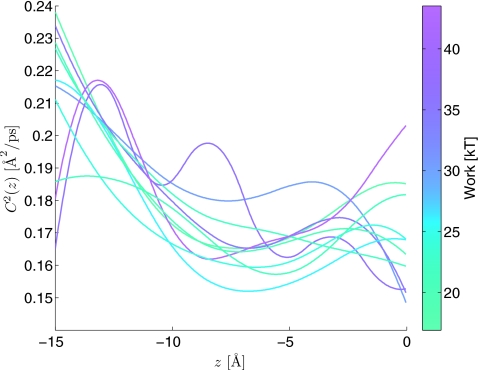
We attempted to compute the effective diffusion coefficient associated with the unbiased system valid at mesoscopic time scales from biased, fast time-scale nonequilibrium trajectories. Both methods 1 and 2 can compute the effective diffusion coefficient as a function of z, but Table 1 focuses on results in the interior of the channel, i.e., 2 Å<∣z∣<11 Å, where the diffusion coefficient is effectively constant (this facilitates comparisons with Ref. 30 data). The results obtained using method 1 are quantitatively close with those reported in Ref. 32 for the entire portion of the channel (see Fig. 5). Method 1 estimated the diffusion coefficient using time-dependent biasing potential whereas Ref. 32 used stationary umbrella sampling windows to obtain this quantity. By “pulling” the potassium ion with a harmonic biasing potential (possessing a well-minimum moving at a constant velocity) and stiff-spring coefficient, we are exploring slightly different physics in the channel. The guiding potential may substantially influence the effective forces and friction experienced by the ion, e.g., in our SMD simulations it appears that some random forces, sometimes believed to induce long-memory effects,^{30, 39} are not felt by the ion because the biasing potential moves the ion in the z direction too quickly to allow the long-memory forces to appreciably accumulate and substantially contribute to the effective diffusion coefficient associated with moving the ion axially across the channel in this exogenously driven system. Note that method 1’s estimate (and hence that of Ref. 32) of the effective diffusion coefficient is substantially higher than the corresponding estimates reported elsewhere.³⁰

Table 1.

Diffusion coefficient estimation. The effective diffusion coefficient $\left(\tilde{D}\right)$ was computed from the SMD data computed in the center of the channel. Two methods were used (see text) to compute this quantity. The top column denotes the initial “state A” and final “state B” for z. For method 1 the SPA diffusion coefficient was evaluated directly from the estimated functions (calibrated from ten SMD curves). For method 2, 100 batches of ten SPA work trajectories were used to compute the PMF and dissipated work. The SPA data also report two times the empirically measured standard deviation of $\tilde{D}$ for both methods. Results from Refs. ³⁰, ³² are included for comparison in the first column (these authors did stationary computations in the channel so the direction of the SMD pulling has no relevance). Note that we assumed that the error bar reported in Ref. 30 was the empirically measured standard deviation of $\tilde{D}$. All diffusion coefficients reported below have units Ų∕ns.

	(−15→0)	(0→−15)	(15→0)	(0→15)
Method 1	181.5±75.3	190.1±52.4	209.6±44.2	182.3±43.3
Method 2 (SPA)	10.97±2.73	9.96±2.14	14.01±4.05	9.38±2.07
Method 2 (SMD)	10.59	10.42	13.63	9.20
Mamonov et al. GLE-HO (Ref. 30)	16±8	⋯	⋯	⋯
Allen et al. GLE-HO (Ref. 32)	246.6	⋯	⋯	⋯

Figure 5.

The diffusion function of the SPA models estimated from ten SMD paths. This function is equal to method 1’s estimate of $\tilde{D}\left(z\right)$. The curves are color coded according to the value of the nonequilibrium work observed in the corresponding SMD trajectory.

It has been suggested that the estimate of the diffusion coefficient reported in Ref. 32 may be significantly biased³⁰ and that the discrepancy between those computed in Refs. ^{30, 32} can be explained by the details of the extrapolation procedure used in the Laplace transform approach originally used in each work. Some modifications³⁰ of the Laplace extrapolation procedure tailored to more accurately include memory effects, induced partially by the channel’s conformational fluctuations interacting with the ion, could help resolve the differences reported in Ref. 32. Both the methods of Refs. ^{30, 32} assumed the generalized Langevin equation harmonic oscillator (GLE-HO) model. Our method 1’s failure to include terms believed to be due in part to long-time memory (e.g., those induced by slow-scale channel fluctuations) is not overly surprising given that our individual SPA models do not attempt to include these types of long-range noise, but the agreement of our diffusion coefficient estimated using nonequilibrium trajectories and that of a “stationary” application³² is intriguing. Method 1 not only ignores memory effects induced by fast-scale non-Markovian noise (e.g., that induced by particle momentum) but also contributions resulting from averaging over different channel conformations; the latter effect can be included in the method reported in Ref. 32 but again may be biased due to the numerical truncation procedure used.

Method 2 for computing the diffusion coefficient indirectly accounts for variation induced by different conformational degrees of freedom.⁸³ The estimate of this method is on par with simulation results accounting for memory and channel fluctuations.³⁰ This suggests that the diffusion coefficient estimation strategy proposed in Ref. 16 does appear to be able to utilize data driven far from equilibrium to predict this system property and the results are consistent with other established techniques.^{30, 46} One benefit that using the SPA models provides when used with method 2 is that confidence intervals can be attached to the estimate. The success of this method 2 requires averaging over an ensemble of trajectories each associated with a different underlying conformational state. By using only a small number of genuine SMD trajectories, i.e., no SPA models, obtaining accurate estimates of uncertainty of the diffusion coefficient is somewhat problematic with method 2. Simulating the SPA models allows one to generate a large batch of statistically independent surrogate trajectories. These can be used to obtain a more reliable estimate of the uncertainty attributable to various random noise sources. A collection of SPA models using different underlying conformations (and the associated dissipated work) can approximate the diffusion coefficient using method 2 consistent with other results,³⁰ but the collection of SPA models still does not account for temporal correlations induced by a “memory kernel.” This suggests that the slowly evolving channel fluctuations contribute significantly to the s→0⁺ limit of the diffusion coefficient computed with the Laplace transform (assuming a GLE-HO model). The ability of method 2 to achieve comparable estimates to other results explicitly including a memory kernel, which in Ref. 30 was constructed to include force autocorrelations, was not a surprise given that we subjected our individual SPA models to goodness-of-fit tests that suggested omitting the effect of this type of memory kernel did not cause the models to be rejected¹⁹ (in Ref. 27 we show that more powerful tests can be applied to stationary MD data). Using an ensemble of SPA models (inherent to method 2) appears to be able to include the contribution that channel fluctuations provide in the diffusion coefficient estimate.

It is difficult to conclusively determine which diffusion coefficient is “closer to reality.” There are systematic differences between the various simulations. For example, the z distance is defined differently in Refs. ^{30, 32}. In addition a variety of other MD simulation details differ slightly between all studies. Note also that the PMFs computed in all references show qualitative differences. The claim was made in Ref. 30 that their results were closer to experiments, but this claim implicitly assumes that a one-dimensional diffusion model can be used to describe the observed experimental fluxes. At experimental time scales, this may be possible, but there is no guarantee that this holds true. This claim also rests on the assumption that the PMF computed with MD simulations is reliable (kinetics and thermodynamics are coupled when comparing to experimental fluxes). It is still unclear how accurately current MD force fields capture the dynamics inside of narrow ion channels.¹⁶ Definitively determining which diffusion coefficient is correct would require experimentally tracking (in an unbiased fashion) the position of individual ions as a function of time our other novel experimental methods.

Before concluding, we would like to mention two speculative ideas and potential future research directions based on the results of this section: (1) Although method 1 appears to estimate a diffusion coefficient believed by some to be too high in comparison to experimental observations of ion diffusion in gA,³⁰ the estimates (if biased) may be relevant to physical systems where an external force (electric field, large pressure gradient, etc.) is used to alter the flow of ions across the channel. This is potentially relevant to nanotechnology applications where systems are designed to benefit from dynamics associated with systems driven far from equilibrium, e.g., Ref. 84. This could be the case if the external forces added are large enough to make long-time memory induced by channel fluctuations, whose time correlation is long and significant in unforced systems, negligible in the far from equilibrium regime. (2) The shape of the state dependent diffusion function, equal to method 1’s $\tilde{D}\left(z\right)$ estimate, varies and shows a partial correlation with the total work introduced into the SMD trajectory used to calibrate the SPA model (see Fig. 5). We have already discussed how slowly evolving conformational degrees of freedom modulate the dynamical response and make using a single (scalar) overdamped diffusion model to accurately describe the stochastic dynamics of the ensemble of paths coming from the many-body SMD simulation problematic at the time and length scales associated with our simulation. Finding collective coordinates that are physically interpretable and correlate with the amount of work dissipation would likely be helpful in designing more efficient phase space sampling schemes based on nonequilibrium trajectories. The SPA model functions estimated can help in identifying such collective coordinates in both equilibrium and far from equilibrium situations.

CONCLUSIONS

We demonstrated how a collection of SPA models could be used to assist various computations commonly encountered in chemical physics (e.g., PMF along a reaction coordinate and the associated diffusion coefficient). The collection of SPA models was used to simulate new sample paths and these surrogate paths could be used to construct confidence bands that accounted for the temporal dependence and continuity of the sample paths while at the same time approximating the variability induced by fast-scale thermal fluctuations¹⁹ and the random initial configuration of the underlying high-dimensional complex system. These confidence bands are applicable to finite time simulations (each trajectory studied here was 1 ns in length). The confidence band width depends on the deterministic nonequilibrium pulling protocol defined by λ(⋅) and the collection of nonequilibrium trajectories (including the initial configuration). To our knowledge this is the first such nonequilibrium method providing confidence bands respecting these various sources of multiscale noise affecting the PMF computation. Accounting for the initial configuration in the gA channel was especially important because the channel could not adequately explore all conformations making relevant contributions to the PMF computation in the 1 ns SMD simulations. Quantitative evidence of this was contained in the pooled work distribution measured from the various work distributions simulated by the SPA models. The collection of SPA models was used to help quantify the initial configuration randomness in the various PMF and diffusion coefficient computations, e.g., a single scalar diffusion model (without memory) would not be able to provide reliable uncertainty estimates in the small set of 1 ns SMD simulations. The fact that a relatively small number of bidirectional nonequilibrium pullings can provide information that is often expensive to compute via equilibrium methods is encouraging from a computational standpoint. Note that using bidirectional pulling data is important in order to obtain accurate results; previous works have already reported problems associated with using unidirectional pulling data to compute the PMF in this system.³¹

One motivation for developing techniques to analyze artifacts introduced by using a collection of simple SPA models calibrated from scalar observables stems from the fact that “good reaction coordinates” can be hard to determine, but progress is being made in this direction.⁸⁵ The larger motivation stems from the fact that in single-molecule experiments one is often limited in the quantities that are experimentally dynamically observable.^{19, 20} Note that the SPA ideas as laid out here could, in principle, be extended to multivariate reaction coordinates.^{23, 24} Modeling tools from semiparametric regression⁷⁶ or functional data analysis⁸⁶ can be used to help one in understanding the information contained within a collection of models^{7, 8, 19, 20} and we see this as a promising future research direction for providing a quantitative understanding of the kinetics and thermodynamics of small biological systems where a low-dimensional set of system observables can be sampled frequently in time.^{1, 2, 3, 4, 5, 87, 88, 89, 90, 91} The SPA modeling ideas are not limited to nonequilibrium situations. The basic ideas behind the methods can also be used to more fully utilize the information contained in umbrella sampling simulations²⁷ and/or experimental time series.

Many new nanotechnology applications^{92, 93} aim to exploit dynamical features associated with small length and time scales, e.g., some molecular motors efficiently extract energy from a surrounding “molecular thermal bath,”⁹³ so quantitative understanding of when a single model or collection of models (of experimentally accessible quantities) is appropriate has potential relevance to nanotechnology design. Methods for quantifying information contained in a collection of models would be helpful in situations where experimentally hard to dynamically monitor conformational degrees of freedom modulate the response of an experimentally accessible quantity.^{19, 20, 27}