Reactive flux and folding pathways in network models of coarse-grained protein dynamics

Abstract

The reactive flux between folded and unfolded states of a two-state protein, whose coarse-grained dynamics is described by a master equation, is expressed in terms of the commitment or splitting probabilities of the microstates in the bottleneck region. This allows one to determine how much each transition through a dividing surface contributes to the reactive flux. By repeating the analysis for a series of dividing surfaces or, alternatively, by partitioning the reactive flux into contributions of unidirectional pathways that connect reactants and products, insight can be gained into the mechanism of protein folding. Our results for the flux in a network with complex connectivity, obtained using the discrete counterpart of Kramers’ theory of activated rate processes, show that the number of reactive transitions is typically much smaller than the total number of transitions that cross a dividing surface at equilibrium.

INTRODUCTION

Discrete coarse-graining of the dynamics is a powerful approach to studying protein folding and other molecular processes that occur on time scales inaccessible to current atomistic simulations.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} Configuration space is first divided into appropriately defined discrete microstates, and then the dynamics is modeled using a master equation that describes stochastic transitions among these microstates. The required rate coefficients can be extracted using a variety of strategies, for instance by monitoring transitions between coarse-grained states in molecular simulations.^{7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17}

Here we establish the relation between the macroscopic kinetics and the underlying microscopic dynamics on a network with complex connectivity (Fig. 1). The focus is on providing a theoretical framework to unravel mechanisms of protein folding when the dynamics is described by a master equation. However, our results are applicable to any discrete kinetic system, such as those that arise in systems biology or the modeling of enzyme catalysis.

Figure 1.

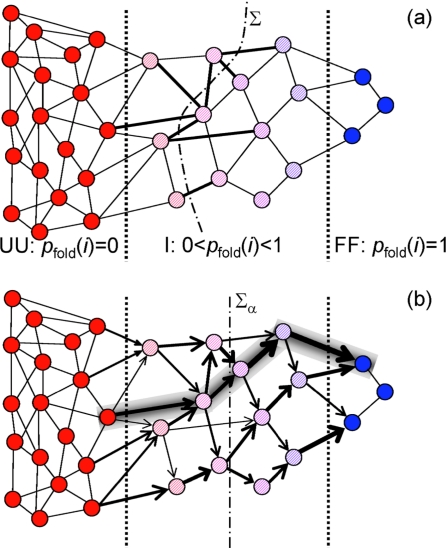
Schematic representation of a network of coarse-grained microstates of a two-state protein (circles). (a) Connectivity network. Reversible transitions among the microstates are denoted by solid lines. Microstates are divided into three groups: Definitely unfolded [UU with p_fold(i)=0; red], intermediate [I with 0<p_fold(i)<1; shaded] and definitely folded [FF with p_fold(i)=1; blue]. The boundaries separating these groups are shown by dashed lines. All transitions between the UU- and FF-microstates occur through the I-microstates, which form the bottleneck. Bold edges indicate the transitions across a dividing surface Σ (shown by the dashed-dotted curve) contributing to the reactive flux. (b) Unidirectional reactive flux diagram showing protein folding currents through the bottleneck region. The direction and thickness of the arrows are proportional to J_i→j defined in Eq. 14. The dominant unidirectional path is indicated by shading. The dashed-dotted line is a dividing surface Σ_α at p_fold=α.

One of the main results of this paper is a remarkably simple expression for the reactive flux in terms of the commitment or splitting probabilities, p_fold, of microstates in the bottleneck region that separates reactants from products. The p_fold of a microstate is defined as the probability that a protein starting from this microstate folds before it unfolds. While this result simplifies the calculation of the rate, its primary importance is that it gives the contribution to the reactive flux of each transition through a dividing surface located in the bottleneck region. By repeating such an analysis for a series of dividing surfaces or from the decomposition of the reactive flux into a sum of contributions of unidirectional pathways, one can gain insight into the mechanism of protein folding.

Our expression for the reactive flux is applicable to discrete dynamics with complex connectivity of the microstates (Fig. 1) and is not based on even an implicit assumption that low-dimensional reaction coordinates exist. We shall show that in general the reactive flux is much smaller than the upper bound given by transition state theory (TST). In TST, which ignores recrossings, the reactive flux is approximated by the number of transitions per unit time that cross a dividing surface in one direction. Our expression for the reactive flux shows that the TST contribution of every transition i→j that crosses the dividing surface is reduced by the difference in p_fold's of microstates j and i. When transitions occur between microstates with similar values of p_fold, this difference is much smaller that unity.

The commitment or splitting probability, p_fold, plays a key role in our analysis. p_fold(i) can be found from trajectories obtained in simulations or in state-resolved single-molecule experiments by counting the fraction of trajectory fragments starting in microstate i that reach the fully folded state before the unfolded state. The importance of this quantity appears to have been first recognized by Ryter¹⁸ who suggested using the stochastic separatrix (the locus of the phase space points for which the splitting probability is equal to 1∕2) as the boundary separating reactants from products. This idea has been exploited in the theory of chemical reactions¹⁹ and was introduced into the protein-folding literature by Du et al.²⁰ who defined the transition state ensemble (TSE) as the set of microstates with p_fold close to 1∕2. In this paper we shall derive the expression for the reactive flux in terms of p_fold using the discrete analogs of the Kramers²¹ and Chandler²² approaches.

THEORY

Our analysis is based on the master equation that describes the evolution of the probability p_i(t) of finding the protein in microstate i at time t, i=1,2,…,N,

$$\frac{d\mathbf{p}\left(t\right)}{dt}=\mathbf{K}\mathbf{p}\left(t\right).$$ (1)

The ij-th element of the N×N rate matrix K, K_ij, is the rate constant for transition j→i (i≠j) and K_jj=−∑_i≠jK_ij. The equilibrium probability of finding the protein in microstate i, p_eq(i), is the solution to Kp_eq=0 with the normalization ${\sum }_{i=1}^N{p}_{\text{eq}}\left(i\right)=1$. The elements of the rate matrix satisfy the condition of detailed balance, K_ijp_eq(j)=K_jip_eq(i), which follows from the requirement that there is no net flux between microstates at equilibrium.

We shall assume that the structure of the rate matrix, K, is such that folding can be accurately described by a phenomenological kinetic scheme

$$U\underset{k_U}{\overset{k_F}{\rightleftarrows }}F,$$ (2)

where k_F and k_U are the folding and unfolding rate constants for transitions between unfolded (U) and folded (F) states of the protein. According to this scheme, the reactive flux in the U→F direction at time t is k_Ff_U(t), where f_U(t) is the population of the unfolded state at time t. At equilibrium this flux, which is the number of U→F transitions per unit time, is equal to the reactive flux in the opposite (F→U) direction. Both fluxes, denoted by J, are given by

$$J=k_F{f}_U^{\text{eq}}=k_U{f}_F^{\text{eq}},$$ (3)

where $f_U^{\text{eq}}$ and $f_F^{\text{eq}}=1-f_U^{\text{eq}}$ are fractional populations of the folded and unfolded states of the protein at equilibrium.

For the kinetics to be described by the scheme in Eq. 2, the majority of the protein population must be localized in two basins separated by a narrow bottleneck, so that the intrabasin relaxation occurs much faster than the interbasin exchange, and thus kinetics of equilibration is essentially single exponential. In such a system all microstates can be separated into three groups: definitely unfolded (UU), definitely folded (FF), and intermediate (I) or bottleneck microstates (Fig. 1). There is some freedom in the choice of the bottleneck boundaries (two dashed lines in Fig. 1) since the reactive flux is rather insensitive to their precise location. Although the equilibrium population of the I-microstates is small, ∑_i∊Ip_eq(i)⪡∑_i∊Lp_eq(i), L=FF,UU, these microstates play an important role since all transitions between the UU- and FF-basins occur only through the bottleneck, UU⇔I⇔FF (i.e., we assume that there are no direct transitions between FF- and UU-basins, K_ij=K_ji=0, i∊UU,j∊FF).

To establish the relationship between the reactive flux at equilibrium and the discrete protein dynamics, we follow Kramers and consider a steady state in which all trajectories entering the FF-basin from the bottleneck are instantly returned to the UU-basin to maintain local equilibrium in this basin. The resulting steady-state distribution, p_ss(i), satisfies

$$\sum _j{K}_{ij}{p}_{ss}\left(j\right)=0$$ (4)

subject to the boundary conditions p_ss(i)=p_eq(i) if i∊UU and p_ss(i)=0 if i∊FF. The reactive flux J is approximated by the steady-state flux through an arbitrary dividing surface Σ in the bottleneck region, which is necessarily crossed by any trajectory connecting the UU- and FF-basins,

$$J=\sum _{i∊F^{\ast },j∊U^{\ast }}\left[K_{ij}{p}_{ss}\left(j\right)-K_{ji}{p}_{ss}\left(i\right)\right],$$ (5)

where F^∗ and U^∗ denote the sets of the microstates in the I region located on the F- and U-sides of Σ that are connected by a single transition.

The solution to Eq. 4 can be written in terms of p_eq(i) and the splitting probability, p_fold(i), defined as the probability of reaching the FF-basin before reaching the UU-basin starting from microstate i. For i∊FFp_fold(i)=1, while for i∊UUp_fold(i)=0. The remaining p_fold's, as indicated in Ref. 23, can be found by solving the discrete version of Onsager’s equation²⁴ for the splitting probability,

$$\sum _i{p}_{\text{fold}}\left(i\right)K_{ij}=\sum _{i∊I}{p}_{\text{fold}}\left(i\right)K_{ij}+\sum _{i∊FF}{K}_{ij}=0,j∊I.$$ (6)

This equation can be derived by considering the relation between the p_fold of microstate j and those of microstates that are connected to it by a single transition (i.e., microstates i for which K_ij≠0). After one transition from microstate j, the protein ends up in microstate i with probability K_ij∕∑_l≠jK_lj. From the probability conservation it then follows that

$$p_{\text{fold}}\left(j\right)=\sum _{i\ne j}{p}_{\text{fold}}\left(i\right)\frac{K_{ij}}{{\sum }_{l\ne j}{K}_{lj}}.$$ (7)

Since ∑_l≠jK_lj=−K_jj, Eq. 7 is equivalent to Eq. 6.

Comparing Eqs. 4, 6 and using the condition of detailed balance, K_ijp_eq(j)=K_jip_eq(i), it can be shown that

$$p_{ss}\left(i\right)=\left[1-p_{\text{fold}}\left(i\right)\right]p_{\text{eq}}\left(i\right).$$ (8)

Substituting this solution for p_ss(i) into Eq. 5 and again using the condition of detailed balance, we obtain one of the main results of this paper,

$$J=\sum _{i∊F^{\ast },j∊U^{\ast }}{K}_{ij}{p}_{\text{eq}}\left(j\right)\left[p_{\text{fold}}\left(i\right)-p_{\text{fold}}\left(j\right)\right],$$ (9)

which is the expression for the reactive flux when the underlying dynamics involves stochastic transitions on a network of microstates with complex connectivity (Fig. 1). One can use this expression to find the folding and unfolding rate constants by means of the flux-over-population formula, $k_{F,U}=J∕f_{U,F}^{\text{eq}}$, [see Eq. 3]. In the special case when the microstates correspond to lattice points in a multidimensional space and the transitions occur only between the nearest neighbors, the continuum limit of Eq. 9 has been obtained by E and Vanden-Eijnden.²⁵ We now rederive the result in Eq. 9 by another method.

To obtain this expression using Chandler’s approach,²² consider the “number” correlation function C_F(t)=⟨I_F(t)I_F(0)⟩, where I_F is unity when the protein is in one of the microstates on the F side of Σ and zero otherwise. In the two-state phenomenological description, Eq. 2, this correlation function is $C_F\left(t\right)=f_F^{\text{eq}}\left[f_F^{\text{eq}}+f_U^{\text{eq}}\text{exp}\left(-\left(k_F+k_U\right)t\right)\right]$, so that its time derivative at t=0 is equal to the reactive flux, $d{C}_F\left(t\right)∕dt{\mid }_{t=o}=f_F^{\text{eq}}{f}_U^{\text{eq}}\left(k_F+k_U\right)=J$. In the framework of the more detailed coarse-grained description, Eq. 1, this correlation function is given by C_F(t)=∑_i,j∊FG_ij(t)p_eq(j), where G_ij(t) is the probability of finding the protein in microstate i at time t, given that it starts from microstate j at t=0. Using the evolution equation, dG_ij(t)∕dt=∑_nK_inG_nj(t) with the initial condition G_ij(0)=δ_ij, the time derivative of the correlation function can be written as,

$$\frac{d{C}_F\left(t\right)}{dt}=\sum _{i,j∊F,n∊U}{K}_{\text{in}}{G}_{nj}\left(t\right)p_{\text{eq}}\left(j\right)+\sum _{i,j,n∊F}{K}_{\text{in}}{G}_{nj}\left(t\right)p_{\text{eq}}\left(j\right).$$ (10)

Using the relations G_ij(t)p_eq(j)=G_ji(t)p_eq(i) and K_ijp_eq(j)=K_jip_eq(i), which follow from the condition of detailed balance, and the fact that ∑_i∊FK_ij=−∑_i∊UK_ij, one can recast Eq. 10 as

$$\frac{d{C}_F\left(t\right)}{dt}=\sum _{i∊F^{\ast },n∊U^{\ast }}{K}_{\text{in}}{p}_{\text{eq}}\left(n\right)\sum _{j∊F}\left[G_{jn}\left(t\right)-G_{ji}\left(t\right)\right],$$ (11)

where i and n are “connected” microstates located on opposite sides of the dividing surface. As t→0, −dC_F(t)∕dt reduces to the TST estimate for the reactive flux through the dividing surface Σ,

$${\phantom{\mid }-\frac{d{C}_F\left(t\right)}{dt}\mid }_{t=0}=J_{\mathrm{TST}}\left(\Sigma \right)=\sum _{i∊F^{\ast },j∊U^{\ast }}{K}_{ij}{p}_{\text{eq}}\left(j\right).$$ (12)

To get a better estimate of the reactive flux, consider −dC_F(t)∕dt on a timescale that is much smaller than the mean interbasin equilibration time, (k_F+k_U)⁻¹, but much larger than the time spent in the bottleneck region by a protein starting in a microstate near the dividing surface. On such a time scale, once the protein reaches the FF- or UU-basin, it does not return to the bottleneck region, so these basins are effectively absorbing. This allows us to approximate the sums in Eq. 11 as: ∑_j∊FG_ji(t)≈∑_j∊FFG_ji(t)≈p_fold(i), i∊U^∗ or F^∗. As a result, −dC_F(t)∕dt in Eq. 11 reduces to the reactive flux in Eq. 9.

One can also obtain the expression for the reactive flux, Eq. 9, using the following simple argument. Consider an equilibrium ensemble of identical proteins. Each protein in the ensemble can be in one of the two basins or in the bottleneck. We denote the fraction of proteins in microstate i,i∊I, that entered the bottleneck from the UU-basin by ν_U(i). The reactive flux is the average number of trajectories that go from the UU-basin to the FF-basin per unit time. The forward (i.e., in the U→F direction) flux through Σ, J_f(Σ), due to such trajectories is given by J_f(Σ)=∑_{i∊F^∗,j∊U^∗}p_fold(i)K_ijp_eq(j)ν_U(j). Since a reactive trajectory can cross Σ several times, the reactive flux is J_f(Σ) minus the flux due to backward transitions of these trajectories through Σ, J_b(Σ)=∑_{i∊F^∗,j∊U^∗}p_fold(j)K_jip_eq(i)ν_U(i). Thus, the reactive flux is

$$J=J_f\left(\Sigma \right)-J_b\left(\Sigma \right)=\sum _{i∊F^{\ast },j∊U^{\ast }}\left[p_{\text{fold}}\left(i\right)K_{ij}{p}_{\text{eq}}\left(j\right){\nu }_U\left(j\right)-p_{\text{fold}}\left(j\right)K_{ji}{p}_{\text{eq}}\left(i\right){\nu }_U\left(i\right)\right].$$ (13)

From the time-reversal symmetry of the underlying microscopic dynamics it follows that, at equilibrium, for any trajectory fragment that goes from microstate j to microstate i in time t, there is a counterpart going in the opposite direction. As a consequence, the fraction of proteins in microstate i, i∊I, that entered the bottleneck from the UU-basin, ν_U(i), is the same as the fraction of proteins that start from this microstate and reach the UU-basin before reaching the FF-basin, so that

$${\nu }_U\left(i\right)=1-p_{\text{fold}}\left(i\right).$$ (14)

Using this relation and the condition of detailed balance, K_ijp_eq(j)=K_jip_eq(i), in Eq. 13, we recover our result for the reactive flux in Eq. 9.

DISCUSSION

As the simplest example, consider the three-state scheme U⇔I⇔F, where k_XY is the rate constant for the transition Y→X with X,Y=U,I,F. When the population of I is small, the rates k_F and k_U can be obtained from the three rate equations by setting dI∕dt=0. For the folding rate this procedure yields k_F=k_FIk_IU∕(k_UI+k_FI). If one chooses the dividing surface to be between the U and I states, our formalism [Eq. 9] predicts that the reactive flux is J=[p_fold(I)−p_fold(U)]k_IUp_eq(U). Since p_fold(U)=0 and p_fold(I)=k_FI∕(k_UI+k_FI), k_F=J∕p_eq(U) agrees with the above result obtained by making the steady-state assumption for the population of I. It can be readily verified that if one chooses the dividing surface to be between I and F, our formalism yields the identical expression for k_F. In fact, it can be shown in general that the reactive flux in Eq. 9 is the same for any dividing surface chosen so that any reactive trajectory unavoidably crosses this surface.

Whereas J is independent of the choice of Σ, individual contributions to the reactive flux may be both positive and negative. However, if we specify Σ using p_fold(i), then all contributions have the same sign. Let us chose the dividing surface Σ_α so that all microstates with p_fold(i)<α are on the U-side of Σ_α, while all microstates with p_fold(i)>α are on the F-side of this dividing surface, 0<α<1. We denote the local reactive flux flowing in the U→F direction from microstate i to microstates j that has a greater p_fold by J_i→j,

$$J_{i\to j}=K_{ji}{p}_{\text{eq}}\left(i\right)\left[p_{\text{fold}}\left(j\right)-p_{\text{fold}}\left(i\right)\right],p_{\text{fold}}\left(j\right)>p_{\text{fold}}\left(i\right).$$ (15)

Since all fluxes J_i→j crossing Σ_α are positive, we can determine the importance of each transition based on the magnitude of its contribution to the reactive flux [Fig. 1b]. By repeating this procedure for a series of dividing surfaces Σ_α, one can evaluate the importance of different folding∕unfolding pathways. Of particular interest are transitions that cross the dividing surface with α=1∕2, since microstates involved in such transitions form the TSE. Using Eq. 9 one can ascertain the dynamically most relevant members of the TSE, i.e., microstates i and j, for which the local reactive flux is the largest. Interestingly, these microstates need not be those with the highest equilibrium populations. Thus, one can determine whether the reactive flux is localized (i.e., only a few pairs of microstates contribute) or delocalized (i.e., there are similar contributions from many transitions). Finally we note that when transitions occur between microstates with similar values of p_fold(i), the difference of the splitting probabilities is much smaller than unity, [p_fold(j)−p_fold(i)]⪡1. The reactive flux in Eq. 9 is then well below its TST upper bound given in Eq. 11, in which recrossings are ignored.

Instead of dividing the total reactive flux into contributions due to transitions crossing a dividing surface, we can decompose it into a sum of contributions due to unidirectional paths connecting the UU- and FF-basins. The local reactive flux between microstate i and j (p_fold(j)>p_fold(i)) is positive, J_i→j>0, and directed in the U→F direction. Because of the probability conservation, the sums of local reactive fluxes entering and exiting a microstate i are equal, ∑_kJ_k→i=∑_jJ_i→j=J_i, where p_fold(k)<p_fold(i)<p_fold(j). One can construct a directed graph that connects the UU- and FF-basins by following the local reactive fluxes [Fig. 1b]. The contribution of each unidirectional path on this graph to the total reactive flux can be determined as follows. A path that starts from i₀∊UU and ends up at i_L∊FF passing through microstates i₁,i₂,…,i_L−1∊I contributes $J\left(i_0\to i_1\to \dots \to i_{L-1}\to i_L\right)=J_{i_0\to i_1}{\prod }_{k=1}^{L-1}\left(J_{i_k\to i_{k+1}}∕J_{i_k}\right)$ to the reactive flux. The sum of all “path” fluxes is equal to the total reactive flux J. The unidirectional path with the largest contribution can be found, for example, by using Dijkstra’s algorithm for the shortest path, identifying ln(J_j∕J_i→j) as the “length” associated with the transition from i to j, and ln(J∕J_i0→i1) as the length associated with the entrance into the bottleneck from the UU-basin.

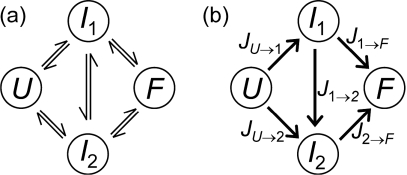
As an illustration consider the four-state model shown in Fig. 2a. In this model the unfolded (U) and folded (F) states of the protein are separated by two bottleneck states I₁ and I₂, through which all U-to-F transitions occur. Given rate constants for which p_fold(I₂)≥p_fold(I₁), the local reactive fluxes obtained from Eq. 15 are shown in Fig. 2b. There are four distinct dividing surfaces in the bottleneck region. Since the total reactive flux J is independent of the choice of the dividing surface we have

$$J=J_{U\to 1}+J_{U\to 2}=J_{1\to F}+J_{2\to F}=J_{U\to 2}+J_{1\to F}+J_{1\to 2}=J_{U\to 1}+J_{2\to F}-J_{1\to 2}.$$ (16)

From this it follows that J_U→1=J_1→2+J_1→F and J_2→F=J_U→2+J_1→2. These relations represent flux conservation at the nodes. Thus, there are only three independent local reactive fluxes. The total reactive flux can be partitioned among the three unidirectional “flux” paths as follows: J(U→I₂→F)=J_U→2, J(U→I₁→F)=J_U→1[J_1→F∕(J_1→2+J_1→F)]=J_1→F, and J(U→I₁→I₂→F)=J_U→1[J_1→2∕(J_1→2+J_1→F)]=J_1→2. The sum of these fluxes is equal to J.

Figure 2.

Four-state model of coarse-grained protein dynamics. (a) Kinetic scheme with two intermediate (or bottleneck) microstates I₁ and I₂. (b) Local unidirectional reactive fluxes for p_fold(I₂)≥p_fold(I₁).

CONCLUDING REMARKS

To summarize, the phenomenological kinetic scheme in Eq. 2 describes the equilibration of the populations of two basins where the majority of the protein population is localized. The equilibration occurs via a sparsely populated bottleneck region, which connects these basins. Although the equilibration rate is determined by dynamics in the bottleneck, this region does not appear in the phenomenological description since the protein spends a small fraction of time there. One of the main results of our analysis is the expression for the reactive flux in Eq. 9, which relates the phenomenological description of two-state protein folding and a more detailed description of the protein dynamics that involves transitions among discrete coarse-grained microstates. This expression allows one to determine how much each transition through a dividing surface contributes to the observed rate. Alternatively, one can divide the total reactive flux into a sum of contributions due to all directed paths connecting the definitely unfolded and definitely folded microstates. Although our primary focus has been on problems where the reactive flux is related to the phenomenological rate constants describing two-state kinetics, the expression in Eq. 9 is actually valid for an arbitrary partitioning of the microstates into three subsets. Specifically, it gives the number of trajectory fragments per unit time that leave the UU region and enter the FF region, irrespective of whether the intermediate microstates are sparsely populated or even exist.