Density Estimation for Protein Conformation Angles Using a Bivariate von Mises Distribution and Bayesian Nonparametrics

Abstract

Interest in predicting protein backbone conformational angles has prompted the development of modeling and inference procedures for bivariate angular distributions. We present a Bayesian approach to density estimation for bivariate angular data that uses a Dirichlet process mixture model and a bivariate von Mises distribution. We derive the necessary full conditional distributions to fit the model, as well as the details for sampling from the posterior predictive distribution. We show how our density estimation method makes it possible to improve current approaches for protein structure prediction by comparing the performance of the so-called “whole” and “half” position distributions. Current methods in the field are based on whole position distributions, as density estimation for the half positions requires techniques, such as ours, that can provide good estimates for small datasets. With our method we are able to demonstrate that half position data provides a better approximation for the distribution of conformational angles at a given sequence position, therefore providing increased efficiency and accuracy in structure prediction.

1. Introduction

Computational structural genomics has emerged as a powerful tool for better understanding protein structure and function using the wealth of data from ongoing genome projects. One active area of research is the prediction of a protein's structure, particularly its backbone, from its underlying amino acid sequence (Dill, Ozkan, Weikl, Chodera, and Voelz 2007).

Based on the fundamental work of Ramachandran, Ramakrishnan, and Sasisekharan (1963), the description of the protein backbone has been simplified by replacing the (x, y, z) coordinates of an amino acid residue's four heavy atoms (N, C_α, C, and O) with the backbone torsion angle pair (φ, ψ) (Fig. 1). A standard visual representation is the Ramachandran plot, in which φ angles are plotted against ψ angles. Because of their importance to structure prediction and their simple representation, a great deal of recent work has sought to characterize the distributions of these angle pairs, with an eye toward predicting conformational angles for novel proteins (Ho, Thomas, and Brasseur 2003; Xue, Dor, Faraggi, and Zhou 2008).

Figure 1.

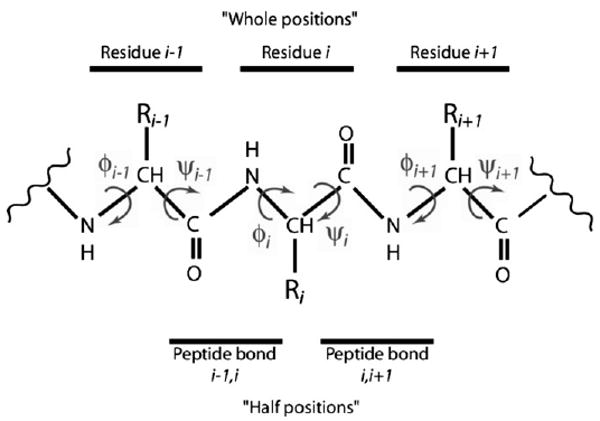
Diagram of protein backbone, including φ and ψ angles, whole positions, and half positions. At the ith residue the φ angle describes the torsion around the bond N_i–C_αi, measuring the angle between the C_i−1–N_i and the C_αi–C_i bonds, whereas the ψ angle describes the torsion around the bond C_αi–C_i, measuring the angle between the N_i–C_αi and the C_i–N_i+1 bonds. (In the graphic, CH represents a C_α atom and the attached hydrogen atom.) The torsion angle pair (φ, ψ) on either side of a residue R is considered a whole position. Three such pairs are shown. The torsion angle pair (ψ, φ) on either side of a peptide bond, between two residues, is considered a half position. Two such pairs are shown.

Datasets from the Protein Structure Databank (PDB) (Berman et al. 2000) can consist of over ten thousand angle pairs, which provide ample data for even relatively unsophisticated density estimation methods. However, when the data are subdivided, based on known characteristics such as amino acid residue or secondary structure type at the relevant sequence position, datasets quickly become small, sometimes having only a few dozen or a few hundred observations. A number of approaches to smooth density estimates from simple binning methods for the (φ, ψ) distributions have been proposed (Hovmoller, Zhou, and Ohlson 2002; Lovell et al. 2003; Rother, Sapiro, and Pande 2008), but they behave poorly for these subdivided datasets. This is unfortunate, because these subsets provide structure prediction that is more accurate, as it utilizes more specific information about a particular sequence position. The issue is further complicated by the circular nature of this data, with each angle falling in the interval (− π, π], which renders traditional techniques inadequate for describing the distributional characteristics. Distributions for angular data, particularly mixture distributions for bivariate angular data, are required.

Some methods have been proposed which exhibit better performance for small bivariate angular datasets. Pertsemlidis, Zelinka, Fonson, Henderson, and Otwinowski (2005) recommend estimating such distributions using a finite number of Fourier basis functions. This method exhibits correct wrapping behavior, but requires the estimation of a large number of parameters that may not be readily interpretable. Other models exhibit more intuitive behavior. Mardia, Taylor, and Subramaniam (2007) fit finite mixtures of bivariate von Mises distributions using the expectation-maximization (EM) algorithm. Dahl, Bohannan, Mo, Vannucci, and Tsai (2008) used a Dirichlet process mixture (DPM) model and bivariate normal distributions to estimate the distribution of torsion angles. However, neither of these methods is entirely satisfactory, as the first requires the selection of the number of component distributions, and the second cannot properly account for the wrapping of angular data.

We propose a nonparametric Bayesian model that takes the best aspects from Mardia et al. (2007) and Dahl et al. (2008). Specifically, we use a bivariate von Mises distribution as the centering and component distributions of a Dirichlet process mixture model. The use of a DPM model offers advantages in that the number of component distributions need not be fixed, and inference accounts for the uncertainty in the number of components. Using a bivariate von Mises distribution, rather than a nonangular distribution, also provides estimates that properly account for the wrapped nature of angular data. In addition, the model readily permits the incorporation of prior information, which is often available for torsion angles.

Although some authors have studied Bayesian models for univariate angular data, to our knowledge the Bayesian analysis of bivariate angular data, such as that arising in protein structure prediction, has not been treated in the literature. We provide the results necessary for Bayesian analysis of bivariate angular data, including the full conditional distributions and conditionally conjugate priors, for a version of the bivariate von Mises distribution known as the sine model (Singh, Hnizdo, and Demchuk 2002). Because of the complexity of this distribution, methods for sampling from the posterior distribution are not obvious. Therefore, we provide a Markov chain Monte Carlo (MCMC) scheme that mixes well without requiring the tuning of any sampling parameters, and show how to produce density estimates from the MCMC sampler.

We use our method to address the bioinformatics question of what distributions should be used when sampling to generate new candidate models for a protein's structure, a matter of considerable interest to the structure prediction community. Recall the illustration in Figure 1, which depicts whole and half positions on a peptide backbone. Current methods use data from whole positions, so the (φ, ψ) angle pairs across positions for a protein are considered independently. An alternative is to use the so-called half positions, which consist of ψ and φ angles on either side of a peptide bond. Treating data as half positions allows for more precise categorization, because these angle pairs are associated with two adjacent residue types, as opposed to a single residue for whole positions. Because they make use of a finer classification of the dataset, half position distributions are more accurate than those of the whole positions, thus providing a better description of backbone behavior. Because of their specificity, datasets for half positions are often relatively small, a situation that our proposed density estimation technique handles well.

Section 2 of this article contains a review of past work in angular data analysis, including recent work in mixture modeling. In Section 3 we describe our DPM model for bivariate angular data that incorporates the von Mises sine model as a centering distribution in the Dirichlet process prior. In Section 4 we also present the groundwork for a Bayesian treatment of the bivariate von Mises distribution and develop the relevant distribution theory, including deriving the full conditional distributions and conditionally conjugate priors for both the mean and precision parameters. We also describe our MCMC scheme for fitting this model, and our associated density estimation technique. Section 5 details the novel results from our method, comparing the use of whole versus half positions for template-based protein structure modeling. Concluding comments are found in Section 6.

2. Review of Previous Statistical Work

As our method builds upon previous univariate and bivariate work with angular data, we provide a review of this field. We also discuss the recent results in bivariate mixture modeling. It should be noted that the terms angular data and circular data are used interchangeably in the literature.

2.1 Univariate Angular Data

A common option for describing univariate circular data are the von Mises distribution (e.g., see Mardia 1975), which can be characterized in terms of either an angle or a unit vector. In terms of an angle φ ∈ (− π, π], the density is written:

$$f(\varphi |\mu ,\kappa )={\{2\pi I_0(\kappa )\}}^{-1}exp\{\kappa cos(\varphi -\mu )\},$$

where κ > 0 is a measure of concentration, μ is both the mode and circular mean, and I_m(x) is the modified Bessel function of the first kind of order m. This distribution is symmetric and goes to a uniform distribution as κ → 0. As discussed by Pewsey and Jones (2005), this distribution can be approximated by a wrapped normal distribution.

There is extensive Bayesian literature for this univariate distribution. Mardia and El-Atoum (1976) derived the full conditional distribution and conditionally conjugate prior for μ, whereas Guttorp and Lockhart (1988) determined the full conditional and conditionally conjugate prior for κ, as well as the conjugate prior and posterior distribution for simultaneous inference on μ and κ. Bagchi and Guttman (1988) developed the more general case including the distributions on the sphere and hypersphere. More recently, Rodrigues, Leite, and Milan (2000) presented an empirical Bayes approach to inference.

2.2 Bivariate Angular Data

The original bivariate von Mises distribution was introduced by Mardia (1975) and was defined with eight parameters. Rivest (1988) introduced a six parameter version. A five parameter distribution is preferable, however, so that the parameters might have a familiar interpretation, analogous to the bivariate normal.

Singh et al. (2002) introduced a five parameter subclass of Rivest's distribution, referred to as the sine model. The density for angular observations (φ, ψ) is of the form:

$$\begin{array}{ll}f(\varphi ,\psi |\mu ,\nu ,{\kappa }_1,{\kappa }_2,\lambda )& =Cexp\{{\kappa }_{1}cos(\varphi -\mu )\\ & +{\kappa }_{2}cos(\psi -\nu )\\ & +\lambda sin(\varphi -\mu )sin(\psi -\nu )\}\end{array}$$ (1)

for φ, ψ, μ, ν ∈ (−π, π], κ₁, κ₂ > 0, λ ∈ (−∞, ∞), and

$$C^{-1}=4{\pi }^2\sum _{m=0}^{\infty }\left(\begin{array}{c}2m\\ m\end{array}\right){\left(\frac{{\lambda }^2}{4{\kappa }_1{\kappa }_2}\right)}^m{I}_m({\kappa }_1)I_m({\kappa }_2).$$ (2)

This density is unimodal when λ² < κ₁κ₂ and bimodal otherwise. In the unimodal situation, this density has a direct analogue to a bivariate normal with mean (μ, ν), and precision matrix Σ⁻¹, where ${\sum }_{11}^{-1}={\kappa }_1$, ${\sum }_{22}^{-1}={\kappa }_2$, and ${\sum }_{12}^{-1}={\sum }_{21}^{-1}=-\lambda$. Note that this normal approximation holds when the variance of the distribution is small (i.e., when κ₁ and κ₂ are large). This correspondence to the bivariate normal distribution provides intuition for the behavior of the sine model for various parameter values.

Bivariate angular data, particularly protein conformational angles, often have a distribution with features that cannot be accommodated by a single von Mises distribution, even when bimodality is permitted. Mardia et al. (2007) developed the cosine model, another five parameter bivariate angular distribution, and suggested using the EM algorithm to fit several finite mixtures of these models, each with a different numbers of components. They employed the Akaike information criterion (AIC) for model selection. With this technique they estimated the density of (φ, ψ) angle pairs in the myoglobin and malate dehydrogenase protein structures.

3. Bayesian Mixture Model with Von Mises Distributions

Our model for bivariate angular distributions offers both the flexibility of the DPM model and the technical accuracy provided by the use of a bivariate angular distribution. The proposed model is

$$({\varphi }_i,{\psi }_i)|{\mu }_i,{\nu }_i,{\Omega }_i\sim p(({\varphi }_i,{\psi }_i)|{\mu }_i,{\nu }_i,{\Omega }_i)$$ (3)

$$({\mu }_i,{\nu }_i,{\Omega }_i)|G\sim G$$ (4)

$$G\sim DP({\tau }_0{H}_1{H}_2),$$ (5)

where p((φ_i, ψ_i)|μ_i, ν_i, Ω_i) is a bivariate von Mises sine model in which Ω_i is a 2 × 2 matrix with both off-diagonal elements equal to − λ_i and diagonal elements κ_1i and κ_2i. This parameterization makes Ω_i analogous to the precision matrix of the bivariate normal distribution. The G is a random realization from DP(τ₀H₁H₂), a Dirichlet process (Ferguson 1973) with mass parameter τ₀ and centering distribution H₁H₂. We take H₁ to be a bivariate von Mises sine model for the means μ and ν, and H₂ to be a bivariate Wishart distribution for the precision matrix Ω. An alternative noninformative prior on the means is obtained using a uniform distribution on the square (−π, π] × (−π, π] for H₁. In either case, the resulting model is a Bayesian mixture model (Antoniak 1974), a broad class of models reviewed by Müller and Quintana (2004).

In contrast, Dahl et al. (2008) modeled the distributions of conformational angles using a DPM model that assumed bivariate normals as the component distributions. They took the sampling model to be a bivariate normal distribution with precision matrix ${\sum }_i^{-1}$ and also took H₁ to be a bivariate normal. This approach is unsatisfactory for circular data and exhibits particular problems when the underlying distribution has significant mass on the boundaries of the (−π, π] × (−π, π] region. Our use of the bivariate von Mises distribution avoids this deficiency. Also, in contrast to our model, the Dahl et al. (2008) model used two separate clusterings: one for the mean parameters and one for the precision parameters.

For our torsion angle application, we are particularly interested in predicting new (φ, ψ) values based on the existing data and our DPM model. Density estimation using DPM models was first discussed by Escobar and West (1995). A nonparametric density estimate of the (φ, ψ) space from data (φ, ψ) = ((φ₁, ψ₁), …, (φ_n, ψ_n)) is the posterior predictive distribution of a new angle pair (φ_n+1, ψ_n+1), namely:

$$\begin{array}{l}p(({\varphi }_{n+1},{\psi }_{n+1})|(\varphi ,\psi ))\\ =\int p(({\varphi }_{n+1},{\psi }_{n+1}),({\mu }_{n+1},{\nu }_{n+1},{\Omega }_{n+1})|(\varphi ,\psi ))d({\mu }_{m+1},{\nu }_{n+1},{\Omega }_{n+1})\\ =\int p(({\varphi }_{n+1},{\psi }_{n+1})|({\mu }_{n+1},{\nu }_{n+1},{\Omega }_{n+1}))\\ \times p(({\mu }_{n+1},{\nu }_{n+1},{\Omega }_{n+1})|(\varphi ,\psi ))d({\mu }_{n+1},{\nu }_{n+1},{\Omega }_{n+1}).\end{array}$$ (6)

We show in the following sections how to estimate this density and how it can be used for protein structure prediction.

4. Model Estimation

The integral of the posterior predictive density in (6) cannot be expressed in closed form, but it can be computed through Monte Carlo integration. Specifically, let $({\mu }_{n+1}^1,{\nu }_{n+1}^1,{\Omega }_{n+1}^1),\dots ,({\mu }_{n+1}^B,{\nu }_{n+1}^B,{\Omega }_{n+1}^B)$ be B samples from the posterior predictive distribution of (μ_n+1, ν_n+1, Ω_n+1) obtained from some valid sampling scheme. Then

$$\begin{array}{l}p(({\varphi }_{n+1},{\psi }_{n+1})|(\varphi ,\psi ))\\ \approx \frac{1}{B}\sum _{b=1}^{B}p(({\varphi }_{n+1},{\psi }_{n+1})|({\mu }_{n+1}^b,{\nu }_{n+1}^b,{\Omega }_{n+1}^b)).\end{array}$$ (7)

Although Equation (7) can be evaluated for any value of (φ_n+1, ψ_n+1), for our purposes we obtain density estimates by evaluating (7) on a grid of points and use linear interpolation between them.

All that remains is to determine how to sample from the posterior distribution of the parameters. The Auxiliary Gibbs sampler of Neal (2000) provides an MCMC update of the allocation of objects to clusters. We are at liberty to choose any valid updating scheme for the mean and precision parameters. Because the joint posterior distribution for all five parameters is intractable, the full conditionals of the mean and precision parameters are a natural choice. We now present our novel results regarding (1) conditionally conjugate priors for this model, (2) full conditional distributions for both conditionally conjugate and uniform priors, and (3) sampling methods for each full conditional distribution.

4.1 Full Conditional Distributions of Mean and Precision Parameters

Note that the sine model can be written either in terms of angles φ_i and ψ_i, or in terms of coordinates on the unit circle x_i = (cos(φ_i), sin(φ_i))^T, and y_i = (cos(ψ_i), sin(ψ_i))^T. Let τ_μ = (cos(μ), sin(μ))^T, τ_ν = (cos(ν), sin(ν))^T, and for a vector δ = (a, b)^T, let δ*: = (−b, a)^T. The sine model density from (1) can now be rewritten as

$$\begin{array}{ll}f(x_i,y_i|{\tau }_{\mu },{\tau }_{\nu },{\kappa }_1,{\kappa }_2,\lambda )& =Cexp({\kappa }_1{\tau }_{\mu }^T{x}_i+{\kappa }_2{\tau }_{\nu }^T{y}_i\\ & +\lambda {\tau }_{\mu }^{\ast T}{x}_i{\tau }_{\nu }^{\ast T}{y}_i).\end{array}$$

This formulation is used in the derivation of the full conditional distribution of the mean parameters given in the Appendix.

The conditionally conjugate prior for the mean parameters is a von Mises sine model with center x₀ = (cos(μ₀), sin(μ₀))^T, y₀ = (cos(ν₀), sin(ν₀))^T, and precision parameters κ₁₀, κ₂₀, and λ₀. Consider a set of observations (x_i, y_i), i = 1, …, n, each with known precision parameters κ_1i, κ_2i, and λ_i. The full conditional distribution is a von Mises sine model with parameters:

$$\begin{array}{l}\stackrel{\sim }{\mu }=arctan\left(\sum _{i=0}^n{\kappa }_{1i}{x}_i\right)\stackrel{\sim }{\nu }=arctan\left(\sum _{i=0}^n{\kappa }_{2i}{y}_i\right)\\ {\stackrel{\sim }{\kappa }}_1=\left|\sum _{i=0}^n{\kappa }_{1i}{x}_i\right|{\stackrel{\sim }{\kappa }}_2=\left|\sum _{i=0}^n{\kappa }_{2i}{y}_i\right|\\ \stackrel{\sim }{\lambda }=\left(\sum _{i=0}^n{\lambda }_i{x}_i^T{y}_i\right){\{cos(\stackrel{\sim }{\mu }-\stackrel{\sim }{\nu })\}}^{-1}.\end{array}$$

The mean parameters of the full conditional distribution are the directions of the sums of the observation vectors, whereas the concentration parameters are the magnitudes of those same vectors. These bivariate results are analogous to the univariate work of Mardia and El-Atoum (1976).

The conditionally conjugate prior can be interpreted as an additional observation with known precision parameters. As observations with higher concentration values have greater weight in determining the posterior distribution parameters, less informative priors are those with κ₁₀, κ₂₀, and λ₀ close to 0. This is consistent with the fact that a noninformative alternative prior to the conditionally conjugate is a uniform distribution on (−π, π] × (−π, π], which is the limit of the sine model prior when λ₀ = 0 and κ₁₀, κ₂₀ → 0.

When considering the full conditional distribution of the precision parameters, it may be assumed that the known means are both 0. The conditionally conjugate prior for the precision parameters is of the form:

$$\begin{array}{ll}\pi ({\kappa }_1,{\kappa }_2,\lambda )& \propto {\left\{4{\pi }^2\sum _{m=0}^{\infty }\left(\begin{array}{c}2m\\ m\end{array}\right){\left(\frac{{\lambda }^2}{4{\kappa }_1{\kappa }_2}\right)}^m{I}_m({\kappa }_1)I_m({\kappa }_2)\right\}}^{-c}\\ & \times exp(R_{\varphi 0}{\kappa }_1+R_{\psi 0}{\kappa }_2+R_{\varphi \psi 0}\lambda ).\end{array}$$ (8)

Here the prior assumes the role of c observations from the von Mises distribution, and the prior parameters R_φ0 and R_ψ0 are the sums of the magnitudes in the x direction of the φ and ψ components, respectively, of these observations. The parameter R_φψ0 is the sum of the products of the magnitudes in the y direction. For this interpretation to hold R_φ0, R_ψ0 and R_φψ0 must all fall between −c and c. Notice that the conditionally conjugate prior, and corresponding posterior distribution, are difficult to sample from because of the infinite sums of Bessel functions. Notice also that these distributions do not guarantee precision parameters that will give unimodal sine model distributions.

4.2 Markov Chain Monte Carlo Sampler

The posterior distribution of our model's parameters in Section 3 can be sampled using MCMC via the Auxiliary Gibbs sampler of Neal (2000). This method requires the ability to directly sample from the centering distribution. Because it is difficult to sample from the conjugate prior for the precision parameters described in (8), we instead use the Wishart distribution for H₂(Ω) in (5). In addition, a Wishart prior guarantees that the sampled matrix will be positive definite, which is equivalent to the restriction that ensures unimodality for the sine model component distributions. Eliminating bimodality both simplifies posterior simulation, and increases the resemblance of the sampling model to that of a mixture of bivariate normal distributions. This substitution is also appealing because, for large values of κ₁ and κ₂, this von Mises model is nearly equivalent to a normal distribution. In this case, the Wishart prior behaves much like the conjugate prior distribution in (8).

Auxiliary Gibbs sampling requires a valid updating scheme for the model parameters. Direct sampling from the full conditional distribution of the means is fairly straightforward. As described previously in Section 4.1, the full conditional distribution of the means is given by a von Mises sine model. A simple method to sample from this distribution is to use a rejection sampler with a uniform distribution as the majorizing density. The implementation requires some care, however, as the full conditional distribution is not always unimodal. The value of the mode in the unimodal case is (μ̃, ν̃), whereas the values in the bimodal case depend on the sign of λ̃ and are given in the Appendix of Mardia et al. (2007).

An update scheme for the concentration matrix Ω of a cluster is less straightforward. Regardless of the choice of prior, the full conditional distribution of the precision parameters would be difficult to sample from directly because of the infinite sum of Bessel functions and the fact that the constant of integration is not known in closed form. However, this distribution is often well approximated by the full conditional of the precision parameters from an analogous model in which the data are assumed to be normally distributed, particularly when a Wishart prior is used. An independence sampler using this equivalent Wishart distribution generally provides a good acceptance rate. Furthermore, this proposal distribution is automatic in the sense that the resulting sampling scheme does not require any tuning parameters. The use of this proposal distribution is also consistent with previous findings for the univariate case, where the full conditional distribution of κ was found to be approximately χ² distributed (Bagchi and Guttman 1988).

Computational Procedure

1. Initialize the parameter values:

   1. Choose an initial clustering. Two obvious choices are: (1) one cluster for all of the angle pairs, or (2) each angle pair in a cluster by itself.

   2. For each initial cluster S of observed angle pairs, initialize the value of the common bivariate von Mises parameters μ, ν, Ω by sampling from the centering distribution H₁(μ, ν)H₂(Ω) of the DP prior.

2. Obtain draws from the posterior distribution by repeating the following:

   1. Given the mean and precision values, update the clustering configuration using one scan of the Auxiliary Gibbs sampler of Neal (2000).

   2. Given the clustering configuration and precision values, update the values of (μ, ν) for each cluster using the full conditional distribution in Section 4.1.

   3. Given the clustering configuration and mean values, update the precision matrix Ω for each cluster using the Wishart independence sampler described in Section 4.2.

5. Template Based Modeling of Protein Structure

5.1 Motivation

In this section we use our proposed density estimation procedure to develop a more efficient method for protein structure prediction. Methods specifically designed for angular data are necessary because consideration of the periodicity is essential for certain amino acids, such as glycine. Figure 2 shows density estimates based on the normal model of Dahl et al. (2008) and our own von Mises sine model. Notice that the normal model is unable to wrap between the angles −π and π. The von Mises model identifies a single peak that includes mass at all four corners, whereas the normal model identifies separate peaks at each corner for this same portion of the data.

Figure 2.

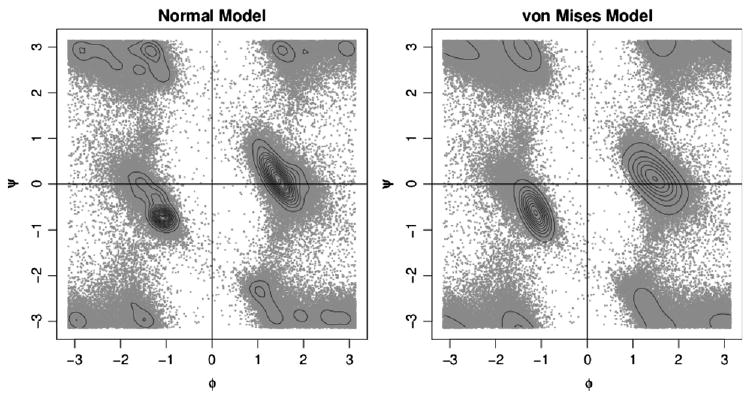
Ramachandran plots for the 121,497 angle pairs that make up the PDB dataset for the residue glycine, along with density estimates based on both the normal and von Mises distributions. The normal model is from the work of Dahl et al. (2008), whereas the von Mises estimate is based on our model in Section 3. Note that glycine spans almost the complete range of values in both φ and ψ, which makes the use of a method that correctly models circular data critical.

We also conducted a quantitative comparison of these two DPM models. To investigate the improvement of the von Mises over the normal, we generated density estimates for subsets of size 200 for each of the 20 amino acid datasets, once using normal centering and component distributions and once using the equivalent von Mises distributions. In each case we used the prior parameter settings and clustering configuration from Dahl et al. (2008), with separate clusterings for mean and precision parameters. We calculated the Bayes factor for the two models using the full amino acid datasets, which ranged in size from 23,000 to 143,000 observations. Our Bayes factor was defined as

$$B((\varphi ,\psi ))=\frac{p((\varphi ,\psi )|M_1)}{p((\varphi ,\psi )|M_2)},$$

where M₁ was our von Mises model estimate and M₂ was the normal model estimate. The logs of the Bayes factors ranged from 216 to 5,040 in absolute value, allowing us to draw clear conclusions as to the superior model in each case. For 14 of the 20 amino acids, the Bayes factor indicated that the von Mises model was superior. When we restricted our test set to only amino acids with more that 2.5% of the observations within π/18 radians (10 degrees) of the border of the Ramachandran plot, 11 of the 12 datasets had a better fit with the von Mises model. Although the normal model fails to capture the wrapped nature of torsion angle data, our method provides robust and elegant estimates of the (φ, ψ) distributions from large or small datasets.

We can use our nonparametric density estimation procedure to estimate the density of backbone torsion angle distributions. This approach allows us to investigate how well distributions obtained from Protein Data Bank (PDB) data approximate the (φ, ψ) distributions at particular positions in a protein fold “family.” This is of interest because one popular technique in protein structure prediction is to generate candidate conformations based on the structures of known similar proteins. These fold families can provide a great deal of information about the unknown structure, but most are very small, often with fewer than 10 members. This means that density estimation purely within a family has not been feasible. In such cases, candidate distributions are generated based on large datasets with similar characteristics to those of the sequence positions in the known structures. As current search methods are mostly random walks in conformation space (Dill et al. 2007; Lee and Skolnick 2008; Das and Baker 2008), improved modeling of these positional densities increases the chance of finding a good structure. To assess the quality of these PDB “category densities,” we compare density estimates from the PDB to those obtained from threefold families: globins, immunoglobulins, and triose phosphate isomerase (TIM) barrels. Each represents a classic architecture in structural biology. The globins consist mostly of α-helical secondary structure, and the immunoglobulins consist mostly of β-sheets. TIM barrels are a mixed structure with both α-helices and β-sheets. These three families are fairly unique in that they have enough known members that density estimation purely within a family is possible.

In contrast to standard methods, we not only consider the torsion angles around a sequence position or residue, but also the (ψ, φ) torsion angle pair around the peptide bond (see Fig. 1). Previously, this peptide centered view of torsion angles has only been applied to short peptides (Anderson and Hermans 1988; Grail and Payne 2000). Recall that we refer to the residue torsion angle pairs (φ, ψ) as “whole positions” and the peptide torsion angle pairs (ψ, φ) as “half positions,” because they reside “half-way” between whole sequence positions. By incorporating the characteristics of two residues, these half positions lead to a finer classification of the dataset, and provide an effective approach to increasing the amount of information known about a particular angle pair without increasing the complexity of the underlying model beyond two torsion angles.

Each whole position can be described by which of 20 amino acid residues is present, and also the type of secondary structure at that location. We define secondary structure in the same manner as the Definition of Secondary Structure for Proteins (DSSP) program (Kabsch and Sander 1983). The normal eight classes are condensed to four: helices (H), sheets (E), coils (C), and turns (T). Residues without any specific structure are assigned to the random coil (C) class. The β-turns and G-turns were combined into the turn (T) class. All helices were classified as (H). Strand and β-bulges were combined into the extended strand (E) class. The 20 residues and 4 secondary structure classes provide 80 possible classifications for whole position data.

Because a half position involves two residues, there are 400 categories when considering only amino acid pairs and 6,400 when the 4 secondary structure classes are included. When considering half positions, we take the same data as used for the whole positions and divide it into a much larger number of groups, which thins out the data considerably. This reduction is worthwhile, however, because every amino acid and secondary structure type exhibits unique behavior visible on the Ramachandran plot. Using adjacent pairs of amino acids and structure types, as the half positions do, gives even more specific information about a sequence position. As we will demonstrate, the use of half positions provides a substantial increase over the available information provided by whole position data.

5.2 Methods and Diagnostics

The torsion angle distributions were estimated for the PDB whole and half positions, as well as the three families of protein folds: globins, immunoglobulins, and TIM barrels. For whole positions, in addition to the categories discussed before, we include a category ignoring secondary structure type, for a total of 100 density estimates. The same was done for half position densities, giving a total of 6,800 estimates.

For each of the three protein fold families, angle pairs for whole and half positions were obtained for each sequence position. For instance, all 92 (φ, ψ) pairs at position 13 based on the globins alignment were used to estimate the relevant density. The same was done for half positions, but the (ψ, φ) angles were centered around the peptide bond between two residues. These alignments produced 183 residue positions for the globins, 343 for the immunoglobulins, and 274 for the TIM barrels.

For each dataset, two chains were run for 6,000 iterations, with the first 1,000 discarded as burn-in. For post burn-in iterations, a draw was taken from the posterior distribution and the resulting von Mises density was evaluated for a grid of 360 × 360 points. Using 1 in 10 thinning, this gave B = 1, 000 samples to estimate the density using (7). For datasets with over 2,000 observations, one run of the MCMC sampler used the full dataset, whereas the other used a subsample of 2,000 observations. We found that subsampling had little impact on the density estimates.

Our von Mises model from Section 3 was used with mean prior parameters μ₀ = ν₀ = 0, and Ω₀ was a diagonal matrix with elements 1/π². The small concentration values made this prior largely noninformative. For the Wishart prior, we used υ=2 degrees of freedom and set the scale matrix B to have diagonal elements of 0.5², and off-diagonal elements of 0 (making the expected value υ/2B⁻¹ = B⁻¹). This again provided a diffuse centering distribution on the radian scale. The mass parameter τ₀ of the Dirichlet process was set to 1.

Convergence was evaluated using entropy as described by Green and Richardson (2001). Figure 3 shows trace plots for the threonine-arginine half position, which provided the best match from the PDB data for the globins 13–14 half position. Notice the rapid convergence for all of our univariate convergence criteria, which was typical for our MCMC scheme.

Figure 3.

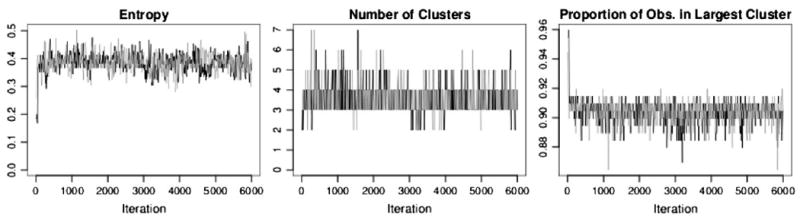
Convergence diagnostics for threonine-arginine half position dataset.

5.3 Comparison of Whole and Half Position Density Estimates

To judge whether the whole or half position density estimates provided a closer match to the density at a particular position of a protein family, we used the Jensen-Shannon divergence:

$$\frac{1}{2}\left(D_{KL}(P,\frac{P+Q}{2})+D_{KL}(Q,\frac{P+Q}{2})\right)$$

as a measure of distributional similarity, where D_KL is the Kullback-Leibler divergence defined by D_KL(P, Q) = Σ_i P(i)log(P(i)/Q(i)). Both P and Q are density estimates from our proposed procedure.

The positional density estimates were compared with all of the estimates from the PDB using this divergence score. Whole position densities from each of the three fold families were compared with the whole position category densities from the PDB, and half positions from the fold families were compared with the half position category densities from the PDB. The best matches, those with the lowest divergence values, are plotted against position in Figure 4. It is evident that the half position comparisons produce lower divergence scores. The mean minimum divergence for whole positions is 0.145, whereas the corresponding half position value is 0.054. The paired sign test of the null hypothesis that the median minimum divergence score for whole positions is less than or equal to that for half positions produced p-values less than 0.0001 for each structure family. The plot shows that the half positions provide better matches at the beginning and ends of the structures, which consist of coil secondary structure, and in the sheet regions of the immunoglobulins. Whole positions perform best in helical regions with a mean divergence of 0.066. Even then, half positions provide a better match for helices with mean divergence 0.031. The worst matching cases are in areas with noncanonical turns or unique coils, which correspond to the highest minimum divergence scores for all structure families.

Figure 4.

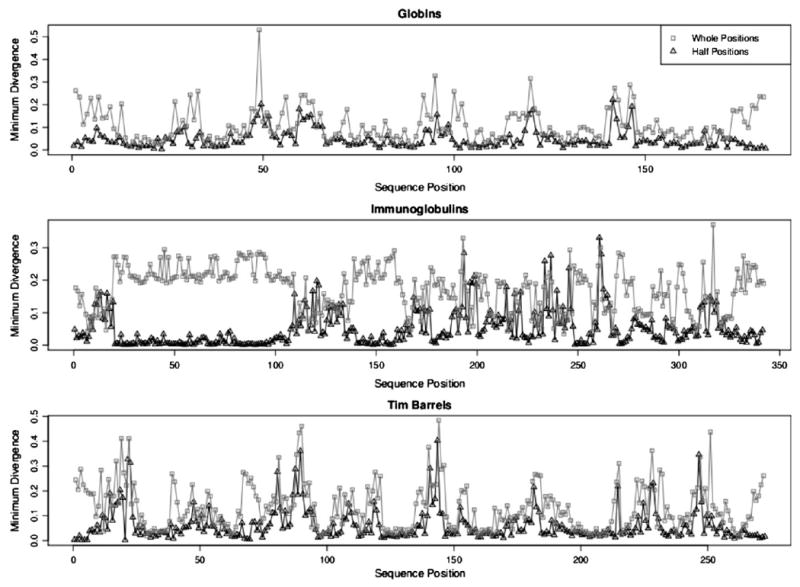
A comparison of minimum divergence scores for whole versus half positions.

A specific example of this behavior can be seen in Figure 5, which shows the globins whole position 13 with the closest matching PDB density compared with the half position 13–14 with its matching half position density from the PDB. It can be readily seen from these figures that the whole position matches fairly well, but also includes extraneous density. By instead considering the half position of the associated peptide, we find a closer match. This is not surprising because of the increased specificity of the half position densities from the PDB, not to mention the increased number of categories available for comparison. For the globins in Figure 5, the whole position density certainly shows a larger cross section of density than the half position. These results suggest that the use of half position data as a substitute for whole position data provides better results.

Figure 5.

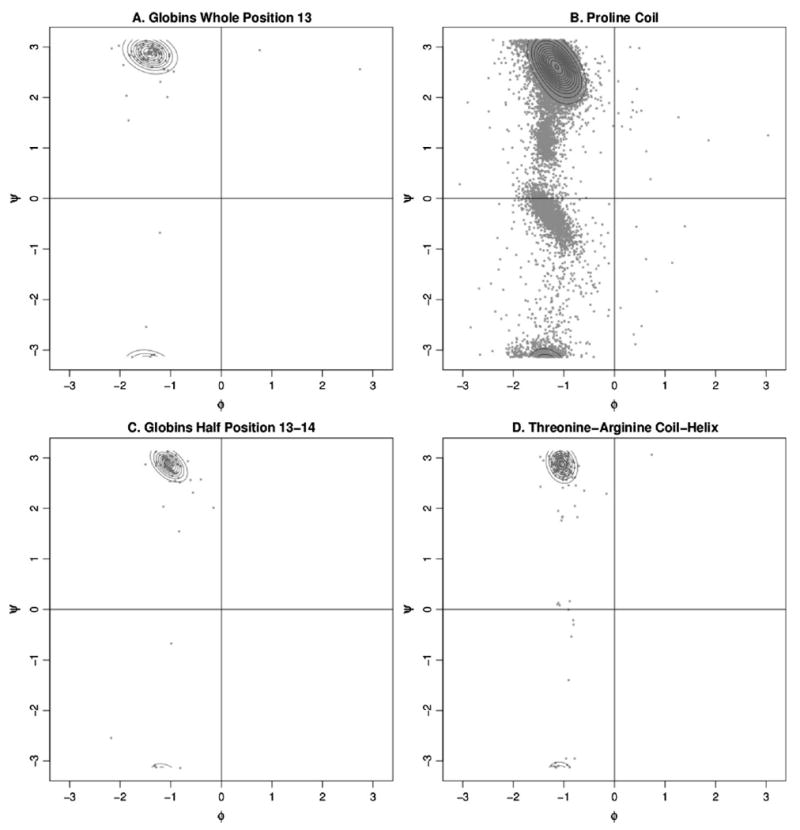
Ramachandran plots around globins position 13. (a) Density estimate and data for whole position 13. (b) Density estimate and data for proline coil whole positions which, at a divergence of 0.204, provide the best PDB match for globins whole position 13. (c) Density estimate and data for half position between residues 13 and 14. (d) Density estimate and data for threonine coil to arginine helix half positions which, at a divergence of 0.028, provide the best PDB match for globins half position 13–14.

6. Discussion

We have presented a novel nonparametric Bayesian method for density estimation with bivariate angular data. This method, unlike many currently used to estimate the density of (φ, ψ) angle pairs, provides smooth estimates without requiring large datasets. This allowed the estimation of the distributions for PDB half position data, as well as positional data from three protein fold families. Using this new technique we were able to evaluate the common practice of using whole position estimates for positional data. Our results indicate that half position densities are more informative than the corresponding whole position estimates.

Our Dirichlet process mixture model performs well for density estimation of bivariate circular data. In contrast to previous work in this area, it does not require the setting of a fixed number of components for the mixture. By incorporating the bivariate von Mises sine model, we are able to account for the wrapping of the data, and the sine model's equivalence to the normal distribution allows for a straightforward interpretation and effective implementation of a MCMC sampling scheme. This was made possible by our results regarding the full conditional distributions for the mean and precision parameters.

We have demonstrated that our approach at half positions provides greater precision than the use of whole positions for protein structure prediction. Unlike the fold families shown here, most protein folds have very limited number of representatives in the PDB. For these fold families, density estimation at each position, even using our method, is not feasible. Therefore, the distributions used to approximate the backbone torsion angle space are obtained from the PDB. When these distributions are inaccurate or too broad, as we see for the whole positions, significant time is spent sampling the wrong areas of backbone conformation space. When searching using a random walk in conformation space, this reduces the chance of finding a good structure. A reliable reduction of the backbone search space using the half position distributions is a significant improvement to all structure prediction methods. The only way such half position distributions can be precisely calculated is by using density estimation methods, such as ours, that properly address the angular nature of the data and cope well with smaller datasets.

We conclude by briefly presenting the results of a sensitivity analysis we performed for the Wishart prior and DP mass parameter. Three different scale matrices were considered for the Wishart prior. Each could be written as c²I, where I was the 2 × 2 identity matrix, and c took values 0.25, 0.5, and 1.0. Figure 6 shows the resulting density estimates for globins position 13. The changes between the density estimates are not dramatic, and the effect is comparable to that of varying the bandwidth in kernel density estimation methods. Other positions showed similar behavior.

Figure 6.

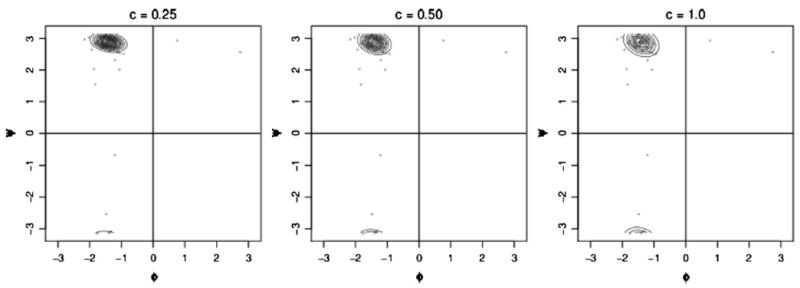
Density estimates for globins positon 13 with different scale matrices for the Wishart prior distribution.

We also investigated the sensitivity to changes in the mass parameter. We set τ₀ to 0.5, 1.0, 2.0, and 5.0. A comparison of these estimates for position 13 is given in Figure 7. The plots all look very similar. This is generally the behavior of the other positions, although sometimes the 5.0 case exhibits slight but noticeable differences.

Figure 7.

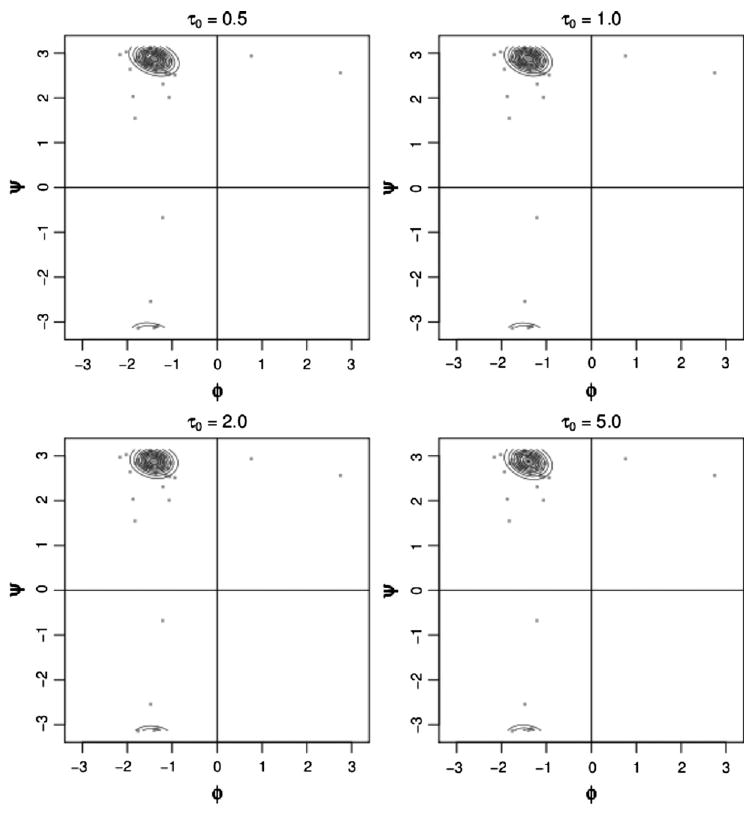
Density estimates for globins position 13 for assorted values of the mass parameter.

Convergence of the Markov chains was generally good, but we did encounter occasional difficulties, particularly when the mass parameter was small. However, although the trace plots of entropy for the two chains might suggest convergence problems, the density estimates generated by the separate chains were very similar. Therefore, we do not consider this to be a major issue. On the other hand, if the mass parameter is very small severe convergence problems can occur. As always, convergence diagnostics should be employed.

Appendix: Derivation of Relevant Distributions

Here we provide the derivations of the results from Section 4.1 regarding the conditionally conjugate prior and posterior distribution for the case when we have data from a bivariate von Mises sine model with unknown mean parameters and known precision parameters.

Recall the parameterization of the von Mises in terms of unit vectors from Section 4.1, where x_i = (cos(φ_i), sin(φ_i))^T, y_i = (cos(ψ_i), sin(ψ_i))^T, τ_μ = (cos(μ), sin(μ))^T, τ_ν = (cos(ν), sin(ν))^T, and for a vector δ = (a, b)^T, δ*: = (−b, a)^T. For observations (x_i, y_i), i = 1, …, n from a bivariate von Mises distribution with known κ_1i, κ_2i, and λ_i, the likelihood for τ_μ and τ_ν is

$$\begin{array}{ll}L({\tau }_{\mu },{\tau }_{\nu }|\mathbf{\text{x}},\mathbf{\text{y}})& \propto \prod _{i=1}^{n}exp({\kappa }_{1i}{\tau }_{\mu }^T{x}_i+{\kappa }_{2i}{\tau }_{\nu }^T{y}_i+{\lambda }_i{\tau }_{\mu }^{\ast T}{x}_i{\tau }_{\nu }^{\ast T}{y}_i)\\ & =exp\{{\tau }_{\mu }^T\sum _{i=1}^n{\kappa }_{1i}{x}_i+{\tau }_{\nu }^T\sum _{i=1}^n{\kappa }_{2i}{y}_i\\ & +\sum _{i=1}^n({\lambda }_i{\tau }_{\mu }^{\ast T}{x}_i{\tau }_{\nu }^{\ast T}{y}_i)\}.\end{array}$$

Notice that ${\tau }_{\mu }^{\ast T}{x}_i{\tau }_{\nu }^{\ast T}{y}_i$ is equal to ${\tau }_{\mu }^{\ast T}{\tau }_{\nu }^{\ast }{x}_i^T{y}_i$, and that for all vectors a, b, we have a*^Tb* = a^Tb, so

$$\begin{array}{ll}L({\tau }_{\mu },{\tau }_{\nu }|\mathbf{\text{x}},\mathbf{\text{y}})\propto & exp\{{\left(\sum _{i=1}^n{\kappa }_{1i}{x}_i\right)}^T{\tau }_{\mu }+{\left(\sum _{i=1}^n{\kappa }_{2i}{y}_i\right)}^T{\tau }_{\nu }\\ & +\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){\tau }_{\mu }^T{\tau }_{\nu }\}\\ \hfill =& exp\{\left|\sum _{i=1}^n{\kappa }_{1i}{x}_i\right|\frac{{\left({\sum }_{i=1}^n{\kappa }_{1i}{x}_i\right)}^T}{\left|{\sum }_{i=1}^n{\kappa }_{1i}{x}_i\right|}{\tau }_{\mu }\\ & +\left|\sum _{i=1}^n{\kappa }_{2i}{y}_i\right|\frac{{\left({\sum }_{i=1}^n{\kappa }_{2i}{y}_i\right)}^T}{\left|{\sum }_{i=1}^n{\kappa }_{2i}{y}_i\right|}{\tau }_{\nu }\\ & +\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){\tau }_{\mu }^T{\tau }_{\nu }\}.\end{array}$$

Notice that the first two terms are consistent with a von Mises likelihood with

$$\begin{array}{c}{\stackrel{\sim }{\tau }}_{\mu }=\frac{\left({\sum }_{i=1}^n{\kappa }_{1i}{x}_i\right)}{\left|{\sum }_{i=1}^n{\kappa }_{1i}{x}_i\right|}{\stackrel{\sim }{\tau }}_{\nu }=\frac{\left({\sum }_{i=1}^n{\kappa }_{2i}{y}_i\right)}{\left|{\sum }_{i=1}^n{\kappa }_{2i}{y}_i\right|}\\ {\stackrel{\sim }{\kappa }}_1=\left|\sum _{i=1}^n{\kappa }_{1i}{x}_i\right|{\stackrel{\sim }{\kappa }}_2=\left|\sum _{i=1}^n{\kappa }_{2i}{y}_i\right|.\end{array}$$

Using this notation, we have

$$\begin{array}{l}L({\tau }_{\mu },{\tau }_{\nu }|\mathbf{\text{x}},\mathbf{\text{y}})\propto exp\left\{{\stackrel{\sim }{\kappa }}_1{\stackrel{\sim }{\tau }}_{\mu }^{\text{T}}{\tau }_{\mu }+{\stackrel{\sim }{\kappa }}_2{\stackrel{\sim }{\tau }}_{\nu }^T{\tau }_{\nu }+\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){\tau }_{\mu }^T{\tau }_{\nu }\right\}\\ =exp\left\{{\stackrel{\sim }{\kappa }}_1{\stackrel{\sim }{\tau }}_{\mu }^T{\tau }_{\mu }+{\stackrel{\sim }{\kappa }}_2{\stackrel{\sim }{\tau }}_{\nu }^T{\tau }_{\nu }+\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){\tau }_{\mu }^T{\tau }_{\nu }{\stackrel{\sim }{\tau }}_{\mu }^T{\stackrel{\sim }{\tau }}_{\nu }{({\stackrel{\sim }{\tau }}_{\mu }^T{\stackrel{\sim }{\tau }}_{\nu })}^{-1}\right\}\\ =exp\left\{{\stackrel{\sim }{\kappa }}_1{\stackrel{\sim }{\tau }}_{\mu }^T{\tau }_{\mu }+{\stackrel{\sim }{\kappa }}_2{\stackrel{\sim }{\tau }}_{\nu }^T{\tau }_{\nu }+\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){({\stackrel{\sim }{\tau }}_{\mu }^T{\stackrel{\sim }{\tau }}_{\nu })}^{-1}{\tau }_{\mu }^T{\tau }_{\nu }{\stackrel{\sim }{\tau }}_{\mu }^{\ast T}{\stackrel{\sim }{\tau }}_{\nu }^{\ast }\right\}\\ =exp\left\{{\stackrel{\sim }{\kappa }}_1{\stackrel{\sim }{\tau }}_{\mu }^{\text{T}}{\tau }_{\mu }+{\stackrel{\sim }{\kappa }}_2{\stackrel{\sim }{\tau }}_{\nu }^T{\tau }_{\nu }+\left(\sum _{i=1}^n{\lambda }_i{x}_i^T{y}_i\right){({\stackrel{\sim }{\tau }}_{\mu }^T{\stackrel{\sim }{\tau }}_{\nu })}^{-1}{\stackrel{\sim }{\tau }}_{\mu }^{\ast T}{\tau }_{\mu }{\stackrel{\sim }{\tau }}_{\nu }^{\ast T}{\tau }_{\nu }\right\}.\end{array}$$

So, in addition to the parameters defined previously, the likelihood is proportional to a von Mises sine model with

$$\stackrel{\sim }{\lambda }=\sum _{i=1}^n({\lambda }_i{x}_i^T{y}_i){({\stackrel{\sim }{\tau }}_{\mu }^T{\stackrel{\sim }{\tau }}_{\nu })}^{-1}.$$

The conjugate prior can be treated as an additional observation in the likelihood, and its interpretation follows directly.