Quantitative evolutionary design of glucose 6-phosphate dehydrogenase expression in human erythrocytes

Abstract

Why do the activities of some enzymes greatly exceed the flux capacity of the embedding pathways? This is a puzzling open problem in quantitative evolutionary design. In this work we investigate reasons for high expression of a thoroughly characterized enzyme: glucose 6-phosphate dehydrogenase (G6PD) in human erythrocytes. G6PD catalyses the first step of the pathway that supplies NADPH for antioxidant defense mechanisms. Normal G6PD activity far exceeds the capacity of human erythrocytes for a steady NADPH supply, which is limited upstream of G6PD. However, the distribution of erythrocyte G6PD activity in human populations reveals a selective pressure for maintaining high activity. To clarify the nature of this selective pressure, we studied how G6PD activity and other parameters in a model of the NADPH redox cycle affect metabolic performance. Our analysis indicates that normal G6PD activity is sufficient but not superfluous to avoid NADPH depletion and ensure timely adaptation of the NADPH supply during pulses of oxidative load such as those that occur during adherence of erythrocytes to phagocytes. These results suggest that large excess capacities found in some biochemical and physiological systems, rather than representing large safety factors, may reflect a close match of system design to unscrutinized performance requirements. Understanding quantitative evolutionary design thus calls for careful consideration of the various performance specifications that biological components/processes must meet in order for the organism to be fit. The biochemical systems framework used in this paper is generally applicable for such a detailed examination of the quantitative evolutionary design of gene expression levels in other systems.

Understanding the quantitative relationship of biological capacities to each other and to the peak natural loads on them, the problem of quantitative evolutionary design (1), is a key issue in integrative biology (2–5). Natural selection against both poor performance and misallocation of resources to superfluous “infrastructure” could be thought to promote a close match between capacities of components operating in series and between these capacities and the peak natural loads. Nevertheless, research at both the molecular (6–9) and the organ (2, 10) levels has shown that ratios between the highest capacities in a series and the lowest ones, as well as between capacities and their loads, are often quite high. In particular, ratios between catalytic capacities (i.e., activities, V_max) of some enzymes, which we will call “excess-activity enzymes,” and the flux capacity of the embedding pathways may exceed 1,000 (11). These ratios remain unexplained.

It has been argued (7) that these high activities are necessary to ensure sufficient net flux in reactions that operate near equilibrium. There are two problems with this argument. First, one must still provide an evolutionary explanation for why the step in question must be near equilibrium. Second, any enzyme whose activity greatly exceeds the pathway flux cannot influence the latter, which is determined by one or more of the enzymes in the pathway that have more modest activities. A slight up-regulation of one of the enzymes that have modest activities would thus more economically achieve the required flux. Thus, the large excess activity primarily determines the proximity to equilibrium, rather than the value of the pathway flux. Furthermore, even if this argument were valid, it would not cover the excess-activity enzymes that are known to operate far from equilibrium.

More general explanations for the high ratios between loads and capacities might also be relevant to the case of excess-activity enzymes. First, the appropriate match between loads and capacities might be physiologically unrealizable owing to physicochemical or developmental constraints (12). Nevertheless, mutants that more closely match loads are known for most excessactivity enzymes. Second, genetic drift, mutational pressure, sexual selection or a neutral excess-activity phenotype might prevent natural selection from balancing capacities to loads (13). However, contrary to expectations were these the responsible factors, mutations that change the expression of excess-activity enzymes are often deleterious (www.ncbi.nlm.nih.gov/omim), and for many enzymes excess activity is pervasive across phylogenetic branches and in large populations. Third, a recent evolutionary or environmental change might have abruptly decreased the peak load and insufficient time elapsed for the now superfluous capacity to decrease by way of natural selection (13). However, this explanation fails if the excess capacity is phylogenetically and geographically prevalent, as is often the case for excess-activity enzymes (14–16). Fourth, the excess capacities may reflect large safety factors, as defense against infrequently high loads (2, 17) or against mutation (18, 19). Where the performance of a component in a serial process is somewhat unpredictable and/or its capacity is cheaply achieved, a high safety factor compared with other components may be selectively advantageous (20). To justify safety factors of 10 or higher, however, there is a need for both the variability of performance and the ratios between costs of performance of the various serial subprocesses to be very high. Fifth, the large capacity of a component may be necessary to fulfill other functions (21). This is a pertinent explanation for the high expression of enzymes that are multifunctional or have broad substrate specificity. Still, there is no evidence for multifunctionality of many specific excess-activity enzymes that have been thoroughly studied. Sixth, the large capacity may be a side effect of fulfilling unappreciated requirements in performing a given function. Research in Biochemical Systems Theory (22) has shown that biochemical networks are often designed to fulfill multiple requirements besides sufficient flux. Examples include robustness to fluctuations of kinetic parameters, sensitive and rapid response to changes of load, and minimal concentrations of reactive intermediates. Higher-level systems likely face similar functional requirements. However, quantitative evolutionary design studies usually address a single functional requirement, often the capacity for sustained flux. Close matches of system design to more demanding but overlooked performance requirements are thus easily misinterpreted as large safety factors for flux capacity. Explanations for apparently superfluous enzyme activities based on criteria other than capacity for sustained flux are implicit in ref. 23 and have been proposed (24), but they have never been substantiated by detailed analysis of a well characterized biochemical network.

In this work, we examine reasons for apparently superfluous expression of an enzyme that is thoroughly characterized biochemically, physiologically, clinically, and genetically: glucose 6-phosphate dehydrogenase (G6PD) in human erythrocytes. After providing the necessary background and describing the mathematical model underlying the analysis, we explain the indices of metabolic performance we consider potentially relevant. Through mathematical analysis we show that two of these indices are sensitive to G6PD activity near normal values. Based on biochemical, clinical, and epidemiological evidence, we then pinpoint physiological processes that set the relevant quantitative functional requirement, and we discuss the implications of the results for quantitative evolutionary design.

Background

G6PD (EC 1.1.1.49) catalyses the first step of the hexose-monophosphate shunt, which provides pentoses for nucleic acid synthesis and regenerates NADPH (Fig. 1a). In erythrocytes, most NADPH is used in the glutathione reductase (GSR, EC 1.6.4.2) reaction (25), which regenerates reduced glutathione (GSH) that is oxidized in the repair of oxidative damage. In mice, and presumably in other organisms, G6PD is dispensable for pentose synthesis but essential for defense against oxidative stress (26). Four lines of experimental evidence suggest that erythrocytes have largely superfluous G6PD activity. First, the highest rate of glucose consumption measured in human erythrocytes is 1.6 μM·s^-1 (27), whereas G6PD activity is 40-fold higher (28). Second, because hexokinase (EC 2.7.1.1), not G6PD, is rate-limiting for the NADPH supply (28) under pronounced oxidative stress, erythrocytes that are moderately deficient in G6PD activity generate NADPH at the same maximal steady-state rate as normal erythrocytes. Third, erythrocytes that are severely deficient in G6PD activity remain in circulation and survive sustained oxidative challenges. G6PD A- is an unstable mutant form of G6PD. G6PD A- erythrocytes that are 63–76 days old are lysed when male G6PD A-patients are treated with primaquine, which causes sustained oxidative stress, but 8- to 21-day-old cells are not (29). Because the activity of the G6PD A- enzyme decays from near-normal values with a half-life of 13 days in erythrocytes (30), by days 21 and 63, G6PD activity is ≈33% and 3% of the initial activity, respectively. By 90 days, the lifespan of G6PD A- erythrocytes (31), the activity is reduced to ≈0.8%. The average G6PD activity in G6PD A- erythrocytes ranges from 5% to 15% normal, despite a shortened cellular lifespan and increased reticulocytosis. Fourth, the average levels of thiobarbituric-acid-reactive substances (an indicator of oxidative damage) in the erythrocytes of young male G6PD A- individuals that are not exposed to oxidative stress do not differ significantly from those in the erythrocytes of normal individuals (32).

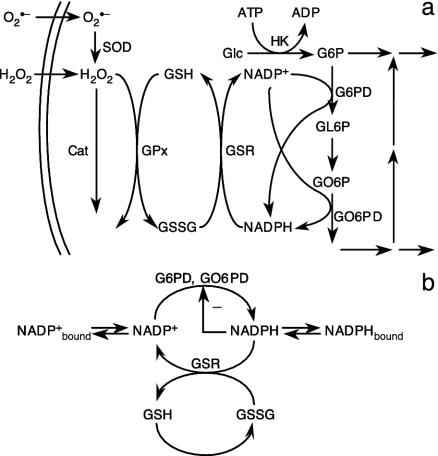
Fig. 1.

Schematic representations of the oxidative part of the hexose-monophosphate shunt and relevant sources of oxidative load (a) and of the simplified reaction network used in our analysis (b). Nonstandard abbreviations: Cat, catalase; G6P, glucose 6-phosphate; GL6P, gluconolactone 6-phosphate; Glc, glucose; GO6P, gluconate 6-phosphate; GO6PD, gluconate 6-phosphate dehydrogenase; GSSG, oxidized glutathione; GPx, glutathione peroxidase; GSR, glutathione reductase; HK, hexokinase; SOD, superoxide dismutase.

On the other hand, G6PD activities are narrowly distributed about the main mode, with typical standard deviations of <17% (33, 34). Moreover, the distribution (34) is also skewed toward high activities. Altogether, these findings suggest that a subtle selective pressure for high G6PD activity is at work. What might be responsible for this selective pressure?

We base our analysis of this question on the model shown schematically in Fig. 1b and described by the following system of differential-algebraic equations (see Supporting Text, Table 1, and Fig. 4, which are published as supporting information on the PNAS web site, for rationale)

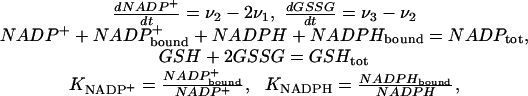with

Criteria for Good Performance

For effective and reliable performance, the oxidative part of the hexose monophosphate shunt should fulfill the following criteria.

Sparing of NADP. NADP undergoes spontaneous hydration to a deleterious product that is not metabolized by hemolyzates (35). Catalase-bound NADPH, however, is stable under prolonged storage (36), prompting us to assume that protein binding protects NADP against degradation. Maintaining unbound NADP at low levels should therefore prevent this loss of material and the concomitant increase in deleterious effects.

Robustness of NADPH Concentration. NADPH is a preferred substrate for various other human erythrocyte enzymes besides GSR (37, 38). Because these enzymes have K_M(NADPH) values near the physiological concentration of NADPH (Table 2, which is published as supporting information on the PNAS web site) their rates of catalysis are sensitive to depletion of the latter. Besides, NADPH is a cofactor for catalase (36) and is essential to prevent catalase inactivation under oxidative stress (39, 40). Because catalase consumes >90% of the incoming hydrogen peroxide (41), a strong depletion of NADPH seriously compromises the erythrocyte's antioxidant defense (42). Robustness is strong where all of the following parameters V_G6PD, K_M,G6P, K_M,NADP⁺, K_d,NADP⁺, K_I,NAPDH, K_I,2,3–DPG, V_GSR, K_M,NAPDH, K_M,GSSG, and K_NADP⁺ have vanishing influences on the concentration of NADPH. That is, where I_NADPH= Σ_i|∂log NADPH/∂ log p_i| << 1, with p_i being the parameters in the previous list. K_NADPH is a “control parameter” whereby the cell can slowly adjust the steady-state concentration of NADPH and, thus, it is appropriate that its influence not be included in the above summation. The case of another important control parameter, k_ox, is addressed next.

Low Gain of NADPH Concentration for the Oxidative Load. A wide range of oxidative loads, represented by values of k_ox, can potentially be imposed on the system by external conditions. So that the various NADPH-dependent erythrocytic processes are minimally disturbed under most physiological oxidative loads it is important that L_NADPH= ∂ log NADPH/∂ log k_ox be small.

Sufficiency of NADPH Supply. The rate of NADPH regeneration (2v₁) should be sufficient to at least cope with the basal oxidative load.

Temporal Responsiveness. The adaptation to increased oxidative loads should be fast enough to cope with environmental variation. We quantify temporal responsiveness by determining the time for half-maximal response of the NADPH supply (t ½,sup) to a 2-fold increase in k_ox. Fast responsiveness corresponds to a small t ½,sup. Because GO6PD responds slower than G6PD to fluctuations in oxidative load (28, 43) our model slightly underestimates t ½,sup.

Functional Demands That Require Normal G6PD Activity

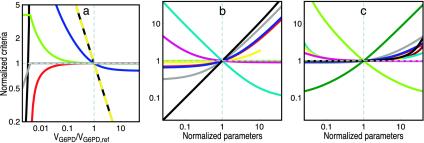
Of the aforementioned performance indices, only t ½,sup, I_NADPH, and L_NADPH are sensitive to G6PD activity around its normal level (Fig. 2). Performance is significantly affected according to these indices when the level of G6PD is between 10% and 90% of the normal value, whereas it remains unaffected according to the others until G6PD levels fall below 1%.

Fig. 2.

Dependence of metabolic performance on parameters affecting the NADPH redox cycle in erythrocytes. (a) Effect of G6PD activity on concentration of unbound NADP (green), concentration of unbound NADPH (red), overall influence on NADPH concentration (dashed yellow), log gain in NADPH concentration with respect to changes in oxidative load (black), NADPH supply (gray), and responsiveness of NADPH supply (blue). Although small L_NADPH values can be achieved with low G6PD activities, these activities are incompatible with good performance according to various criteria. For instance, such activities limit NADPH supply. (b and c) Effect of various parameters on the log gain in NADPH concentration with respect to changes in oxidative load and on responsiveness of NADPH supply, respectively: K_M,NADP⁺ (gray), K_I,NADPH (magenta), K_M,G6P/G6P and K_d,NADP⁺ (red), 2-DPG/K_I,2,3-DPG (blue), V_GSR (light green), K_M,NADPH (dark red), K_M,GSSG (dark green), κ = NADPH/(NADPH + NADPH_bound) = 1/(1 + K_NADPH) (yellow), k_ox (black), and NADP_tot (cyan). In b, the curves for V_GSR, K_M,NADPH and K_M,GSSG overlap. Parameters and performance indices are normalized with respect to their values in the wild type.

I_NADPH has little relevance in natural selection for high G6PD activities because it is small even at 10% residual G6PD activity, and the parameters defining this influence are much less changeable than k_ox. To further assess the relevance of L_NADPH and t ½,sup, we note that after a sudden increase of oxidative load, the concentration of NADPH gradually approaches a lower steady-state on the time scale of t ½,sup and relaxes back to the initial value after the pulse (Fig. 5, which is published as supporting information on the PNAS web site). The t ½,sup is most relevant when G6PD activities are low, the increase in oxidative load large, and the duration of the pulse not much longer than t ½,sup. When G6PD levels are close to normal, the change in the steady-state level of NADPH diminishes (L_NADPH becomes smaller) and the response time becomes less relevant. Thus, the two relevant indices reflect synergistic aspects of performance that during selection move G6PD levels toward the normal value. Once the normal value is achieved in the population, the selective effectiveness of L_NADPH is essentially eliminated and, because of the synergistic action of the two, the effectiveness of t ½,sup is also greatly diminished. Altogether, these results suggest that the normal level of G6PD in human erythrocytes was tuned by natural selection to ensure sufficient robustness of the NADPH concentration and responsiveness of the NADPH supply.

If low L_NADPH and t ½,sup are indeed relevant performance requirements, two outcomes are expected from natural selection. First, other relevant biochemical parameters should have values that are consistent with the minimization of both L_NADPH and t ½,sup. Second, L_NADPH and t ½,sup should themselves be robust to fluctuations of the parameters about their normal values. The normal parameterization of the system is indeed consistent with both expectations (Fig. 2 b and c). Normal values of the parameters are such as to warrant near minimal and near insensitive values of L_NADPH and t ½,sup and, remarkably, tend to be close to the parameters' breakpoints for L_NADPH or t ½,sup. In the case of L_NADPH, the exceptions are the control parameters NADP_tot and k_ox. These exceptions do not negate the selective relevance of L_NADPH. The value of k_ox is imposed by the cell's environment, and higher NADP_tot can only decrease L_NADPH at the expense of longer t ½,sup and increased NADP degradation. In the case of t ½,sup, the exceptions are K_M,GSSG and V_GSR, which are kinetic parameters of GSR. These exceptions also do not negate the selective relevance of t ½,sup. Because the increase in demand for NADPH first leads to an increase in NADP⁺, which subsequently leads to an increase in the supply of NADPH, the responsiveness of the supply (t ½,sup) can be no faster than the responsiveness of the demand (t ½,dem) that is determined by K_M,GSSG and V_GSR. [The high GSR activity is required for maintenance of a robustly low concentration of the deleterious GSSG (unpublished data).] As G6PD activity increases relative to GSR activity, t ½,sup asymptotically approaches t ½,dem. Under physiological conditions, t ½,sup (1.2 s) is already close to its lower bound (t ½,dem = 0.94 s), and therefore normal G6PD activity does not limit responsiveness of the NADPH supply as much as GSR activity. This situation best avoids rapid NADPH depletion under pulses of oxidative load.

The evidence above supports the hypothesis that a functional requirement for small gain of the NADPH concentration in response to oxidative load and for fast responsiveness of the NADPH supply drive natural selection for high G6PD activity in human erythrocytes. However, this hypothesis is plausible only if erythrocytes are occasionally exposed to oxidative loads that would cause substantial NADPH depletion under mild G6PD deficiency.

Is There a Physiological Requirement for Strong Robustness of NADPH Concentration and Fast Responses of NADPH Supply to Oxidative Loads?

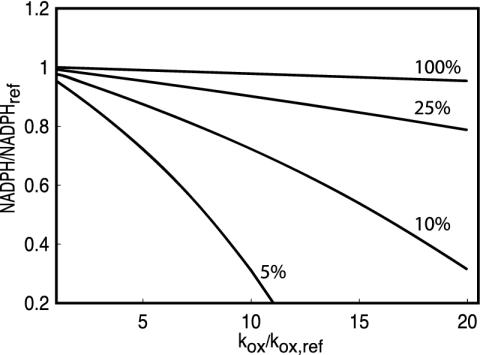
Physiological and pathological conditions known to increase the oxidative load on erythrocytes include hyperlipidemia (44), diabetes (reviewed in ref. 45), Friedrich's ataxia (46), various modalities of physical exercise (47, 48), atherosclerosis (49, 50), and infection (reviewed in ref. 51). Levels of glutationylhemoglobin are 7-fold higher in diabetics than in normal individuals (52), suggesting that k_ox is elevated by approximately the same factor. Reliable quantitative data for other conditions is lacking, but changes in various markers of oxidative stress suggest average oxidative loads ranging from 1.5 to 5 k_ox,ref. Arguably, these oxidative loads are too mild to cause relevant NADPH depletion under moderate G6PD deficiency (Fig. 3). However, the previous estimates are based on experiments that detect only averaged effects of oxidative load on erythrocytes, whereas in most conditions mentioned above the sources of oxidative load are spatially localized. Hence, average effects that are observed experimentally in blood collected at distant sites might actually be due to very high local oxidative loads on erythrocytes. Localized sources of oxidative load would expose circulating erythrocytes to pulses of oxidative stress, each lasting a few seconds. To avoid fast depletion, the supply of NADPH must respond to the increased demand within this time scale. Because t ½,sup = 1.2 s at normal G6PD activities, the latter functional requirement might not be fulfilled even under mild G6PD deficiencies.

Fig. 3.

Predicted effect of oxidative load on NADPH concentration at the residual G6PD activities indicated above each curve. Two facts are relevant in interpreting this figure. First, our model underestimates NADPH depletion at high (≥10 k_ox,ref) oxidative loads. In this condition G6P depletion is not negligible, and NADPH consumption by processes that our modeling neglects is exacerbated. Second, G6PD activities in normal erythrocytes change over an ≈6-fold range. The enzyme is inhibited by various metabolites, NADPH, 2,3-diphosphoglycerate, and ATP, whose concentrations change over the circulatory cycle as well as with environmental conditions. G6PD activity declines to 26% of the initial value over the erythrocyte's life span (30).

What physiological processes could account for such high locally imposed oxidative loads? Most conditions mentioned above have in common activation of the immune system (44, 47, 49–51). Activated phagocytic cells produce vast amounts of superoxide and hydrogen peroxide (53, 54). Hydrogen peroxide easily permeates erythrocyte membranes (55) and is a substrate for glutathione peroxidase and catalase. Superoxide enters erythrocytes through the anionic channel (56) and then undergoes rapid superoxide dismutase (SOD)-catalyzed dismutation, producing hydrogen peroxide. Furthermore, high concentrations of superoxide exacerbate NADPH consumption by catalase (40), a process that our model neglects.

Erythrocytes can adhere to phagocytes (57), and there is evidence that adhesion to activated neutrophils does indeed cause a substantial oxidative load, whose effects are more pronounced in G6PD-deficient erythrocytes. A 2-h coincubation of one neutrophil per 20 opsonized erythrocytes under conditions leading to formation of immune complexes caused GSH levels to fall by a minimal amount in normal erythrocytes, by 33% in erythrocytes from G6PD A- patients (with 12% of normal G6PD activity), and by 59% in erythrocytes from Caucasian G6PD-deficient patients (with 2% of normal G6PD activity) (58). Under some conditions, activated neutrophils (54) and monocytes (53) can even lyse normal erythrocytes. The vigorous action of phagocytes is not surprising as its function is to kill pathogens.

In vivo, erythrocytes get nearby or adhere to activated phagocytes as they circulate through sites of inflammation or atherosclerotic lesions. The immune clearance process, which in primates is mediated by erythrocytes, may also expose erythrocytes to brief pulses of high oxidative load. In this process, immune complexes bound to the erythrocyte complement receptor 1 (CR1) are cleared from circulation by phagocytes (mostly Kupffer cells) in the liver, without erythrocyte destruction (59). The transfer of immune-complex substrates from the erythrocyte to the phagocyte involves close contact between these cells. Monocytes produce a considerable amount of oxidant species even in the absence of phagocytosis (60), and the formation of “rosettes,” which mimic the association between erythrocytes and monocytes, is sufficient to generate an oxidative burst (61). In vitro, with a monocytic cell line, this close contact typically lasts for ≈30 s (62), and in primates immune complexes are cleared from circulation with a t_1/2 of ≈5 min (63).

These data indicate that oxidative damage to erythrocytes caused by contact with phagocytes does set a functional requirement for the low L_NADPH and t ½,sup that hold in the normal range of G6PD activities in erythrocytes. If this functional requirement mediates the selective pressure for maintenance of high G6PD activity in human erythrocytes, then NADPH depletion owing to G6PD deficiency should decrease fitness.

Is There Evidence for a Selective Disadvantage of Moderate G6PD Deficiency? If So, Is NADPH Depletion a Plausible Cause of This Disadvantage?

Clinical data reveal a selective disadvantage of moderate G6PD deficiency and suggest that this disadvantage is mediated by interactions with the immune system. Moderate G6PD deficiency predisposes patients to infection-induced hemolysis (reviewed in ref. 51) as predicted. [Phagocytes from G6PD-deficient subjects show a normal oxidative burst (64).] Furthermore, G6PD-deficient patients with the A- variant show increased risk of sepsis upon severe trauma injury (65). The experimental evidence suggests that transient NADPH depletion and accumulation of oxidative damage in G6PD-deficient erythrocytes mediate this negative clinical outcome. Prostaglandin E₂ is produced by activated macrophages (66) and monocytes (67), and attenuates the cytotoxicity of these cells (67, 68). Human erythrocytes do not produce prostaglandins but contain NADPH-dependent prostaglandin-E₂ 9-reductase (EC 1.1.1.189) (69, 70). Owing to prostaglandin-E₂ catabolism by this enzyme, the close association between erythrocytes and activated phagocytes may exacerbate the cytotoxicity of the latter and thus facilitate the killing and phagocytosis of opsonized pathogens. In contrast, NADPH depletion owing to G6PD deficiency would lead to less effective destruction of pathogens. NADPH depletion can also disturb immune function more indirectly by hampering repair of oxidative damage to erythrocytes, because interaction with oxidatively modified erythrocytes dramatically alters the cytokine production of monocytes (71).

Epidemiological studies correlating the clinical outcome of infection with near normal erythrocyte G6PD activities are lacking. Nevertheless, the evidence above supports the following hypothesis. The need to avoid depletion of NADPH caused by close erythrocyte–phagocyte contact provides the selective pressure for maintenance of high G6PD activity in human erythrocytes. There is evidence suggesting that the G6PD A- phenotype was much more disadvantageous in the past (72). Our hypothesis provides a straightforward explanation for this. The more septic and hazardous environment then made infection more prevalent than today. Consequently the immune system was more active, with more frequent immune adhesion events, leading to more frequent pulses of oxidative stress. This situation would have exacerbated the effect of G6PD deficiency on oxidative damage in erythrocytes. In turn, this led to higher incidence of hemolysis and sepsis upon infection and/or trauma among G6PD-deficient patients than today.

Closing Remarks

The lack of reliable data for estimating the maximal oxidative load on erythrocytes prevents calculation of safety factors for the relevant performance indices. Still, the results presented above show that “investment” in G6PD expression is much more closely matched to the organism's functional requirements, namely for robustness of NADPH concentration and responsiveness of NADPH supply in response to naturally occurring oxidative challenges, than anticipated from the ratio of activities between G6PD and hexokinase. At 25% residual G6PD activity, substantial NADPH depletion occurs in response to a physiologically plausible oxidative challenge (Fig. 3). The clinical and epidemiological data discussed above also reveal a distinct impact on fitness at 10% residual G6PD activity, and the sharp mode at normal values in the population distribution of erythrocyte G6PD activity (33) suggests that even slight deficiency has a relevant effect on fitness. Therefore, the amount of G6PD in the wild type is not largely superfluous.

Functional requirements for robustness and/or responsiveness may explain the excess activity of many other enzymes. The importance of robustness (as reflected by small sensitivities and log gains) as a criterion of good performance of biochemical systems has long been recognized (73), and this criterion has helped to understand the design of various biochemical regulatory networks (22). There are two widely used strategies, often in combination, for maximizing robustness of metabolite concentrations. One is maximizing the kinetic order of the enzyme that consumes the metabolite. This is achieved by the enzyme normally working at a small fraction of its catalytic capacity. If the metabolite concentration is to be robust even when the pathway flux is maximal, then the consuming enzyme must be an excess-activity enzyme. The other strategy uses one or more negative feedback loops from the metabolite or a downstream product to a previous step in the pathway. In unbranched biosynthetic pathways, for instance, there is usually a negative feedback loop from the final product to the first enzyme. A strong feedback endows the pathway with robust intermediate concentrations (74) but potentially makes long pathways unstable. Instability is avoided by making some intermediate steps have a much larger capacity than others (23). This tradeoff between feedback strength (gain) and stability is intrinsic to negative feedback control (75), which pervades biological systems. Both strategies above also improve the temporal responsiveness of the metabolite concentration (23).

Large excess activities may evolve to meet still other functional requirements. For instance, because high concentrations of many metabolic intermediates are deleterious, these concentrations and their changes should be minimal. An effective way to decrease the concentration of an intermediate and its changes is by turning the consuming enzyme into an excess-activity enzyme (22).

Survival of any organism depends on swift, robust, and sensitive physiological responses to environmental events. These performance requirements are often more demanding on system design than that for high flux, and may apply with different intensities to different components of a serial process. Fulfillment of such requirements is thus a likely explanation for large excess capacities in many systems. Thus, the principle of symmorphosis (3), that the quantity of structure incorporated into an organism's functional system is matched to what is needed, may hold more generally than hitherto appreciated. To properly quantify the mismatch between required and actual structure, quantitative evolutionary design studies should start with the identification of the costliest performance requirements, and safety factors should be calculated with reference to these. The quantitative systems framework used in this paper seems appropriate for this endeavor.