Normal Mode Analysis of Biomolecular Structures: Functional Mechanisms of Membrane Proteins

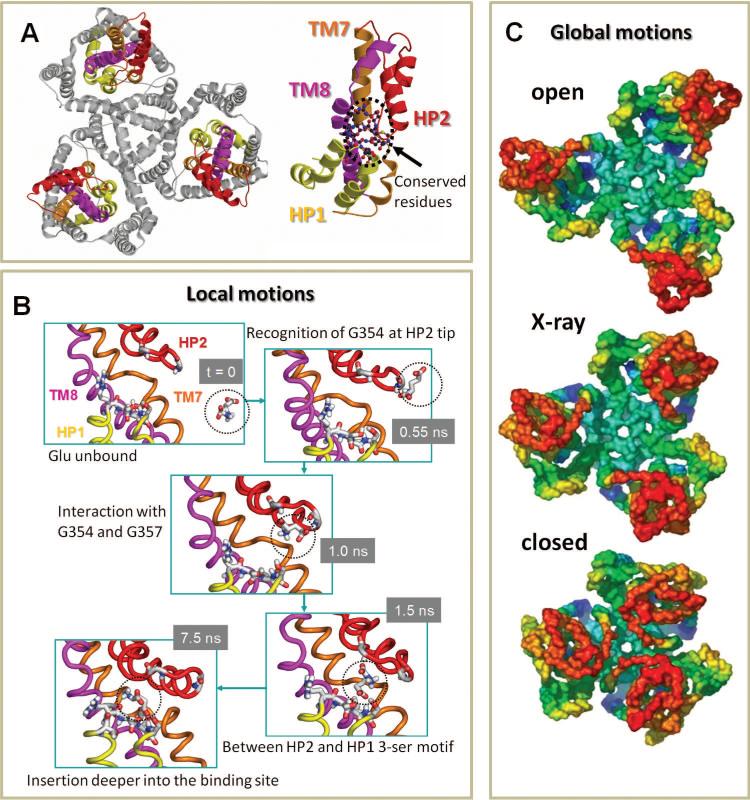
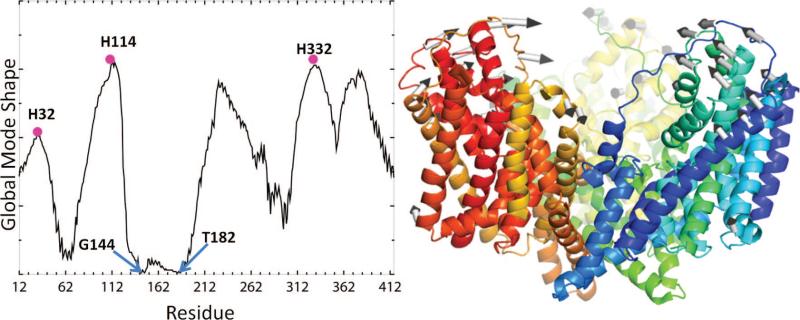
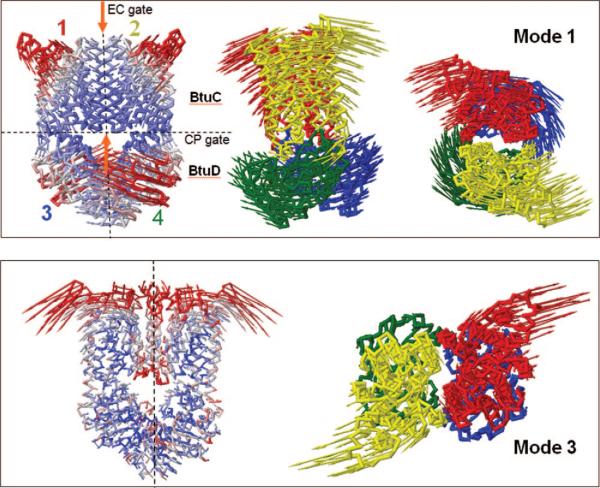
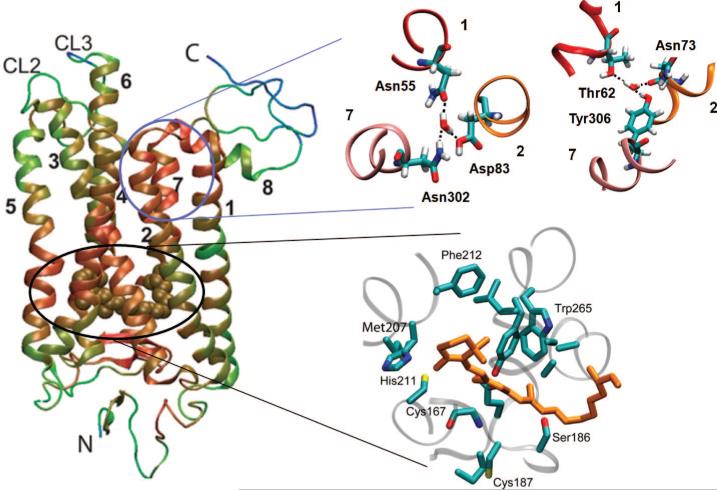
1. Introduction

1.1. Protein Dynamics and Allostery

1.1.1. Dynamic Equilibrium between Pre-existing Conformations

The ability of macromolecules to sample an ensemble of conformations has been evident for decades, starting from the statistical mechanical theory and simulations of polymers.^1–3 A polymer chain of N atoms enjoys 3N – 6 internal degrees of freedom, which gives rise to infinitely many conformations. Even a simple model of N = 100 atoms where bond lengths and bond angles are fixed, and dihedral angles are restricted to discrete isomeric states—say three states per bond—has access to 3^N–3 = 1.9 × 10⁴⁶ conformations. Proteins, too, are polymers, and have access to ensembles of conformations. The main structural difference between proteins and other chain molecules is that, under physiological conditions, proteins sample a significantly narrower distribution of conformations compared to disordered polymers. Their conformational variations are confined to the neighborhood of a global energy minimum that defines their “native state”.

While the native state has been traditionally viewed as a “unique structure” selected or encoded by the particular amino acid sequence, it is now established by theory, computations, and experiments, after the work of pioneering scientists in the field,^4–15 that the native state actually represents an ensemble of microstates: these microstates maintain the overall “fold” and usually share common secondary structure, but they differ in their detailed atomic coordinates. Differences are manifested by variations in bond lengths, bond angles, dihedral angles, loop conformations, substructure packing, or even entire domain or subunit positions and orientations.

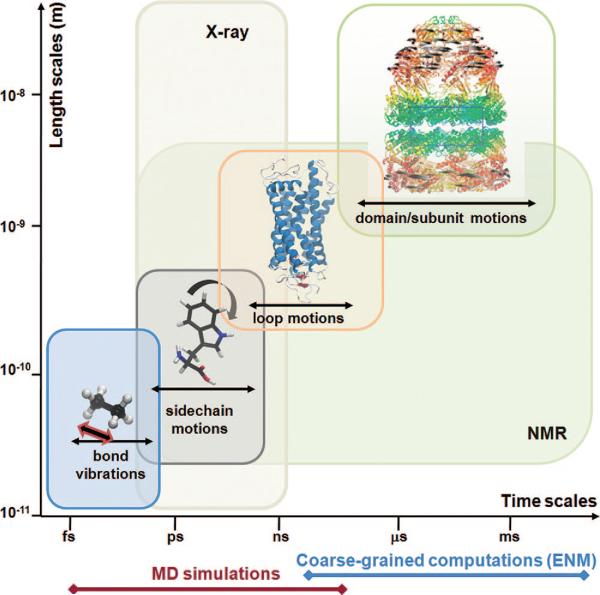
Importantly, these microstates are not static: there is a dynamic equilibrium which allows for continual interconversions between them while maintaining their probability distribution. These “jigglings and wigglings of atoms” as expressed by Feynman,¹⁶ and clearly observed in molecular dynamics (MD) simulations, were originally viewed as random events, or stochastic properties, hardly relevant to biological function. They essentially account for local relaxation phenomena in the nanoseconds regime, which may facilitate, for example, the diffusion of oxygen into the heme cavity of myoglobin¹⁷ or the permeation of ions across selectivity filters in ion channels.^18–20 However, recent studies indicate that these thermal fluctuations may not only passively facilitate but also actively drive concerted domain movements and/or allosteric interactions, such as those required for substrate binding, ion channel gating, or catalytic function.^15,21–34 Figure 1 provides an overview of the broad range of equilibrium motions accessible under native state conditions, ranging from bond length vibrations, of the order of femtoseconds, to coupled movements of multimeric substructures, of the order of milliseconds or seconds.

Figure 1.

Equilibrium motions of proteins. Motions accessible near native state conditions range from femtoseconds (bond length vibrations) to milliseconds or slower (concerted movements of multiple subunits; passages between equilibrium substates). X-ray crystallographic structures span length scales up to several hundreds of angstroms. Fluctuations in the subnanosecond regime are indicated by X-ray crystallographic B-factors. NMR spectroscopy is restricted to relatively smaller structures, but NMR relaxation experiments can probe a broad range of motions, from picoseconds to seconds, including the microseconds time range of interest for several allosteric changes in conformation. Also indicated along the abscissa are the time scales of processes that can be explored by MD simulations and coarse-grained computations. Molecular diagrams here and in the following figures have been generated using Jmol (http://www.jmol.org/), PyMol (http://www.pymol.org/), or VMD³⁵ visualization software.

1.1.2. Functional Significance of Collective Motions

In the last two decades, there has been a surge in the number of studies based on principal components analysis (PCA)³⁶ of biomolecular structures and dynamics. These studies have proven useful in unraveling the collective modes, and in particular those at the low frequency end of the mode spectrum, that underlie the equilibrium dynamics of proteins.³⁷ Normal mode analysis (NMA) of equilibrium structures,^38,39 essential dynamics analysis (EDA) of the covariance matrices retrieved from MD runs,⁴⁰ and singular value decomposition (SVD) of MD or Monte Carlo (MC) trajectories^41–43 all fall in this category of PCA-based methods. Recently, a server has been developed to efficiently perform such calculations using a variety of input structures.⁴⁴

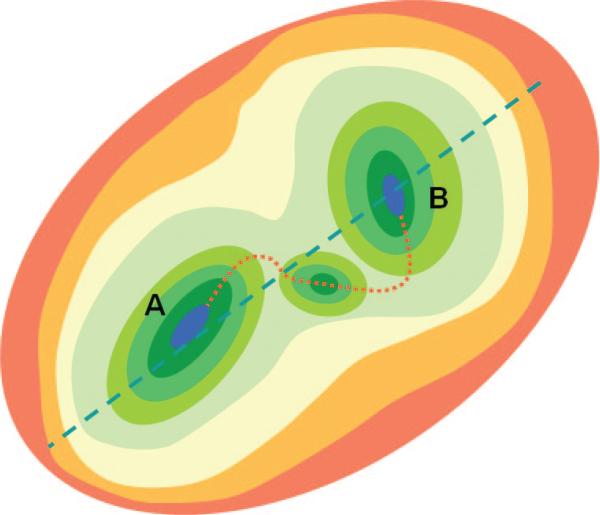
PCA-based studies provide increasing support to the view that the apparently random fluctuations of proteins under native state conditions conceal contributions from highly cooperative movements (e.g., concerted opening and closing of domains) that are directly relevant to biological function. Functional movements indeed involve passages between collections of microstates or substates that coexist in a dynamic equilibrium (Figure 2). The most cooperative motions usually occur at the low frequency end of the mode spectrum. These modes engage large substructures, if not the entire structure, hence their designation as global or essential modes. They are intrinsically accessible to biomolecules, arising solely from structure. In a sense, in the same way as sequence encodes structure, structure encodes the equilibrium dynamics. We refer to these global movements that are collectively encoded by the 3-dimensional (3D) structure as intrinsic motions of the examined protein, intrinsic to the protein fold or topology of native contacts. Biomolecular structures conceivably evolved to favor the global modes that help them achieve their biological or allosteric functions.²¹ Briefly, the emerging paradigm is structure-encodes-dynamics-encodes-function, and an evolutionary pressure originating from functional dynamics requirements may have selected the relatively small space of functional structures.

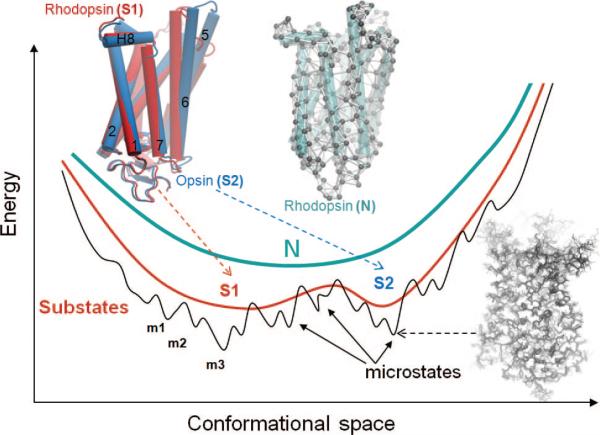
Figure 2.

Energy profile of the native state modeled at different resolutions. N denotes the native state, modeled at a coarse-grained scale as a single energy minimum. A more detailed examination of the structure and energetics reveals two or more substates (S1, S2, etc.), which in turn contain multiple microstates (m1, m2, etc.). Structural models corresponding to different hierarchical levels of resolution are shown: an elastic network model representation where the global energy minimum on a coarse-grained scale (N) is approximated by a harmonic potential along each mode direction; two substates S1 and S2 sampled by global motions near native state conditions; and an ensemble of conformers sampled by small fluctuations in the neighborhood of each substate. The diagrams have been constructed using the following rhodopsin structures deposited in the Protein Data Bank: 1U19 (N); 1U19 and 3CAP (S1 and S2); and 1F88, 1GZM, 1HZX, 1L9H, 1U19, 2G87, 2HPY, 2I35, 2I36, 2I37, 2J4Y, 2PED, 3C9L, and 3C9M (microstates).

The predisposition of proteins to undergo functional changes in structure is now supported by numerous experimental and computational studies, and an increasing amount of data demonstrates that allosteric responses are driven by intrinsically accessible motions.^{15,23,24,45–51} These studies have brought a new understanding to the role of collective dynamics in protein functions, demonstrating in particular how the functions of membrane proteins such as signal transduction, pore opening, ion gating, or substrate translocation are enabled by the cooperative movements of symmetrically arranged subunits. These findings are in support of the original Monod–Wyman–Changeux (MWC) view of allosteric effects,^52,53 the main tenets of which are predisposition of the structure to access alternative conformations via cooperative changes in structure (simultaneously engaging all subunits) and selection from this pool of accessible conformation to achieve biological function in the presence of ligand/substrate binding. Recent findings on the relevance of global modes to functional dynamics are presented below for select, widely studied membrane proteins. The goal here is to review NMA-based computational methods and their applications to membrane proteins. We will also discuss recent developments for improving the methodology and its implementation in structure refinement and drug discovery methods.

1.1.3. Normal Mode Analysis: An Old Technique That Recently Found a Revival in Molecular Biology

Normal mode analysis provides information on the equilibrium modes accessible to a system, assuming that the system is stabilized by harmonic potentials. It has been used for several decades in studying classical physical phenomena such as atomic vibrational spectra and transport in the solid state. Its application to proteins dates back to the early 1980s.^54–57 However, only in the past decade has it become a tool widely used for exploring functional motions. A major reason behind its broader use is the observation that global modes elucidated by NMA bear functional significance. This feature became even more evident with the use of simplified models in coarse-grained (CG) NMA.³⁸

From a physical perspective, the global modes simply represent reconfigurations along directions (principal axes) that are most easily accessible (require the least energy ascent for a given size deformation) on the multidimensional energy landscape. Mode frequency (squared) provides a measure of the curvature (or stiffness) of the energy landscape along a given mode direction, with lower frequency modes being softer motions. Given that the energy landscape is, in turn, defined by the molecular structure, the global modes are structure-encoded by definition.

A striking feature of NMA and other PCAs of biomolecular structures is the observed robustness of the global modes to details in atomic coordinates or specific interatomic interactions. The global modes are defined by the entire structure (or architecture). Their insensitivity to local interactions, or to the specific energy functions and parameters that define the force field, presumably results from their systemic nature. As evidenced by the pioneering study of Tirion,⁵⁸ a hypothetical force field with uniform (single-parameter) harmonic potentials yields global modes almost indistinguishable from those obtained from a detailed force field with specific nonlinear terms. The property that apparently dominates the shape of the global modes is the network of inter-residue contacts, which is a purely geometric quantity defined by the overall shape, form, or native contact topology of the protein.^59,60

1.1.4. Elastic Network Models Inspired by the Robustness of Global Modes

The insensitivity of global modes to structural and energetic details has now been confirmed in many studies^61–66 and led to the following question: If these modes are not sensitive to structural and energetic details, why not use CG models to elucidate such collective movements? This line of thought opened the way to the adoption of elastic network models (ENMs) for exploring protein dynamics.^38,39 ENMs take rigorous account of the topology of contacts. In this respect, they may be viewed as Go models which are also based on native contact maps.^4–6 The major difference is, however, that the network representation adopted in ENMs permits us to take advantage of methods of NMA or spectral graph theory to obtain analytical solutions for equilibrium dynamics that can be readily implemented in efficient computational algorithms. The main advantages of ENM-based approaches are indeed (i) their ability to provide an exact solution for the unique dynamics of each structure and (ii) their applicability to large biomolecular complexes and assemblies beyond the range of atomic simulations.

The first such simplified model, the Gaussian network model (GNM), was introduced a decade ago,^67,68 inspired by the work of Tirion.⁵⁸ GNM is based on the theory of elasticity set forth by Flory and co-workers^69–73 for polymer networks. The structure is represented as a network of nodes (α-carbons) and elastic springs. The springs connect the α-carbon pairs that are closer than a cutoff distance, R_c, in the native structure. A Kirchhoff matrix of inter-residue contacts, Γ, is the sole determinant of equilibrium dynamics. The accessible spectrum of relaxation modes is computed using statistical mechanical theories of solid state physics and/or graph-theoretic methods that have found wide utility in other applications. The GNM has been shortly followed by other ENMs, including, in particular, Hinsen's model with distance-dependent force constants^74,75 and the anisotropic network model (ANM),^76–79 which will be described in some detail in section 2.3.2.

A major reason behind the broadening recognition of NMA as a tool for exploring functional motions of proteins is the observation that global modes elucidated by NMA bear functional significance. For example, the allosteric change in conformation undergone by hemoglobin from its tense (T) form to its relaxed (R) form has been shown by both full atomic NMA⁸⁰ and ANM³¹ to match closely the collective motions along the second lowest frequency mode intrinsically accessible to the original structure. The ratchet-like motion of the two subunits of the ribosome is enabled by the third slowest mode;^81,82 or in general, the opening/closing of domains/subunits in many enzymes conforms to their low frequency modes.^32,79 It is now broadly recognized that ligand binding cooperatively triggers collective movements and stabilizes conformers that are already favored by, or accessible to, the unbound protein structure.³⁰

In recent years, ENM-based NMAs have contributed to improving our understanding of the collective dynamics of membrane proteins, among other allosteric systems. Understanding the functional motions of membrane proteins is significant from both biological and pharmaceutical points of view, as described in section 1.2.1. Progress in this field has been slow, however, due to the scarcity of structural data and the complexity of the involved multiscale interactions. The majority of structure-based computations performed for membrane proteins in the past decade focused on localized events, such as passage of ions across a selectivity filter, which are observable by MD simulations of tens of nanoseconds. The computational study of events such as ion/substrate gating, on the other hand, has been limited by the more cooperative nature of associated changes in structure. Models and methods designed to observe longer time or larger size windows, not obscured by atomic details or random noise, are needed in this case. CG NMAs and their extensions and combinations with atomic simulations^44,83–88 are beginning to fill this gap. The applications summarized in section 3 permit us to observe for the first time a new regime of motions at residue-level detail, providing insight into mechanisms of pore opening, ion gating, or allosteric signal transduction by membrane proteins.

1.2. Structural Dynamics of Membrane Proteins: Significance and Challenges

1.2.1. Classification, Biological Role, and Pharmacological Importance

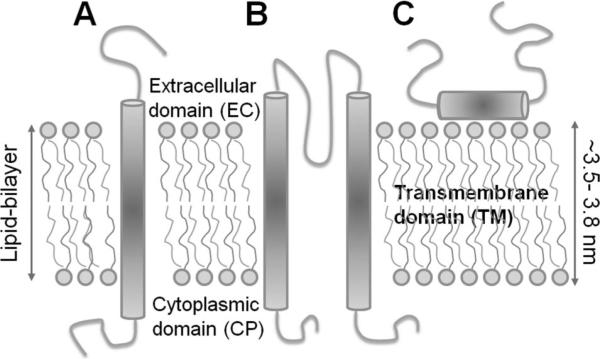
Membrane proteins are classified into two broad groups: integral membrane proteins (IMPs) and peripheral membrane proteins. IMPs are permanently located at the membrane; peripheral membrane proteins are temporarily attached, either to IMPs or to the peripheral regions of the membrane. IMPs include channels, receptors, transporters, and enzymes, in addition to cell adhesion and energy transduction proteins. They are divided into two broad groups depending on the degree to which they span the lipid bilayer: transmembrane (TM) (or polytopic) and integral monotopic. Integral monotopic proteins are attached to the membrane from one side, while TM proteins are typically composed of three domains: extracellular (EC), intracellular/cytoplasmic (CP), and TM domains (Figure 3). The present review focuses on the equilibrium dynamics of selected TM proteins that have been explored by NMA-based approaches in recent years (section 3).

Figure 3.

Schematic representation of different types of integral membrane proteins. (A) Single helical TM protein (a bitopic membrane protein), (B) a polytopic TM protein composed of multiple TM elements (here two helices), and (C) an integral monotopic membrane protein.

The continual flow of ions and metabolites across the membranes is essential for many of life's processes. The membrane acts as an insurmountable barrier for the passage of ions and/or solutes into or out of the cell under equilibrium conditions, thus maintaining a net voltage difference between the cell interior and exterior, known as the resting membrane potential. TM proteins maintain the equilibrium concentrations of ions/substrates in the EC and CP regions, elicit or regulate cell signaling and energy transduction processes, regulate cell volume, or secrete electrolytes.^89,90 In particular, ion pumps and ion exchangers “actively” transport ions: they pump ions against their gradient by coupling the “uphill” process to an energy source such as ATP hydrolysis or the “downhill” movement of an ion or substrate. Likewise, carriers transport substrates, against their concentration gradient in many cases, assisted by proton or ion counter- or cotransport. Ion channels, on the contrary, are usually viewed to be “passive” membrane proteins: they allow for “downhill” permeation of ions and may exhibit very high conduction rates.⁹¹ The electrochemical gradients built by ion pumps serve as a driving source for ion channels and other transporters.⁸⁹

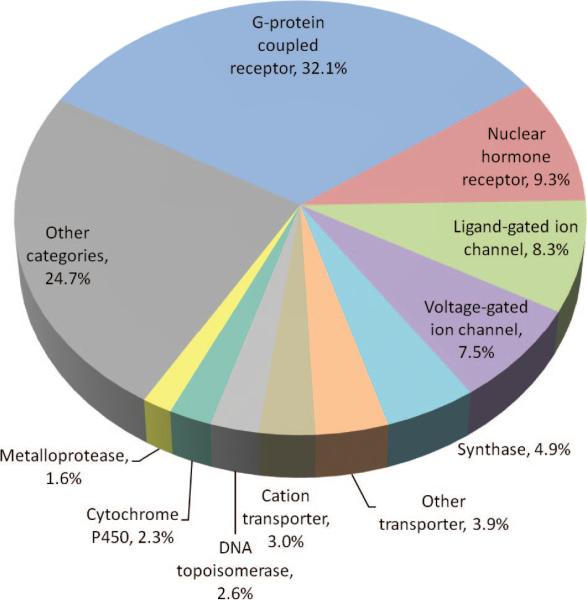
With their locations at cell boundaries, membrane proteins are involved not only in the transport of endogenous substrates/ions but also in drug uptake⁹² and drug action. While approximately 30% of sequenced genes encode membrane proteins, the fraction of membrane proteins among drug targets has been estimated to be 70% in 2001.⁹³ An updated distribution of drug targets is presented in Figure 4. The pie chart refers to 965 U.S. Food and Drug Administration (FDA) approved small-molecule drugs, obtained from DrugBank (http://www.drugbank.ca)⁹⁴ as primary source and refined using Therapeutic Target Database (DB),⁹⁵ Super-Target DB,⁹⁶ and the literature.⁹⁷ A total of 380 proteins are targeted by these drugs, most of which belong to the human genome. The corresponding molecular functions, retrieved from the PANTHER Classification System,⁹⁸ are grouped into 71 functional categories. Figure 4 displays the most frequently targeted ten such categories. The top-ranking four categories are G-protein coupled receptors (GPCRs), nuclear hormone receptors, ligand-gated ion channels, and voltage-gated ion channels. These constitute targets for more than half of the drugs. These results are consistent with those recently compiled by Hopkins and co-workers,⁹⁹ apart from minor differences, presumably due to differences in the data set.

Figure 4.

Distribution of small molecule drugs based on the targeted molecular function. The distribution is shown for the top-ranking ten functional categories targeted by 965 FDA-approved small molecule drugs, excluding biotechnology drugs, nutraceuticals such as vitamins and amino acids, and those with uncertain targets. The top ten categories shown in the pie chart are associated with more than 75% of the drugs in the data set. The distribution is based on 1008 drug–protein associations. A given category is counted once if a given drug targets multiple proteins in that category.

The membrane proteins that are most frequently targeted by small molecule drugs are histamine H1 receptors, α1-adrenergic receptors, and D2 dopamine receptors. All three are members of the GPCR family of proteins. These are succeeded by γ-aminobutyric-acid (GABA) A receptor α1, a ligand-gated ion channel. These proteins are still being investigated in relation to a broad spectrum of diseases including central nervous system disorders, allergies, inflammation, respiratory disorders, headache, and sleep disorders.¹⁰⁰ Notably, most of the drugs currently in use were not initially developed to interact with a specific target protein but to induce certain phenotypes in cultured cell or animal assays.¹⁰¹ The identification of the targets followed the completion of the drug discovery process (a trial-and-error process using combinatorial chemistry rules). The importance of assessing drug targets and understanding the mechanistic aspects of drug–target associations became clear only in recent years. Knowledge of structure and dynamics of target proteins is now recognized to be a crucial element in making progress in rational drug discovery.¹⁰²

1.2.2. Increasing Structural Data on Membrane Proteins

Although atomic resolution crystal structures of soluble proteins have historically been reported with an exponentially increasing frequency, similar progress has not been made for membrane proteins. Determination of membrane protein structures is difficult for a number of reasons. Their crystallization requires disruption of the bilayer, usually with detergents, which renders many of the physical methods of crystallization difficult or impractical. The amphipathic nature of membrane proteins and their inherent conformational flexibility also poses a problem for crystallization.¹⁰³ Yet another reason for the limited structural data on membrane proteins is their low concentrations in tissues, i.e., the difficulties in overexpressing and purifying them at the milligram level.

In spite of these limitations, important progress has been made in recent years in determining membrane protein structures.¹⁰⁴ With the advances in high-throughput techniques in structural biology, multiple protein targets are being cloned, expressed, and purified in parallel, with clones being generated on multiwell plates and crystallization trials being completed at the rate of 100 plates per day.^105,106 These techniques are now being advantageously used in membrane protein structure determination. Membrane proteins are unstable in detergent micelles, and finding conditions that stabilize them helps in protein crystallization. Often, a series of detergents are tested, and the one that extracts the maximum quantity of soluble, active, homogeneous protein is used. Dodecyl maltoside is a detergent that provides such conditions.¹⁰⁷ The recently solved full-length KcsA structure is a nice example of engineering an enhanced stability at the C-terminal domain of the membrane protein by the use of synthetic antigen-binding fragments as crystallographic chaperones. We refer our readers to comprehensive reviews^{103,104,108,109} for more information on advances in NMR spectroscopy,^108–116 X-ray crystallography,^117–122 electron crystallography of 2D crystals in the presence of lipids,⁹³ and infrared spectroscopy (IR).¹²³

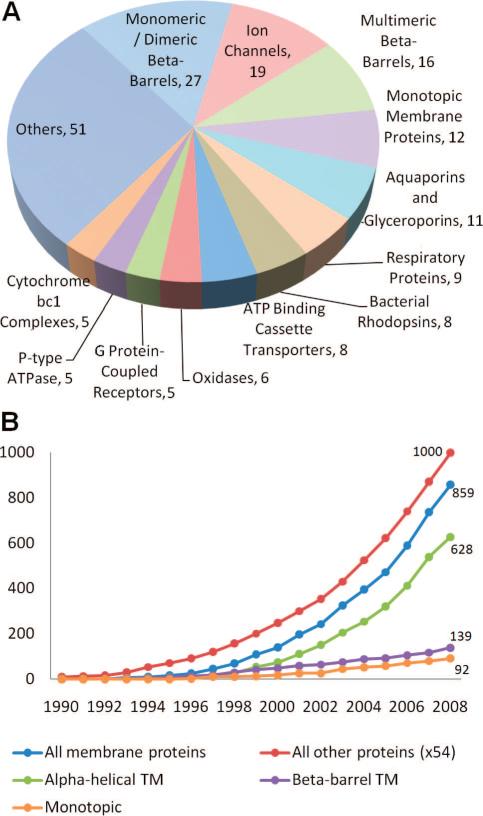
These advances resulted in a remarkable increase in the number of structurally known membrane proteins: while at the end of 2003, there were about 326 resolved membrane proteins (75 of them being unique), this number jumped to 859, including 182 unique structures by the end of 2008 (Figure 5). A comprehensive summary of membrane protein structures available to date is provided by the site (http://blanco.biomol.uci.edu/Membrane_Proteins_xtal.html) maintained by Stephen White's lab. Access to all membrane protein structures in the Protein Data Bank (PDB) is provided by databases such as the PDB of Transmembrane Proteins¹²⁴ (http://pdbtm.enzim.hu/) and the Membrane PDB¹²⁵ (http://www.mpdb.ul.ie). The rapidly growing data in the PDB now holds promise for exploring the structure-based dynamics of membrane proteins.⁹¹ The NMA-based studies presented in section 3 provide some examples of such explorations.

Figure 5.

PDB statistics for membrane proteins. (A) Structures of 182 unique membrane proteins are available in the PDB, as of January 2009. The pie chart displays the distribution of these structures among different functional/structural categories. (B) Growth of released membrane protein structures and other protein structures starting from 1990. Note that the number of “other” proteins is reduced by a factor of 54 in the curve, for display purposes. We also show the breakdown of membrane proteins into different structural groups: α-helical TM, β-barrel TM, and monotopic. An exponential growth with an R2 value of 0.99 is observed in the last ten years for both membrane proteins and all other proteins. The corresponding growth rates are 0.23 and 0.18, respectively; that is, they are higher for membrane proteins due to initiatives in that direction.

1.2.3. Multiscale Dynamics of Membrane Proteins Probed by Experiments

The biological function of many membrane proteins involves a transient change in structure, with the associated processes usually spanning a broad range of time scales (Figure 1). Since the early days of electrophysiology, theories and models have been developed to gain a better understanding of the structural basis of biological function and biochemical data.⁸⁹ Spectroscopic methods for examining conformational vibrations have been applied to proteins as early as 1952, long before the availability of detailed X-ray structures.¹²⁶ Their successful application to membrane proteins has been possible only after the development of sensitive instrumentation and sophisticated analysis techniques.¹²³

Here, we briefly point to two spectroscopic methods, NMR and electron paramagnetic resonance (EPR), that emerge as powerful tools for probing protein dynamics over broad time scales, and we refer our readers to excellent reviews^127–136 for more information.

Structural dynamics probed by NMR

Many of the experimental data showing that structural dynamics play a central role in protein function currently originate from NMR spectroscopy.^{22,131,135,137} While traditionally NMR studies have been limited to relatively small proteins (typically <50 kDa), the dynamics of significantly larger structures are now being explored with advances in labeling technology and solution NMR,¹³² and motions in both short (pico- to nanoseconds) and long (micro- to milliseconds) time scales are being probed.^{116,131,138–140} Using ¹³C- and ²H-NMR relaxation rates, Kay and co-workers showed that site-specific quantitative data could be collected for the correlation times of methyl groups for proteins of the order of 100 kDa;^141,142 for example, picoseconds-to-nanoseconds cross-correlation rates for intramethyl ¹H–¹H dipolar spin relaxation have been measured for a half proteasome complex.¹³³ Not all methyl sites undergo such fast dynamics, however. Those embedded in regions that undergo highly concerted subunit motions exhibit relaxation times of the order of milliseconds, as observed¹⁴³ in the α-rings of the 20S core particle proteasome—a molecular machine of 670 kDa. Finally, the ability of NMR experiments to separate local and global changes in conformation is noteworthy. A classical example is the T → R transition of aspartate transcarbamoylase,¹⁴⁴ the 2D ¹H–¹³C spectra of which clearly evidenced the pre-existence of a dynamic equilibrium between the two forms and the stabilization of one (R) upon ligand binding.¹⁴⁵ Residual dipolar couplings (RDCs) observed in NMR spectra are increasingly providing information on collective motions in the nano- to microsecond regime.^26,130,146 The PCA-based comparison of an ensemble of NMR models refined against RDCs²⁶ for ubiquitin with the X-ray structures of the same protein in the presence of different substrates showed (i) the accord between the conformations sampled in solution by the unbound protein and those assumed upon complexation with different substrates and (ii) the fact that conformational variations could be explained to a large extent by a few low frequency modes intrinsically accessible to the structures.

Structural dynamics probed by site-directed spin labeling (SDSL) combined with EPR^{127–129,147}

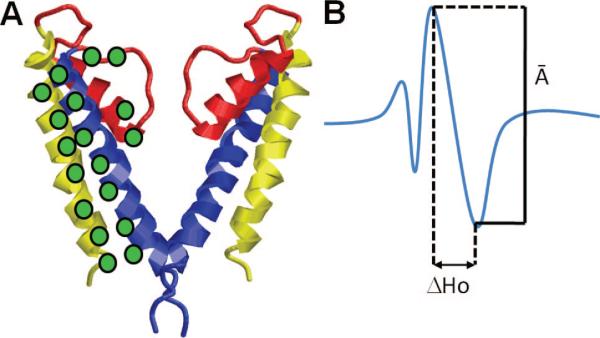
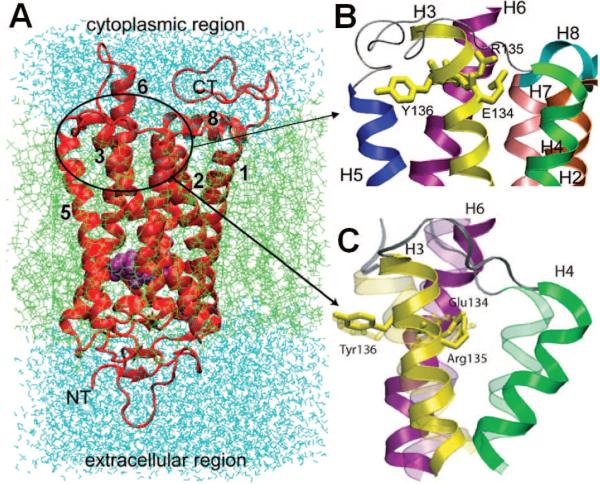
In this technique, residues at selected sites are substituted, mostly by cysteines, followed by the selective modification of the sulfhydryl group with a nitroxide radical that serves as an EPR spin label/probe. A set of spin-labeled proteins is thus prepared, differing by the position of spin-labeled cysteines (Figure 6). The experiments allow for characterizing the mobilities of the spin-labeled residues and the changes in the distances between them. Applications of time-resolved SDSL-EPR to membrane proteins (e.g., to bacteriorhodopsin^148,149 and rhodopsin^{134,150–155} by Hubbell, Khorana, and co-workers, to the K⁺ channel from Streptomyces lividans (KcsA),^156–159 and to a prokaryotic mechanosensitive channel (MscL)¹⁶⁰ by Perozo and co-workers) have successfully provided information on interhelical movements or changes in tertiary contacts accompanying their functional rearrangements. Notably, fluctuations and correlations over wide time scales, from nanoseconds to milliseconds, can be examined by this technique, and changes in distance between pairs of labels separated by 20–60 Å can be probed by double electron resonance (DEER) with a resolution better than 1 Å.¹⁶¹ A recent application to rhodopsin clearly demonstrated, for example, that the activation of the molecule is accompanied by an outward movement of TM helix 6 by about 5 Å.¹⁶¹

Figure 6.

Site-directed spin-labeling coupled with EPR illustrated for a potassium channel. (A) Molecular model of KcsA (omitting two of the four subunits for clarity). The green discs indicate the positions of the spin-labeled residues (probes) on TM1 (yellow), TM2 (blue), and the selectivity filter (red). (B) Measurement of the structural parameter from the spectral line shape of an EPR-spectrum. The amplitude (A^–) of the normalized central resonance line M = 0 and the mobility parameter ΔH_o (the peak-to-peak width at M = 0) are shown. Changes in two structural parameters are usually examined: (i) probe mobility (ΔH_o) and (ii) spin–spin interaction parameter W. Changes in the probe mobility, ΔΔH_o, indicate rearrangements in tertiary or quaternary contacts, while the W parameter obtained from the ratio of the normalized amplitude spectra (A^–) in different forms reports changes in the intersubunit probe-to-probe proximity. Such measurements performed by Perozo and co-workers for the open and closed conformations of KcsA as a function of pH¹⁵⁷ revealed the coupled rigid-body rotations of TM helices TM1 and TM2 of the four subunits and the opening of the permeation pore (gating) induced by the concerted rotations of the TM2 helices while the selectivity filter remained practically immobile.

1.2.4. Structure-Based Models, Theory, and Computations

According to Moore's law, the cost of computing halves roughly every 1.5 to 2 years.¹⁶² Looking back at MD simulations of biomolecules at atomic resolution, we have indeed progressed from tens of picoseconds in the early 1980s to tens of nanoseconds at present, roughly consistent with Moore's law. The progress in recent years in MD simulations of membrane proteins^163–166 has been enabled by advances in computing technology, algorithms, and methods.^167,168 Classical examples include the simulations of aquaporin,^33,169–172 gramicidin,^20,173–175 and KcsA.^18,176–179 Yet, the time scales of tens of nanoseconds, or even tenths of microseconds,¹⁸⁰ being accessed in advanced MD simulations still fall short of providing an accurate sampling of the complete conformational space that many multimeric membrane proteins explore under physiological conditions. Indeed, multimeric structure is recognized as essential for enabling highly cooperative structural rearrangements.⁵² Physics-based CG models such as ENMs emerge as approximate structural models that provide analytical solutions for the collective dynamics of such complex systems, which cannot be determined with MD.

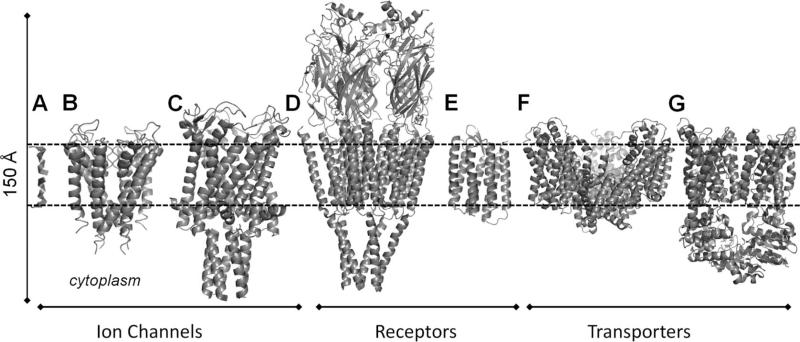
Here we present recent progress in exploring the dynamics of membrane proteins using NMA with ENM-based models. The proteins considered are grouped into three categories: ion channels, receptors, and transporters, presented in the respective sections 3.1–3.3, and among them we present NMA-based studies on gramicidin A (GA), potassium channels (KcsA and others), a MscL, the nicotinic acetylcholine receptor (nAChR), rhodopsin (as a prototypic GPCR), a glutamate transporter (Glt_Ph), and an ATP binding cassette (ABC) transporter (BtuCD) (Figure 7). Note that, in many cases, there is no clear-cut distinction between these categories; some receptors or transporters may also function as ion channels (e.g., nAChR is a ligand-gated ion channel, or glutamate transporter also functions as a chloride channel).

Figure 7.

Transmembrane proteins studied by NMA, considered in the present review: (A) gramicidin A, (B) KcsA, (C) MscL, (D) nAChR, (E) rhodopsin, (F) glutamate transporter (Glt_ph), and (G) BtuCD. The bilayer is indicated by the dashed lines. The ribbon diagrams were constructed using the respective structures 1NRU, 1K4C, 2OAR, 2BG9, 1L9H, 1XFH, and 1L7V available in the PDB.

Membrane proteins are one of the most challenging biomolecular systems from theoretical and computational aspects, because their functional mechanisms involve not only the global dynamics of multiple subunits but also the highly specific local interactions (e.g., ionic interactions, solvation) in the presence of lipid bilayer and water molecules. The former group of motions is conveniently explored by CG models such as ENMs, but the latter requires detailed full atomic geometry and energy considerations and cannot be studied by ENMs. This broad range of events also spans a hierarchy of functionally significant time scales, which in turn requires adopting multiscale approaches. The combination of atomic-level resolution with high-level (low resolution) computational approaches is deemed as a promising path for interpreting experimental observations and determining structure–function relations.^20,181 Attempts at developing such integrated approaches by steering MD simulations along ENM directions⁸⁵ or sampling transition pathways using adaptive ENM methods have recently been undertaken. These will be presented in section 4.2. Other recent studies support the utility of ENM-based approaches, not only for assessing functional dynamics but also for flexible docking of substrates and refining low resolution structures, and will be presented in section 4.2.

2. Theory

2.1. Principal Component Analysis of Experimentally Resolved Conformations

2.1.1. Definitions of System and Parameters

Principal component analysis of ensembles of structures is an orthogonal linear transformation that transforms data from the Cartesian coordinate system into a new system of collective coordinates.³⁶ The goal is to gain a simplified view of the structural variability in the examined data set by identifying the dominant directions of structural changes. The new coordinate system is such that the greatest variance in the data set lies along the first principal component (PC) axis, followed by the second PC axis, and so on. Here we will focus on the application of PCA methods to extract information on equilibrium dynamics. PCA is performed in this case for an ensemble of conformers such as the PDB structures for the same protein determined in the presence of different substrates, or NMR models for the same protein.⁴⁴ Alternatively, an ensemble of MD snapshots may be used. The utility of PCA for understanding functional dynamics is clearly demonstrated by a recent study of ubiquitin structures in which a single mode of motion was found to largely account for ubiquitin's recognition ability.²⁶

Let us consider an ensemble of M conformations, for a protein of N interaction sites (N atoms or residues, or any CG representation of an interaction site). Each conformation, k, is described by a 3N-dimensional vector consisting of the position vectors R_i^(k) = (x_i^(k) y_i^(k) z_i^(k))^T of the N sites (1 ≤ i ≤ N) in that particular conformation, organized as

$$\begin{array}{cc}\hfill & 6{\mathbf{q}}^{\left(k\right)}={({\left({{\mathbf{R}}_1}^{\left(k\right)}\right)}^{\mathrm{T}},\dots ,{\left({{\mathbf{R}}_N}^{\left(k\right)}\right)}^{\mathrm{T}})}^{\mathbf{T}}=\hfill \\ \hfill & {({x_1}^{\left(k\right)},{y_1}^{\left(k\right)},\dots ,{x_N}^{\left(k\right)},{y_N}^{\left(k\right)},{z_N}^{\left(k\right)})}^{\mathbf{T}}\hfill \end{array}$$ (1)

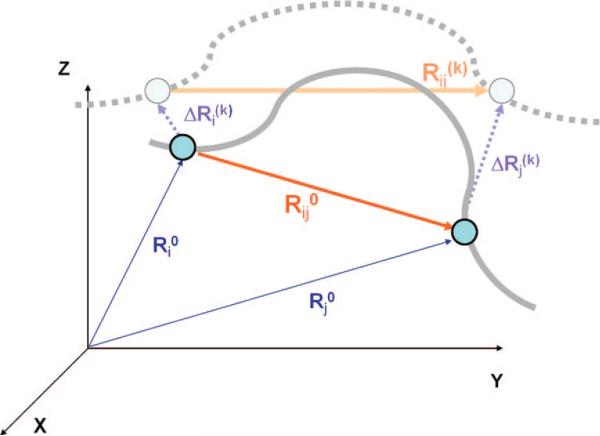
Likewise, we define a 3N-dimensional fluctuation vector Δq^(k) = q^(k) – q⁰ for each conformation, describing the departure ΔR_i^(k) = R_i^(k) – R_i⁰ in the position vectors of the N sites from their equilibrium position R_i⁰ = (x_i⁰ y_i⁰ z_i⁰)^T (Figure 8). The equilibrium positions may be identified by the average over all snapshots from MD trajectories or over all optimally superimposed PDB structures. The PDB coordinates are usually assumed to be the equilibrium positions when performing NMA of a given structure using the ENM, as will be described below.

Figure 8.

Schematic view of interaction sites and their displacements. In the initial conformation, CG sites i and j are located respectively at R_i⁰ and R_j⁰, and the vector R_ij⁰ = R_j⁰ – R_i⁰ defines the distance vector between these sites. Upon displacement along mode k, the CG sites move to R_i⁰ + ΔR_i^(k) and R_j⁰ + ΔR_j^(k), and the distance vector becomes R_ij^(k). The solid gray line represents the structural details of the initial-state protein that are above the resolution of the coarse graining, and the broken gray line indicates the structure after a displacement along mode k.

2.1.2. Covariance Matrix: A Measure of Correlations between Residue Motions

In many applications, it is of interest to understand the type and strength of coupling between the variations in different degrees of freedom. The cross-correlations between the components of the fluctuations vectors are given by the averages 〈Δq_iΔq_j〉 over all conformations, which are conveniently organized in a 3N × 3N covariance matrix C,

$$\mathbf{C}=M^{\text{-}1}\sum _k\Delta {\mathbf{q}}^{\left(k\right)}\Delta {\mathbf{q}}^{\left(k\right)\mathbf{T}}$$ (2)

A detailed description of equilibrium motions, including the mean-square fluctuations of individual sites and their cross-correlations, is provided by the covariance matrix C. The elements of C may alternatively be viewed as N × N blocks (or submatrices of size 3 × 3), C_ij each of the form

$${\mathbf{C}}_{ij}=\left[\begin{array}{ccc}\hfill \langle \left(\Delta x_i\Delta x_j\right)\rangle \hfill & \hfill \langle \left(\Delta x_i\Delta y_j\right)\rangle \hfill & \hfill \langle \left(\Delta x_i\Delta z_j\right)\rangle \hfill \\ \hfill \langle \left(\Delta y_i\Delta x_j\right)\rangle \hfill & \hfill \langle \left(\Delta y_i\Delta y_j\right)\rangle \hfill & \hfill \langle \left(\Delta y_i\Delta z_j\right)\rangle \hfill \\ \hfill \langle \left(\Delta z_i\Delta x_j\right)\rangle \hfill & \hfill \langle \left(\Delta z_i\Delta y_j\right)\rangle \hfill & \hfill \langle \left(\Delta z_i\Delta z_j\right)\rangle \hfill \end{array}\right]$$ (3)

Here we use boldface subscripts to designate a (sub)matrix or vector and lightface subscripts for scalars (e.g., elements of vectors or matrices). The sum of the diagonal elements of C_ij,

$$\mathrm{tr}\left\{{\mathbf{C}}_{ij}\right\}=\langle \Delta x_i\Delta x_j\rangle +\langle \Delta y_i\Delta y_j\rangle +\langle \Delta z_i\Delta z_j\rangle =\langle \Delta {\mathbf{R}}_i•\Delta {\mathbf{R}}_j\rangle$$ (4)

provides a measure of the cross-correlation between the fluctuations ΔR_i and ΔR_j of sites i and j; similarly, the mean-square fluctuations in the positions of individual sites are given by the trace of the diagonal submatrices, i.e., tr{C_ii} = 〈(ΔR_i · ΔR_i)〉 = 〈(ΔR_i)²〉 using i = j in eq 4. In many applications, it proves useful to analyze the N × N covariance matrix, C̄, composed of the correlations between the fluctuation vectors ΔR_i, themselves,

$$\stackrel{‒}{\mathbf{C}}=\left[\begin{array}{cccc}\hfill \langle {\left(\Delta {\mathbf{R}}_1\right)}^2\rangle \hfill & \hfill \langle \Delta {\mathbf{R}}_1•\Delta {\mathbf{R}}_2\rangle \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \langle \Delta {\mathbf{R}}_2•\Delta {\mathbf{R}}_1\rangle \hfill & \hfill \langle {\left(\Delta {\mathbf{R}}_2\right)}^2\rangle \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \langle \Delta {\mathbf{R}}_N•\Delta {\mathbf{R}}_1\rangle \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \langle {\left(\Delta {\mathbf{R}}_N\right)}^2\rangle \hfill \end{array}\right]$$ (5)

The fluctuations in the Cartesian space are mapped onto the space spanned by the 3N (or N) principal axes upon diagonalizing the covariance matrix C (or C̄) as

$$\mathbf{C}={\mathbf{PSP}}^{\mathrm{T}}=\sum _{k=1}^{3N}{\sigma }_k{\mathbf{p}}_k{{\mathbf{p}}_k}^{\mathbf{T}}$$ (6)

where P is the unitary matrix of normalized displacements along the principal axes, also called the principal modes of structural changes, each given by a column p_k, (1 ≤ k ≤ 3N), and S is the diagonal matrix of eigenvalues σ₁, σ₂, ..., σ_N, usually ordered in descending order. The eigenvalues are directly proportional to the variance along the principal axes such that the fractional contribution of p_k to the structural variability in the data set is f_k = σ_k/∑_Iσ_i, where the summation is performed over all 3N modes. Equation 6 permits us to assess the contribution of each mode or subset of modes to the observed covariance. For example, the square displacements in the position of the i^th interaction site induced by the top ranking m PC modes are

$${\phantom{\mid }{\left(\Delta {\mathbf{R}}_i\right)}^2\mid }_{1\le k\le m}=\mathrm{tr}\left\{{\left[\sum _{k=1}^m{\sigma }_k{\mathbf{p}}_{\mathit{k}}{{\mathbf{p}}_{\mathit{k}}}^{\mathbf{T}}\right]}_{\mathit{ii}}\right\}$$ (7)

2.2. Normal Mode Analysis

2.2.1. Assumptions and Limitations

The mathematical theory of NMA is detailed in any classical mechanics text;¹⁸² hence, here we will present only an outline of the theory as it pertains to its recent applications to proteins and their complexes. The essence of NMA is again the diagonalization of a 3N × 3N matrix H, called the Hessian, the inverse of which yields the covariance matrix C.

The underlying assumption in NMA is that any given equilibrium system fluctuates about a single well-defined conformation and that the nature of these thermally induced fluctuations can be calculated assuming a simple harmonic form for the potential. This directly leads to a basic limitation of NMA: it is only valid in proximity to the equilibrium. As the system is displaced from its equilibrium conformation, the extent to which the harmonic approximation holds grows increasingly uncertain. The excursions from equilibrium along the normal modes must be closely monitored, lest one propose a conformational change in excess of the model's capabilities. In situations where the potential is calculated using exact units, for example when an atomistic force field is used as the kernel for the potential energy surface, then the magnitude of the excursions along the normal modes might be approximated by the absolute temperature of the system. When further coarse-graining is used, for example in the ENMs, then the absolute magnitudes of the interactions are unknown and even greater care must be used.

A second caveat to NMA is that the normal modes represent instantaneous displacements and are tangent to the direction of motion at equilibrium. The molecule often contains additional internal distance constraints that are not explicitly included in the NMA, such as fixed bond lengths or bond angles. All but the smallest distortions along the normal modes will violate these constraints unless measures are taken to satisfy them.^183,184 As a result, (i) NMA results are “accurate” in the immediate vicinity of the energy minimum, where the “direction” of motion is accurately predicted; large excursions in the conformational space may necessitate the use of an adaptive scheme to re-evaluate normal modes at a minimum, and (ii) NMA with ENMs is most useful for predicting the large-scale motions, which are insensitive to structural and energetic details; localized highly specific interactions, including in particular electrostatic interactions, cannot be precisely accounted for. Increasingly, NMA is used in conjunction with traditional MD or other simulation methods to explore large-scale motions in the presence of detailed atomic interactions.^{85,183,185–189}

2.2.2. Underlying Potential and Hessian Matrix

For our purposes, the physical system under consideration is a molecular system containing N interaction sites, the Cartesian coordinates of which are given by eq 1. We will omit the superscript k here, since NMA is performed for a single structure (M = 1). Near the equilibrium conformation, q⁰, the potential energy can be expanded as a power series in q as

$$\begin{array}{cc}\hfill V\left(\mathbf{q}\right)=& V\left({\mathbf{q}}^0\right)+\sum _i{\left(\frac{\partial V}{\partial q_i}\right)}^0(q_i-q_i^0)+\hfill \\ \hfill & \frac{1}{2}\sum _{i,j}{\left(\frac{{\partial }^{2}V}{\partial q_i\partial q_j}\right)}^0(q_i-q_i^0)(q_j-q_j^0)+\dots \hfill \end{array}$$ (8)

where superscripts of zero indicate the equilibrium conformation. The first term is the minimum value of the potential, which may be set to zero. The second term is identically zero at any local minimum of the potential. To second order, the potential is then a sum of pairwise potentials

$$\begin{array}{cc}\hfill V\left(\mathbf{q}\right)& =\frac{1}{2}\sum _{ij}{\left(\frac{{\partial }^{2}V}{\partial q_i\partial q_j}\right)}^0(q_i-q_i^0)(q_j-q_j^0)\hfill \\ \hfill & =\frac{1}{2}\sum _{i,j}(q_i-q_i^0)H_{ij}(q_j-q_j^0)=\frac{1}{2}\Delta {\mathbf{q}}^{\mathbf{T}}\mathbf{H}\Delta \mathbf{q}\hfill \end{array}$$ (9)

where H is the Hessian matrix obtained from the second derivatives of the potential with respect to the components of q (or Δq):

$$H_{ij}={\left(\frac{{\partial }^{2}V}{\partial q_i\partial q_j}\right)}^0$$ (10)

In the same way as the covariance matrix C is organized, H may be thought of as an N × N matrix of 3 × 3 submatrices, each of which describes the energetic contribution from the interaction of two CG sites. Two important properties of the Hessian arise from eq 10. First, H is real and symmetric by construction and is therefore diagonalized by an orthogonal transformation. Where H not symmetric, its eigenvectors would not form an orthonormal basis over the full space of molecular motions and NMA could not be performed. Second, none of the eigenvalues of H can be negative if H is constructed at a local potential energy minimum. The sign of a given eigenvalue indicates the local curvature of the potential along the corresponding mode directional vector or eigenvector: Positive eigenvalues indicate local minima, and negative eigenvalues, local maxima. The local potential energy landscape for a system in a potential energy minimum will have only positive or zero curvature in all directions. Eigenvalues that are identically zero indicate conformational changes that have no effect on the system's (internal) potential energy. Typically, H has six zero eigenvalues, corresponding to the rigid-body rotations and translations of the molecule. Obtaining the proper form of the Hessian can be a difficult process that must be handled delicately and will be discussed later.

2.2.3. Equation of Motion and Its Solution

The Hessian does not contain the full story of NMA. Because NMA is applied to the study of dynamics, it is necessary to account for kinetic energy as well as potential energy. In doing so, the form of the matrix that is to be diagonalized changes slightly, but the physical interpretation of the results is more transparent. By considering the system to be a collection of classically behaving particles, the equation of motion can be written as

$$\mathbf{M}\frac{{\mathrm{d}}^2\Delta \mathbf{q}}{\mathrm{d}{t}^2}+\mathbf{H}\Delta \mathbf{q}=0$$ (11)

Here the diagonal matrix M contains the masses of the particles. Each mass is repeated three times, once for each of the particle's three Cartesian coordinates. A solution to eq 11 is the 3N-dimensional vector u_k(t) = a_k exp{–iω_kt}, where a_k is a complex vector containing both amplitude and phase factor, and ω_k is the frequency of the mode of motion represented by u_k(t). Substituting this solution into eq 11, the equation of motion becomes

$${\mathbf{Hu}}_k={\omega }_k^2{\mathbf{Mu}}_k$$ (12)

which is a generalized eigenvalue equation. The complete set of solutions u_k(t), 1 ≤ k ≤ 3N, and the corresponding squared frequencies ω_k² may be organized as the respective columns of the matrix U and the elements λ_k = ω_k² of the diagonal matrix Λ to rewrite the set of 3N equations represented by eq 12 in compact notation as

$$\mathbf{HU}=\mathbf{MU}\Lambda$$ (13)

Equation 13 is usually solved by transforming it to a standard eigenvalue equation H̃Ũ= ŨΛ in mass-weighted coordinates through the transformations Ũ = M^1/2Uand H̃ = M^–1/2HM^–1/2. The mass-weighted Hessian, H̃, retains the symmetry of the original Hessian, and its eigenvectors ũ_k = M^1/2u_k form an orthonormal basis set (i.e., Ũ^TŨ = 1). These are the normal modes of the system. Their Cartesian counterparts are found through the inverse transformation U = M^–1/2Ũ and satisfy the orthonormality condition U^TMU = 1. If the interaction sites have all equal mass m, M reduces to the identity matrix multiplied by m, Ũ = m^1/2U, and H̃ = m^–1 H.

2.2.4. Significance of Normal Modes and Dominance of Slow Modes

The energy associated with a given normal mode is directly proportional to the square of its frequency (or its eigenvalue λ_k = ω_k²). This can be seen by rewriting eq 9 for a single mode k:

$$V\left({\mathbf{u}}_k\right)=\frac{1}{2}{\mathbf{u}}_k^{\mathrm{T}}{\mathbf{Hu}}_k=\frac{{\omega }_k^2}{2}$$ (14)

Displacements along high-frequency modes are therefore energetically more expensive than those of equal magnitude along low-frequency modes. The vibrational energy is, on average, equally partitioned among all the modes, such that the average amplitude of oscillation along mode k scales with 1/ω_k². Thus, the molecule experiences the greatest displacement along the lowest frequency, or “slowest”, modes. Conceptually, the energy landscape slopes most gently along the slow modes, and these are consequently the most accessible. These modes are also of highest interest when seeking to determine the most probable global fluctuations of a molecule. Large eigenvalues, on the other hand, indicate directions of steep energetic ascent, and excursions along these modes will quickly raise the system's energy.

The cross-correlations 〈Δq_iΔq_j〉 between the displacements of the interaction sites along different coordinates are calculated as statistical mechanical averages of the form

$$\begin{array}{cc}\hfill & \langle \Delta q_i\Delta q_j\rangle =\frac{1}{Z}\int d^{3N}q{e}^{-1∕\left(2k_{\mathrm{B}}T\right)\Delta {\mathbf{q}}^{\mathrm{T}}\mathbf{H}\Delta \mathbf{q}}\Delta q_i\Delta q_j=\hfill \\ \hfill & k_{\mathrm{B}}T{\left({\mathbf{H}}^{-1}\right)}_{ij}\hfill \end{array}$$ (15)

using the configurational integral

$$Z=\int d^{3N}q{e}^{-1∕\left(2k_{\mathrm{B}}T\right)\Delta {\mathbf{q}}^{\mathrm{T}}\mathbf{H}\Delta \mathbf{q}}={\left(2\pi k_{\mathrm{B}}T\right)}^{3N∕2}{\left[\text{det}\left({\mathbf{H}}^{-1}\right)\right]}^{1∕2}$$ (16)

Here the integrations are performed over the complete space of equilibrium fluctuations, k_B is the Boltzmann constant, T is the absolute temperature, and (H^–1)_ij designates the ij^th element of the inverse of H. Because only internal motions affect the system's potential energy, H has exactly six eigenvalues that are identically zero, corresponding to the three translational and three rotational degrees of freedom. The inverse of H is therefore replaced by the pseudoinverse, which is the inverse evaluated only in the space corresponding to the nonzero eigenvalues,

$${\tilde{\mathbf{H}}}^{-1}=\sum _{k=1}^{3N-6}\frac{{\tilde{\mathbf{u}}}_k{\tilde{\mathbf{u}}}_k^{\mathrm{T}}}{{\omega }_k^2}$$ (17)

The importance of the slow modes is again highlighted in these equations: The lowest frequency modes contribute most to the spatial partition function because det(H̃^–1) is the product of the reciprocal nonzero eigenvalues of H̃.

2.2.5. Covariance Computed from NMA: Bridging with PCA of Structural Ensembles

The cross-correlation 〈Δq_iΔq_j〉 on the left-hand side of eq 15 is simply the ij^th element of the covariance matrix C; therefore, eq 15 may be rewritten in compact notation as

$$\mathbf{C}=k_{\mathrm{B}}T{\mathbf{H}}^{\text{-}1}$$

This equation establishes the bridge between the PCA of ensembles of conformations and NMA of a given structure. In the former case, the top ranking (principal) modes of structural changes are extracted from experimental data (or sets of known structures for a given protein). In the latter, the same such structural changes are predicted by the theory using one structure to construct H.

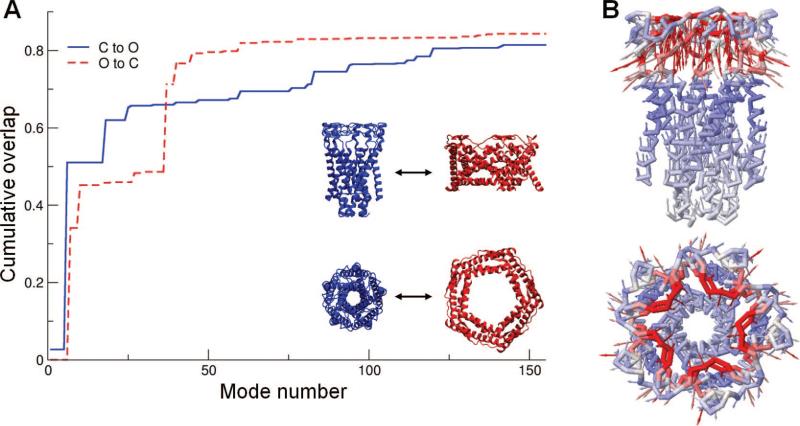
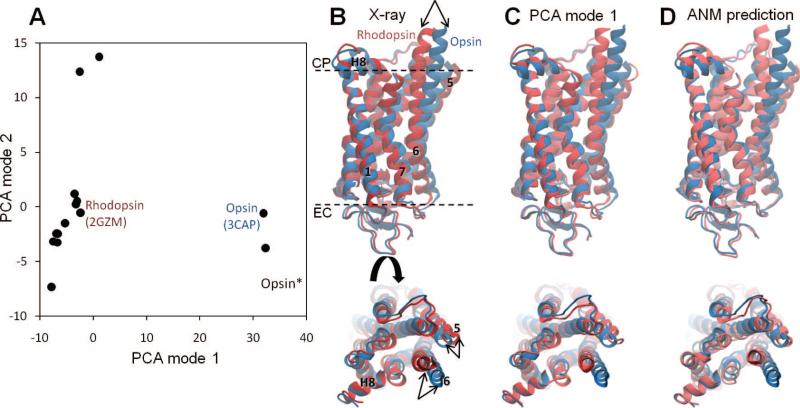
The top-ranking modes obtained by PCA should, in principle, be comparable to the lowest frequency modes derived by NMA (i.e., λ_i ~ 1/σ_i, and p_i ~ u_i), provided that (i) the data set of conformations subjected to PCA represents an equilibrium distribution and (ii) the Hessian in NMA provides an accurate description of dominant interactions. Recent PCAs performed for ensembles of PDB structures exhibit good agreement with the global modes predicted by CG NMAs.^44,190 Notably, ENMs have been adopted in those NMAs. The relevance of ENM predictions for a given protein to PC modes derived from sets of structures experimentally resolved for the same protein (under different conditions, in the presence of different ligands) lends support to the use of ENMs for assessing functional changes in structure. Similar results will be presented below for rhodopsin.

2.2.6. Using Normal Modes for Exploring the Potential Energy Surface

The harmonic approximation only holds in the immediate vicinity of a local potential energy minimum, but what if we wish to explore structures that are far away from this minimum? One method for exploring remote regions of the potential energy surface is the normal mode following (NMF) technique.¹⁹¹ In this method, one starts at an energy minimum and iteratively moves the structure along its slowest eigenmode while remaining at a minimum for all the other modes. Eventually one of the eigenvalues will become negative, indicating the neighborhood of a saddle point or a transition state. From that point, other local minima can be found by iteratively distorting the structure along the potential energy gradient.

The NMF method has recently been enhanced through using the Metropolis MC criterion to control the size of the steps taken.¹⁹² As discussed in section 3.1.1, this technique has proven useful in revealing the gating mechanism of gramicidin A. Similar techniques that take advantage of movements along the mode coordinates have been exploited for investigating transition pathways between known minima, as described in section 4.4.

2.3. Elastic Network Models

NMA requires knowledge of a symmetric and nonnegative Hessian. An energy minimization is required prior to performing NMA on a protein crystal structure to ensure that the first derivative of the total potential is zero with respect to all degrees of freedom and to evaluate the second derivatives (elements of H). Energy minimization is a computationally expensive task and generally distorts the initial conformation, resulting in NMA being performed on a structure altered from the original. Lu and Ma have demonstrated that the problem of initial energy minimization can be overcome by mathematically moving the minimum to the initial structure.¹⁹³ Their technique involves decomposing the Hessian into submatrices, replacing each submatrix with its nearest symmetric positive semidefinite matrix, and reconstructing the Hessian. Far easier is adopting an ENM that by design accepts the initial structure, usually taken from the PDB, to be an energy minimum.

The ENM representation is readily scalable to any level of coarse-graining and requires very few parameters. The ENM approximates the protein's potential energy as that of a classical network of masses coupled by springs: each node in the network is a CG site, and each edge is a spring. The network topology is defined by the native structure, with edges placed between nodes/sites that lie within a prespecified cutoff distance from each other. Comparisons of predicted rms fluctuations to motions inferred from crystallographic B-factors have identified optimal cutoff distances of 7.3 Å for the GNM and 18 Å for the ANM, provided that nodes are identified by the C^α-atoms.^78,194 As to the spring constants, the simplest ENMs use a uniform force constant for all interactions; Hinsen proposed using a force constant that decays rapidly with distance.⁷⁴ Sen and Jernigan empirically investigated how the force constants should vary with the residues’ coordination numbers.¹⁹⁵ The adoption of stiffer springs for sequentially neighboring residues¹⁹⁶ or amino acid-specific force constants^197,198 has been shown to improve the agreement with experiments.

The choice of the specific spring constants has little, if any, effect on the global modes. The global modes of motion are widely recognized to be intrinsic properties of the 3D shape of the protein and have been verified in several studies to be insensitive to model parameters^61–66 and almost identically reproduced at various hierarchical levels of resolutions.^45,61,199 The robustness of global modes permits us to utilize ENMs in the study of membrane proteins. One might conceivably adopt different force constants for the internal and interfacial regions of membrane proteins and even differentiate between the interactions with lipid molecules and those with water molecules in the EC or CP regions. However, as will also be illustrated below, comparisons of ENM results with those obtained from full atomic NMAs conducted in the presence of explicit water/lipid molecules have shown that the global modes of membrane proteins are essentially dictated by the protein architecture/fold/shape, similar to the cases for other proteins, and are robust to small variations in the EN topology and environmental effects. Furthermore, the structural changes along the global modes are observed to correlate well with those experimentally observed for particular membrane proteins that are structurally characterized in different states (e.g., apo vs ligand-bound forms).

Several ENM servers have been developed to date, which permit users to readily retrieve results based on the ENMs and their extensions to several applications.^{78,186,200–205} Below we present the theory and assumptions underlying commonly used ENMs, and sections 3 and 4 will illustrate their applications and extensions.

2.3.1. Gaussian Network Model

The GNM is based on the assumption that all residue fluctuations (and inter-residue distances) are Gaussianly distributed around their equilibrium coordinates,^67,68 similar to the statistical mechanical behavior of polymer networks.^69–73 The equilibrium coordinates are identified by the position vectors R_i⁰ of C^α-atoms in the PDB structures. Residue pairs are connected by a spring of force constant γ_ij, provided that they are located within a cutoff distance R_c. The fluctuations in residue positions and their cross-correlations are fully controlled by the N × N Kirchhoff matrix, Γ, defined in terms of the spring constants as

$${\Gamma }_{ij}=-{\gamma }_{ij}$$ (19)

for all i ≠ j, and

$${\Gamma }_{ii}=\sum _j{\gamma }_{ij}$$

where the summation is performed over all off diagonal terms in the row i (or column j). Γ is the N × N counterpart of H. Its pseudoinverse, Γ^–1, scales with the covariance matrix C̄^67,68,206 (see eq 5)

$$\stackrel{‒}{\mathbf{C}}=3k_{\mathrm{B}}T{\Gamma }^{-1}$$ (20)

The above equation is obtained from a statistical mechanical average similar to eqs 15 and 16, where the overall interaction potential is replaced by^207,208

$$V_{\mathrm{GNM}}=\frac{1}{2}\sum _{ij}{\gamma }_{ij}({\mathbf{R}}_{ij}-{\mathbf{R}}_{ij}^0)({\mathbf{R}}_{ij}-{\mathbf{R}}_{ij}^0)=\frac{1}{2}\sum _{ij}{\gamma }_{ij}{\left(\Delta {\mathbf{R}}_{ij}\right)}^2$$ (21)

The above summation is performed over all connected pairs. A major simplification in the GNM is the adoption of a uniform spring constant γ_ij = γ for all residue pairs (i, j) that are connected. As a result, Γ reduces to the adjacency matrix, or Lagrangian, multiplied by γ. Note that the absolute value of γ does not affect the mode shapes (or eigenvectors) but uniformly scales their squared frequencies (eigenvalues).

To date, the GNM has been tested in numerous applications and proven to yield results in reasonable agreement with a wealth of experimental data, including X-ray crystallographic B- factors for amino acids^194,204 and nucleotides,²⁰⁵ root-mean-square deviations in residue coordinates for NMR models,²⁰⁹ H/D exchange free energy costs,²¹⁰ hinge sites in many enzymes and their spatial proximity to catalytic sites,³² NMR order parameters^211,212 and changes in NMR parameters upon ligation,²¹³ highly conserved core amino acids,²⁰⁶ unfolding pathways²¹⁴ and folding nuclei²¹⁵ in proteins (e.g., rhodopsin),²¹⁶ or the common dynamics of families of proteins applied to globins,²¹⁷ and potassium channels.²¹⁸ The good correlation between GNM predictions and experimental data observed in numerous applications despite the simplicity of the model highlights the important role of native contact topology in defining the collective dynamics.

The eigenvalue decomposition of Γ permits us to assess the contribution of different modes to equilibrium dynamics. Γ has N – 1 nonzero eigenvalues, with the lowest corresponding to the first (global) mode. Typical outputs from GNM mode decomposition include the displacement of residues along each mode axis (global hinge sites being located between sequence segments that undergo opposite direction movements along slowest modes), cross-correlations between residues in individual modes, and square displacement profiles of residues driven by individual modes or subsets of modes. No information on the 3-dimensional directions of motions can be obtained with the GNM, because the main ingredient of the theory is an N × N matrix (as opposed to the 3N × 3N Hessian in NMA). The anisotropic network model, described next, is the simplest ENM that provides information on directionalities.

2.3.2. Anisotropic Network Model

The most broadly used ENM is the anisotropic network model.^76–79 The positions of the nodes in the ANM are identified by the coordinates of C^α-atoms for amino acids, and P, C_4*, and C₂-atoms for nucleotides. ANM analysis is simply a CG NMA, subject to the potential^74,75

$$V=\frac{1}{2}\sum _{ij}{\gamma }_{ij}{(R_{ij}-R_{ij}^0)}^2$$ (22)

Note that there is a central difference between V_GNM and the above potential. Here V = 0 if R_ij = R_ij⁰, irrespective of the direction of the corresponding distance vectors. In the case of the GNM, on the other hand, changes in the distance vector incur a potential energy increase, even if the inter-residue distance is maintained (see eq 21). The mean-square fluctuations and cross-correlations predicted by GNM have been shown in comparative studies to yield better agreement with experimental data than the ANM predictions.^{38,39,207,208}

Using the ANM, it is possible to readily write a closed form expression for H using eq 22 in eq 10. The second derivatives of the potential in this case are simply given by

$$\frac{{\partial }^{2}V}{\partial x_i\partial y_j}=-\frac{{\gamma }_{ij}(x_j-x_i)(y_j-y_i)}{R_{ij}^2}$$ (23)

Using the notation x_ij⁰ = (x_j⁰ – x_i⁰) and similarly for y_ij⁰ and z_ij for the three components of the instantaneous distance vector R_ij⁰, the off-diagonal 3 × 3 submatrices of H take in the ANM the form

$${\mathbf{H}}_{ij}=-\frac{{\gamma }_{ij}}{{\left(R_{ij}^0\right)}^2}\left[\begin{array}{ccc}\hfill {\left(x_{ij}^0\right)}^2\hfill & \hfill x_{ij}^0{y}_{ij}^0\hfill & \hfill x_{ij}^0{z}_{ij}^0\hfill \\ \hfill x_{ij}^0{y}_{ij}^0\hfill & \hfill {\left(y_{ij}^0\right)}^2\hfill & \hfill y_{ij}^0{z}_{ij}^0\hfill \\ \hfill x_{ij}^0{z}_{ij}^0\hfill & \hfill y_{ij}^0{z}_{ij}^0\hfill & \hfill {\left(z_{ij}^0\right)}^2\hfill \end{array}\right]$$ (24)

and the diagonal submatrices satisfy the identity

$${\mathbf{H}}_{ii}=-\sum _{j;j\ne i}{\mathbf{H}}_{ij}$$ (25)

This simple expression for H is readily used in NMA to determine the collective dynamics. We note that the amino acid specificity can be included in ENM-based studies by adopting residue-specific force constants, and indeed we have deliberately presented the GNM Kirchhoff matrix and ANM Hessian (respective eqs 19 and 24) in terms of force constants, γ_ij, that are dependent on the identity of the amino acids i and j connected in the network. However, in most applications, γ_ij is taken as a constant, γ, for all pairs of residues connected in the network. Equation 22 with a single parameter γ_ij = γ has been originally used by Tirion for representing interatomic interactions (as opposed to inter-residue interactions considered in all succeeding ENM studies, starting from the GNM) and demonstrating the reproducibility of global modes obtained by detailed atomic force fields.⁵⁸ As mentioned above, the absolute value of γ for a given level representation does not affect the mode shapes (i.e., the eigenvectors, u_k, (1 ≤ k ≤ 3N – 6) of H) but their frequencies, because the eigenvalues of H, λ_k, are proportional to γ. Likewise, the global modes are insensitive to the adoption of residue-specific force constants. A more detailed assessment of the specific role of particular residues in these global modes and the redistribution of interactions (e.g., salt bridges) resulting from global movements, and their effect on allosteric pathways will be given below.

A major utility of the ANM is its ability to generate alternative conformations (substates or microstates) in the close neighborhood of a given structure upon deforming the original structures along the dominant (lowest frequency) modes. Similar to eq 7, the change in the square fluctuations of residue i contributed by the movement along a given mode k is given in terms of the kth eigenvector (u_k) and eigenvalue (λ_k) of H as

$${\phantom{\mid }{\left(\Delta {\mathbf{R}}_i\right)}^2\mid }_k=\mathrm{tr}\left\{{\left[{{\lambda }_k}^{-1}{\mathbf{u}}_k{{\mathbf{u}}_k}^{\mathbf{T}}\right]}_{ii}\right\}$$ (26)

Or the alternative conformations induced upon moving along a given mode are simply³¹

$$\begin{array}{cc}\hfill & {\mathbf{q}}^{\left(k\right)}={({\left({{\mathbf{R}}_1}^{\left(k\right)}\right)}^{\mathrm{T}},\dots ,{\left({{\mathbf{R}}_N}^{\left(k\right)}\right)}^{\mathrm{T}})}^{\mathbf{T}}=\hfill \\ \hfill & {({\left({{\mathbf{R}}_1}^0\right)}^{\mathrm{T}},\dots ,{\left({{\mathbf{R}}_N}^0\right)}^{\mathrm{T}})}^{\mathbf{T}}\pm \mathbf{s}{{\lambda }_k}^{-1∕2}{\mathbf{u}}_{\mathit{k}}\hfill \end{array}$$ (27)

where the coefficient s scales with (k_BT)^1/2. In principle, given the uncertainty in the absolute value of γ, which is reflected on the eigenvalues, a range of s values giving rise to movements comparable in size to those experimentally observed may be generated and used for further calculations (such as generating an ensemble of conformations to be used in docking simulations; see section 4.2). Alternatively, the choice of s may be based on the correlation cosine or overlap²¹⁹

$$I_k=\left(\Delta {\mathbf{q}}_{\mathrm{AB}}•{\mathbf{u}}_k\right)∕\mid \Delta {\mathbf{q}}_{A\mathrm{B}}\mid$$ (28)

between the normalized directional vector u_k and the targeted direction of deformation Δq_AB = q^(B) – q^(A), provided that the goal is to explore the transition from substate A to B. The potential contribution of subsets of modes to such a transition may be deduced from the cumulative overlap [∑_kI_k²]^1/2, where the summation is performed over the subset of modes of interest, usually starting from the lowest-lying modes. Note that this summation is identically equal to unity if it is performed over all 3N – 6 modes/eigenvectors, which form a complete orthonormal basis set for the 3N – 6 dimensional space of conformational changes. Another quantity of interest is the degree of collectivity, κ_k, for mode k, defined as²²⁰

$${\kappa }_k={\mathit{N}}^{\text{-}1}\text{exp}\{-\sum _{i=1}^N\alpha {\phantom{\mid }{\left(\Delta {\mathbf{R}}_i\right)}^2\mid }_k{\phantom{\mid }\text{log}{\left(\alpha \Delta {\mathbf{R}}_i\right)}^2\mid }_k\}$$ (29)

where α is the normalization constant ∑_i α(ΔR_i)²|_k = 1. The form of eq 29 suggests that the degree of collectivity has an entropic significance. The mode with the highest degree of collectivity has the highest entropy: it is distributed over a larger number of residues rather than being orderly confined to a few residues. Lower frequency modes are usually more collective; their high degree of collectivity is indeed needed for triggering cooperative (allosteric) responses. Of interest is to identify the most collective modes toward disclosing potentially functional movements intrinsically favored by the overall structure. Sections 3.1, 3.2, and 3.3 will present applications of the ANM to ion channels, receptors, and transporters, respectively.

2.3.3. Rotating-Translating Blocks Model

A key strength of ENMs is their scalability. Because the interactions are all pairwise and harmonic, once the CG sites are defined, the ENM can be constructed and its Hessian determined. Scalability is particularly useful when modeling very large systems, as it is often the case that the memory required for diagonalizing H exceeds that currently accessible. The slow modes predicted by NMA are robust to the level of coarse-graining, and bundling 20 or more residues into a single CG site still produces slow modes that overlap well with the global modes of the full C^α representation.^61,199 The disadvantage of excessive coarse-graining is the loss of information on the detailed local movements. Although global motions are accurately reproduced with high levels of coarse-graining, reconstructing their details can be daunting. Mixed models^221–223 that use detailed descriptions only for specific regions of interest and CG descriptions for most of the molecule are helpful in retaining desired detail while discarding unnecessary information.

In special cases, the size of the Hessian can be reduced by exploiting the symmetry of the system. Group theoretical calculations were used to represent the Hessian of icosahedral viral capsids in reduced forms.^224–226 Alternatively, by making the assumption that all repeat units in a symmetric system behave identically, one can construct a reduced Hessian that has only symmetrical modes.²²⁷ A more general method for reducing the complexity of H without eliminating any structural detail is the rotations and translations of blocks (RTB)²²⁸ or the block normal mode²²⁹ (BNM) method. This method assumes that the system is constructed of n_b rigid blocks and that the normal modes can be expressed as rigid body rotations and translations of its constituent blocks. Each block has six degrees of freedom (three translational, three rotational). The number of degrees of freedom thus reduces from 3N to 6n_b. The blocks are defined as seen fit for the application at hand: An all-atom protein model might be simplified by assuming that each residue forms a rigid block, or a C^α-only model might be simplified into blocks of secondary structure. Furthermore, the size of the blocks is not restricted: If some domain is known to be particularly rigid, it might be modeled as a block, whereas a small but flexible loop may consist of several blocks. The limitation of the RTB method is that it does not reproduce internal motions of the blocks, so that a great deal of information can be lost if flexible regions with high internal mobility are assumed to be rigid.

Consider a system of N particles that can be collected into n_b < N rigid blocks connected by elastic springs. Define the 3N × 6n_b projection matrix, P, from the 3N-dimensional space of all particles into the 6n_b-dimensional space of rotations and translations of the rigid blocks. The original Hessian is projected into the space of rigid blocks with the transformation

$${\mathbf{H}}_{\mathrm{BLK}}={\mathbf{P}}^{\mathrm{T}}\mathbf{HP}$$ (30)

H_BLK is diagonalized with V_BLK^THV_BLK = Λ_BLK, and the resulting eigenvectors are projected back into the full 3N-dimensional space with the inverse projection V = P^TV_BLK. Thus, 6n_b – 6 normal modes result from the rigid block approximation. Each mode is 3N dimensional.

This method was first applied to small proteins by Durand et al.,²³⁰ who used it to simplify conventional MD force fields by grouping atoms into rigid amino acids. It has since been used to investigate the role of intrinsic dynamics in conformational changes in molecular motors,^229,231 to study the motion of the ribosome,⁸¹ the maturation of cowpea chlorotic mottle virus,²³² and the mechanical properties of icosahedral viral capsids.²³³

2.3.4. Extensions for Treating Environmental Effects

Methods based on ENMs have been enhanced to include the effect of viscous drag,^234–236 and altered to include the environmental perturbations.^28,237 In order to systematically assess the effect of environment on protein dynamics, Ming and Wall^28,238 and Zheng and Brooks²³⁷ proposed a method that relies on separating the problem into a system that contains all relevant degrees of freedom and an environment that contains all other degrees of freedom. The Hessian matrix is then composed of four blocks that relate the system with itself (H_ss), the environment with itself (H_ee), and the system with the environment (H_se),

$$\mathbf{H}=\left(\begin{array}{cc}\hfill {\mathbf{H}}_{\mathrm{ss}}\hfill & \hfill {\mathbf{H}}_{\mathrm{se}}\hfill \\ \hfill {\mathbf{H}}_{\mathrm{se}}^{\mathrm{T}}\hfill & \hfill {\mathbf{H}}_{\mathrm{ee}}\hfill \end{array}\right)$$ (31)

At a minimum of the potential energy, the pseudo-Hessian, H̄, is found as

$$\stackrel{‒}{\mathbf{H}}={\mathbf{H}}_{\mathrm{ss}}-{\mathbf{H}}_{\mathrm{se}}{\mathbf{H}}_{\mathrm{ee}}^{-1}{\mathbf{H}}_{\mathrm{se}}^T$$ (32)

H̄ has the same dimension as H_ss but includes the effects of the environment. Its eigenmodes can be directly compared to those of any system of equal size. This technique has been used to study a range of phenomena, including the coupling of motor protein binding pocket dynamics to global protein structure,²³⁷ substrate induced conformational changes,²³⁹ and allostery in membrane proteins.^29,240

Another method for introducing viscous damping into a vibrational system is to use the Langevin equation,

$$\mathbf{M}\frac{{\mathrm{d}}^2\Delta \mathbf{q}}{\mathrm{d}{t}^2}+\mathbf{Z}\frac{\mathrm{d}\Delta \mathbf{q}}{\mathrm{d}t}+\mathbf{H}\Delta \mathbf{q}+\xi \left(t\right)=0$$ (33)

Here the elements of the friction matrix, Z, provide velocity-dependent damping, and the white noise vector ξ accounts for thermal energy transferred to the molecule from the solvent. The elements of this vector obey the properties

$$\langle {\xi }_i\left(t\right)\rangle =0$$ (34)

$$\langle {\xi }_i\left(t\right){\xi }_j\left(t^{\prime }\right)\rangle =2Z_{ij}{k}_{\mathrm{B}}T\delta (t-t^{\prime })$$ (35)

From eq 34 it is seen that the net external force incident on each CG center averages to zero. Equation 35 indicates that the external force is random in time and provides as much energy as is lost due to damping. The solution to eq 33 for macromolecules was given by Lamm and Szabo²⁴¹ and has further been modified to incorporate the use of rigid blocks.⁸³ When compared with MD, the Langevin models provide insight into the role of friction in protein dynamics.^234,236,242 This technique has been used in conjunction with ENMs to calculate scattering functions of proteins,²⁴³ to investigate the sources behind damping in global protein motions,²⁴⁴ and to estimate the fractional free energy loss in the myosin power stroke.²³⁵

We note that, in a related study,⁸³ the response of membrane-embedded gramicidin A dimer to a sudden velocity kick near one end was explored by examining the time evolution of the molecule, modeled as a collection of harmonic oscillators, under the Langevin equation. Calculations shortly referred to as Langevin dynamics (conceptually similar to NMA, but in the phase space of displacements and momenta) were repeated twice, for the fully atomic model and for a mixed model where the eight indole groups on the molecule were represented by the RTB model. Detailed comparison of the results from the two sets of calculations showed that the results from RTB-Langevin dynamics closely agreed with those from full atomic Langevin dynamics, in support of the adoption of the RTB model for structural elements that are known to be nearly rigid.

3. Intrinsic Dynamics of Membrane Proteins and Their Functional Significance

3.1. Ion Channels

Ion channels are usually accepted to be passive transport proteins: they allow for the conduction of ions when the electrochemical gradients are shifted away from the equilibrium membrane potential. Their functions include establishing a resting membrane potential, controlling cell volume, and regulating the flow of ions across the epithelial cell.⁸⁹ Their role of “facilitator” is achieved by undergoing changes between open and closed conformations. Fundamental questions associated with ion channel functions concern the location of the activation gate as well as the conformational changes that ensure the reversible occlusion of the channel. Here, we will present the NMA results for gramicidin A, potassium channels, and MscL.

We note that, among the global modes predicted for symmetric structures (e.g., homotetrameric potassium channels and homopentameric MscL), a group of modes maintain the structural symmetry; that is, they induce the same type of deformation in all monomers. These modes are nondegenerate; that is, they have unique eigenvalues. Nondegenerate modes play a dominant role in enabling the cooperative transitions of large multimeric, structurally symmetric proteins (or assemblies), by simultaneously exploiting the intrinsic preferences of individual subunits. It will be shown below that such nondegenerate modes are instrumental in initiating the gating process in ion channels.

3.1.1. Gramicidin A

Gramicidin A is the first membrane protein that has been examined by NMA.²⁴⁵ It is also the smallest ion channel known to date: it is a dimer, with each monomer being simply a left-handed helix of 16 amino acids. The two helices are stacked head-to-head and allow for the selective permeation of small cations (e.g., Cs⁺, K⁺) and water molecules through a narrow opening along the helical axes (Figure 7A). The original NMA of GA dimer by Roux and Karplus was one of the earliest studies of membrane proteins, if not the first, that overruled the use of rigid, or nearly rigid, models as appropriate approximations to simulate ion permeation.²⁴⁵ The GA was demonstrated therein to enjoy considerable structural flexibility. Another interesting observation, which probably was one of the early indications of the robustness of low frequency modes, was the observed insensitivity of the low frequency modes to changes in the strength of hydrogen bond interactions. Computations performed by varying the partial charges assigned to carbonyl dipoles showed that the frequencies below 75 cm^–1 remained virtually unchanged; and since these low frequency modes had a dominant effect on the fluctuation behavior, the overall GA dynamics exhibited little dependence on the strength of hydrogen bond interactions.

Extensive computational studies have been performed for gramicidin since then.²⁰ The gating mechanism and the slow conformational transitions undergone by GA have now been identified to be a counter-rotation of the two helices around the pore axis, accompanied by a slight expansion of the channel mouths at the EC and CP ends. To elucidate this mechanism, Miloshevsky and Jordan performed¹⁹² a series of computations, including MC-NMF (see section 2.2.6) coupled with a Metropolis algorithm, full atomic NMA, NMA with the one-residue-per-block RTB approach, and NMA with the ANM (using the elNémo server²⁰²). Notably, the global mode predicted by these models of various complexities was invariably observed to be the counter-rotation of the two helices around the pore axis (Figure 9). The global mode shape obtained with the ANM was reported therein to look “as accurate as that obtained with the all-atom CHARMM22 force field”. It is worth noting, however, that the global mode frequency predicted by the RTB and ANM is significantly larger than that (~6.5 cm^–1) observed in full atomic NMA. Therefore, while the functionally relevant mechanism of motion can be accurately predicted by these CG models, the time scales are not. This is understandable, as the slow modes are dampened by solvent and these CG models do not take account of the viscous drag effect.

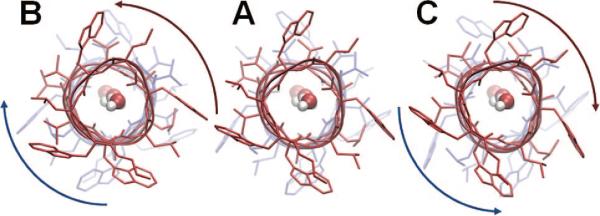
Figure 9.

Counter-rotations of the two helical dimers of gramicidin A, viewed from the EC side along the channel axis. This is the lowest frequency ANM mode of motion of the dimer. It is accompanied by a lateral expansion at the helical termini near the CP and EC regions. This mode was found to be crucially important for the initiation of the dissociation of the monomers needed for ion channel gating. Calculations were performed on an ANM server⁷⁸ (http://ignmtest.ccbb.pitt.edu/cgi-bin/anm/anm1.cgi), using the PDB structure 1JNO. Panel A displays the PDB structure, and panels B and C show two conformations fluctuating in opposite directions along the lowest frequency mode. Water molecules were placed inside the pore using Sybyl 8.3. (figure inspired by ref 192).

The conservation of the mode shape between ANM- and CHARMM-based NMAs is in accord with compelling evidence that the directionality of the structural changes natively accessible to proteins is not altered by the solvent effect or the use of highly simplified potential functions.⁶⁶ Miloshevsky and Jordan concluded that the predicted gating mechanism is an inherent property of GA architecture and should not be changed by the surrounding lipid and water molecules.¹⁹²

It is also worth noting that in contrast to the generally accepted gating model of two states, closed and open, involved in GA's functional transitions, the simulations show that the GA may exist in multiple intermediate states, consistent with experiments.^246,247 Finally, the effective sampling of the transition state using the MC-NMF supports the view that the movements along the global mode predicted by NMA (either full atomic or using ANM) form the crucial step for initiating pore opening. Motions along the lowest eigenvalue modes encountered at the later stages of the transition pathway via adaptive NMF exhibited some departures, however, from those predicted by RTB and ANM for the initial state.

3.1.2. Potassium Channels

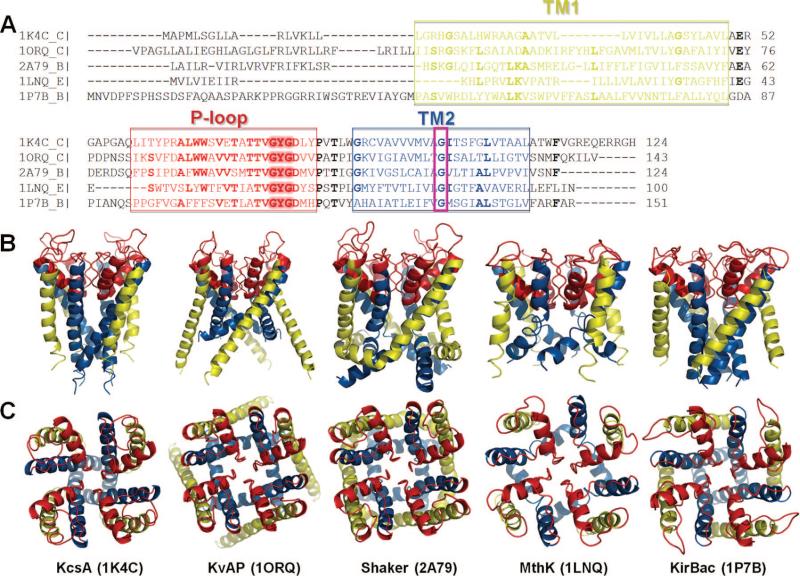
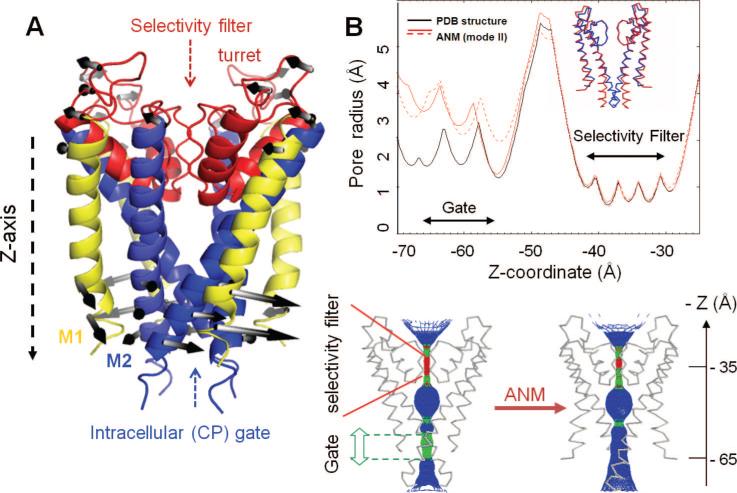
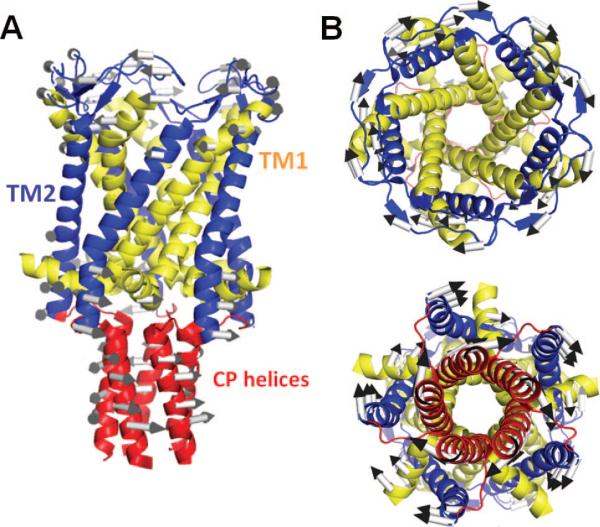
Potassium channels are tetramers, cylindrically arranged to form a bundle of TM helices, enclosing a central pore, or a channel, through which ions are conducted. The pore regions of most K⁺ channels are considered to have similar structure, despite significant differences in sequence (Figure 10). They all contain two TM helices, TM1 (yellow) and TM2 (blue), per monomer, connected by a stretch of 30 residues, known as the P-loop region (red). The P-loop contains three structural elements: a narrow selectivity filter of ~10 Å length near the EC entrance of the pore region; the P-helix, which spans only the upper half of the bilayer; and the exposed loops, also known as the turret, at the EC side. The selectivity filter is followed by a large cavity in the middle of the core region, which ends in a CP gating region, as illustrated in Figure 11A for KcsA, the first K⁺ channel that has been crystallized and structurally resolved.¹¹⁸ The outer helices (TM1) are exposed to the lipid environment; the inner helices (TM2) line the pore. The four P-loops together form the EC vestibule, which opens up into a large central aqueous cavity (of ~10 Å diameter in KcsA).

Figure 10.

Sequence and structure of the pore region of five structurally known K⁺ channels. (A) Alignment of the pore region sequences. The regions corresponding to the helices TM1 and TM2 and the P-loop are indicated by the boxed green, blue, and red letters, respectively. The alignment was performed using ClustalW.²⁴⁸ Fully or highly conserved amino acids are written in boldface. Two regions of interest are the signature motif GYG (highlighted) at the selectivity filter and the conserved glycine on TM2 (e.g., G83 in MthK) enclosed in a magenta box. (B and C) Structural comparison of the pore forming regions aligned in panel A. These are all tetrameric structures. The monomers contain either two TM helices (KcsA, MthK, and KirBac, with PDB ID's 1K4C, 1LNQ, and 1P7B, respectively) colored yellow (TM1) and blue (TM2) or six TM helices (KvAP and Shaker with PDB ID's, 1ORQ and 2A79, respectively). The helices S5 and S6 of KvAP and Shaker are equivalent to the respective helices TM1 and TM2 of the other K⁺ channels and are displayed here, along with the P-loop region, colored red. The channels are viewed from side (B) and from the top (EC region) (B) (see ref 218 for more details).

Figure 11.

Opening up of the potassium channel pore by the global twisting mode. (A) Ribbon diagram of KcsA illustrating the basic structural regions and the motion along the second slowest ANM mode. This is a global twisting (nondegenerate) mode that induces counter-rotations at the EC and CP regions, indicated by the white/gray arrows. (B) Top panel: The pore-radius profile as a function of the pore axis (Z-axis), calculated for the X-ray structure (black curve) and for two conformations visited by fluctuations in opposite directions along the global twisting mode (red curves). The inset shows the backbone trace of two of the monomers in the X-ray structure (blue) and the ANM-predicted conformation (red). The separation between the inner (TM2) helices at the gate is enlarged by about 1.5 Å. Bottom panel: A mesh-wire representation of the channel pore before (left) and after (right) reconfiguration along the second ANM mode. Color code: blue, radius > 3 Å; green, 3 Å > radius > 2 Å; red, radius < 2 Å. For visual clarity, only two monomers of the tetramer are shown (see ref 218 for more details).

The KcsA structure is proposed to be in the closed form.¹⁵⁶ The structure of a calcium-dependent K⁺ channel from Methanobacterium thermoautrophicum (MthK)¹²⁰ is considered to be the open form, containing a wide open intracellular pore of ~16 Å. Since the determination of the KcsA structure,¹¹⁸ many more K⁺ channel structures have been resolved in either open or closed forms (Figure 10).

The availability of these structures allows NMA-based studies exploring the collective movements of the potassium channels and assessing, in particular, the pore opening mechanism. One of the first studies in that direction was a NMA of KcsA by Ma and co-workers, in 2002.²⁴⁹ The study pointed for the first time to the concerted rotational motion of all four TM2 helices as a collective mode favored by the tetrameric structure. More recent examination of a series of potassium channels using the ANM demonstrated that the core domains favor exactly the same mechanism of global motion in all cases, which allows for pore opening.²¹⁸ This global mode of motion is a counter-rotation of the two halves of the molecule about the cylindrical axis of symmetry, akin to a concerted twisting-and-torsion motion of all TM helices. This nondegenerate mode equally distorts all four subunits and confers a remarkable expansion at the gate region (Figure 11B) by swinging the M2 helices away from the cylindrical axis, while the selectivity filter region remains fairly rigid. A striking observation is the appearance of a kink in the TM2 helices which further enhances the pore opening.²¹⁸

Notably, the movement of the M2 helices is consistent with the displacement observed in the MthK crystal structure.¹²⁰ Furthermore, the change in the relative positions of the four TM2 helices at the gate is also consistent with the spin-labeling experiments of Perozo et al.^157,158 and single molecule techniques²⁵⁰ which point to an increase in the distances between the M2 helices (or diameter) at the pore region and a kink at G83 in MthK TM2 (counterpart of G99 in KcsA and G134 in KirBac1.1; see Figure 10A), in accord with ANM results. The comparison of the pore-radius profiles for the wild type protein and its “deformed” form predicted by the ANM in Figure 11B clearly illustrates the increase in the pore-radius at the CP gate region.

The recently resolved X-ray structure of a nonselective cation channel NaK (PDB ID: 3E86) in the open form²⁵¹ provides an elegant example of the role of kink-formation in opening up the cation channel. This structure, when superimposed onto the closed form (PDB ID: 2AHY)²⁵² indicates the selectivity filter to be static during gating,²⁵¹ in agreement with ANM predictions²¹⁸ and SDSL-EPR measurements^157,158 described above. The major conformational change is a helix bending at the highly conserved G87, which acts as a hinge. The counterpart of this glycine, conserved in potassium channels’ TM2 helices (Figure 10), has been pointed out to act as a hinge site,²¹⁸ which also exhibits a kink during the gating motion. Furthermore, a comparison of the open and closed forms of NaK also shows a global-twisting motion around the helical axis of the inner helix,²⁵¹ in agreement with experiments²⁵⁰ as well as ANM predictions.²¹⁸

Miloshevski and Jordan applied their MC-NMF method (successfully used in their earlier examination of GA channel gating; see Figure 9) to KcsA. Their study also confirmed that the gating mechanism of KcsA involves a rotation and unwinding of the TM2 bundle away from the channel axis, leading to an open state with an inner vestibule of ~5–7Å radius, in agreement with the computational models described above.¹⁸⁹ Haliloglu and Ben-Tal²⁵³ also analyzed the transition between the closed and open structures (KcsA and MthK, respectively) using the ANM and in silico alanine-scanning mutagenesis data. Their ANM study again confirmed the global torsion motion as the dominant mechanism of pore opening, while the alanine-scanning mutagenesis study identified a network of energetically and dynamically coupled residues between the selectivity filter and the CP region, consistent with experimental data.²⁵⁴

3.1.3. Mechanosensitive Channels

One of the most basic demands of primitive cells is to tolerate changes in the environment, such as tonicity, without bursting. This function involves regulation of cell volume by ion flow.²⁵⁵ MscL is an ion channel that is able to detect and relieve such tensions in the membrane.^256–259

The crystal structure of the homopentameric MscL from Myobacterium tuberculosis has been resolved at 3.5 Å by Chang and co-workers.¹¹⁷ Each subunit contains three α-helices: two TM (TM1 and TM2) and one CP (Figure 12A). An aqueous cavity opening, approximately 18 Å in diameter, leads from the EC side, through a pore lined with hydrophilic residues narrowing down at the CP side, to an occluded hydrophobic apex, which is proposed to be the gate.¹¹⁷ The five subunits are organized into two domains, the TM and CP domains, both exhibiting a 5-fold symmetry. Their respective diameters are 50 and 15 Å. The pore-lining helix of each subunit, TM1 (yellow in Figure 12A), is connected to the outer helix, TM2 (blue), by an EC loop of 44–68 residues, forming a flap at the EC surface. TM2 is connected to the CP helix by a shorter loop of 10–12 residues. The TM1 and TM2 helical axes are tilted by about 28° with respect to the 5-fold axis while the CP helix is tilted by 15°. The radius of the pore varies between 2 and 18 Å and is partially occluded at the CP region. In the open form, the cross-sectional diameter of the TM domain is estimated to be between 30 and 40 Å,²⁶⁰ suggesting a substantial increase in the size of the channel pore.

Figure 12.

Global dynamics of M. tuberculosis MscL predicted by the ANM. (A) Side view of the pentameric structure, and (B) views from the EC (top) and CP (bottom) regions. The TM helices are colored yellow (TM1) and blue (TM2), which are the inner and outer helices, respectively. CP helices are colored red. The TM and CP helices rotate in opposite directions in the slowest ANM mode. The directions of the arrows in panel B refer to the rotations as viewed from the EC and CP regions, hence their “apparent” rotation in the same direction. We also note that the structure fluctuates between two conformers where the TM helices and CP helices undergo counter-rotations, in either direction; that is, the arrows displayed in the figure represent one of the two opposite direction movements along this mode axis. The ribbon diagrams are generated using the structure (PDB ID: 2OAR) resolved by Chang et al.¹¹⁷

The dynamical properties of MscL from E. coli have been explored by NMA²⁶¹ using the homology models for the closed form based on the M. tuberculosis MscL structure^258,261 and other structural models proposed by Sukharev and co-workers.²⁵⁸ The study identified two major kinds of motions: type I, a symmetrical motion that corresponds to an overall twisting and tilting of all TM helices around the cylindrical axis, exhibited by the first nondegenerate ANM mode, and type II, a global bending, via modes 2 and 3. The “twist to open” motions²⁶¹ are consistent with the iris-like mechanism proposed by Sukharev and co-workers²⁵⁸ to be implicated in the gating process.

Figure 12 displays the structural changes driven by the lowest nondegenerate ANM mode (mode 1), calculated for the M. tuberculosis MscL. As indicated by the arrows, the TM domain undergoes a global twist in this mode, with the EC and CP regions undergoing counter-rotations about the cylindrical axis. The amplitude of the motion is higher at the CP ends than at the EC ends. Calculations performed with and without the CP domain show that the same mechanism of motion is maintained at the TM domain, irrespective of the presence or the excision of the CP domain, except for shifting the location of the hinge region by no more than three or four residues.

A small subset of low frequency modes accessible to the initial substate have been shown in previous work to account for 65% of the conformational change observed between the closed and open states.²⁶¹ The contribution of the individual modes to the transition between two states may be assessed by examining the overlap (eq 28) between the eigenvectors predicted for a given starting conformation and the difference vector Δq_AB = q^(B) – q^(A) between the two end points. Here we focus on the difference vector Δq_OC between an open form (O) modeled by Sukharev et al.²⁵⁸ and the closed form (C). Figure 13 displays the cumulative overlap between Δq_OC and the modes predicted by the ANM. ANM calculations were repeated with the open (red dashed curve) and the closed (blue, solid curve) structures. It is clearly seen that although the pentameric structure has access to 3N – 6 modes (i.e., 1539 modes in the present case, with N = 515), only a small number of modes make a distinctive contribution (see the jumps in the curves). The fact that the transition is achieved by moving in such a small subspace is remarkable. The modes that make the largest contributions are the nondegenerate slow modes. These modes maintain the pentameric symmetry of the channel. In panel B of Figure 13, the motions induced in the second lowest nondegenerate mode (mode 6) are illustrated by the color-coded ribbon diagrams (red, most mobile; blue, most rigid) and arrows along the deformation directions. It can be clearly seen that this motion tends to contract/expand the channel along the cylindrical axis, with the strongest effect exerted on the partially disordered segments exposed to the EC region.

Figure 13.

Cumulative contribution of ANM modes to the structural change between the open and closed forms of MscL. The ordinate displays the cumulative overlap between the ANM modes (eigenvectors) predicted for the starting conformation and the targeted direction of structural change. ANM calculations were performed using either the closed (C) form (blue, solid curve) or open (O) form (red, dashed) as the starting substate. In either case, a cumulative overlap of about 0.8 is achieved by the top-ranking ~120 modes (less than 1/10th of accessible modes). Concrete (stepwise) contributions are made by the nondegenerate modes. The 2nd lowest nondegenerate mode accessible to the closed form (mode 6) is illustrated in panel B. This mode induces a contraction/expansion along the pentameric axis, mainly the portion close to the EC region, as seen from the side (top) and EC (bottom) views of the channel.

3.2. Receptors

3.2.1. Nicotinic Acetylcholine Receptor

Communication between nerve cells takes place at junctions called synapses. The presynaptic cells release, upon activation, neurotransmitters into the synapse, which bind to ligand-gated ion channels (LGICs) on the surface of the postsynaptic cells. Binding of neurotransmitter causes the channels to open, allowing the ions to flow across the postsynaptic cell membrane. The opening and closing of LGICs rapidly convert chemical signals into an electrical output, regulating the flow of information. Mutations in LGICs lead to a number of “channelopathies”, such as congenital myasthenic syndromes, epileptic disorders, and hereditary hyperekplexia.²⁶² Approximately 8.3% of small-molecule drugs target LGICs (Figure 4).

The nicotinic acetylcholine receptor is a member of a superfamily of pentameric transmitter-gated ion channels, also called Cys-loop receptors, which include the serotonin 5-HT3, GABA A and GABA C, and glycine receptors. Members of this superfamily contain a signature loop of 13 residues closed by a disulfide bridge, called the Cys-loop, at the interface between the EC and TM domains of their respective monomers.²⁶³ The nAChR activity is triggered by binding of acetylcholine (ACh) or nicotine.

The structure of nAChR in the closed state has been determined by cryo-EM of tubular crystals grown from the electric organ of Torpedo marmorata.^264,265 The structure consists of five subunits (α, β, δ, α, and γ), two of which (α-subunits) have a slightly distorted (closed or tense, T) conformation compared to the other three (open, relaxed, R), hence the pseudosymmetric organization of the quaternary structure. The receptor is organized into three domains (Figure 7D): a large N-terminal EC domain involved in binding the neurotransmitter, a TM pore domain, and a smaller CP domain. The N-terminal domain of each subunit is composed of an N-terminal α-helix and two β-sheets arranged in a curled β-sandwich connected by the Cys-loop (Figure 14A). The same fold is exhibited by the soluble ACh binding protein (AChBP).²⁶⁶ There are two ACh binding sites at the interfaces between the α–δ and α–γ subunits’ EC domains. The TM domains of individual subunits are composed of four helices, M1–M4, overall forming a cluster of 20 TM helices. The pore lining helix, M2, is tilted radially inward toward the central axis up to the middle of the membrane. The outer helices (M1, M3, and M4) tilt both radially toward and tangentially around the central 5-fold axis.²⁶⁴ Comparison of the ligand-free nAChR and ligand-bound AChBP structures suggests that ACh binding induces a local structural rearrangement (closure of two loops around ACh) to convert the α-subunits to their open (relaxed, R) state, which cooperatively triggers a transient opening of the channel pore at a distance of about 40 Å, thus allowing cations, particularly Na⁺ and K⁺, to pass through.

Figure 14.

Ligand-gated ion channel nAChR structure and dynamics. (A) Structure of the EC and TM domains of nAChR²⁶⁵ (PDB ID: 2BG9). The secondary structure of one of the monomers (α) is colored to display the β-sandwich fold (red) of the EC domain and the four TM helices (M1–M4; blue) of the TM domain; and the remaining four monomers are shown in gray. The lowest frequency ANM mode induces a quaternary symmetric twist, as indicated by the arrows shown for monomer α. (B) CP end of TM domain (bottom) and close up view of one of the monomers (monomer α, colored) (top). Red dashed circle indicates the channel pore. Arrows indicate the collective movements of M2 helices along ANM mode 1. Green circles represent the CP end of the M2 helices after deformation along ANM mode 1. (C) Comparison of bacterial homopentameric LGICs ELIC (2VL0) and GLIC (3EAM) shows the contribution of this quaternary twist mode to the conformational changes involved in activation. One subunit (closest to the viewer) is omitted to display the channel pore.

Several models have been proposed for elucidating the gating mechanism of nAChR.^267–272 NMAs performed by different groups for the complete structure of nAChR²⁷⁰ and for the EC-TM domains of the homopentameric α₇ nAChR models based on the nAChR and AChBP structures^271,272 invariably showed that the lowest frequency mode is a concerted quaternary twist with counter-rotations of the EC and CP domains around the 5-fold symmetry axis (Figure 14A). Like all vibrational modes, this global mode gives rise to two sets of conformers, corresponding to positive and negative movements along the mode axis, manifested as opposite torsions in this case. Of these two sets, one is found to induce an opening in the TM channel of nAChR: the counterclockwise torsional rotation of the TM domain accompanied by clockwise rotation of the EC domain when viewed from the CP region. As can be seen in Figure 14B, the five M2 helices lining the pore are displaced slightly away from the center during this particular quaternary twisting. The calculation of the pore size profile along the TM channel (using HOLE²⁷³) shows that a relatively small (up to ~3Å) increase in diameter is induced in the constriction zone, the original value of which is 5.7 Å in the known structure. The diameter of the first hydration shell of a monovalent cation is typically around 8 Å. This small opening of the pore induced by the global mode is thus expected to enable the passage of hydrated cations.²⁷¹

An increase in the pore radius by ~1.5 Å has indeed been suggested by MD and Brownian dynamics simulations to be sufficient to raise the computed conductance to ~22 pS—a value comparable to the experimental measurements for the open channel.²⁷⁴ The above results from NMAs (including those obtained with ENMs) support the view that small but concerted rearrangements of the M2 helices lining the pore readily allow for an expansion of this size in the pore, thus providing an efficient gating mechanism. Concerted rigid-body motions of M2 helices were inferred by Unwin from early comparisons of the original structures at various resolutions.²⁷⁵ Grosman and co-workers made extensive single-channel electrophysiological measurements to analyze the change in the microenvironment of the helices M1, M2, and M3 between the open and closed forms of the channel.^276,277 Mainly, they examined the position-dependent proton transfers (or pK_a shifts) for ionizable residues that have been engineered in the inner faces of these helices. These experiments led them to conclude that nAChR pore dilation involved subtle rearrangements, if any, of these three helices.^276,277 Notably, the twisting mode predicted by the NMA does not necessarily implicate any significant change in the orientation of the M2 helix side chains with respect to the channel lumen but small rotations of about ~15° that presumably induce minimal changes in the exposure of side chains, which may explain the experimental observations. The changes induced by the NMA-predicted quaternary twisting mode, in the exposure of M2 residues’ side chains to the central pore, were indeed pointed out by Changeux and co-workers to be compatible with the experimental data from Grosman and co-workers.²⁷¹

The global twisting-to-open motion of nAChR resembles those observed in other multimeric ion channels, discussed above. The collective modes of the M2 bundle (pore-lining helices) predicted by NMA are also observed in PCA of MD simulation trajectories.²⁶⁸ Conventional MD simulations of 30 ns for nAChR embedded in an explicit lipid bilayer also indicate²⁶⁹ the concerted rotations of M1 and M2 helices accompanying the shrinking of the ACh binding pocket, and the open–close transition of the structure can be driven by introducing a torsional rotation around the pore axis in steered MD. The accord between NMA results for the nAChR, in the absence of a lipid environment, and MD trajectories conducted in explicit water and lipid bilayer corroborates the dominant role of the membrane proteins’ intrinsic features in defining the movements that facilitate essential functions such as gating.

In addition to gating, the mechanism of signal transduction from the ACh binding site to the pore, which presumably triggers the channel gating, has been a topic widely studied by both experiments and computations. In particular, the allosteric roles of individual residues and loops potentially involved in communicating agonist binding have been examined. Sine and co-workers identified, for example, the loops at the interface of the EC and TM domains that are required to couple the ligand-binding and pore domains in the serotonin type-3A receptor²⁷⁸ and identified the key residues within these loops, which signal agonist binding.²⁷⁹ Single-molecule measurements of open-like vs closed-like propensities (in terms of Φ-values) of individual residues at the transition state of the receptor^280,281 suggested a Brownian cascade of domain motions, whereby the transmitter binding domain assumes an open state and the M2 helices move toward the open state in discrete steps. Such a sequential cascade of discrete changes is not compatible with the all-or-none MWC-type allosteric motions predicted by NMA. The normal mode motions in the low frequency regime are smooth and concerted movements that simultaneously engage both the ACh binding and pore domains, rather than gradually progressing from one site to another. More recently, Sine and co-workers showed that the closed-to-open transition of the receptor involves two primed closed states independent of agonist binding.²⁸² The primed closed states elicit short- or long-lived openings. Structural mapping of these states eludes computational studies due to the limitations in the resolution of the structures and those of the computational methods themselves.

The recently resolved X-ray structures of two bacterial homopentameric ligand-gated ion channels shed further light into pore opening/closing mechanisms. These are the closed state structure of the Erwinia chrysanthemi ligand-gated ion channel (ELIC)²⁸³ and two open-state structures of the Gloebacter Violaceus ligand-gated ion channel (GLIC).^284,285 These structures do not include the CP helical bundle but bear EC and TM domains comparable in size and fold to their counterparts in nAChR. In particular, their EC domain superimposes closely with AChBP and with the EC domain of nAChR, except for a missing α-helix. The most striking difference between the ELIC and nAChR structures is at their pore domain: the EC half of the ELIC pore is occluded with Phe246 and Leu239 side chains that narrow down the pore diameter to less than 1 Å, while the remaining CP half is wide open (diameter of 6 Å). The two GLIC structures, on the other hand, are in the open state, being crystallized in the presence of an activating ligand proton. Figure 14C compares the ELIC and GLIC structures after their optimal superimposition. In addition to a symmetric tilt of the pore forming helices, the most visible difference is a quaternary twist similar to that observed in nAChR. Bocquet et al.²⁸⁴ reported that the lowest ENM mode, a quaternary twist of the two domains, explains 29% of the structural difference between the cores of the structures. Overall, these structural data are consistent with a model of pore opening involving a quaternary twist and tertiary deformation.²⁸⁴

3.2.2. Rhodopsin

G-protein coupled receptors constitute one of the largest protein superfamilies in the human genome, with more than 800 members. Among the five families that form this superfamily, the rhodopsin family is the largest, with 701 members.²⁸⁶ All GPCRs share a common architecture of seven TM α-helices (H1–H7) (Figure 7E). They transmit EC signals to the CP region via allosteric movements of TM helices. The resulting changes in the CP surface facilitate G-protein binding and activation, which, in turn, triggers a cascade of cellular responses.^287,288

The vast majority of the structure-based computations for GPCRs have been done using the bovine rhodopsin structure, originally resolved by Palczewski and co-workers.²⁸⁹ In addition to the bundle of seven TM helices, referred to as opsin, the structure contains an 11-cis-retinal (chromophore) deeply embedded in the core (Figure 15A). The EC domain consists of the N-terminus and three interhelical loops EC1–EC3; the CP domain contains three interhelical loops CL1–CL3 connecting respective pairs of helices H1–H2, H3–H4, and H5–H6, and a C-terminal helix H8 that runs parallel to the membrane. The EC domain contains a β-sheet, which serves as a lid to the chromophore binding pocket, stabilized by a highly conserved disulfide bond between Cys110 and Cys187. The retinal, covalently bound Lys296 on H7, undergoes a cis/trans isomerization upon light activation. This gives rise to a local conformational strain that propagates through the concerted rearrangement of the TM helical bundle to the CP domain, inducing an opening at the conserved D(E)RY motif, which is recognized by the G-protein (Figure 15B). The active form, metarhodopsin II, is reached after a series of photointermediates. It binds the heterotrimeric G-protein, transducin, and interacts with several other signaling proteins.

Figure 15.

Rhodopsin structure and its ERY motif at the CP region. (A) Ribbon diagram of the first rhodopsin structure determined by Palczewski and co-workers,²⁸⁹ shown in a lipid bilayer. This is a seven TM helix structure, enclosing a chromophore (cis-retinal, shown in space filling, magenta). The C- and N-termini are labeled as CT and NT, along with some of the TM helices that can be distinguished clearly. Note that there is an eighth helix, at the CP region, that runs parallel to the membrane surface. (B) Enlarged view of the CP region containing the ERY motif (E134–R135–Y137) on the TM helix 3 (or H3), involved in G-protein recognition. (C) Reconfiguration of the ERY-motif-containing domain upon cis–trans isomerization of the retinal induced by light activation, suggested by an ANM analysis⁸⁵ of rhodopsin dynamics.

Recent years have witnessed a remarkable progress in the number of newly solved GPCR structures.²⁹⁰ Comparison of the structures of bovine opsin in its G-protein-interacting form (referred to as opsin*)²⁹¹ and rhodopsin shows, for example, an outward tilt of 6Å in TM6, and pairing of TM5 to TM6, in agreement with aforementioned experimental data and the above computational model proposed for metarhodopsin II. Comparison of the ligand-free opsin²⁹² and opsin*, on the other hand, shows little structural difference, suggesting that the opsin conformational population is shifted toward the activated state in the absence of retinal and G-protein. In addition to opsin structures, the structures of four other unique GPCRs were recently determined,²⁹⁰ including the β₂ adrenergic receptor (β₂AR) structure by the Kobilka lab, an additional β₂AR structure that pointed to the stabilizing role of cholesterol,²⁹⁰ the structures of an antagonist-bound A_2A adenosine receptor,²⁹³ turkey β1-adrenergic receptor,²⁹⁴ and squid rhodopsin.²⁹⁵ All together, these structures provide important information on the divergent EC regions, differences in the ligand binding sites, and convergent features of the TM domains.

The type and extent of conformational changes undergone upon activation of rhodopsin have been extensively examined by various experiments^{128,134,150–155,161,296–298} and computations.^{85,180,216,299–306} GNM and ANM studies^216,300 show that the global mode is controlled by a broad hinge-bending region that includes the chromophore binding pocket and a number of highly constrained conserved residues in the close neighborhood (e.g., E113, T118, E122 on H3, F261 and W265 on H5, Y268 on H6, and C187 on β4) such that the structural changes locally induced upon the isomeric transition of the cis-retinal are efficiently propagated through cooperative rigid-body movements of the TM helices, toward both the CP and EC regions. An effect of these cooperative movements is opening the CP ends of the TM helices 3, 4, and 6, thus exposing the ERY motif at the G-protein binding site (Figure 15C). A model for the Meta II state has been proposed³⁰⁰ by analyzing the lowest ANM modes in conjunction with experimental data. The model was shown to correctly predict 93% of the experimentally observed effects in 119 rhodopsin mutants for which the decay rates and misfolding data have been reported, including a systematic analysis of Cys → Ser replacements.³⁰⁰

With the elucidation of a large number of structures, we are now in a position to examine more closely the correlation between the experimentally observed structural differences and theoretically predicted conformational changes. We performed a PCA of currently available rhodopsin and opsin structures and compared the resulting PC modes to ANM modes. Our data set includes 16 structures, comprised of 14 rhodopsin and two opsin X-ray structures. Out of N = 348 residues, 312 are commonly resolved in the data set of examined structures, excluding the segments 230–240 on CL3, 311–313 between H7 and H8, and 327–348 at the C-terminus. The distribution of the structures along the first two principal modes is shown in Figure 16 panel A. These two modes contribute about 62% and 12%, respectively, to the structural variability in the data set. The PCA clearly separates the structures into two clusters along the first principal axis. These two clusters may be viewed, in a sense, as the two substates illustrated in Figure 2. Notably, the first cluster includes all the 14 rhodopsin structures in the inactive (sub)state and the second, two opsin conformations in the putative active (sub)state. Mode 1 therefore unambiguously distinguishes between these two substates, representative conformations of which are displayed in Figure 16 panel B. The second principal mode, on the other hand, further disperses the structures within the first cluster. This mode essentially refers to the changes in loop conformations and termini orientations. These can be viewed as the microstates in the inactive substate.

Figure 16.

PCA and ANM calculations for rhodopsin. (A) Distribution of 16 X-ray structures in the subspace spanned by the PCA mode directions 1 and 2. These respective modes account for 62% and 12% of the structural variability in the data set. The principal axis 1 differentiates the inactive and (putative) activated structures which are clustered in two distinctive groups, and the PCA axis 2 further differentiates between the structures in the cluster of inactive rhodopsins (B). Superimposition of experimentally determined rhodopsin and opsin structures, indicated by the labels on panel A. (C) Rhodopsin structure generated by deforming the opsin structure along the first principal mode, p₁. (D) Rhodopsin conformation predicted by deforming the opsin structure along the 20 lowest frequency ANM modes. The 14 rhodopsin structures in the analyzed set include, in addition to the ground state²⁸⁹,³⁰⁷–³¹¹ and various photoactivated states, lumirhodopsin,³¹² bathorhodopsin,³¹³ 9-cis-rhodopsin,³¹⁴ photoacivated deprotonated intermediate,³⁰⁹ and thermostabilized mutants.³¹⁰,³¹⁵ These microstates are dispersed along the second principal axis. These calculations have been performed for the C_α atoms only; the remaining backbone atoms were reconstructed with the BioPolymer module of Sybyl 8.3 (Tripos). ANM calculations were performed using the relatively short cutoff distance of R_c = 8 Å, so as to release interhelical constraints.

Rhodopsin thus provides an excellent example of how functional modes can be determined through PCA and NMA. One utility of PCA is to provide us with a simple organization of the ensemble of conformations accessible to a given protein, and this use will become increasingly valuable with the growth in PDB structures for the same protein, hence the development of PCA servers to perform such tasks.⁴⁴ The second utility is to assist in our assessment of the dominant changes in structure, which is usually described by the 3N-dimensional PCA mode 1, p₁, and the corresponding amplitude of motion scales with σ₁^1/2 (see eq 7). Panel C in Figure 16 illustrates how the rhodopsin conformation (red) is closely reproduced upon reconfiguring the opsin structure along p₁. Comparison of the range of the principal axes 1 and 2 in Figure 16 shows that the size of motions along p₁ is at least twice as large as that along p₂. Third, and most importantly, the principal modes may be directly compared with those predicted by NMA. The PCA modes are exclusively based on experimental data for an ensemble of structures, while ANM modes are predicted by the theory for a single structure. Comparison of the two sets can help benchmark the computational predictions, provided that the experimental data set represents a more or less complete ensemble (see, for example, the study performed by the Jernigan lab for HIV-1 protease¹⁹⁰), or consolidate the results, given that both sets involve approximations. In the present case, the set of PDB structures is far from complete. Yet, ANM calculations performed for the two representative structures (labeled) from each cluster showed that p₁ exhibits a cumulative overlap of 0.79, with the first 20 ANM modes intrinsically accessible to opsin, and a cumulative overlap of 0.74, with the first 20 ANM modes accessible to rhodopsin. Thus, 2% of ANM modes in the low frequency regime provide a reasonable description of the change observed experimentally. The reconfiguration predicted by moving the opsin structure along these ANM modes is shown in panel D. These results again confirm the view that the relative movements of the TM helices 5 and 6 observed upon light activation are intrinsic properties encoded in the rhodopsin architecture.

3.3. Transporters

Transporters are generally active carriers. They require an energy-producing process to translocate a substrate against its concentration gradient. Secondary active transporters take advantage of the movement of a solute down a concentration gradient, so as to translocate another substrate across the membrane. Glutamate transporter, discussed below, is an example of such a transporter, where the uphill translocation of glutamate is coupled to downhill Na⁺ transport.

3.3.1. Glutamate Transporters

The concentration of glutamate in the EC space may increase by 10³–10⁴ fold during periods of synaptic activation, and it is critical to have a mechanism in place to clear the excess glutamate, which, otherwise, may have neurotoxic effects. Glutamate transporters clear the excess glutamate molecules. They are located on neurons and glia (Figure 17). Their precise functioning (glutamate uptake and reuptake) is essential not only to protect against excitotoxicity^316,317 but also to regulate glutamatergic signal transmission by preventing sustained activation and desensitization of ionotropic receptors and modulating the activation of metabotropic receptors.³¹⁸ Members of this family, including the human excitatory amino acid transporters (hEAATs), utilize Na⁺-derived electrochemical gradients to transport glutamate, hence their classification as the family of dicarboxylate/amino acid: cation symporters,³¹⁹ also referred to as the glutamate transporter family.³²⁰ Notably, these transporters also function as chloride channels.^321,322

Figure 17.

Release, uptake, and reuptake of glutamate at an excitatory synapse. Upon arrival of an action potential at the presynaptic axon terminus, voltage-sensitive Ca²⁺ channels trigger the fusion of vesicles with the cell membrane to release glutamate molecules in the synaptic cleft. Glutamates bind and activate receptors on the postsynaptic cell membrane. Excess glutamate is cleared by glutamate transporters, which are more abundant and efficacious in the glia in the vicinity of the synapse.

The first member structurally resolved in this family is an archaeal aspartate transporter, Glt_Ph, from Pyrococcus horikoshii.^323,324 Glt_Ph provided for the first time a structural model for gaining insights into the molecular basis of glutamate transport by the human orthologs, hEAAT1–5.³²⁵ The top view (from the EC side) and side view of Glt_Ph can be viewed in the respective Figures 18A and 19B. As can be seen, Glt_Ph is a homotrimer, the three monomers of which are arranged cylindrically to form a bowl-shaped basin of ~50 Å diameter and ~30 Å depth toward the EC surface at the center of the protein. Each subunit is composed of two domains: the N-terminal domain consists of TM1–TM6 (gray in Figure 18A), and the C-terminal core is comprised of the helices TM7 and TM8, and helical hairpins HP1 and HP2 (colored in Figure 18A).³²⁴

Figure 18.

Structure and dynamics of glutamate transporter. (A) The homotrimer, viewed from the EC region. The N-terminal region (TM1–TM6) is displayed in gray; the C-terminal core HP1–TM7–HP2–TM8 is colored yellow–orange–red–violet and labeled in the figure on the right. (B) Snapshots from MD simulations, illustrating the time-resolved recognition and binding events, starting from t = 0, where the substrate is in the aqueous cavity, up to t = 7.5 ns, where the substrate is sequestered at the binding site and remains therein for the remaining duration of the simulation, of ~20 ns.³²⁶ (C) Symmetric opening/closing mode of Glt_Ph, as observed in ANM. The middle diagram displays the Glt_Ph structure viewed from the EC side (PDB: 1xfh); the top and bottom diagrams display the ANM-predicted open and closed conformations, respectively. In the X-ray structure, the basin is exposed to the EC aqueous environment, while in the closed form contacts between neighboring subunits occur (see, for example, the L34 loops colored red).

Figure 19.

Global dynamics of the aspartate transporter Glt_Ph predicted by the ANM. (A) Distribution of square displacements of residues, (ΔR_i)²|₁ + (ΔR_i)²|₂ (see eq 26), induced in the asymmetric stretching–gcontraction mode (a 2-fold degenerate mode). The same profile is induced in all three subunits upon superposition of these two lowest frequency modes, leading to a cylindrically symmetric reconfiguration. Peaks refer to the most mobile residues, and minima to the hinge centers (e.g., Gly144 and T182) controlling the concerted movements of the subunits. The large amplitude swinging movements of the extracellular histidines suggest a possible role in facilitating the attraction of the anions or engulfing them into the central basin. (B) Mechanism of motion in the first nondegenerate ANM mode (see also panel C in Figure 18). The arrows indicate the direction of the concerted movements of the three subunits (note that the third subunit in the back is lightly visible).

We note that TM7 has an unusual structure, with two helical segments connected by a partially unwound conserved motif N₃₁₀MDGT₃₁₄.³²⁴ This motif is in a sense “frustrated”, containing potentially hydrogen-bond-forming groups that lack partners, hence the role of this motif in binding the substrate (confirmed in simulations³²⁶) and the clustering of several conserved residues near this region (Figure 18A). In other words, the irregularity of this helix at its central portion is actually functional. We note that this region is located exactly near the tips of the two loops HP1 and HP2. Another region important in substrate recognition is indeed the serine-rich tip of the HP1 loop, which is in van der Waals contact with the tip of HP2. The amphipathic TM8 helix also shows irregularities, which have been observed in simulations³²⁶ to be involved in substrate binding and channeling.³²⁸ HP8 has indeed been proposed to form a portion of the transport pathway.³²⁰ Intersubunit contacts are confined to the N-terminal domain, suggesting that the three core domains function independently of each other, as also suggested by experiments.³²⁷

We recently examined the substrate recognition and binding events of Glt_Ph by MD runs of tens of nanoseconds.³²⁶ Our simulations clearly showed that the HP2 hairpin acts as an “EC gate”, in accord with the mechanisms inferred³²⁴ from structural data. The fluctuations of this gate between its open and closed substates occur within the time scale of nanoseconds. Figure 18B illustrates the sequence of events observed³²⁶ in a typical run, starting from diffusion of the substrate toward the partially open “gate” and continuing with the recognition of conserved glycines (G354 and G357) at the HP2 tip, gradual insertion into the region between HP1 and HP2, near a conserved 3-Ser motif on HP1, and subsequent stabilization at a site near the unwound portion of TM7. The latter site and geometry are in close agreement with the binding pose experimentally observed³²³ for aspartate in the high resolution structure of Glt_Ph.

These conventional MD simulations thus provided ample information on the early recognition and binding events. However, no substrate translocation could be observed in these simulations. Instead, we performed nonequilibrium steered MD (SMD) simulations,³²⁸ which helped elucidate two substrate translocation pathways, one of which is more readily accessible, along with the key interactions and energy barriers encountered during the translocation. The SMD thus provided information on “slower” events, which would otherwise be inaccessible via classical MD.

Notably, both substrate binding and substrate translocation events examined in these two sets of simulations are local events that involve the core regions in each subunit, and they appeared to occur independently in the three subunits, consistent with experimental observations. There is, however, yet another dimension: the movements that cooperatively engage all three subunits, which may perhaps explain the raison d'être for the functioning of glutamate transporter as a trimer, rather than as three monomeric proteins. ANM analysis of the global dynamics of Glt_Ph yields the movements depicted in Figure 18C as the first nondegenerate mode (mode 3), along with a doubly degenerate asymmetric stretching/contraction mode accessible to the transporter. In mode 3, the three subunits undergo concerted opening/closing movements to alternately expose and cover the central basin. The diagrams in the figure are color coded, with the red portions corresponding to the most mobile regions. The largest movements are undergone in this case by the N-terminal domain residues that are exposed to the EC region and the aqueous basin. It is interesting to note the possible occurrence of intersubunit contacts between the EC-exposed portions of TM8 and HP2 during the concerted movements of the three subunits in this mode. The diagram and arrows in Figure 19 panel B illustrate the same movement, viewed from the side; and Figure 19A displays the corresponding mobility profile (normalized distribution of residue square displacements driven by this mode). G144 and T182 exhibit minimal mobilities. These two residues are located at the base of the aqueous basin on the EC and IC sides, respectively, and are proposed to play a role in modulating the concerted motion of the subunits. The base of the EC vestibule indeed remains rigid and immobile during these movements, which may be a requirement to maintain the integrity of the trimer. As to the peaks in the mobility profile, we note a number of histidines exposed to the EC region. It is interesting to note, in this context, that Vandenberg and co-workers observed that Zn²⁺ ions inhibited the anion conductance of EAAT4 and attributed this inhibition to the binding of Zn²⁺ to His146 and His154 conserved in EAAT1, -2, -4, and -5.³²⁹ Interestingly, these two histidines lie very close, both sequentially and spatially, to the top-ranking residue (His114 in Glt_Ph or Lys152 in EAAT1) in the global mode profile, suggesting that the peak residues observed here could possibly serve as “sensors” for capturing negatively charged substrates.

3.3.2. ATP Binding Cassette Transporter BtuCD

ATP binding cassette transporters mediate the transport of various substrates, including ions, drugs, lipid molecules, and small proteins, across the membranes via an ATP-dependent mechanism.^330,331 BtuCD is a member of the family of ABC transporters that transports vitamin B₁₂ in E. coli, and it has been investigated by both structural and computational studies.

The BtuCD complex, like most ABC transporters, consists of four subunits, arranged as two homodimers: the TM dimer, BtuC, that forms the specific substrate translocation pathway, consisting of 20 TM helices; and the CP dimer, BtuD, composed of two nucleotide-binding domains (NBDs) where the ATP binding and hydrolysis activities take place.^332–334 The TM dimers of ABC transporters usually exhibit little sequence similarity, with their sequence being specific to the particular substrate that they recognize and translocate. The NBDs, on the other hand, are highly conserved, sequentially and structurally. They share the common motifs Walker A and Walker B typical of many ATP-binding domains, as well as a signature sequence, also called the C motif, that completes the ATP binding site at the interface between the two NBDs.

Examination of the crystal structure of BtuCD³³² and MD simulations performed for BtuCD³³⁵ and MalK (an ABC transporter with similar architecture³³⁶) suggests that ATP binding to the BtuD dimer triggers conformational changes that propagate to BtuC. ATP binding induces a closing at the interface between the two NBDs of the BtuD dimer and stabilizes the interactions (or reduces the fluctuations) at the interface, as confirmed by MD simulations³³⁷ of the dimer. However, the extent to which these structural changes occur in the presence of the BtuC dimer has been questioned, given that the MD simulations for the tetramer did not exhibit the decrease in the inter-NBD distance observed upon ATP binding in the BtuD dimer.³³⁷ A related question of interest is the role of BtuF, the protein that delivers the vitamin B₁₂ to the periplasmic entrance of the BtuCD, on the dynamics of the transporter.

NMA of BtuCD dynamics was recently performed by Ma and co-workers toward elucidating the intrinsic dynamics of the transporter.³³⁸ In this study, the lowest frequency modes accessible to the two dimers, BtuC and BtuD, were analyzed separately with ANM, as were those accessible to the tetrameric BtuCD structure (of ~1100 residues). This analysis demonstrated that the lowest mode accessible to the tetramer, ANM mode 1, is a highly cooperative motion that involves the reverse rotations of the two halves of the BtuCD transporter, as illustrated in Figure 20, top panel. Interestingly, the relative movements of the two TM domains in this mode correlate (with an overlap of 0.83, after removing the rigid-body contributions) with the mode 1 accessible to the BtuC dimer alone,³³⁸ suggesting that the intrinsic dynamics of BtuC strongly affects this global mode of the tetramer. This mode was also shown to be insensitive to BtuF capping.³³⁸

Figure 20.

Global dynamics of the ABC transporter BtuCD. Top and bottom panels display the collective motions of the tetramer in the ANM modes 1 and 3, respectively, recently examined by Weng et al. (2008). The color-coded diagrams on the left in both panels display the size of motions (red, most mobile; blue, almost rigid) induced in these modes. The other diagrams display the relative motions of the two TM domains (1, red; 2, yellow) of the BtuC dimer, and the two NBDs (3, blue; 4, green) of the BtuD dimer, that compose the BtuCD tetramer, viewed from the side (middle diagram in top panel) or from the EC region (right diagrams in both panel). The two gates (EC and CP gates) of the substrate (vitamin B₁₂) translocation pore are indicated by the orange arrows in the left diagram of the top panel.

The mechanism of BtuCD mode 1 is more clearly visualized from the side (middle diagram in Figure 20 top panel, obtained by rotating the diagram on the left by 90° around the vertical 2-fold symmetry axis). This view shows that monomers 2 and 4 (belonging to the respective dimers BtuC and BtuD; see labels in panel A) rotate almost rigidly together, while monomers 1 and 3 undergo an opposite rotation with the pivot located near the CP gate of the translocation pathway.³³⁸ As a result, this movement induces a simultaneous shear opening between the pairs of NBDs (3 and 4) or their ATP binding sites and between the pairs of TM domains (1 and 2) near the EC ends of the TM helices, while the CP gate undergoes minimal, if any, displacement (see also the color-coded diagram on the left). Thus, closing of NBDs upon ATP binding is accompanied by a simultaneous closing of the EC pore, which prior to this allosteric effect was sufficiently large to accommodate vitamin B₁₂ entry to the translocation pathway. Thus, Weng et al. proposed that the vitamin B₁₂ molecule is trapped into the periplasmic cavity rather than transported to the CP region, upon ATP binding.³³⁸ Weng et al. further proposed that the conformational change required for substrate translocation and the opening of the CP end of the pore is associated with ATP hydrolysis (rather than ATP binding). In particular, mode 3 has been proposed to contribute largely to the conformational change powered upon ATP hydrolysis. As can be seen in the bottom panel of Figure 20, this mode induces an opening at the pore region of the BtuC dimer. BtuF capping appears to restrict these movements, while another mode (mode 7, not shown) has been pointed out to effectively enable substrate transport. Modes 3 and 7 of the tetramer have been shown to be similar in shape to the lowest two modes favored by the BtuD dimer structure,³³⁸ which supports the significance of these intrinsically accessible modes in mediating the ATP-dependent coupling of the dimers.

4. Conclusion

Over the years, many techniques have been developed to tackle an ever broadening range of problems using NMA in general and ENMs in particular. The linearity of the theory endows it with considerable flexibility, and the clever applications of matrix algebra to NMA have expanded its utility. In particular, ANM and its extensions have been of great use in studying dynamic phenomena that exceed the time or length scales of MD, such as investigations of Megadalton-scale structures’ dynamics,^{64,81,207,232,233,339} exploring the CG transition pathways,^340–346 and studying the effects of crystal packing on protein dynamics.^{194,347–350} Other studies have taken advantage of the computational efficiency of the GNM/ANM to perform serial analyses of large data sets and gain insights into design principles. An example is the colocalization of global hinge sites and catalytic sites in enzymes, which appears to be a mechanism of efficiently coordinating the mechanical and chemical activities of the protein.³² Another example is the intrinsic ability of the proteins in the unbound form to undergo structural changes that are stabilized upon substrate binding.^21,30,351 We presented several applications to membrane proteins in section 3. Below, we present an overview of insights into mechanisms and principles of functional dynamics gained from ENM-based studies (section 4.1) and recent extensions that are anticipated to be exploited and further developed in future studies (section 4.2).

4.1. Robustness and Functionality of Global Modes

4.1.1. Robustness of Global Modes: A Requirement in Evolutionary Selection of Structures

Designable protein structures are usually referred to as structures that are the lowest energy conformer for a multitude of sequences; that is, these structures can usually tolerate sequence substitutions with minimal change in their overall fold. This type of insensitivity to sequence variations is what makes a stable structure, in a sense. But stability does not necessarily imply functional aptitude.

Function, on the contrary, requires a well-defined flexibility and conformational malleability, within a coarse-grained view of the global energy minimum, perhaps evidenced by substates that are accessible via small energy barriers. In the same way that stable structures are those which are insensitive to sequence variations, one can think of functional proteins as those whose dynamics are insensitive to structural details. Indeed, the success of ENM-based NMAs presumably originates from the insensitivity of global modes to structural and energetic details.

The observed robustness of global modes may reflect an evolutionary pressure. Stable structures are those mapped onto by many sequences, according to the designability principle set forth by Wingreen and co-workers.³⁵² Functional structures, on the other hand, are proposed to be those that intrinsically favor the global modes that facilitate/accommodate biological functions such as substrate binding, translocation, or gating by membrane proteins; the global modes are in this case favored, or mapped onto, by the overall architecture despite minor changes/perturbations in structure.

4.1.2. Toward Gaining Insights into Functional Dynamics of Membrane Proteins

Biomolecular dynamics is a complex process. In particular, the transitions between conformational states separated by high energy barriers, such as the folding of proteins, continue to pose a challenging problem—except for small proteins where some success has been recently achieved. The transitions between microstates within a global energy well, or between substates separated by relatively low energy barriers, on the other hand, appear to be a more tractable problem, with the development and applicability of elastic network models and PCA-based methods. The rapidly increasing structural data now permit us to test and improve these coarse-grained models and methods. In the present review, we illustrated the recent applications to membrane proteins, as a group of proteins that are extremely important from biological and pharmaceutical points of view.

These studies provide us with insights into the collective mechanisms of motions preferentially accessed by membrane proteins. A striking observation is the occurrence of a global twisting as a mechanism of pore opening or ligand gating in many membrane proteins. The “twist-to-open” mechanism instrumental in the gating function of most of the membrane proteins discussed here suggests a common mechanism of pore-opening when the pore architecture exhibits a cylindrical symmetry with funnel-like organization of a bundle of helices. Another observation is the high cooperativity of the motions, which becomes even more pronounced by the structural symmetry or multimerization. In this respect, nAchR presents a unique structure, being a heteropentamer. Yet, the dominant mechanism conducive to channel opening is again observed to be a global twist. It is also interesting to note that the transition between the closed and open forms has been observed in many applications, to be realized by a small subset of modes at the low frequency regime, and among them, nondegenerate modes usually provide the most productive paths leading to functional substates in the case of structurally symmetric multimers. The passage between the open and closed forms of the MscL achieved by a few nondegenerate modes is a typical example (Figure 13).

ENM-based NMAs not only provide insights into the most easily accessible movements of quaternary structures but also point to sites that may play a critical role in mediating or propagating allosteric signals. In the same way as there are particular amino acids whose substitution may be deleterious (conserved residues) to stability, there are particular sites on the structure whose perturbation could impair the global dynamics (e.g., hinge sites in the global modes). We have learned that these sites are utilized by proteins to elicit cooperative responses, e.g., ligand binding pockets that efficiently transmit allosteric signals, especially if fueled by the energy released by an exothermic reaction (e.g., ATP hydrolysis) in the vicinity. These sites are referred to as mechanically critical sites³² or sites with a high allosteric potential.^238,239 Not surprisingly, more and more structures show us that active sites, the drug binding sites, or residues that are known to mediate allosteric effects, or ATP binding sites, coincide with, or closely neighbor, such mechanically critical sites. It is clear that an improved understanding of the structural basis for allosteric and chemical communications in these proteins will assist in the rational discovery of drugs against the various channelopathies or signaling diseases.

4.1.3. Many Functional Motions of Membrane Proteins Are Intrinsic to Their 3D Structure, Independent of Membrane Environment

Evidence for the dominance of intrinsic dynamics in defining certain collective motions and/or allosteric mechanisms of membrane proteins (such as gating or signaling), independent of the membrane environment, is provided by the applications presented in section 3.

We began with gramicidin A, for example, in section 3.1.1. The calculations performed by Miloshevsky and Jordan unambiguously demonstrated the equivalence of the NMA results from ENMs and those from full atomic models in the presence of explicit lipid and water molecules subject to the CHARMM22 force field.¹⁹² In particular, the gating mechanism (counter-rotation of the two helices) was concluded to be an inherent property of the GA architecture, independent of surrounding lipid and water molecules. Likewise, the ANM calculations performed for a series of potassium channels by Shrivastava and Bahar²¹⁸ yielded results (cooperative rotational/twisting motions of M2 helices to induce pore opening) in excellent agreement with SDSL EPR data from Perozo's lab^157,158 and confirmed by recent structural data (kink region) determined for a newly resolved cation channel (NaK),²⁵¹ again showing that the rigorous consideration of the native contact topology permits us to predict global movements relevant to function regardless of the potential perturbation of the membrane environment. In the case of nAChR, the quaternary twist model from ANM studies^270–272 not only agrees with the mechanisms inferred from MD and Brownian dynamics simulations^268,269,274 but also compares favorably with the newly elucidated closed and open structures of the ligand-gated ion channels GLIC^284,285 and ELIC.²⁸³ The global movements of the archaeal aspartate transporter Glt_Ph, on the other hand, drive the cooperative opening/closing of the three subunits around the central aqueous basin, which were not observed in tens-of-nanoseconds simulations. The computations with Glt_Ph using MD,³²⁶ steered MD,³²⁸ and ANM indeed provide a nice example of the complementarity of results and the utility of exploiting multiple scale computations. An even better approach is to develop integrated MD-ANM approaches, like the ANM-steered MD applied to rhodopsin,⁸⁵ which simultaneously provided access to global movements while viewing atomic interactions and rearrangements. A striking observation in this case is the close correspondence between ANM modes and the dominant modes derived from the PCA of 16 X-ray structures resolved for rhodopsin in different forms. The fact that a small subset (2%) of ANM modes in the low frequency regime yields an overlap of ×0.75 with the principal modes of deformations derived from experimental data again lends strong support to the physical and biological significance of ANM modes, which are based exclusively on the protein structure, independent of membrane environment.

The mechanisms of collective movements essential to certain functions such as gating or allosteric signaling thus appear to be intrinsic to protein structure, in accord with ENM-based predictions exclusively based on the inter-residue contact topology of the membrane protein. However, the function of membrane proteins involves many other specific and subtle interactions that cannot be studied by CG models and NMA, such as the selection of particular ions at the selectivity filter, recognition and binding of substrate by specific interactions, and the assistance of substrate translocation by cotransported ions. Moreover, ENM-based NMA cannot provide information on the absolute time scales of the movements either, due to lack of a proper consideration of the frictional drag or other environmental factors that may affect the relative frequencies or probabilistic occurrence of different modes of motions. Essentially, the ENM-based studies provide information on the “accessible” most cooperative movements that are selected/recruited functions. However, there also exist several accessible, energetically favorable movements at local scales, including side chain isomerizations or specific reorientations of polar groups, which require full atomistic and, in some cases, even quantum mechanical calculations. Adding to the complexity is the potential coupling between local events and global movements, hence the need for developing multiscale methodologies that take advantage of the capabilities of both MD and NMA.

4.1.4. Entropic vs Enthalpic Effects, or Geometry vs Specificity

It is important to note that ENM-based approaches are based on purely geometric considerations such as inter-residue contact topology or overall shape/architecture of the examined structure. As a result, the predicted movements are those which are entropically favored, as originally proposed for polymeric networks,^69,70 and do not contain contributions from specific (enthalpic) interactions. ENM-based approaches are therefore useful to the extent that geometry or topology plays a dominant role in the process being explored. The machinery of supramolecular systems could be a prime example for processes dominated by collective mechanics, rather than specific/local chemical events. However, in many applications it may be important, if not indispensable, to invoke both effects and adopt hybrid or multiscale approaches. Recent years have indeed seen a large number of studies in that direction, which have been partly reviewed here. Overall, it is important to interpret the ENM-predicted dynamics as one aspect of the complex mechanochemical process, mainly that intrinsically preferred by the particular architecture, in the absence of perturbations from specific intra- and intermolecular effects.

4.2. Extensions of Coarse-Grained NMA and Future Directions

4.2.1. Hybrid Methods That Integrate CG NMA and MD

As discussed above, MD simulations realistically explore, in the presence of explicit solvent and/or membrane, events on the nanosecond time scale for biomolecules of a few hundreds of residues, while their application to larger systems (e.g., multimeric proteins) and longer processes (e.g., of the order of microseconds or slower) suffers from sampling inaccuracies. NMA with ENMs provide an understanding of the global movements of Megadaltons systems, but at the cost of loosing accuracy and specificity at the local scale. The above-described applications of MD and NMA- methods to membrane proteins nicely illustrate the capabilities and limitations of the two sets of computations. For example, the CG modeling and the atomistic simulations of inward rectifying potassium channel Kir3.4.1³⁵³ provided similar pictures of the overall dynamics of the ligand-binding domain, suggesting dimer-of-dimers motion as an intrinsic property of the CP domain of this K⁺ channel. Thus, combining the data from these alternative computational approaches may help consolidate the inferred mechanisms, if a consistent behavior is captured. Likewise, the PCA of MD trajectories generated for BtuCD in a lipid bilayer supports the hypothesis that ATP-binding drives closure of the nucleotide binding domains in BtuD, while the apo state of BtuD randomly switches between open and closed substates,³³⁷ consistent with ANM analysis of the same dimer. It is not generally sufficient, however, to perform and compare two independent sets of computations, such as MD and CG NMA, to make inferences on multiscale dynamics. Instead, there is a need to develop hybrid methodologies or more integrated approaches that exploit the complementary utilities of the two methods and take account of possible couplings between these different scale events.

A new protocol that steers MD along ANM modes has been recently developed to this aim and used to study of the conformational changes associated with photoactivation signal transmission in rhodopsin.⁸⁵ In this method, global conformational changes that are not accessible via conventional MD trajectories can be sampled, while motions and interactions at atomic scale can be observed in the presence of explicit solvent and lipid bilayer. Two stable regions were identified by this method for rhodopsin, one clustered at the chromophore and the second at the CP end of the TMs 1, 2, and 7 (Figure 21). These simulations elucidate the redistribution of the interactions between the retinal and its neighboring residues on H3–H6, induced upon cis → trans isomerization of retinal. Eleven of the 16 residues identified to participate in the central hinge region near the retinal have been tested by experiments and confirmed to play a critical role in stabilizing the activated state. Furthermore, these simulations draw attention to the possible role of water molecules in coordinating the interactions between conserved residues at the CP ends of the helices H1, H2, and H7, illustrated in Figure 21.

Figure 21.

Critical interactions near the chromophore binding pocket and CP ends of TM1, TM2, and TM3 in rhodopsin. The ribbon diagram on the left is color-coded (from red, least mobile, to blue, most mobile) by the RMSDs observed in the positions of residues during ANM-steered MD simulations of rhodopsin activation. Two regions enlarged on the right are distinguished by their highly constrained dynamics: the chromophore binding pocket and the CP end of helices 1, 2, and 7. The tight packing in the former region ensures efficient propagation of the local conformational strains (induced upon cis → trans isomerization of the retinal) to distant regions, including in particular the ERY-binding motif at the CP end of helices H3 and H6 (note the enhanced mobility at this region). Water molecules play an important role in stabilizing the CP ends of TM1, TM2, and TM7. For more details, see ref 85.

Another study in the same spirit is the examination of the allosteric changes in the conformation of BtuCD TMDs. These movements that appear to be induced upon ATP binding to the BtuD dimer have been examined by Tieleman and co-workers using the perturbed ENM (see subsection 2.3.4) and biased MD simulations.²⁴⁰ The results support the MalK model for the transport mechanism; that is, a closure of the nucleotide binding domain upon ATP binding is predicted, which results in closing of the TMD toward the CP side while inducing an opening toward the periplasmic side.

4.2.2. Docking and NMA in Drug Discovery

Understanding the mechanism of interactions between the target protein and a small molecule inhibitor is of crucial importance in drug discovery.¹⁰² Molecular docking is the primary computational tool to model these interactions³⁶² and screen compound libraries of small molecules with potential inhibitory/agonistic/antagonistic activities.³⁶³ There are numerous successful applications of docking to membrane proteins. Predix Pharmaceuticals, for example, targeted five different GPCRs in in silico screens of commercially available libraries and identified 11 compounds per target, with an average hit rate of 17%.³⁶⁴ In another study, Wang and co-workers targeted dopamine (D₃) receptors and identified four compounds that bind at 100 nM levels, with 60% hit rates.³⁶⁵

The ligand-selective conformational heterogeneity of GPCRs has been recognized, however, as a limiting factor in in silico efforts.^287,366 The binding site geometries of GPCRs differ, depending on the functionality and the potency of bound ligands.³⁶⁷ Kinetic measurements and single molecule spectroscopy both reveal that the 7TM helix bundle samples distinguishable conformational states in the absence or presence of ligand, and the populations of these conformational states shift upon ligand binding.^368,369 State-of-art docking programs usually allow for only partial binding site flexibility limited to optimizing a small number of side-chain rotations or short loop conformers. Overlooking such conformational flexibilities hampers the success of in silico drug discovery.

Abagyan and co-workers made prominent contributions to developing algorithms and tools that take account of target protein conformational flexibility,^370,371 which have been successfully applied to GPCRs.³⁷² In particular, a ligand-steered homology modeling approach was developed, which uses existing ligands to shape and optimize the GPCRs binding site.³⁷³ The idea therein is to start with hundreds of crude homology models as probable conformations of the target protein and then filter them based on their interaction energy with known ligands probed by flexible docking and on their ability to detect known ligands in virtual screening tests. The utility of this approach was demonstrated by its application to melanin-concentrating hormone receptor 1, where a 10-fold improvement over random high-throughput-screening was achieved and six novel antagonists were identified. In a similar recently published study,³⁷⁴ β₂AR interactions with agonist/antagonist were examined upon generating multiple conformations of β₂AR. The models were reduced and further refined by flexible docking of selected agonists in the light of mutagenesis data to obtain models that outperformed rhodopsin-based models. In accord with these findings, Kobilka and co-workers reported that rhodopsin-based homology models of β₂AR developed prior to β₂AR structure resolution were more similar to rhodopsin rather to β₂AR,³⁷⁵ stipulating the need to consider more distinctive target conformations.

The generation of multiple conformations for the target protein emerges from the above and other studies^376–381 as an important component of computational tasks for modeling and simulating protein–inhibitor interactions. NMA with ENMs appears to be particularly suitable for generating backbone rearrangements. It suffices to have but one structure to generate a distribution of energetically favorable conformations in its neighborhood. Likewise, the method can be used to refine/broaden an existing collection of conformations.

Figure 22 illustrates three cases where such NMA-based generation of alternative conformers improved the performance of docking simulations. Panel A shows the results for cyclic AMP-dependent protein kinase.³⁸² A ligand binding loop in this protein is known to assume different conformations in the presence of different ligands. Alternative loop conformations favored by the structure were determined in this case by selecting from the ensemble of low-to-medium frequency modes those that specifically induce reorientations in this particular loop. The use of this ensemble in docking simulations was shown to improve the discrimination rate between binders and nonbinders.³⁸² Panel B refers to the study of matrix metalloproteinases inhibitors by Perahia and co-workers.³⁸³ The global mode that directly affects the opening/closing of the ligand binding cavity was identified in this case to be the second lowest mode, and a set of conformations was generated by gradually reconfiguring the protein along that mode. Docking of inhibitors to the resulting target ensemble was shown to improve docking in all cases compared to docking to a single energy-minimized structure. Finally, May and Zacharias used NMA to improve protein–protein and ligand–DNA docking in a number of studies.^379,384,385 Panel C illustrates the application to cyclin-dependent kinase 2.³⁸⁴ An ensemble of ligands were randomly placed in the binding site of the protein in this case, and the protein–ligand interactions were optimized by deforming the protein along the lowest ten modes accessible to the structure.³⁸⁴ The approach improved all poorly docked cases, at only a modest increase in computational cost. Two more studies from Perahia's lab support the utility of NMA-based modeling, one involving a protein that interacts with a membrane protein (CD47 receptor), and the other showing how collective motions (of a synthase) relate to its catalytic activity.^386,387

Figure 22.

Use of NMA in modeling protein–ligand interactions. Alternative conformations for the target protein were generated for (A) cAMP-dependent protein kinase³⁸² (PDB ID, 1JLU; inhibitor PDB ID, 1REK), (B) matrix metalloproteinase-3³⁸³ (PDB ID, 1UEA; inhibitor PDB ID, 1HY7), and (C) cyclin-dependent kinase 2³⁸⁴ (complex PDB ID, 1G5S), by reconfiguring these target proteins along the global modes of motions indicated by the arrows. See text for details.

4.2.3. Normal Modes for Structural Refinement

An obstacle to understanding the chemistry of biological molecules has always been the determination of their structures to atomic precision. Unless a protein readily crystallizes or is sufficiently small to produce a clean NMR signal, its structure cannot be determined to high resolution. In many cases, the structure can be predicted by homology modeling and then refined to locate the optimal conformation for the particular sequence. Feig and co-workers showed³⁸⁸ that a good set of decoy structures against which to refine can be generated by distorting a homologous template along its slowest normal modes. Indeed, because these slowest modes indicate the easiest directions of motion, refinement using normal modes produces higher resolution structures than does refinement using other CG methods or MD.³⁸⁸

Normal modes are also used in refining electron microscopy (EM) structures. The idea is to use structural data available from X-ray crystallography or homology modeling for substructures (e.g., individual domains, subunits, etc.) and exploit their NMA-predicted alternative conformers to optimally fit cryo-EM data for the intact structure. Several methods have been developed for structural refinement using ENMs,^389–395 some of which are available as software packages.^201,396 The basic technique in these approaches is to start with a known high-resolution structure and iteratively alter it along its normal modes, preferably the slow modes, until its structure agrees with the EM density map.

Vector quantization-based techniques have also been used to predict the collective motions of macromolecules from low-resolution structures.^397,398 The underlying idea therein is that an ENM constructed around the EM density map produces the same dynamics as an ENM constructed using the detailed structure that is represented by the density map. The map is divided into a set of discrete points that act as nodes in the ENM, and the global dynamics are calculated with NMA. This technique has been shown to predict motions in accord with experimentally observed fluctuations.³⁹⁹

Recently, the combination of MD and NMA results for DHFR complexed with nicotinamide adenine dinucleotide phosphate by the Perahia lab demonstrated that the inelastic neutron scattering spectrum may reflect proteins trapped in different conformations (at 120 K), in addition to the vibrational modes of different conformations, leading to inhomogeneous broadening of the spectrum.⁴⁰⁰

4.2.4. Exploring Allosteric Transitions in Large Biomolecular Systems

Proteins usually sample multiple substates, prompted by an external event, such as ligand binding or assembly with another protein, especially if an allosteric change in conformation is triggered. The details of the transition from one state to the other are in most cases only marginally understood; the transition likely does not follow a single linear trajectory but instead winds through a complex energy landscape. Nonetheless, these global transitions appear to proceed, or are at least initiated, via the collective global mode directions that are studied with NMA, and it has been shown in many applications that biomolecular structural transitions between functional substates are largely accounted for by a few slow modes. This observation puts ENMs among the primary tools for theoretical studies of transition pathways.

Since NMA is valid only in the local region surrounding a potential energy minimum, its application to nonequilibrium events such as conformational changes must be handled delicately. When studying the simplest case of a system with two stable conformation—call them “A” and “B”—it is assumed that each conformation resides at the bottom of a harmonic potential energy well and that the transition state is sufficiently close to both end points as to be within the range of the harmonic approximation about each conformation. The system can then transition smoothly from the harmonic surface surrounding A to the harmonic surface surrounding B.

An early technique for studying transition pathways using ENMs³⁴⁰ involves constructing two ENMs for the initial conformation (Figure 23). The topology of the first ENM is determined by the contacts in state A, and the topology for the second is determined by the native contacts in state B. The system is initially modeled with the EN for state A only, and the transition proceeds by gradually reducing the effects of the state A EN while increasing the contribution of the state B EN. Throughout the transition, intermediate conformations are calculated by minimizing a cost function based on the instantaneous EN. This method has since been adapted to use rigid clusters or combinations of rigid clusters and pointlike beads.³⁴¹ A related method^342,343 involves constructing an ENM for the initial state only and then slowly perturbing the structure to satisfy known distance constraints from the final structure. A similar “nonlinear” elastic model, in which the modes are continuously modified in a series of small steps through the transition, was used to study the open to closed transition of adenylate kinase.³⁴⁵ All three methods are capable of generating putative transition pathways with low computational cost.

Figure 23.

Schematic representation of the energy landscape for two substates. The cartoon shows the putative free energy landscape around a conformational transition for a two-state system. Both conformations, A and B, are contained within a global free energy well, represented here as the outermost oval. The slowest mode of the well, indicated by the broken blue line, is expected to overlap with the transition between states A and B. Each stable conformation lies at the bottom of its own local well. The transition between states (red dotted line) is expected to proceed along the slowest local mode in the vicinity of each end point. The slow modes accessible to the metastable intermediate conformation between the end points provide further information on the pathway near the transition point.

Another technique, the plastic network model,³⁴⁴ combines the potentials about states A and B into an analytical double-well potential. The transition states are defined as conformations on the cusp between states A and B. This model was also used to investigate the allosteric transition in adenylate kinase. A similar “mixed ENM” was used to investigate the helix-to-sheet transition of the Arc repressor,⁴⁰¹ as well as transitions of kinesin and myosin.²³⁷ The plastic network model was modified⁴⁰² to make the potential a double-well for all interactions. The resulting potential energy landscape is unlike the original but has multiple local extrema. This model, too, was used to investigate the open-to-closed transition of adenylate kinase, revealing an alternative transition pathway. Yet another method, the adaptive ANM of Yang et al.³⁴⁶ gradually moves the structures from both end points along their respective slow modes until a common structure is reached at the assumed transition state. It is also worth noting that not all NMA-based methods of generating transition pathways are strictly analytical. The MC normal mode following method of Miloshevsky and Jordan¹⁹² utilizes normal modes to guide simulations. An advantage of this technique is that it does not require two conformations but generates an approximate potential energy landscape from the initial conformation alone.

Besides the proteins discussed in this review article, there are also other membrane proteins where the normal modes predicted by CG NMA have been observed to correlate closely with experimental observations on gating mechanisms, for example acid-sensing ion channel (Asc1).⁴⁰³ In this very recent study, modes 1 and 3 induce a twisting of the entire TM domain coupled to the motions of a β-turn, which in turn induces an opening of the channel pore. The predicted mechanism is consistent with mutagenesis and electrophysiological experiments. To quote the authors, “This result indicates that the structure of the closed, desensitized state of Asc 1 intrinsically tends to undergo a twisting motion to open the gate”. This study reinforces the point made in this review, namely, the “twisting-to-open” motion is a common mechanism for gating membrane proteins with an inherent cylindrical symmetry.

Biography

Ivet Bahar is the John K. Vries Founding Chair of the Department of Computational Biology, School of Medicine, University of Pittsburgh, and Director of the Joint Ph.D. Program in Computational Biology between Carnegie Mellon University and University of Pittsburgh. She served as an Assistant (1986–87), Associate (1987–93), and Full Professor (1993–2001) at the Chemical Engineering Department of Bogazici University, Istanbul, Turkey, before joining the University of Pittsburgh. Her research areas are biomolecular systems structure, dynamics, and interactions. She authored in over 170 papers in the areas of polymer chemistry, molecular biophysics, and computational structural biology. She has been an elected member of EMBO since 2000, a principal member of the Turkish Academy of Sciences, an elected member of the Biophysical Society Council, and an Executive Committee Member of the International Society of Quantum Biology and Pharmacology.

Timothy Lezon received his B.S. in physics from the University of Illinois at Urbana–Champaign in 1997 and his Ph.D. in physics from the Pennsylvania State University in 2007. His research interests include the application of statistical physics techniques to biological systems, particularly in the development of coarse-grained models for exploring protein structure and dynamics.

Ahmet Bakan received his undergraduate education at Koç University, Istanbul. He is currently pursuing his Ph.D. degree in computational biology at the University of Pittsburgh. His interests focus on protein–ligand interactions, protein dynamics, and the role of dynamics in recognition and binding events.

Dr. Indira Shrivastava is currently a Research Associate at the Department of Computational Biology at the University of Pittsburgh. She received her Ph.D. in Quantum Chemistry from the Department of Chemistry at University of Pune, India, in 1993. She did postdoctoral work at the Indian Institute of Science, Bangalore, EMBL, Heidelberg, and the Structural Biology Unit, at the University of Oxford, and was a visiting fellow at the National Institutes of Health, Maryland. Her research interests include molecular modeling and simulations of membrane proteins to explore functional dynamics of these proteins by an integrated approach of macroscopic, microscopic, and submicroscopic simulations. She dedicates this review article to her father, Mr. Harigovind Shrivastava, upon his 75th birthday.