Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2010 Jan 19;107(5):2147–2152. doi: 10.1073/pnas.0909000107

Mobile elements reveal small population size in the ancient ancestors of Homo sapiens

Chad D Huff a, Jinchuan Xing a, Alan R Rogers b, David Witherspoon a, Lynn B Jorde a,1
PMCID: PMC2836654  PMID: 20133859

Abstract

The genealogies of different genetic loci vary in depth. The deeper the genealogy, the greater the chance that it will include a rare event, such as the insertion of a mobile element. Therefore, the genealogy of a region that contains a mobile element is on average older than that of the rest of the genome. In a simple demographic model, the expected time to most recent common ancestor (TMRCA) is doubled if a rare insertion is present. We test this expectation by examining single nucleotide polymorphisms around polymorphic Alu insertions from two completely sequenced human genomes. The estimated TMRCA for regions containing a polymorphic insertion is two times larger than the genomic average (P < <10−30), as predicted. Because genealogies that contain polymorphic mobile elements are old, they are shaped largely by the forces of ancient population history and are insensitive to recent demographic events, such as bottlenecks and expansions. Remarkably, the information in just two human DNA sequences provides substantial information about ancient human population size. By comparing the likelihood of various demographic models, we estimate that the effective population size of human ancestors living before 1.2 million years ago was 18,500, and we can reject all models where the ancient effective population size was larger than 26,000. This result implies an unusually small population for a species spread across the entire Old World, particularly in light of the effective population sizes of chimpanzees (21,000) and gorillas (25,000), which each inhabit only one part of a single continent.

Keywords: human effective population size, human evolutionary history, Alu, coalescent theory, population genetics

Mobile elements make up about half of the human and primate genomes (reviewed in refs. 1–3). Despite their ubiquity in the genome, mobile element insertion events are rare compared to other types of mutational events. The single nucleotide mutation rate is ≈2.2 × 10−8 per base pair (bp) per generation, or about 130 mutations per birth in humans (4). By comparison, mobile element insertion events are at least three orders of magnitude rarer, with Alu insertion rates estimated at 1 in 21 to 22 births and LINE1 (L1) rates estimated at 1 in 212 births (5, 6). Because of the rarity of mobile element insertion events, they are most likely to be observed in genomic regions that have ancient coalescence times (i.e., deep genealogies).

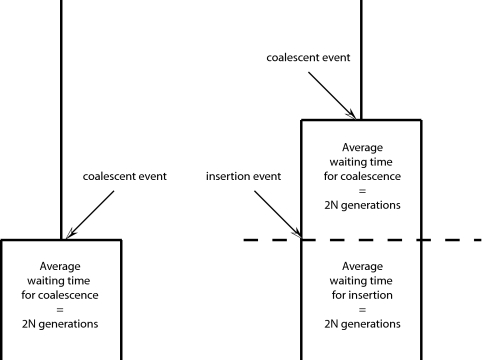
Consider the coalescent processes for different regions of the genome, with a distribution of gene trees of various lengths. When insertion events are very rare, each genealogy contains a single event with probability proportional to the total length of the gene tree. The longer the tree, the more likely it is to contain a polymorphic insertion. Tajima (7) developed theory that showed that the length of a coalescence interval that contains a rare event, such as a mobile element insertion, should be approximately twice as long as a coalescence interval that does not contain a rare event (see Fig. 1 for details). This is because an interval that includes a rare insertion event contains two subintervals, one preceding the insertion and the other following. The lengths of these subintervals are independent, and given the rarity of mobile element insertions, each subinterval has an expected length that approximates that of a random (unconditioned) coalescent interval.

Fig. 1.

Fig. 1.

Open in a new tab

Genealogies conditioned on the presence of a rare polymorphic insertion. In a genealogy of two gene copies from a randomly mating haploid population with a constant size of 2N individuals, a coalescent event occurs with probability 1/2N per generation, and an insertion event with probability 2μ, where μ is the insertion rate at the locus. The probability of an event of either type is 1/2N + 2μ, which is ≈1/2N if μ is small. The mean waiting time until the first event (of either type) is thus ≈ 2N. We are considering only those genealogies in which this first event is an insertion. Consequently, there is a second subinterval to consider. By an identical argument, its expected length is also ≈2N. Therefore, the total length of a genealogy conditioned on the presence of a rare mutation is ≈4N, twice the unconditional expectation of 2N. So in the simple case of two samples in a population of constant size, the presence of a rare polymorphic insertion doubles the expected length of the genealogy.

Here, we use human whole-genome DNA sequence data to demonstrate that Tajima’s prediction is very accurate. In addition, we take advantage of the fact that regions that contain mobile element insertion events provide unique information about ancient population history because of their deep genealogies. Surprisingly, the information contained in just two genome sequences provides sufficient resolution to estimate the effective population size of human ancestors living more than 1.2 million years ago (Mya).

Results

The argument outlined above implies that the expected time to most recent common ancestor (TMRCA) between two samples is twice as long at a genomic region containing a polymorphic mobile element than at a typical genomic locus. However, this result assumes random mating and constant population size. To evaluate the influence of these assumptions, we measure the pairwise nucleotide diversity in the haploid human reference genome (hg18) and the diploid genome of Craig Venter (HuRef). Here, “pairwise” denotes that diversity is measured as a comparison between the reference sequence and one HuRef chromosome at each locus (6). The genome average pairwise nucleotide diversity between HuRef and the human reference sequence is 8.13 × 10−4, corresponding to a TMRCA of 462 thousand years ago (kya). For the 638 HuRef-specific mobile element insertions in our analysis, we observed 9,609 SNPs in the 10-kb regions surrounding the insertions, for a mean pairwise nucleotide diversity of 1.51 × 10−3. This corresponds to a TMRCA of 856 kya, which is 1.85 times the genome average (see Materials and Methods for details). With a genome average nucleotide diversity of 8.13 × 10−4, we expect 5,190 SNPs in a sequence length of 6,380 kb and we observed 9,609. The 99% confidence interval (CI) for nucleotide diversity in regions within 10 kb of an insertion (measured from 100,000 bootstrap samples over 638 loci) was 1.39 × 10−3 to 1.66 × 10−3, which is well above the point estimate for genome-wide nucleotide diversity (8.13 × 10−4).

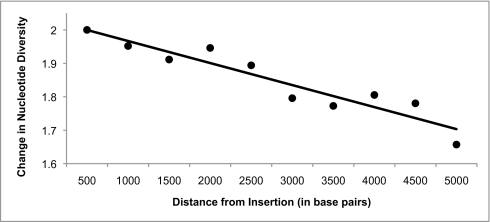
Because we expect about one recombination event per million years in a 1.5-kb region (8), not all sites in the 10-kb region will be in complete linkage disequilibrium with the polymorphic insertion. Sites closer to the insertion site are linked more tightly to the insertion and therefore are a better reflection of its diversity. Therefore, the diversity in the 10-kb region surrounding the insertion underestimates the diversity at the insertion site. Fig. 2 demonstrates this effect by plotting the increase in nucleotide diversity as a function of distance from the insertion. Nucleotide diversity increases linearly with proximity to the insertion (correlation coefficient r = 0.94), so that between 4,500 and 5,000 bases away the nucleotide diversity is only 166% the genome average, but between 0 and 500 bases it has increased to 200%. Therefore, despite the well-known deviations from random mating and constant population size in human history, the observed increase in nucleotide diversity near polymorphic insertions fits the theoretical prediction very well.

Fig. 2.

Fig. 2.

Open in a new tab

Increase in nucleotide diversity between HuRef and the reference assembly in regions near a polymorphic insertion. Nucleotide diversity measurements are from 500-bp regions. Diversity decreases linearly as the region moves away from the insertion as a result of recombination (correlation coefficient r = 0.94). At 4,500 to 5,000 bases from the insertion, the diversity is 1.72 times the genome average, while at 0 to 500 bases the diversity is 1.99 times the genome average.

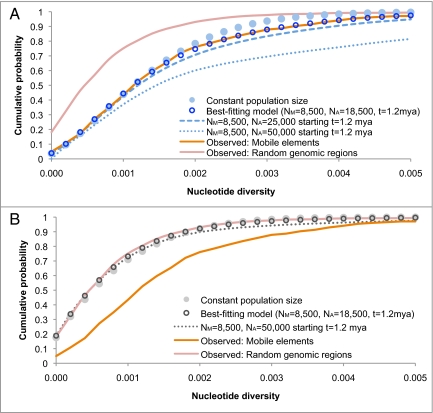
Because genomic regions near polymorphic mobile element insertions have on average twice the nucleotide diversity of a typical region, the genealogies of these regions are on average twice as old. So although the mean TMRCA between HuRef and the reference sequence is 462 kya, the mean TMRCA within 500 bp of a polymorphic mobile element is 924 kya. Because these genealogies extend back almost 1 million years on average, they may contain unique insights about ancient human population history. To explore this possibility, we evaluate a three-parameter demographic model where modern effective population size (NM), ancient effective population size (NA), and time of population size change (t) are allowed to vary, incorporating a recombination rate of 1 cm/Mb. Our test statistic for each parameter set is the likelihood of the observed distribution of nucleotide diversity (orange line in Fig. 3). Our maximum likelihood estimate for the three-parameter model is NA =18,500 before t = 1.2 Mya, with NM = 8,500 (95% CI 8,100–8,750) for the last 1.2 million years (Figs. 3 and 4). Holding NM constant, the 95% confidence region for NA and t is bounded by NA = 14,500–26,000 and t = 0.9–1.5 Mya. The best-fitting model is significantly more likely than one in which the effective population size has always been constant (P = 2.5 × 10−16; Fig. 3). Our estimate for NM is smaller than the worldwide modern human effective population size because it is strongly influenced by the European ancestry of the HuRef genome. However, because NA is an estimate of population size before the divergence of modern human populations, the European origin of the genome samples should have little or no influence on our estimate for NA. Our results demonstrate that the effective population size of human ancestors living over 1 million years ago was 1.7 to 2.9 times greater than it is today.

Fig. 3.

Fig. 3.

Open in a new tab

Cumulative probability distribution of SNP nucleotide diversity between HuRef and the reference sequence in 5,000-bp regions. (A) The distributions from simulated demographic models conditioned on the presence of a polymorphic insertion (demographic models shown in blue). (B) The unconditional distributions of the demographic models (show in gray). The orange line is the observed distribution in regions surrounding polymorphic insertions, while the red line is the observed distribution of 2,432 randomly chosen genomic regions. The best-fitting demographic model is the maximum likelihood estimate among all three-parameter demographic models considered, with a large ancient population size of NA = 18,500 starting t = 1.2 Mya (see Materials and Methods). Because genealogies that contain polymorphic mobile elements are ancient, the best-fitting model is clearly differentiated from the constant population size model in A. In contrast, the two models are nearly indistinguishable in B, demonstrating that the unconditional distribution of nucleotide diversity contains relatively little information about ancient population history, with only very large changes in ancient population size producing a noticeable effect (NA = 50,000). For the constant population-size model, the effective population size is n = 9,244, which is the effective population size for HuRef and the reference sequence based on genome-wide estimates of nucleotide diversity (23). The best-fitting model is significantly more likely than the constant population-size model (P = 2.5 × 10−16, likelihood-ratio test). The differences in the observed distributions for regions surrounding polymorphic insertions and regions chosen at random are highly significant (P < <10−30, χ2; Table S1). Nucleotide diversity is also stochastically greater in regions surrounding polymorphic insertions compared to regions chosen at random (P < <10−30, Mann-Whitney U).

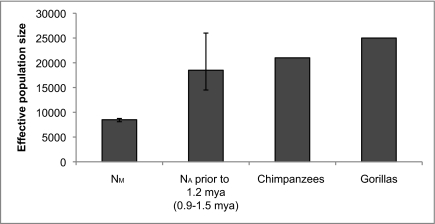
Fig. 4.

Fig. 4.

Open in a new tab

Maximum likelihood estimate and confidence region for ancient human effective population size (NA) under a three-parameter demographic model. Estimates for chimpanzee and gorilla effective population size are from ref. 21. The error bar and date range for NA and t are from the two-parameter 95% confidence region (with NM fixed at 8,500 individuals).

Implicit in the above analysis is the assumption that mutation rates in genomic regions containing polymorphic mobile element insertions are not different from rates in the rest of the genome. Tian et al. (9) reported a 40% increase in nucleotide divergence in regions immediately surrounding indels vs. regions far from indels in a comparison between chimpanzees and humans (see figure 1a in ref. 9). The pattern of excess substitutions is characterized by a 50% increase in the proportion of transversions (see figure 3h in ref. 9). The authors hypothesize that the observed increase in substitution rate is the result of heterozygous indels inducing nucleotide mutations in the surrounding DNA. If this explanation is correct, then the mechanism should apply to heterozygous mobile element insertions as well, which would cause us to underestimate the mutation rate near polymorphic mobile elements and, hence, overestimate effective population size. To test for possible mutagenic effects of mobile elements, we selected 3,705 genomic regions that contain human-specific Alu insertions and compared the nucleotide diversity between the human and the chimpanzee genome in these regions. For the 100-bp region surrounding these insertions, both the nucleotide divergence and the proportion of transversions were near the genome average and significantly lower than the observed values for indels in Tian et al. (9), demonstrating that the mutagenic properties of indels do not apply to Alu elements (Table 1).

Table 1.

Nucleotide divergence and proportion of transversions between chimpanzees and humans in 100-bp regions around lineage specific Alus and indels

Alus Genome average Indels* P(Alus=Indels)†
Nucleotide divergence 0.01346 0.01430 0.0154 P < <10−30
Proportion of transversions 0.3476 0.3452 0.47 P < <10−30
Open in a new tab

*From Tian et al. (9)

†χ2 goodness of fit, two-sided.

Discussion

Because genomic regions with polymorphic mobile elements are among the oldest in the genome, these regions provide windows into ancient population history that are unavailable in other comparably sized samples. For these loci, the distribution of nucleotide diversity is highly reflective of ancient population size, as shown in Fig. 3. One consequence of a larger ancient effective population size is a decrease in the rate of coalescence during the time when the population is large, which is evidenced by an increase in nucleotide diversity. This is visible in Fig. 3A as a decrease in the proportion of genomic regions with intermediate levels of nucleotide diversity. The distributions under the constant population-size model and the observed data clearly diverge where the nucleotide diversity is between 0.002 and 0.004, with 99% of the distribution below 0.004 in the constant population-size model vs. only 94% in the observed data (Fig. 3A). This change in nucleotide diversity can be explained by an increase in ancient effective population size, demonstrated by the best-fitting model in Fig. 3A. From this model, we estimate that ancient human effective population size (NA) was 18,500 before 1.2 Mya, which is roughly twice as large as the modern human effective population size.

Previous studies have suggested that human effective population size has been ≈10,000 for the last 2 million years (10, 11). Our results demonstrate that the effective population size of human ancestors living before 0.9 to 1.5 Mya was between 14,500 and 26,000. Interestingly, our point estimate of an ancient population size of 18,500 is strikingly similar to a previous estimate of modern effective population size from Sherry et al. of 17,500, measured from fixed and polymorphic Alu insertions (12). However, the similarity is coincidental, as the latter estimate was a measure of more recent population size (12). As we have demonstrated here, genomic regions that contain polymorphic mobile elements are on average older than other regions of the genome, and this effect introduced a bias in the previously published analysis, inflating the estimate of recent human effective population size (12).

A model of constant population size is significantly less likely than any of the models in our 95% confidence region; still, the expected 100% increase in nucleotide diversity under the constant population-size model provides an excellent approximation for the observed increase in average nucleotide diversity near polymorphic insertions (Fig. 2). An expected 100% increase in diversity is also a good approximation for the best-fitting three-parameter model, with a 97% increase in expected diversity within 2,500 bp of an insertion. Therefore, for genomic regions containing polymorphic insertions, a 2-fold increase in expected nucleotide diversity in a sample size of two is a prediction that appears robust to changes in population size, at least for the types of fluctuations that are relevant to human evolutionary history.

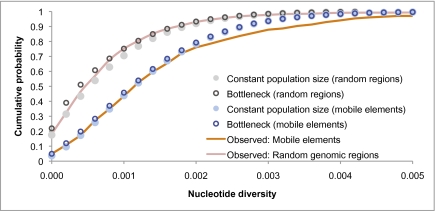
The applicability of a model of constant population size to human demographic history may at first seem surprising, given the ubiquitous genetic signature throughout the human genome of population decline and subsequent expansion between 40,000 and 90,000 years ago (13–15). However, because of the age of genealogies with polymorphic mobile elements, they are not heavily influenced by relatively recent population history. Because a mobile element insertion is unlikely to have occurred in shorter genealogies that coalesced during a population bottleneck, most of the genealogies with polymorphic insertions should be unaffected by the bottleneck. This theory is demonstrated in Fig. 5, which models a bottleneck that reduced the population size by more than 99% for one generation around 90,000 years ago. As shown, this severe bottleneck has little effect on the distribution of nucleotide diversity near a polymorphic insertion.

Fig. 5.

Fig. 5.

Open in a new tab

Effect of a population bottleneck on the distribution of nucleotide diversity. The orange line is the observed distribution in regions surrounding polymorphic insertions; the red line is the observed distribution of 2,432 randomly chosen genomic regions. While the unconditional distribution (random genomic regions) is sensitive to a recent population bottleneck, the effect on the conditional distribution (genomic regions that contain a mobile element insertion polymorphism) is very minor. The effective population size in the constant population-size model is n = 9,244 (Fig. 3). The bottleneck model is identical to the constant population-size model except for a single bottleneck event 3,500 generations ago of size F = 0.085, where F is the inbreeding coefficient (timing and severity of the bottleneck are from parameter estimates of the Out-of-Africa bottleneck in ref. 14).

Our observation that the nucleotide divergence between chimpanzees and humans in regions within 100 bp of a new Alu insertion is not greater than the genome-wide average contrasts with the increased indel-associated divergence observed by Tian et al. (9). Both observations could be accounted for if the mutations associated with small (1–100 bp) indels were generated during the same biochemical events that created the indels themselves, instead of being induced later by some property of heterozygous indels. The processes that result in small indels are probably heterogeneous, ranging from strand slippage (reviewed in ref. 16) to nonhomologous end-joining following double-strand breakage triggered by any of a variety of DNA lesions (reviewed in ref. 17). These processes sometimes involve strand resection and error-prone DNA synthesis or DNA repair, which could occasionally cause a nearby nucleotide mutation. Indeed, nonhomologous end-joining is adaptively used for the purpose of generating such variation during the maturation of the mammalian immune system (reviewed in ref. 18). Alu insertions, on the other hand, are created by a specific, evolved retroposition process that relies on the endonuclease and reverse transcriptase functions encoded by LINE-1 retrotransposons (19). Under this “messy repair” hypothesis, the difference between Alu insertions and the small indels studied by Tian et al. (9) lies in the mechanism of their creation, not in their properties in heterozygotes.

Although our results clearly indicate that the effective population size of human ancestors was once larger than it is in modern humans, the difference is surprisingly modest: With 95% confidence, the effective population size of human ancestors was no greater than 26,000 before 0.9 to 1.5 million years ago. This finding implies an unusually small population size for a species spread across the entire Old World (20), particularly in light of the estimated effective population sizes of chimpanzees (21,000) and gorillas (25,000), which together inhabit only one part of a single continent (21). Possible explanations may include repeated population bottlenecks or periodic replacement events from competing subspecies of Homo. Exploring this problem in greater detail may provide important clues about the evolutionary history of Homo ergaster, Homo erectus, and archaic Homo sapiens.

Materials and Methods

Our analysis is based on a comparison between the human reference genome (hg18) and Craig Venter’s genome (HuRef). Because HuRef is diploid but the reference genome is haploid, our initial sample size was three. This complicates the comparison, as the shape of the gene tree at any given locus is unknown: at some loci both alleles of the HuRef genome share a common ancestor before coalescing with the reference genome; at other loci one allele of the HuRef genome shares a common ancestor with the reference genome before coalescing with the other allele. To simplify the problem, we restrict our attention to haploid contigs in HuRef that contain an insertion not present in the reference genome, so that our sample size is always two.

In previous work, we identified 639 autosomal HuRef-specific retrotransposition insertions, including 574 Alu, 51 L1, and 14 SVA insertions (6). We estimated the TMRCA from SNP data using the pairwise nucleotide diversity between the reference genome and the HuRef genome, with a per nucleotide mutation rate of 2.2 × 10−8 per generation and a 25-year generation time (4). Here, “pairwise” denotes that diversity is measured as a comparison between the reference sequence and one HuRef chromosome at each locus. Using a three-step process to filter out sequencing errors, Levy et al. (22) identified 3,074,686 SNPs between HuRef and the reference sequence out of a total of 2,782,357,138 nucleotides. Of those, 1,450,860 were homozygous in HuRef and 1,623,826 were heterozygous. Thus, the number of SNPs between the reference genome and the average haploid HuRef genome is 2,262,773, for a genome average pairwise nucleotide diversity of 8.13 × 10−4.

To estimate the pairwise nucleotide diversity for the 639 regions with HuRef-specific retrotransposon insertions, we aligned the reference sequence with the HuRef haploid contigs used to identify the insertions, including 5 kb of sequence on each side of an insertion. One contig did not contain enough sequence for the full 10-kb alignment and was excluded from subsequent analysis. We restricted our attention to those SNPs that met the filtering criteria in Levy et al. (22). For SNPs previously identified as heterozygous in HuRef and polymorphic between the reference sequence and HuRef, we evaluated the allelic state of each SNP from the HuRef-reference alignments. For SNPs previously identified as homozygous in HuRef, we used the allelic states reported in Levy et al. (22).

For the comparison between chimpanzee and human, we downloaded full genome alignments from University of California Santa Cruz (UCSC) (http://hgdownload.cse.ucsc.edu) (23). We identified human-specific Alu insertions from RepeatMasker table available from UCSC (http://hgdownload.cse.ucsc.edu) (24).

The test statistic for the three-parameter demographic model is the likelihood of the observed distribution of nucleotide diversity conditioned on the presence of a polymorphic insertion (this distribution is shown as the orange line in Fig. 3). Although our data include 10 kb surrounding each Alu insertion, we used only half of each region in our likelihood calculations: 2.5 kb on either side of each insertion. This allows us to use 5-kb regions in simulations, reducing the computational burden. We simulated a set of genealogies conditioned on the presence of a polymorphic insertion under each three-parameter model to obtain the expected nucleotide diversity distribution for each model. We then estimated the likelihood of the observed distribution of nucleotide diversity for each model from the simulated genealogies, as described below.

To simulate genealogies conditioned on the presence of a polymorphic insertion, we first generated a set of unconditional genealogies using standard coalescence algorithms (25). We then applied importance sampling to these genealogies, with the sampling weight for the ith simulation, Wi, equal to the probability that a single insertion event occurs in genealogy i (26, 27). The log likelihood, gx, that there are x segregating sites in a given mobile element region is estimated by:

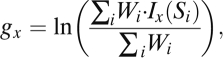graphic file with name pnas.0909000107eq1.jpg

where Si is the number of segregating sites in the ith simulation, and Ix is the indicator function for x, with Ix(Si) = 1 if the simulated number Si of segregating sites equals x, and Ix(Si) = 0 otherwise. Because mobile element insertion events are exceedingly rare, Wi is approximately proportional to Ti, the total number of generations in the genealogy at the insertion site. Therefore, we replace Wi with Ti in the above equation. We estimated g with at least 100,000 simulations for each three-parameter model (Tables S2–S4). We calculated the log likelihood of each three-parameter model, L, by summing over g for all observed mobile element polymorphism regions:

graphic file with name pnas.0909000107eq2.jpg

where kj is the number of nucleotide differences at the jth locus. This calculation assumes that polymorphic insertions are unlinked. To accommodate this assumption, we identified all pairs of insertions that were within 0.05 cm of each other and removed one member of each pair (genome recombination map from ref. 28). We chose 0.05 cm as our cutoff because it corresponds to an r2≤0.2 in human populations (29). In this pruning procedure, we removed 28 insertions, resulting in a dataset of 610 mobile elements for the likelihood calculations.

We established the initial confidence region by comprehensive exploration of the parameter space on a coarse three-dimensional grid. One dimension, representing time, ranged from 0.1 to 2.5 Mya, with grid points separated by 100,000 years. The other two dimensions, representing NA and NM, each ranged from 5,000 to 50,000 individuals, with grid points separated by 5,000 individuals. After establishing the confidence region on this coarse grid, we then refined it by simulating around its edges on a finer grid. On this finer grid, points on the two population size axes were separated by 500 individuals, while points on the time axis were still separated by 100,000 years. In this process, we performed more than 350 million simulations to evaluate more than 2,200 models (see Tables S2–S4 for the estimated likelihood of each model). We derived point estimates for NM, t, and NA, from the model with the maximum likelihood among all models considered. We estimated the 95% confidence region for t and NA from a 2-parameter likelihood-ratio (LR) test between the maximum likelihood model and all other models, which includes all models with LR less than 20 (χ2α=0.05,df = 2<−2ln[LR]). Because of the strong statistical support for NM = 8,500, we could not derive a meaningful confidence interval for NM at a resolution of 500 individuals. Therefore, we separately estimated this confidence interval by evaluating NM in units of 25 individuals, holding NA and t constant at their maximum likelihood estimates of NA = 18,500 and t = 1.2 mya. For all simulation results, the mutation rate was 2.2 × 10−8 per site per generation and the recombination rate was 1 cm/Mb, with a 25-year generation time (4).

Supplementary Material

Supporting Information
supp_107_5_2147__index.html (847B, html)

Acknowledgments

We thank two anonymous reviewers for their helpful comments on previous versions of the manuscript. This work was supported by National Institutes of Health Grant GM-59290 (to L.B.J.), Primary Children’s Medical Center Foundation National Institute of Diabetes and Digestive and Kidney Diseases (DK069513), and The University of Luxembourg–Institute for Systems Biology Program.

Footnotes

The authors declare no conflict of interest.

*This Direct Submission article had a prearranged editor.

This article contains supporting information online at www.pnas.org/cgi/content/full/0909000107/DCSupplemental.

References

  • 1.Belancio VP, Hedges DJ, Deininger P. Mammalian non-LTR retrotransposons: for better or worse, in sickness and in health. Genome Res. 2008;18:343–358. doi: 10.1101/gr.5558208. [DOI] [PubMed] [Google Scholar]
  • 2.Goodier JL, Kazazian HH., Jr Retrotransposons revisited: the restraint and rehabilitation of parasites. Cell. 2008;135:23–35. doi: 10.1016/j.cell.2008.09.022. [DOI] [PubMed] [Google Scholar]
  • 3.Xing J, Witherspoon DJ, Ray DA, Batzer MA, Jorde LB. Mobile DNA elements in primate and human evolution. Am J Phys Anthropol. 2007;(Suppl 45):2–19. doi: 10.1002/ajpa.20722. [DOI] [PubMed] [Google Scholar]
  • 4.Nachman MW, Crowell SL. Estimate of the mutation rate per nucleotide in humans. Genetics. 2000;156:297–304. doi: 10.1093/genetics/156.1.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Cordaux R, Hedges DJ, Herke SW, Batzer MA. Estimating the retrotransposition rate of human Alu elements. Gene. 2006;373:134–137. doi: 10.1016/j.gene.2006.01.019. [DOI] [PubMed] [Google Scholar]
  • 6.Xing J, et al. Mobile elements create structural variation: analysis of a complete human genome. Genome Res. 2009;19:1516–1526. doi: 10.1101/gr.091827.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Tajima F. Evolutionary relationship of DNA sequences in finite populations. Genetics. 1983;105:437–460. doi: 10.1093/genetics/105.2.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Burgess R, Yang Z. Estimation of hominoid ancestral population sizes under Bayesian coalescent models incorporating mutation rate variation and sequencing errors. Mol Biol Evol. 2008;25:1979–1994. doi: 10.1093/molbev/msn148. [DOI] [PubMed] [Google Scholar]
  • 9.Tian D, et al. Single-nucleotide mutation rate increases close to insertions/deletions in eukaryotes. Nature. 2008;455:105–108. doi: 10.1038/nature07175. [DOI] [PubMed] [Google Scholar]
  • 10.Harpending HC, et al. Genetic traces of ancient demography. Proc Natl Acad Sci USA. 1998;95:1961–1967. doi: 10.1073/pnas.95.4.1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Takahata N, Satta Y. Selection, convergence, and intragenic recombination in HLA diversity. Genetica. 1998;102-103:157–169. [PubMed] [Google Scholar]
  • 12.Sherry ST, Harpending HC, Batzer MA, Stoneking M. Alu evolution in human populations: using the coalescent to estimate effective population size. Genetics. 1997;147:1977–1982. doi: 10.1093/genetics/147.4.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Rogers AR, Harpending H. Population growth makes waves in the distribution of pairwise genetic differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
  • 14.Schaffner SF, et al. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Fagundes NJ, et al. Statistical evaluation of alternative models of human evolution. Proc Natl Acad Sci USA. 2007;104:17614–17619. doi: 10.1073/pnas.0708280104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Garcia-Diaz M, Kunkel TA. Mechanism of a genetic glissando: structural biology of indel mutations. Trends Biochem Sci. 2006;31:206–214. doi: 10.1016/j.tibs.2006.02.004. [DOI] [PubMed] [Google Scholar]
  • 17.Lieber MR. The mechanism of human nonhomologous DNA end joining. J Biol Chem. 2008;283:1–5. doi: 10.1074/jbc.R700039200. [DOI] [PubMed] [Google Scholar]
  • 18.Xu Z, et al. DNA lesions and repair in immunoglobulin class switch recombination and somatic hypermutation. Ann N Y Acad Sci. 2005;1050:146–162. doi: 10.1196/annals.1313.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Dewannieux M, Esnault C, Heidmann T. LINE-mediated retrotransposition of marked Alu sequences. Nat Genet. 2003;35:41–48. doi: 10.1038/ng1223. [DOI] [PubMed] [Google Scholar]
  • 20.Klein RG. The Human Career: Human Biological and Cultural Origins. Chicago: University of Chicago Press; 1999. [Google Scholar]
  • 21.Yu N, et al. Global patterns of human DNA sequence variation in a 10-kb region on chromosome 1. Mol Biol Evol. 2001;18:214–222. doi: 10.1093/oxfordjournals.molbev.a003795. [DOI] [PubMed] [Google Scholar]
  • 22.Levy S, et al. The diploid genome sequence of an individual human. PLoS Biol. 2007;5:e254. doi: 10.1371/journal.pbio.0050254. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Chiaromonte F, Yap VB, Miller W. Scoring pairwise genomic sequence alignments. Pac Symp Biocomput. 2002;7:115–126. doi: 10.1142/9789812799623_0012. [DOI] [PubMed] [Google Scholar]
  • 24.Smit AFA, Hubley R. Green P (1996–2007.) RepeatMasker Open-3.0. http://www.repeatmasker.org, accessed July 1, 2009. [Google Scholar]
  • 25.Hudson RR. In: Oxford Surveys in Evolutionary Biology. Antonovics J, Futuyama D, editors. Oxford: Oxford University Press; 1990. pp. 1–44. [Google Scholar]
  • 26.Hudson RR. In: Mechanisms of Molecular Evolution. Takahata N, Clark AG, editors. Sunderland, Mass.: Sinauer; 1993. pp. 23–36. [Google Scholar]
  • 27.Tavaré S, Balding DJ, Griffiths RC, Donnelly P. Inferring coalescence times from DNA sequence data. Genetics. 1997;145:505–518. doi: 10.1093/genetics/145.2.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Frazer KA, et al. International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Consortium TIH International HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_107_5_2147__index.html (847B, html)
0909000107_st01.doc (59.5KB, doc)
0909000107_st02.doc (758.5KB, doc)
0909000107_st03.doc (44KB, doc)
0909000107_st04.doc (1.6MB, doc)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES