Analysis of stability of neural network with inhibitory neurons

Abstract

Phase coding in a neural network composed of neural oscillators with inhibitory neurons was studied based on the theory of stochastic phase dynamics. We found that with increasing the coupling coefficients of inhibitory neural oscillators, the firing density in excitatory population transits to a critical state. In this case, when we increase the inhibitory coupling, the firing density will come into dynamic balance again and tend to a fixed value gradually. According to the phenomenon, in the paper we found parameter regions to exhibit those different population states, called dividing zones including flat fading zone, rapid fading zone and critical zone. Based on the dividing zones we can choose the number ratio between inhibitory neurons and excitatory neurons in the neural network, and estimate the coupling action of inhibitory population and excitatory population. Our research also shows that the balance value, enabling the firing density to reach the dynamic balance, does not depend on initial conditions. In addition, the critical value in critical state is only related to the number ratio between inhibitory neurons and excitatory neurons, but is independent of inhibitory coupling and excitatory coupling.

Introduction

Since the 1960’s, the theory of phase resetting was applied to the studies of physiological rhythms by Winfree, and had obtained lots of improvements (Winfree 1970, 1980), subsequently the theory was extended to study the synergistic effect of brain (Haken 1980, 1996) and to research neural information processing and the evolution of the neural information. The theory was triumphantly used to neurologic disease such as the physical therapy of Parkinson’s disease in Medicine and Biology, and considerable effects had been implemented (Tass 1999; Tass et al. 2003). Furthermore, in recent years the theory of the phase dynamics has been successfully used for studying neural networks and cognitive neurodynamics. The reason why the computational neuroscientists and neurosurgery experts have shown much interest in the theory is mostly owing to its incomparable advantages (Yamaguchi et al. 2004; Alexander et al. 2007; Wagatsuma and Yamaguchi 2005), such as the theory can fully embody the frequency, firing density, mutual coupling and amplitude changes of neural coding in complex network. Besides, it can describe the collective activities in large-scale neural oscillator population and the response to stimulations. Meanwhile it also can simplify the modeling of neural oscillator population under different coupling conditions. Although the simplified model is rough, it has many advantages. First, it can describe the neural activities of neuronal population which consists of large number of neurons. Second, it can reflect the dynamic properties of neural information processing, such as synchronous oscillation, dynamic coupling and rapid convergence. In addition it can express neuronal plasticity and so on. In a word, the simplified model can achieve analogical effect that other neuron models can reach.

The applications of stochastic phase dynamics in cognitive neurodynamics mainly emphasize the study of collective activities in neural oscillator population (Wang and Zhang 2006, 2009, 2003, 2007; Wang and Jiao 2006; Jiao and Wang 2009; Wang et al. 2008, 2006). From the actual researches obtained, we can see that the study on neural oscillator population lean to the study of excitatory neural oscillator population. However, in actual neural system excitatory neurons interact with inhibitory neurons. Although the number of inhibitory neurons is small, they play an extremely important role in synchronous motion of neural oscillator populations and the evolution of neural coding. In our former studies, we proposed a stochastic nonlinear phase dynamic model under coupling action of inhibitory neurons, and analyzed the spontaneous behavior and the dynamic evolution of average number density under the condition of simulation (Liu et al. 2009). In this paper, according to the dynamic model and the phenomenon in spontaneous behavior, we further analyze the stability on phase neural coding in the presence of inhibitory neurons through computer stimulation.

Dynamic model

We assume that there are N neurons in a synchronous neuronal group, where excitatory neural oscillators are considered as a population with eigenfrequency Ω₁, and the number and phase of oscillators are denoted by N₁ and θ₁. Inhibitory neural oscillator is another population composed of N₂ neurons with eigenfrequency Ω₂, oscillator phase is denoted by θ₂ where, N = N₁ + N₂.

For spontaneous behavior, the phase of every oscillator obeys the following phase dynamic equation:

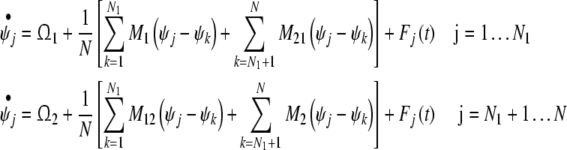where F_j(t) is random force. For the sake of simplicity, F_j(t) is modeled by Gaussian white noise. Thus,

are the mutual coupling interactions between excitatory coupling oscillators and inhibitory coupling oscillators, Ω₁ and Ω₂ are the eigenfrequencies of excitatory population and inhibitory population respectively. Q is the constant noise amplitude..

where,

In our research, coupling parameters C_m, C_1m, G_m, G_1m are all considered to be zero, that is C_m = 0, C_1m = 0, G_m = 0, G_1m = 0. K_m, K_1m, L_m, L_1m denote mth order coupling coefficients between neurons. And the coupling coefficients of excitatory neural oscillators are defined as positive values. And the coupling coefficients of inhibitory neural oscillators are negative, that is K_m > 0, K_1m > 0, L_m < 0, L_1m < 0.

According to phase dynamic equation,we can get the Fokker–Planck equation of probability density f

f expresses the probability density of the oscillators’ phases at time t. Let f = f(ψ₁, ···ψ_N, t)

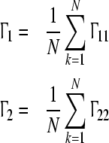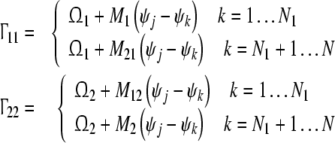The Fokker–Planck equation is a n-dimensional equation. In order to reduce the dimensions and analyze expediently, the number density of the neural oscillators is introduced.

The number density is defined as follows:

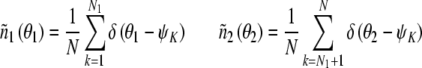The stochastic aspect of the dynamics is taken into account by introducing the average number of the oscillators.

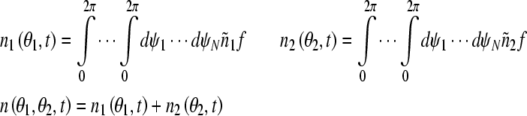The average number density and global average number density meet boundary conditions below.

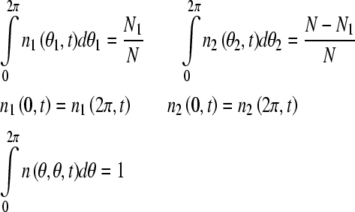Where n₁(θ₁, t) and n₂ (θ₂, t) represent the average number of excitatory neural oscillator population and inhibitory neural oscillator population respectively. According to these equations above, we get the phase dynamic model in spontaneous behavior

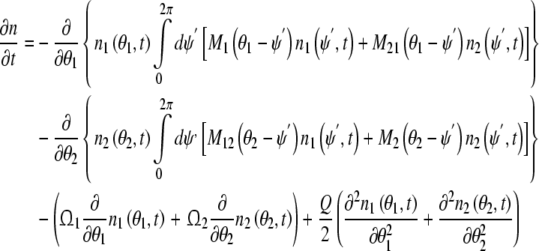Analysis on stability

Critical state

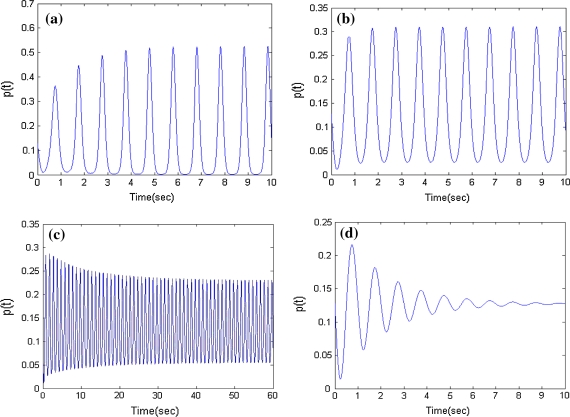
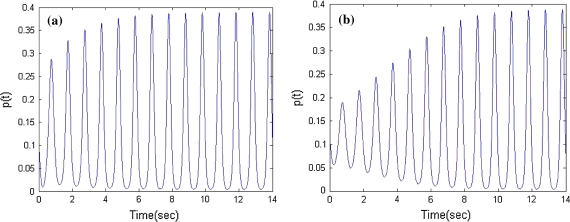
In our former research (Liu et al. 2009), we found that with increasing the coupling coefficients of inhibitory neural oscillators, the average number density shows a uptrend firstly, and then goes through a critical state, finally will be in downtrend (Fig. 1). The amplitude of firing density keeps constant in Fig. 1b. In this case, when decreasing the coupling of inhibitory oscillators, the firing density in excitatory population will rise and arrive dynamic balance (Fig. 1a). In contrast, when increasing the inhibitory coupling, the firing density will decline and reach dynamic balance (Fig. 1c) or tend to a fixed value (Fig. 1d). Here, the state of Fig. 1b is defined as critical state. And the balance value in the state is named as critical value.

Fig. 1.

Firing density in the different inhibitory couplings p(t) = n₁(0,t)

In the paper, the initial conditions were chose as sinusoidal which was given by

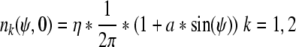Where η is a normalization factor. a is a parameter and according to the nonnegativity of average number density, 0 < |a| ≤ 1 holds. For a = 0, the average number density and firing density are in perfectly desynchronized state, in which neural oscillators trend to uniform distribution and new neural coding can’t emerge. So in this paper a = 0 was replaced by a small value 0.00001.

According to the definition mentioned above, we get balance values and densities of inhibitory coupling in critical state under the condition of different number ratios, such as Tables 1 and 2.

Table 1.

Parameters in critical state when K₁ = 3

K1 = 3
a		N2/N = 0.3	N2/N = 0.25	N2/N = 0.2	N2/N = 0.15	N2/N = 0.1
a = 0.00001	L1	−3.75	−5.07	−7.1	−10.4	−17.2
	Critical value	0.1114	0.1194	0.1273	0.1353	0.1432
a = 1	L1	−3.15	−4.38	−6.2	−9.31	−15.5
	Critical value	0.2703	0.2896	0.3110	0.3275	0.3451

Table 2.

Parameters in critical state when a = 0.5

a = 0.5
K1		N2/N = 0.3	N2/N = 0.25	N2/N = 0.2	N2/N = 0.15	N2/N = 0.1
K1 = 3	L1	−3.63	−4.95	−6.95	−10.25	−16.9
	Critical value	0.1752	0.1881	0.2	0.2132	0.2250
K1 = 2	L1	−1.29	−1.95	−2.95	−4.58	−7.9
	Critical value	0.1757	0.1881	0.2	0.2133	0.2250

N₂ is the number of inhibitory neurons. N is the summation of excitatory neurons and inhibitory neurons. L₁ is the coefficient of inhibitory coupling. K₁ is the coefficient of excitatory coupling

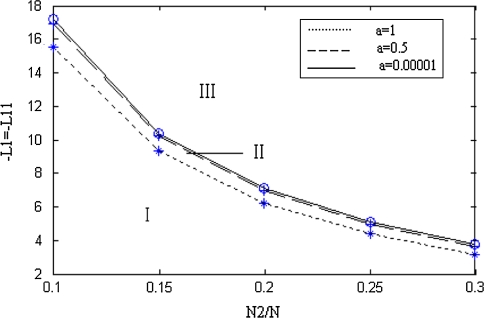
The number density and firing density are in uniform distribution when a = 0.00001. Here, we name the critical line corresponding to a = 0.00001 as totally inhibited critical line. Figure 2 clearly shows that two critical lines divide three continuous regions in the parameter space K₁ = 3. The firing densities tend to uniform distribution in the zoneIII located outside of totally inhibitory critical line. And in the zoneI the firing density rises firstly and goes into balance state. There may be the case that the firing density declines firstly and goes into balance state in the zoneII. And the value of a determines the size of zoneII. Figure 2 describes the maximal region of zoneII. The diving regions can be considered as the base for choosing the number ratio between inhibitory neurons and excitatory neurons in the neural network, and estimating the coupling action of inhibitory population and excitatory population in later research.

Fig. 2.

Zone map when K₁ = 3

Critical state in different excitatory coupling

Tables 3 and 4 show the critical states under the condition of different excitatory coupling. From the tables we can know that under the same excitatory coupling, with increasing the number of inhibitory oscillators, critical values decrease and inhibitory coupling in the critical state also decrease. And this is easily comprehensive. Under different excitatory coupling and the same number ratio, the critical values are the same. If we neglect the errors in stimulation, the deviation between the two critical lines are also basically the same in above tables.

Table 3.

Parameters in critical state when K₁ = 2

K1 = 2
a		N2/N = 0.3	N2/N = 0.25	N2/N = 0.2	N1/N = 0.15	N2/N = 0.1
a = 0.00001	L1	−1.4	−2.1	−3.1	−4.8	−8.2
	Critical value	0.1114	0.1194	0.1273	0.1353	0.1432
a = 1	L1	−0.82	−1.38	−2.2	−3.64	−6.5
	Critical value	0.2699	0.2896	0.3110	0.3277	0.3451

Table 4.

Parameters in critical state when K₁ = 4

K1 = 4
a		N2/N = 0.3	N2/N = 0.25	N2/N = 0.2	N2/N = 0.15	N2/N = 0.1
a = 0.00001	L1	−6.05	−8.1	−11.1	−16.1	−26.2
	Critical value	0.1114	0.1194	0.1273	0.1353	0.1432
a = 1	L1	−5.48	−7.38	−10.2	−14.97	−24.5
	Critical value	0.2706	0.2896	0.3110	0.3279	0.3451

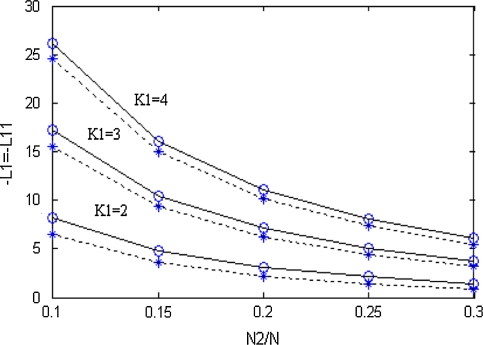
Figure 3 shows the zone maps in different excitatory couplings. From the figure, we can see that with increasing coupling in excitatory population, the size of zoneI increases, but the size of zoneII is changeless. It can be seen that the maximal range of zoneII is independent of excitatory coupling. And according to the figure, we can speculate that when the excitatory coupling is less than a certain value, the size of zoneI will always decrease and maybe reduce to zero, namely the zoneI disappear. Because even if there is no inhibitory neurons, there is a critical value which determine that whether or not the firing density can reach to balance state (Tass 1999).

Fig. 3.

Critical states in different excitatory couplings

Comparing Tables 2, 3 and 4, we can see that the critical values are the same under the same value of a, and Table 1 also validate this fact. According to this fact, it can be seen that the critical value is only related to the number ratio between inhibitory neurons and excitatory neurons under the same initial condition. And the lager the number of inhibitory neurons is, the smaller the critical value is.

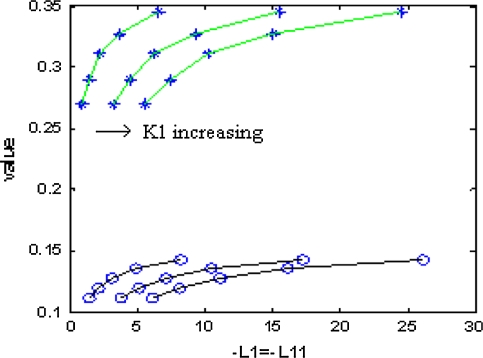
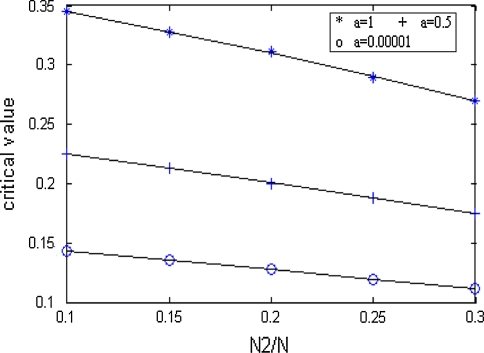
In Figs. 4 and 5, “*” denote critical values for a = 1. And “o” denote critical values for a = 0.00001. “+” denote critical values for a = 0.5. In Fig. 4, the same critical values correspond to the same number ratio. In Fig. 5, there is only one set of curves on number ratio and critical values. And this fact also conforms that critical values are the same under different excitatory couplings. In Figs. 4 and 5, the part beyond the “*” line corresponds to zoneIin Fig. 3, and the part below the “o” line corresponds to zoneIII. The part between the two lines corresponds to zoneII.

Fig. 4.

Relationship between critical value and inhibitory coupling

Fig. 5.

Relationship between critical value and number ratio

The equations of three lines in Fig. 5 are separately given by:

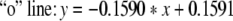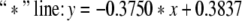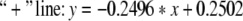If we neglect the errors in stimulation, the three lines above are approximately parallel. Thus it can be seen that the critical value and the number ratio between inhibitory neurons and excitatory neurons meet certain linear relationship.

Balance value changes in subarea

According to above results, we can see that the critical state is related to initial conditions, so the critical values are also influenced. We address here a question of whether balance values in subarea are related to critical condition or not. Figures 6 and 7 validate the doubt. Figures 6 and 7 show a compassion between the two balance values under different initial conditions.

Fig. 6.

Firing density. aa = 1 ba = 0.05

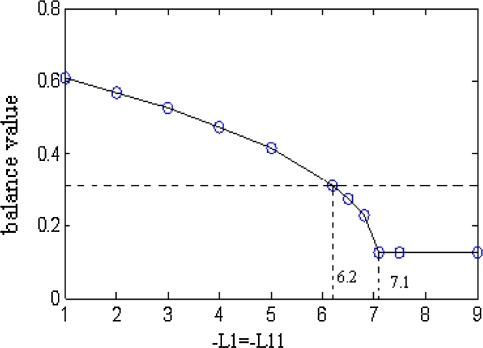
Fig. 7.

Change of balance values in subarea

Comparison with Figs. 6 and 7, we can find that although initial conditions are different, the balance values are the same. And the parameter a is only related to the time when it reaches to dynamic balance. This fact shows that initial conditions don’t influence balance value of firing density. Hence, it can be seen that balance values of firing density are only related to the excitatory coupling, inhibitory coupling and the number ratio between inhibitory neurons and excitatory neurons.

Table 5 shows a set of balance values on firing density in different inhibitory couplings. It shows that the balance values of firing density keep a fixed value (about 0.1273) and change no longer when the absolute value of L₁ is more than 7.1. With a comparison between Tables 5 and 1 and Fig. 2, the inhibitory couplings between −6.2 and −7.1 belong to the range of zoneII. The firing density gets to uniform distribution and tend to a fixed value when the absolute value of inhibitory coupling is more than 7.1.

Table 5.

Balance values under different inhibitory couplings

N2/N = 0.2 K1 = 3
L1	−1	−2	−3	−4	−5	−6.2	−6.5	−6.8	−7.1	−7.5
Balance value	0.6082	0.5685	0.5244	0.4740	0.4131	0.3110	0.2749	0.2283	0.1273	0.1273

The plane in Fig. 7 is divided into two parts by the dashed line. The above part corresponds to zoneI in Fig. 2. The below part correspond to zoneII and zoneIII. Balance value in zoneIII is a fixed value and changes no further. According to Fig. 7, it can be seen that the change of balance values located in above part is flatter. But in the below part balance values change rapidly. So corresponding to balance values, zoneI is named as flat fading zone on balance values of firing density. And zoneII is named as rapid fading zone.

Conclusion

In the paper, according to the conclusion in our former researches, we further analyze the stability on phase neural coding in the presence of inhibitory neurons through computer stimulation. And we study different states which are divided into three zones according to the former researches. ZoneI is a upward balance zone in which the firing density rises firstly and goes into balance state. In zoneII, a downward balance state may exist. And the firing densities tend to uniform distribution in zoneIII. The study on the dividing zones is considered as the reference basis of choosing the number ratio between inhibitory neurons and excitatory neurons in the neural network, and estimating the coupling action of inhibitory population and excitatory population. According to balance values when the firing density reach to dynamic balance, zoneI is named as flat fading zone in which balance values change slowly. zoneII is considered as rapid fading zone in which balance values change rapidly.

The analytical simulation also shows that initial conditions don’t influence balance values of firing density. Furthermore, the values of firing density in critical state are approximately the same under the same initial conditions and number ratio of neurons. That is critical values are only related to the number ratio between inhibitory neurons and excitatory neurons, and is unrelated to inhibitory coupling and excitatory coupling. And the value of firing density in critical state meets a certain linear relationship.