Surface-coupled proton exchange of a membrane-bound proton acceptor

Abstract

Proton-transfer reactions across and at the surface of biological membranes are central for maintaining the transmembrane proton electrochemical gradients involved in cellular energy conversion. In this study, fluorescence correlation spectroscopy was used to measure the local protonation and deprotonation rates of single pH-sensitive fluorophores conjugated to liposome membranes, and the dependence of these rates on lipid composition and ion concentration. Measurements of proton exchange rates over a wide proton concentration range, using two different pH-sensitive fluorophores with different pK_as, revealed two distinct proton exchange regimes. At high pH (> 8), proton association increases rapidly with increasing proton concentrations, presumably because the whole membrane acts as a proton-collecting antenna for the fluorophore. In contrast, at low pH (< 7), the increase in the proton association rate is slower and comparable to that of direct protonation of the fluorophore from the bulk solution. In the latter case, the proton exchange rates of the two fluorophores are indistinguishable, indicating that their protonation rates are determined by the local membrane environment. Measurements on membranes of different surface charge and at different ion concentrations made it possible to determine surface potentials, as well as the distance between the surface and the fluorophore. The results from this study define the conditions under which biological membranes can act as proton-collecting antennae and provide fundamental information on the relation between the membrane surface charge density and the local proton exchange kinetics.

Energy conversion in living cells typically involves proton translocation across a membrane, via proton transporters. These transporters maintain a proton electrochemical gradient utilizing free energy provided, for example by electron transfer or light. The free energy stored in this gradient is used, e.g., for transmembrane transport, motility, or synthesis of ATP by the ATP synthase. Results from a range of studies indicate that the membrane plays an important role in these processes, in addition to serving as a barrier. The membrane surface may also provide a proton link between the various membrane-embedded proteins, where the mere two-dimensional confinement of the reactants can also play a role. Enhancement of reaction rates between solute molecules and their target molecules on the surface and in the vicinity of biological membrane interfaces (e.g. ligand binding to membrane proteins) has been demonstrated in several studies and explained in terms of initial nonspecific binding of the solute molecules to the membrane followed by diffusion along the surface to their target molecules (1–8). Studies on some specific membrane-bound proton pumps, for example cytochrome c oxidase or bacteriorhodopsin (9–12), have revealed higher than diffusion-limited rates of proton uptake (9, 13–15). It has been hypothesized that these proteins have a surface proton-collecting antenna, consisting of negative and buffering groups, aiding the proton uptake (12, 16, 17). Theoretical studies also indicate that the membrane itself can contribute to this proton uptake (18–20). More recently, using fluorescence correlation spectroscopy (FCS), increased protonation rates were observed at membrane interfaces for single fluorophores conjugated to small unilaminar vesicles (SUVs) (21) and for single fluorophores conjugated to membrane-reconstituted cytochrome c oxidase (22). Proton exchange measurements using FCS have several advantages. In particular, the measurements are performed under equilibrium conditions without perturbing the sample, buffering effects of the fluorophores can be neglected due to low fluorophore concentrations, and the measurements reflect the local proton exchange dynamics directly at the site of the fluorophore.

Previous studies (21–22) showed that the enhancement of the protonation rates could be attributed to the proton-collecting antenna effect. However, these investigations were performed only at low proton concentrations (pH > 8), around the pK_a value of the used fluorophore (Fluorescein). In the present study, we included an additional fluorophore, Oregon Green, with a lower pK_a, and extended the measurements to a wider proton concentration range (pH 6–10). This approach allowed us to identify two distinct regimes for the proton exchange rates. In the range of low proton concentrations, the proton exchange rate increased rapidly with increasing proton concentrations, and the slope was consistent with the membrane acting as a proton-collecting antenna for the fluorophore. In contrast, at high proton concentrations the increase in the proton exchange rate was slower and the slope was comparable to that of direct protonation of the fluorophore from the bulk solution. The observed switch from a fast membrane-mediated protonation at low proton concentrations to a protonation increasingly dictated by direct protonation at higher proton concentrations has been predicted theoretically (18–19), but its direct experimental observation as well as the quantitative characterization has not been reported before. The protonation rates of the fluorophores were found to be significantly higher for negatively charged membranes than for neutral membranes and this membrane-charge effect was diminished at high bulk ion concentrations. Additionally, the proton exchange rates at low pH (< 7) were essentially identical for both fluorophores in spite of their different intrinsic pK_as. In conclusion, this study provides direct evidence for how the local pH determines the mode of protonation for proton acceptors at the surface of biological membranes; to which extent a membrane-mediated proton-collecting antenna contributes to this exchange; and how the protonation is modulated by charge densities on the membranes.

Results and Discussion

The proton exchange in the immediate environment of the pH-sensitive fluorophore was monitored using FCS. Fluorescence intensity fluctuations, originating from individual protonation and deprotonation events of the fluorophores (free in solution or liposome-conjugated) and their diffusion through a confocal observation volume, provides the normalized auto-correlation function G(τ) given by (23)

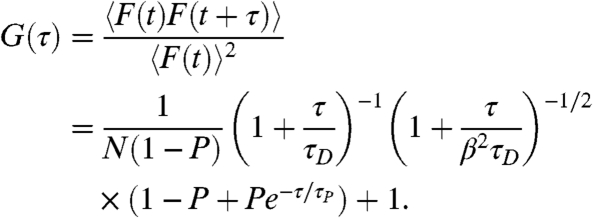[1]

Here, F(t) is the detected fluorescence intensity at a time t, τ is the correlation time, τ_D is the average translational diffusion time of the fluorescent species through the observation volume, N the mean number of fluorophores in the observation volume, and β the relationship between the axial and lateral extension of the observation volume. P signifies the fraction of protonated fluorophore, and τ_P = 1/k_P is the proton relaxation time, where k_P is the proton relaxation or proton exchange rate. For a one-step reversible protonation reaction in a nonbuffered water solution, k_P is given by the sum of the deprotonation rate constant, k_-1, and the protonation rate, k₊₁[H⁺]_bulk, of the fluorophore:

[2]

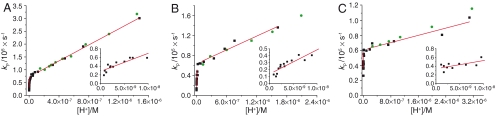
In this study we used the pH-sensitive dyes Fluorescein (Flu) and Oregon Green (OG) with pK_a values of 6.4 and 4.7, respectively, as determined from static pH titrations in water solution using a spectrofluorometer (Table 1). Data from FCS measurements indicate that the lower pK_a of OG is mainly due to a ∼25 times higher deprotonation rate for OG than for Flu. When the lipid-conjugated Flu or OG was incorporated into SUVs, an increase in the pK_as by approximately two units could be observed in the static measurements for each of the dyes (see Table 1). The underlying changes in the protonation and deprotonation rates were determined using FCS. Fig. 1 shows the proton exchange rates, k_p, as a function of the proton concentration for Flu- and OG-labeled DOPG and DOPC SUVs in 0.15 M NaCl or 0.60 M NaCl in the pH range ∼5.5 to ∼9. The data collected at pH values > 8 corroborate the results from our previous study (21), performed under similar conditions. The slopes in the k_p(H⁺) plots were > 10¹² M^-1 s^-1, which is consistent with a membrane-assisted acceleration of the protonation rate. However, at pH values < 7 the slopes were significantly smaller, displaying values between ∼10¹⁰ to ∼10¹¹ M^-1 s^-1, consistent with direct protonation of the dye. Thus, for both DOPG and DOPC SUVs, the Flu-labeled SUVs (solid black squares in Fig. 1) show two distinct phases of proton exchange, with a breaking point between pH 7 and 8. No such breaking point was found when measurements were performed with dyes in solution. This suggests that the different protonation behavior in the two pH ranges is a consequence of the membrane, and not due to an inherent property of the dyes themselves. As already mentioned above, the dye OG has a lower intrinsic pK_a compared to Flu (Table 1), which allowed us to more easily perform measurements in a lower pH range than for Flu. However, the lower pK_a prevented us from recording FCS data in the high-pH range, where the fraction of protonated fluorophores, P, is too small to allow τ_P to be precisely determined (see Eq. 1) (21–23). For OG-labeled SUVs (solid green circles in Fig. 1), the proton exchange rate increased linearly with increasing proton concentrations, and there was a perfect overlap with the corresponding rates for Flu-labeled DOPG SUVs. This comparison suggests that when the two different dyes are conjugated to SUVs, they are both subject to protonation and deprotonation rates that are determined by the local membrane environment; and that the corresponding rate constants are independent of the intrinsic pK_as of these dyes.

Table 1.

pK_as from static spectrofluorometer titrations for Fluorescein and Oregon Green, free in solution and conjugated to membranes

Sample	pKa
Fluorescein in H2O	6.4 ± 0.1
Fluorescein—DOPG (0.15 M NaCl)	8.2 ± 0.1
Fluorescein—DOPG (0.60 M NaCl)	7.9 ± 0.1
Fluorescein—DOPC (0.15 M NaCl)	8.3 ± 0.1
Oregon Green in H2O	4.7 ± 0.1
Oregon Green—DOPG (0.15 M NaCl)	6.7 ± 0.1
Oregon Green—DOPG (0.60 M NaCl)	6.3 ± 0.1
Oregon Green—DOPC (0.15 M NaCl)	6.3 ± 0.1

Fig. 1.

Proton exchange rates measured by FCS vs. proton concentration. The insets show the data for pH > 8. (A) Flu-labeled DOPG SUVs (black squares) and OG-labeled DOPG SUVs (green circles) in 0.15 M NaCl, shown for the complete proton concentration range and for pH > 8 (inset). The red lines show linear fits to the proton exchange rates for the Flu data above pH 8 and below pH 7. Above pH 8, the fit yields an apparent protonation second-order rate constant of 4.1 ± 0.7 × 10¹² M^-1 s^-1 and a corresponding deprotonation rate constant of 2.8 ± 0.3 × 10⁴ s^-1, and below pH 7, an apparent protonation second-order rate constant of 1.6 ± 0.4 × 10¹¹ M^-1 s^-1 and a corresponding deprotonation rate constant of 7.2 ± 0.3 × 10⁴ s^-1. (B) Flu -labeled DOPG SUVs (black squares) and OG-labeled DOPG SUVs (green circles) in 0.60 M NaCl, shown for the complete proton concentration range and for pH > 8 (inset). The red lines show linear fits to the proton exchange rates for the Flu data above pH 8 and below pH 7. Above pH 8, the fit yields an apparent protonation second-order rate constant of 3.5 ± 0.6 × 10¹² M^-1 s^-1 and a corresponding deprotonation rate constant of 1.4 ± 0.3 × 10⁴ s^-1, and below pH 7, an apparent protonation second-order rate constant of 4.6 ± 0.6 × 10¹⁰ M^-1 s^-1 and a corresponding deprotonation rate constant of 6.4 ± 0.5 × 10⁴ s^-1. (C) Flu-labeled DOPC SUVs (black squares) and OG-labeled DOPC SUVs (green circles) in 0.15 M NaCl, shown for the complete proton concentration range and for pH > 8 (inset). The red lines show linear fits to the proton exchange rates for the Flu data above pH 8 and below pH 7. Above pH 8, the fit yields an apparent protonation second-order rate constant of 1.9 ± 0.8 × 10¹² M^-1 s^-1 and a corresponding deprotonation rate constant of 3.4 ± 0.4 × 10¹⁰ s^-1, and below pH 7, an apparent protonation second-order rate constant of 1.2 ± 0.2 × 10¹⁰ M^-1 s^-1 and a corresponding deprotonation rate constant of 6.1 ± 0.4 × 10⁴ s^-1.

Dependence of the Protonation Rate on the Bulk Ion Concentration.

Both DOPG and DOPC liposomes have a pK_a of ∼3 (SI Text). In the measured pH range, DOPG lipids are negatively charged, while DOPC lipids are zwitterionic. The data shown in Fig. 1A and C indicate that at high proton concentrations, the proton exchange rates for both OG- and Flu-labeled DOPC SUVs are lower than the corresponding rates for the DOPG SUVs. To investigate whether this difference is due to a higher proton concentration near the surface of the DOPG membranes as compared to the DOPC membranes, we performed measurements on OG-labeled DOPG SUVs at different NaCl concentrations (Fig. 2). Addition of salt is expected to screen the membrane charges of the DOPG vesicles, reducing the possible electrostatic attraction of protons to the membrane surface.

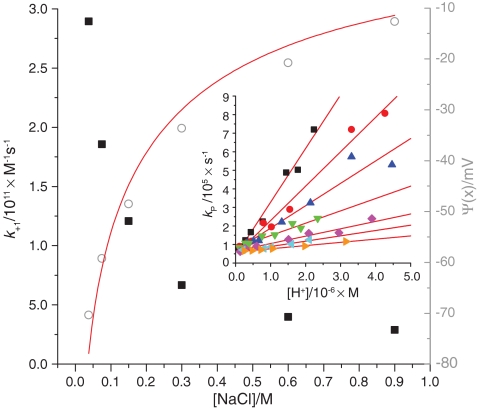
Fig. 2.

Dependence of the protonation rate coefficient with the ion concentration for OG-labeled DOPG SUVs (solid squares). Estimated electrostatic potentials as sensed by OG-labeled DOPG SUVs at 37.5 mM–900 mM NaCl (open circles). Fit to the data using Eqs. 4 and 5 shown as a red line. In this fit, the distance between the surface and the fluorophore, x, was taken as a fitting parameter. Inset: Proton exchange rates measured by FCS vs. proton concentration for OG-labeled DOPG SUVs in an aqueous solution at NaCl concentrations 37.5 mM (black squares), 75 mM (red circles), 150 mM (blue triangles), 300 mM (green triangles), 600 mM (magenta squares), and 900 mM (cyan triangles) and OG-labeled DOPC SUVs in 0.15 M NaCl (orange triangles).

For a given proton concentration, both k_p and the corresponding pK_a value were found to noticeably decrease with increasing NaCl concentrations (see Table 1). In contrast, only a minor pK_a shift (from 4.7 to 4.5) was observed for free OG fluorophores in an aqueous solution when increasing the NaCl concentration from 0 to 0.90 M NaCl (SI Text). For DOPG SUVs and at NaCl concentrations approaching 1 M, k_P approaches the rates observed for the zwitterionic DOPC SUVs. The measured k_P for these latter vesicles thus presumably represents an intrinsic proton exchange rate, unaffected by membrane-related electrostatic effects. For the OG-labeled DOPC SUVs, Eq. 2 was used to fit the data and we obtained an apparent protonation second-order rate constant of k₊₁ = 1.7 ± 0.1 × 10¹⁰ M^-1 s^-1.

The increase in k₊₁ and pK_a for OG-labeled DOPG SUVs with decreasing NaCl concentrations (inset, Fig. 2) suggests that the proton concentration is higher near the membrane surface due to the electrostatic attraction of protons. Apparent pK_a shifts for pH-sensitive fluorophores conjugated to micelles, membranes, and proteins have been observed in previous studies (24–26) and were attributed to a surface potential enhancing the local proton concentration near the membrane surface.

The relationship between the local proton concentration [H⁺]_local and the bulk proton concentration [H⁺]_bulk in the presence of an electrostatic potential is determined by the Boltzmann equation:

[3]

where Ψ is the electrostatic potential, q the proton charge, k_B the Boltzmann constant, and T is the temperature. The electrostatic potential Ψ(x), in the aqueous phase near a charged planar surface with homogeneously distributed charges, depends on the distance from the surface, x. The relationship between the surface potential, Ψ(0), and the surface charge density, σ, of the surface in the presence of a monovalent salt solution can be described by Gouy-Chapman theory (24, 26–29):

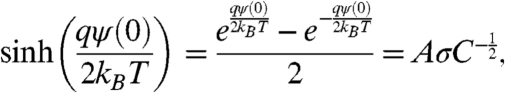[4]

where C is the monovalent salt concentration, N_A is the Avogadro constant, ε is the dielectric constant, ε₀ the permittivity of free space, and A is a constant:

A protonatable molecule conjugated to a charged membrane, a distance x from the membrane, experiences a potential:

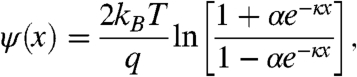[5]

where 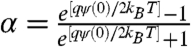, and κ = (2e²N_AC/εε₀k_BT)^1/2 is the inverse of the Debye length and equals 3.305 × C^1/2 (in units nm^-1) at 22 °C.

The proton exchange rate of a pH-sensitive fluorophore k_P, as extracted from an FCS measurement, is found by inserting Eq. 3 into Eq. 2:

[6]

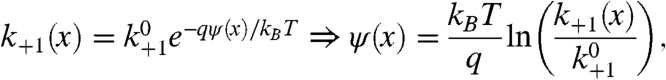[7]

where k₊₁ is the apparent second-order protonation rate constant and 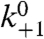is the corresponding protonation rate constant in the absence of an electrostatic potential.

The data in Fig. 2 (inset) were fitted according to Eq. 2. Based on the observation that at high proton concentrations (pH < 7) the protonation appears to occur via direct protonation of the fluorophore from the bulk (Fig. 1), the apparent k_-1 and k₊₁ rate constants at different NaCl concentrations were extracted. The decrease in the k₊₁ rate constants with increasing ion concentration (Fig. 2) correlates with the observed shift in pK_a determined from static pH titrations. Upon increasing the NaCl concentration from 0.15 M to 0.60 M, the pK_a of OG-labeled DOPG SUVs decreased by 0.4 pH units (see Table 1). The corresponding shift determined from the FCS measurements is 0.5 pH units, assuming that the off-rate is the same for the two ion concentrations.

Given that the decrease in k_P in Fig. 2 (inset) with increasing NaCl concentration is due to ionic screening of surface charges and that the intrinsic protonation rate constant, 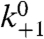, corresponds to the on-rate constant for OG-labeled DOPC SUVs, the electrostatic potential at different NaCl concentrations can be calculated using Eq. 7. Fitting the resulting potentials to Eqs. 4 and 5 (Fig. 2, red line) yields a value of x = 5 Å. In this fit a surface charge density of 1/(50 Å²) was used, obtained from the number of lipids per liposome and liposome size (surface area). The number of lipids per liposome was determined from a series of FCS and dynamic light scattering (DLS) measurements: by varying the membrane concentration of Flu, and by determining the size and brightness per liposome (SI Text). The distance x can probably change with the ion concentration if the linker between the acceptor and surface is flexible enough. However, in this study the linker was short (∼1 Å) and this effect should be small compared to the size of the proton acceptor itself (the fluorophore).

We note that the pK_a for OG labeled to SUVs obtained from FCS measurements, defined as the logarithm of the ratio of the protonation and deprotonation rate constants, does not agree with the pK_a determined from the spectrofluorometer titrations. For OG labeled to DOPC SUVs the FCS measurements yield a pK_a of ∼5.3 as compared to a pK_a of 6.3 by spectrofluorometer measurements (see Table 1). The discrepancy in the pK_a values obtained using the two methods shows that the increase in the pK_a for OG when conjugated to an SUV is not simply an effect of a decreased deprotonation rate constant.

Surface-Coupled Proton Exchange.

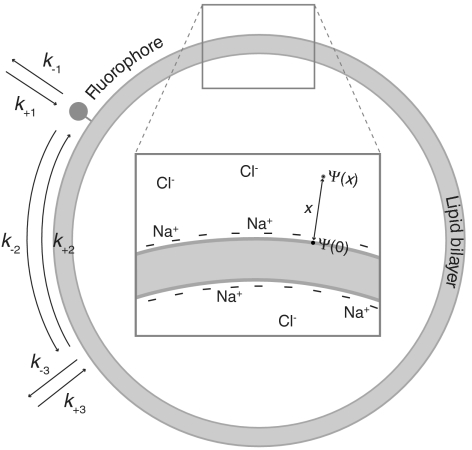
To explain the pH-dependent change in the protonation mode of SUV-conjugated fluorophores, as observed for the Flu samples (see Fig. 1), we consider a model including both protonation via the membrane and protonation from the bulk solution (see Fig. 3).

Fig. 3.

Schematic model including a membrane surface with a fluorophore, the paths of proton exchange, and the corresponding rate constants.

For a protonatable fluorophore conjugated to a lipid of an SUV with a radius r in a water solution, the direct exchange of protons between the fluorophore and the bulk solution is described by

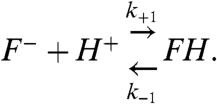[8]

Here, F^- and FH are the nonprotonated and protonated forms of the fluorophore, respectively, and k₊₁ and k_-1 denote the corresponding fluorophore protonation and deprotonation rate constants. The protonation rate is proportional to the proton concentration close to the fluorophore, [H⁺]_local. In addition, the protonation rate constant, k₊₁, depends on the proton diffusion coefficient in water D_P = 9.3 × 10^-5 cm²/s (9), and on the proton collision cross-section radius of the fluorophore a. If the fluorophore is a perfect sink for protons, binding every proton that reaches the fluorophore (removing the proton from the system), then k₊₁ is given by (2, 4)

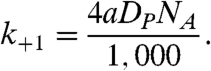[9]

Here it is assumed that the proton collision radius of the fluorophore is much smaller than the radius of the SUV (a ≪ r).

For a protonatable SUV, the first protonation and deprotonation step of the whole SUV is described by

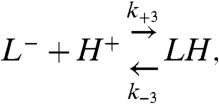[10]

where LH and L^- denote the SUV when a proton resides on its surface and a nonprotonated SUV, respectively, and k₊₃ and k_-3 are the protonation and deprotonation rate constants, respectively. The apparent pK_a of the first protonation step of the SUV is given by 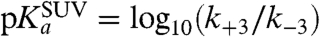. When the whole SUV surface is a perfect sink for protons, it has been shown for analogous systems that k₊₃ is given by (2)

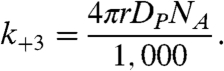[11]

For a fluorophore conjugated to a lipid within an SUV, that can be protonated both via the bulk solution and via the membrane surface, the proton exchange with the bulk solution is described by expression 8 and its proton exchange with the SUV surface by

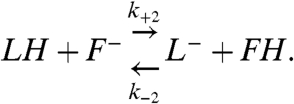[12]

Here, k₊₂ and k_-2 are the protonation and deprotonation rate constants of the fluorophore via the membrane surface; k₊₂ is the inverse of the mean time it takes for the proton to be captured by the fluorophore after arrival to the surface. If the proton diffusion coefficient along the surface is sufficiently high, and the fluorophore acts as a perfect proton sink, then the whole SUV surface would also act as a perfect sink for protons. When the proton concentration is low enough (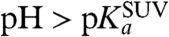) such that the surface of the SUV is not saturated with protons, these conditions can be considered valid. The protonation of the fluorophore is then described by expressions 10 and 12. The effective protonation rate constant of the fluorophore would then be equal to that for the whole SUV, as given by Eq. 11. On the other hand, for high proton concentrations (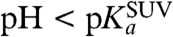), the protonation rate of the SUV surface from the bulk solution is higher and the SUV surface is saturated with protons. In this pH range, the protonatable fluorophore cannot be considered a perfect sink with irreversible absorption of protons, but rather a molecule that reversibly binds protons for a time t_off and exchanges protons with the environment as described by expressions 8 and 12.

The experimental data indicate that at low proton concentrations (pH > 8), the protonation rates of liposome-associated fluorophores are strongly enhanced (see Fig. 1). A linear fit to the proton exchange rates for Flu-labeled DOPC SUVs above pH 8 (see Fig. 1C) yields an apparent protonation second-order rate constant of 1.9 ± 0.8 × 10¹² M^-1 s^-1 and a deprotonation rate constant of 3.4 ± 0.4 × 10⁴ s^-1 from the slope and the intercept, respectively. Based on the assumptions outlined above (i.e. that protonation of the fluorophore is described by Eq. 11, and that the whole SUV membrane is involved in the protonation of the fluorophore), the radius of the SUV can be estimated from Eq. 11 to be 27 ± 11 nm. This reasonably concurs with the radius of 15 nm obtained from measurements using DLS and FCS (see Materials and Methods). When conjugated to an SUV, the fluorophore resides close to the membrane surface. Protons released from the fluorophore to the bulk are then subject to recurrent reassociation back to the membrane and k_-1 = 0. The deprotonation rate constant obtained from the linear fit above therefore represents k_-2.

In contrast, measurements on Flu-labeled DOPC SUVs below pH 7 (see Fig. 1C) yield an apparent protonation second-order rate constant of 1.2 ± 0.2 × 10¹⁰ M^-1 s^-1 and a corresponding deprotonation rate constant of 6.1 ± 0.4 × 10⁴ s^-1. The observed increase in k_p of the fluorophore with increasing proton concentrations is then presumably attributed to direct proton transfer from the bulk solution. By using Eq. 9, the proton collection radius can then be estimated to a = 0.5 ± 0.1 nm, which is consistent with the molecular radius of a Flu molecule (∼0.5 nm).

Two distinct modes of protonation of the fluorophore are observed, with a transition from a protonation mode at low proton concentrations (pH > 8) governed by a membrane-mediated pathway (expressions 10 and 12) into a mode at high proton concentrations (pH < 7), where the protonation is increasingly dictated by direct protonation of the fluorophore via the bulk solution (expression 8). The transition is presumably a consequence of a saturation of the protonation path via the membrane (see expression 12) when the SUV surface is saturated with protons. We note that the change of protonation mode occurs approximately in the range where there is on average one or more protons on the SUV surface, which is likely to strongly contribute to the saturation of the membrane-mediated protonation path. The average number of protons can be calculated from the pK_a of the lipids and number of lipids per SUV (SI Text).

Conclusions

The data presented in this study shows that the proton exchange rate of a membrane-bound proton acceptor is highly dependent on the ionic strength of the solution and the membrane properties, such as the lipid charge. For Flu conjugated to phospholipid membranes, a dramatic enhancement in the protonation rate constant was observed at low proton concentrations (pH > 8). However, at high proton concentrations (pH < 7) this enhancement was weakened and the protonation rate constant was comparable to that expected from direct protonation of the Flu dye from the solution. Measurements on OG conjugated to the same type of membranes displayed almost identical proton exchange rates for high proton concentrations. Because the pK_a of this dye in its free form is very different from that of Flu, we conclude that the deprotonation rate constants of the dyes, when associated to the membrane, are determined by the local environment close to the membrane and not by their intrinsic pK_as. The data show protonation rate constants in agreement with the physical size of the SUVs and the corresponding cross-sections of the fluorophores. Furthermore, the study determined the electrostatic potential as sensed by the proton acceptor and an approximate distance between the probe and the surface.

In identifying the role of the membrane in proton transfer at the surface of biological membranes, this study found that ion concentration bears an impact on proton exchange rates, and that this could be explained by changes in the local surface potential. Furthermore, the data indicate that the mode of protonation of a membrane-associated proton acceptor can switch from a membrane-promoted to a direct exchange with the bulk solution. This protonation mechanism is likely to be a general feature also for a wide range of membrane-associated proton transporters, such as cytochrome c oxidase, photosynthetic reaction centers, and bacteriorhodopsin (9, 15, 30) in living cells.

Materials and Methods

Liposome Preparation.

SUVs were prepared by mixing 2.5 ml of a 10  mg/ml chloroform solution of the glycerophospholipid DOPG (1,2-dioleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] or DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine), Avanti Polar Lipids, Inc., Alabaster, AL) with 50 μl of a 2.5 μg/ml chloroform solution of Fluorescein-DHPE [N-(Fluorescein-5-thiocarbamoyl)-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine)] (Invitrogen, Carlsbad, CA) or 50 μl of a 2.5 μg/ml chloroform solution of Oregon Green-DHPE [Oregon Green 488-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine)] (Invitrogen, Carlsbad, CA) in a flask. Following evaporation under nitrogen flow, the lipids were dissolved in a 4 ml NaCl solution, to 37.25 mM to 900 mM M depending on the sample.

The lipid mixture was shaken for 30 min, using a vortex mixer, to form multilaminar liposomes, and then sonicated, using a tip sonicator, until the solution became transparent. To remove residual dye from the bulk solution the salt solution was changed using a PD10 column (GE Healthcare UK Limited, Little Chalfont, UK).

The liposome solution was then centrifuged for 40 min (10,000 g) to remove residual multilaminar liposomes and metal particles from the sonicator tip. The ratio of Fluorescein-DHPE to nonfluorescent lipids was 1∶300,000 to ensure that each liposome contained only one fluorophore. The sonicated liposomes were determined to approximately 15 nm in radius by DLS measurements, corresponding well with the radius determined by FCS.

FCS Measurements.

Before starting measurements, the sample was subjected to CO₂-free air in order to remove dissolved CO₂ and then kept under a CO₂-free air atmosphere throughout the measurements. The pH was continuously monitored with a pH-electrode (Inlab Semi-Micro, Mettler-Toledo International Inc., Columbus, OH) coupled to a pH-meter (Jenway 3510, Jenway, Dunmow, UK). FCS measurements were performed on a home-built confocal setup, consisting of an Olympus IX-70 microscope body and a linearly polarized Ar-ion laser (Siemens Laser, LGK 7812-1, Siemens, München, Germany) operated at 488 nm. The laser beam was focused by a 40×, NA 1.2, UPlanApo Olympus objective, down to a 1/e² radius of ∼0.5 μm. Emitted fluorescence was collected by the same objective, focused by a 150-mm achromatic lens onto a 50 μm-diameter pinhole in the image plane, passed through a band-pass filter (HQ532/70, Chroma Technology Corp., Rockingham, VT), and after recollimation split by a 50/50 beam-splitter cube, and finally detected by two avalanche photodiodes (APDs) (SPCMAQR-14/16, Perkin-Elmer Optoelectronics, Wellesley, MA). The detection volume was assumed to be a three-dimensional Gaussian with an axial 1/e²-extension β times the transverse 1/e²-radius. The APD signals were processed by an ALV-5000/E correlator (model ALV-5000-E, ALV, Langen, Germany, with an ALV 5000/FAST Tau Extension board). Excitation power was kept constant, and at a low level (9 μW yielding an irradiance in the focus of 1.2 × 10³ W/cm²), to minimize the contribution from triplet state kinetics in the correlation curves (31), which can otherwise overlap with and disturb the readout of the protonation-related processes at high proton concentrations.

Spectrofluorometer Measurements.

The spectrofluorometer measurements were performed on a FluoroMax 3 spectrofluorometer (Horiba Jobin Yvon, Edison, NJ). For each pH titration series, a recording was performed at low pH (∼3), where the fluorescence signal was negligible and only scattered light from the SUVs contributed to the signal. This measurement was used for background subtraction.

Data Analysis.

The recorded correlation curves and spectrofluorometer data were analyzed in OriginPro 7.5 (OriginLab, Northampton, MA).