The tolerance–fecundity trade-off and the maintenance of diversity in seed size

Abstract

Seed size commonly varies by five to six orders of magnitude among coexisting plant species, a pattern ecologists have long sought to explain. Because seed size trades off with seed number, small-seeded species clearly have the advantage in fecundity, but what is the countervailing advantage of large seeds? Higher competitive ability combined with strong competitive asymmetry can in theory allow coexistence through a competition–colonization trade-off, but empirical evidence is inconsistent with this mechanism. Instead, the key advantage of large seeds appears to be their tolerance of stresses such as shade or drought that are present in some but not all regeneration sites. Here I present a simple, analytically tractable model of species coexistence in heterogeneous habitats through a tolerance–fecundity trade-off. Under this mechanism, the more tolerant species win all of the more stressful regeneration sites and some of those that are less stressful, whereas the more fecund species win most but not all of the less stressful sites. The tolerance–fecundity trade-off enables stable coexistence of large numbers of species in models with and without seed limitation. The tolerance–fecundity mechanism provides an excellent explanation for the maintenance of diversity of seed size within plant communities and also suggests new hypotheses for coexistence in animal and microbial communities.

Seed size varies strikingly among plant species, even within the same community (1). Seed mass commonly varies over five to six orders of magnitude among coexisting plant species (2) and over two to three orders among coexisting species sharing the same life form and mature size (3). Ecologists have long puzzled over this variation in seed size, given that simple models suggest that one size should be optimal for any given set of conditions (4, 5). Because seed size varies so widely within communities, any mechanism that maintains seed size diversity would contribute substantially to explaining maintenance of plant species diversity.

Many empirical studies illuminate the relative advantages of seeds of different sizes (6). A given reproductive effort can produce many small or few large seeds; thus small-seeded species have the advantage in seed production, as clearly demonstrated by analyses that control for plant size (7, 8). In contrast, large-seed species have higher average seed and seedling survival (9, 10). This advantage does not manifest itself uniformly under all conditions—instead, it reflects the advantages of large seeds in providing resources that can be allocated to tolerate particular stresses, such as shade, drought, or defoliation (9, 11). Thus, large seeds have the advantage in stress tolerance and small seeds in fecundity (12).

Although the empirical evidence indicates that large seeds are advantageous only under some conditions, theoretical explanations for the maintenance of diversity of seed size have thus far focused exclusively on average performance, without considering habitat variation. The most frequently invoked explanation is founded on a trade-off between competitive ability and fecundity (13–16). Larger seeds, when present, disproportionately win regeneration sites, so smaller-seeded species must escape their larger-seeded competitors to persist. Seed size diversity is maintained by a competition–colonization trade-off (17–19), a mechanism that requires very strong competitive asymmetry–that is, the better competitor must virtually always win no matter how slight its advantage (20). However, empirical tests show that competition is not sufficiently asymmetric in favor of large-seeded species for the competition–colonization trade-off to explain observed variation in seed size (6, 21).

Other authors argue that the advantage of small-seeded species in seed production is largely or completely canceled out by the advantage of large-seeded species in survival (22) or survival, life span, and mature size combined (10). If these relationships canceled perfectly (which is by definition infinitely unlikely), then seed size would be a purely neutral trait—a conclusion at odds with the huge literature on seed biology (23). If they only partially cancel, maintaining seed size diversity still requires some other stabilizing mechanism, albeit a weaker one than would be required in the absence of this equalizing mechanism (24).

Here, I develop a theoretical framework for understanding the maintenance of diversity in seed size—a framework based on an interspecific trade-off between stress tolerance and fecundity and on variation in stressfulness among potential regeneration sites (Fig. 1) (20, 25). I present a simple, analytically tractable model of the coexistence of species via this tolerance–fecundity trade-off. The predictions of this model are consistent with empirical evidence and enhance our understanding of real communities. I discuss the robustness of the results to modifications of model assumptions and the future research directions opened up by this theory.

Fig. 1.

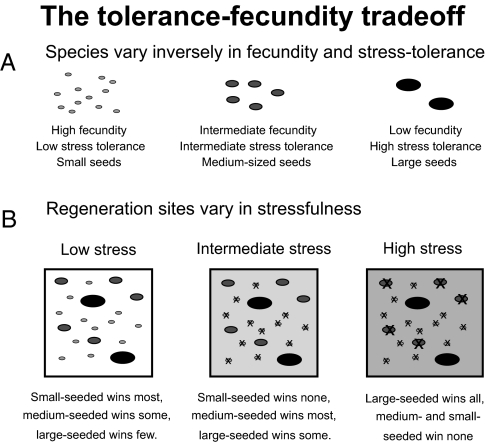
The tolerance–fecundity trade-off rests on two sets of assumptions. (A) Species must vary inversely in fecundity and stress tolerance, such that those species with high fecundity have low stress tolerance and those with high stress tolerance have low fecundity. This could be mediated by seed size, as depicted here, although it need not be. (B) Potential regeneration sites for establishment vary in stressfulness, and this stress acts as a filter disproportionately impacting the regeneration odds of the less stress-tolerant and more fecund species. In low stress sites, all species are able to recruit, and thus the species with high fecundity are more likely to win the site. In contrast, in the high stress sites, most species are unable to regenerate (as indicated by x's); only the species with high stress tolerance can recruit and win. In sites of intermediate stressfulness, the least stress-tolerant species are unable to recruit, and the site is won often by species of intermediate stress tolerance and intermediate fecundity and sometimes by species of high stress tolerance and low fecundity.

Model and Results

I examine coexistence conditions in a simple model in which species vary only in their fecundity and their stress tolerance at the regeneration stage (Fig. 1A). There is a single axis of stressfulness of potential regeneration sites, and each species has a discrete threshold stressfulness value: It can recruit in sites that are less stressful and it cannot recruit in those that are more stressful (Fig. 1B). Thus, each species can recruit in a subset of available regeneration sites, and these subsets are perfectly nested—the sites in which the least tolerant species can recruit are a subset of those in which the next least tolerant can recruit, and so on. Species differ only in their fecundity, defined here as seed production per individual, and in the proportion of sites in which they can regenerate—and they differ inversely in these two traits. Space is implicitly divided into discrete regeneration sites. For simplicity of analytical analyses, I initially assume that dispersal is uniform and that abundances and fecundities are sufficiently large that all regeneration sites receive seeds of all species every year (i.e., there is no seed limitation). This assumption is later relaxed.

Two-Species Case.

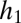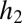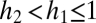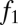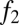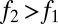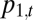Suppose we have two species and that species 1 is the more tolerant, whereas species 2 has the higher fecundity. Let and be the proportion of the regeneration sites that species 1 and species 2 can recruit in, with these proportions nested and . Let and be the fecundities of species 1 and species 2, with . Let and 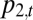denote the abundances of species 1 and 2 at time t, in proportion occupancy of total habitat in the community (so 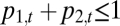). Let m be the mortality or disturbance rate, such that a fraction 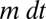of the sites occupied by adults of the two species become available for new recruits in time 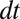. Then

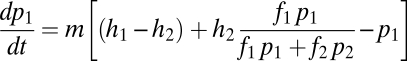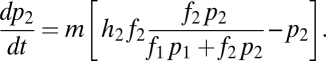In words, the change in abundance of each species reflects losses (deaths) in proportion to each species’ current abundance (last term in each equation) and gains from recruitment into sites opened by deaths. Species 1 obtains all of the open sites in which it is the only species that can regenerate 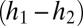, plus a fraction of 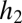proportional to the abundance of its seeds as a fraction of all seeds. Species 2 obtains only the remaining fraction of .

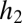Equilibrium abundances, 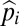, are necessarily constant in time and thus must satisfy

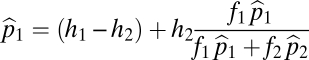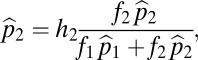which has solution 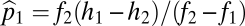, 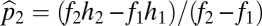. This equilibrium is stable, as shown in SI Text, and has a convenient graphical interpretation (Fig. 2A). Note that in the limit as 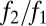goes to infinity, 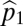goes to 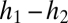(the area in which only species 1 is able to recruit), and 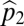goes to .

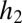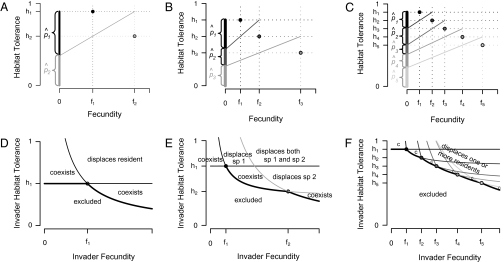
Fig. 2.

Graphical representation of equilibrium abundances, 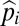(A–C), and conditions for coexistence and invasion (D–F) in the tolerance–fecundity model, for different numbers of species. Here species 1 (black) has lowest fecundity and highest habitat stress tolerance (the proportion of habitat in which it can recruit), species 2 (gray) has higher fecundity and lower stress tolerance, species 3 (lighter gray, if present) has still higher fecundity and lower stress tolerance, and so forth. When expressed as the proportion of total area occupied, the equilibrium abundances sum (or “stack”) to 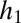(stacked bars in A–C). The point at which a line drawn from 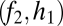through 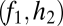intersects the y axis determines the division between 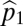and 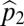(A–C). Similarly, the division between 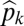and 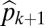is defined by the line drawn from 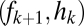through 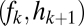and on to the y axis (B and C). Coexistence is possible only if these lines intersect the y axis at a 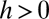, a condition met if 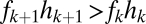, and if the lines do not cross, which requires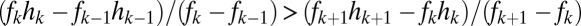 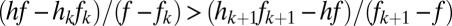. The fate of a new species with parameter values f and h introduced into a community depends on its position relative to the curved lines that define these two sets of conditions for the resident species, distinguished here by thin and thick lines, respectively, as well as on its position relative to the horizontal line 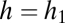(D–F). All these lines are omitted where they do not influence invader fate. Depending on the parameter combination, the invader may be able to invade and coexist with all residents (“coexists” or simply “c”), be unable to invade and thus be excluded (“excluded”), or invade and displace one or more residents (“displaces sp. 1”, etc.).

Not all combinations of two species satisfying 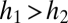and 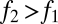can coexist. For coexistence, both equilibrium abundances must be greater than zero, and thus we must have 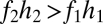. Invasion conditions follow (Fig. 2D) (see SI Text for proofs).

N-Species Case.

We can similarly consider the case of an arbitrary number n > 2 of species. Suppose species 1 is the most tolerant and least fecund and species n the least tolerant and most fecund, with perfect inverse ranking in between, such that 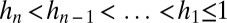and .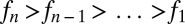

If the species coexist, then at equilibrium

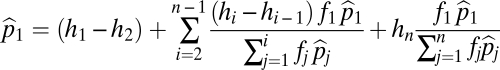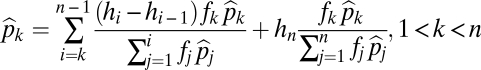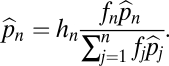The equilibrium abundances are

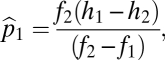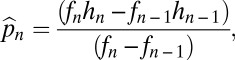and

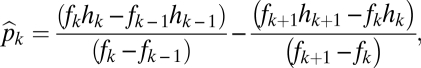These abundances again have a convenient graphical interpretation (Fig. 2 B and C). Note that the abundances of the species have no necessary relationship to their ranking in fecundity and habitat tolerance. Instead, a species’s abundance depends on how its own parameter values compare with the parameter values of the species on either side. All other things being equal, a focal species’ abundance will be higher if it has a greater advantage in fecundity over the next least fecund species and a greater advantage in tolerance over the next least tolerant species. It will also be more abundant if the next most fecund species has a smaller advantage in fecundity over it and if the next most tolerant species has a smaller advantage in tolerance.

The combination of two or more resident species places restrictions on potential values for a coexisting intermediate species above and beyond those that each presents individually (Fig. 2 E and F). Coexistence requires not only 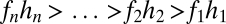but also

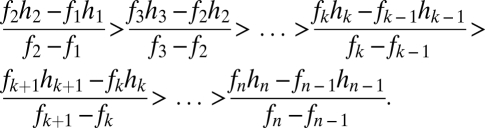Provided these conditions are met, an arbitrary number of species can in theory coexist via the tolerance–fecundity trade-off (although of course in practice the number is limited by drift whose influence depends on the size of the community and each species’ potential equilibrium abundance in that community).

Adding Seed Limitation.

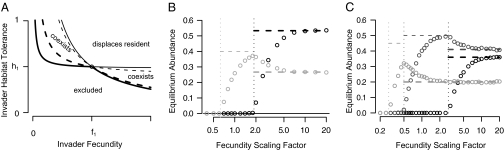
Seed limitation can be introduced into the basic tolerance–fecundity model by substituting Poisson seed rain for uniform seed rain. With this change, the conditions for coexistence become more restrictive (Fig. 3A). For example, coexistence in the two-species case requires 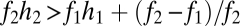and 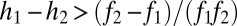(SI Text). Thus, if fecundities are too low, the species cannot coexist (Fig. 3B). 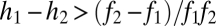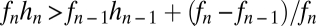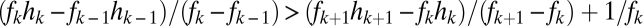In the n-species case, generalization from the three-species case (SI Text) suggests that the requirements are , , and for 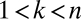, a conjecture supported by simulation results (Fig. 3C, SI Text). The 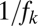term in the last condition introduces a clear limit to the number of coexisting species, a limit that is more restrictive for lower fecundities.

Fig. 3.

The effects of seed limitation in the form of Poisson seed rain on equilibrium abundances and possibilities of coexistence. (A) Seed limitation shifts and restricts parameter combinations compatible with coexistence (compare with Fig. 2D), and these become ever more restricted as fecundity decreases, here from 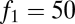(solid lines) to 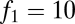(dotted lines); in all cases 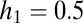. (B) Equilibrium abundances (circles) in simulations of a more tolerant (black) and a more fecund (gray) species. The fecundity scaling factor is the fecundity of the more tolerant species 1; species 2 always has four times this fecundity. Habitat tolerances are 0.8 and 0.4, respectively. As fecundity increases, equilibrium abundances converge on those found under uniform dispersal with no seed limitation (thick dashed lines). For very low fecundities, neither species can persist or invade. When the fecundity of species 2 passes above the threshold 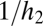(dotted gray line), its equilibrium abundance becomes nonzero and increases toward its equilibrium in isolation under uniform seed rain (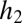, dashed thin gray line). When the fecundity of species 1 passes above the threshold 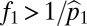(dotted black line), its equilibrium abundance becomes nonzero and above this value both species converge on their equilibrium abundances in the case of uniform dispersal. (C) Similar dynamics play out in the case of three species: At low fecundities no species can persist, then as fecundity increases first only species 3 can persist, then species 2 and 3, and finally all three species. Here the fecundities of species 2 and 3 are four and eight times as large as that of species 1, and habitat tolerances are 0.97, 0.7, and 0.45.

Discussion

Implications for Understanding Plant Communities.

The tolerance–fecundity trade-off constitutes a powerful stabilizing mechanism for the maintenance of diversity of seed size. Under this trade-off, seed size diversity is maintained through partitioning of exogenous variation among regeneration sites. The key assumptions of this model are that species vary inversely in fecundity and stress tolerance and that potential regeneration sites vary in stressfulness. To explain diversity of seed size, I assume that large-seeded species have high stress tolerance at the initial regeneration stage and low fecundity, whereas small-seeded species have low stress tolerance and high fecundity. In sites having low stressfulness, all or most species have the opportunity to recruit, and thus these sites are disproportionately—but not exclusively—won by small-seeded species, because they produce more seeds. In sites having high stressfulness, small-seeded species are unable to recruit, leaving large-seeded species to “win” the site (Fig. 1). This is consistent with field data, where small-seeded species disproportionately fail to generate in some “stressful” sites, whereas large-seeded species can be found regenerating on a wider variety of sites (26).

The tolerance–fecundity model provides a far better explanation for the maintenance of diversity of seed size than does the traditional competition–colonization trade-off model or any other mechanism proposed to date. In the competition–colonization model, the key advantage of large seeds is higher competitive ability, realized as a higher per capita probability of winning any site. Yet the advantages of large seeds accrue almost entirely in sites that present stresses (9), as reflected in the tolerance–fecundity model. Further, the diversity-maintaining power of the competition–colonization trade-off relies critically on high competitive asymmetry (14, 20, 27)—and this degree of asymmetry is absent from plant communities (6, 21, 28). As for the idea that the higher fecundity of small-seeded species is cancelled out by the larger survival (and perhaps longer life span and larger mature size) of large-seeded species (10, 22), it is certainly true that these quantities vary inversely among species. But it is infinitely unlikely for them to exactly cancel to the point where seed size would be a neutral trait (29)—and even small deviations from perfect neutrality would lead to rapid dominance (30), in this case by a single seed size. This is inherently an equalizing mechanism (24)—it can reduce competitive differences among species thereby slowing competitive exclusion, but it cannot in and of itself maintain diversity of seed size.

Previous theories for species diversity maintenance have often involved species differences either in habitat-specific performance or in fecundity (31); the tolerance–fecundity model uniquely combines the two and trades them off against each other (20, 25). Tolerance–fecundity theory also specifically offers an explanation for changes in species composition over the course of succession—for example, changes over time in the plant community found on abandoned agricultural land (32). In the past, such changes were explained by the competition–colonization trade-off and/or a successional niche model in which species differed in their performance in the different environments present over the course of succession (some species doing better in early-successional environments and others in late-successional environments) (33). The relative importance of these two mechanisms could in theory be distinguished with seed addition and “niche removal” experiments (33). The tolerance–fecundity model offers distinct predictions for the effects of seed addition, disturbance, and other manipulations (34, 35), predictions that should be considered as alternatives. For example, adding seeds of all species in large numbers would greatly accelerate succession in communities governed by the competition–colonization trade-off (because it would speed the arrival of the superior competitor), while having no effect where the successional niche operated alone (33). For communities in which the tolerance–fecundity trade-off drove succession, the effects of seed addition would depend crucially on any associated changes in the relative abundances of species in the seed rain.

Robustness of the Mechanism.

The tolerance–fecundity trade-off model, like all models, is a caricature of reality—it does not attempt to reproduce all processes but strives to capture some essential features. How robust are the results to more realistic representations of seed rain and seed limitation, habitat variation and plant adaptations to habitat variation, and interspecific differences in plant life history?

Many plant populations are seed limited, with seeds failing to arrive at some or even most suitable regeneration sites, especially in diverse communities where many species are very rare (34–39). In contrast, in the basic tolerance–fecundity model presented in the main text, seed rain is assumed to be uniform and sufficiently high that seeds of all species arrive at all regeneration sites. Analysis of the model with Poisson seed rain (SI Text) shows seed limitation constricts the parameter combinations compatible with coexistence and alters equilibrium abundances. However, even with the addition of realistic levels of seed limitation, there is ample scope for species coexistence via the tolerance-fecundity trade-off. This is consistent with previous results, which show that when species partition exogenous habitat heterogeneity, seed limitation enhances drift, reducing the number of species that coexist (40). [In contrast, the addition of seed limitation in purely neutral models or those in which species coexistence is unrelated to habitat partitioning allows more species to coexist (41).]

In the simple model here, there is a single axis of habitat stressfulness, and plant species have a threshold response to that axis—for stress values lower than their threshold they are able to establish, and for stress values higher, they are absolutely unable to establish. In reality, stress and species adaptations to it are both multidimensional, and the probability a given species will successfully establish usually varies gradually with any given axis of habitat stressfulness (11). Successful establishment in some habitats requires not simply more provisions, but often specific utilization of those provisions (e.g., deep roots to tolerate drought) or even specific kinds of provisions (e.g., nutrients), and the strategies that succeed there may reduce success in other habitats (42). More complex relationships of establishment ability to a single axis of habitat stressfulness can easily be explored in simulation models and are expected to alter the precise parameter combinations that enable coexistence without fundamentally changing the manner in which this trade-off contributes to stabilizing coexistence. The multidimensionality of stressfulness and related adaptations is a more challenging problem. In some systems this may be well represented as a combination of the tolerance–fecundity trade-off and one or more independent axes of differences in allocation and/or design strategies, thus leaving the mechanism of the tolerance–fecundity trade-off intact. In other cases, the two axes may interact in more complex ways that require more complex models.

Coexisting plant species typically span tremendous variation in mature size and life span (12), quite unlike the model here. The influence of these differences on the maintenance of diversity of seed size must be considered because these traits are in part correlated with seed size and because juveniles generally compete regardless of mature size (10). I argue that this is best treated as three independent, albeit interacting questions: the maintenance of diversity in mature size, the cause of systematic variation in mean seed size with mature size, and the maintenance of diversity of seed size for any given mature size (typically two to three orders of magnitude) (10). Life history theory offers insight into the increase in mean seed size with mature size (3, 43–45). Various niche models explain the maintenance of diversity of mature sizes, without considering seed size (e.g., ref. 46). And the tolerance-fecundity model now provides an explanation for the maintenance of the observed variation in seed size not explained by mature size. The interaction of these three mechanisms is an important area for future research.

Importance and Future Directions.

The question of what mechanisms maintain diversity is not merely academic—it provides key insights into what species are most at risk for extinction from habitat destruction and environmental change. A highly influential study of relative extinction risk of species coexisting under the competition–colonization trade-off, for example, found that the most competitive (least fecund) species were at highest risk under habitat destruction, even though they generally had the highest abundances (47). Indeed, a key result was that these species could be doomed to extinction even if habitat destruction alone still left a substantial population size, because future recruitment would fall short of mortality, thus creating an “extinction debt” (47, 48). In contrast, under the tolerance–fecundity trade-off, the key to continued coexistence is the maintenance of a variety of habitats varying in stress tolerance. Habitat destruction that is equally severe across all types of regeneration habitat would be expected to pose the biggest risk to the rarest species because of their increased vulnerability to demographic stochasticity. Environmental change that makes all habitats more stressful is likely to place the least stress-tolerant species at highest risk; environmental change that makes all habitats less stressful will disproportionately endanger the most tolerant species. This is similar to endangerment risks inferred under pure habitat partitioning mechanisms, but the nested structure of habitat use under the tolerance–fecundity mechanisms leads to differences in the relative magnitude of impacts. In particular, environmental change that disproportionately reduces the area of habitat at some intermediate stress value will most endanger species whose habitat tolerance thresholds are just above the range in which habitat area is reduced.

Although the focus in the present work has been on how the tolerance–fecundity trade-off combined with spatial variation in regeneration habitat stressfulness can explain maintenance of diversity in seed size in plant communities, essentially the same mechanism may also play a role in other settings. Strong temporal variation in stressfulness among and within years (49) can offer similar opportunities for coexistence via a tolerance–fecundity trade-off . Just as seed size can mediate a tolerance–fecundity trade-off in plants, offspring size and per-offspring investment more generally may mediate similar trade-offs in animals or even microbes. And like the competition–colonization trade-off, the tolerance–fecundity trade-off may also be relevant for understanding coexistence of different strains of pathogens in systems where hosts vary systematically in defenses and pathogen strains vary inversely in their reproductive rates and their ability to overcome these defenses.

In conclusion, seed size varies tremendously among coexisting species, and explaining this variation and its role in plant community dynamics has remained an enduring challenge. Clearly, the seed size–number trade-off is central, and the advantage of high number (fecundity) is clear. Large size potentially offers multiple advantages, which can be difficult to characterize. These have often been designated with the vague term “competitiveness” and thus thought to be well represented by the theoretically powerful competition–colonization trade-off. As empirical reviews show, however, the true advantage of large seeds is not that they can take over from smaller seeds under any conditions (competitiveness in the competition–colonization trade-off), but that they can tolerate a variety of stresses encountered during regeneration—a trait I refer to as “tolerance” (6, 12). The model presented here shows how this tolerance enabled by large seed size, and its trade-off with fecundity enabled by small seed size, facilitates coexistence in communities where regeneration habitats vary in stressfulness. The tolerance–fecundity trade-off offers a clear explanation for coexistence of species varying in seed size and may be relevant in many other cases of variation in offspring size or provisioning. As such, it also has important implications for understanding the threats posed to individual species and to communities by anthropogenic habitat destruction and alteration.