Encoding properties of haltere neurons enable motion feature detection in a biological gyroscope

Abstract

The halteres of dipteran insects are essential sensory organs for flight control. They are believed to detect Coriolis and other inertial forces associated with body rotation during flight. Flies use this information for rapid flight control. We show that the primary afferent neurons of the haltere’s mechanoreceptors respond selectively with high temporal precision to multiple stimulus features. Although we are able to identify many stimulus features contributing to the response using principal component analysis, predictive models using only two features, common across the cell population, capture most of the cells’ encoding activity. However, different sensitivity to these two features permits each cell to respond to sinusoidal stimuli with a different preferred phase. This feature similarity, combined with diverse phase encoding, allows the haltere to transmit information at a high rate about numerous inertial forces, including Coriolis forces.

Rapid input from mechanosensors is a crucial component of flight control in many insects (1). Behavioral studies have demonstrated that the information transmitted by mechanoreceptors, particularly by gyroscopic organs like dipteran halteres (2, 3) and lepidopteran antennae (4), is necessary for stable flight. In particular, the kinematics of dipteran halteres allow them to experience Coriolis forces resulting from body rotations (3, 5), and thus potentially to act as gyroscopic organs for flight control (6, 7). The base of the haltere is equipped with a rich array of dome-shaped campaniform sensilla that occur in patches on the dorsal and ventral surfaces (8, 9). Of these fields, three [dF1, dF3, and vF1, in the terminology of Gnatzy et al. (9)] are oriented parallel to the long axis of the haltere, and one field (dF2) and the large chordotonal organ are oriented orthogonal to the long axis. The directional orientation (8, 9) and selectivity (10) of the fields suggest that the haltere can detect forces moving in multiple directions using the diverse patches of campaniform sensilla.

Although kinematic (5) and behavioral (6) evidence suggests that the haltere’s primary function is to encode Coriolis forces that result from body rotations during flight, little is known about the response of primary afferent neurons to haltere motions. The diverse orientations (9) and directional sensitivity (10) of the campaniform sensilla suggest that they could employ a variety of encoding strategies to capture different aspects of complex mechanical stimuli, but a particular strategy remains to be shown. For example, the different campaniform sensilla could be tuned to different frequencies of stimuli, responding best to specific kinds of motion. Alternatively, the sensilla could be broadly tuned to respond to a range of frequencies, and the stimuli that activate them would be filtered by the structure of the organ itself. The utility of these potential coding strategies for producing controlled flight behavior remains an open question.

In previous research (10), we used step and sinusoid stimuli to describe the latency and frequency responses of dipteran halteres. However, stimulating the halteres with such simple patterns permits only a linear analysis of their encoding properties. Here, we examine nonlinear characteristics using band-limited white noise stimuli (11). We focused on the feature selectivity and information processing capabilities of these neurons. These encoding characteristics are particularly important, because at least some of the information can be transmitted directly to a motor neuron via an electrotonic gap junction (12), and thus is not further refined in the central nervous system before affecting behavior (13, 14). By characterizing the encoding properties, we are able to examine neural information processing at the earliest sensory and immediate premotor levels simultaneously. In doing so, we reveal the mechanisms by which neurons convert complex stimuli into a train of spikes that can be immediately used to control a complex behavior.

Results

Haltere Afferents Show Diverse Responses to Complex Stimuli with High Timing Precision and Short Latency.

Our goal was to determine which components of a complex time-varying stimulus drive the haltere primary afferents to fire, and thereby to infer the motion information that spikes transmit to the brain and the downstream motor neurons.

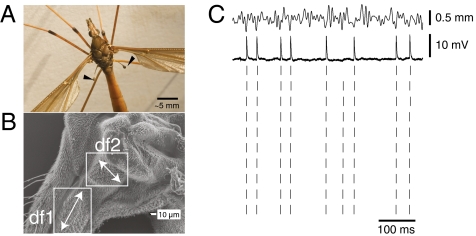
When halteres are mechanically driven by simple motion stimuli (steps and sine waves), haltere primary afferents show highly temporally precise spiking responses with short latencies (10). Here, we measured these encoding properties in response to complex stimuli. We evaluated the spike timing jitter by repeating a 10-s long segment of a white noise random motion stimulus at least 20 times; cells with fewer than 50 defined firing events (15) were not analyzed. The spike responses to these repeated trials, illustrated in Fig. 1, are highly repeatable, with small variations, from trial to trial. The mean temporal jitter, measured as the SD of the spike arrival time for each discrete event, averaged over events, for the 18 analyzed cells was 0.81 ± 0.15 ms (median = 0.78 ms), consistent with previous estimates (10). This degree of temporal precision is very high relative to the natural wing-beat period of 25 ms, also the period of oscillation of the halteres.

Fig. 1.

(A) Photograph of the crane fly Holorusia hespera. Black pointers indicate the tips of the large halteres. (Scale bar: ∼5 mm.) (B) Scanning electron micrograph of halteres of Tipula showing fields of campaniform sensilla and their approximate orientation [according to Fox and Daniel (10)]. (Scale bar: 10 μm.) (C) Haltere primary afferent responses to stimuli are highly repeatable with low jitter. Stimulus (Top), spike response (Middle), and raster plot (Bottom) of a haltere primary afferent neuron’s response to repeated presentations of the same segment of white noise.

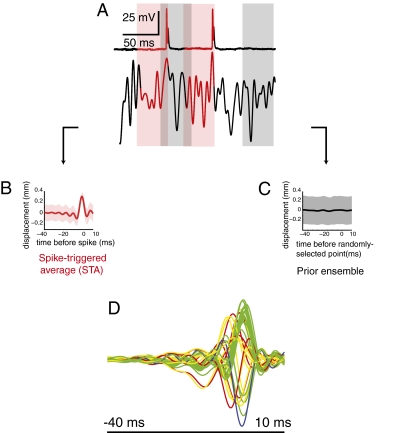
To identify the specific patterns of haltere motion that cause spiking, we used reverse correlation methods to analyze the structure of spike-triggering stimuli. We collected the set of stimulus segments immediately preceding each spike (Fig. 2A); we used segments 40 ms in length as for times earlier than 40 ms, the stimulus did not have a net effect on the arrival of a spike. The mean of this set of stimulus segments is the spike-triggered average (STA) (Fig. 2B). The STA provides a first-order estimate of what feature of the motion stimulus causes the cell to fire; it is the optimal linear estimator of the stimulus that results in a spike (16). We used the STA to estimate the response latency by finding the time at which the STA reached its maximum excursion from zero (i.e., the largest peak or trough of the STA). The mean latency of the 36 recorded cells was 3.02 ± 2.8 ms, again consistent with previous measurements (10). As a second measure of latency, we found the point at which the SD of the STA reached a minimal value. The mean time of this reduction in variance was 4.44 ± 3.8 ms before the spike. To determine the magnitude of the reduction in variance, we compared the minimum variance with that of the variance at the start of our time window (40 ms before the spike). The mean percentage reduction in variance was 51 ± 9% (Fig. 2B).

Fig. 2.

First-order analysis of white noise data. (A) Raw spike responses showing examples of stimulus segments included in the STE (pink, stimuli preceding each spike) and the prior ensemble (gray, stimuli preceding randomly chosen points). (B) STA ± SD. (C) Average of prior ensemble ± SD. (D) STAs for all 36 cells from 40 ms before to 10 ms after the spike. The color of each STA reflects the cell’s position in the scheme shown in Fig. 7B.

Given that the STA is an estimate of the feature in the stimulus to which a cell is selective, we compared the feature selectivity of all cells by overlaying their STAs (Fig. 2D). The STAs of this population of cells are diverse in their time courses (both time to peak and width of peak), their amplitudes, and even their signs. This first-order analysis of the response suggests that haltere primary afferent neurons are selective for different stimulus features.

All Cells’ Responses Contain Two Components that Resemble a Single Feature and Its Derivative.

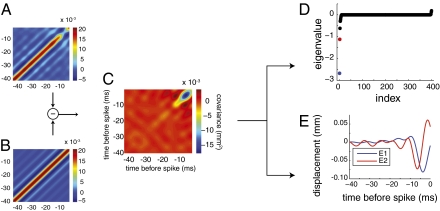
Given this diversity of average spike-triggering features, we sought to determine if there was some common structure in the neuronal responses using a more sensitive characterization. Examination of the second-order moments through principal component analysis of the spike-triggering stimuli allows one to determine multiple stimulus components that are associated with spiking activity (17 –20). Along with the ensemble of stimulus segments associated with spikes, we also sampled 40-ms segments from the stimulus at random to create a collection of stimuli that were unrelated to spiking (Fig. 2C). We refer to this random stimulus set as the “prior ensemble”; this set is used to sample the statistics of the stimulus itself, independent of the neural responses. We then computed the covariance matrices of the spike-triggering and random stimulus sets (Fig. 3 A and B) and found the difference between them (Fig. 3C). Diagonalizing the resulting matrix yields a set of eigenmodes characterizing the stimulus features that best capture what it is about the stimulus that leads to a spike.

Fig. 3.

Covariance analysis of white noise data. (A) Covariance matrix of the STE. (B) Covariance matrix of the prior ensemble. (C) Overall covariance matrix (A − B). (D) All eigenvalues of the subtracted covariance matrix; a small number are significantly different from zero. The two largest values are labeled in color. (E) Eigenvectors corresponding to the two largest eigenvalues, representing the most relevant stimulus features.

These eigenmodes allow one to reparametrize the stimulus in terms of features that are relevant to spiking by reexpressing each stimulus sample in terms of its similarity to each eigenmode. The corresponding eigenvalues quantify how important each stimulus component is for spiking by measuring the difference in its variance in the sets of spiking and random stimuli. For example, if a given component is irrelevant for spiking, its distribution in the spike-triggered and prior ensembles will be identical, the covariance matrices will cancel out, and the corresponding covariance will be zero. If a given feature is highly constrained in the spike-triggering ensemble, for instance, if the system must cross threshold with respect to a given stimulus component to spike, the variance in the spike-triggered ensemble (STE) for that component will be less than in the prior, and that component will be associated with a significant negative eigenvalue. Thus, examining the eigenvalues of the diagonalized matrix allows one to identify a smaller set of stimulus descriptors (relative to the original 40-ms time sequence) required to capture the input/output properties of the system. We found that most eigenvalues of the diagonalized matrix are close to zero but that a small number are significantly different from zero (Fig. 3D). In Fig. 3E, we show the relevant eigenmodes or features corresponding to the most significant eigenvalues for an example cell.

In all cells, we noted that a pair of the most significant eigenvectors had the property that one was close to the derivative of the other (20). In 30 of the 36 cells, the eigenvector corresponding to the second-largest negative eigenvalue was close to the derivative of the eigenvector corresponding to the largest negative eigenvalue (Fig. 3 D and E). Of the remaining 6 cells, 4 showed a feature-derivative relationship between the largest negative and largest positive eigenvectors; 1 had such a relationship between the second-largest positive and largest positive eigenvectors; and in 1 cell, the largest negative eigenvector resembled the derivative of the second-largest negative eigenvector.

Most Cells Are Selective in Multiple Stimulus Dimensions.

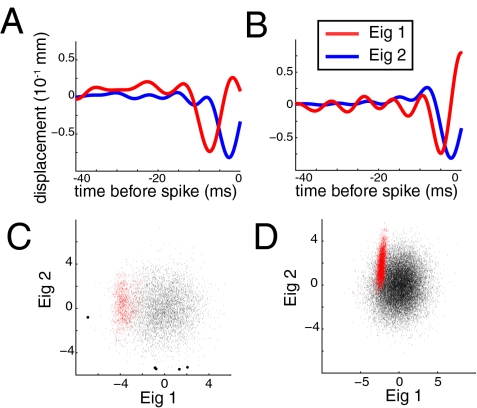
The preceding analysis allows us to represent the stimulus using only the few stimulus components that are relevant to the cell’s response. For each cell, we plotted each stimulus segment in terms of its similarity to (i.e., linear projection onto) the derivative pair features f₁, f₂ (Fig. 4 A and B). Neural selectivity for motions that are similar to either of the features can be seen by comparing the distribution of that component in the spike-triggering stimuli with that in the prior ensemble. A cell was selective to a particular stimulus feature if the distribution of spike-triggering stimuli (Fig. 4 C and D, red dots) was very different from the distribution of the randomly chosen stimuli (Fig. 4 C and D, black dots). We see that some cells are primarily selective only in a single dimension (Fig. 4C, 7 cells), whereas others are sharply selective in two dimensions (Fig. 4D, 29 cells).

Fig. 4.

(A and B) Relevant features (two largest eigenvectors of the covariance matrix) for two different cells. Each cell had at least two relevant eigenvectors, one of which resembled the derivative of the other. (C and D) Dot products (projections) of each stimulus segment from the STE (red) and prior ensemble (black) and the derivative pair features shown in A. (Left) Figures show a cell selective in one dimension: The distribution of spike-triggering segments differs from that of the prior segments along only one axis. (Right) Figures show a cell selective in two dimensions: The spike-triggering segments have a different distribution than the prior segments along both axes.

The Encoding of All Haltere Neurons Can Be Described by a Single Pair of Population Features and a Phase.

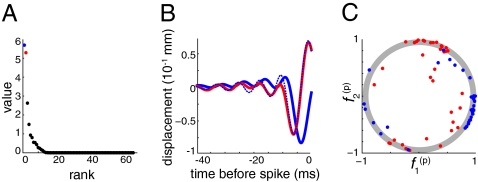
Each cell had a distinct STA and a unique set of derivative pair features (f ₁ ⁱ, f ₂ ⁱ) (indexed by the cell label i) that described its selectivity. To examine underlying similarities among these features, we used singular value decomposition to analyze the set of features comprising the derivative pairs collected from individual cells. Because the covariance analysis described previously exposed the unifying features in each cell’s set of spike-triggering stimuli, singular value decomposition of the set of individual cell features allows us to find feature selectivity that is common among the entire population of cells. The singular values of the nonsquare matrix constructed from this list of features revealed that two dominant “population features,” f ₁ ^(p) and f ₂ ^(p) (Fig. 5A), account for the majority (57%) of the variance in the feature set. These population features also form a derivative pair (Fig. 5B). Representing each cell’s individual features in the 2D plane described by the population features (Fig. 5C) shows that most cell features (f ₁ ⁱ, f ₂ ⁱ) are indeed well described as a linear combination of f ₁ ^(p) and f ₂ ^(p): When the population feature pair accounts for the majority of the structure of the original pair, the length of the vector in the [f ₁ ^(p), f ₂ ^(p)] plane is close to 1 (points falling inside the shaded area; Materials and Methods). Thus, the main difference between the features that drive individual cells is captured by the specific linear combination a f ₁ ^(p) + b f ₂ ^(p), which approximates a given f ⁱ. For each cell, the coefficients (a, b) describe different points around the unit circle, and can thus be reduced to a single number, the phase on the unit circle.

Fig. 5.

Results of singular value decomposition of the derivative pair features from all 36 cells. (A) Singular values. (B) Population features corresponding to largest singular values (blue, first feature; red, second feature; dotted blue, calculated derivative of first feature). (C) Projections of each cell’s most significant feature (blue) and the derivative-like feature (red) onto the population features. The shaded circle includes linear combinations with vector length ranging from 0.9 to 1.

These Population Features Capture Much of the Information Captured by the Individual Cells.

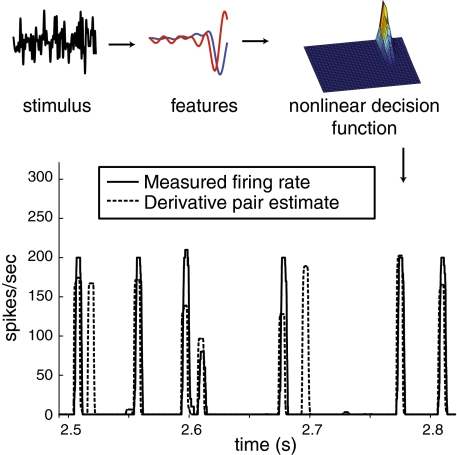
From the individual cell features and the population features, we constructed low-dimensional models that allowed us to predict spiking responses to arbitrary stimuli. These models also allowed us to compute the mutual information—a measure of correlation between stimulus and response—captured by both each cell’s measured features and the population features. The spike-rate predictions constructed using the derivative pair eigenvectors all predicted spike events accurately when given a unique arbitrary white noise stimulus (Fig. 6). These models captured >99% of the recorded spiking events, with falsely predicted events comprising 15% of the predicted spikes. Approximately half of these falsely predicted events occurred less than 20 ms after a correctly predicted firing event, suggesting that cell refractoriness (not included in the model) suppresses some bursting.

Fig. 6.

(Upper) Schematic of 2D spike-predicting models. An arbitrary stimulus is projected onto the two derivative pair features. These projections, combined with a 2D histogram of projections of the STE and prior ensemble onto the two features, predict the firing rate. (Lower) Model’s predictions of firing rate response to an arbitrary white noise stimulus. The measured firing rate is a response to a repeated white noise segment rather than to the continuous white noise used to extract the features and construct the histogram.

We used a direct method of estimating mutual information (21) in the group of 25 cells for which we had obtained a sufficient number of responses to repeated stimuli. Eight of these cells were included in the group of 36 cells used in our covariance analysis. Direct estimates of information rate found an average mutual information of 4.42 ± 1.79 bits per spike for the 25 cells measured. 2D models using each cell’s individual features captured, on average, 3.34 ± 0.97 bits per spike (75% of the measured information). The population features captured an average of 2.90 ± 1.08 bits per spike (66% of the measured information). Models based on the population features capture, on average, 86 ± 14% of the information captured by models based on the derivative pairs.

Predictions of Responses to Sine Wave Stimuli Show a Broad Range of Phase Responses.

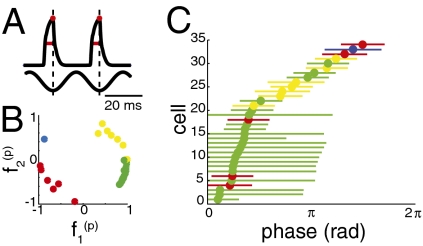
Given that the feature selectivity of each cell can be described as a unique combination of two common features, how might these particular phases in the [f ₁ ^(p), f ₂ ^(p)] plane allow the cells to respond differently to simple stimuli? Using the derivative pair eigenvectors and decision functions of each cell, we predicted the responses to sine wave stimuli at wing-beat and twice wing-beat frequencies and at several stimulus amplitudes. In each cell, we calculated the mean phase of the peak firing rate and estimated the cell’s phase precision by measuring the width at half of the maximum firing rate (Fig. 7A). We divided the cells into four groups based on the projection of the dominant feature onto the [f ₁ ^(p), f ₂ ^(p)] plane (Fig. 7B). Each cell’s peak firing rate occurred at a unique phase, and the population of cells from which we recorded contained cells whose peak phases spanned nearly the entire cycle (Fig. 7C). Although the preferred phase of individual cells changed slightly with stimulus frequency and amplitude, the distribution of phases across the sine wave cycle did not. For many cells, the preferred phase was correlated with the phase relationship of its derivative pair features. For example, if the projection of the cell’s dominant feature onto f ₁ ^(p) was positive and its projection onto f ₂ ^(p) was negative, the predicted response to sine waves was greatest at an earlier phase (Fig. 7C, green dots).

Fig. 7.

Each cell’s peak firing rate occurs at a unique phase. Firing rates in response to sine wave stimuli were predicted using the method shown in Fig. 6. (A) Schematic for determining preferred stimulus phase (red dot) and approximate phase error (red line, width at half-maximal height) from the predicted firing rates. (B) Each cell’s first eigenvector projected onto the two population features (see Fig. 5C), colored according to quadrant. (C) Predicted preferred stimulus phases, with approximate errors, for all cells in response to a 40-Hz sine wave stimulus. Cells with a predicted firing rate of zero are excluded.

Discussion

By stimulating the haltere with white noise motion while recording from its primary afferent mechanoreceptors, we were able to determine the feature selectivity of these crucial flight-control organs. Haltere primary afferent mechanoreceptors are able to encode stimuli over a broad range of frequencies using a small number of stimulus dimensions and transmit this information at a high rate to the central nervous system. The similarities of these two stimulus dimensions across all cells, and the ability of the two population features to capture a large fraction of the information contained in the cells’ individual features, is evidence that there is a single encoding strategy employed by haltere neurons. Furthermore, each cell’s dominant features are sufficient to predict spiking activity in response to complex stimuli with relatively high accuracy, which is a significant improvement over previous linear analyses of haltere function (10).

Haltere Afferents Are Selective in Multiple Dimensions.

Although the STA, as measured in terms of haltere position, reflects some general properties of the stimuli that trigger spiking, it does not capture the full dimensionality of the response. The stimulus contains numerous higher order modes (e.g., velocity, acceleration, impulse), and we have used principal components analysis to find those aspects of the stimulus that are most relevant to spiking activity. Although a few cells were primarily selective for a single dimension of the stimulus (Fig. 4 A and C), a majority of cells showed very sharp thresholds in two stimulus dimensions (Fig. 4 B and D). In many of these cells, the second feature strongly resembled the derivative of the first feature. The projection of an arbitrary stimulus onto these features and the cell’s nonlinear decision function could be combined to create a reasonably accurate reconstruction of the cell’s firing rate (Fig. 6), suggesting that these two features are sufficient to capture the cell’s encoding activity.

Encoding Is Similar Across All Cells.

The advantage of considering each neuron’s response selectivity in multiple dimensions is evident from our analysis of the population. Despite the broad range of forms in the STAs, we found, using singular value decomposition of the two leading features from each cell, that two population features captured most of the feature selectivity of the entire group of cells. Projections of the individual cells’ leading features onto the population features (Fig. 5C) show that the feature selectivity of most cells can be described by a linear combination of these two features. The population features capture an average of 86% of the information captured by the cell’s individual derivative pair eigenvectors, suggesting that most haltere afferents share selectivity to the same two stimulus dimensions but with differing weights. We were able to relate these weights to the neurons’ preferred phase of response to a sinusoidal stimulus (Fig. 7 B and C).

Similarity of Encoding Provides Further Evidence of Structural Rather Than Neural Specialization.

Previous studies on the encoding properties of halteres found latency, phase, and bandwidth among haltere primary afferents that suggested the potential encoding of many different forces, including Coriolis forces (10). The present study supports this hypothesis by exploring the potential responses of halteres with white noise and finding only minor differences in their responses, suggesting that all campaniform sensilla share a multidimensional feature selectivity that would permit detection of diverse forces. Similarities between the neural responses of haltere primary afferents and the homologous campaniform sensilla on the wings of the fly (22) suggest that there may be a generalized encoding strategy used by all flight-associated campaniform sensilla.

A Population of Campaniform Sensilla with a Common Encoding Strategy and Diverse Phase Sensitivity Permits Detection of Numerous Forces, Including Coriolis Forces.

Given that the main difference in encoding between neurons is the phase of the leading features, we hypothesize that the large population of primary afferents both increases the acuity of strain sensing in the haltere and opens the possibility for more complex coincidence-detection algorithms at higher levels.

The phase shift between neurons of the haltere could arise from two sources: first, the cells may simply be experiencing the features of the stimulus at slightly different times because of their positions on the haltere (23), or, second, there could be some intrinsic delay in spike generation that differs from cell to cell. Although the first scenario seems more likely, either case results in a population in which spatiotemporal resolution is increased as a result of a larger number of campaniform sensilla.

Although an array of sensory cells could serve a functional purpose in any mechanoreceptive system, the haltere’s function as a gyroscopic organ begs the question: How might an array of similar sensors with distinct preferred phases work to encode Coriolis forces? The differential phase encoding among the campaniforms allows the possibility of higher level processing to address the fundamental problem of detecting small out-of-plane motions (attributable to Coriolis forces) among the background of the large in-plane signal caused by the haltere’s oscillation during flight (3, 24). The haltere oscillates in a sinusoidal or triangle-wave pattern (5, 24), and rotations of the body introduce small deviations to this pattern in the plane orthogonal to the axis of oscillation. These motions can change the shape of the haltere’s tip trajectory from a simple line into an ellipse or a figure-of-eight, depending on the plane of rotation (24). The phase of the wing stroke at which peak strain occurs will shift depending on the magnitude of the body rotation. Given that each haltere neuron responds to a sinusoid stimulus at a preferred phase, the identity of the first neurons activated by the stimulus will also vary with the magnitude of the body rotation. The differential activation of specific campaniform sensilla in response to various forces, combined with high spike-timing precision (10), would allow the campaniform array to detect complex stimuli accurately while executing complex flight behavior.

Materials and Methods

Preparation and Recording.

All recordings were performed on adult female crane flies (Holorusia hespera) caught in Snohomish and King Counties in Washington State during July and August 2008. Crane flies were kept at 4 °C in sealed individual containers with a moist paper towel until they were removed for an experiment. In preparation for recording, legs and wings were removed and the dorsal aspects of the thorax and abdomen were attached with dental wax to a metal rod mounted on a micromanipulator. We dissected the lateral aspect of the thorax by removing the anepisternum, anepimeron, and much of the thoracic musculature to expose the haltere nerve. A hypodermic syringe needle was bent into a hook, attached to a micromanipulator, and placed underneath the haltere nerve to stabilize it for intracellular recordings. This syringe also delivered insect saline [150 mM NaCl, 3 mM CaCl₂, 3 mM KCl, 10 mM N-Tris(hydroxymethyl)methyl-2-aminoethanesulfonic acid buffer, and 25 mM sucrose, pH 6.5–7.5] (25) to the preparation. We used quartz glass microelectrodes with a resistance of 30–150 MΩ that were made with a Sutter Instruments P-2000 puller and filled with 1 M KCl to record action potentials from single afferent axons in the haltere nerve. Given the large number of campaniform sensilla and small numbers of other sensors (chordotonal organs or sensory hairs) (26), we assume that we are recording from campaniform sensilla afferents. Membrane voltages were amplified with a Neuroprobe 1600 amplifier (AM Systems), converted to audio signals, and recorded using a data acquisition board (USB-6251; National Instruments) at 10 kHz, which was sufficiently fast to capture the times of spike occurrences to 0.1-ms accuracy.

Because preliminary recordings showed that haltere primary afferents were not spontaneously active, we mechanically oscillated the haltere with a low-frequency (5–15 Hz) sinusoidal stimulus before and during cell impalement. The absence of spikes between stimulation events in our records confirmed that these cells were not spontaneously active. The electrode was advanced with a piezoelectric motor (MPM-10 Piezo translator with DC3001 motorized micromanipulator; World Precision Instruments) until spikes were audible. We recorded spiking responses from a total of 53 cells in eight animals. During recording, we stimulated the haltere using a capillary tube (internal diameter = 0.75 mm, external diameter = 1.0 mm) attached to a small motor (MicroMax Series 671; Cambridge Technology, Inc.). The haltere tip was placed inside the capillary tube and oscillated either in the approximate natural stroke plane (dorsoventral) or in the plane orthogonal to the stroke plane (anteroposterior). Because we did not find any directional differences between spike responses in our analyses, data from both planes were pooled. To measure the motion of our motor directly, we placed a photodiode underneath the tip of the capillary tube and oscillated the motor with the same white noise stimulus as used in experiments. We obtained an approximate voltage-to-distance conversion factor by using the micromanipulator to move the motor 1 mm while recording the voltage in the photodiode. We then recorded the photodiode’s voltage while oscillating the motor with our experimental stimuli to obtain the stimulus voltage-to-distance conversion. We found that, on average, a change in stimulus voltage of 1 V corresponded to 0.5 mm of translation. Given an approximate haltere length of 4 mm and a maximum stimulus voltage amplitude difference of 2.5 V, the maximum haltere excursion during noise stimulation was ≈17°. Additionally, we tested the motor’s ability to deliver the noise stimulus accurately by oscillating the motor with our experimental stimuli and recording the photodiode’s voltage. A Bode plot of the gain and phase between the stimulus voltage and the photodiode’s voltage showed no significant gain or phase shift between the input voltage and the resulting output.

The voltage input to the servo-motor was driven by the data acquisition board, which was controlled with custom Matlab (The Mathworks) code. We oscillated the motor using band-limited Gaussian noise (BLGN) with a frequency range of 1–150 Hz, which includes frequencies below, at, and above the frequency of naturally occurring Coriolis forces. In some recordings, we recorded continuously for as long as possible. For these stimuli, we considered the dataset to be sufficiently large if we were able to collect >1,000 spikes. Thirty-six such recordings were obtained in seven animals, lasting a mean of 5.56 min and capturing a mean of 6,193 spikes. In other recordings, we interleaved 10 s of random white noise with a single 10-s segment of white noise. These repeated segments were used to generate raster plots and information calculations. We obtained between 20 and 60 responses 10 s in length to repeated segments in 25 cells in seven animals (six of which were also used in the continuous-recording experiments above). Eight of these 25 cells were among the 36 cells mentioned previously in which we obtained continuous recordings with BLGN.

Data Analysis.

Data were analyzed with custom-built Matlab software. Cell voltages were bandpass-filtered (80–1,000 Hz), and spike times were discriminated using a thresholded sliding-window algorithm (custom Matlab code by M.S. Tu, University of Washington, Seattle, WA).

Jitter Calculation.

Responses to repeated stimuli were binned into histograms at a resolution of 1 ms. We defined a response event as any 1-ms bin in which the mean firing rate was 10 times the cell’s baseline firing rate. From the collections of all response events in the dataset, we determined which events consisted of single spikes with no contaminating spikes in a 5-ms window around the event (15). We found the time of the spike in this window for each trial and calculated jitter as the SD of the event time across all trials.

Covariance Analysis in Single Cells.

We used covariance analysis to find the stimulus features that had the most significant influence on the spike response (20). Using the continuous responses of 36 cells under BLGN stimulation, we built the STE by selecting the stimulus history in a 40-ms time window before each recorded spike in each cell. We excluded any spikes that occurred less than 3 ms after the previous spike, thus eliminating secondary spikes in bursts. The mean of the STE is the STA. For each cell, we found the covariance matrix of the STE and subtracted the covariance matrix of the prior stimulus ensemble to find the overall covariance matrix. We then found the eigenvalues and the corresponding eigenvectors of this matrix (Fig. 3).

Singular Value Decomposition in the Population of Cells.

We used singular value decomposition to examine whether a small number of features could capture the response properties of haltere primary afferents as a group (27, 28). Using covariance analysis as described previously, we found the four most significant positive and negative features for each cell and identified a pair of features within this set in which the second selected feature resembled the derivative of the first. The singular value decomposition of a matrix of these feature pairs was used to derive population features that described the feature selectivity of the entire group of cells from which we recorded.

Modeling Neural Responses Using Low-Dimensional Models.

Using the methods of Fairhall et al. (20), we used the principal components of our covariance matrices to predict spike rates to arbitrary stimuli. We used Bayes’ rule (20):

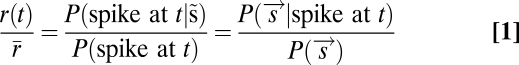Here, the vector 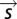is some representation of the stimulus: in principle, the full time series of the input. In practice, we wished to use a lower dimensional representation of the stimulus that captures most of the dependence of the spiking output on the input. This is provided by the features derived through reverse correlation. In this case, 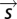denotes the components of the stimulus corresponding to the identified features. Thus, we projected the STE and prior ensemble, respectively, onto one or more relevant features (the first eigenvector, the derivative eigenvectors, or the population features) and binned the resulting values to fi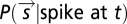nd and 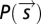. The quotient of these two probability histograms (Eq. 1) is a nonlinear function of 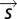that predicts the time-varying firing rate 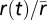(Fig. 6). The firing rate for a given arbitrary stimulus is therefore found by projecting it onto the relevant feature(s) to determine 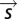and then looking up the corresponding firing rate from the decision function.

We used data from the continuous white noise recordings to construct the model and tested its ability to generalize to an arbitrary stimulus by predicting the firing rate in response to a novel 10-s random stimulus. In the recording session, we repeated this random stimulus multiple times to allow us to estimate the repeatability of the stimulus through calculations of jitter and information.

Information Calculations.

We used a method to measure information transmission directly from the spiking responses. To measure information using this “direct” method (21), we used the responses to repeated BLGN segments to compute

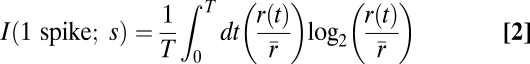where T is the total time of the repeated segment, r(t) is the mean spike rate at a given time (averaged over several repeats), and 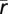is the overall spike rate for the random segment. Because the spike rates and the computed information content are dependent on the time bin resolution, we measured information using decreasing bin sizes from 10 to 1 ms and extrapolated to infinitely small bins using linear regression to calculate a 95% confidence interval for the extrapolated point. Similarly, we ensured that we had a sufficiently large number of repetitions by subsampling the data using a fraction of the total repetitions and recalculating the information (given a fixed bin size). We found that the information estimate stabilized quickly with increasing repetitions. In all cells in which we collected more than 20 repetitions, the estimate reached an asymptote by 20 repetitions, suggesting that 20 repetitions were sufficient to obtain a reliable direct information estimate from all 25 cells. We removed any repeats during which the firing rate was more than 20% above or below the mean firing rate across all trials for that cell. We calculated information using the direct method on the set of 25 cells and removed one large outlier with a very low firing rate from our dataset.

To calculate information captured by the low-dimensional models, we used the following equation developed by Fairhall et al. (20):

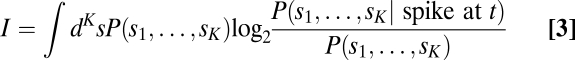where K is the number of dimensions used to construct the model. This equation was used to compare the information content of models constructed with an individual cell’s derivative pair eigenvectors with models made using the population features.