Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2010 Feb 4;107(8):3864–3869. doi: 10.1073/pnas.0906765107

Mechanical amplification by hair cells in the semicircular canals

Richard D Rabbitt a,b,1, Richard Boyle c, Stephen M Highstein b
PMCID: PMC2840494  PMID: 20133682

Abstract

Sensory hair cells are the essential mechanotransducers of the inner ear, responsible not only for the transduction of sound and motion stimuli but also, remarkably, for nanomechanical amplification of sensory stimuli. Here we show that semicircular canal hair cells generate a mechanical nonlinearity in vivo that increases sensitivity to angular motion by amplification at low stimulus strengths. Sensitivity at high stimulus strengths is linear and shows no evidence of amplification. Results suggest that the mechanical work done by hair cells contributes ∼97 zJ/cell of amplification per stimulus cycle, improving sensitivity to angular velocity stimuli below ∼5°/s (0.3-Hz sinusoidal motion). We further show that mechanical amplification can be inhibited by the brain via activation of efferent synaptic contacts on hair cells. The experimental model was the oyster toadfish, Opsanus tau. Physiological manifestation of mechanical amplification and efferent control in a teleost vestibular organ suggests the active motor process in sensory hair cells is ancestral. The biophysical basis of the motor(s) remains hypothetical, but a key discriminating question may involve how changes in somatic electrical impedance evoked by efferent synaptic action alter function of the motor(s).

Keywords: active process, auditory, hair bundle, inner ear, motor

Vestibular organs resembling those of modern humans first appeared in primitive fish over 400 million years ago (1) and have remained relatively unchanged to provide sensations of gravity, motion, and vibration. These inner-ear organs rely on sensory hair cells to convert mechanical motion of their microvilli (stereocilia) bundle at the apical end of the cell into synaptic neural transmission at the basal end. In auditory organs, hair cells are known to have a dual role and serve not only as mechanosensitive transducers but also as motors that mechanically amplify quiet sounds within the ear (2). In mammals this amplification is partially the result of piezoelectric-like somatic electromotility of cochlear outer hair cells (3), motility that requires expression of the protein prestin in the plasma membrane (4, 5). Hair-cell amplification is controlled by the brain through an extensive centripetal efferent innervation in the cochlea synapsing on outer hair cells (6). Activation of medial olivocochlear efferent neurons sharply reduces the mechanical vibration and tuning of the cochlear organ of Corti (7, 8) through the inhibitory action of efferent neurotransmitter(s) on the motor output of outer hair cells (9, 10). Taken together, these findings reveal that the mammalian cochlea is an active electromechanical amplifier controlled by the brain to be exquisitely sensitive to low sound pressure levels of interest to the organism. Whether an amplification strategy is a general principle of sensory hair-cell organs or is limited to a subset of hearing organs remains a topic of debate. We know that somatic electromotility and the protein prestin are specialized to the mammalian cochlea and are not present in other hair-cell organs (11). Nonetheless, there is evidence that a similar active amplification process may be at play (12 –14). Short hair cells of the avian auditory organ (15), for example, exhibit active hair-bundle movements (16) in the absence of somatic electromotility (17). These hair cells are recipients of an extensive efferent innervation (18) that may control the active bundle-based amplification analogous to control of somatic motility in mammalian outer hair cells (19). It also has been shown that saccular hair bundles of the bullfrog (20) and semicircular canal hair bundles of the eel (21) move in response to transepithelial electric fields and may generate physiologically relevant forces during transduction. Hair bundles from the saccule exhibit an active process, compressive nonlinearity, that enhances mechanical motion for low stimulus strengths (22), and spontaneous oscillations (23, 24) demonstrating the ability of the hair bundle to do mechanical work on the environment. Mechanical power output and amplification by the hair bundle can be evoked by driving the motion of the hair bundle with flexible fiber (25). These features are fundamentally nonlinear and suggest that hair bundles may be poised on the brink of a limit cycle oscillation to maximize tuning and amplification (26). The extent to which this active process is physiologically relevant to semicircular canal vestibular sensation is unclear. Analogous to the mammalian cochlea and other auditory organs, the vestibular semicircular canals generally receive an extensive efferent innervation that controls sensitivity to physiological stimuli (27 –30), but it is not known if efferent activation alters hair-bundle motion or amplification. These and related data compel the hypothesis that vestibular organs are active electromechanical amplifiers that are controlled by the brain via the efferent system. To test this hypothesis, we measured the motion of fluorescent microbeads attached to the cupula overlying hair bundles in the vestibular semicircular canals in response to physiological stimuli in vivo. Results demonstrate an active process that amplifies cupula movements for low stimulus strengths in the semicircular canals. The micromechanical nonlinearity and amplification were eliminated by electrical activation of the brainstem efferent vestibular nucleus, thus proving the hair-cell origin of the mechanical amplification reported here.

Results and Discussion

Each semicircular canal forms a toriodal loop of fluid that displaces in response to angular acceleration of the head. This fluid displacement compels deflection of a gelatinous diaphragm, the cupula, that spans the entire cross-section of the ampulla and covers the sensory epithelium. Deflection of the cupula leads to sensory transduction through gating of mechanosensitive ion channels located in the stereocilia of hair cells and, potentially, reversing transduction and amplification through active forces generated by the hair cells and/or hair bundles. Using the approach illustrated in Fig. 1, we measured motion of fluorescent microbeads adhered to the surface of the cupula and recorded single-unit afferent discharge in response to micromechanical indentation of the canal duct [which mimics angular rotation of the head (31)], both with and without bipolar electrical stimulation of the efferent vestibular nucleus [which mimics neural control of vestibular sensation (32)]. We used a teleost fish, Opsanus tau, as the experimental model to facilitate the approach (30, 33). Fig. 2 shows typical displacements of the cupula (Fig. 2 B and E) and the discharge rate in spikes per second (skp/s) of two selected afferents (Fig. 2 A and D) in response to an ∼20-μm mechanical indentation of the duct (Fig. 2 C and F). A 20-μm (peak-to-peak) sinusoidal mechanical indentation has been shown to produce endolymph displacement and afferent responses equivalent to a peak-to-peak sinusoidal angular head velocity of ∼80 °/s (31). Cupula motion followed the sinusoidal stimuli (Fig. 2B) and exhibited slow adaptation in response to step stimuli (Fig. 2E). It is important to note that motion was measured near the center of the cupula and, because the cupula deflects like a diaphragm attached around its entire periphery (34), hair-bundle deflections would be considerably smaller in magnitude (33). Consistent with previous reports in this species, afferents exhibited more harmonic distortion relative to the cupula and multiple time constants of adaptation to step stimuli, with some units entering cut-off during inhibitory stimuli (35). These discharge patterns quantify the neural code transmitted to the brain by the semicircular canals.

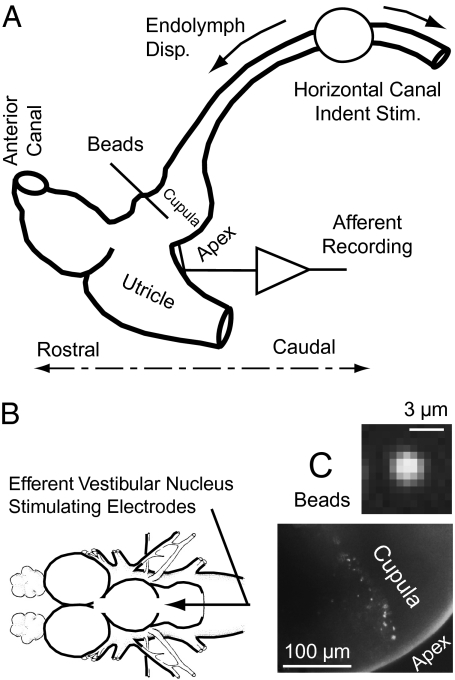
Fig. 1.

Fig. 1.

Open in a new tab

Experimental set-up. (A) Schematic of surgically exposed region of the membranous labyrinth showing location of indentation stimulus, single-unit afferent recording, and fluorescent microbead placement. (B) Bipolar stimulating electrodes placed in the brainstem efferent vestibular nucleus. (C) (Lower) Fluorescent microbeads adhered to the cupula. (Upper) Intensity of a single bead viewed through the transparent membranous labyrinth in the living animal.

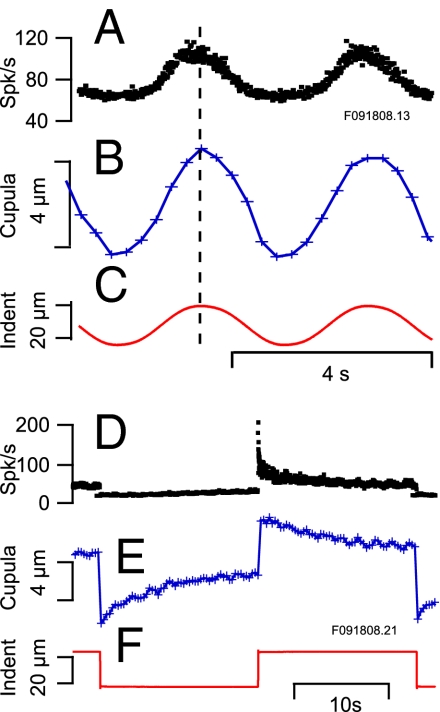
Fig. 2.

Fig. 2.

Open in a new tab

Afferent discharge and cupula displacement. (A–C) Afferent discharge (A) and cupula motion (B) recorded simultaneously in response to sinusoidal mechanical indentation of the membranous duct (C). The electronic shutter of the CCD camera was open ∼50 ms to collect each image. Image acquisition times (“+” in B and E) define the times when bead positions were measured; straight lines connect the data points to clarify the waveform. (D–F) Afferent discharge and cupula motion for step indentation stimuli showing the excitatory–inhibitory asymmetry adaptation of afferent discharge that was not present in cupula motion (which was nearly symmetric at these stimulus levels) and differences in time constants of afferent vs. cupular adaptation. Note that 1-μm sinusoidal mechanical indentation evokes afferent responses and cupula displacements equivalent to ∼4 °/s angular velocity of the head (31); hence the 20-μm stimuli are equivalent to an angular head velocity of 80 °/s (peak-to-peak). The small periodic oscillations in D and E are the result of an uncorrected respiration movement artifact.

Also consistent with previous reports in this species, activation of the efferent system typically evoked an increased average discharge rate and reduced gain that varied in time course and magnitude between individual afferents (30, 32). The change in average discharge and gain in one example unit is illustrated in Fig. 3A for a sinusoidal stimulus (Fig. 3C). Concomitant efferent-evoked changes in cupula motion were not present (Fig. 3B). Rather, efferent effects on afferent discharge were caused primarily by inhibitory synaptic contacts on hair cells that underlie the reduced gain and by excitatory synaptic contacts on afferents that underlie the increased background discharge (30). Although the predominant efferent effects are on the neural level (compare Fig. 3 A and B), we were interested specifically in determining if a mechanical component was present at low stimulus levels where a hair-cell active process might be observable. To investigate this question, we used tonic efferent activation. Tonic activation of the efferent vestibular system generates an initial transient increase at the onset of the stimulus followed by tonic changes in afferent discharge rate and gain (29, 30). One example from the present set of experiments is shown in Fig. 3 D and E where the discharge rate of this afferent adapted to a tonic level with no obvious change in the adaptation time constant (*) to mechanical stimuli (35). Subsequent results shown in Fig. 4 and Fig. 5 were obtained during this form of tonic efferent activation.

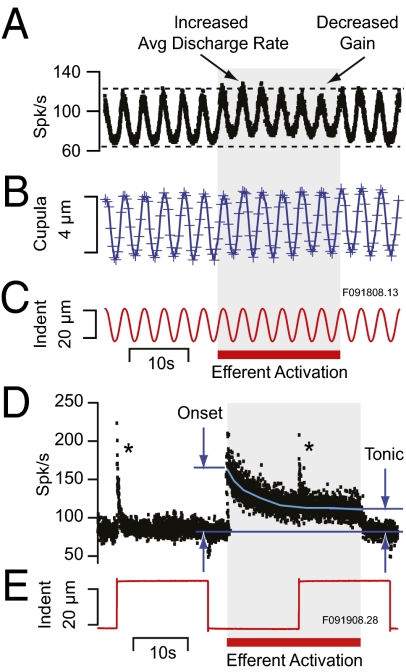
Fig. 3.

Fig. 3.

Open in a new tab

Efferent action on afferent discharge. (A–C) Activation of the efferent vestibular system by delivering 200 shocks per second to the brainstem (30) typically increased the average discharge rate (spk/s) of sensitive afferents and reduced the peak-to-peak amplitude of modulation. For sinusoidal stimuli greater than ∼2-μm indentation (equivalent to ∼8°/s angular head rotation), efferent activation had no obvious effect on displacement of the cupula (e.g., B). (D and E) Continuous activation of the efferent system evoked tonic changes in afferent discharge rates far outlasting transient discharge modulations induced by mechanical stimuli (*). Subsequent results shown in Figs. 4 and 5 report changes in cupula motion during tonic efferent activation.

Fig. 4.

Fig. 4.

Open in a new tab

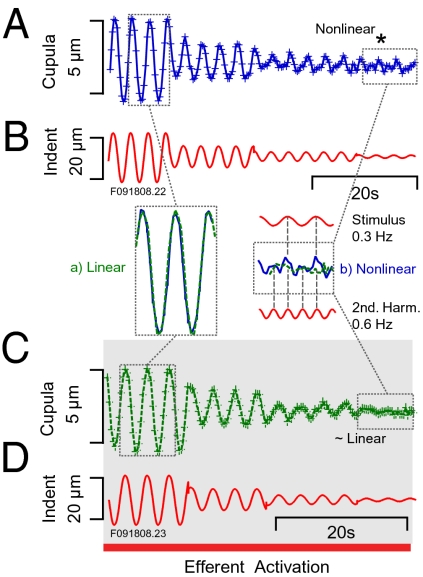
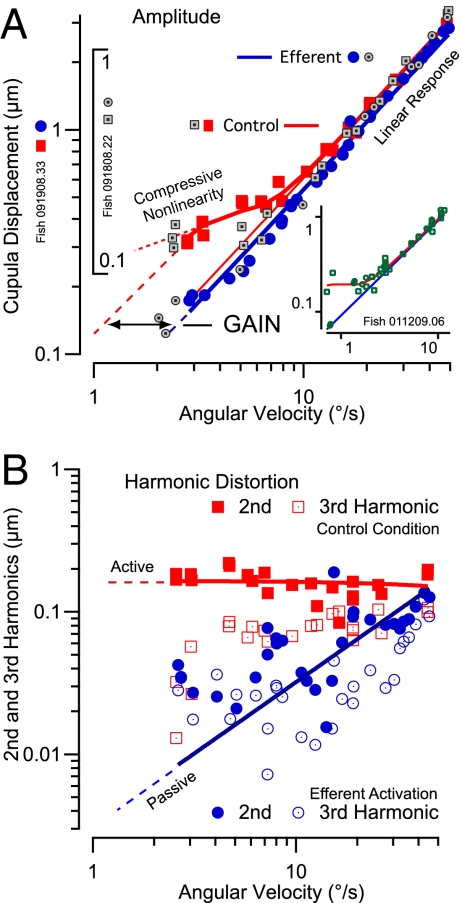
Nonlinear micromechanical displacements for stimuli near the threshold of sensation. (A and B) Displacement of the cupula as a function of stimulus level at 0.3 Hz. Cupula motion linearly followed the stimulus at high levels of stimulation. At low stimulus levels cupula motion exhibited increased harmonic distortion and higher gain associated with nonlinearity in response. (C and D) At high mechanical stimulus strengths, electrical activation of the efferent system had no effect on motion of the cupula, but at low stimulus strengths harmonic distortion and nonlinear gain observed in the control condition were eliminated. Insets show direct comparisons of responses in the control (A) and the efferent activated conditions (C) for high (a, linear) and low (b, nonlinear) stimulus strengths.

Fig. 5.

Fig. 5.

Open in a new tab

Mechanical compressive nonlinearity and elimination by efferent activation. (A) First plus second harmonic displacement of the cupula as a function of equivalent angular head velocity for sinusoidal stimuli at 0.3 Hz in three animals (indicated by red and blue symbols, by gray symbols, and (in Inset) by green symbols, respectively). A compressive nonlinearity amplifying the response of the cupula was present for cupula displacements below ∼500 nm (red curves, filled squares). The nonlinearity was eliminated by electrical activation of the efferent vestibular system (linear growth with stimulus; blue line, filled circles). (B) Nonlinearity is manifested primarily in the second harmonic illustrated here for the first animal from A. The second harmonic of cupula motion shows an active process that feeds mechanical power into the response (active, solid red line). The large second harmonic was eliminated during efferent activation (blue filled circles). Third harmonics are shown also (open symbols) and were consistent with passive harmonic distortions that grow in linear proportion to the stimulus (passive; solid blue line). See Results and Discussion for further details.

We measured the micromechanical response as a function of stimulus strength to examine if cupula movements involved active power output by hair cells. Fig. 4A provides raw data illustrating a nearly linear response for large-magnitude stimuli that became nonlinear and distorted for low-magnitude stimuli (Fig. 4A). This behavior was eliminated by tonic activation of the efferent vestibular nucleus (Fig. 4C), activation that is known to disable a subset of hair cells in the semicircular canal by opening a large ionic conductance in the basal membrane (30). Insets in Fig. 4 directly compare cupula displacements in the control condition (solid blue line) and displacements with efferent activation (green dashed line). For large-strength stimuli (a), responses in the two conditions were virtually identical and tracked the 0.3-Hz sinusoidal stimulus. Responses for large-strength stimuli were dominated by the first harmonic, with low harmonic distortion and only one peak per cycle. For low-strength 0.3-Hz sinusoidal stimuli (b), cupula displacements in the control condition exhibited a large second harmonic component (at 0.6 Hz), manifested in this example as two peaks per cycle and resembling a rectified response. This second harmonic was greatly reduced during efferent activation (green dashed line). Dependence of cupula displacements on stimulus strength and efferent activation are quantified in Fig. 5. Fig. 5A plots the amplitude (first plus second harmonics) as a function of angular velocity of the head. Results for three animals were converted to equivalent angular head velocity using a 1-μm indentation as equivalent to a 4 °/s angular velocity (31). The response was nearly linear for cupula motions >500 nm and mechanical stimuli >7 °/s but deviated from linearity at lower levels. In rhe five animals tested, the mechanical stimuli above which the response was linear averaged 4.5 °/s (SE 1.2°/s).

Activation of the efferent system extended mechanical linearity to the entire range studied (∼100 nm–3 μm; solid blue diagonal line intercepting zero). For cupula motions less than ∼500 nm, micromechanical displacement of the cupula was amplified. This increased displacement compresses a broad range of stimulus strengths into a narrower range of cupula responses and therefore is termed a “compressive nonlinearity.” Results are analogous to the compressive micromechanical response of the basilar membrane in the mammalian cochlea (36). For low-strength stimuli, the amplification gain associated with compression was about 6 dB. This amplification gain was computed using the formula GdB = 20log(A/P), where GdB is the gain, A is the cupula displacement in the active control condition, and P is the cupula displacement in the passive condition during tonic efferent activation. We were not able to discover the lower limit of the mechanical compressive response or the full gain associated with the effect (Fig. 5A, dotted vs. dashed red lines) because of experimental limitations. For sinusoidal stimuli, the additional gain arose primarily from a second harmonic that grew relative to the first harmonic as the stimulus magnitude was reduced (Fig. 5B). The second harmonic was greatly attenuated with efferent activation (Fig. 5B, filled red boxes vs. filled blue circles). This second harmonic is analogous to a rectified response and compelled positive cupula displacements during both the excitatory and inhibitory phases of the sinusoidal stimulus. This is consistent with a quadratic or even-order nonlinearity (37) and may underlie an active process similar to the nonlinearity implicated as essential to otoacoustic emissions and sensitivity in auditory hair-cell organs (26, 38). Efferent activation eliminated both the compressive nonlinearity (Fig. 5A) and the large second harmonic (Fig. 5B). There was considerable variability between animals (n = 6) in the magnitude of the first harmonic gain (average 61 nm per °/s; range 15–120 nm per °/s), probably resulting from differences in the spatial locations of microbeads on cupulae. For stimuli below 3 °/s, the second harmonic nonlinearity during activation of the efferent system (average 37 nm; range 12–55 nm; n = 5) was significantly (P < 0.05) less than observed in the control condition (average 66 nm; range 23–177 nm; n = 6). It is likely that uncontrolled physiological variables (bead location, age, sex, and other factors) contributed to the interanimal variability in the active process and second harmonic component. Absent any other efferent-controlled cells capable of displacing endolymph in the canals, sensitivity to efferent activation strongly indicates that sensory hair cells underlie the amplification reported here. Present data cannot determine whether efferent neurons modulate cycle-by-cycle (39) to coordinate the timing of the amplification with the stimulus or whether the amplification is intrinsic to an active process within the hair bundle that is triggered by the mechanosensitive transduction current as shown previously (2, 22).

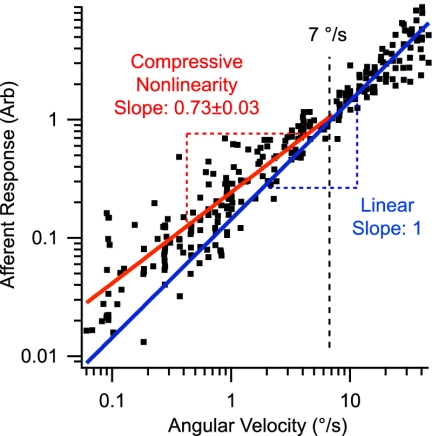
To investigate whether the micromechanical nonlinearity reported above might be reflected in the neural signal transmitted to the brain, we recorded a population of afferent responses in the semicircular canal over a broad range of low-strength stimuli. Measurements were done in the living animal without opening the membranous labyrinth. Single-unit afferent responses (e.g., Figs. 2 and 3) were recorded for sinusoidal stimuli, and discharge rates were fit with a two-term Fourier series, identical to the approach used to quantify cupula displacements. Population results (n = 14) showing the magnitude of the afferent discharge modulation (first plus second harmonic) vs. the magnitude of the stimulus (converted to °/s) are summarized in Fig. 6. Individual afferent responses had discharge modulations ranging from ∼0.5–23 spk/s per °/s angular head velocity and, to investigate nonlinearity of the population, were scaled by their sensitivity to a 7 °/s stimulus and plotted together in Fig. 6. Consistent with micromechanical results reported in Fig. 5A, most afferent responses at high stimulus strengths were scattered around a 45° line (slope of 1 on a log-log scale) as required for a linear response. A subset of high-gain afferents showed a reduction in gain at high stimulus levels because of a saturating nonlinearity reported previously (29). For lower-strength stimuli, a majority of responses were above the linear prediction, and the slope of the data demonstrated a statistically significant nonlinearity (slope of 0.73 + 0.03 SD log-log scale). Therefore, a compressive nonlinearity similar to that observed in the micromechanics also was present in neural responses to low-strength stimuli.

Fig. 6.

Fig. 6.

Open in a new tab

Afferent compressive nonlinearity. The first plus second harmonic discharge rate (spk/s) modulation of semicircular canal afferent neurons is shown as a function of stimulus strength for sinusoidal motion at 2 Hz (three animals, 14 neurons). Afferent data were normalized by their responses at 7°/s to allow multiple units to be compared using a single vertical axis. The solid blue line with a slope of 1 (log-log scale) illustrates the response of a linear system in which doubling the stimulus doubles the response. For stimuli below ∼7°/s, most afferent responses fell above the blue line and were more sensitive than would be expected from linear theory. Results for low-strength stimuli exhibited a compressive nonlinearity as demonstrated by a slope significantly <1.

Unlike the otolith organs, semicircular canal hair cells are morphologically aligned with each other such that all cells are excited or inhibited for motions in the same direction. Hence, mechanical power generated by the hair cells summates to drive motion of the cupula reported here. This cupula movement works against the viscous drag of the endolymph, thereby allowing us to estimate the active power output by comparing the motion under the control conditions with the passive linear condition during efferent activation. The difference in the cupula motion between the active and passive conditions was primarily the presence of the second harmonic motion (e.g., Figs. 4A and 5 B). 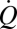Based on the power dissipated by endolymph fluid drag compelled by the second harmonic, the active power output per hair cell would need to be at least Inline graphic where Inline graphic is the second harmonic component of the endolymph volume velocity, c is the hydraulic resistance of endolymph flow in the slender endolymphatic duct, and M is the number of hair cells contributing. Integrating this power over one cycle and assuming power is delivered during half of the cycle provides the active work done per cycle. We estimated the hydraulic resistance (c = 3.3 × 1010 N-s/m3) (40), cupula area (Ac = 1.8 × 10−6 m2) (41), upper limit on the number of hair cells in the semicircular canal crista of the adult toadfish (M = 9000), cupula volume velocity (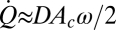Inline graphic), and, from the present results, the active displacement of the cupula (D∼1 × 10−7 m), and frequency (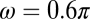Inline graphic rad/s). This calculation results in an estimate of 97 zJ (97 × 10−21 J) per hair cell per cycle, a result that compares favorably with a previous estimate of 79 zJ from isolated bull frog saccular hair cells under quite different experimental conditions (25).

It is remarkable that the compressive nonlinearity, amplification, and efferent control reported here in the semicircular canals are similar to that observed previously in modern species including in the mammalian cochlea (7, 8, 42 –44). Results support the idea that the active amplification process is a general principle of hair-cell sensory organs implemented to increase sensitivity to submicron bundle displacements. The absence of the protein prestin in semicircular canal hair cells (11) and established hair-bundle–based motors in other hair-cell organs (2, 16, 25, 36, 45 –50) indicates that the hair bundle is the most likely source of the amplification reported here. Alternatively, it remains possible that some yet to be described somatic process compelled displacement of the hair bundles and cupulae in these experiments. Whatever the specific biophysical origin may be, the present results demonstrate an active process in the semicircular canal hair cells of a teleost, thus suggesting that the mechanism is ancestral and may underlie the broad appearance of hair-cell active processes in birds, mammals, reptiles, and amphibians.

Both the somatic and hair-bundle motors are controlled by the brain via efferent synaptic contacts on hair-cell somata. In the semicircular canals, efferent-evoked changes in hair-cell somatic electrical impedance are substantial (30, 51) and may underlie the relatively fast control of the motor described here. Precisely how this control is accomplished remains unclear, particularly because sensitivity to somatic impedance may not be consistent with popular models of hair-bundle motor action. At least three motors in the hair bundle have been identified in a variety of species: (i) an unconventional actin-myosin motor that contributes to slow (in ms) adaptation of the mechanosensitive current and slow hair-bundle movements (46, 52, 53); (ii) Ca2+-dependent fast (in μs) adaptation and fast hair-bundle movements (20, 47, 54 –58); and (iii) fast electrically driven bundle movements that occur in response to changes in membrane potential (59 –61). The semicircular canals are known to transduce angular head motions with flat gains down to very low frequencies (29, 62) and with very little adaptation in the present experimental model (35). Therefore it seems unlikely that an actin-myosin adaptation motor underlies the amplification reported here. Movement driven by Ca2+ entering the mechanotransduction channels is a possibility, but it is not yet clear if such a mechanism would be consistent with efferent effects. Efferent activation shunts the receptor potential modulation in semicircular canal hair cells and increases the transduction current as the result of the decrease in hair-cell somatic impedance (30, 51). This activity suggests that Ca2+ flow into stereocilia via the transduction channels increases during efferent activation, and hence one might expect increased Ca2+ binding. Because the mechanical power output was shown here to be reduced by efferent activation, it seems compelling that the mechanical power stroke does not reflect Ca2+ influx directly but instead requires a process that is inhibited by efferent activation. One possibility is that efferent-evoked changes in somatic impedance might control the efficiency of the hair-bundle motor through electrical means (60). If so, Ca2+ influx and the transduction channel complex may control the temporal properties of hair-bundle movements, and the bundle mechanical power output might draw significantly from the electrochemical potential energy between the endolymph and perilymph, in analogy to a transistor with power output modulated by temporal signals applied to the base.

Methods

Experimental procedures and animal care were designed to advance animal welfare and were approved by the University of Utah and the Marine Biological Laboratory animal care and use committees. The oyster toadfish, Opsanus tau, was used as the experimental model because of the biomechanical homology to humans (41, 63) and to facilitate experiments involving microbead tracking and efferent activation in vivo. Fish were lightly anesthetized by immersion in a solution of tricaine methanesulfonate (5 mg/L in seawater) (Sigma) and immobilized in a plastic tank filled with bubbled seawater. The dorsal surface of the animal was exposed to allow surgical access to the labyrinth via a small craniotomy dorsal to the horizontal canal ampulla. The surgical procedure, placement of fluorescent microbeads on the surface of the cupula, micromechanical indentation stimuli, efferent system activation, neural recording, and microbead motion tracking followed methods detailed previously (30, 33). Briefly, mechanical indentation (compression) of the slender limb of the horizontal canal duct (Fig. 1) causes endolymph to displace away from the point of stimulation and compels deflection of the cupula in the excitatory direction (64). Both excitatory and inhibitory mechanical stimuli were generated by compressing the canal with a preload and moving the indenter with small sinusoidal movements around this preload condition. Responses of individual afferent neurons in the toadfish show that the 1-μm zero-to-peak 0.3-Hz sinusoidal indentation at the physical location used in the present study generates the same afferent responses and cupula displacements as 4 °/s zero-to-peak 0.3-Hz sinusoidal angular head rotation (25). Thus we could record cupula motion without rotating the animal or the microscope. Fluorescent microspheres (1–3 μm) (Bangs Laboratories) were surface modified to bind wheat germ agglutinin to promote adherence to the surface of the cupula (33). To introduce the fluorescent beads, we covered the ampulla with electrically insulating fluorocarbon (FC-75; 3M) and used a custom tungsten cutting electrode (ValleyLab) to electrocauterize a fistula ∼75 μm in diameter in the membranous ampulla at a distance ∼300 μm medial to the cupula. A fistula of this size is known not to alter canal mechanics or afferent responses because the high surface tension of the fluorocarbon–endolymph interface seals the fistula (65). Neutrally buoyant fluorescent beads were allowed to diffuse to the cupula from a glass pipette tip placed in the fistula. Bead motion was tracked over 2–10 cycles of the 0.3-Hz sinusoidal stimulus using a QImaging Retiga-EXi CCD camera (1,392 × 1,040, 50-ms open shutter time) configured on an upright microscope (Carl Zeiss AxioTech; Mitutoyo 5–20× Plan Apo objectives). Bead movements over consecutive cycles were fit with a three-term Fourier series to define the first, second, and third harmonics of the movement. Bead motions were viewed from a dorsal vantage point so that movements were recorded only in the horizontal plane of the animal. In all experiments, we recorded single-unit semicircular canal afferent responses (EXT-02F; npi Electronics) to physiological stimuli to ensure normal function of the canal, and during electrical activation of the efferent vestibular nucleus to ensure efferent stimulus effectively evoked responses in afferents. Afferent discharge patterns in response to sinusoidal stimuli were combined over 10–500 cycles using stimulus-triggered histograms, and the first and second harmonic modulation were computed using the Fourier approach described previously (35). Electrical stimulation of the efferent vestibular nucleus used bipolar electrodes placed on the midline of the brainstem and excited using 200 electrical shocks per second, with the amplitude adjusted while recording individual afferents to reproduce previously reported physiological responses (29, 30). Mechanical stimuli and afferent responses were amplified, filtered at 2 kHz (LHBF-48×; npi Electronics), sampled, and digitized at 5 kHz (ITC-18; HEKA Instruments). Custom software was written to acquire data and control the camera shutter and stimuli (Igor Pro; WaveMetrics). The motion of individual beads was tracked using the method of Thévanaz and Unser (66) as implemented by IgorPro 6 (WaveMetrics). Bead movements were calculated in the x and y directions of the CCD array but were reported in the direction perpendicular to the surface of the cupula (e.g., perpendicular to the line of beads in Fig. 1C). In all experiments, bead movements were tracked relative to the crista and membranous labyrinth so that results provided the deflection of the cupula uncontaminated by any small movements of the animal or sensory epithelium relative to the recording optics (33). The noise floor for bead motion tracking was <200 nm.

Acknowledgments

Curtis King assisted with design of the instruments, Dr. Kathryn D. Breneman assisted with preliminary data analysis, and Dr. Angela Yamaucui assisted with preliminary data collection. Financial support was provided by Grant R01 DC006685 from the National Institute on Deafness and Other Communication Disorders.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

  • 1.Stensiö E. The Downtonian and Devonian vertebrates of Spitsbergen. Part I, Family Cephalaspidae. Skr . Svalbard Nordishavet. 1927;12:1–391. [Google Scholar]
  • 2.Hudspeth AJ. Making an effort to listen: Mechanical amplification in the ear. Neuron. 2008;59:530–545. doi: 10.1016/j.neuron.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Brownell WE, Bader CRB, Bertrand D, de Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 1985;227:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
  • 4.Zheng J, et al. Prestin is the motor protein of cochlear outer hair cells. Nature. 2000;405:149–155. doi: 10.1038/35012009. [DOI] [PubMed] [Google Scholar]
  • 5.Liberman MC, et al. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 2002;419:300–304. doi: 10.1038/nature01059. [DOI] [PubMed] [Google Scholar]
  • 6.Liberman MC. Efferent synapses in the inner hair cell area of the cat cochlea: An electron microscopic study of serial sections. Hear Res. 1980;3:189–204. doi: 10.1016/0378-5955(80)90046-5. [DOI] [PubMed] [Google Scholar]
  • 7.Murugasu E, Russell IJ. The effect of efferent stimulation on basilar membrane displacement in the basal turn of the guinea pig cochlea. J Neurosci. 1996;16:325–332. doi: 10.1523/JNEUROSCI.16-01-00325.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Russell IJ, Murugasu E. Medial efferent inhibition suppresses basilar membrane responses to near characteristic frequency tones of moderate to high intensities. J Acoust Soc Am. 1997;102:1734–1738. doi: 10.1121/1.420083. [DOI] [PubMed] [Google Scholar]
  • 9.Dallos P, et al. Acetylcholine, outer hair cell electromotility, and the cochlear amplifier. J Neurosci. 1997;17:2212–2226. doi: 10.1523/JNEUROSCI.17-06-02212.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Fuchs PA, Murrow BW. Cholinergic inhibition of short (outer) hair cells of the chick’s cochlea. J Neurosci. 1992;12:800–809. doi: 10.1523/JNEUROSCI.12-03-00800.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Adler HJ, et al. Expression of prestin, a membrane motor protein, in the mammalian auditory and vestibular periphery. Hear Res. 2003;184:27–40. doi: 10.1016/s0378-5955(03)00192-8. [DOI] [PubMed] [Google Scholar]
  • 12.Manley GA. Cochlear mechanisms from a phylogenetic viewpoint. Proc Natl Acad Sci USA. 2000;97:11736–11743. doi: 10.1073/pnas.97.22.11736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Manley GA, Köppl C. What have lizard ears taught us about auditory physiology? Hear Res. 2008;238:3–11. doi: 10.1016/j.heares.2007.09.011. [DOI] [PubMed] [Google Scholar]
  • 14.Manley GA. Spontaneous otoacoustic emissions from free-standing stereovillar bundles of ten species of lizard with small papillae. Hear Res. 2006;212:33–47. doi: 10.1016/j.heares.2005.10.007. [DOI] [PubMed] [Google Scholar]
  • 15.Tanaka K, Smith CA. Structure of the chicken’s inner ear: SEM and TEM study. Am J Anat. 1978;153:251–271. doi: 10.1002/aja.1001530206. [DOI] [PubMed] [Google Scholar]
  • 16.Hudspeth AJ, Choe Y, Mehta AD, Martin P. Putting ion channels to work: Mechanoelectrical transduction, adaptation, and amplification by hair cells. Proc Natl Acad Sci USA. 2000;97:11765–11772. doi: 10.1073/pnas.97.22.11765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.He DZ, et al. Chick hair cells do not exhibit voltage-dependent somatic motility. J Physiol. 2003;546:511–520. doi: 10.1113/jphysiol.2002.026070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Fischer FP. General pattern and morphological specializations of the avian cochlea. Scanning Microsc. 1994;8(2):351–363. discussion; 363–354. [PubMed] [Google Scholar]
  • 19.Fettiplace R, Fuchs PA. Mechanisms of hair cell tuning. Annu Rev Physiol. 1999;61:809–834. doi: 10.1146/annurev.physiol.61.1.809. [DOI] [PubMed] [Google Scholar]
  • 20.Bozovic D, Hudspeth AJ. Hair-bundle movements elicited by transepithelial electrical stimulation of hair cells in the sacculus of the bullfrog. Proc Natl Acad Sci USA. 2003;100:958–963. doi: 10.1073/pnas.0337433100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Rüsch A, Thurm U. Spontaneous and electrically induced movements of ampullary kinocilia and stereovilli. Hear Res. 1990;48:247–263. doi: 10.1016/0378-5955(90)90065-w. [DOI] [PubMed] [Google Scholar]
  • 22.Martin P, Hudspeth AJ. Compressive nonlinearity in the hair bundle’s active response to mechanical stimulation. Proc Natl Acad Sci USA. 2001;98:14386–14391. doi: 10.1073/pnas.251530498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Martin P, Bozovic D, Choe Y, Hudspeth AJ. Spontaneous oscillation by hair bundles of the bullfrog’s sacculus. J Neurosci. 2003;23:4533–4548. doi: 10.1523/JNEUROSCI.23-11-04533.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Le Goff L, Bozovic D, Hudspeth AJ. Adaptive shift in the domain of negative stiffness during spontaneous oscillation by hair bundles from the internal ear. Proc Natl Acad Sci USA. 2005;102:16996–17001. doi: 10.1073/pnas.0508731102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Martin P, Hudspeth AJ. Active hair-bundle movements can amplify a hair cell’s response to oscillatory mechanical stimuli. Proc Natl Acad Sci USA. 1999;96:14306–14311. doi: 10.1073/pnas.96.25.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Eguíluz VM, Ospeck M, Choe Y, Hudspeth AJ, Magnasco MO. Essential nonlinearities in hearing. Phys Rev Lett. 2000;84:5232–5235. doi: 10.1103/PhysRevLett.84.5232. [DOI] [PubMed] [Google Scholar]
  • 27.Holt JC, Lysakowski A, Goldberg JM. Mechanisms of efferent-mediated responses in the turtle posterior crista. J Neurosci. 2006;26:13180–13193. doi: 10.1523/JNEUROSCI.3539-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Goldberg JM, Fernández C. Efferent vestibular system in the squirrel monkey: Anatomical location and influence on afferent activity. J Neurophysiol. 1980;43:986–1025. doi: 10.1152/jn.1980.43.4.986. [DOI] [PubMed] [Google Scholar]
  • 29.Boyle R, Highstein SM. Resting discharge and response dynamics of horizontal semicircular canal afferents of the toadfish, Opsanus tau . J Neurosci. 1990;10:1557–1569. doi: 10.1523/JNEUROSCI.10-05-01557.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Boyle R, Rabbitt RD, Highstein SM. Efferent control of hair cell and afferent responses in the semicircular canals. J Neurophysiol. 2009;102:1513–1525. doi: 10.1152/jn.91367.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Rabbitt RD, Boyle R, Highstein SM. Mechanical indentation of the vestibular labyrinth and its relationship to head rotation in the toadfish, Opsanus tau . J Neurophysiol. 1995;73:2237–2260. doi: 10.1152/jn.1995.73.6.2237. [DOI] [PubMed] [Google Scholar]
  • 32.Boyle R, Highstein SM. Efferent vestibular system in the toadfish: Action upon horizontal semicircular canal afferents. J Neurosci. 1990;10:1570–1582. doi: 10.1523/JNEUROSCI.10-05-01570.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Rabbitt RD, et al. Dynamic displacement of normal and detached semicircular canal cupula. J Assoc Res Otolaryngol. 2009;10:497–509. doi: 10.1007/s10162-009-0174-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Hillman DE, McLaren JW. Displacement configuration of semicircular canal cupulae. Neuroscience. 1979;4:1989–2000. doi: 10.1016/0306-4522(79)90070-8. [DOI] [PubMed] [Google Scholar]
  • 35.Rabbitt RD, Boyle R, Holstein GR, Highstein SM. Hair-cell versus afferent adaptation in the semicircular canals. J Neurophysiol. 2005;93:424–436. doi: 10.1152/jn.00426.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Kunuth KH. Mathematics of distortion product otoacoustic emission generation: A tutorial. In: Berlin CI, editor. Otoacoustic Emissions. Basic Science and Clinical Applications. Singular Publishing Group, San Diego; 1998. pp. 149–159. [Google Scholar]
  • 38.Long GR, Tubis A, Jones KL. Modeling synchronization and suppression of spontaneous otoacoustic emissions using Van der Pol oscillators: Effects of aspirin administration. J Acoust Soc Am. 1991;89:1201–1212. doi: 10.1121/1.400651. [DOI] [PubMed] [Google Scholar]
  • 39.Sadeghi SG, Goldberg JM, Minor LB, Cullen KE. Efferent-mediated responses in vestibular nerve afferents of the alert macaque. J Neurophysiol. 2009;101:988–1001. doi: 10.1152/jn.91112.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Rabbitt RD, Damiano ER, Grant JW. Biomechanics of the Semicircular Canals and Otolith Organs. In: Highstein SM, Popper A, Fay R, editors. The Vestibular System, Springer Handbook of Auditory Research. Spirnger, New York: 2004. pp. 153–201. [Google Scholar]
  • 41.Ghanem TA, Rabbitt RD, Tresco PA. Three-dimensional reconstruction of the membranous vestibular labyrinth in the toadfish, Opsanus tau . Hear Res. 1998;124:27–43. doi: 10.1016/s0378-5955(98)00108-7. [DOI] [PubMed] [Google Scholar]
  • 42.Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Rhode WS. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mössbauer technique. J Acoust Soc Am. 1971;49(suppl 2):1218. doi: 10.1121/1.1912485. [DOI] [PubMed] [Google Scholar]
  • 44.Brown MC, Nuttall AL, Masta RI. Intracellular recordings from cochlear inner hair cells: Effects of stimulation of the crossed olivocochlear efferents. Science. 1983;222:69–72. doi: 10.1126/science.6623058. [DOI] [PubMed] [Google Scholar]
  • 45.Manley GA. Evidence for an active process and a cochlear amplifier in nonmammals. J Neurophysiol. 2001;86:541–549. doi: 10.1152/jn.2001.86.2.541. [DOI] [PubMed] [Google Scholar]
  • 46.Howard J, Hudspeth AJ. Mechanical relaxation of the hair bundle mediates adaptation in mechanoelectrical transduction by the bullfrog’s saccular hair cell. Proc Natl Acad Sci USA. 1987;84:3064–3068. doi: 10.1073/pnas.84.9.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Wu YC, Ricci AJ, Fettiplace R. Two components of transducer adaptation in auditory hair cells. J Neurophysiol. 1999;82:2171–2181. doi: 10.1152/jn.1999.82.5.2171. [DOI] [PubMed] [Google Scholar]
  • 48.Kennedy HJ, Evans MG, Crawford AC, Fettiplace R. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat Neurosci. 2003;6:832–836. doi: 10.1038/nn1089. [DOI] [PubMed] [Google Scholar]
  • 49.Vollrath MA,, Eatock RA. Time course and extent of mechanotransducer adaptation in mouse utricular hair cells: Comparison with frog saccular hair cells. J Neurophysiol. 2003;90:2676–89. doi: 10.1152/jn.00893.2002. [DOI] [PubMed] [Google Scholar]
  • 50.Fettiplace R, Ricci AJ, Hackney CM. Clues to the cochlear amplifier from the turtle ear. Trends Neurosci. 2001;24:169–175. doi: 10.1016/s0166-2236(00)01740-9. [DOI] [PubMed] [Google Scholar]
  • 51.Flock A, Russell I. Inhibition by efferent nerve fibres: Action on hair cells and afferent synaptic transmission in the lateral line canal organ of the burbot Lota lota . J Physiol. 1976;257:45–62. doi: 10.1113/jphysiol.1976.sp011355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Assad JA, Corey DP. An active motor model for adaptation by vertebrate hair cells. J Neurosci. 1992;12(9):3291–3309. doi: 10.1523/JNEUROSCI.12-09-03291.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Holt JR, et al. A chemical-genetic strategy implicates myosin-1c in adaptation by hair cells. Cell. 2002;108:371–381. doi: 10.1016/s0092-8674(02)00629-3. [DOI] [PubMed] [Google Scholar]
  • 54.Howard J, Hudspeth AJ. Compliance of the hair bundle associated with gating of mechanoelectrical transduction channels in the bullfrog’s saccular hair cell. Neuron. 1988;1:189–199. doi: 10.1016/0896-6273(88)90139-0. [DOI] [PubMed] [Google Scholar]
  • 55.Crawford AC, Evans MG, Fettiplace R. The actions of calcium on the mechano-electrical transducer current of turtle hair cells. J Physiol. 1991;434:369–398. doi: 10.1113/jphysiol.1991.sp018475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Choe Y, Magnasco MO, Hudspeth AJ. A model for amplification of hair-bundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction channels. Proc Natl Acad Sci USA. 1998;95:15321–15326. doi: 10.1073/pnas.95.26.15321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Beurg M, Nam JH, Crawford A, Fettiplace R. The actions of calcium on hair bundle mechanics in mammalian cochlear hair cells. Biophys J. 2008;94:2639–2653. doi: 10.1529/biophysj.107.123257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Assad JA, Shepherd GM, Corey DP. Tip-link integrity and mechanical transduction in vertebrate hair cells. Neuron. 1991;7:985–994. doi: 10.1016/0896-6273(91)90343-x. [DOI] [PubMed] [Google Scholar]
  • 59.Ricci AJ, Crawford AC, Fettiplace R. Active hair bundle motion linked to fast transducer adaptation in auditory hair cells. J Neurosci. 2000;20:7131–7142. doi: 10.1523/JNEUROSCI.20-19-07131.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 60.Breneman KD, Brownell WE, Rabbitt RD. Hair cell bundles: Flexoelectric motors of the inner ear. PLoS One. 2009;4:e5201. doi: 10.1371/journal.pone.0005201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 61.Cheung EL, Corey DP. Ca2+ changes the force sensitivity of the hair-cell transduction channel. Biophys J. 2006;90:124–139. doi: 10.1529/biophysj.105.061226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 62.Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J Neurophysiol. 1971;34:635–660. doi: 10.1152/jn.1971.34.4.635. [DOI] [PubMed] [Google Scholar]
  • 63.Ifediba MA, Rajguru SM, Hullar TE, Rabbitt RD. The role of 3-canal biomechanics in angular motion transduction by the human vestibular labyrinth. Ann Biomed Eng. 2007;35(7):1247–1263. doi: 10.1007/s10439-007-9277-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Dickman JD, Correia MJ. Responses of pigeon horizontal semicircular canal afferent fibers. I. Step, trapezoid, and low-frequency sinusoid mechanical and rotational stimulation. J Neurophysiol. 1989;62:1090–1101. doi: 10.1152/jn.1989.62.5.1090. [DOI] [PubMed] [Google Scholar]
  • 65.Rajguru SM, Rabbitt RD. Afferent responses during experimentally induced semicircular canalithiasis. J Neurophysiol. 2007;97:2355–2363. doi: 10.1152/jn.01152.2006.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 66.Thévenaz P, Ruttimann UE, Unser M. A pyramid approach to subpixel registration based on intensity. IEEE Trans Image Process. 1998;7:27–41. doi: 10.1109/83.650848. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES