Singular Value Decomposition-based Alternative Splicing Detection

SUMMARY

Altered alternative splicing has been identified as an important factor in tumorigenesis. The Affymetrix exon tiling array is designed for detecting alternative splicing events in a transcriptome-wide fashion; however, there are currently few analysis tools that are well studied for effective detection of alternative splicing events. We propose a new screening procedure based on singular value decomposition (SVD) of the residual matrix from a robust additive model fit to probe selection region (PSR) data. With this approach, we analyze the exon tiling array data from a brain cancer study conducted at the M. D. Anderson Cancer Center, and show that the proposed SVD-based approach is able to better accommodate outlying measures and capitalize on the multidimensional group-by-PSR gene expression profiles for more effective detection of group-specific alternative splicing events as well as the PSRs that are most likely associated with the alternative splicing. Lab validation confirmed some of our findings, but the list of candidates detected with our proposed method may provide a better signpost to guide further investigations.

1 Introduction

In the 1970s it was discovered that a number of DNA segments called exons, interrupted by segments called introns, constitute the final gene transcription product, messenger RNA (mRNA), through a post-transcriptional process called RNA splicing (Berget et al., 1977; Chow et al., 1977; Gilbert 1978). Only a few years after the initial discovery of exons and RNA splicing, it was found that an additional level of gene regulation occurs through alternative RNA splicing. While an intriguing finding at the time, there was really no way to completely predict the impact that this finding would have on our understanding of gene expression. Early studies labeled alternative splicing as a specialized phenomenon that would likely impact the regulation of a small set of genes. As the genome initiative pressed forward, the number of genes found to undergo some type of alternative splicing gradually increased. As the size of the Expressed Sequence Tags (EST) database grew, so did the realization that a significant number of genes indeed utilize some form of alternative RNA processing to generate genetic diversity. With the sequencing of the human genome completed, it appears that much of human phenotypic diversity may stem from alternative RNA splicing. Since alternative splicing is associated with important biological and pathological processes, understanding how any given cell ultimately forms its final mRNA complements from a well-defined pool of RNA precursors would help gain insights into the disease genesis and strategy for treatments. For this reason, the study of alternative slicing has become an integral part of genomic and proteomic research.

With regards to the role of alternative splicing in cancer, calcitonin and fibronectin were the first genes identified to have aberrant RNA splicing associated with tumorigenesis (Steenbergh et al., 1984; Castellani et al., 1986). Since their identification, more than forty genes have been reported to generate tumor-specific splicing isoforms, creating a correlation of altered splicing products with cancer development. While changes in RNA splicing are clearly associated with many types of cancers, the specific underlying mechanisms responsible for these changes are less clear. In most cases, investigators have reported merely the correlation of specific splicing variants with particular cancers. Point mutations of donor/acceptor splicing sites or enhancer/silencer elements of genes have caused aberrant splicing in some cases (e.g., Lee and Haber, 2001; Scheffer et al., 2000). Krawczak et al. (1992) estimated that 15% of the point mutations that result in human genetic disease create an RNA splicing defect. Specific examples of point mutations that alter RNA splicing and lead to cancer formation are those involving the p53 gene (e.g., Ghosh et al., 2004). It is clear that altered splicing leads to a loss of p53 function.

Recently, Affymetrix developed the exon tiling array system, which is one of the first high throughput technology to investigate the alternative splicing on a genome-wide scale. The detailed description of the exon tiling array design is available in Affymetrix (2005). Validation of alternative splicing has relied on labor-intensive reverse-transcriptase (RT) PCR. Even with RT-PCR, some important forms of alternative splicing are difficult to validate. With the advent of exon tiling arrays, researchers are now able to cost-effectively analyze gene expression at the level of transcript diversity on a whole-genome scale and use the information to identify promising candidate isoforms for downstream validation.

A research area of primarily biological interest is to identify alternative splicing that is associated with a disease phenotype, say, brain cancer, which is the focus of our study in this paper. In this type of experiment, exon tiling arrays are made from tissue samples collected from the two groups of cancer patients and disease-free subjects, where the expression intensities of Probe-Selection-Region (PSR) are measured. The PSRs are different RNA segments in exon regions on a chromosome. The occurrence of alternative splicing is manifested by the presence of PSRs that show different degrees of differential expression between two groups from the other PSRs. At the present time, only a small number of methods are available to analyze the exon tiling arrays. Pattern-based Correlation (PAC; see French et al. 2007) used in the Affymetrix data analysis software suits experiments with a relatively large number of sample types. A widely used method is the two-way ANOVA model applied to expression data that use the log-2 transformed PLIER signal intensity estimates (Hubbell, 2005) extracted from the arrays in Affymetrix ExACT 1.0 software. This ANOVA-based approach was followed by Affymetrix in developing their Analysis of Splice Variation, ANOSVA (Cline et al. 2005), which can handle both the exon-level and PSR-level data analysis. Basically, the ANOVA model includes the group and PSR as the main effects, and the presence of alternative splicing is measured by the significance for the interaction effects.

However, it has been empirically observed that the ANOVA approach is often problematic, mainly due to several factors: (i) the analysis is susceptible to the presence of individual outlying values of the expression intensity; (ii) it intends to detect the average interaction strength instead of the interactions that are due to individual PSRs, but splicing is more likely to occur when a small number of PSRs are responsible; and (iii) true alternative splicing events could be overlooked by ANOVA because of heterogenous variations of signal intensities across PSRs.

To overcome these drawbacks of the ANOVA approach, we propose in Section 2 a robust procedure that utilizes the median regression methodology and robust SVD of the residual matrix. The median regression is fit to an additive model with group and PSR as main effects, and the residual matrix is approximated by the first one or two singular dimensions so that the interesting structure or patterns in the residuals can be discerned through the left and right singular vectors. The work of Hu, Wright and Zou (2006) and Hu and He (2007) showed the value of using low rank approximations of the gene expression data matrix. The proposed method in this paper is partially motivated by the earlier work on SVD. We use the proposed method on a brain cancer study (Cheung et al., 2008) in Section 3 and demonstrate how it can lead to more specific and more informative splicing candidates in these cancer data. A detailed analysis of the exon array data shows that many of the candidates missed by ANOVA can be detected by our proposed method. A higher proportion of such splicing candidates identified by our proposed method is either known to be associated with brain cancer in the literature or validated in our lab through RT-PCR.

Beyond the statistical concerns discussed here, false splicing events may also be induced by other biologically relevant factors. For example, if there is a large group-and-PSR interaction occurring at a PSR site where one group has the average signal intensities falling in the region of background noises, the statistical screening based on interactions is likely to lead to false splicing discovery. In such cases, the specific PSR is not really measurable. Towards this direction, Affymetrix has adopted the MIDAS algorithm (Gardina et al. 2006), which implements the filtering at several levels to screen out the PSRs that are likely to be noninformative or unreliable. We note that our proposed method and MIDAS address different issues in a somewhat complementary manner to achieve the goal of obtaining a more reliable list of alternative splicing candidates so that experimental costs related to biological validation can be controlled. In our study of brain cancer in Section 3, the filtering by MIDAS is also used together with our proposed method.

2 Motivation and Method

2.1 Basic notations

We start with the standard analysis of variance (ANOVA) method in alternative splicing detection. Let y_ijk be the log-2 transformed signal intensity of the j^th PSR in sample k of group i for a probe set. To legitimize the log transformation, a constant 1 is added to all the intensity measures in the analysis. The ANOVA model with interaction can be expressed as

$$y_{ijk}=c_i+s_j+e_{ij}+{ϵ}_{ijk,}$$ (1)

where c_i stands for the effect of group i, s_j for the effect of the j^th PSR, e_ij for the group-and-PSR interaction effect, and ϵ_ijkfor measurement error. A reduced ANOVA model takes the form

$$y_{ijk}=c_i+s_j+g_i{p}_j+{ϵ}_{ijk,}$$ (2)

with a multiplicative interaction effect e_ij = g_ip_j, where g_i and p_j denote the contributions to the interaction effect from group i and PSR j, respectively. The splicing candidates selected by ANOVA are those with significant overall interaction effect based on the F test for the null hypothesis H₀: e_ij = 0 for all (i, j). For those detected genes, it is possible that no individual PSR interacts with group sufficiently strongly to suggest the occurrence of the splicing.

We find that the variabilities of the residuals to the ANOVA model vary with groups, and often more so with PSRs. Thus, a better practice in the ANOVA approach to detecting splicing candidates is to take the PSR-specific variability into account in the statistical test. Later in the paper, we refer to this variant as the weighted ANOVA method, or WANOVA. The same idea will be used for re-scaling residuals in Section 2.3 for our proposed method.

For the remaining part of the paper, we shall consider the case of two groups (e.g., i = 1 for the normal tissues and i = 2 for the cancer tissues) with n_i samples for each group. Two-group problems are common, but the methodology we describe here applies equally to problems with more groups.

Step 1 of our proposed method is, for each gene, to fit an additive model

$$y_{ijk}=c_i+s_j+{ϵ}_{ijk}^{*},$$ (3)

by the least absolute deviation method, and store the residuals r_ijk into a J-by-L residual matrix Ω, where J is the number of PSRs, L = n₁ +n₂ is the number of arrays, and the first n₁ columns of Ω correspond to group 1.

The least absolute deviation methods finds c_i and s_j by minimizing

$${\displaystyle \sum _{ijk}\left|y_{ijk}-c_i-s_j\right|,}$$

which could be solved as the median regression problem using the library quantreg in R. The median regression estimates are closely related to median polish in the literature, but quantreg does the minimization more accurately. For the details on quantreg, we refer to Koenker (2005).

We will perform a robust low-rank approximation to Ω and use the first or second singular vectors to facilitate screening for alternative splicing candidates. While the exact procedure will be described in Section 2.3, we note that our basic idea is to look for specific rows of the matrix (corresponding to PSRs) that can explain the group profile information in the residual matrix Ω.

2.2 Connection with ANOVA

Singular value decomposition is frequently used to decompose the row effects and the column effects of a data matrix according to the effect sizes. In this paper we use the first two singular structures

$$\mathrm{\Omega }=d_1{u}_1{v}_1^T+d_2{u}_2{v}_2^T+\zeta ,$$ (4)

where u₁ and u₂ are the first two singular row vectors, υ₁ and υ₂ are the first two singular column vectors, and d₁ ≥ d₂ are the first two singular values of Ω. The remaining term ζ represents the summation of all the higher-order singular components.

If we ignore the difference between the least squares estimation and the least absolute deviation estimation in estimating c_i and s_j, the reduced ANOVA approach (2) can be compared to using the rank one approximation of Ω, while our proposed method uses the rank two approximation. Hu, Wright, and Zou (2006) established the relationship between SVD and the multiplicative interaction estimation. Hu and He (2007) used more than the first singular structure in SVD to recover gene profile information. The earlier work mentioned above provided the motivation for our proposed method here.

2.3 The proposed method

Following Step 1 described in Section 2.1, We propose to use the residual matrix Ω as well as a scaled version of it to locate PSR-group interactions. In empirical investigations, we observed that the variabilities of the signal intensities in a group vary across PSRs, a phenomenon similar to the probe-level data described in Hu, Wright, and Zou (2006). We also noticed that the variation is particularly substantial in the cancer group, possibly due to the biological heterogeneity among cancer patients. Without accounting for heterogenous variability in the data, a PSR with a large variance may dominate the first or second singular structure, and then mask biologically interesting patterns related to alternative splicing that occur at other locations.

We compute the scaled residual matrix Ω*, whose (j, l)-th element is

$${\omega }_{jl}^{*}=\frac{{\omega }_{jl}}{\sqrt{s_j^2+c_0}},$$ (5)

where ω_jl is the (j, l)-th element of Ω, $s_j^2$ is the pooled sample variance of {y_1jk: k = 1, ⋯, n₁} and {y_2jk: k = 1, ⋯, n2}, and c₀ is a small positive constant. We observed that some PSRs do not express at all (taking the value of 0 for the intensity measurements), so this constant is there to stabilize the scaling factor in the same spirit as in Efron et al. (2001) and Tusher et al. (2001). We recommend using the 10th percentile of $s_j^2$ across all the genes as the choice of c₀ (see Efron et al., 2001).

Step 2 of our proposed method is to perform the robust SVD on Ω* to obtain

$${\mathrm{\Omega }}^{\ast }=d_1^{*}{u}_1^{*}{v}_1^{*T}+d_2^{*}{u}_2^{*}{v}_2^{*T}+{\zeta }^{*},$$ (6)

which can be carried out by the robust low-rank approximation algorithm of Chen, He and Wei (2008).

If $d_1^{*}/d_2^{*}\ge 3$, which happens in about 10% of the time in our empirical studies, we will focus on the first singular structure only, because the magnitude of the second singular level is not practically significant relative to the first singular level. Otherwise, we look at both singular levels. Let $v_{11}^{*}$ and $v_{12}^{*}$ be the sub-vectors of $v_1^{*}$ with the first n₁ (normal samples) and the last n₂ elements (cancer samples), respectively. The two-sample t-test applied to $v_{11}^{*}$ versus $v_{12}^{*}$ is used to detect the significant group difference through the first singular vector. If the group difference is significant, we say that this gene is a “stage 1” candidate for alternative splicing, and then we will look for outstanding PSRs from $u_1^{*}$ and u₁ as “stage 2”.

The n_c smallest and n_c largest elements of $u_1^{*}$ (with n_c = max(2, [J/10])), corresponding to PSRs, are singled out as candidates. So we allow the number of candidates to increase with the number of PSRs, but it is unlikely that we can reliably identify interesting PRSs beyond n_c (or 10% for J > 20) outlying cases. The set of PSR indices of these candidates is denoted by C₁. To see if they are “outstanding”, we interrogate both $u_1^{*}$ and u₁. The rationale of examining u₁ at the original scale is to help find the PSR whose interaction effect is strong relative to the others but the array-to-array variability at this PSR is high so that the corresponding value at $u_1^{*}$ may not be outlying. Explicitly, we examine the outlyingness of these PSRs in the vector u₁, the first left singular vector of Ω. Let M₀ and M₁ be the median and median absolute deviation (MAD), respectively, of all the elements in u₁ = (u₁₁, ⋯, u_1J), and let

$$h_j=\left|u_{1j}-M_0\right|/M_1.$$ (7)

Similarly, we define $h_j^{*}$ for $u_1^{*}$ based on the scaled residuals.

Step 3(i) of our proposed method is, for any “stage 1” candidate gene, to declare that the jth PSR is outstanding as an alternative splicing site for any j ∈ C₁, and either h_j > 3 or $h_j^{*}>3$. This is analogous to the 3σ rule used for identifying outlying values. If at least one outstanding PSR is found, we call this gene a “stage 2” candidate.

If $d_1^{*}/d_2^{*}<3$, we follow up Step 3(i) with Step 3(ii) by performing the same screening procedure described above on the second singular structure. The candidates found in both Steps 3(i) and 3(ii) are taken together as the final candidates for alternative splicing. For “stage 2” candidates, specific PSRs are singled out as likely alternative splicing sites.

In our cancer study with most genes having J < 20 PSRs, we consider at most four possible PSRs in Step 3(i), and possibly another four in Step 3(ii); the output from our approach contains no more than eight PSRs, and usually much fewer. If the two-sample t-tests on the group differences through both the first and the second singular vectors are non-significant, we would exclude this gene from consideration. However, it is possible that the group difference is non-significant in $v_1^{*}$ but significant in $v_2^{*}$. The consideration of the second singular structure is often valuable in finding candidates of alternative splicing.

To summarize, we have a 3-step procedure for detecting alternative splicing candidates. Step 1 is to obtain the residual matrix from an additive fit. Step 2 is to perform SVD on the residual matrix in its raw scale as well as in a variability-adjusted form. Step 3 is to look for stage 1 and stage 2 candidate genes based on the the singular values and singular vectors obtained from Step 2.

3 A brain cancer study

Exon array profiling of 24 brain tumor cases, more specifically glioblastoma multiforme (GBM), and 12 control samples were conducted as described (Cheung et al., 2008). For demonstration of the proposed method, we focus our subsequent studies on 685 probe sets representing 550 unique genes having at least 5 PSRs on chromosome 9 to screen for cancer-specific alternative splicing candidates.

We implemented the ANOVA approach, the weighted ANOVA, and our proposed SVD-based method on these genes and summarized the results in Table 1. For the SVD method, we take the p-value threshold of 0.05 for the group tests on the first two right singular vectors. A gene can be a candidate either because (1) the group test on the first right singular vector $v_1^{*}$ is significant or (2) the group test on the second singular vector $v_2^{*}$ is significant and $d_1^{*}/d_2^{*}<3$. The overall significance level of the group test for a gene is between 0.05 and 0.1, so we take the p-value threshold of 0.1 for ANOVA in our comparison. In some sense, those p-value thresholds would give the ANOVA approach more chance to include more splicing candidates. We hasten to add, however, that our focus in this paper is screening, not formal hypothesis testing, so we do not make multiple testing adjustments. The evaluation of false positive rates will be made with external information in Sections 3.4 and 3.5.

Table 1.

Comparison of splicing detection between ANOVA and the SVD method.

number of detected genes
ANOVA	187
Weighted ANOVA	277
SVD	1st singular structure	2nd singular structure	both
	stage 1
	115	218	28
Overlapping with ANOVA	67	74	26
Overlapping with weighted ANOVA	92	105	27
	stage 2
	67	154	8
Overlapping with ANOVA	48	55	8
Overlapping with weighted ANOVA	56	72	8

The p-values can be useful for ranking the splicing candidates. In our proposed SVD method, we use the p-values on the group differences at stage 1. If $d_1^{*}/d_2^{*}\ge 3$ the p-value obtained from $v_1^{*}$ is used; Otherwise, the smaller p-value between $v_1^{*}$ and $v_2^{*}$ is used. These p-values can be used to rank “stage 1” or “stage 2” candidates.

The SVD-based method detected a total of 361 “stage 1” candidate genes, where 115 genes were identified only from (1), 218 were identified only from (2), and 28 genes were identified due to both (1) and (2). In contrast, the ANOVA approach found a much smaller number of 187 genes, and WANOVA flagged in 277 genes. Note that in this application, a large number of genes were detected from the second singular structure in the SVD-based method, suggesting that a uni-dimensional summary of the residual matrix is often insufficient (more details will be provided later).

The SVD-based approach found 229 “stage 2” candidate genes, in which 67 genes are detected by (1) only, 154 genes are detected by (2) only, and 8 genes are detected by both (1) and (2). Out of the 187 genes detected by ANOVA, 167 of them are “stage 1” candidates and 111 of them are “stage 2” candidates found by the SVD-based method. The WANOVA candidates overlap more (than the ANOVA candidates) with the SVD candidates identified through the first singular level, but a substantial number of SVD candidates identified through the second singular level are missed by either ANOVA or WANOVA. To understand why, we examine some of the genes in detail in the next few sub-sections to show the advantage of the proposed SVD-based approach over ANOVA.

3.1 Robustness against single outlying intensity

As discussed earlier, the L₁ fit and robust SVD used in the proposed method makes it resistant to the effect of single outlying intensities in the data. We found through empirical studies that the presence of outliers is far from an exception in the microarray data.

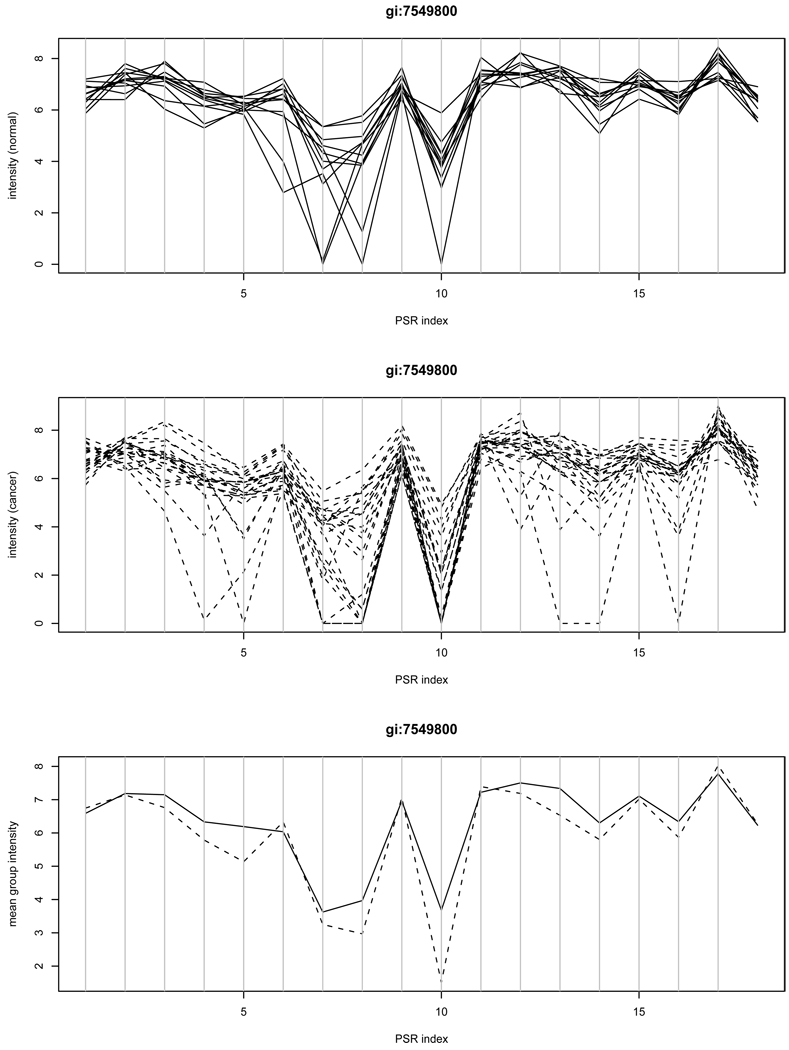
Figure 1 shows one exemplary gene ANAPC2 represented by the gi accession number gi:7549800 for illustration. This gene is not a candidate found by our SVD method, but both ANOVA and WANOVA yield the significant p-value of 0.001 mainly due to the intensities at PSR 10. We further interrogated the intensities of individual samples at this PSR. We observed that many cancer samples have unreliable intensity measurements that lie in the background noise region. In particular, we found 11 out of 24 cancer samples with the intensity value of 0 and 6 other cancer samples with the intensity measure below 4. By not using these unreliable measurements, the p-value from ANOVA would increase to 0.219, which again demonstrates that the ANOVA result is vulnerable to outliers and prone to false positive detection. This pattern of false positives was observed frequently in our empirical studies.

Figure 1.

Intensities of example gene gi:7549800: the group-PSR interaction was detected by ANOVA but not by the SVD method. Unreliable measurements at PSR 10 may lead to a false positive. The top panel contains the plot of intensities of individual normal samples versus PSRs; The middle panel contains the plot of intensities of individual cancer samples versus PSRs; The bottom panel contains the average intensities of normal samples (solid) and cancer samples (dashed) versus PSRs.

It is worth pointing out that our analysis does not exclude the possibility that a tumor-subtype specific splicing event might be occurring. A careful analysis of subtype specific alternative splicing is beyond the scope of this paper.

3.2 Usefulness of the second SVD structure

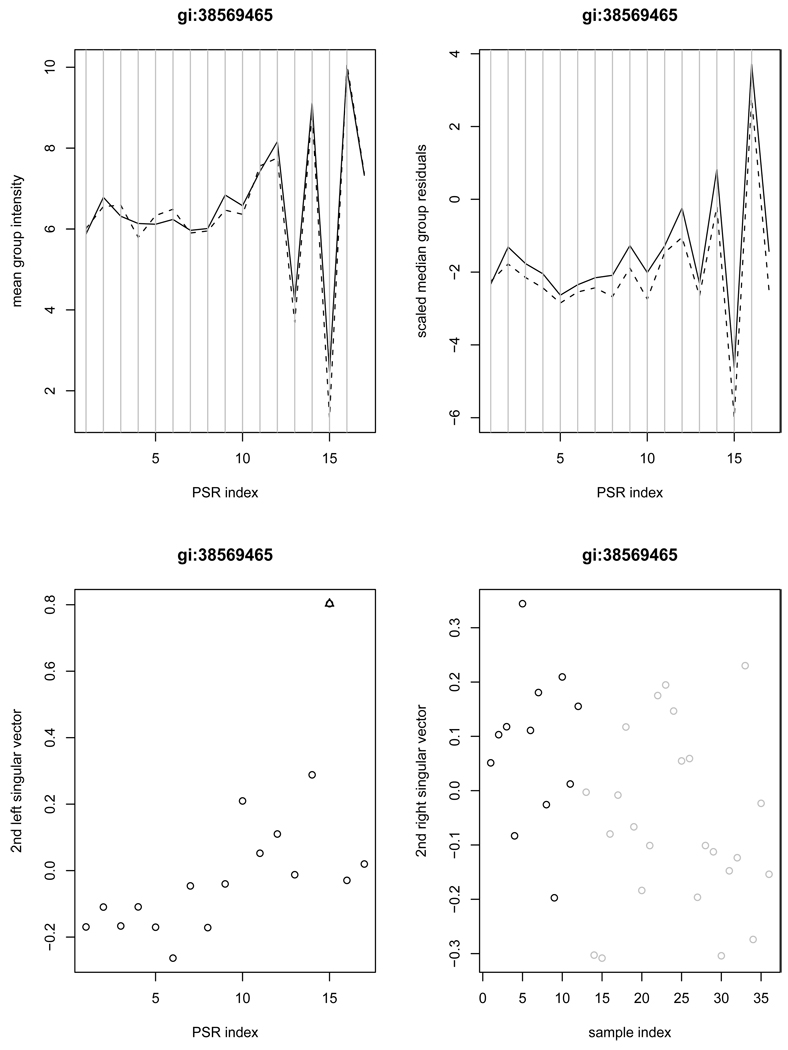
As mentioned earlier, our proposed SVD method is able to utilize the second SVD structure unless its magnitude measured by the singular value is negligible relative to the first. To see the benefit of doing so, we hereby show one gene example, ROD1 (gi:38569465), for demonstration.

The upper left panel of Figure 2 gives the mean intensities at all PSRs for gene gi:38569465. There is not much to be said about the means, but PSR 15 looks distinct in the scaled median residuals shown at the upper right panel of Figure 2. Not surprisingly, ANOVA failed to detect the interaction between group and PSR 15 (p-value=0.469 and 0.440 for ANOVA and WANOVA, respectively) while the SVD method was able to pick it up in the second structure with the significant group difference (p-value=0.011). The second singular vectors for the scaled residual matrix are displayed in the second row of Figure 2. Clearly, PSR 15 is seen as a good candidate site for alternative splicing, most likely an alternative promoter. But it does not show up clearly in the first singular vector.

Figure 2.

Example gene gi:38569465 demonstrates the usefulness of the second SVD structure in detecting possible alternative splicing. The left upper panel contains the average intensities of normal samples (solid) and cancer samples (dashed) versus PSRs; The right upper panel contains the median scaled residual values of normal samples (solid) and cancer samples (dashed) versus PSRs; The left lower panel contains the plot of the second left singular vector along with the PSRs (an outlying PSR indicated by triangle); The right lower panel contains the second right singular vector versus samples (black-normal; grey-cancer).

3.3 Interaction dominated by individual PSRs

Since ANOVA aims to detect overall interaction between group and PSR, a significant interaction effect is not of much use for indicating alternative splicing that is associated with a small number of PSRs. In the brain cancer study, there are 76 genes with p-values less than 0.1 from the ANOVA test but no outlying PSRs are found by the proposed SVD method, which does look for individual PSRs that may relate to group-specific alternative splicing. It is unclear if such candidates are as valuable in searching for cancer-specific splicing genes.

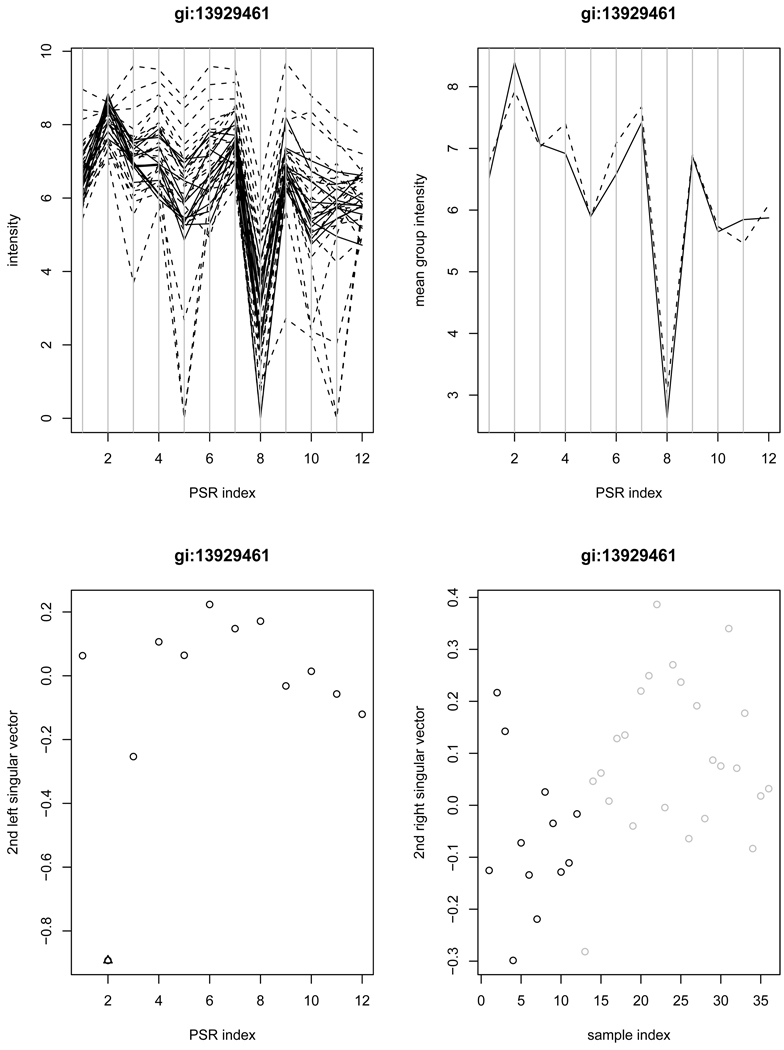
We further investigate the set of 118 genes that are detected by the SVD method as the “stage 2” but not by ANOVA. One representative gene B4GALT1 (gi:13929461) is shown in Figure 3, for which the ANOVA yields a p-value of 0.878 (and the WANOVA gives a p-value of 0.250). From the profile plots in row 1, we note that the mean group intensities are lower for the cancer patients only at PSR 2 and PSR 11, but PSR 11 is associated with high array-to-array variability, which led to a lack of power in the ANOVA approach. However, PSR 2 stood out in the second singular vector under the proposed SVD method, despite high variabilities at some other PSRs.

Figure 3.

Example gene gi:13929461 is detected by the SVD method as the “stage 2”, but missed by ANOVA. The left upper panel contains the plot of intensities of individual samples versus PSRs (solid-normal; dashed-cancer); The right upper panel contains the average intensities of normal samples (solid) and cancer samples (dashed) versus PSRs; The left lower panel contains the plot of the second left singular vector along with the PSRs (an outlying PSR indicated by triangle); The right lower panel contains the second right singular vector versus samples (black-normal; grey-cancer).

To summarize the results from the empirical investigation, we find that the proposed SVD method is robust in the presence of individual outlying intensities, able to retrieve useful information related to alternative splicing from the second singular structure, and can help detect the group-PSR interaction attributed to individual PSRs that are likely to be associated with group-specific alternative splicing events.

3.4 Biological Validation

We applied Affymetrix’s MIDAS algorithm on 118 “stage 2” candidate genes selected by the SVD method but overlooked by ANOVA to further refine the list of splicing candidate genes. A total of 64 of them passed the MIDAS threshold. A public domain database (http://genome.ucsc.edu) provides information on possible splicing events/isoforms of genes in the whole human genome. We find that 48 out of the 64 genes are indicated for alternative splicing to have some type of splicing events (isoforms), based on the NCBI Reference Sequence (RefSeq) that so far has the most reliable sequencing information. Only one out of the 64 genes cannot be found in the database. The high hit rate of 75% for biological relevance in this subset of genes indicates that the proposed SVD method is useful in retrieving information that is missed by ANOVA.

For comparison, we did the same to the 20 genes that are detected by ANOVA but not by the SVD method at stage 1. Among them, 10 passed the MIDAS threshold, and 5 out of those 10 genes are indicated for splicing events by the RefSeq database. The lower hit rate of 5 out of 10 confirms that the proposed SVD method is preferable.

However, we caution that the NCBI Reference Sequence database does not contain information to validate the cancer-specific splicing events, which are of real interest to us. We have to draw upon other studies to look into those genes that have been known to be associated with brain cancer.

So far, our RT-PCR validation experiment has confirmed two glioma-specific cassette exon splicing events in chromosome 9: LCA (gi:6005992) and TNC (gi:4504548). Gene gi:6005992 is identified by both ANOVA and SVD (through the second singular structure). However, gi:4504548 was missed by ANOVA (with p-value= 0.661), flagged by WANOVA (with p-value=0.041), while the second singular structure in the SVD method detected this with a significant group difference (p-value= 0.005) and an outlying PSR 2.

Our discussion of the brain cancer study has been so far focusing on chromosome 9. We also find it interesting to consider two genes (CALD1 and EGFR) on chromosome 7 that have been documented in the literature to have splicing events related to brain cancer. In the same brain cancer study, ANOVA and WANOVA gave the p-value of 0.143 and 0.0002, respectively, for CALD1 (gi:15149468, see Zhang et al., 2004), while the proposed SVD method flagged it as a “stage 1” candidate with the p-value of 0.00004 on the second right singular vector with $\frac{d_1}{d_2}=\frac{20.973}{7.835}<3$. No outlying PSRs are identified for this gene.

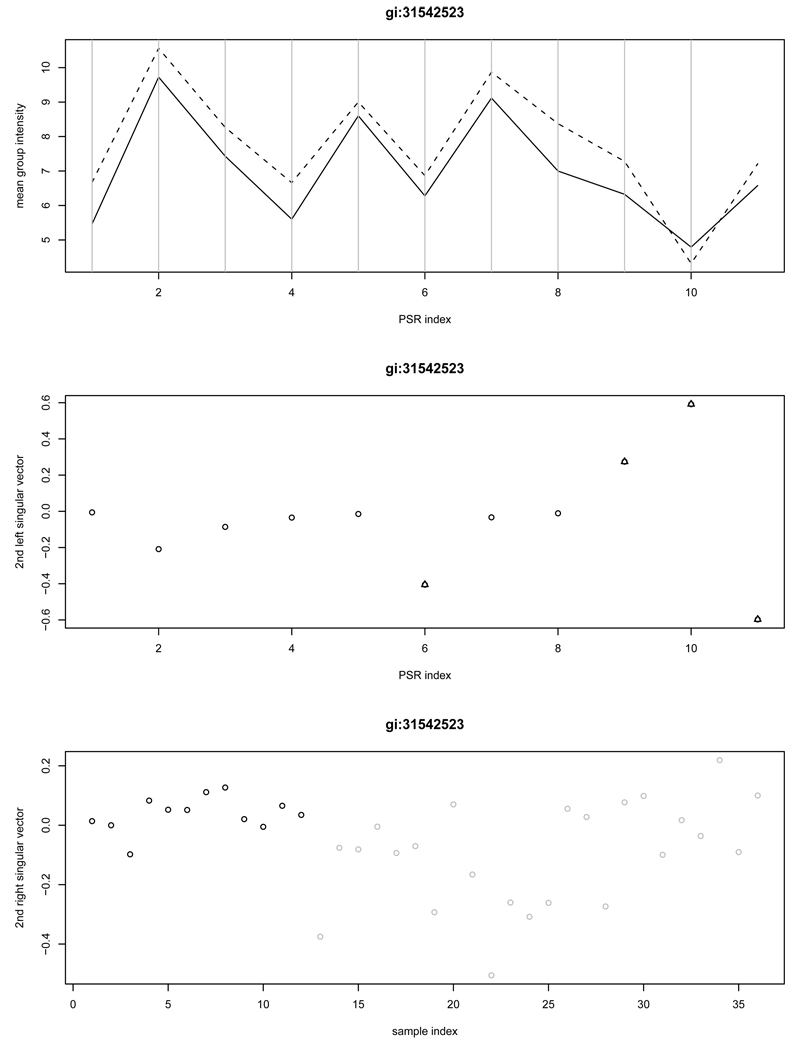
It is more intriguing to take a look at gene EGFR, whose splice variants have been functionally related to glioma formation (Nagane, et al. 2001; Mellinghoff et al. 2005; Frederick, et al. 2000). The corresponding probe set, gi:29725608, was given the p-value of 0.999 by ANOVA and 0.976 by WANOVA. In contrast, the SVD method yields a very significant group difference (p-value= 2.79 × 10⁻¹¹) on the second right singular vector with outlying PSRs 1, 10, 14, and 17. However, our proposed SVD method would miss it with this probe set, because the second singular value is not large enough, with $\frac{d_1}{d_2}>3$. The gene is also represented by another probe set gi:31542523, named as ECOP (EGFR-coamplified and overexpressed protein mRNA). The p-values from ANOVA and WANOVA for this probe set were 0.062 and 0.256, respectively, but our proposed SVD method flagged it as a “stage 2” candidate. As shown in Figure 4, the exon region that contains PSRs 9 – 11 is a promising site for the splicing event. In fact, it is believed to represent alternative promoters.

Figure 4.

A validated gene EGFR on chromosome 7 is detected by the SVD method at the second stage but missed by ANOVA. The top panel contain the plot of the average group intensities versus the PSRs; The middle and bottom panels contain the second left singular vector and the second right singular vector, respectively. In the top panel, normal and cancer groups are indicated by solid and dashed line, respectively; In the bottom panel, normal and cancer groups are indicated in black and grey, respectively.

3.5 Comparison of Top-ranked Genes

The statistical tests and the associated p-values used in the ANOVA methods and the proposed SVD method are not adjusted for multiple testing, because they are used for the purpose of screening and ranking. In this sub-section, we examine 50 top-ranked genes (based on p-values), as a supplementary study to that of the previous subsection.

It is fair to compare ANOVA to the stage 1 result of the SVD method because both approaches focus on the overall interaction between PSR and group. We take 50 top-ranked candidates each from ANOVA, WANOVA and SVD. It turned out that ANOVA and SVD overlap 18 times, and WANOVA and SVD overlap for 23 times out of 50.

Using the RefSeq information in the UCSC genome database, we found that 23 out of the 32 genes (72%) identified by SVD but not by ANOVA are indicated for exon splicing events, but only 16 out of the 32 genes (50%) identified by ANOVA but not by SVD are indicated. If the weighted ANOVA is used, we found that 20 out the 27 genes (74%) identified by SVD but not by WANOVA are indicated, as compared to 16 out of the 27 genes (59%) identified by WANOVA but not by SVD. The relative comparisons here are in line with those discussed in Section 3.4, showing once again that the use of weights in ANOVA is helpful, but the proposed SVD method is the overall winner for identifying exon splicing events.

4 Discussion

In this paper, we have introduced a robust alternative splicing method based on singular value decomposition. In comparison to the currently available methods, in particular, the two-way ANOVA model, our proposed method aims to target the group-by-PSR interaction that is due to one or a small number of PSRs, which is generally more biologically relevant when identifying alternative splicing events. The method is robust against single outliers and accounts for unequal variances of the signal intensity across PSRs. More importantly, it is capable of retrieving nontrivial information from a second-order singular structure, which has been empirically demonstrated to be biologically interesting and informative for a large number of genes.

Our studies indicate that the weighted ANOVA method accommodating the PSR-specific variance generally outperforms the ordinary ANOVA method used in the existing software. However, it does not suggest splicing-associated PSRs, and lags the proposed SVD method in overall reliability and accuracy.

Detecting group-specific alternative splicing is a challenging task, and a number of open questions remain. For example, our proposed method incorporates screening and diagnostic procedures with tuning parameters that are not fully data adaptive. A data-adaptive test on the statistical significance is yet to prove its worth. In another front, the MIDAS software from Affymetrix performs filtering of unreliable PSRs/exons/samples/genes at several levels prior to using ANOVA. Therefore, it will be biologically useful and statistically interesting to develop statistical models and analysis tools that incorporate filtering and testing in a unified framework.

Lab validation of group-specific alternative splicing is not easy either. Targeted RT-PCR focused on important glioma-specific cassette exon events, and only two genes were confirmed for this event on chromosome 9. However, the detection of other types of splicing events, such as overlapping exon splicing and alternative 3′ (or 5′ ) end variation, is also important for cancer research. The proposed SVD method has a real potential for finding promising candidates and the likely splicing sites for a wide variety of group-specific alternative splicing events.