Abstract
DNA supercoiling is one of the mechanisms that can help the unlinking of newly replicated DNA molecules. Although DNA topoisomerases, which catalyze the strand-passing of DNA segments through one another, make the unlinking problem solvable in principle, it remains difficult to complete the process that makes the separation of the sister duplexes possible. A few different mechanisms were developed by nature to solve the problem. Some of the mechanisms are very intuitive while the others, like topology simplification by type II DNA topoisomerases and DNA supercoiling, are not so evident. A computer simulation and analysis of linked sister plasmids formed in Escherichia coli cells with suppressed topo IV topoisomerase suggest an insight into the latter mechanism.
Keywords: DNA unlinking, DNA supercoiling, supercoiling free energy, DNA gyrase
Introduction
The double-stranded nature of DNA imposes a problem related to its replication: the parental DNA strands must be unlinked to make the separation of daughter chromosomes possible. Clearly, the separation is impossible for linked circular DNA molecules without passing one segment of the double helix through other segments. Although there is no such topological problem for linear DNA due to the free ends of the molecules, their very large length makes the problem nearly equally as tough. Clearly, the helical structure of DNA makes unlinking especially difficult. This very difficult problem was recognized immediately after the discovery of DNA structure and even led some theorists to solutions involving a paranemic (side-by-side) model for DNA (as opposed to the plectonemic Watson and Crick structure).1–3
A quantitative measure of the type of linking occurring between complementary strands of the double helix is the linking number, Lk, which may be defined in the following way. One of the strands defines the edge of an imaginary surface (any such surface gives the same result). The Lk is the algebraic (i.e., sign-dependent) number of intersections between the other strand and this spanning surface. The value of Lk depends only on the topological state of the strands and hence is maintained through all conformational changes that occur in the absence of strand breakage. By convention, the Lk of a closed circular DNA formed by a right-handed double helix is positive. The Lk between complementary strands of circular DNA is close to the number of base pairs divided by the DNA helical repeat, which equals 10.5 base pairs per turn. Thus, the value of Lk for the Escherichia coli chromosome is about 400,000. If each of the complementary strands is replicated without any unlinking, the above number would be the linking number for the sister DNA molecules, Ca (although Ca stands for the same mathematical term as Lk — in biological literature the former refers to the linking number between two double-stranded DNAs, while the latter specifies the linkage between the complementary strands of a single circular DNA). Failure to reduce this huge number to exactly zero will result in the failure to partition the daughter chromosomes. Thus, the unlinking mechanism must be rapid and accurate.
Unlinking would not be possible without DNA topoisomerases, even for linear chromosomes. By creating breaks in DNA through which they pass other DNA segments, topoisomerases are able to reduce Lk of the complementary strands during the replication and Ca of new daughter DNA molecules after completion.4–8 However, unlinking is a stochastic process, and topoisomerases can not only unlink but also can introduce links between DNA molecules. Special mechanisms are needed to provide complete unlinking, and a few such mechanisms were developed by nature.
In many cases the directionality of strand-passing events catalyzed by the enzymes is directed by a mechanical stress. Torsional stress in the double helix created by the moving replication complex promotes very efficient unlinking of the parental DNA strands, so the great majority of interlinks are removed before the end of replication.6,8 Mechanical forces which stretch linked daughter chromosomes during mitosis and meiosis create a different kind of stress that also strongly promotes unlinking.9,10
The problem of complete unlinking is such a difficult one because DNA molecules are so long and thin. Thus, their compaction into thick and relatively short eukaryotic chromosomes dramatically simplifies the problem. It is exactly the same trick, spooling, that is used to keep very long and thin threads in order. There is no comparable DNA compaction in prokaryotic cells, however, and the mechanism is much less important there.
Topological Equilibrium and DNA Supercoiling
There are two more not-so-intuitive mechanisms that contribute to complete unlinking. These mechanisms are related to the thermodynamic concept of topological equilibrium. Let us assume that we have a solution of circular DNA molecules. Let us imagine that their backbones are phantoms, so the molecule segments can easily pass through one another. In such case thermal motion would permanently change the topology of the molecules. However, after some time the fractions of all topological states approach their equilibrium values. Of course, these fractions and the fraction of linked DNA molecules in particular depend on DNA length, concentration and other parameters. One can imagine that given a very high concentration of DNA in contemporary organisms (around 20 mg/ml in bacterial nucleoids), the equilibrium fraction of linked circular DNAs would not be small. Type II topoisomerases catalyze strand passing and therefore make DNA segments, to some extent, phantoms.11 If the enzymes drive circular DNA molecules to topological equilibrium, they would hardly solve the unlinking problem. It turned out, however, that type IIA topoisomerases, the major unlinking enzymes, do a better job, reducing the fraction of linked circular DNAs to a level that is many times lower than that at the equilibrium.12 It is a puzzling story how the enzymes manage to do this but it is beyond the scale of these short comments (see ref. (13) for review).
The second of the latter mechanisms is based on shifting the topological equilibrium to a smaller fraction of linked molecules. This is achieved via DNA supercoiling. Prokaryotic circular DNA molecules are always negatively supercoiled inside the cells — the Lk of the complementary strands, is smaller, by 5–7%, than the value which corresponds to the torsionally unstressed molecules, Lk0.14 This deficit in the Lk, or the linking number difference, ΔLk= Lk − Lk0, causes the torsional deformation of the double helix and also results in the interwinding of DNA segments (see refs. (14–17) for details). Although the overall sizes of supercoiled and torsionally relaxed DNA molecules are not so different, interwound conformations of supercoiled DNA are much tighter than the conformations of relaxed molecules (Fig. 1). It is much less probable that a random line will pass inside the interwound superhelix than inside a loose random coil formed by a relaxed circular DNA. Thus, supercoiling greatly reduces the probability that two DNA molecules will be linked with one another at equilibrium. The reduction of the equilibrium linking probability due to supercoiling has been shown both experimentally and theoretically.18 It was also shown that type II topoisomerases, which catalyze the strand passage of one double-stranded DNA segment through another, very efficiently unlink pairs of DNA molecules when at least one of them is supercoiled.19,20
Fig. 1.
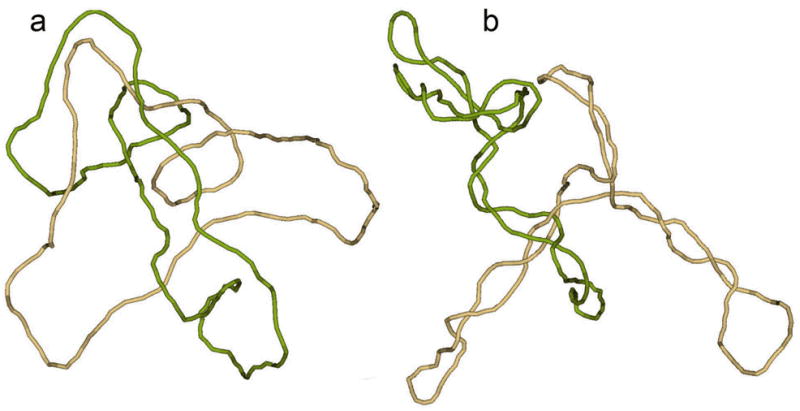
Topological equilibrium between linked and unlinked circular DNAs. The equilibrium distribution of topological forms could be obtained if the segments of circular molecules easily pass through one another during thermal motion, a condition that is easy to provide in computer simulation. Typical simulated conformations of singly linked catenanes, corresponding to DNA molecules 4 kb in length, show why supercoiling decreases the equilibrium fraction of catenanes. (a) Relaxed circular molecules have very loose conformations and are often linked at equilibrium if their centers of mass are close to one another. (b) Two supercoiled molecules can also form a link, but their tight conformations dramatically reduce the equilibrium probability of such an event even if the molecules are very close to one another.
Supercoiling of Topologically Linked Sister Plasmids
Recently Martinez-Robles et al. addressed the relationship between supercoiling and catenation from another angle.21 If it is less probable to have two supercoiled molecules linked with one another at equilibrium, that means it should be more difficult to introduce supercoiling into linked DNAs than into unlinked ones. The authors of the study wanted to show this directly for plasmids replicated in Escherichia coli cells. Supercoiling in bacterial cells is introduced by DNA gyrase, and the authors guessed that the enzyme adds more and more negative supercoiling into newly synthesized daughter plasmids when their linking number, Ca, is reduced by topoisomerases. This very reasonable suggestion was supported by a computer simulation. In this computationa DNA molecule was modeled by a closed chain of cylinders, so that one cylinder corresponded to 30 base pairs (the same model was used in the examples of catenanes shown in Fig. 1). It has been shown that this model quantitatively describes all known large-scale properties of the double helix (reviewed in ref. (22)). The bending rigidity constant between the adjacent cylinders is chosen so that the persistence length of the model chain is equal to DNA persistence length, which is 150 base pairs.23. The diameter of the cylinders accounts for electrostatic repulsion between DNA segments and therefore exceeds the geometric diameter of the double helix. For ionic conditions close to the physiological ones it equals 5 nm.24–26 To model DNA supercoiling, we need to introduce one more parameter into the model: the DNA bending rigidity. Its value is also known from many independent studies (see refs. (27–31). Martinez-Robles et al. used the Monte Carlo simulation to sample equilibrium ensembles of catenanes with a chosen value of Ca and fluctuating values of ΔLk. In this way they generated the equilibrium distributions over ΔLk for different values of Ca, and converted the distributions into the free energy of supercoiling. The simulations were performed for DNA catenanes that consisted of one relaxed and one supercoiled molecule. It was found that the free energy needed to introduce the same level of ΔLk increases for the catenanes with larger values of Ca.
It turned out to be more difficult to prove the relationship between supercoiling and catenation in the newly replicated plasmids experimentally. The fraction of linked plasmids is very small in the samples extracted from the normal cells due to very fast unlinking of the daughter DNAs after replication. Therefore, the authors used a special cell line in which unlinking could be inhibited by selectively suppressing Topo IV, the main enzyme responsible for unlinking.32–34 Martinez-Robles et al. wanted to show that the level of supercoiling is lower for linked plasmids with higher values of Ca. The plasmids, grown in this cell line, were separated by 2D gel electrophoresis with different concentrations of the agarose for each direction. Since the catenanes are separated differently depending on the agarose concentration, the researchers managed to identify distinctive families of spots on the gel that corresponded to the catenanes between two nicked plasmids, one nicked and one supercoiled molecule, and two supercoiled DNAs. The diagram corresponding to the second family is shown in Fig. 2. The individual spots correspond to the catenanes with different values of Ca. Adjacent spots in the diagram differ by 1 in the values of Ca that can have only integer values. Some spots with low values of Ca were further separated by electrophoresis in the second direction on up to a dozen smaller spots. The latter spots correspond to the catenanes with different ΔLk values of the supercoiled plasmid (although ΔLk is not an integer, its possible values form an arithmetic progression with the difference of 1 so that they can form a discrete set of spots in the gel). If the plasmids with different ΔLk can be separated, this opens a way to determine ΔLk for the supercoiled plasmids in catenanes of different complexities. It is known how to solve this problem for isolated supercoiled molecules,35–37, but it is a much more difficult task for these complex objects. Unfortunately, the separation of the catenanes with different ΔLk values was not possible for highly linked catenanes, and this left no chance of determining ΔLk for supercoiled molecules in these catenanes. Still, the authors found some indirect indications that the absolute values of ΔLk are indeed smaller for the catenanes with larger Ca. Overall, the obtained data supports the suggestion that increasing linking between the sister plasmids presents an obstacle for their supercoiling, and, correspondingly, supercoiling promotes unlinking.
Fig. 2.
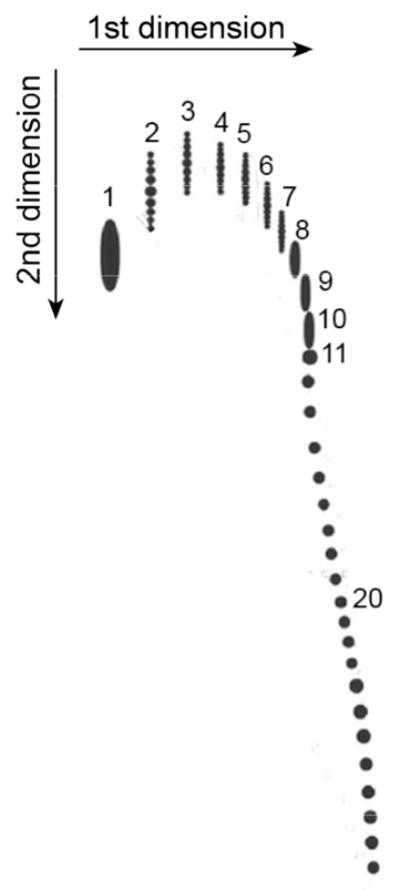
Separation of DNA catenanes by 2D gel electrophoresis. The diagram reproduces the data by Martinez-Robles et al. for a family of catenanes formed by one nicked and one supercoiled plasmid 4383 bp in length.21 The agarose gels of 0.4 % and 1% were used for electrophoresis in the first and second directions, respectively. The gel for the second dimension contained chloroquine, a dye that intercalates between DNA base pairs and changes the supercoiling. The numbers near the spots correspond to values of Ca in the catenanes. The catenanes with low values of Ca and different values of ΔLk are also separated into sets of vertical spots. The latter separation decreases when the value of Ca is grows, and for the linked plasmids with Ca larger than 7 it becomes impossible to separate molecules with different ΔLk at any concentration of chloroquine.
Perspective
Very different and sometimes very sophisticated mechanisms are used by nature to provide complete unlinking of daughter chromosomes. Probably, all of these mechanisms are needed since none of them guarantee that the unlinking will be complete. However, the importance of each of these mechanisms in different organisms varies. DNA supercoiling is important for the unlinking of bacterial chromosomes that have a level of compaction much lower than that of eukaryotic chromosomes. Supercoiling should be even more important for bacterial plasmids since mechanical forces do not contribute there to the unlinking of the replicated DNA molecules. It would be important to show that the contribution of supercoiling to the unlinking of the newly replicated sister plasmids is really critical. It can probably be done in a cell line in which DNA gyrase, which introduces negative supercoiling, can be suppressed. If supercoiling is critical for plasmid unlinking, the fraction of linked plasmids should grow upward in such cells after the gyrase suppression. This result has been obtained by Cozzarelli and co-workers for linked plasmids formed inside Escherichia coli cells by site-specific recombination.38
DNA supercoiling affects many DNA functions in bacterial cells. It changes the level of transcription of at least 7% of the Escherichia coli genome.39 It definitely can help in the unlinking of the newly replicated DNA molecules. So, it may be that facilitating DNA unlinking is one of the major functions of DNA supercoiling.
Acknowledgments
A. V. acknowledges support from the National Institutes of Health (Grant GM 54215).
References
- 1.Rodley GA, Scobie RS, Bates RHT, Lewitt RM. A possible conformation for double-stranded polynucleotides. Proc Natl Acad Sci USA. 1976;75:4092–4096. doi: 10.1073/pnas.73.9.2959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pohl WF, Roberts GW. Topological considerations in the theory of replication of DNA. J Math Biology. 1978;6:383–402. doi: 10.1007/BF02463003. [DOI] [PubMed] [Google Scholar]
- 3.Sasisekharan V, Pattabiraman N, Gupta G. Some implications of an alternative structure for DNA. Proc Natl Acad Sci U S A. 1978;75:4092–6. doi: 10.1073/pnas.75.9.4092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Champoux JJ, Been MD. Topoisomerases and the swivel problem. In: Alberts B, editor. Mechanistic studies of DNA replication and genetic recombination: ICN-UCLA symposia on molecular and cellular biology. XIX. New York: Academic Press, Inc; 1980. pp. 809–815. [Google Scholar]
- 5.Varshavsky A, Sundin O, Ozkaynak E, Pan R, Solomon M, Snapka R. Final stages of DNA replication: multiply intertwined catenated dimers as SV40 segregation intermediates. In: Cozzarelli NR, editor. Mechanisms of DNA replication and recombination, UCLA symposia on molecular and cellular biology. Vol. 10. New York: Alan R. Liss, Inc; 1983. pp. 463–494. [Google Scholar]
- 6.Wang JC, Liu LF. DNA replication: topological aspects and the roles of DNA topoisomerases. In: Cozzarelli NR, Wang JC, editors. DNA topology and its biological effects. Cold Spring Harbor, New York: Cold Spring Harbor Laboratory Press; 1990. pp. 321–340. [Google Scholar]
- 7.Ullsperger CJ, Vologodskii AV, Cozzarelli AV. Unlinking of DNA by topoisomerases during DNA replication. Nucl Acids and Mol Biol. 1995;9:115–142. [Google Scholar]
- 8.Alexandrov AI, Cozzarelli NR, Holmes VF, Khodursky AB, Peter BJ, Postow L, Rybenkov V, Vologodskii AV. Mechanisms of separation of the complementary strands of DNA during replication. Genetica. 1999;106:131–40. doi: 10.1023/a:1003749416449. [DOI] [PubMed] [Google Scholar]
- 9.Hiraga S. Chromosome and plasmid partitioning in Escherichia coli. Ann Rev Biochem. 1992;61:283–306. doi: 10.1146/annurev.bi.61.070192.001435. [DOI] [PubMed] [Google Scholar]
- 10.Page B, Snyder M. Ann Rev Microbiol. Vol. 47. 1993. Chromosome segregation in yeast; pp. 231–261. [DOI] [PubMed] [Google Scholar]
- 11.Wang JC. Moving one DNA double helix through another by a type II DNA topoisomerase: the story of a simple molecular machine. Q Rev Biophys. 1998;31:107–144. doi: 10.1017/s0033583598003424. [DOI] [PubMed] [Google Scholar]
- 12.Rybenkov VV, Ullsperger C, Vologodskii AV, Cozzarelli NR. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science. 1997;277:690–693. doi: 10.1126/science.277.5326.690. [DOI] [PubMed] [Google Scholar]
- 13.Vologodskii A. Theoretical Models of DNA Topology Simplification by Type IIA DNA Topoisomerases. Nucl Acids Res. 2009;37:3125–3133. doi: 10.1093/nar/gkp250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bauer WR. Structure and reactions of closed duplex DNA. Ann Rev Biophys Bioeng. 1978;7:287–313. doi: 10.1146/annurev.bb.07.060178.001443. [DOI] [PubMed] [Google Scholar]
- 15.Fuller FB. The writhing number of a space curve. Proc Natl Acad Sci USA. 1971;68:815–819. doi: 10.1073/pnas.68.4.815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vologodskii AV, Cozzarelli NR. Conformational and thermodynamic properties of supercoiled DNA. Ann Rev Biophys Biomol Struct. 1994;23:609–643. doi: 10.1146/annurev.bb.23.060194.003141. [DOI] [PubMed] [Google Scholar]
- 17.Bates AD, Maxwell A. DNA topology. Oxford: Oxford University Press Inc; 2005. p. 198. [Google Scholar]
- 18.Rybenkov VV, Vologodskii AV, Cozzarelli NR. The effect of ionic conditions on the conformations of supercoiled DNA. II Equilibrium catenation. J Mol Biol. 1997;267:312–323. doi: 10.1006/jmbi.1996.0877. [DOI] [PubMed] [Google Scholar]
- 19.Marians KJ. DNA gyrase-catalyzed decatenation of multiply linked DNA dimers. J Biol Chem. 1987;262:10362–8. [PubMed] [Google Scholar]
- 20.Roca J, Wang JC. The probabilities of supercoil removal and decatenation by yeast DNA topoisomerase II. Genes Cells. 1996;1:17–27. doi: 10.1046/j.1365-2443.1996.01001.x. [DOI] [PubMed] [Google Scholar]
- 21.Martínez-Robles ML, Witz G, Hernández P, Schvartzman JB, Stasiak A, Krimer DB. Interplay of DNA supercoiling and catenation during the segregation of sister duplexes. Nucl Acids Res. 2009;37:5126–5137. doi: 10.1093/nar/gkp530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vologodskii A. Simulation of equilibrium and dynamic properties of large DNA molecules. In: Lankas F, Sponer J, editors. Computational Studies of DNA and RNA. Dordrecht, The Netherlands: Springer; 2006. pp. 579–604. [Google Scholar]
- 23.Hagerman PJ. Flexibility of DNA. Ann Rev Biophys Biophys Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 24.Stigter D. Interactions of highly charged colloidal cylinders with applications to double-stranded DNA. Biopolymers. 1977;16:1435–1448. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- 25.Brian AA, Frisch HL, Lerman LS. Thermodynamics and equilibrium sedimentation analysis of the close approach of DNA molecules and a molecular ordering transition. Biopolymers. 1981;20:1305–1328. doi: 10.1002/bip.1981.360200615. [DOI] [PubMed] [Google Scholar]
- 26.Rybenkov VV, Vologodskii AV, Cozzarelli NR. The effect of ionic conditions on DNA helical repeat, effective diameter, and free energy of supercoiling. Nucl Acids Res. 1997;25:1412–1418. doi: 10.1093/nar/25.7.1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shore D, Baldwin RL. Energetics of DNA twisting. II Topoisomer analysis. J Mol Biol. 1983;170:983–1007. doi: 10.1016/s0022-2836(83)80199-5. [DOI] [PubMed] [Google Scholar]
- 28.Horowitz DS, Wang JC. Torsional rigidity of DNA and length dependence of the free energy of DNA supercoiling. J Mol Biol. 1984;173:75–91. doi: 10.1016/0022-2836(84)90404-2. [DOI] [PubMed] [Google Scholar]
- 29.Shibata JM, Fujimoto BS, Schurr JM. Rotational dynamics of DNA from 10e-10 to 10e-5 seconds: comparison theory with optical experiments. Biopolymers. 1985;24:1909–1930. doi: 10.1002/bip.360241006. [DOI] [PubMed] [Google Scholar]
- 30.Klenin KV, Vologodskii AV, Anshelevich VV, Klisko VY, Dykhne AM, Frank-Kamenetskii MD. Variance of writhe for wormlike DNA rings with excluded volume. J Biomol Struct Dyn. 1989;6:707–714. doi: 10.1080/07391102.1989.10507731. [DOI] [PubMed] [Google Scholar]
- 31.Bryant Z, Stone MD, Gore J, Smith SB, Cozzarelli NR, Bustamante C. Structural transitions and elasticity from torque measurements on DNA. Nature. 2003;424:338–41. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 32.Adams DE, Shekhtman EM, Zechiedrich EL, Schmid MB, Cozzarelli NR. The role of topoisomerase IV in partitioning bacterial replicons and the structure of catenated intermediates in DNA replication. Cell. 1992;71:277–288. doi: 10.1016/0092-8674(92)90356-h. [DOI] [PubMed] [Google Scholar]
- 33.Khodursky AB, Zechiedrich EL, Cozzarelli NR. Topoisomerase IV is a target of quinolones in Escherichia coli. Proc Natl Acad Sci USA. 1995;92:11801–11805. doi: 10.1073/pnas.92.25.11801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zechiedrich EL, Cozzarelli NR. Roles of topoisomerase IV and DNA gyrase in DNA unlinking during replication in Escherichia coli. Genes & Develop. 1995;9:2859–2869. doi: 10.1101/gad.9.22.2859. [DOI] [PubMed] [Google Scholar]
- 35.Keller W. Determination of the number of superhelical turns in simian virus 40 DNA by gel electrophoresis. Proc Natl Acad Sci USA. 1975;72:4876–4880. doi: 10.1073/pnas.72.12.4876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lee CH, Mizusawa H, Kakefuda T. Unwinding of double-stranded DNA helix by dehydration. Proc Natl Acad Sci USA. 1981;78:2838–42. doi: 10.1073/pnas.78.5.2838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Du Q, Livshits A, Kwiatek A, Jayaram M, Vologodskii A. Protein-induced local DNA bends regulate global topological complexity of recombination products. J Mol Biol. 2007;368:170–182. doi: 10.1016/j.jmb.2007.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zechiedrich EL, Khodursky AB, Cozzarelli NR. Topoisomerase IV, not gyrase, decatenates products of site-specific recombination in Escherichia coli. Genes Dev. 1997;11:2580–92. doi: 10.1101/gad.11.19.2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Peter BJ, Arsuaga J, Breier AM, Khodursky AB, Brown PO, Cozzarelli NR. Genomic transcriptional response to loss of chromosomal supercoiling in Escherichia coli. Genome Biol. 2004;5:R87. doi: 10.1186/gb-2004-5-11-r87. [DOI] [PMC free article] [PubMed] [Google Scholar]


