A Bayesian approach to modeling associations between pulsatile hormones

Abstract

Many hormones are secreted in pulses. The pulsatile relationship between hormones regulates many biological processes. To understand endocrine system regulation, time series of hormone concentrations are collected. The goal is to characterize pulsatile patterns and associations between hormones. Currently each hormone on each subject is fitted univariately. This leads to estimates of the number of pulses and estimates of the amount of hormone secreted; however, when the signal-to-noise ratio is small, pulse detection and parameter estimation remains difficult with existing approaches. In this paper, we present a bivariate deconvolution model of pulsatile hormone data focusing on incorporating pulsatile associations. Through simulation, we exhibit that using the underlying pulsatile association between two hormones improves the estimation of the number of pulses and the other parameters defining each hormone. We develop the one-to-one, driver-response case and show how birth-death MCMC can be used for estimation. We exhibit these features through a simulation study and on the relationship between luteinizing and follicle stimulating hormones.

1 Introduction

Hormones in the endocrine system interact to regulate important functions such as the growth, stress, and reproduction (Sherwood, 2005). Many of the hormones in these systems are pulsatile hormones, where the hormone is secreted into the circulatory system via boluses of hormone, called pulses. To understand the mechanisms behind endocrine diseases, endocrinologists and other biomedical investigators are most interested in characterizing the features that define the pulsatile secretion in a time series of hormone concentrations. To study pulsatile hormones, blood samples are collected from subjects every 5–15 minutes over a period of 6 to 24 hours. Hormone assays are run on the samples resulting in time series of hormone concentrations. Traditionally, each individual hormone series on each subject is characterized separately in analysis. Then, in a second stage analysis, the pulsatile characteristics (pulse frequency, pulse mass, total secretion, and half-life) are compared between groups of subjects. Various statistical models have been developed to characterize a single hormone series on a subject (Guo, Wang, and Brown, 1999; Kushler and Brown, 1991; Veldhuis and Johnson, 1992; Johnson, 2003; Liu and Wang, 2006). By far, the most commonly applied approach is based on deconvolution (Veldhuis and Johnson, 1992).

The above methods work well in characterizing pulsatile hormones such as luteinizing hormone (LH) and growth hormone (GH), but there are various hormones where pulse detection and parameter estimation is still difficult. For adrenocorticotropic hormone (ACTH) and cortisol the coefficient of variation is larger than that seen with LH and GH. In the case of follicle stimulating hormone (FSH), the pulse mass relative to the half-life is small and the signal-to-noise ratio is small, making pulse detection and parameter estimation additionally challenging using existing methods.

Driver-response pulsatile associations are known to exist between many sets of hormones (Clarke and Cummins, 1982; Clarke et al., 1984; Dorin et al., 1996; Marshall et al., 1992). In a driver-response model of pulsatile association, a pulse in one hormone results in a pulse in another hormone after a short period of time. Despite the possible estimation benefits when incorporating these known pulsatile associations, development of bivariate models has been limited because of the complexity of jointly estimating two sets of pulsatile parameters. To our knowledge, there is only one model that includes a pulsatile association component (Guo and Brown, 2001). This model is limited in that it assumes an instantaneous pulse secretion and only has a discrete measure of the temporal association between the pulses. These restrict the hormones to which this model can be applied. Other bivariate approaches for hormone data relate hormone concentrations or the underlying circadian rhythms (Diggle, 1990; Wang, Guo, and Brown, 2000). They are not appropriate for modeling pulsatile associations when decay rates or secretion lengths differ between the hormones, as is the case with most hormone pairs.

In this paper, we develop a new bivariate model of pulsatile hormones. We focus on incorporating a pulsatile association component because it is the major component of association in pulsatile hormone time series and is the mechanism that biologically ties together pairs of hormones most strongly. We show that in situations where there is known to be an association between pulses, incorporating the pulsatile association improves estimation of the pulsatile parameters. This is especially true in hormones that are difficult to estimate univariately. In Section 2 we develop the one-to-one driver-response pulsatile association model. We describe the birth-death MCMC (BDMCMC) estimation algorithm for the one-to-one driver-response model in Section 3. In Section 4, we apply the model to our motivating data set, a pair of LH-FSH series, in which FSH pulsatility is characterized poorly when fitted alone. In Section 5, we investigate the estimation properties and improvements over a univariate BDMCMC fitting algorithm for simulated data similar to LH and FSH. Discussion and model extensions is offered in Section 6.

Before defining the model, we note that in this paper driver-response terminology, which often implies causality, is not meant to imply that the underlying association in the model must be causal. The application of the following models is equally viable in situations where one series exhibits a temporal association such that pulses in one series are followed in time by pulses in another series with no causal element. This also implies that this class of models cannot be used to prove or disprove causality.

2 The bivariate deconvolution model

Deconvolution is the most widely used model to fit pulsatile hormones and is applicable to a wide range of hormones (Dorin et al., 1996; Kasa-Vubu et al., 2002; Matt et al., 1998). This makes the interpretation of the parameters familiar to clinical investigators. It is for these reasons that we base our association model on this mathematical framework; however, other frameworks are equally plausible. The general forms of the deconvolution approach for pulsatile hormone data are covered in detail by Veldhuis and Johnson (1992) and more recently extended to the Bayesian framework by Johnson (2003). Thus, we move to our bivariate deconvolution model. In this section we focus on developing the one-to-one model, where the driver and response pulses exist in pairs. It is the most common pulsatile association and applicable to our motivating example. However, the model is generalizable to non-one-to-one driver-response associations. Extensions are discussed in Section 6 and implementation is considered future work.

2.1 The one-to-one deconvolution model

Let {x_t} be the time series of concentrations of the driver hormone and {y_t} be the time series of concentrations of the response hormone for one subject, where t = 1, …, n. Parameters and functions subscripted by x will refer to the driver hormone. Parameters and functions subscripted by y will refer to the response hormone.

In the deconvolution framework, the observed hormone concentrations are represented by the convolution integral plus error: $log(x_t)=log({\int }_{-\infty }^t{S}_x(z)E_x(t-z)dz)+{\epsilon }_{x_t}$ and $log(y_t)=log({\int }_{-\infty }^t{S}_y(z)E_y(t-z)dz)+{\epsilon }_{y_t}$. S_y(·) define the hormone secretion functions, E_x(·) and E_y(·) define the hormone elimination functions, and ε_xt and ε_yt are the errors consisting of both biological and technical components. The hormone concentration is modeled on the log scale to account for the fact that hormone concentrations are positive. Alternatively, one could model the hormone concentration on the natural scale and assume a constant coefficient of variation (CV) error structure. In further development, the secretion and elimination representations are similar for the driver and response hormone but with the subscript of y replacing the subscripts of x. Thus, we only describe, in detail, the driver hormone.

In deconvolution models of hormone data, the secretion function is specified by, $S_x(·)=b_x+{\sum }_{i=-\infty }^k{f}_{xi}\{t;{\theta }_{xi}(t)\}$. The first part of the sum, b_x, is a non-pulsatile, basal secretion rate and assumed constant over time, as is the case for most hormones. Each component in the summation defines one of the k pulsatile secretion events. Each pulse is defined by a rate function, f_xi{t; θ_xi(t)}, where θ_xi(t) is a set of pulse specific parameters (such as the location and pulse mass) where the complete set of pulse specific parameters is denoted as θ_x = (θ_x1, …, θ_xk). In this implementation, the secretion rate functions had a similar Gaussian form for each hormone and each pulse; $f_{xi}\{t;{\theta }_{xi}(t)\}=A_{xi}exp[-0.5{\{(t-t_{xi})/{\sigma }_x\}}^2]/\sqrt{2\pi {\sigma }_x^2}$. Each Gaussian curve has the set of pulse specific parameters θ_xi(t) = (t_xi, A_xi), where the ith pulse is centered at the location, t_xi and has mass A_xi. The pulse width ${\sigma }_x^2$ is assumed common across pulses because estimation in noisy series is difficult. The Gaussian form has been the most commonly used functional form of the pulsatile secretion; however, other positive functional forms could easily be considered in the Bayesian framework.

In implementation, an initial concentration, C_0x is added to the model to represent the concentration at the start of observation that is due to pulsatile secretion occurring, but not completely decaying, before the start of observation. Essentially C_0x represents the components of the sum that occurs before the first pulse in the observation period (i.e., i ≤ 1). Finally, we assume that the elimination function, E_x(t), is modeled as a single exponential decay where λ_x is the constant decay rate.

When explicitly combining the model specifications, we arrive at the following model of hormone concentration for the driver hormone:

$$\begin{array}{l}{x}_t=C_{0x}exp\{-{\lambda }_{x}t\}+\\ {\int }_{-\infty }^t\underset{S_x(t)}{\underbrace{\left[b_x+{\displaystyle \sum _{i=1}^k}{A}_{xi}\frac{1}{\sqrt{2\pi {\sigma }_x^2}}exp\{-1/2{(\frac{t_{xi}-z}{{\sigma }_x})}^2\}\right]}}\underset{E_x(t)}{\underbrace{exp\{-{\lambda }_x(t-z)\}}}dz+{\epsilon }_{xt}.\end{array}$$

2.2 Priors

To complete the Bayesian specification of the model, we define a set of priors and hyperpriors and assume that some of the priors depend upon a set of hyperparameters, ω, such that the prior factors as follows:

$$\begin{array}{c}p({\mathrm{\sum }}_e,b_x,b_y,{\lambda }_x,{\lambda }_y,{\sigma }_x^2,{\sigma }_y^2,{\theta }_x,{\theta }_y,\omega ,k)\\ =p({\mathrm{\sum }}_e)p(b_x)p(b_y)p({\lambda }_x)p({\lambda }_y)p({\sigma }_x^2)p({\sigma }_y^2)p({\theta }_x,{\theta }_y\mid \omega ,k)p(\omega )p(k).\end{array}$$ (1)

We note that the prior on the pulse specific parameters is a joint prior and used to define the pulsatile association component of the model.

There are two association components relating the pulse locations, t_x and t_y, and the pulse masses, A_x and A_y. Given the close timing of the driver and response pulses in a one-to-one model, the one-to-one assumption results in the same number of pulses in each series. Thus, in the model, we assume for each driver pulse there exists a response pulse such that t_yi = t_xi + τ_i where τ_i ~ Gamma(α, β), i.e., the lag time between the driver and response pulses is a random effect with hyperparameters α and β. In addition, the pulse masses, log(A_xi) and log(A_yi), are linearly associated. We impose the linear association by assuming that the masses are random effects with a bivariate log normal distribution, (log(A_xi), log(A_yi))′ ~ BivNormal(log(μ_mx, μ_my)′, Σ_m). The log normal distribution was chosen to accommodate the positivity constraint of the pulse masses. Other distributions, such as a truncated normal or t-distribution are equally plausible. With these specifications the prior on the pulse component factors as: $p({\theta }_x,{\theta }_y\mid \omega ,k)={\prod }_{i=1}^{k}p(A_{xi},A_{yi}\mid \omega ,k)p({\tau }_i\mid \omega ,k),p(t_{xi}\mid \omega ,k)$.

2.3 Parameter specification in the Priors

In implementing the one-to-one model we specified the following priors. We assumed, a priori, that the distribution of the number of pulse pairs was a truncated Poisson(λ), truncated at 50. This upper boundary is above the number of pulses that occur in pulsatile hormone series in one day. In the LH-FSH example, λ = 23 and λ = 13 in the simulation. These values were based on previous research. However, the estimation is not sensitive to the value of λ.

Conditional on the number of pulse pairs, k, the driver locations, t_xi, are distributed as a random permutation of every third order statistic from 3k + 2 i.i.d. uniform(−40,T+10) random variates (Green, 1995; Stephens, 2000a; Johnson, 2003). This choice increases the probability that each pulse is modeled as one Gaussian without becoming too periodic. To accommodate partial pulses at the beginning and ending of a series, we choose values for pulse locations slightly before and after the start and end of observation (T).

Table 1 contains information about the priors on the common parameters and association components. For the lag distribution, we focused on estimating the mean and assumed that the mean and the variance are the same in the lag distribution (i.e., β = 1). We used the congugate hyperpriors for the pulse mass distribution and the pulse mass variance-covariance matrix. The hyperpriors on the mean of the log(pulse mass) were vague with a mean of 1.5 for the driver (LH) and 0 for the response (FSH). The variance-covariance matrix in the hyperprior of the pulse masses was set as a 2 × 2 diagonal matrix with diagonal components (10, 000, 10, 000). The priors and hyperpriors on the variances of the random effects are shown in Table 1. The priors on the variance-covariance matrix of the masses and widths were informative to reflect our belief that the mass and widths are similar. We chose the actual values based on Johnson (2003) and scaled the values to match modeling the log of the pulse masses. For the baseline, decay rates, and initial concentration we choose uniform priors over ranges that are much larger than biologically plausible values (see Table 1). For example, the baseline cannot be larger than the maximum of the data, so we chose a value higher than the maximum of both datasets. C0 would be unlikely to be much more than the maximum of the data or the size of a few pulses depending on the decay rate. Here the maximum of the data was larger than the pulse masses and we conservatively took a multiple of the maximum hormone concentration. The half-life is well defined for many hormone so we set a boundary that was 4 times that the larger of the reported value in the literature of the two hormones under study.

Table 1.

Prior information for the simulation and LH-FSH example. A “•” is used when the values were similar for the driver and response hormones.

b•/λ•	Unif(0, 50]
λ•	Unif(0, 1000]
C0•	Unif{0, 2 × max(xi)}, Unif{0, 2 × max(yi)}
${\mathrm{\sum }}_m^{-1}$	Wishart4[Sm]
$S_m^{-1}$	diag(20, 20)
α	Gamma(1.5, 0.1)
${\mathrm{\sum }}_e^{-1}$	Wishart2[Se]
$S_e^{-1}$	diag(100, 100)

The parameters choices for the univariate analyses were analogous to what was defined above.

3 Estimation of the 1-1 model

To estimate the posterior distribution we used BDMCMC (Stephens, 2000a). The major assumption of BDMCMC is that the joint posterior of the pulse specific components and the number of pulse pairs must be exchangeable. In our situation, the exchangeable assumption implies that the labeling of the pulse pairs be unimportant. In the examples in this paper, the biological process (i.e., the parameters) does not change over the course of one day of study. Thus, the labeling of the pulse pairs is not important. In the one-to-one setting, the pulse specific parameters can be represented as a pair (e.g., (A_xi, A_yi) and (t_xi, τ_i)) and Johnson’s (2003) BDMCMC algorithm can be extended with just a larger set of parameters associated with each birth or death in the process.

The mathematical derivations of the birth-death stage of the algorithm can be found in the Supplemental Material. In the MCMC stage, we used a Metropolis-Hastings/Gibbs sampler (Tierney, 1994) to update the parameters conditioned on the number of pulses at the end of the birth-death stage. When full conditionals did not have a closed form, we used a random walk Metropolis-Hastings sampler to simulate the distributions.

For the univariate models, the BDMCMC estimation algorithm was applied as described in Johnson (2003).

3.1 BDMCMC implementation

For the LH-FSH example and each of the simulated bivariate and univariate series, we ran the BDMCMC chain for 250,000 iterations. The birth rate, λ_b, and the simulation time, t₀, between MCMC updates in the BDMCMC algorithm are related and fairly arbitrary. We set t₀ = 1 and λ_b = mean number of pulses in the Poisson prior on the number of pulses. We investigated the sensitivity of our choice of t₀ and λ_b on a subset of the simulated series. As expected, when t₀ was larger, the time in the birth-death simulation was longer; however, the results did not change. The results for λ_b were similar for values in a wide range of λ_b. We discarded the first 20,000 iterations as burn-in. Every 50th iteration was saved and used for summarizing the posterior distributions. The variances in the proposal distributions for the Metropolis-Hastings steps were chosen to obtain acceptance rates between 25 and 50%. We assessed convergence and mixing visually using serial plots of the draws.

We initialized the algorithm by assuming there was one pulse, i.e., k = 1. We started the chains at various points over reasonable ranges of the parameters to assess the sensitivity of the starting value. As long as the values were not extreme, the results were similar. For both real data example and the simulations, we used historical knowledge about the values of the half-lives (Schally, et al., 1971) of LH and FSH (LH=60 minutes and FSH=240 minutes). The pulse widths were initialized at 10 and 30 minutes² for LH and FSH, respectively based on preliminary univariate analyses. The minimum of the data was used to guide the starting value for the baseline. When initializing the pulse masses, pulses were more likely to be modeled as one component if the initial mean pulse mass in the pulse mass hyper-prior was larger than truth. We initialized the mean of the pulse mass distribution at a value approximately 0.25 log(concentration) units larger than truth.

Our modeling situation is similar to modeling mixtures of distributions which results in label switching. Label switching means at different iterations the same pulse pairs will be labeled with a different index. Usually the pulses are adequately separated in time such that sorting by their location in time resolves most of the label switching; however, when one pulse is modeled as two components, ordering via time does not always resolve the issue. In post-simulation processing, we resolved this situation by combining pulse specific parameters when the driver locations occurred within 4 sampling units of one another. This minimized the remaining label switching. The algorithm that was used to combine the secretion events is presented in the Supplemental Material. Alternate approaches to post simulation processing may also be applied (Johnson, 2003, 2006; Stephens, 2000b).

To assess model fit we generated a sample from the posterior predictive distribution and calculated the χ² discrepancy as outlined by Gelman, et al (1995).

4 Motivating real data example

LH and FSH are two pulsatile hormones of interest in the reproductive system. In general, LH pulses are more clearly defined, but FSH pulses are often difficult to detect and characterize because of the smaller pulse masses and longer half-life. In a natural setting, both LH and FSH are driven by GnRH (Schally et al., 1971; Marshall et al., 1992). Thus, we would ideally use the GnRH-FSH driver-response relationship to characterize FSH. However, GnRH hormone levels are often below assay sensitivity in human blood. Thus, GnRH pulse detection is not possible in human studies. Since both LH and FSH are driven by GnRH and the LH response to GnRH is earier than FSH, the LH-FSH pair of series can be modified to exhibit a driver-response association (without the causal element). In this example, we focus on improving the estimation of FSH pulatile characteristics by using the LH-FSH relationship. In our example, blood was collected every 7.5 minutes for 24-hours. We shifted the LH observations two sampling units backward in time (15 minutes) prior to analysis to guarantee FSH pulses occur after LH pulses regardless of any noise in estimating the locations.

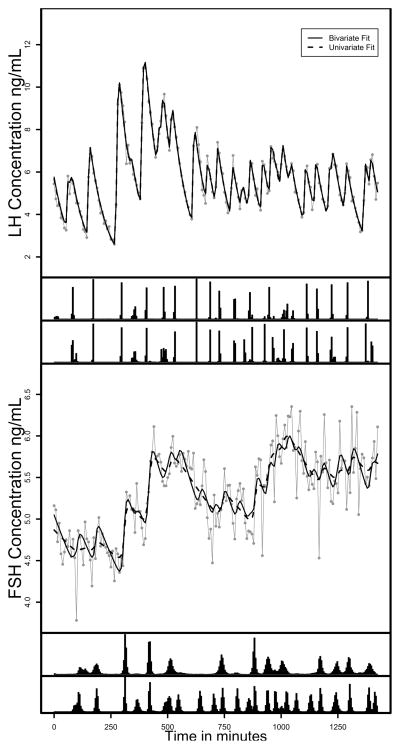
Figure 1 shows the observed and fitted values along with the joint posteriors of the pulse locations for both fits for the LH-FSH series. For LH, we note that the pulse locations are similar between the univariate and bivariate fits. The fitted lines are also similar for both methods of fitting LH and both fit the observed data well indicating that adding the less clean FSH series to the model does not degrade the fit for LH. For FSH, the number and precision of the pulse locations is less in the univariate fit compared to the bivariate fit. The univariate fit shows that the larger trends are being fitted with many pulses being smoothed through. None of the fits indicated significant lack of fit using the posterior predictive distribution.

Figure 1.

Observed and expected LH and FSH concentrations for one subject. The top figure is LH, and the bottom is FSH. The solid grey lines are the observed hormone concentration profiles and the solid black line is the mean of the posterior predictive distribution for the bivariate fit and the dashed black line is the expected curve for the univariate fits. The histograms on the bottom axes represent the joint posteriors of the pulse locations for the univariate fit (top) bivariate fit (bottom). The data are from Pincus et al. (1998).

Table 2 contains the mean and 95% equal tails credible intervals for the parameters estimates for the two fits. The parameter estimates and credible intervals are similar for the LH series. Notable differences for FSH include the substantially fewer number of pulses in the univariate fit and much less precision in the locations of the pulses. This results in a much lower estimate of the total pulsatile secretion. In addition, the half-life and pulse width estimates for FSH are much higher than the bivariate fit and much higher than is usually considered biologically plausible by endocrine investigators. This along with the large difference in the number of pulses between LH and FSH are the major indictors that something may be incorrect in the univariate fit of FSH and would suggest alternative models might be useful. When studying the pulses that are detected in the bivariate fit and not in the univariate fit, we note that the pulses were not systematically smaller and were not essentially zero (Supplemental Table 1). In fact, the average size of the missing pulses was only slightly lower with an average of 0.5 concentration units compared to 0.6 concentration units for the pulses detected in the univariate FSH fit. This reassures the authors that the one-to-one model is valid.

Table 2.

Summary statistics for the common parameters for the example LH-FSH series from the bivariate and univariate fits: Mean=mean of the posterior and CI=credible interval

	LH		FSH
	Bivariate	Univariate	Bivariate	Univariate
Parameter	Mean (95% CI)	Mean (95% CI)	Mean (95% CI)	Mean (95% CI)
No. Pulses	22.60 (21,24)	23.55 (23,25)	–	11.33 (5,16)
No. Secretion Events	28.62 (27,31)	28.20 (25,31)	28.6 (27,31)	11.6 (5,16)
Baselinea	0.98 (0.2,1.6)	1.03 (0.2,1.6)	2.25 (0.31,3.81)	2.95 (0.6,4.5)
Half-Lifeb	53.47 (44.19,65.06)	53.70 (44.41,65.69)	253.73 (110.56,460.90)	438.64 (143.31,804.41)
Secretion Widthc	8.20 (4.43,12.58)	8.72 (4.61,13.79)	40.67 (1.07,127.77)	76.67 (2.62,302.32)
Total pulse sec.a	87.19 (81.46,93.67)	88.00 (81.12,95.71)	13.02 (9.91,17.12)	6.23 (2.96,9.62)
Mean of Lag Dist’nb	15.39 (10.73,20.25)	–	–	–
Mean Log(Sec.) Mass	1.02 (0.82,1.20)	1.03 (0.81,1.24)	−0.88 (−1.30, −0.54)	−0.74 (−1.79, −0.24)
Log(Sec.) Mass Var	0.20 (0.10,0.38)	0.25 (0.12,0.48)	0.18 (0.041,0.53)	0.47 (0.015,2.63)
Mass Correlation	0.61 (0.13,0.87)	–	–	–

^aunits=ng/mL

^bunits=minutes

^cunits=minutes²

5 Simulation

To further assess the bivariate model and to confirm our use of the bivariate model in the LH-FSH case, we simulated 100 bivariate hormone series under a one-to-one driver-response association. We fitted each set of series with the bivariate model and also fit each univariate series with the analogous BDMCMC univariate model and fitting algorithm. The parameters in the simulation were chosen to represent hormone profiles similar to LH and FSH data presented in the previous section. In the simulation, we assumed a sampling interval of 7.5 minutes for a duration of 24 hours. The pulse masses were drawn simultaneously from a bivariate log normal distribution with a mean of 1.24 for the driver hormone and −0.74 for the response hormone. The variance of the driver masses was 0.15 and 0.14 for the response hormone. The masses had a correlation of 0.85. The pulse widths were 10 minutes² for the driver and 30 minutes² for the response. The half-lives (λ_•/log(2)) were 60 minutes and 240 minutes for the driver and response, respectively. The baselines (b_•=λ_•) were 0.65 concentration units for the driver and 3.0 concentration units for the response, where a • is used when the driver or response designation is not important. For the driver series, the inter-pulse interval was drawn from a gamma distribution with a mean of 98 minutes (13 sampling units) and a variance of 52.5 minutes² (7 sampling units²) (Mauger et al., 1995). In addition, a minimum inter-pulse interval of 4 sampling units was imposed to prevent two pulses from occurring simultaneously. The time between a driver and response pulse was drawn from a gamma distribution with a mean of 15 minutes and a variance of 20.0 minutes². Finally, for both series, the errors were drawn independently from two Gaussian distributions with a variance of 0.05 for the driver hormone and a variance of 0.005 for the response hormone.

5.1 Simulation results

Table 3 contains the true parameter values and the summarizations of the posterior distributions, average biases, and equal tails 95% credible intervals. We used the mode of the posterior distribution of the pulse number after post-simulation processing to summarize false positives and negatives for the pulse locations. For the bivariate model there were 27 false negatives out of 1463 pulses (1.8% false negative rate) and 3 false positives (1 in each of 3 series). There were an average of 14.6 pulse pairs per series. Sixteen series had 1–3 pulses missing (average=1.3) and one had 6 missing. The average frequency of the model of the posterior distribution of the number of pulses was 71%. The estimates of the common pulse parameters and the pulse specific parameters had minimal bias with the exception of the response half-life and pulse width, which are both biased high. However, the bias and precision are improved using the bivariate fit. The total pulse secretion was estimated well and the coverage is good for all parameters. There was no evidence of lack-of-fit based on the posterior predictive density and the χ²-discrepancy statistic.

Table 3.

Parameter summary statistics for the common parameters for 100 simulated series estimated using bivariate and univariate models. D=driver hormone, R=response hormone, units in parentheses, PM=posterior mean, CI=credible interval

		Bivariate				Univariate
Parameter	True Value	Mean of PM	(SD)	Width of 95% CI	Coverage of 95% CI	Mean of PM	(SD)	Width of 95% CI	Coverage of 95% CI
D Baseline (conc.)	0.65	0.84	(0.37)	0.39	96	0.94	(0.43)	0.41	94
D Half-Life (min.)	60	56.89	(9.74)	10.22	96	55.85	(10.85)	11.01	93
D Pulse Width (min.2)	10	15.15	(10.06)	10.80	98	15.04	(10.18)	10.76	98
R Baseline (conc.)	3.00	2.38	(0.59)	0.79	92	3.02	(0.37)	0.68	99
R Half-Life (min.)	240	330.05	(87.99)	120.36	97	487.76	(87.84)	170.08	68
R Pulse Width (min.2)	30	89.54	(59.57)	79.38	99	122.80	(54.11)	126.41	100
Mean of Lag Dist’n (min.)	15	13.86	(3.10)	3.60	95	–	–	–
D Mean Log(Mass) (log(conc.))	1.24	1.23	(0.13)	0.14	96	1.23	(0.13)	0.16	95
R Mean Log(Mass) (log(conc.))	−0.74	−0.75	(0.19)	0.23	97	−1.32	(2.70)	0.87	100
D Var Log(Mass) (log(conc.)2)	0.15	0.14	(0.069)	0.081	94	0.21	(0.10)	0.14	97
R Var Log(Mass) (log(conc.)2)	0.14	0.12	(0.077)	0.10	91	0.47	(2.51)	1.10	100
Mass Correlation	0.85	0.61	(0.23)	0.27	92	–	–	–

Bias in total secretion and pulse specific parameters
Parameter	True Value	Mean Bias of PM	(SE)	95% CI	Coverage of 95% CI	Mean Bias of PM	(SE)	95% CI	Coverage of 95% CI
Number of Pulses	14.6	−0.24	(0.078)	(−1.06,0.94)	99
D Univariate	–	−0.31	(0.010)	(−1.39,1.02)	98
R Univariate	–	−4.63	(0.12)	(−8.42, −0.35)	63
Total D secretion (conc.)	55.1	0.93	(0.66)	(−9.7,13.8)	92	0.59	(0.73)	(−11.0,14.2)	91
Total R secretion (conc.)	7.6	0.24	(0.14)	(−2.3,3.6)	95	−3.08	(1.27)	(−5.0, −0.02)	54
D location (min.)a	–	0.24	(0.17)	27.10b	97	−0.029	(0.18)	22.75	93
D masses (conc.)	3.46	0.10	(0.018)	2.64	93	0.086	(0.019)	2.35	88
R locations (min.)	–	−0.85	(0.21)	34.90	96	−1.22	(0.77)	179.78	98
R masses (conc.)	0.48	0.025	(0.0037)	0.56	96	−0.094	(0.0059)	0.58	84

^aN=1436 for bivariate, N=1413 for univariate driver, N=985 for univariate response

^bAverage width of 95% CI

For the univariate deconvolution method, the driver series has a slightly higher false negative rate of 3% (44 false negatives) and a slightly higher false positive rate of 0.5% with 7 series having one false positive each. The false negatives were spread across 20 series with 1–6 false negatives each (mean=2.2 pulses). The mode of the posterior distribution of the number of pulses had an average frequency percentage of 66%, slightly lower than the bivariate fit. The parameter estimation was similar between the bivariate and univariate fits, with the parameter estimates having minimal bias. This confirms that going with a bivariately fitting when one series is not well defined does not decrease the estimation performance of a fairly clean series. In fact, there is some indication that bivariate fitting may help to define the parameter estimates and the number of pulses slightly better.

For the response series, only 2 series had the correct number of pulses estimated. There were 1–9 pulses missing in each series with an average of 5 pulses missing in each series. The posterior distribution of the pulse mass was wide and the posterior mode had an average frequency percentage of only 22%. The parameter estimate is quite biased for the half-life and pulse width, such that the estimates are moving into non-biologically plausible ranges. The coverage is low for the half-life (60%) and the width of the 95% credible interval is very wide for the pulse width. The total secretion is biased low and the estimate is on average only estimating 50% of the true pulse secretion in the series.

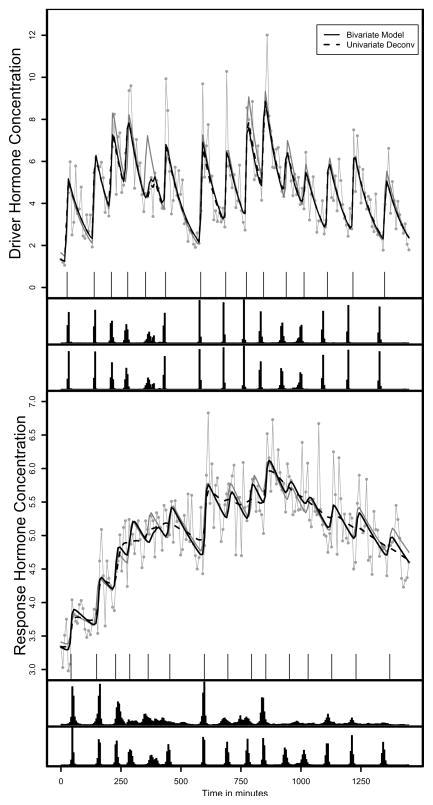
Figure 2 contains the simulated and expected values for one example simulated pairs of series. Supplemental Table 2 contains the parameter estimates for the example in Figure 2. The fitted hormone concentrations are essentially identical for the driver series. In general, the driver series is fitted well with both methods. However, the size of the fifth pulse is underestimated in both fits because randomly the noise resulted in consistently low hormone concentration values. For the response hormone, neither models produce the close fit to the observed data compared to LH, which is an artifact of the low signal-to-noise ratio in the response series. However, the bivariate model represents the more classical pulsatile fit we expect, while the univariate fit seems to be overly smooth and modeling the more global trends in the data. In addition, the bivariate model is fitted the true concentration curve quite closely. However, none of the fits exhibit lack of fit using the posterior predictive distribution.

Figure 2.

An example expected and simulated hormone concentrations. The top figure is the driver hormone, and the bottom the response hormone. The true pulse locations are the ticks just under the observed series. The grey lines with the “dots” are the observed data, the solid grey lines are the true hormone concentrations. The solid black lines are the expected bivariate fits and the dashed black lines the expected univariate fits. The histogram below each series is the joint posterior distribution of the pulse locations for the univariate fit (top) and the bivariate fit (bottom).

6 Discussion

In this paper, we presented a new model of a pulsatile driver-response association between two hormones. The framework behind the model is more flexible than the exist bivariate model because it incorporates both temporal and pulsatile mass associations. Although we focused on a one-to-one pulsatile association, the model framework is not restricted to a one-to-one associations. Two examples of non-one-to-one driver-response associations include an imperfect driver association where a response pulse is more likely to occur for larger driver pulses and a two driver situation where, in truth, there are two drivers of the response hormone but only one driver was collected in the experiment. In the first case, there would be missing response pulses and in the second case, there would be missing driver pulses relative to the one-to-one model. These extensions might be incorporating by the introduction of an indicator function, r_i. For the imperfect driver model, when r_i = 1, a corresponding response pulse is generated according to p(A_yi|A_xi) based on the bivariate log normal defined in the one-to-one model. The response pulse location would be generated according to one-to-one timing model. If r_i = 0, (A_yi, t_yi) is missing. The probability of a response pulse occurring could be modeled by a logit: logit[p(r_i = 1)/{1 − p(r_i = 1)}] = a + bA_xi.

For the two-driver model, the response hormone contains more information than the driver hormone and the model would be conditioned on the response mass. Although this does not follow the temporal ordering of the biology, all pulses are observed at the time of analysis. Thus, one may condition on either the driver or mass information when modeling the association. In this extension, if r_i = 1, there is a corresponding driver pulse generated according to p(A_yi|A_xi), which is based on the bivariate normal defined in the one-to-one model and the driver pulse location is generated using a slight variation of the one-to-one timing model: t_xi = t_yi −τ_i. When r_i = 0, (A_xi, t_xi) are missing. The probability of a driver pulse being observed could be modeled by a logit: logit[p(r_i = 1)/{1−p(r_i = 1)}] = c+dA_yi.

In further extensions to the model, one could consider associations between the non-pulsatile components, such as the baseline or decay rates. However, the pulsatile associations are often of most interest to the investigator. In addition, the secretion mechanism is thought to be most tightly linked as the elimination kinetics are farther down the pathway. Although the single subject model is easily extended to incorporate additional pulsatile associations, the estimation extension likely requires modeling all subjects together on series of 24 hours or less in length to provide enough pulses for adequate estimation. Modeling all subjects together has yet to be accomplished in with pulsatile hormone series. Thus, we focused on the one-to-one model, which is estimable using a single bivariate series. We leave the model extensions as future work.

For the one-to-one driver-response case, we showed that by using the underlying biologic pulsatile association, one is able to improve estimation of the number of pulses. This results in less biased estimates of other parameters for hormones that are not estimated well univariately. Bivariate fitting may be particularly useful when neither the driver nor response hormones are accurately characterized when analyzed alone. Although, we focused on the situation where one series is very difficult to characterize to match with the data we had received.

It is interesting to note that the global measure of fit is not sensitive to detecting differences between the bivariate and univariate fits. This may be because of the flexibility and almost over parameterization of all pulsatile hormone models. This implies that model fit may not be most useful in helping to identify the appropriate association structure and deciding when to use a bivariate model. Many other aspects of the estimation offer clues to whether the one-to-one association assumption is appropriate. First, it is reassuring that the bivariate model cannot be used to claim pulsatility in a series when there is none. When fitting series where at least one of the series was not pulsatile (i.e. random noise around a mean), the estimation algorithm does not run in almost every case. In the rare instance that the program does not hang, the MCMC chains do not converge.

Additionally, when the user fits two pulsatile series that are not associated assuming a one-to-one association, the mean of the pulse lag distribution is usually very large (50–75 minutes for over half the series fitted in our simulation) and the correlation between the masses is zero or negative. On close inspection the user would also find pulses of size zero (or essentially zero) in one or both of the series matching with larger pulses in the corresponding series indicating an artificial association. Finally, it is likely that the univariate pulse locations would not be a subset of the bivariate fit. Similar problems arise when a pulsatile association exists but it is not one-to-one. Although there was strong biology behind the one-to-one assumption for the LH-FSH example, we did compare the pulses detected in the bivariate fit but not in the univariate fit. As one might expect, the pulses detected in the bivariate fit are slightly smaller on average(as is likely the reason they weren’t detected univariately), but they are not systematically below the univariate fit and certainly not close to zero. However, formally testing these concepts requires population models.

So, how might one determine when a bivariate association might be of use? The usual indication that something isn’t correct in the univariate fit lies in the estimates of the parameters, mainly the half-life and pulse width. Much is known about the half-life of our hormones and endocrine investigators would certainly claim that the parameter estimates in the univariate fit of FSH are not biologically plausible. In addition, the number of pulses differs vastly between two hormones that are known to work in tandem. Finally, the fitted curves in the univariate fit appear overly smooth compared to the usual pulsatile models in a hormone that is known to be pulsatile. In conclusion, using the known pulsatile association between two pulsatile hormone series can help with the parameter estimation of pulsatile series that are difficult to fit univariately. The general underlying idea of incorporating biological associations may also be useful in many other areas of physiological modeling.