The Reopening Rate of the Fingers Domain Is a Determinant of Base Selectivity for RB69 DNA Polymerase

Abstract

Two divalent metal ions are required for nucleotide incorporation by DNA polymerases. Here we use the bacteriophage RB69 DNA polymerase (RB69 pol) and the metal ion exchange-inert nucleotide analogue rhodium(III) deoxythymidine triphosphate (Rh·dTTP) to investigate the requirements of metal binding to the “A” site and to the “B” site, independently. We show that while binding of a metal ion to the A site is required for the nucleotidyl transfer reaction to occur, this metal binding is insufficient to initiate the prechemistry enzyme isomerization that has been observed with this polymerase. Moreover, we show that binding of a deoxynucleoside triphosphate (dNTP), in the absence of a catalytic metal ion, is sufficient to induce this conformational change. In this report, we also present several lines of evidence (from pulse–chase, rapid chemical quench-flow, and stopped-flow fluorescence experiments) for the reverse rate of the enzyme isomerization, closed to open, of a DNA polymerase complex. The implications of these data for the fidelity of DNA polymerization by RB69 pol are discussed.

DNA polymerase is the central component of a multiprotein complex (replicase) that is responsible for faithfully copying the genomes of all living organisms. Although all four deoxynucleoside triphosphates are potential substrates, replicative DNA polymerases insert “wrong” bases only once in every 1 million incorporation events. The main reason for the low error rate is the high level of base discrimination exhibited by these enzymes (for reviews, see refs 1–4). If the wrong base is inserted, it is quickly removed via a potent exonuclease activity either inherent in the polymerase polypeptide or in a subunit associated with the replication complex which increases the overall fidelity by at least 100-fold (5–11). High on the list among the outstanding unsolved problems in DNA replication is the mechanism used by DNA polymerases to discriminate against three of the four dNTPs that do not form Watson–Crick (W–C) hydrogen bonds with the templating base. As has been noted many times, the difference in free energy, between base pairs that can form W–C hydrogen bonds and those that cannot, is insufficient to account for the degree of base selectivity that has been observed with replicative DNA polymerases (3, 12). In this paper, we report results of kinetic studies with RB69 DNA polymerase (RB69 pol)¹ that provide some insight into this process.

In the preceding paper (13), we investigated the effect that occupancy of either the “A” or “B” metal ion site would have on (i) the affinity of an incoming dNTP, (ii) the rate of conformational change, and (iii) the rate of primer extension. This was possible because we took advantage of the “exchange-inert” properties of the rhodium(III) cation (Rh³⁺) (14). Since the Rh³⁺ cation forms stable complexes with deoxynucleoside triphosphates (14), we were able to saturate the B metal ion site and the nucleotide binding pocket by adding a sufficient Rh·dTTP concentration to the RB69 pol–dP/T binary complex while leaving the A metal site unoccupied. We showed that the RB69 pol–dP/T–Rh·dTTP collision complex could proceed to a closed form even when the A metal ion site was empty. In the absence of Mg²⁺ or Mn²⁺ in the A site, chemistry does not take place. However, we wanted to know whether Mg²⁺ can enter the closed form of the ternary structure to allow the nucleotidyl transfer reaction to occur. If there were no barriers to free diffusion of Mg²⁺ into the A site in the closed ternary complex, then the rate of nucleotide incorporation would be expected to equal the rate that was observed when Mg²⁺ was included in the reaction mixture before addition of Rh·dTTP. On the other hand, if the closed structure has to relax, at least partially to a more open form, before Mg²⁺ can access the A site, then it should be possible to determine the rate of relaxation, providing that this process is slower than the rate of nucleotidyl transfer. The rate of relaxation or reopening corresponds to k₋₃ in the minimal kinetic scheme (Scheme 1) for the nucleotidyl transfer reaction catalyzed by RB69 pol as shown below:

Scheme 1.

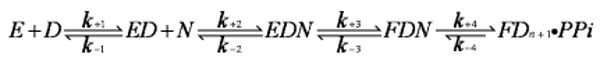
The closed ternary structure is designated as FDN because it is in a fluorescent state different from that of the EDN collision complex that forms upon introduction of a dNTP(N) to an RB69 pol–dP/T(ED) complex where a 2-aminopurine (dAP) residue is the templating base. Previous studies have shown that when a saturating dTTP concentration is introduced into a solution of this type of binary complex, the fluorescence of dAP is rapidly quenched at a rate, k₊₃, that exceeds the rate of dTMP incorporation (15, 16). When all of the ternary complexes are in the FDN state, chemistry occurs at the maximal rate (k₊₄) and is essentially irreversible. In this report, we show that when Mg²⁺ is excluded from the reaction until the ternary complex is formed, the rate of dTMP incorporation is much slower (4 s⁻¹) than when Mg²⁺ is present at the time when the components are first mixed (85 s⁻¹). We propose that the 4 s⁻¹ rate represents the reopening rate of the ternary complex that can be observed by rapid chemical quench and limits the rate of dTMP incorporation under these circumstances. The other means of estimating the reopening rate are indirect and rely on the rate of dAP fluorescence enhancement when dTTP is released from an RB69 pol–dP/T–dNTP ternary complex. As discussed later, an experiment designed to determine the reopening rate of the ternary complex by trapping dTTP as it dissociates from the ternary complex revealed two rates of fluorescence enhancement with equal amplitudes, 50 and 4 s⁻¹. These determinations were made with the correct incoming dNTP. As we show later when an incorrect dNTP is part of a ternary complex, the reverse isomerization (reopening) rate is very rapid. Given these results, the question is whether they provide any additional insight into how RB69 pol is able to exert such a high level of base discrimination.

There have been proposals published that ascribe base selectivity to differences in the relative energy barriers of the transition state for the incorporation of correct and incorrect bases (11, 12, 17–19). Other schemes to account for base discrimination invoke a rate-limiting step (conformational change) that acts as a checkpoint before chemistry (2, 3, 20). Recently, a kinetic explanation was advanced which stated that base discrimination is dependent on the relative ratio of the nucleotidyl transfer rate (k₊₄) to the rate of reopening (k₋₃) of ternary complexes that contain either a correct or an incorrect dNTP (21).

We decided to test this latter proposal by attempting to estimate the reversal rate (k₋₃) of FDN, the closed, isomerized RB69 pol ternary complex, a state that exists just prior to the nucleotidyl transfer step, as shown in Scheme 1. As mentioned above, we have used pulse–chase, chemical-quench and stopped-flow fluorescence procedures for this purpose. We found that the value of k₋₃ was much smaller than k₊₄, the rate of chemistry, for insertion of correct incoming dNTPs but is very rapid for incorrect dNTPs. As a consequence, only a small percentage of ternary complexes with an incorrect dNTP populate the FDN state. A low flux of incoming nucleotides through the FDN state would account for the dramatically reduced efficiency for incorporation of incorrect bases into the growing primer strand and is consistent with the proposal of Tsai and Johnson (21) for base selectivity exhibited by T7 pol. The implications of this hypothesis for the fidelity of RB69 pol and other B family replicative DNA polymerase are discussed.

Materials and Methods

Escherichia coli strain BL21(DE3) was obtained from Stratagene Corp. DH5α cells and dNTPs were purchased from Invitrogen. [γ-³²P]ATP was purchased from Perkin-Elmer Life Sciences Inc. Ni-NTA resin was obtained from Qiagen. Rhodium chloride was purchased from Sigma-Aldrich, Inc. Dowex 1×2-100 mesh ion-exchange resin was purchased from ACROS Organics. Biogel P2 was ordered from Bio-Rad Laboratories. Other chemicals were analytical grade from Sigma-Aldrich, Inc. RB69 DNA pol cDNA was a gift from J. Karam (Tulane University, New Orleans, LA). Oligonucleotides were purchased from the W. M. Keck Foundation Biotechnology Resource Laboratory (Yale University). The sequences of the primer-templates are listed in Table 1.

Table 1.

Oligonucleotides Employed in the Rapid Chemical-Quench, Pulse–Chase, Chemical-Quench, Equilibrium Fluorescence, and Stopped-Flow Experiments with RB69 pol

oligonucleotide	sequence
13pC primera	CCG ACC ACG GAA C
20tA templatea	GGC TGG TGC CTT G A* G GGG AAd
14pT primerb	GC GGA CTG CTT ACT
18tA templateb	GCG CCT GAC GAA TGA ACT
13pC primerc	GC GGA CTG CTT AC
18tG templatec	GCG CCT GAC GAA TGG ACT-Cy3

^aOligonucleotides (dP/T*) used in rapid chemical-quench, pulse–chase, chemical-quench, equilibrium fluorescence, and stopped-flow experiments for RB69 pol.

^bOligonucleotides (dP/T⁺) used with Sequenase in trapping dTTP.

^cOligonucleotides (dP/T) used for equilibrium fluorescence titrations to determine the binding affinity of dCTP for the Sq–dP/T complex.

^dA*, 2-aminopurine (dAP).

Protein Expression and Purification

Expression and purification of the exonuclease deficient mutant of the bacteriophage RB69 pol were accomplished as previously described (22). The gene for this enzyme was cloned into a pET21 vector (Invitrogen) that encoded a C-terminal hexahistidine tail. The six appended His residues allowed facile purification of the expressed protein by Ni-NTA affinity chromatography (23). Protein concentrations were determined using the Bio-Rad assay according to the manufacturer's instructions. The active site titration for RB69 pol was performed using a burst assay with a known concentration of duplex DNA (24).

Preparation of Rh·dTTP

Rh·dTTP was prepared as previously described (13). A brief summary of this synthesis follows. Rhodium chloride hydrate was boiled in HClO₄ for 2 h to convert it to [Rh(H₂O)₆](ClO₄)₃ (25). Equal concentrations of this reagent and Na·dTTP were mixed, adjusted to pH 3, and heated at 80 °C for 20 min. This solution was chilled to 4 °C on ice and then applied to a 1.6 cm × 20 cm Dowex 1×2-100 mesh ion-exchange resin column, which had been previously washed with nanopure water (adjusted by HCl to pH 3) until the eluate had a pH of 3. The column was eluted with nanopure water and then with 100 mM HCl. The eluate was monitored by absorption at 260 nm, and two peaks were observed. The first peak contained inactive rhodium complexes, and the second peak contained Rh·dTTP which was concentrated by rotory evaporation and adjusted to pH 5. This solution was then desalted on a 150 cm × 1.5 cm P2 column that was equilibrated with 2 mM NaAc buffer (pH 5). Incubation of Rh·dTTP with RB69 pol and a primer-template containing dA as the templating base in the absence of Mg²⁺ showed no dTMP incorporation in 30 min. On the basis of this result, we concluded that the Rh·dTTP and the buffers used were free of Mg²⁺.

Preparation of Synthetic Oligonucleotide Substrates

The oligonucleotides used as primers in the rapid chemical-quench experiments were 5′-labeled with ³²P with T4 polynucleotide kinase per the manufacturer's instructions (New England Biolabs). Termination of the reaction was performed by heating the mixture to 95 °C for 5 min. We accomplished primer-template annealing by mixing equimolar ratios of the primer and template, heating the mixture to 95 °C, and allowing it to cool slowly to 25 °C. The templates for stopped-flow fluorescence and Sequenase trapping experiments as well as equilibrium fluorescence titration experiments were annealed to primers as described above. The sequences of the primers and templates employed in all experiments are listed in Table 1.

Rapid Chemical-Quench Assay Conditions

Due to the rapid rates of product formation, all assays employed a RQF-3 rapid chemical-quench-flow instrument (Kintek Corp., Austin, TX). Single-nucleotide incorporation assays were carried out at 24 °C in a buffer containing 50 mM MOPS (pH 7.0) and varying concentrations of MgCl₂, from 0.5 to 100 mM. RB69 pol (200 nM) and duplex oligonucleotide substrates (180 nM) were assembled and allowed to pre-equilibrate for 5 min. The reaction was initiated with the addition of Rh·dTTP. As the chemical reaction also requires a divalent metal ion, MgCl₂ was present in the RB69 pol–dP/T sample, the Rh·dTTP solution, or both solutions. The reaction was terminated by the addition of 0.5 M EDTA.

Pulse–Chase Experiments

The final concentrations in the pulse–chase experiments were as follows: 100 nM RB69 pol, 90 nM dP/T, 50 mM MOPS (pH 7.0), 10 mM MgCl₂, and varying concentrations of Na·dTTP, Ca·dTTP, or Rh·dTTP. For the experiments involving Ca²⁺, the final concentration of CaCl₂ was 2 mM, and it was present in all samples prior to mixing. A solution containing RB69 pol and dP/T was rapidly mixed with a solution containing either Na·dTTP, Ca·dTTP, or Rh·dTTP and allowed to incubate for 0.01 s. After the incubation period, a solution containing MgCl₂ was added such that the final concentration of MgCl₂ was 10 mM. The reaction was terminated by the addition of 0.5 M EDTA.

Product Analysis

Products were separated on 20% denaturing urea polyacrylamide gels, imaged on a Storm 840 phosphorimager, and quantified using ImageQuaNT (Molecular Dynamics, Sunnyvale, CA).

Equilibrium Fluorescence Titrations

(i) 2-Aminopurine-Labeled dP/T

Emission spectra of dP/Ts containing dAP and RB69 pol–dP/T complexes were acquired at 24 °C with a Photon Technology International Alphascan scanning spectrofluorometer. The reaction mixture contained 200 nM P/T (13/20mer) with dAP as the templating base (Table 1), 1 μM RB69 pol, 2 mM CaCl₂, 50 mM MOPS (pH 7.0), and different matched dTTP or mismatched dCTP concentrations. Samples were excited at 313 nm so that inner filter effects from nucleoside bases were negligible (16). Fluorescence emission spectra were recorded from 330 to 460 nm. The intensities were corrected for the intrinsic fluorescence of RB69 pol and dTTP. No photobleaching could be detected after 10 min. Peak emission intensities at 365 nm were plotted as a function of dTTP or dCTP concentration and fit to a hyperbolic equation enabling us to estimate the overall dissociation constants (K_dg^app) for dNTP binding.

(ii) Cy3-Labeled dP/T

Emission spectra of dP/T labeled with Cy3 at the 5′ end of the templateand the Sequenase–dP/T complex were acquired at 24 °C with a Photon Technology International Alphascan scanning spectrofluorometer. The reaction mixture contained 2 nM dP/T (13/18mer) (Table 1), 200 nM Sequenase, 2 mM CaCl₂, 50 mM MOPS (pH 7.0), and different dCTP concentrations. Samples were excited at 546 nm, and emission spectra were recorded from 555 to 590 nm. Peak emission intensities at 570 nm were plotted as a function of dCTP concentration and fit to a hyperbolic equation enabling us to estimate the overall dissociation constants (K_dg^app) for dCTP binding.

Stopped-Flow Fluorescence Experiments

Experiments were performed using an Applied Photophysics (Leatherhead, U.K.) SX18MV-R stopped-flow apparatus thermostated at 24 °C. The excitation wavelength for dAP was 313 nm. A 345 nm long pass glass filter was used for monitoring dAP fluorescence emission. A solution containing 400 nM dP/T, 2 μM RB69 pol, and 2 mM CaCl₂ in 50 mM MOPS buffer was mixed rapidly with varying dTTP concentrations in the same buffer with 2 mM CaCl₂. The final reaction mixture consisted of 50 mM MOPS (pH 7.0), 200 nM dP/T, 1 μM RB69 pol, 2 mM CaCl₂, and varying dTTP concentrations. Similar experiments were performed with dCTP opposite dAP. The final reaction mixtures consisted of 50 mM MOPS (pH 7.0), 200 nM dP/T, 1 μM RB69 pol, 2 mM CaCl₂, and varying dCTP concentrations. The fluorescence scans were corrected for the intrinsic fluorescence of dCTP.

Sequenase–dP/T Trapping of dTTP Released from the RB69 pol–dP/T–dTTP Ternary Complex

Sequenase (Sq) (2.4 μM) and dP/T⁺ (3 μM) in syringe A were rapidly mixed with 2 μM RB69 pol, 2 μM dP/T* (Table 1) (dAP as the templating base), and 2 μM dTTP in syringe B (Table 2). Both solutions contained 2 mM CaCl₂ and 50 mM MOPS (pH 7.0). The experiments were performed using an Applied Photophysics SX18MV-R stopped-flow instrument thermo-stated at 24 °C. The excitation wavelength for dAP was 313 nm. A 345 nm long pass glass filter was used when monitoring dAP fluorescence emission. As a control, the experiment described above was performed under the same conditions except that syringe A contained buffer only [2 mM CaCl₂ and 50 mM MOPS (pH 7.0)] but no Sq–dP/T⁺ complex.

Table 2.

Components, Concentrations, and Percentages of Complexes before and after Mixing in Sequenase Trapping Experiments

	initial concentration (μM)	before mixing		5 s after mixing
		concentration (μM)	% of complex	concentration (μM)	% of complex
syringe A
Sequenase	2.4
dP/Ta	3
Sequenase–dP/Ta		2.3	97.1	0.3	14
Sequenase–dP/Ta–dTTP		0	0	2	99.8
syringe B
RB69 pol	2
dP/Tb	2
dTTP	2	0.4		0
RB69 pol–dP/Tb		0.2	10.6	1.8	90.3
RB69 pol–dP/Tb–dTTP		1.6	79.9	0.004	0.2

^adP/T⁺ is 14pT/18tA in Table 1.

^bdP/T* is 13pC/20tA in Table 1. 2-Aminopurine is the templating base.

Data Analysis

Data from chemical quench or stopped-flow experiments were fit to a single-exponential equation using Origin. The dNTP concentration dependence of k_obs fit to an equation for a rectangular hyperbola of the form k_obs = k_max[dNTP]/(K_d + [dNTP]), where k_obs is the first-order rate constant and k_max is the maximum value for the conformational change rate before chemistry (stopped-flow fluorescence). The incorporation rate (k_pol) was determined by rapid chemical quench; K_d is the ground-state dissociation constant for dissociation of dNTP from the RB69 pol–dP/T binary complex. Data from the equilibrium fluorescence experiments were fit to a hyperbolic or a quadratic equation of the form

$$\Delta Q=\frac{Q_m\left[E_0+S_0+K_d-\sqrt{{(E_0+S_0+K_d)}^2-4E_0{S}_0}\right]}{2E_0}$$

where ΔQ is the fluorescence signal change, Q_m is the maximum value for the fluorescence signal change at saturating substrate concentrations, E₀ is the total enzyme concentration, and S₀ is the total dNTP concentration. K_d is the ground-state dissociation constant for dissociation of dNTP from the RB69 pol–dP/T binary complex. The solution of these equations provided an estimate of the apparent dissociation constants of dNTP. The data collected from stopped-flow fluorescence experiments for dCTP binding to the RB69 pol–dP/T binary complex were fit to kinetic Scheme 2 using KinTekSim.

Scheme 2.

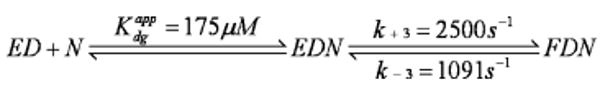
Minimal Kinetic Scheme for “Incorrect” dCTP Binding to the RB69 pol–dP/T* Complex and Isomerization in the Presence of Ca²⁺

Results

Effect of Mg²⁺ Concentration on the Rate of dTMP Incorporation

Prior to conducting pulse–chase experiments in which Mg²⁺ was added after assembly of the ternary complex, we found it was necessary to determine the effect of Mg²⁺ concentration on the rate of dTMP incorporation when it occupied only the A metal binding site. To probe the effects of Mg²⁺ binding at the A site, without confounding effects due to Mg²⁺ binding at the B metal binding site, we employed a metal exchange-inert rhodium(III) derivative of dTTP. This derivative has previously been shown to be stable for at least several hours at pH 7 (13) and has been used before to parse metal site specific effects in RB69 pol and pol β (13). Three experiments were conducted to determine the effects of Mg²⁺ binding to the A site on the rates of the conformational change and chemistry with the following results. (i) When a solution containing Rh·dTTP and MgCl₂ was added to a solution containing RB69 pol and DNA, the maximum observed rate of dTMP incorporation was 92 ± 15 s⁻¹ at 5 mM MgCl₂ (Figure 1A). (ii) When Rh·dTTP was added to a solution containing RB69 pol, DNA, and MgCl₂, the maximum observed rate was 77 ± 6 s⁻¹ at 10 mM MgCl₂ (Figure 1B). (iii) When MgCl₂ was present in both solutions, the maximum observed rate was 80 ± 10 s⁻¹ at 2.5 mM MgCl₂ (Figure 1C). In all cases, inhibitory effects of high MgCl₂ concentrations (>10 mM) prevented us from being able to calculate a k_max for the reactions or an apparent dissociation constant for Mg²⁺ binding (Figure 1D). However, there were qualitative similarities in the rate versus MgCl₂ concentration profiles in the three experiments mentioned above that allowed us to conclude the following: (i) The observed maximum rate of reaction was approached at or around a Mg²⁺ concentration of 5 mM. (ii) The observed maximum rates were simulated for all the experiments. (iii) There were apparent inhibitory effects of MgCl₂ at concentrations greater than 10 mM, suggesting that the order of addition does not have an effect on Mg²⁺ binding or on the rate of the subsequent enzymatic reactions.

Figure 1.

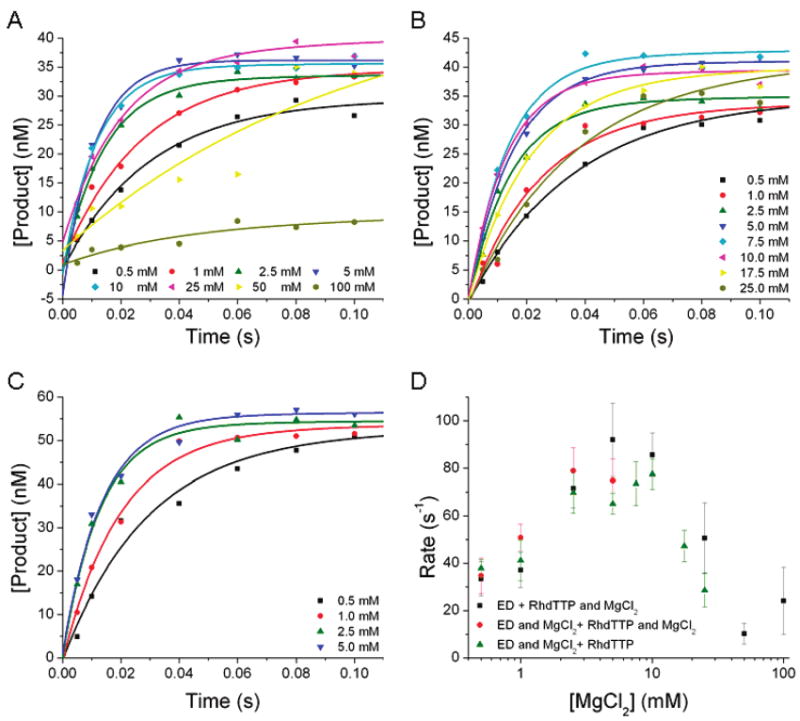
Incorporation of Rh·dTTP opposite dA at varying concentrations of MgCl₂. The final reaction conditions for all experiments depicted consisted of 100 nM RB69 pol, 90 nM DNA, 250 μM Rh·dTTP, 50 mM MOPS (pH 7.0), and varying concentrations of MgCl₂ from 0.5 to 100 mM. (A) The reaction was initiated by premixing Rh·dTTP and MgCl₂ and then rapidly mixing this solution with one containing RB69 pol and DNA. The incorporation rate is 92 ± 15 s⁻¹. (B) The reaction was initiated by premixing RB69 pol, DNA, and MgCl₂ and then rapidly mixing this solution with one containing Rh·dTTP. The incorporation rate is 77 ± 6 s⁻¹. (C) The reaction was initiated by premixing RB69 pol, DNA, and MgCl₂ and then rapidly mixing this solution with one containing Rh·dTTP and MgCl₂. The incorporation rate is 80 ± 10 s⁻¹. (D) The rates of product formation are plotted vs MgCl₂ concentration for each of the three experiments depicted in panels A–C. Regardless of when MgCl₂ is added, the observed maximum rate of the reaction fits to approximately 80 s⁻¹, at a MgCl₂ concentration of approximately 10 mM. Because of the mixing procedure, each solution was prepared at twice the final reported concentration. The product concentrations were plotted vs time and fit to a single-exponential equation.

Pulse–Chase, Chemical-Quench Experiments

To assay the effects of binding a metal ion in the A site on the overall rate of nucleotide incorporation, in the presence of a metal-bound deoxynucleoside triphosphate occupying the B and nucleotide binding sites, we used pulse–chase, chemical-quench experiments to sequentially add Na·dTTP, Ca·dTTP, or Rh·dTTP followed by MgCl₂ to a solution containing RB69 pol and a dP/T. Experiments employing Na·dTTP were conducted with a Na·dTTP concentration increasing from 100 to 2000 μM, and the product formation versus time profile was fit to a single-exponential equation. Because these experiments were designed to observe incorporation only in the second phase of the experiment, after MgCl₂ addition, it was necessary to determine whether product incorporation could be observed during the first phase of the reaction, after Na·dTTP addition. To assess this possibility, a “zero point” was collected at each concentration of nucleotide, where 0.5 M EDTA was added during the second addition in place of 10 mM MgCl₂. No product was observed in any of these zero points. While the product formation was fit to a single-exponential equation, the actual data were biphasic, exhibiting both a fast, unresolved time phase and a slower, time-resolved phase. The data were interpreted as representing two populations of RB69 pol–dP/T complexes present in the reaction mixture upon addition of MgCl₂. There was little variation in the observed rates for the time-resolved phase at any concentration of Na·dTTP assayed, and the average rate of this phase was 8 ± 4 s⁻¹. Although the rate of this phase was relatively constant, the amplitude of this phase increased with an increase in Na·dTTP concentration (Figure 2A). Because the fraction of RB69 pol–dP/T complexes represented by the slow phase of the reaction increased with an increase in Na·dTTP concentration, we have interpreted the slow phase as representing RB69 pol–dP/T-Na·dTTP ternary complexes and the unresolved phase as representing RB69 pol–dP/T binary complexes not bound to Na·dTTP.

Figure 2.

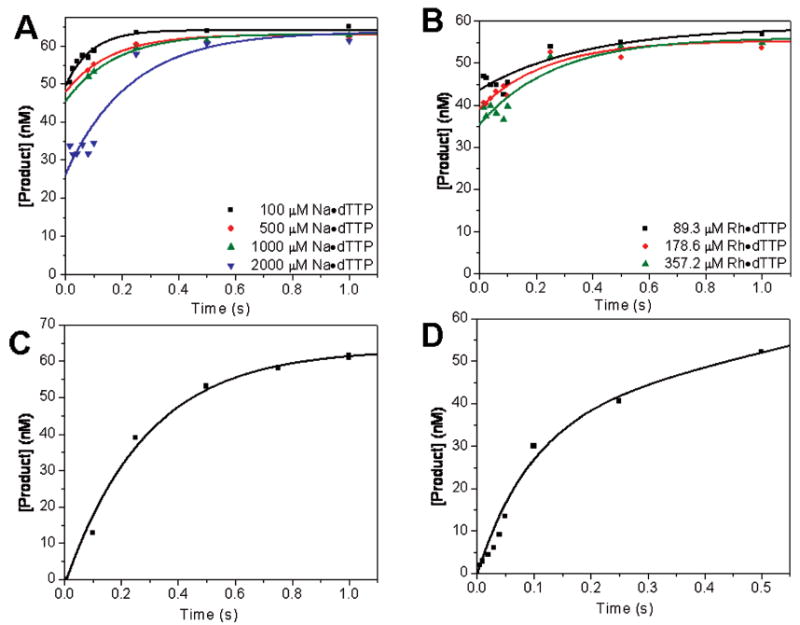
Pulse-chase, chemical-quench experiment. (A) RB69 pol was preincubated with DNA, then rapidly mixed with various Na·dTTP concentrations, and allowed to incubate for 0.01 s. (B) RB69 pol was preincubated with DNA, then rapidly mixed with various Rh·dTTP concentrations, and allowed to incubate for 0.01 s. (C) RB69 pol was preincubated with DNA, then rapidly mixed with 500 μM dTTP and 4 mM CaCl₂, and allowed to incubate for 0.01 s. After preincubation, each reaction mixture was rapidly mixed with MgCl₂ and allowed to react for variable amounts of time before the reaction was quenched with 0.5 M EDTA. The data from panels A–C were fit to a single-exponential equation, and the average rates are 8 ± 4, 4 ± 1, and 3.5 ± 0.4 s⁻¹, respectively. (D) dTTP (500 μM) was preincubated with 4 mM CaCl₂ and 10 mM MgCl₂ and then rapidly mixed with a solution containing RB69 pol, DNA, and 10 mM MgCl₂. The reaction was quenched at various times with 0.5 M EDTA, and the data were fit to a burst equation. The burst rate is 11 ± 4 s⁻¹. The final reaction conditions included 100 nM RB69 pol, 90 nM DNA, 50 mM MOPS (pH 7.0), and 10 mM MgCl₂.

Experiments employing Rh·dTTP were conducted at three concentrations of Rh·dTTP (89, 179, and 357 μM). Because of the limited solubility of the Rh·dTTP substrate, we were unable to perform this assay at higher Rh·dTTP concentrations. The product versus time plots were fit to a single-exponential equation and, like the experiments with Na·dTTP, exhibited both a fast unresolved phase and a slow time-resolved phase. The average rate of the slow phase was 4 ± 1 s⁻¹ (Figure 2B). The amplitudes of the slow phase of the reactions increased with increasing Rh·dTTP concentrations. Like the experiments with Na·dTTP, no product formation was observed at the zero points. We have interpreted these data in a manner analogous to that of the Na·dTTP data, where the time-resolved phase represents the RB69 pol–dP/T complexes bound to Rh·dTTP and the unresolved phase represents the RB69 pol–dP/T complexes not bound to Rh·dTTP.

The experiment employing Ca·dTTP was conducted only at 500 μM. Like the previously described experiments, the zero point showed no product formation, but unlike the previously described experiments, the product versus time profile showed no unresolved phase. It fit best to a single exponential, with a rate of product formation of 3.5 ± 0.4 s⁻¹ (Figure 2C).

To show that the slow rate and single-exponential nature of the Ca·dTTP experiment were not due to inhibitory effects of the CaCl₂ present in the reaction mixture, a single nucleotide incorporation experiment was conducted to determine the rate of the chemical reaction in the presence of 2 mM CaCl₂. The plot of product concentration versus time fit best to a burst equation (y = e^−kt + bt, where y is the amplitude of the burst phase, k is the rate of the burst phase, and b is the slope of the linear phase). The data fit to a burst rate of 11 ± 4 s⁻¹ (Figure 2D). These data suggest that in the Ca·dTTP pulse–chase reaction, there is a slow reaction (ternary complex relaxation) occurring prior to chemistry at a rate of 4 s⁻¹, based upon the mechanism shown in Scheme 3 and the equation k_obs = (k_slowk_chem)/(k_slow + k_chem).

Scheme 3.

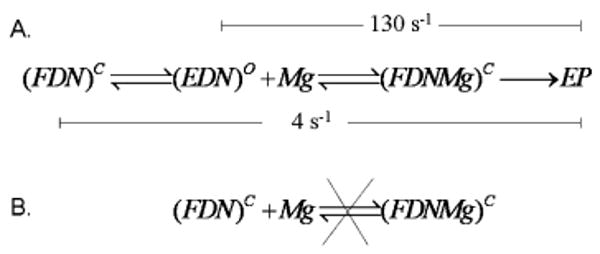
(A) Kinetic Scheme for Pulse–Chase, Chemical-Quench Experiments for the RB69 pol–dP/T–dTTP Ternary Complex (FDN)^a and (B) Kinetic Scheme Indicating That Mg Is Not Able To Enter the Closed Ternary Complex

^a (FDN)^C indicates the closed state of the ternary complex. (ED*N)^O indicates a collision ternary complex in the open form. Mg indicates Mg²⁺. EP represents the product of the reaction. (FDNMg)^C indicates the ternary complex with Mg²⁺ occupying the A metal site. For part 3A, k_slow = 4 s⁻¹ and k_chem = 130 s⁻¹.

Affinity of Correctly Matched dTTP and a Mismatched dCTP for an RB69 pol–P/T Binary Complex

In the presence of Ca²⁺, a dP/T with dAP as the templating base can be used to determine the affinity of dNTPs for an RB69 pol–dP/T binary complex. Representative equilibrium fluorescence scans of matched dTTP binding to the RB69 DNA pol–dP/T complex are shown in Figure 3A. The K_dg^app for dTTP binding was 53 nM (Figure 3B). In contrast, the K_dg^app for the mismatched dCTP was 53 μM (Figure 3C). The 10³-fold difference in binding affinity between dTTP and dCTP is much greater than what was observed when the overall K_d^app for the incorporation of matched or mismatched dNTPs was determined by the rapid chemical quench.

Figure 3.

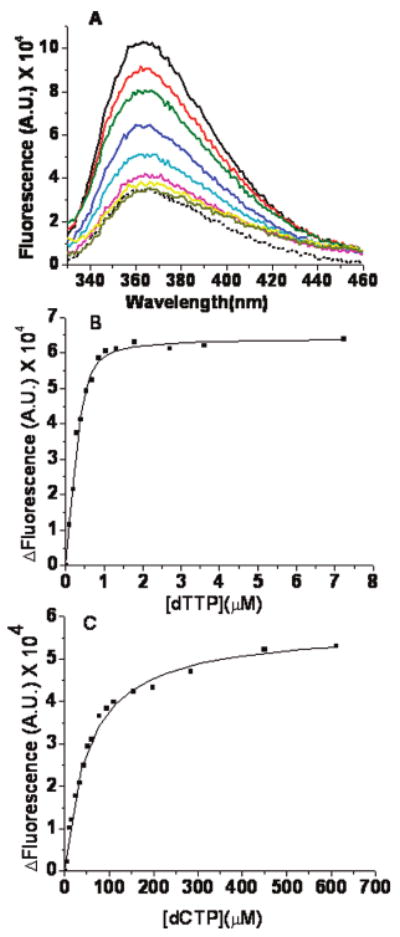
Equilibrium fluorescence titrations for dTTP or dCTP binding to the RB69 DNA pol–dP/T complex. (A) Representative fluorescence emission spectra of dTTP binding to wild-type RB69 pol in the presence of a 13/20mer dP/T (Table 1), with dAP as the templating base (shown by the solid lines) and 2 mM CaCl₂. The concentration of dP/T was 200 nM, and that of RB69 pol was 1 μM. The dTTP concentrations (from top to bottom) were 0, 0.1, 0.2, 0.3, 0.55, 0.9, 2.9, and 7.9 μM. The dotted line is the fluorescence trace for the dP/T alone. (B) dP/T (dAP as the templating base, 200 nM) in the presence of 2 mM Ca²⁺. The change in fluorescence vs dTTP concentration fit best to a quadratic binding equation with a K_dg^app of 0.053 ± 0.015 μM. (C) dP/T (dAP as the templating base, 200 nM). The change in fluorescence vs dCTP concentration fit best to a hyperbolic equation with a K_dg^app of 53 ± 3 μM. The change in fluorescence (ΔF) is in the direction of quenching. The ΔF of the binary complex is normalized to zero in the absence of dNTP, and the ΔF increases with an increase in dNTP concentration.

Forward and Reverse Isomerization Rates of Ternary Complexes Containing Correct and Incorrect dNTPs

Having determined the K_dg^app values for dNTP binding to an RB69 pol–dP/T* complex, we next compared the rates of conformational change induced by incoming dNTPs. For this purpose, we compared the rates of dAP fluorescence quenching when a correct (dTTP) or an incorrect (dCTP) deoxynucleoside triphosphate was rapidly mixed with a RB69 pol–dP/T binary complex. The first experiments were carried out with the RB69 pol–dP/T* complex, dTTP, and 2 mM Ca²⁺. As shown in Figure 4A, there was no change in start points with an increase in dTTP concentration and the scans fit a single-exponential equation at all dTTP concentrations. When the observed rates were plotted versus dTTP concentration, the extrapolated k_max value was ∼1200 s⁻¹ (Figure 4B). The rapid forward rate (k₊₃) of fluorescence quenching likely reflects Fingers domain closing as represented by the EDN ⇌ FDN step in Scheme 1. One estimate of the rate of Fingers reopening (k₋₃) was obtained by extrapolating the hyperbolic curve in Figure 4B to a dTTP concentration of zero. Although there is a large error inherent in this extrapolation, the rate of reversal of FDN to EDN is <24 s⁻¹, which is much lower than the forward rate (k₊₃) of 1200 s⁻¹ so that the FDN species predominates when the incoming dNTP is complementary to the templating base. When a dP/T* and Mg²⁺ are components of the FDN complex, the rate of product formation (FD_n+1·PP_i) reaches a maximum value with a saturating dTTP concentration.

Figure 4.

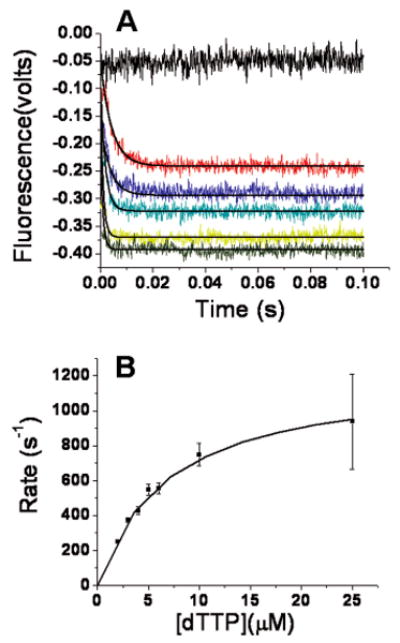
Stopped-flow fluorescence with dTTP opposite dAP with a dP/T (Table 1). (A) One syringe contained 400 nM DNA and 2 μM RB69 pol in 50 mM MOPS buffer (pH 7) at 24 °C. The other syringe contained varying dTTP concentrations (0, 2, 4, 5, 10, and 25 μM from top to bottom) in 50 mM MOPS buffer (pH 7). Both syringes contained 2 mM CaCl₂ and 0.1 mM EDTA. The plots of fluorescence vs time fit a single-exponential equation. The scans are in color, and the fitting curves are in black. (B) The rates from the single exponential vs dTTP concentration fit a hyperbolic equation with a k_max of 1200 ± 50 s⁻¹ and a K_dr^app of 6.8 ± 0.6 μM. The Y-intercept is −10 ± 24 s⁻¹.

Stopped-flow fluorescence experiments were performed under the same conditions with a mismatched dNTP (dCTP), an RB69 pol–dP/T complex, and 2 mM Ca²⁺. In contrast to the results obtained with the correct incoming nucleotide, when dCTP was introduced there was a very rapid fluorescence quench whose amplitude was dependent on dCTP concentration as indicated by the decrease in start points (Figure 5A). When the amplitude for dAP quenching from stopped-flow experiments was plotted as a function of increasing dCTP concentration, the resulting curve fit a hyperbolic equation giving an apparent K_da^app of 67 ± 12 μM (Figure 5B), consistent with the K_dg^app value of 53 ± 3 μM determined by equilibrium fluorescence (Figure 3C). The stopped-flow fluorescence results indicated that both the forward and reverse rates of the ternary complex isomerization were too fast to measure. However, we were able to model the reaction using the minimal kinetic Scheme 2 by fixing the starting and end points. We also included a parameter for the intrinsic quenching of dCTP fluorescence that varied with dCTP concentration. This was determined in a control experiment where the change in fluorescence was measured and the dCTP concentration was varied from 0 to 1 mM (Figure 1 of the Supporting Information). The start point changes with an increase in dCTP concentration indicated that there was a rapid reversal rate (>1000 s⁻¹) of the ternary complex containing the incorrect dNTP, from the closed to the open state. This reversal rate (>1000 s⁻¹) with the incorrect dCTP is much faster than the reversal rate when the correct dTTP was a component of the ternary complex (Figure 4B). From these data, it is clear that with dCTP, the open EDN complex is greatly favored over the closed FDN complex that is poised for chemistry.

Figure 5.

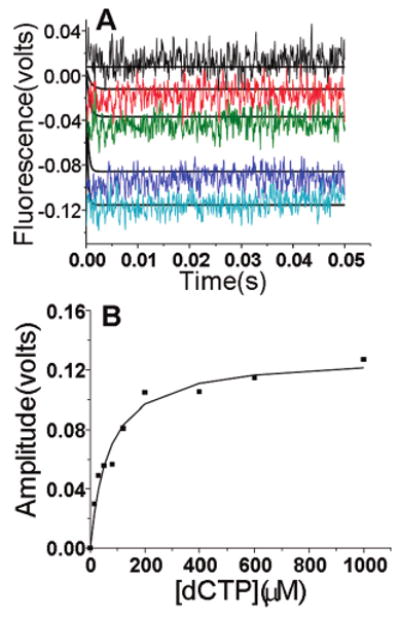
Stopped-flow fluorescence scans with dCTP opposite dAP with a dP/T. (A) One syringe contained 400 nM DNA and 2 μM RB69 pol in 50 mM MOPS buffer (pH 7) at 24 °C. The other syringe contained varying dCTP concentrations (0, 15, 50, 400, and 1000 μM from top to bottom) in MOPS buffer. Both syringes contained 2 mM CaCl₂. The fitting plot was obtained from the estimated parameters based on Scheme 2. The experimental scans are in color, and the fitting curves are in black. (B) The amplitude vs dCTP concentration fit a hyperbolic equation with a K_da^app of 67 ± 12 μM.

Estimation of the dTTP Release Rate Using a Sequenase–dP/T⁺ Complex To Trap dTTP When It Dissociates from the RB69 pol–dP/T*–dTTP Complex

To determine the rate of release of dTTP from the closed ternary complex, using an independent assay, we conducted a competition experiment in which we rapidly mixed the ternary RB69 pol–dP/T*–dTTP complex (dAP as the templating base) with excess Sq–dP/T⁺ binary complex in the stopped-flow fluorescence instrument (Table 2). The Sq–dP/T⁺ binary complex rapidly bound the dTTP that was released from the RB69 pol ternary complex with high affinity, resulting in fluorescence enhancement of dAP as the RB69 pol ternary complex reverted to the binary complex. The plot of fluorescence versus time (Figure 6) fit a double-exponential equation with rates of 50 and 4 s⁻¹. The amplitudes of the fast and slow phases were approximately equal. We modeled all the rates and binding parameters using two possible kinetic schemes for the acquired data (Scheme 4) which are discussed in detail in the Supporting Information. For the EDN to FDN isomerization, the maximum forward rate (1200 s⁻¹) was estimated from the k_obs versus dTTP concentration plot (Figure 4B). The 50 and 4 s⁻¹ rates obtained from the Sequenase trapping experiment were much slower than the forward rate of 1200 s⁻¹. To estimate the constant for dissociation of dTTP from the Sequenase ternary complex, we titrated a Cy3-labeled Sq–dP/T binary complex (Table 1) with an increasing dCTP dissociation and found a value of 0.83 ± 0.29 nM (Figure 2 of the Supporting Information), which was sufficiently low to ensure almost complete trapping of the released dTTP, assuming that the K_d for dTTP versus dA is in the same range as that for dCTP versus dG.

Figure 6.

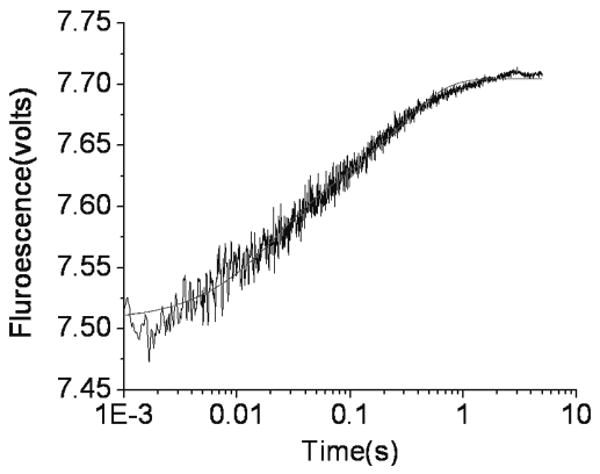
Sq–dP/T⁺ binary complex trapping of dTTP released from a RB69 pol–dP/T*–dTTP ternary complex using stopped-flow fluorescence with dTTP opposite dAP with a dP/T (Table1). The fluorescence vs time fit best to a double-exponential equation with rates of 50 and 4 s⁻¹.

Scheme 4.

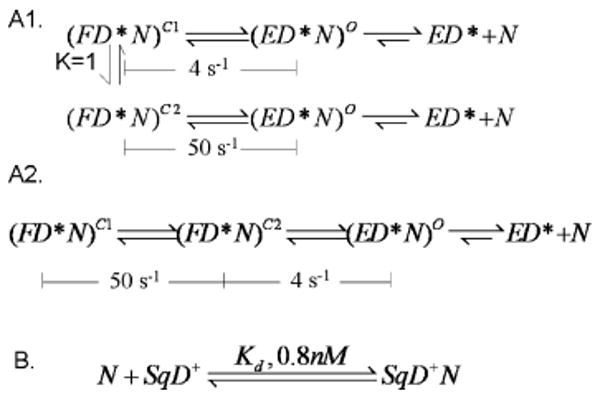
Kinetic Schemes for Sequenase–dP/T⁺ (SqD⁺) Trapping of dTTP(N) Released from the RB69 pol–dP/T*–dTTP Ternary Complex (FD*N)^a

^a We assume that ED* + N and (ED*N)^O are in rapid equilibrium as (ED*N)^O is a collision complex. (FD*N)^C1 and (FD*N)^C2 are in a different fluorescent state than (ED*N)^O. Scheme A1 or A2, combined with scheme B, is consistent with the experimental data. The superscripts C1, C2, and O denote two putative closed forms of the ternary complex and the open, collision complex, respectively. D* indicates a dP/T with dAP as the templating base, and D⁺ indicates a dP/T labeled at the 5′ end of the template with Cy3.

The key requirements for the Sequenase trapping experiment to yield useful information were as follows. (i) The concentrations of RB69 pol, dP/T*, and dTTP had to be adjusted so that there would be a sufficiently large difference between the percent of the dAP-labeled dP/T* in the RB69 ternary complex before and after mixing the components in syringe B with the Sq–dP/T⁺ complex in syringe A to obtain a significant amplitude change in dAP fluorescence. We were able to satisfy this requirement using the concentrations listed in Table 2. (ii) The K_d for dTTP binding to the Sq–dP/T⁺–dTTP ternary complex had to be much lower than the corresponding K_d for dTTP binding to the RB69 pol ternary complex. We showed that this requirement was met by determining the K_dg^dCTP for the Sq–dP/T⁺ complex by titrating a Cy3-labeled Sq–dP/T complex with dCTP and measuring the change in Cy3 fluorescence as a function of dCTP concentration (Figure 2 of the Supporting Information). The affinity of dNTP for the Sq–dP/T complex was 0.8 nM, compared to 53 nM for the RB69 pol–dP/T* complex, which clearly met this requirement. (iii) The dissociation constant of the Sq–dP/T⁺ binary complex had to be sufficiently low so that greater than 90% of the dP/T⁺ would be in the binary complex. This requirement should have been satisfied on the basis of the dissociation constant for a T7 pol–dP/T binary complex reported in the literature (26). (iv) The free dTTP concentration had to be sufficiently low that it would not fully saturate the Sq–dP/T⁺ complex before the dTTP, which dissociates from the RB69 pol ternary complex, had a chance to be sequestered by the Sq–dP/T⁺ complex. This requirement was met by calculating the free dTTP concentration left after the RB69 pol–dP/T–dTTP complex was formed and showing that it was below that threshold. The initial and final concentrations of all the components before and after mixing are listed in Table 2 along with the percentages of the respective binary and ternary complexes before, and 5 s after, mixing. The dTTP trapping experiment provided direct evidence for slow dNTP dissociation when the correct incoming base, dTTP, was a component of the ternary complex. Given the high K_d values for binding of incorrect dNTPs to the RB69 pol–dP/T complex, it was not possible to conduct this experiment with incorrect dNTPs because the free dNTP concentration would be too high to obtain reliable results.

Discussion

Deciphering the mystery of how replicative DNA polymerases are able to discriminate among the four potential dNTP substrates with such exquisite specificity has been a cherished goal of investigators for many years.

Among the competing models that have been proposed to explain base discrimination, the induced fit hypothesis is the one that has been cited most frequently (2). In this model, binding of the incoming dNTP induces a conformational change that involves closing of the Fingers domain, a step that was believed to be rate-limiting and thus would serve as a checkpoint for severely restricting formation of a closed ternary complex with incorrect dNTPs. Results from pulse–chase and pulse-quench experiments lent support to this notion since, for many DNA polymerases, the rate of the internal isomerization step (conformational change) was believed to be slower than the rate of correct dNMP incorporation. T4 pol was cited as a possible exception because, in pulse–chase experiments, the yield of product was identical, no matter whether the reaction was quenched with HCl or EDTA (3, 24). A caveat for this conclusion about T4 pol, however, was that it required a slow step, product release, to be rate-limiting which, although it has been assumed to hold for most DNA pols, does not apply to T4 pol (3). When stopped-flow fluorescence was used to study the rates of conformational change (presumably Fingers closing), it became clear that the forward rate of the isomerization step (k₊₃ from Scheme 1) was faster than k₊₄, the rate of product formation (15, 16).

About this time, another attempt was made to explain base discrimination on purely thermodynamic grounds. This proposal asserted that the difference between the free energy barriers for incorporation of correct versus incorrect dNMPs could satisfactorily account for observed levels of base discrimination (11, 19, 27). This explanation required that chemistry be rate-limiting for both correct and incorrect dNTPs. While there is evidence that supports this proposal for pol β (14, 28), data for other DNA polymerases, such as T7 pol and the Klenow fragment, suggest that there is a step prior to nucleotidyl transfer that is rate-determining for correct incoming dNTPs but that chemistry limits the dNMP incorporation rate when an incorrect dNTP is a component of the ternary complex (3).

Recently, another proposal was advanced by Tsai and Johnson to account for base discrimination by T7 pol, a replicative polymerase belonging to the A family (21). The novel aspect of their proposal was that the conformational change prior to chemistry, which commits the incoming dNTP to proceed through the transition state to product, eliminates the rate of the chemical step from the specificity constant (k_cat/K_m). This is because the specificity constant is independent of the nucleotidyl transfer rate (k₊₄) when the reversal rate of the internal isomerization (k₋₃) is slow relative to chemistry. As a consequence, base selectivity cannot be explained solely on thermodynamic grounds.

It should be clear from the discussion given above that to test the general validity of Tsai and Johnson's proposal, it would be important to obtain values for the reverse isomerization rate constant, k₋₃ (FDN reconverting to EDN), for ternary complexes of DNA polymerases containing correct and incorrect dNTPs other than T7 pol. It would also be valuable to evaluate k₋₃ with assays that monitor different properties of the ternary complexes to ensure that the same process is being monitored in every case. To address this issue, we have used four different approaches. (i) The first was to assemble a ternary RB69 pol–dP/T–Rh·dTTP complex in the absence of Mg²⁺. This complex was assumed to be in the fully closed form on the basis of the observation that the fluorescence of dAP, the templating base, was fully quenched. No product was formed from this complex, but upon addition of Mg²⁺, the rate of product formation was ∼4 s⁻¹, a value much lower than the 80 s⁻¹ incorporation rate observed when Mg²⁺ was present in the mixture prior to the start of the reaction. Similar experiments were carried out where the ternary complex, with a correct dNTP, was assembled with Ca·dTTP or Na·dTTP followed by addition of Mg²⁺. The rate of product formation in these experiments was also in the range of ∼4 s⁻¹, indicating that it was the initial absence of Mg²⁺ in the A site rather than the identity of the metal ion complexed with the incoming dNTP that was responsible for the 20-fold difference in rates of dTMP incorporation. Additionally, it should be noted that the amplitude of the slow phase increased with an increase in dTTP concentration. This is consistent with a model in which nucleotide binding saturates the closed state of the enzyme complex. The fast unresolved time phase seen in Figure 2 represents those enzyme molecules that are in the open state and can readily bind Mg²⁺. The slow phase represents the population of enzyme molecules in the FDN state that have to reopen and then close prior to chemistry. (ii) The second approach was to use a dP/T complexed with RB69 pol in the presence of Ca²⁺, to prevent product formation, and to estimate the rate of dAP quenching as a function of increasing dTTP concentration. By extrapolating the hyperbolic curve that was obtained by plotting k_obs versus dTTP concentration to the Y axis (where the dTTP concentration approaches zero in Figure 4B), we were able to obtain an approximate value of k₋₃. This experiment was also carried out with a ddP/T which also prevents product formation, again with dAP as the templating base, but in the presence of Ca²⁺ or Mg²⁺. From these experiments, k₋₃ values in the range of 4–30 s⁻¹ were obtained. This rather large spread in values stems from the difficulty in obtaining an accurate estimate of the Y intercept because the precision of the measurements decreases as the dTTP concentration approaches zero. However, the reversal rate of FDN to the EDN collision complex is clearly much slower than either the forward isomerization rate (k₊₃) or the dTMP incorporation rate (k₊₄). As a consequence of these rate differences, the FDN state becomes more highly populated when a correct dNTP is part of the ternary complex and it is the FDN complex that is poised for nucleotidyl transfer. When the reaction mixture contains Mg²⁺ and an extendable primer, FDN will be converted to product (FD_n+1PP_i). Since the k_obs for product formation is proportional to FDN concentration, the lower the reverse isomerization rate (k₋₃), the higher the observed rate of product formation. This is entirely consistent with the pulse–chase rapid chemical-quench result described above. (iii) The third approach involved a dTTP trapping experiment designed to measure the rate at which dTTP was released from the RB69 pol–dP/T–dTTP ternary complex (complex I). The underlying assumption is that complex I has to relax, or partially reopen, to release the bound dTTP so that it can be trapped by the Sq–dP/T⁺ binary complex (complex II) which we have shown to have a much higher affinity (0.8 nM) (Figure 2 of the Supporting Information) for dTTP than complex I (53 nM) (Figure 3B). The rates of fluorescence enhancement that were observed (50 and 4 s⁻¹) reflect the rates of dAP unstacking, and the direction of the fluorescence change is the opposite of that of the quenching that occurs during the formation of the ternary RB69 pol complex. These rates then can be considered to be a measure of the relaxation rate of the ternary complex. To account for why two rates with nearly equal amplitudes were observed, we have to assume either that there are two populations of molecules in the FDN state that relax at different rates along parallel pathways as shown in Scheme 4A1 or that the process follows a single pathway that starts with a more rapid relaxation of FDN (50 s⁻¹) followed by a slower opening of the putative partially relaxed intermediate, at a rate of 4 s⁻¹, to give the fully open EDN^O collision complex which is in rapid equilibrium with ED + N (Scheme 4, A2). (iv) The aim of the fourth experiment was to estimate k₋₃ when the RB69 pol–dP/T binary complex was challenged with an incorrect dNTP. Again we depended on changes in dAP fluorescence to monitor partitioning of the RB69 pol–dP/T–dNTP complex between the EDN and FDN states. By using Ca²⁺, we were able not only to block chemistry but also to increase the affinity of the incoming dNTP for the binary complex. When stopped-flow fluorescence experiments were performed with dCTP opposite dAP as the templating base, the rate of quenching exceeded the 2 ms dead time of the stopped-flow instrument as shown by the decrease in start points as a function of dCTP concentration (Figure 5A). The end points were also dependent on dCTP concentration, as expected, because of the reversibility of the isomerization. As pointed out in Results, modeling this process using KinTekSim provided estimates for the forward and reverse isomerization rates. Each of these rates exceeded 1000 s⁻¹ (Scheme 2). It is clear from the stopped-flow fluorescence results (Figure 5A) that the FDN to EDN reversal rate is much faster for an incorrect, as opposed to a correct, incoming dNTP. This is consistent with the concept advanced by Tsai and Johnson (21) that the internal isomerization step represents an important checkpoint for base discrimination in this system.

Although our principle aim in this study was to obtain insight into the mechanism of base discrimination, our experimental approach differed from that used by Tsai and Johnson (21). Whereas they used a dye-labeled T7 pol to determine the reverse isomerization rate for their ternary complexes that contained either correct or incorrect dNTPs using stopped-flow fluorescence, we used a Sq–dP/T⁺ complex to trap dTTP released from the ternary complex and a pulse–chase, chemical quench to determine the rate of dTMP incorporation after addition of Mg²⁺ to the closed, Mg²⁺ deficient, RB69 pol ternary complex.

We determined the rates of release of dTTP (50 and 4 s⁻¹) from the RB69 pol ternary complex with the Sq–dP/T trapping experiment and found that the rates were much slower than the forward isomerization rate (k₊₃ > 1000 s⁻¹) but were consistent, in part, with the rate of 4 s⁻¹ from pulse–chase, chemical-quench experiments. Since the time-resolved phase of pulse–chase, rapid chemical-quench experiments had relatively low amplitudes, detecting the presence of a second 50 s⁻¹ phase was not possible. Although the same process may be monitored in both assays, the pulse–chase, rapid chemical-quench experiment reports the slowest rate while the readout of the Sq–dP/T⁺ trapping experiment is the rate of dAP fluorescence enhancement. Since this depends on dAP unstacking, it is an indirect way of monitoring conformational changes in the complex, and it is not clear just when unstacking occurs. For example, the ternary complex could be opening and closing very rapidly, but the presence of a correct dNTP would greatly favor the closed form. In this scenerio, a correct dNTP might be expected to dissociate more slowly from the open form than an incorrect dNTP because of complementary base pairing. It is conceivable that the full extent of dAP fluorescence enhancement is realized only when the dTTP actually dissociates from the open complex. As depicted in Scheme 4, there could be relaxation of the closed form with partial unstacking followed by dissociation of dTTP to give the fully open binary complex which we had previously shown to have the highest fluorescence.

In principle, the slow rate of dTMP incorporation observed in the pulse–chase, chemical-quench experiments could have been due to slow Ca²⁺ release followed by Mg²⁺ binding or just to slow diffusion of Mg²⁺ into the A site in the closed ternary complex because, in chemical-quench experiments (Figure 1), it has the same incorporation rate for Rh·dTMP when both solutions in syringes A and B contained Mg²⁺ or when just one of the solutions contained Mg²⁺. It suggested that the diffusion of Mg²⁺ into the A site is a rapid process, which occurs faster than dTMP incorporation. Divalent metal ion binding is generally thought to be diffusion-controlled, a very rapid process, and in most reports, the assumption has been made that the catalytic metal ion should be freely exchangeable while the complex is in the closed state (14, 29, 30). This view has been bolstered by the fact that structures of the closed forms of many DNA polymerases do not have any residues whose side chains could act as steric barriers to prevent access or exchange of divalent metal ions into, or out of, the A site. However, there are many highly ordered water molecules in the vicinity of the A site, as seen in high-resolution structures of ternary RB69 pol complexes (M. Wang and J. Wang, unpublished results) that could restrict diffusion of divalent cations particularly because divalent cations such as Mg²⁺ and Ca²⁺ have large hydration shells. This could account for our findings that Mg²⁺ and Ca²⁺ do not appear to be freely exchangeable with other divalent metal ions in the A site when the RB69 pol ternary complex is fully closed. The dTMP incorporation rate from pulse–chase, chemical-quench experiments agrees both with the values obtained from the stopped-flow experiments described above in section (ii), which are independent of metal binding, and the Sq–dP/T experiments designed to trap dTTP as it is released from the ternary complex as discussed in section (iii). Taken together, it seems unlikely that the results from (i) the pulse–chase, quench-flow experiment, (ii) the extrapolation of the dAP fluorescence quench rate versus dTTP concentration plot to the Y axis, and (iii) the Sequenase trapping experiment would report the same rates for different processes. Thus, it seems reasonable to conclude that the ∼4 s⁻¹ rate, observed with the three different methods, represents the slowest rate of relaxation or reopening of the ternary complex when it is in the closed, FDN state and when a correct dNTP is part of the FDN complex. The 50 s⁻¹ rate found with the dTTP trapping experiment may represent an intermediate in the reopening pathway or a parallel pathway that also leads to (EDN)^O as shown in Scheme 4.

Clearly, the behavior of the ternary complex containing an incorrect dNTP differs markedly from the behavior of the ternary complex with a correct dNTP. Because the forward and reverse rates of the internal isomerization are so rapid in the presence of an incorrect dNTP, the only way that we could approximate the rates was by attempting to obtain the best fit to the stopped-flow fluorescence scans that were obtained with different dCTP concentrations and by modeling the kinetics data using KinTekSim. Despite the imprecision inherent in this approach, the results were fully consistent with the idea that the closed complex with an incorrect dNTP either reopens or releases the dNTP much more rapidly than a ternary complex with a correct dNTP. As a consequence, partitioning of the incoming incorrect dNTP between the EDN and FDN states strongly disfavors the FDN complex, and thus, the rate of incorrect dNMP incorporation is greatly reduced compared to the situation with a correct dNTP.

Comparison of RB69 pol with Pther DNA pols with Respect to Metal Binding, Conformational Change, and Fidelity

We have already mentioned how our results with RB69 pol relate to those obtained with T7 pol. The only other DNA pol for which these issues have been extensively studied is pol β. Attempts have been made to assess the role of divalent metal ions in the kinetics of DNA synthesis catalyzed by pol β. In Scheme 1 of ref 14, the catalytic metal ion is shown entering the E·D_n·N complex in step 3 after the ternary collision complex, E·D_n·N, has already closed. The slow step that they observed occurs after addition of Mg²⁺ to the closed ternary complex (step 3). The slow fluorescence change that accompanied the Mg²⁺ addition had the same rate as dNMP incorporation. They assigned this slow rate, after adding Mg²⁺ to the closed complex, to the chemical step and indicate that it is not caused by the chemical reaction itself but that its rate is limited by chemistry. They also state that the slow fluorescence change most likely reflects the reopening of the closed form after chemistry (step 6 in their Scheme 1). The major distinction between our study and that of Bakhtina et al. (14), aside from the fact that we are working with a different DNA polymerase, is that we ascribe the slow step, observed after addition of Mg²⁺ to the closed ternary complex, to its relaxation which would allow entry of Mg²⁺ to the A site before chemistry. In contrast, with pol β the slow fluorescence change is posited to occur after chemistry and would also reflect reopening of a closed complex but one where nucleotide addition had already occurred. It is certainly possible that the behavior of pol β and RB69 pol could be due to inherent differences between the two enzymes. For instance, the residues in the closed complex of pol β do not envelop the nascent base pair as tightly in the vicinity of the A site compared to RB69 pol, and thus, Mg²⁺ might actually access the A site more easily. Another possibility is that the behavior of both enzymes could be accommodated by a common kinetic scheme and that it is just our interpretation of the results that differs (14). In the case of pol β, there was an implicit assumption that Mg²⁺ can access the A site while the complex is fully closed. If this assumption is accepted, their results and interpretations are internally consistent. But what if Mg²⁺ cannot access the A site when the ternary complex is fully closed? If this were the case, there would have to be another step before Mg²⁺ could enter and bind to the A site, an essential requirement for nucleotidyl transfer. When the closed complex harbors a correct dNTP, it might be expected to reopen slowly, and this could be the process that Bahktina et al. was monitoring by observing the change in dAP fluorescence. Its rate of change then would also limit the rate of dNMP incorporation. If so, this step, step 2, in which E′·D_n·N reverts to E·D_n·N, could allow entry of Mg²⁺, but this would have to happen before, not after, chemistry.

We want to emphasize that we have created a situation in our study that is not normally encountered by DNA polymerases in vivo or in vitro, since Mg²⁺ is present throughout the nucleotide addition cycle. The purpose here was to obtain an estimate of k₋₃, the rate of relaxation of the ternary complex with correct and incorrect incoming dNTPs. Since the relative values of this reverse isomerization rate for correct and incorrect dNTPs were shown to be the most important factor in determining the extent of base discrimination with T7 pol, it was of great interest to see if this analysis would hold for a replicative DNA polymerase from another family which is one of the reasons we attempted to obtain k₋₃ values for RB69 pol. While we have not yet been able to use a fluorescently labeled RB69 pol to explore the reverse isomerization rates for correct and incorrect dNTPs, as was done for T7 pol, we have been able to estimate k₋₃ values for RB69 pol using the three approaches described in this report. Since they all gave similar numbers, we believe they were reporting the same process.

While we would like to test this scheme further with an appropriate dye-labeled RB69 pol, we think that the approaches we have used here could be applied effectively with other DNA polymerases to test the generality of this scheme and to see if it could serve as a universal basis for explaining DNA polymerase fidelity.