Classification of Spatially Unaligned fMRI Scans

Abstract

The analysis of fMRI data is challenging because they consist generally of a relatively modest signal contained in a high dimensional space: a single scan can contain over 15 million voxel recordings over space and time. We present a method for classification and discrimination among fMRI that is based on modeling the scans as distance matrices, where each matrix measures the divergence of spatial network signals that fluctuate over time. We used single-subject Independent Components Analysis (ICA), decomposing an fMRI scan into a set of statistically independent spatial networks, to extract spatial networks and time courses from each subject that have unique relationship with the other components within that subject. Mathematical properties of these relationships reveal information about the infrastructure of the brain by measuring the interaction between and strength of the components. Our technique is unique, in that it does not require spatial alignment of the scans across subjects. Instead, the classifications are made solely on the temporal activity taken by the subject's unique ICs. Multiple scans are not required and multivariate classification is implementable, and the algorithm is effectively blind to the subject-uniform underlying task paradigm. Classification accuracy of up to 90% was realized on a resting-scanned Schizophrenia/Normal dataset and a tasked multivariate Alzheimer's/Old/Young dataset. We propose that the ICs represent a plausible set of imaging basis functions consistent with network-driven theories of neural activity in which the observed signal is an aggregate of independent spatial networks having possibly dependent temporal activity.

1. Introduction

Existing neuroimaging classification methods for functional Magnetic Resonance Imaging (fMRI) data have shown much promise in discriminating among cerebral scans, but are limited in the types of data they can handle, and in the numbers of outcomes they can predict (Ford et al. (2003)) (Zhang and Samaras (2005)). In general, fMRI discrimination methods require preprocessing steps such as spatial alignment of the scans and are only infrequently suitable for multivariate classification problems (Calhoun et al. (2007)) because of their utilization of bivariate classifiers. Spatial alignment algorithms often are constructed assuming a subject has a normal brain, and therefore may be less accurate when warping scans of patients with physical anomalies. Existing classification methods typically require knowledge of the task paradigm thereby limiting their application to subjects who are able and willing to perform such tasks. Here we introduce a procedure called spectral classification that is capable of multivariate discrimination among single-session fMRI scans taken during both a tasked and “mind-wandering” (task-free) state. The methods classify based on the temporal structure of the data rather than the spatial structure, thereby bypassing the need for spatial alignment of the scans. We call this method spectral classification because of its usage of spectral graph-theory measurements for discrimination. We demonstrate here a non-spatial method of classification having cross-validation accuracy rates as high as 90% for bivariate classification. Mathematically we introduce a method for comparing and classifying objects represented by distance matrices. In this paper an entire matrix describes an fMRI scan where the entries contain the “distances” between the activity of two components' timeseries; however these methods are generally applicable to any problem in which the elements are described as matrices rather than isolated points and discrimination is desired among these objects.

Temporally recorded neuroimaging data pose a unique challenge to classification because of the high-dimensional structure of the data sets. One scan can contain more than 120,000 recordings that often are highly correlated both in only four effective dimensions consisting of space and time. Because of this, practical classification procedures require an initial dimension-reduction stage where discriminating signal is extracted from the noisy data. In spatial-based discrimination methods, localized summaries of the temporal signal are used to compress the temporal dimension into a single point at every spatial location. The spatial regions containing discriminating summary statistics are extracted and used to create a classification machine. (Zhang and Samaras (2005)) (Ford et al. (2003))

The summary statistics used for describing temporal activity include mean signal intensities or p-values measuring association with a known task-paradigm. These regional summary statistics are compared across subjects when training the classifier, requiring the scans be spatially aligned to a common atlas space. The most often used alignment algorithms (Woods et al. (1998)) are 12-parameter affine transformations that warp a subject's brain to a common atlas space. Alignment precision is limited with normal patients by the low geometric flexibility of the algorithms, and is potentially more difficult to achieve with subjects having structural inconsistencies associated with mental disorders. For example, it is known that people with schizophrenia have significantly larger ventricles (Shenton et al. (2001)) and that Alzheimer's sufferers show brain atrophy(Ridha et al. (2006)); standard structural alignment tools cannot take into account the unique differences existing in these patients. Thus, spatially-based discrimination methods may fail in classifications across individuals due simply to poor spatial alignment.

A known task-function is often correlated regionally with timeseries to identify regions closely associated with a task. Improved alignment methods notwithstanding, localized low-order summary statistics of the regional BOLD signal may not capture higher-order discriminating information contained in the temporal domain. If functional anatomy is similar among patient groups, then the temporal information of the scans offer a new dimension with potentially discriminative information. If the group differences exist not in the spatially localized signal summary but in the native temporal activity taken by the brain, classification methods relying on summary statistics could fail to distinguish between groups. A method that instead reduced the often-redundant spatial dimension while keeping intact the temporal structure would capitalize on signal differences existing in the temporal domain rather than spatial. The method proposed here is agnostic to the task function and yields similar accuracy results discriminating among identically tasked scans and untasked scans in two datasets tested here.

Because of the limitations of spatial discrimination methods, there is a need for a classification method that is both insensitive to spatial alignment and independent of low order statistical summaries. Using unaligned scans our method classifies on temporal activity patterns between independent components within a subject. The blind source separation method of Independent Components Analysis (ICA) is capable of decomposing a sequence of three dimensional images into sources consisting of statistically independent spatial maps acting over time according to possibly dependent activity patterns. When applied to fMRI data, ICA decomposes a four-dimensional single fMRI scan into a set of statistically independent spatial components (Hyvärinen and Oja (2000)). These spatially independent components have corresponding time courses that show statistical dependence with the time courses of other components. The strength of the relationship between components is indicated by coupling, or correlated intensities over time.

It is not known which if any of the spatial components identified by ICA represent functional neural networks, however it has previously been shown that ICA-methods yield identifiable stable neurological patterns. Damoiseaux et al (JS Damoiseaux (2006)) were able to identify 10 consistent resting state networks common across their population that appear to correspond to identifiable phenomena such as motor function, visual processing, executive functioning, auditory processing, memory, and even the default-mode network, however the identification of these components is not required with our approach to classification yet remains a hidden layer that might be useful for neuroscientific interpretation. The general goal of our work is to develop a classification method that is independent of any trained user interaction making the tool more practically applicable and less sensitive to experimenter bias. One consequence of this, as implemented here, is that the classification itself may be based on signals that are not directly interpretable as neural in nature. For example, it is possible that group specific artifacts, such as head motion, might be contributing to the classifier. For the moment, we note that even in the face of this potential limitation, the classifier appears quite robust. In the future, we intend to use automated means to detect and reject identifiable artifacts (such as motion.) Because the time courses alone are used for discrimination our method does not require us to associate the spatial components with a known biological process to classify a scan; rather, we are concerned with the temporal structure that these components take, how similar they are with other components in that subject, and how this dependency varies across subjects and groups.

In the classification method described here, inter-subject component comparisons do not require multiple scans or knowledge of the underlying task paradigm. We describe here the application of our methods using two separate datasets. The first consists of blocked-task designed scans from Normal Old, Normal Young, and Alzheimer's patients, while the second dataset consists of resting-state scans of Schizophrenia subjects and Normal controls. We estimated the classification testing accuracy using cross-validation (C.V.) and the out-of-bag error from the random forests (R.F.) (Breiman (2001)) classifier, where the accuracy is an estimate of how well the classifier would do if given a new scan from a previously unseen subject.

Random forests is a decision-tree machine learning method that creates many classification trees by resampling from both the observations and classifiers at each node and subsequently making decision rules to minimize the misclassification rate of the sampled data within each tree. Many decision trees are constructed and combined to create a “forest” that decides an observation's class by voting over the decisions made by each tree. The tree is then tested on observations that weren't selected in the initial sampling, to give the “out-of-bag” error which is usually an unbiased estimate of the testing error.

2. Materials and Methods

2.1. Overview

The first step in spectral classification is to perform ICA individually on the scans to reduce the dimensions of the data and extract the time courses of the components. We then create distance matrices that capture the relationship between the temporal signals within a subject, and extract features from these similarity matrices using the principal (largest) eigenvalues. Finally, we train a random forests classifier on the extracted features and evaluate the out-of-bag and cross-validation errors as measures.

The implementation of the spectral classification procedure can be summarized as follows:

• Step 1: Decompose a scan into spatial networks and timecourses using Independent Components Analysis (ICA).

• Step 2: Create a distance matrix describing temporal correlations among spatial components within a subject.

• Step 3: Unwrap the distance matrix by calculating the geodesic distance among components and extract principal eigenvalues from distance matrix to create feature vector.

• Step 4: Train a (multivariate) random forests classifier using eigenvalues as features, and evaluate it by using cross-validation.

2.2. Data Characteristics

All subjects, both schizophrenia patients and healthy controls, gave written informed consent and were recruited and studied under a protocol approved by the UCLA and the Greater Los Angeles VA Health Care System Institutional Review Boards. The Schizophrenia/Normal dataset consists of 14 clinically stable schizophrenia outpatients (diagnosed according to DSM-IV-R criteria using a structured clinical interview) and 6 healthy controls, matched to the affected individuals for age, gender, race, handedness and parental education level. Subjects were scanned at rest on a Siemens Allegra 3T scanner (Erlangen, Germany) in supine position, wearing acoustic noise protectors. To facilitate later coordinate alignments, we collected a high-resolution 3D MPRAGE data set. (Scan parameters: TR/TE/TI/Matrix size/Flip Angle/FOV/Thickness= 2300/2.9/1100/160×192×192/20/256×256/1 mm). We then collected a set of T2-weighted EPI images (TR/TE/Matrix size/Flip Angle/FOV/Thickness=5000/33/128×128×30/90/200×200/4.0mm) with bandwidth matched to the later BOLD studies, covering 30 horizontal slices in the same plane of section used for activation studies. These data are inherently in register with the subsequently collected functional series as they share the same metric distortions. For the latter, multi-slice echo-planar imaging (EPI) was used to measure Blood Oxygenation Level Dependent (BOLD)-based signals (TR/TE/Matrix size/Flip Angle/FOV/Thickness= 2500/45/64×64×30/90/200×200/4.0mm) The fMRI procedure detects signal changes that indicate neuronal signaling indirectly through changes in signal intensity that reflect relative blood oxygenation and thus metabolic demands. We preprocessed the scans using motion correction (MCFLIRT in FSL) and then performed skull-stripping using FSLs BETALL (Smith et al. (2004)).

The Alzheimer's Young/Old dataset was obtained from the fMRI Data Repository Center, collected originally by Randy Buckner (Buckner et al. (2000)). A history of neurological or visual illness served as exclusion criteria for all potential subjects. Further, older adults were excluded if they had neurologic, psychiatric or mental illness that could cause dementia. A total of 41 participants (14 young adults, 14 nondemented older adults, and 13 demented older adults) were included in the dataset. The task paradigm used an event-related design consisting of presentation of a 1.5 second visual stimulus. Subjects pressed a key with their right index fingers upon stimulus onset. The visual stimulus was an 8-Hz counterphase flickering (black to white) checkerboard subtending approximately 12 of visual angle (6 in each visual field). Stimulus onset was triggered at the beginning of the image acquisition via the PsyScope button box.

The methods presented in this paper were performed using tools in FSL (Smith et al. (2004)) and routines coded in R (R Development Core Team (2008)).

Constructing an automatic classifier required us to reduce the dimensionality of the data, construct activity manifolds on which to calculate the geodesic distances (Tenenbaum et al. (2000)), create feature vectors using properties of these manifolds, and to perform classification of the subjects.

2.3. Dimension Reduction

As fMRI data is very high-dimensional it is necessary to first reduce the data in a manner that preserves its temporal structure. When ICA is performed on an fMRI scan, the data is broken down into a set of spatial activation maps and their associated time courses.

A scan of time length T and spatial dimension S and can be expressed as a linear combination of N ≤ T components and the corresponding timecourses:

$$X_{\mathit{\text{ts}}}=\sum _{\mu =1}^N{M}_{t\mu }{C}_{\mu s}$$ (1)

Where X_ts represents the raw scan intensity at timepoint t ≤ T and spatial location s ≤ S, M_tμ is the amplitude of component μ at time t, and C_μs is the spatial magnitude for component μ at spatial location s.

In the ICA decomposition, the spatial components are assumed to be statistically independent, however, there is no assumption of independence for their time courses. ICA is run on each subject, extracting all relevant components that are found within that subject. The Laplacian Approximation to the Model Order is used to derive the number of components existing in each subjects, as has been found effective in estimating the underlying number of signal sources (Minka (2000)). The consequences of using other methods to determine the number of components are discussed in Section 5.1.

The net result is that the dimensionality is reduced from an initially four-dimensional dataset into a selection of time series and a small number of spatial maps representing the spatial signatures of the independent components within a subject. We use the time series of the components for classification as they are not dependent on proper spatial alignment over the population. In addition, the time series represent a more compact description of the data than the spatial maps because of the smaller dimensionality of a 1-effective dimension timeseries compared to a 3-effective dimension spatial map. This in turn allows for more flexibility in the discrimination methods available because of computational efficiency.

2.4. Manifold Construction

Each independent component can be considered a node on an unknown graph or manifold unique to each subject, and we can model the connection between two nodes by measuring the similarity between two components' timeseries. The metric of similarity presented here is based on the measure of cross-correlation, but the classification methods were tested successfully also with frequency domain signal strength, fractal dimension, and standard statistical correlation.

Graphically we want to measure the randomness taken by the bivariate path of two components. Let M_α and M_β be the timecourses from two different independent components within a subject. The bivariate plot of the first and second timecourse within two random subjects is shown in Figure 1, where the two timecourses are selected as being those that explain the most variance out of all extracted timecourses, and are unique within each subject. We wish to see if the patterns observed in the interactions of components are consistent and strong enough to discriminate among patient groups.

Figure 1. Phase Space for Primary Components.

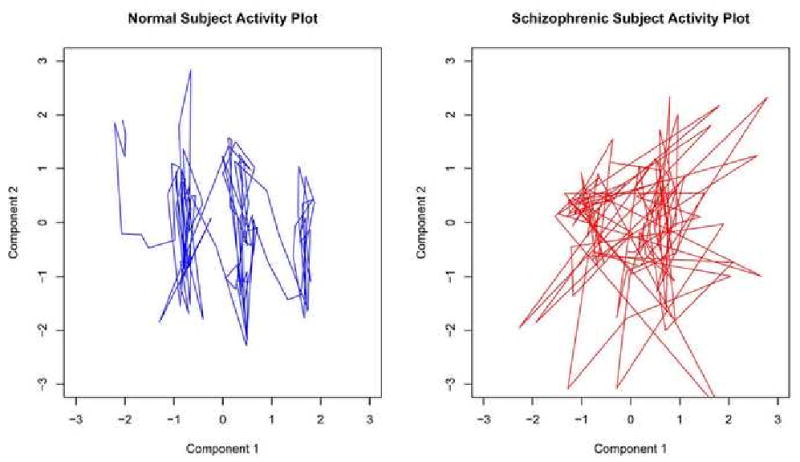
To quantify the relatedness between pairs of temporal components we compute a distance metric based on the cross-correlation function, which is a linear measure of the similarity between two time series and may be computed for a wide range of lags. Time Series based measures have been used to explore directed influences between neuronal populations in fMRI data (Roebroeck et al. (2005)) using Granger causality and have found increased correlation among independent components in schizophrenia patients compared to normal controls (Jafri et al. (2007)) using the cross-correlation. We used the maximal absolute correlation between two time series over a range of lags as an indicator of the amount of information shared between them and how similarly they act over time.

$$\mathit{\text{CCF}}(M_{\alpha },M_{\beta },l)=\frac{E[(m_{\alpha ,t+l}-\overline{M_{\alpha }})(m_{\beta ,t}-\overline{M_{\beta }})]}{\sqrt{E[{(m_{\alpha ,t}-\overline{M_{\alpha }})}^2]E[{(m_{\beta ,t}-\overline{M_{\beta }})}^2]}}$$ (2)

where m_α,t+l is time-shifted version m_α,t, l is the time lag separating the two timeseries M_α and M_β, and $\overline{M_{\alpha }}$ is the mean of the entire timeseries M_α = (m_α,1, m_α,2, …, m_α,T). The timeseries are calculated at lags ranging from 0 to 20% of the timeseries length, as higher lags results in fewer time points to calculate the correlation and a more noisy estimate. The distance function is a transformation of the maximal absolute cross-correlation between two timeseries.

$$d(M_{\alpha },M_{\beta })=\frac{1}{{\mathit{\text{max}}}_{\mathit{\text{lags}}}[|\mathit{\text{CCF}}(M_{\alpha },M_{\beta })|]}-1$$ (3)

To test the dependency of our method on a particular metric, we compared the results of our chosen metric with three other distance metrics derived from the raw correlation, fractal dimension, and a measure of Fourier signal strength. Similar accuracy results were obtained which are discussed further in Table 3,4.

Table 3.

Cross-Validation Accuracy

Groups	Method 1 CV Accuracy	Method 2 CV Accuracy	Chance Accuracy
Alzheimer's, Old, Young	65.9%	53.7%	34.1%
Alzheimer's, Old	74.1%	74.1%	51.9%
Alzheimer's, Young	62.9%	59.3%	51.9%
Old, Young	89.2%	89.2%	50%
Schizophrenic, Normal	80%	80%	70%

Table 4.

Classification Accuracy by Component Selection Criterion

Criterion Criterion	Method 1 Accuracy	Eigenvalue Dimension	Method 2 Accuracy	Eigenvalue Dimension
AIC	65%	5	75%	1
BIC	70%	7	95%	8
LAP	80%	3	90%	3

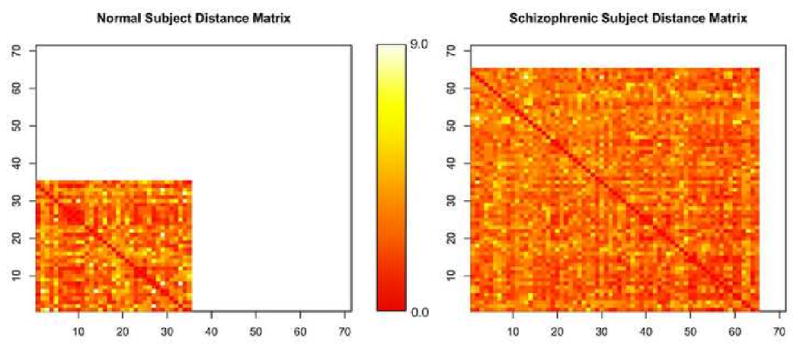
Within a subject i calculating the distance between all N_i temporal components yields a distance matrix Φ_Ni×Ni. The dimensionality of each subject's matrix corresponds to the number of independent components initially extracted as shown in Figure 2 and may therefore differ. The darker intensity in Figure 2 indicates a smaller distance, while a lighter color shows a greater distance. The distances range in value from (0, 9) and the colors are normalized within each matrix so that darkest lightest color corresponds to the greatest intensity. The rows and columns in the distance matrices have no direct correspondence across subjects. The temporal components are extracted individually within each subject using ICA, leading to a unique structure in the temporal associations within that subject's distance matrix, Φ_Ni×Ni.

Figure 2. Subject Matrices showing unequal number of component.

2.5. Feature Selection

Each matrix Φ_Ni×Ni represents the connectivity over time of independent components M_α embedded on some unknown manifold that is unique to each subject. Distances between points d(M_α, M_β) quantify the temporal similarity between two components represented by timeseries M_α and M_β. It is unreasonable to assume that the graphical structure represented by a matrix for subject i, Φ_Ni×Ni, lies on a linear space, as only a very small subset of all the spaces on which a manifold could lie will be linear. To account for this, an intermediary step will be performed prior to feature extraction that will warp the graphical structures represented by the matrices to account for the potential non-linearity of the manifolds.

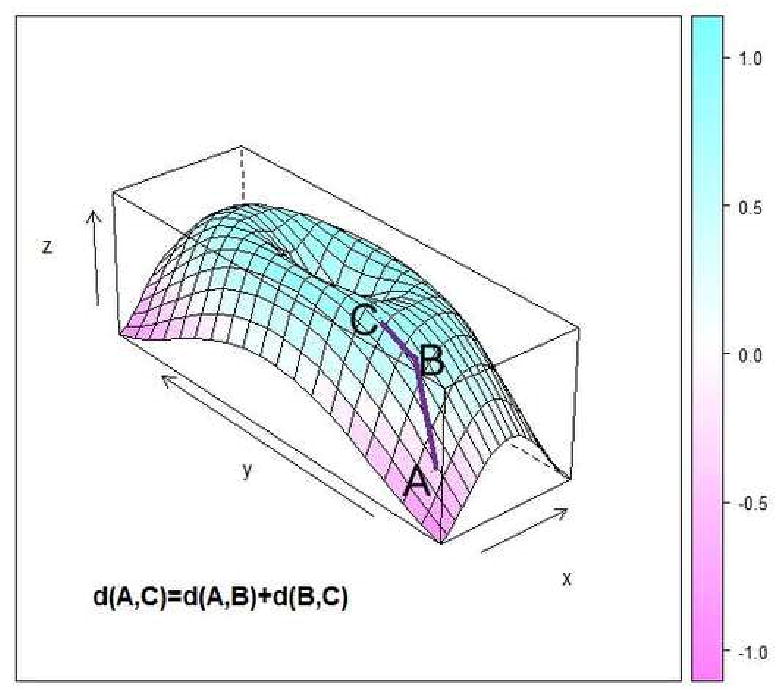
The matrices are warped for each subject using the same principles underlying the manifold embedding technique of ISOMAP (Tenenbaum et al. (2000)). Within each subject, the original matrix is transformed by recalculating the distances among components using a non-linear metric, the geodesic distance (Tenenbaum et al. (2000)). The geodesic distance measures distances between non-neighboring points as the shortest path connecting points through their neighbors as in Figure 4, where the distance between A and C is calculated as the manifold path distance from A to B to C instead of directly from A to C. Points are considered connected if they fall within a set of k-nearest neighbors, where k is chosen to minimize the Bayesian Information Criterion (BIC) (Hogg et al. (2000)) of the goodness of fit within the subject. Further discussion on the choice of neighborhood size and embedding dimension in presented in Section 3.5. Using the geodesic distance, each matrix Φ_Ni×Ni is warped separately by recalculating the distances among points (components) prior to extracting features to create a new matrix ${\Phi }_{N_i\times N_i}^{\ast }$.

Figure 4. Geodesic Distance Calculation.

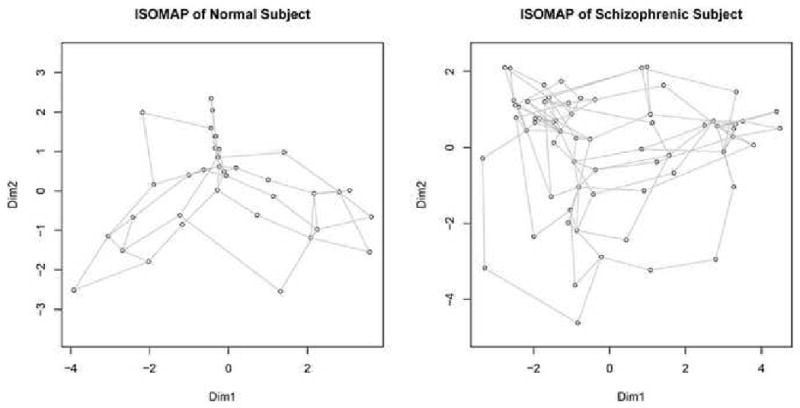
We illustrate the graphical structures these matrices ${\Phi }_{N_i\times N_i}^{\ast }$ represent by embedding them individually in a two dimensional-space using ISOMAP, shown in Figure 3. To perform the embedding the distance matrix is projected onto the eigenvectors corresponding to the two principal eigenvalues of the decomposition of the geodesic distance matrix (Tenenbaum et al. (2000), Kruskal (1964)). Every vertex represents an independent component, while the edge length between vertices corresponds to the geodesic distance between two components. The complete relationship of spectral classification to other methods such as ISOMAP is discussed in Section 5.3.

Figure 3. Embedding of Matrices.

The manifold defined by ${\Phi }_{N_i\times N_i}^{\ast }$ can be described by the eigenvalues λ of the distance matrix that measure the variance explained along the different dimensions. ${\Phi }_{N_i\times N_i}^{\ast }=Q\Lambda Q^{-1}$ where Q is the matrix of eigenvectors and Λ is the matrix of eigenvalues. The largest n_i ≤ N_i eigenvalues for subject i are used to create a feature vector λ⃗_i = (λ_1i, λ_2i, …, λ_ni). Extracting eigenvalues from each graph bypasses the issue of the structures all lying on a unique self-defined manifold, because we are using the properties of the subjects' manifolds to classify instead of the points (components) comprising it. For classification purposes we enforce that n_i = c ∀i where c is some constant chosen as in Section 3.5, because it is necessary to use the same number of features for classification per subject. The principal eigenvalues of the geodesic distance matrix give the strength along the primary dimension and reveal the “skew” in the connective structure of the components. The geodesic distance matrix is analogous to the weighted adjacency matrix of the graph; hence, the spectral decomposition of this matrix lends itself to the procedure name of spectral classification.

2.6. Subject Classification

Once feature vectors λ⃗ have been extracted for all subjects a classifier is trained using Random Forests (Breiman (2001)). Random Forests is well-suited for multivariate classification problems as it decides outcomes by voting, and is less likely to overfit in practice than other methods because of its usage of resampling. The algorithm operates by repeatedly sampling from the data and predictors to construct decision trees. A group of classification trees become a forest, which classifies an observation by having the trees that had not previously seen that observation vote for an outcome. The predicted class of an observation is taken to be the category with the maximal votes by all the trees. The cross-validation error of the classification forest is taken to be the out-of-bag error, and the average error is taken to be the best estimate of the accuracy of this predictor on a completely new scan. However, because the parameters are selected with respect to the out-of-bag error, the testing error is biased. Because of this, we performed cross-validation outside of the parameter selection process to obtain an unbiased testing error estimate.

3. Results and Discussion

The Spectral Classification procedure was run on both the Schizophrenia/Normal and the Alzheimer's/Old/Young Dataset to obtain bivariate and multivariate classification results. The Alzheimer's/Old/Young dataset was also grouped into pairs to further test bivariate classification. There were two parameters involved in fitting the manifold: the neighborhood size, $\frac{1}{k}$, and n_i, the number of dimensions in which to embed. We present the results using two different parameter selection methods. For more details on these selection methods see section 5.1.

3.1. Method 1: Optimized Single Parameter Selection

We will describe here a method of selecting model parameters (n, k_i) such that k_i is selected within a subject by optimizing a model fit, and n is optimized with respect to minimizing the classification error over all subjects. The embedding dimension n is a global parameter held constant for all subjects, while k_i is allowed to vary within subject.

For a given n we will select the fitting parameter $\frac{1}{k_i}$ within a subject by minimizing the Bayesian Information Criterion (BIC) for the goodness of fit. The goodness of fit measure, L_i, is the sum of the eigenvalues used in the partial fitting normalized by the total absolute value of all the eigenvalues.

$$L_i=\frac{{\sum }_{\mu =1}^n{\lambda }_{\mu i}}{{\sum }_{\mu =1}^{N_i}|{\lambda }_{\mu i}|}$$ (4)

where N_i is the number of components within the ith subject, λ_μ is the μth largest eigenvalue, $\frac{1}{k_i}$ is the fraction of total components considered to be neighbors and n is the number of eigenvalues used to describe the subject's distance matrix such that n ≤ 10 ≤ N_i. The upper bound of 10 is selected as a search parameter range since all N_i ≥ 10. The BIC for a subject's embedding of N_i components using k_i is

$$\mathit{\text{BIC}}(N_i,k_i,n)=-2\ast \mathit{\text{log}}(L_{(k_i,n)})+k_i\ast \mathit{\text{log}}(N_i)$$ (5)

For a given n, select the k_i that minimizes the BIC for that subject. The k_i is treated as the degrees-of-freedom parameter because a neighborhood size is calculated as $\frac{N_i}{k_i}$. If k_i increases, the neighborhood size decreases, and there are fewer connections defined between nodes on the graph. This leads to an increased flexibility in the location which points can take. More connections necessarily lead to more restrictions on how the object can be embedded. Because of this, the BIC of the model bears an inverse relationship to the connectedness of the graph. As k_i increases, the connectivity decreases and the BIC increases.

The eigenvalue dimension, or eigendimension, indicates the number of eigenvalues used in the classifier. The eigendimension parameter n must be held constant across all subjects in order to train a classifier, so a random forests model is created for all n ∈ (1, 10), where the parameter k_i will be selected to maximize the goodness of fit as described above. The eigendimension parameter n is selected that maximizes the classification accuracy across subjects.

The results are presented in Table 1.

Table 1.

Classification Accuracy

Groups	Maximum Accuracy	Eigenvalue Dimension	Median Accuracy	Chance Accuracy
Alzheimer's, Old, Young	65.9%	1	50.0%	34.1%
Alzheimer's, Old	74.1%	1	48.2%	51.9 %
Alzheimer's, Young	74.1%	1	66.3%	51.9 %
Old, Young	89.3%	1	66.1%	50 %
Schizophrenic, Normal	80%	3	80%	70%

Although the accuracy is decreasing with sample size, the relative classification accuracy with respect to chance improves with sample size. When trying to increase the number of possible labels in a set, the chance rate of accuracy decreases. With multivariate classification, the “chance” accuracy classification rate (Alzheimer's/Old/Young) was 34.1%, whereas with the bivariate classification of subgroups (Alzheimer's, Old), (Alzheimer's, Young), and (Old, Young) the “chance” accuracy rate was 51.9%, 51.9%, and 50% respectively. Relative to the chance accuracy, the multivariate classifier actually has improved results with more samples, with respective accuracy ratios of classification accuracy/chance accuracy of 1.9326 for the multivariate classification compared to 1.6416, 1.4277, 1.7206 classification ratios for the bivariate runs, using Method 2 accuracy results in Table 2.

Table 2.

Classification Accuracy

Groups	Maximum Accuracy	Eigenvalue Dimension	Nearest Neighbors	Median Accuracy	Chance Accuracy
Alzheimer's, Old, Young	65.9%	1	1/2	51.2%	34.1%
Alzheimer's, Old	85.2%	1	1/4	63.0%	51.9%
Alzheimer's, Young	74.1%	2	1/7	70.4%	51.9%
Old, Young	89.3%	1	1/2	71.4%	50%
Schizophrenic, Normal	90%	3	1/10	80%	70%

An investigation into the classification error within category are discussed in 5.2.

3.2. Method 2: Optimized Dual Parameter Selection

In this section we present a method where the two parameters n and k for fitting the neighborhood are optimized simultaneously within the model. Both n and k are global parameters and are constant across subjects. The out-of-bag error using this approach is artificially lower than the testing error. Because two parameters are being optimized with respect to the out-of-bag error, Method 2 produces a more biased estimate of the training error than does Method 1, which optimizes only a single parameter. This hypothesis is tested below, when cross-validation is run outside of the random-forests parameter selection stage.

The neighborhood size parameter k will be held constant across all subjects within each model evaluation, where k ∈ (2, 10). The eigenvalue dimension n ∈ (1, 10)

The results appear in Table 2.

Because there may exist multiple pairs (n*, k*) corresponding to the same maximum classification accuracy over all possible parameter combinations (n, k), we select the minimum n yielding the optimal accuracy. In the event that multiple (n, k) pairs yield the same classification accuracy for the smallest n, the minimal k is use as a tiebreaker. For example, in the Schizophrenia/Normal dataset, there were 9 total (n*, k*) combinations yielding 90% classification accuracy, so the smallest n rule yielded a (n*, k*) parameter pair as (2, 10).

3.3. Cross-Validation

Both Method 1 and Method 2 optimized neighborhood fit parameters by minimizing the out-of-bag error, or maximizing the out-of-bag-accuracy. To compensate for the bias created by training our classifier on the out-of-bag error, we performed leave-one-out cross validation on top of the resampling already involved in the random forests procedure. This cross-validation is performed outside of the entire model fitting and parameter selection stage to ensure that the testing-accuracy remains unbiased Simon et al. (2003) Demirci et al. (2008). A single observation is omitted from the dataset containing n observations, the model is constructed using the n − 1 observations with the eigendimension parameter and neighborhood size parameter optimized as above. The predictive model is chosen with the eigendimension that maximizes the classification accuracy (minimizes the out-of-bag error) on the n − 1 observations, and this model is then tested on the nth observation that was originally set aside. This procedure is performed repeatedly leaving out a single observation each time for the entire dataset, and the classification accuracy is computed based on the cross-validation accuracy leading to a truly unbiased estimate. The results are shown in Table 3.

A difference between the cross-validation and out-of-bag error cannot be interpreted directly as a measure of bias in the original model creation. Because of the relatively small sample size, leaving out a single observation significantly reduces the dataset size on which the model is created. For example, using leave-one-out on the Schizophrenia/Normal dataset reduces the training set size by 5%. A difference between the out-of-bag error and the cross-validation error then may be attributed to this difference, and not because of bias introduced with the parameter optimization procedure.

Because there may exist multiple (n*, k*) parameters that yield the same maximal classification accuracy in Method 2, there exists some flexibility in the choice of (n, k) on which to estimate the cross-validation accuracy. For simplicity, here we use the (n, k) pair with the smallest n over all pairs yielding the same maximal classification accuracy. If there exists more than one (n, k) corresponding the maximal classification accuracy and the same minimum n, we then select the pair with the minimum k as well. This is equivalent to the n, k chosen to represent the eigenvalue dimensions in Method 2. For further details see Section 3.5.

3.4. Sensitivity to Distance Metric Choice

In this section we will test the methods developed above using three other distance metrics: the correlation distance, the fractal distance, and a new metric we call the phase distance. In this manner we will see how sensitive spectral classification is to the distance metric used to describe the association between independent components.

3.4.1. Correlation

The cross-correlation of two timeseries is merely a lagged version of the correlation. The correlation is a linear metric describing the relationship between increases and decreases in signal amplitude over time.

$$\mathit{\text{Correlation}}(M_{\alpha },M_{\beta })=\frac{E[(m_{\alpha ,t}-\overline{M_{\alpha }})(m_{\beta ,t}-\overline{M_{\beta }})]}{\sqrt{E[{(m_{\alpha ,t}-\overline{M_{\alpha }})}^2]E[{(m_{\beta ,t}-\overline{M_{\beta }})}^2]}}$$ (6)

Results using this metric are shown in Table 5.

Table 5.

Classification Accuracy

Groups	Method 1 RF Accuracy	Method 1 CV Accuracy	Method 2 RF Accuracy	Method 2 CV Accuracy
Alzheimer's, Old, Young	61.0%	42.9 %	65.9%	58.5%
Alzheimer's, Old	63.0%	59.3%	70.4%	37.0 %
Alzheimer's, Young	81.5%	74.1%	81.4%	63.0%
Old, Young	82.1%	71.4 %	92.9%	71.4 %
Schizophrenic, Normal	80%	75%	90%	70%

3.4.2. Phase Distance

To quantify the relationship between pairs of components within a subject, we will create a metric called phase distance that measures the change in activation levels between pairs of components over time.

A shift in energy between two timecourses M_α and M_β between time (t, t + 1) can be calculated as the Euclidean distance

$$D_E(m_{\alpha ,t},m_{\beta ,t})=\sqrt{{(m_{\alpha ,t}-m_{\alpha ,t-1})}^2+{(m_{\beta ,t}-m_{\beta ,t-1})}^2}$$ (7)

This is an extension of the univariate concept of “phase distance”, where univariate movement over time is plotted with the two axis being the observation at time (t, t + 1). Performing this calculation over the range of time yields a vector, D_E(M_α, M_β).

If this energy shift were systematic, one could argue there existed a relationship between the independent components represented by M_α and M_β. The periodogram of the distance vector D_E(M_α, M_β) would exhibit dominant frequencies if this energy shift were ordered, and equal amplitude at all frequencies if there was no regular pattern. “White noise” is defined by this equal distribution of amplitude across all frequencies, and the variance of the amplitudes across all frequencies would be small. A dominant frequency would increase the standard deviation of the periodogram frequencies.

The phase distance between two independent components timecourses is constructed around the regularity of energy shifts among pairs of independent component timecourses.

$$d(M_{\alpha },M_{\beta })=\frac{1}{\mathit{\text{S D}}(D_E(M_{\alpha },M_{\beta }))}$$ (8)

This metric is calculated for all possible component pairs within a subject to form a distance matrix. Results using this metric are shown in Table 6.

Table 6.

Classification Accuracy

Groups	Method 1 RF Accuracy	Method 1 CV Accuracy	Method 2 RF Accuracy	Method 2 CV Accuracy
Alzheimer's, Old, Young	48.8%	29.3 %	58.5%	46.3%
Alzheimer's, Old	70.4%	59.3%	85.2%	81.4%
Alzheimer's, Young	51.9%	29.6%	81.4%	70.4%
Old, Young	64.3%	57.2 %	78.6%	75%
Schizophrenic, Normal	80%	75%	75%	75%

3.4.3. Fractal Correlation Dimension

A fractal measure of dimensionality is used to quantify the complexity of this bivariate trajectory. The correlation dimension Grassberger and Procaccia (1983) computes the dimensionality of a space occupied by a set of random points, and is measured as a density limit of the number of points contained within an ε-ball where the number of points sampled approaches infinity as the radius of the ball ε approaches zero. We compute the density of points in a 2-dimensional space, where the first dimension is the set of points M_α, and the second dimension is the set M_β. A single point in the space at time t is (m_α,t, m_β,t). Although these points are embedded in a two-dimensional space, the distribution of the fractal dimension of these points is bounded above by two and is actually lower than this.

The fractal dimension is calculated using a parameter called the confidence parameter, α, which allows extremely distant points in the set to be removed. This reduces the effects of possible outliers in the calculation by removing an observation that is atypical with respect to the other points. The default parameter in R of α = .2 is used here.

Results using this metric are shown in Table 7.

Table 7.

Classification Accuracy

Groups	Method 1 RF Accuracy	Method 1 CV Accuracy	Method 2 RF Accuracy	Method 2 CV Accuracy
Alzheimer's, Old, Young	53.7%	41.5 %	53.7%	36.7%
Alzheimer's, Old	55.6%	37.0%	63.0%	22.2%
Alzheimer's, Young	77.8%	63.0%	77.8%	55.6%
Old, Young	67.9%	60.7 %	78.6%	39.3 %
Schizophrenic, Normal	80%	75%	85%	75%

The results for this metric are suboptimal with respect to the other parameters. A reason for this may be in the instability of this metric because of the number of points. The fractal dimension is an estimate of density as N → ∞, however our N here is limited to roughly 125 points for both datasets. As such, the number of points we have may lead to instable estimates of an infinite limiting density.

3.5. Sensitivity to Parameter Choice

Here we will examine the effect the parameter choice has on the classification accuracy.

3.5.1. Method 1: Single Parameter Optimization

Method 1 discussed the selecting model parameters (n, k_i) such that k_i is selected within a subject by optimizing a model fit, and n is optimized with respect to minimizing the classification error over all subjects. We will discuss here the change in classification accuracy associated with the change in n.

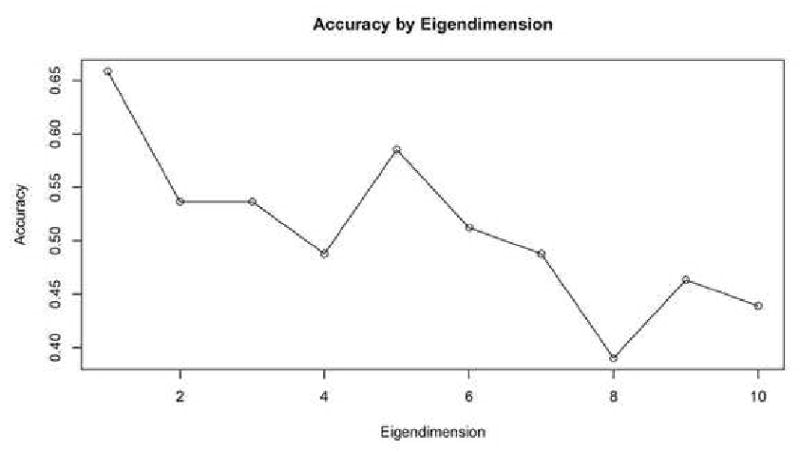
For the Schizophrenia/Normal dataset, the maximal classification accuracy was obtained with eigenvalue dimension n = 3, and the accuracy stayed constant with successive dimensions in Figure 6. This is an indicator that the smaller dimensions were the better predictors at between-group differences. For the Alzheimer's/Old/Young dataset, the maximal classification accuracy was obtained with an eigendimension of n = 1 in Figure 7. Extracting successive eigenvalues into the feature vector served to lower the classification accuracy.

Figure 6. SZ Accuracy by Extracted Eigenvalues.

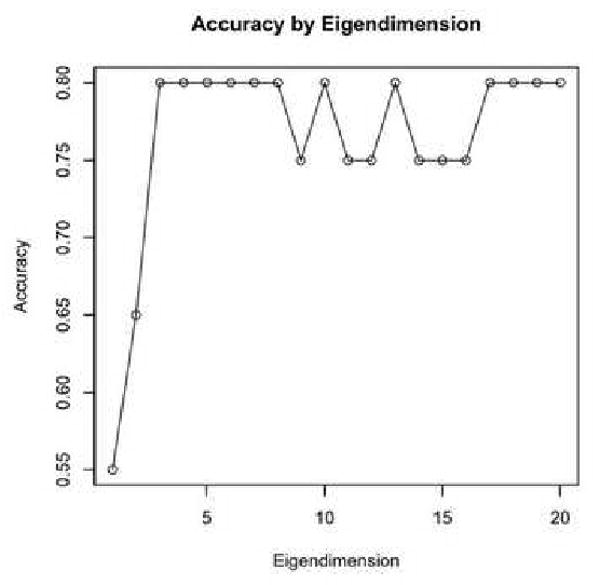
Figure 7. AD Accuracy by Extracted Eigenvalues.

3.5.2. Method 2: Dual Parameter Optimization

The procedure has two free parameters that are optimized: the eigendimension n and the neighborhood size k.

The number of principal eigenvalues used to create a feature vector for a subject is a free parameter bounded above by the minimum number of components existing over all subjects. The number of eigenvalues n used to construct a classifier are by themselves an indicator of the level of variation among the groups; if there existed significant differences between groups, one would see a large number of principal eigenvalues along which there existed between-group variations.

Another parameter to be selected is the fraction of nearest-neighbors to be considered when calculating the geodesic distances. Because all subjects had a unique number of components, we will take a constant percentage of the total number of components to determine the neighborhood size. The eigenvalue dimension will be selected between 1 and 10, while between 10%-50% $(\frac{1}{k},k\in \left(2,10\right))$ of the total number of components within a subject will be used for neighborhood selection.

We will examine the influence of these parameters on the classification accuracy by altering the free parameters.

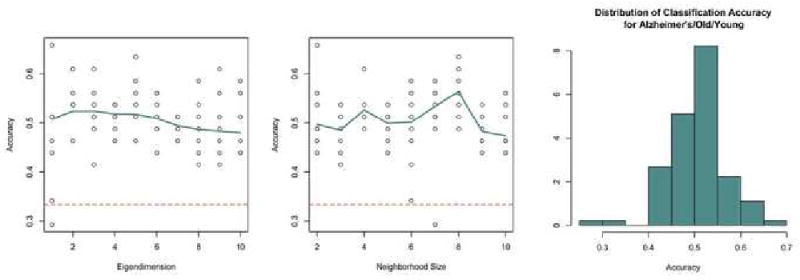
As shown in Figure 8, the accuracy of the classifier for the Old/Young/Alzheimer's dataset improves when using smaller numbers of eigenvalues, which is an indicator that the most difference exists among the first few dimensions. The trend is not as clear in the effect of neighborhood size in the predictive accuracy. The dashed line indicates the random classification accuracy of 33.3%. The median classification accuracy was 51.4%, and the maximum accuracy was 65.9%. The distribution of the accuracy for all possible free parameters for the Alzheimer's/Old/Young dataset shows a unimodal shape with the middle 50% of parameters having accuracy between 46.4% and 53.7%.

Figure 8. AD Parameter Choice.

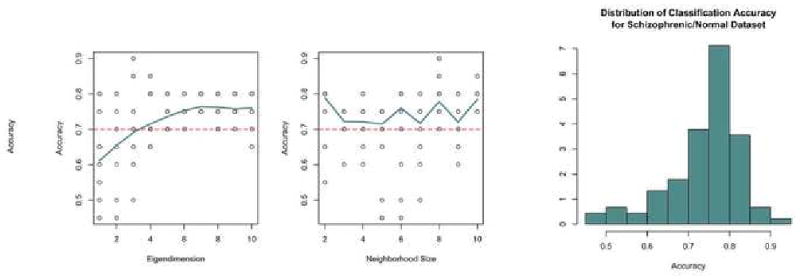
For the Schizophrenia/Normal dataset the accuracy of the classifier improves using greater numbers of eigenvalues in Figure 9. This may be true because there existed initially more components in this dataset than the Alzheimer's/Old/Young dataset, which would lead to a greater number of dimensions on which to discriminate. Similar to the first dataset, there does not appear to be a consistent pattern between the neighborhood size and classification accuracy. The distribution of accuracies over all possible parameters is roughly symmetric with a left skew.

Figure 9. SZ Parameter Choice.

4. Conclusion

The methods developed here can be seen as comparing interactions of spatially independent components over time within a subject and seeking differences in these interactions across groups. Mathematically, we are trying to discriminate among distance matrices, while geometrically we are comparing a group of points (components) in some unknown subject-defined space to another group of points in a different subject's space. Using the geodesic similarity unwinds the shape that each group of point forms, thereby increasing the effectiveness of a linear eigendecomposition on a non-linear subspace. Then, we extract the eigenvalues of the similarity matrix to obtain the strength of the primary dimensions. We are then comparing the size of our unknown manifolds along the primary dimensions across subjects and using differences across subjects to construct a classifier.

We have demonstrated that the temporal information alone contains a signal strong enough for discrimination. The eigenvalue dimension indicates the number of principal eigenvalues along which the groups exhibit significant variation. The need for the geodesic distance transformation demonstrated that the temporal connectivity among the components is highly nonlinear. This may be related to the non-linearity of the initial dimension reduction method ICA. The geodesic transformations of the association matrices smooth the non-linear manifold joining components, improving the features extracted during the eigen-decomposition.

A proposed future direction is to combine spatial and temporal classification models to create a more powerful time-space hybrid classifier. Both methods offer valuable discriminative power along different domains, so a combination could only serve to strengthen existing models. In addition, the existing algorithm could developed using aligned scans with group component extraction, which would allow one to identify what hypothesized neurological networks behave differently across groups. This would allow direct comparisons of components across subjects instead of comparing properties of subject connectivity.

The approach presented here circumvents many problems that otherwise make classification based on neuroimaging data difficult. First we perform dimension reduction using a method, ICA, that extracts discriminating features of the images automatically. ICA can be seen as an element from a class of dimension-reduction methods that effectively extract basis functions that describe the images in a compact manner. Although there were 125 total possible independent components within a randomly selected normal subject, the top 10 independent components sorted by variance explained cumulatively were able to explain roughly 27.0% of the total temporal variance. The independent components have the further attractive feature that the spatial signatures are reported by neuroscientists in many cases to correspond roughly to identifiable functional networks. Thus our classifier may be operating on meaningful functional architecture of the brain. Our method operates using all the independent components within a subject, so no human interpretation is required to achieve classification of the data. Because of the anatomical variability of human brains- and presumably the added variability of the presence of certain function circuits- as crucial advantage of our method is the obviation of the need for structural alignments.

5. Appendix

As the procedure was created with the free parameters of neighborhood size choice and eigendimension, we wish to see how the selection of these parameters changes the accuracy of the classifier. We also will discuss how the algorithm methods presented here relates to two popular machine-learning algorithms: ISOMAP (Tenenbaum et al. (2000)) and spectral clustering (Ng et al. (2001)).

5.1. Sensitivity to Component Number Approximation Method

The number of components was initially chosen using the Laplace Approximation to the Model Order (LAP) (Minka (2000)), which has been found previously to best estimate the number of ICAs in a subject compared to other methods such as Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and the Minimum Description Length (MDL). We will examine the impact of changing the method in which the number of independent components are selected within the Schizophrenia/Normal dataset by comparing the results using LAP to select the parameters compared to AIC and BIC.

There exists a consistent trend in the number of components extracted by criterion method used, shown in Figure 5. The AIC consistently estimates the greatest number of components, while the LAP is second, and the BIC selects the lowest number of components. Using the components extracting for each of these three methods, we will investigate the effect changing the criterion has on classification accuracy using Method 1 and Method 2 for the Schizophrenia/Normal Dataset.

Figure 5. Number of Components Extracted by Selection Method.

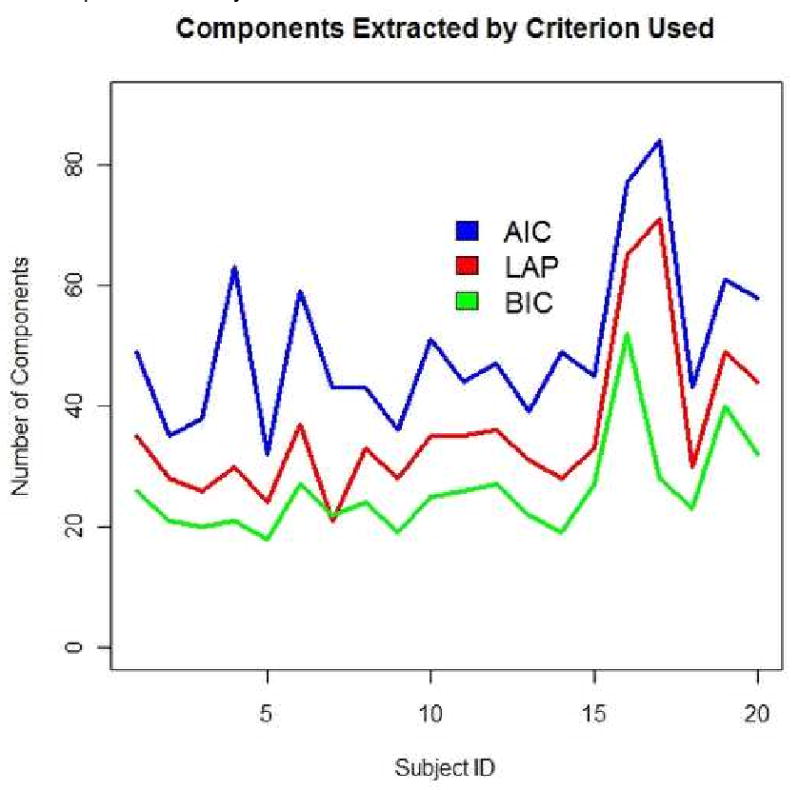
Changing the estimation method yields lower classification methods for both criteria using Method 1, yet yields slightly better results for BIC than LAP in Method 2, as shown in Table 4. As Method 2 is a biased estimate of the testing error because of its extreme use of parameter optimization, this result may be a result of overfitting. As the LAP method has previously been shown to be the best manner of estimating the number of component sources, it appropriately yields the highest average accuracy over the other selection methods of AIC and BIC.

5.2. Missclassification Error Rates

The missclassification rate by category is shown for both datasets using the optimal model selected in Method 1.

For the Alzheimer's/Old/Young dataset, the easiest category to identify was Old, while the most difficult category to identify was Alzheimer's in Table 8.

Table 8.

Missclassification Matrix

Variable	Young	Old	Alzheimers	Classification Error
Young	9	2	3	35.7%
Old	1	11	2	21.4%
Alzheimer's	2	4	7	46.2%

The missclassification matrix for the bivariate Schizophrenia/Normal classification run shows that the easiest class to identify was the Normal category, while the most difficult was the Schizophrenia class in Table 9.

Table 9.

Missclassification Matrix

Variable	Schizophrenic	Normal	Classification Error
Schizophrenic	4	2	33.3%
Normal	2	12	16.7%

5.3. Relationship to Existing Methods

5.3.1. Independent Components Analysis (ICA)

The methods presented here are largely dependent upon the initial step of dimension reduction, where ICA is used to decompose the data into source signals.

ICA operates under the assumption that an observation x is actually a linear combination of independent source signals s_i such that x = As (Hyvärinen and Oja (2000)). The source signals are assumed to be non-Gaussian, because if they were Gaussian and independent the estimating multivariate Gaussian joint distribution would be symmetric, thus leading to source estimations that are estimable only up to orthogonal rotations. The algorithm used for this analysis, FAST-ICA, estimates the source signals by maximizing the negentropy using Newton's method.

5.3.2. ISOMAP

This classification method uses concepts from the ISOMAP algorithm (Tenenbaum et al. (2000)) which transforms a Euclidean distance matrix into a geodesic distance matrix before projecting the data on the principal eigenvectors corresponding to the principal eigenvalues. ISOMAP can be understood as a geodesic transformation of a distance matrix followed by traditional multidimensional scaling. While spectral classification transforms the distance matrix using geodesic distances, spectral classification uses the eigenvalues of the primary dimensions for classification rather than using the principal eigenvectors for projection. Calculating the geodesic distances transforms the original distance matrix into a weighted adjacency matrix by using nearest neighbors to determine adjacency.

5.3.3. Spectral Clustering

Spectral Clustering procedures group points using on the spectral properties of the Laplacian matrix of a graph (Ng et al. (2001)). For a weighted adjacency matrix W_(n,n) that gives the weighted connections for n points, the degree of a point is defined as $d_i={\sum }_{j=1}^n{w}_{ij}$. If two points i and j are not connected, w_ij = 0. For a set of n points the degree matrix D_(n,n) is a diagonal matrix where d_i,j = degree(i) if i = j, and 0 otherwise. The adjacency matrix A_(n,n) describes the connectivity of a graphs, where a_i,j = 1 if points i and j are connected, and 0 otherwise. The Laplacian of a graph then is computed as L = D − A. Spectral clustering operates by extracting the eigenvectors of L that correspond to the minimum eigenvalues and creating a matrix V with the columns of V corresponding to the eigenvectors of L. Points y_i are constructed by taking the rows of V and are clustered into a predetermined number of k groups using the k-means clustering technique.

Spectral Classification differs from Spectral Clustering by using a spectral decomposition of the weighted adjacency matrix W instead of the Laplacian L of W. The principal eigenvalues are used for classification in Spectral Classification, while the minimal eigenvectors are used for clustering in Spectral Clustering.