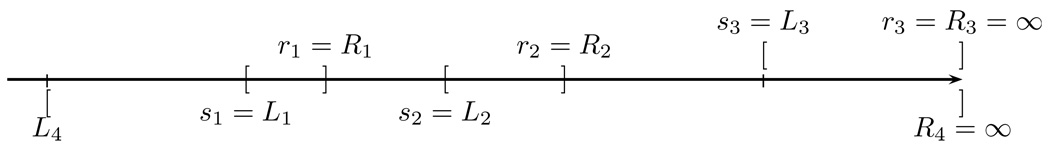A Semiparametric Regression Cure Model for Interval-Censored Data

Abstract

Motivated by medical studies in which patients could be cured of disease but the disease event time may be subject to interval censoring, we presents a semiparametric non-mixture cure model for the regression analysis of interval-censored time-to-event datxa. We develop semiparametric maximum likelihood estimation for the model using the expectation-maximization method for interval-censored data. The maximization step for the baseline function is nonparametric and numerically challenging. We develop an efficient and numerically stable algorithm via modern convex optimization techniques, yielding a self-consistency algorithm for the maximization step. We prove the strong consistency of the maximum likelihood estimators under the Hellinger distance, which is an appropriate metric for the asymptotic property of the estimators for interval-censored data. We assess the performance of the estimators in a simulation study with small to moderate sample sizes. To illustrate the method, we also analyze a real data set from a medical study for the biochemical recurrence of prostate cancer among patients who have undergone radical prostatectomy. Supplemental materials for the computational algorithm are available online.

1. INTRODUCTION

Medical advancements have made it possible for patients to be cured of certain types of diseases. Monitoring for a non-fatal disease event, such as cancer biochemical recurrence or AIDS drug resistance, is usually carried out through periodic clinical visits of patients (Lindsey and Ryan, 1998). The exact time of the disease event is only known to have occurred during two consecutive clinical visits if it did happen; however, a complication is that the disease event may never happen because the patient can be cured of the disease. This type of interval-censored event-time data with possibility of cure is commonly encountered in medical studies, especially in follow-up studies when the cure of non-fatal event is of clinical interest.

For example, it is of routine practice to monitor serum prostate-specific antigen (PSA) for cancer biochemical recurrence among patients who have undergone radical prostatectomy for their clinically localized prostate cancer. Radical prostatectomy removes the entire prostate gland and presumably all tumor cells. Patients who are free of PSA for two to three years after surgery are generally considered of being cured of biochemical recurrence because the operation has successfully removed all PSA-generating tumor cells (Dillioglugil et al., 1997; Pound et al., 1999). However, PSA may reappear in serum after surgery, which is called biochemical recurrence, indicating the operation is not success and the cancer has come back. Investigators would like to know why some patients are cured of the biochemical recurrence but not the others, and how these relate to patient’s baseline characteristics such as cancer clinical stage and tumor histology. During the follow-up, biochemical recurrence is found out by detectable PSA level in serum as ascertained at periodic clinic visits for about every three months after surgery. The actual time of biochemical recurrence is only known to have occurred between two consecutive visits, or may not even happen for some patients who are cured of the disease. It is therefore of great interest to develop new method for analyzing the probability of cure for the interval-censored data in the regression-analysis framework for including the patient baseline characteristics.

Extensive statistical literature has been devoted to interval-censored data, but without incorporating the possibility of cure. The nonparametric maximum likelihood estimator (NPMLE) for the distribution function for interval-censored data was first studied by Peto (1973) and then by Turnbull (1976) using a self-consistency algorithm. Groeneboom and Wellner (1992) proposed an iterative convex minorant algorithm for current status data and case-2 interval-censored data. Wellner and Zhan (1997) discussed some efficient algorithms for obtaining the NPMLE for these cases. Strong consistency of the NPMLE was proved for interval-censored data under a L₁ topology (Schick and Yu, 2000; Yu et al., 2001) and under the Hellinger metric (van der Vaart and Wellner, 2000). Semiparametric regression methods for interval-censored data have been investigated for the proportional hazards model (Finkelstein, 1986), the proportional odds model (Rabinowitz et al., 1995), and the accelerated failure time model (Betensky et al., 2001). Semiparametric models have also been proposed for regression analysis of current status data (Huang, 1996; Rossini and Tsiatis, 1996; Lin et al., 1998; Tian and Cai, 2006). In addition, Lam and Xue (2005) considered a mixture cure model for current status data using the estimating equation approach.

Two major approaches to model the cure rate are the mixture cure model and the non-mixture cure model (Chen et al., 1999). The mixture cure model is a mixture of two separate regression models for the cure rate of the cured population and the survival function for the non-cured population, which has been investigated extensively in the literature (Berkson and Gage, 1952; Yamaguchi, 1992; Taylor, 1995; Maller and Zhou, 1996; Sy and Taylor, 2000; Li et al., 2007, among others). Chen, Ibrahim and Sinha (1999) pointed out that the mixture cure model did not maintain the assumed survival model structure, e.g. proportional hazards, for the whole population. As an alternative, the non-mixture cure model was proposed to keep the proportional hazards structure for the whole population, while allowing for a straight-forward interpretation of the covariate effects on the probability of cure (Tsodikov, 1998; Chen et al., 1999; Tsodikov et al., 2003). As described by Chen et al. (1999) and Zeng et al. (2006), the non-mixture cure model has a biological interpretation of tumor cell growth, for which the model is also called the promotion time cure model. The works for both the mixture and the non-mixture cure models are largely based on right-censored data, not on interval-censored data.

In this article, we consider the regression analysis of interval-censored data for a semiparametric non-mixture cure model. Let T be a nonnegative random variable representing the event time and let Z be the vector of covariates. The survival function of T conditional on the covariate Z is assumed to satisfy the following cure model:

$$S(t|\mathit{Z})=P(T\ge t|\mathit{Z})=\text{exp}\left(-e^{\alpha +\beta \prime \mathit{Z}}F(t)\right),$$ (1)

where (α, β) are the regression coefficients, and F is a completely unspecified cumulative distribution function. For right-censored data, Tsodikov (1998) considered a cure model with a bounded function F, where the intercept is not allowed. The regression model (1) is a natural structure to keep the proportional hazards assumption while allowing a nonzero probability of cure as t → ∞. When F is an unbounded cumulative hazard function, the model becomes the Cox proportional hazards model by setting α = 0. Letting F be bounded by 1, we will show that the model (1) is identifiable and leads to an improper survival function.

The paper is organized as follows. In Section 2, we describe the model, the identifiability issue and the likelihood function. In Section 3, we develop the maximum likelihood estimation (MLE) based on an expectation-maximization (EM) approach for interval-censored data. The computation utilizes the expectation conditional-maximization (ECM) algorithm of Meng and Rubin (1993), which alternates the M-step for (α, β) and the M-step for F in addition to the E-step. The M-step for F is the nonparametric MLE, which imposes challenge for numerical calculation. We apply a convex optimization method to develop a self-consistency-type algorithm in the spirit of Turnbull (1976). In Section 4, we prove strong consistency of the MLE estimators under the Hellinger distance using the modern empirical processes of van der Vaart and Wellner (1996). In Section 5, we describe the simulation studies to evaluate the performance of the proposed method, and illustrate the method through analysis of data for serum PSA recurrence among prostate cancer patients. We provide concluding remarks in Section 6 and the technical proofs in Supplemental Materials.

2. MODEL AND LIKELIHOOD

2.1. The Model

Under the non-mixture cure model (1), the overall survival distribution falls in the framework of a proportional hazards model with the cumulative hazard function e^αF(·). The intercept α in the regression part of the cure model allows for the easy interpretation of covariate effects while keeping a exible baseline function. When t → ∞, the probability of cure for a given Z is exp(−e^α+β′Z), the complimentary log-log regression. The proposed method can be easily extended to a general regression model by replacing exp(·) with a known positive convex function. When Z = 0, the baseline cure rate is simply exp (−e^α), which depends on the intercept α.

Let E₀ denote the expectation under the true values α₀, β₀ and F₀ that satisfy model (1). We assume that $E_0[\text{exp}({\mathit{\beta }}_0^{\prime }\mathit{Z})]<\infty$ and |α₀| < ∞. It is clear that the baseline survival function S₀(t) = exp(−F₀(t)) is not a proper survival function because lim_t→∞ S₀(t) = 1/e. The marginal survival function P₀(T ≥ t) = E₀[P₀(T ≥ t|Z)] is also not a proper survival function by Jensen’s inequality ${\text{lim}}_{t\to \infty }{P}_0(T\ge t)=E_0[\text{exp}(-\text{exp}({\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z}))]\ge \text{exp}\{-E[\text{exp}({\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z})])\}$, always greater than 0.

In order to ensure the identifiability of model (1), we require F to be a regular distribution function with lim_t→∞ F(t) = 1. To show the identifiability, let (α_*, β_*, F_*) be a set of parameters that satisfies (1), i.e., $S_{*}(t|\mathit{Z})=\text{exp}[-e^{{\alpha }_{*}+{\mathit{\beta }}_{*}^{\prime }\mathit{Z}}{F}_{*}(t)]$. Fixing ω in a set of probability 1 in the underlying probability space, then S_*(t|Z(ω)) = S(t|Z(ω)) implies that for each t ∈ (0,∞), $e^{{\alpha }_{*}+{\mathit{\beta }}_{*}^{\prime }\mathit{Z}(\omega )}{F}_{*}(t)=e^{\alpha +\mathit{\beta }\prime \mathit{Z}(\omega )}F(t)$. Letting t → ∞ yields $e^{{\alpha }_{*}+{\mathit{\beta }}_{*}^{\prime }\mathit{Z}(\omega )}=e^{\alpha +\mathit{\beta }\prime \mathit{Z}(\omega )}$ because lim_t→∞ F_*(t) = lim_t→∞ F(t) = 1. This implies that ${\alpha }_{*}+{\mathit{\beta }}_{*}^{\prime }\mathit{Z}=\alpha +\mathit{\beta }\prime \mathit{Z}$ with probability 1. Suppose that if P(b′Z = a) = 1 for a real number a and any real vector b, then a = 0 and b = 0. This implies that α_* = α and β_* must be equal to β. Hence, F_*(t) = F(t) for each t ∈ (0, ∞).

2.2. Data and Likelihood

We consider a setting in which the event time T may not be observed exactly, but instead is known to have occurred in an interval [L, R]. Here, L is the latest examination time before the event, and R is the earliest examination time after the event, where R = ∞ if the event has not happened before the last follow-up. The data are n i.i.d copies of (L, R, Z), denoted by (L_i, R_i, Z_i) for patient i, where L_i < R_i for i = 1, ⋯, n. Denote θ′ = (α, β′) and ${\tilde{\mathit{Z}}}_i^{\prime }=(1,{\mathit{Z}}_i^{\prime })$. Then model (1) can be re-expressed as S_Zi (t) = S_θ,F (t|Z_i) = exp (−e^θ′Z̃_iF(t)), where the function SZ_i (t) is left continuous, with right limits. If R_i < ∞,

$$P_{\mathit{\theta },F}(L_i\le T_i\le R_i|{\mathit{Z}}_i)=\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(L_i-)\right)-\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(R_i+)\right),$$

where P_θ,F is the probability measure under the parameters θ and F. If R_i = ∞, then there are two possibilities for the ith patient: the patient is cured, or the event of interest for that patient occurs after the last examination time, which can be calculated by

$$P_{\mathit{\theta },F}(L_i\le T_i\le \mathrm{\infty }|{\mathit{Z}}_i)=e^{-\text{exp}(\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i)F(L_i-)}.$$

The likelihood function for the n observed interval-censored data is then

$$L_n(\mathit{\theta },F)={\displaystyle \prod _{i=1}^n{\left[e^{-\text{exp}(\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i)F(L_i-)}-e^{-\text{exp}(\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i)F(R_i+)}\right]}^{1(R_i<\mathrm{\infty })}{\left[e^{-\text{exp}(\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i)F(L_i-)}\right]}^{1(R_i=\mathrm{\infty })}.}$$ (2)

Note that unlike the standard Cox model, the full likelihood function derived under the cure model (1) needs to account for the probability of cure.

To obtain the maximum likelihood estimators (MLE) based on (2) for (θ, F), we now show that the nonparametric MLE for F is only unique up to an equivalent class. This derivation is an extension of the method of Peto (1973) and Turnbull (1976) for the NPMLE of interval-censored data without covariates. Define a finite number of disjoint intervals ${\{[s_j,r_j]\}}_{j=1}^{m+1}$ constructed as follows: s_j ∈ {L_i : i = 1, ⋯, n} and r_j ∈ {R_i : i = 1, ⋯, n}, the interval (s_j , r_j) does not contain any members of {L_i,R_i, i = 1, ⋯, n}, and s₁ ≤ r₁ < s₂ ≤ r₂ ⋯ < s_m ≤ r_m < s_m+1 < r_m+1 = ∞. It is possible that s_j = r_j , j = 1, ⋯,m. Here s_m+1 is the observed longest follow-up time. Let $\mathcal{C}={\cup }_{j=1}^m\left[s_j,r_j\right]$. Note that function x ↦ e^{−exp(θ′Z)x} is nonincreasing in x.

We first examine the maximization of the likelihood function with respect to F for an arbitrary but fixed θ. For given data and fixed θ, the maximization of the likelihood function (2) depends on F only through its values on 𝒞 but not on the outside of 𝒞. For fixed values of ${\{F(s_j-),F(r_j+)\}}_{j=1}^m$, the likelihood function does not change with the value of F in (s_j, r_j). Let p_j = F(r_j+) − F(s_j−) for j = 1, ⋯, m. Then the vector p ≡ (p₁, ⋯, p_m) where ${\displaystyle {\sum }_{j=1}^m{p}_j=1\text{and}{p}_j\ge 0}$ defines an equivalence class of cumulative distribution functions that are constant outside 𝒞. Thus, we can limit our search for the MLE of F in the equivalence class of the following step functions that have right-hand limits and are continuous from the left:

$$t\mapsto {\displaystyle \sum _{j=1}^m{p}_{j}1(t\ge r_j),}$$

, with the constraint ${\displaystyle {\sum }_{j=1}^m{p}_j=1}$. Without loss of generality, we still denote the function by F in the equivalence class. The function is continuous from the right F(t) = F(t+) and takes a constant value on [r_j , s_j+1], which is equal to F(r_j) for j = 1, ⋯, m. Further, F(0) = 0 and F(r_m) = F(s_m+1) = 1. The function F has jumps of size p₁, ⋯, p_m right before r₁, ⋯, r_m, respectively. Subsequently, the survival function of T given Z_i can be written as:

$$S_{{\mathit{Z}}_i}(t)=S_{\mathit{\theta },F}(t|{\mathit{Z}}_i)=\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(t)\right)=\text{exp}\left[-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{\displaystyle \sum _{j=1}^m{p}_{j}1(t\ge r_j)}\right].$$ (3)

In particular, for j = 1, ⋯,m, S_Zi(s_j−) = exp [−e^θ′Z̃i(p₀ + p₁ + ⋯ + p_j−1)], and

$$S_{{\mathit{Z}}_i}(r_j+)=\text{exp}\left[-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}(p_0+p_1+\cdots +p_j)\right]=S_{{\mathit{Z}}_i}(s_{j+1}),$$

where p₀ ≡ 0 for the convenience of notation.

The likelihood function (2) of the observed data is now a function of the parameters p = (p₁, ⋯, p_m) and θ. Let δ_ij indicate whether [s_j, r_j ] belongs to [L_i, R_i] for j = 1, ⋯, m+1. In particular, δ_i,m+1 = 1 indicates whether the ith person has completed the follow-up without the occurrence of the event (i.e. R_i = ∞). Using the above notation, we write the log-likelihood function of (2) as

$$l_n(\mathit{\theta },F)\equiv l_n(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\text{log}\left\{{\displaystyle \sum _{j=1}^m{\delta }_{\mathit{\text{ij}}}(S_{{\mathit{Z}}_i}(s_j-)-S_{{\mathit{Z}}_i}(r_j+))+{\delta }_{i,m+1}{S}_{{\mathit{Z}}_i}(s_{m+1})}\right\}.}$$ (4)

Since we assume a cure in our application, the data have at least one event-free subject (R_i = ∞) whose follow-up time is longer than r_m. It follows that the term δ_i,m+1S_Zi(s_m+1) does not vanish from (4). The likelihood contribution of event-free subjects is determined by comparing their follow-up times with r_m. Only the subjects who are event-free and have L_i > r_m contribute to the likelihood as the cured subjects. The random times {r_m, s_m+1} essentially serve the same role as the deterministic “cure threshold” proposed by Zeng, Yin, and Ibrahim (2006) for right-censored data. As with all cure modeling, the viability of this model requires the follow-up of a study to be sufficiently long so that s_m+1 is large enough for some subjects to be considered cured in the given scientific context.

Due to the complexity of data notation, we use a hypothetical data example with 4 subjects to illustrate the derivation of the equivalent class for the likelihood function as depicted in Figure 1. The cases for patients i = 1, 2, 3 are straightforward. We only describe the case for patient i = 4, where δ_4,1 = δ_4,2 = δ_4,3 = 1. The contribution of patient i = 4 to the log-likelihood function (4) is ${\displaystyle {\sum }_{j=1}^2{\delta }_{4,j}(S_{{\mathit{Z}}_4}(s_j-)-S_{{\mathit{Z}}_4}(r_j+))+{\delta }_{4,3}{S}_{{\mathit{Z}}_4}(s_3)}$ which is equal to S_Z4(s₁−) in the equivalent class for the likelihood function (2).

Figure 1.

A hypothetic example with n = 4. Each pair of brackets [ ] corresponds to a patient data.

In summary, we have derived the nonparametric MLE F̂_n(θ) = argmax_Fl_n(θ, F) by an equivalence class argument for a fixed but arbitrary θ. The MLE for θ can then be obtained by maximizing the profile log-likelihood θ ↦ l_n(θ, F̂_n(θ)), which is equivalent to maximizing the function θ ↦ sup_F L_n(θ, F). Maximizing the profile log-likelihood yields the semiparametric maximum likelihood estimator (θ̂_n, F̂_n).

3. COMPUTATIONAL ALGORITHM AND PROPERTIES

We now develop the computational algorithm to obtain the MLE from (4). It is numerically difficult to maximize the log-likelihood function (4), while the dimension of F̂_n can increase with the sample size n. To overcome this dificulty, we first consider an EM method for interval-censored data as an extension of the method for the nonparametric estimation when the covariates are absent (Kalbeisch and Prentice, 2002, page 80–81). The resulting expected log-likelihood function has the appealing property of being concave. We then replace the M-step by two conditional M-steps that alternate the M-step for θ and the M-step for p, which allow us to utilize diffierent optimization techniques for maximizing the expected log-likelihood function for θ and p, separately. This is essentially the ECM algorithm of Meng and Rubin (1993), but we further exploit convex optimization techniques for a numerically stable and efficient algorithm for the M-step. Our algorithm forces the search of p in the interior of a constrained convex parameter space for obtaining MLE.

3.1. EM Method: Expectation-step

To simplify the notation in (4), for i = 1, ⋯, n, j = 1, ⋯, m, we define

$$\begin{array}{c}{\gamma }_{i,j}(\mathit{\theta },\mathit{p})\equiv S_{{\mathit{Z}}_i}(s_j-)-S_{{\mathit{Z}}_i}(r_j+)=S_{{\mathit{Z}}_i}(s_j)\left[1-\text{exp}\left(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\right)\right]>0,\hfill \\ {\gamma }_{i,m+1}(\mathit{\theta },\mathit{p})\equiv {\gamma }_{i,m+1}(\mathit{\theta })=S_{{\mathit{Z}}_i}(s_{m+1})=\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\right).\hfill \end{array}$$

The log likelihood function (4) is then

$$l_n(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\text{log}\left({\displaystyle \sum _{j=1}^{m+1}{\delta }_{\mathit{\text{ij}}}{\gamma }_{\mathit{\text{ij}}}(\mathit{\theta },\mathit{p})}\right)},$$ (5)

where ${\displaystyle {\sum }_{j=1}^{m+1}{\gamma }_{i,j}(\mathit{\theta },\mathit{p})=1}$ for each i = 1, ⋯, n.

By the equivalence of (2) and (4), the interval-censored data are now represented by Δ_i = (δ_i,1, ⋯, δ_i,m, δ_i,m+1) for i = 1, ⋯, n. We may view Δ_i as the incomplete data arising from an (m+1)-class multinomial distribution with index 1. Specifically, we consider the complete data as denoted by X = {X_i ≡ (X_i,1, ⋯, X_i,m,X_i,m+1), Z_i : i = 1, ⋯, n}. Conditional on the covariate Z_i, X_i is assumed to have an m+1 class multinomial distribution with index 1, and for j = 1, ⋯, m + 1,

$$\text{Pr}(X_{\mathit{\text{ij}}}=1|{\mathit{Z}}_i)={\gamma }_{\mathit{\text{ij}}}(\mathit{\theta },\mathit{p})>0.$$

The X_i for i = 1, ⋯, n are assumed to be independent of each other so the complete data log-likelihood is

$$l_X(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^m{X}_{\mathit{\text{ij}}}\left[\text{log}{S}_{{\mathit{Z}}_i}(s_j)+\text{log}\left(1-\text{exp}(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})\right)\right]-X_{i,m+1}{e}^{\mathit{\theta }\prime {\tilde{Z}}_i}}\right\}.}$$ (6)

From the incomplete data {Δ_i, i = 1, ⋯, n}, we know that the ith outcome falls into one of the classes j as indexed by δ_ij but we do not know the specific class into which it actually falls, except for the trivial cases. For example, in Figure (1), the event for patient 4 is known to have occurred in either (s₁, r₁), (s₂, r₂) or (s₃, r₃), but in exactly which one is unknown. Under this missing mechanism, the log-likelihood of the incomplete data is identical to (4).

The E-step is to calculate the expected log-likelihood function of (6). Given data {Δ_i, Z_i : i = 1, ⋯, n} and current parameter estimation (θ^(k), p^(k)) of the k-th step,

$$X_{\mathit{\text{ij}}}^{(k)}\equiv E[X_{\mathit{\text{ij}}}|{\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)},{\mathbf{\Delta }}_i,{\mathit{Z}}_i]=\frac{{\delta }_{\mathit{\text{ij}}}{\gamma }_{\mathit{\text{ij}}}({\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)})}{{\displaystyle {\sum }_{j\prime =1}^{m+1}{\delta }_{\mathit{\text{ij}}\prime }{\gamma }_{\mathit{\text{ij}}\prime }({\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)})}}\ge 0, j=1,\cdots ,m+1.$$ (7)

Then the expected log-likelihood at the kth step is

$$\begin{array}{c}{l}^{(k)}(\mathit{\theta },\mathit{p})\equiv E(l_X(\mathit{\theta },\mathit{p})|{\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)},{\mathbf{\Delta }}_i,{\mathit{Z}}_i,i=1,\cdots ,n)\hfill \\ ={\displaystyle \sum _{i=1}^n\{{\displaystyle \sum _{j=1}^m{X}_{\mathit{\text{ij}}}^{(k)}\left[-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{\displaystyle \sum _{j\prime =1}^m{p}_{j^{\prime }}1(s_{j^{\prime }}\le s_{j-1})+\text{log}\left(1-\text{exp}(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})\right)}\right]}}\hfill \\ \hfill -X_{i,m+1}^{(k)}{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\},\end{array}$$

where s₀ is set to be −∞ for notational convenience. Denote $c_{\mathit{\text{ij}}}^{(k)}={\displaystyle {\sum }_{j\prime =1}^m{X}_{\mathit{\text{ij}}\prime }^{(k)}1(s_j\le s_{j\prime -1})\ge 0}$, which is independent of the parameters θ and p. The expected log-likelihood can be expressed as

$$l^{(k)}(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^m\left[-c_{\mathit{\text{ij}}}^{(k)}{p}_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}+X_{\mathit{\text{ij}}}^{(k)}\text{log}\left(1-\text{exp}(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})\right)\right]-X_{i,m+1}^{(k)}{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}}\right\}}.$$ (8)

The following proposition shows that the expected log-likelihood is a concave function with respect to both θ and p_j > 0, j = 1, ⋯, m, which implies that any local maximizer of the function is also a global maximizer on the set defined by ${\displaystyle {\sum }_{j=1}^m{p}_j=1,p_j>0,j=1,\cdots ,m}$ and θ in an open convex set.

Proposition 1

The function l^(k)(θ, p) is a concave function for each p_j > 0, j = 1, ⋯, m, and for each θ that belongs to an open compact set.

Proof

The function l^(k) (θ, p) is a summation of functions of (θ, p) ↦ −p_je^θ′Ẑ_i and (θ, p) ↦ log(1−exp(−p_je^θ′Z_i)), which are concave by noting that (x, y) ↦ −x exp(y) is concave and (x, y) ↦ log(1 − exp(−xe^y)) is strictly concave for x > 0 and −∞ < y < ∞, respectively. A summation of concave functions is still a concave function.

The M-step will be followed to maximize the expected log-likelihood function using the ECM algorithm: the maximization with respect to θ for fixed p, and the maximization with respect to p for fixed θ, iteratively.

3.2. Maximization Step for Covariate Coefficients θ

The number of covariates is often much smaller than n, so it is straightforward to maximize l^(k)(θ, p) directly with respect to θ for a fixed p, for example, by a quasi-Newton method such as the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm (Boyd and Vandenberghe, 2004, Chapter 9). The first partial derivative of l^(k)(θ, p) with respect to θ is

$${\nabla }_{\mathit{\theta }}{l}^{(k)}(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^m\left[-c_{\mathit{\text{ij}}}^{(k)}+\frac{X_{\mathit{\text{ij}}}^{(k)}}{\text{exp}(p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})-1}\right]p_j-X_{i,m+1}^{(k)}}\right\}{\tilde{\mathit{Z}}}_i{e}^{\mathit{\theta }\mathrm{\prime }{\tilde{\mathit{Z}}}_i}.}$$

The second partial derivative of l^(k)(θ, p) with respect to θ is

$$\begin{array}{c}{\nabla }_{\mathit{\theta }}^2{l}^{(k)}(\mathit{\theta },\mathit{p})\hfill \\ \hfill \hspace{1em}=-{\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^m\left[c_{\mathit{\text{ij}}}^{(k)}+\frac{X_{\mathit{\text{ij}}}^{(k)}\left[1+\text{exp}(p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})(p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}-1)\right]}{{[\text{exp}(p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})-1]}^2}\right]p_j+X_{i,m+1}^{(k)}}\right\}{\tilde{\mathit{Z}}}_i{\tilde{\mathit{Z}}}_i^{\prime }{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}.}\end{array}$$

We may apply the inequality 1 − x < e^−x for x < 1 to confirm that the gradient is positive definite whenever the covariate matrix ${\mathbf{Z}}_i{\mathbf{Z}}_i^{\prime }$ is positive definite. For every i, j, the second term in the above display is always nonnegative when p_je^θ′Ẑ_i ≥ 1. When p_je^θ′Ẑ_i < 1, this term is still positive by noting that p_je^θ′Ẑ_i − 1 > −exp(−p_je^θ′Ẑ_i). Proposition 1 also infers that for each fixed p, l^(k) (θ, p) is strictly concave when the matrix $n^{-1}{\displaystyle {\sum }_{i=1}^n{Z}_i{Z}_i^{\prime }}$ is positive definite and θ is in a bounded convex set ℬ in ℝ^d+1. The concavity implies that a local maximizer is also the unique global maximizer.

3.3. Maximization Step for F: Optimality Conditions

The next step in the ECM algorithm is to maximize the expected log-likelihood function with respect to p conditional on θ. Although the maximization in p is numerically challenging, we note that the function p ↦ l^(k) (θ, p) is strictly concave by Proposition 1 when not all p_j ∈ [0, 1] are zero for j = 1, ⋯, m, and not all $X_{\mathit{\text{ij}}}^{(m)}$ are zero for j = 1, ⋯, m. Thus, if we can find a local maximizer for p, it is also the unique global maximizer for p in the conditional maximization step. We first explore the optimality conditions for the maximization step for p by convex optimization techniques (Boyd and Vandenberghe, 2004, Section 5.5). To develop a numerically efficient and stable algorithm, we apply the primal-dual interior-point method for constrained optimization (Boyd and Vandenberghe, 2004, page 609–613), which yields a self-consistency algorithm for p in the sense of Turnbull (1976) and keeps the point mass p_j positive.

For notational convenience, denote for j = 1, ⋯, m,

$$a_j={\displaystyle \sum _{i=1}^n\left[e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{\displaystyle \sum _{j\prime =1}^m{X}_{\mathit{\text{ij}}\prime }^{(k)}1(s_j\le s_{j\prime -1})}\right],}$$

where $X_{\mathit{\text{ij}}}^{(k)}$ is defined in (7) and k is the index for the current EM iteration. Here both θ and k are fixed, so a_j, e^θ′Ẑ_i and $X_{\mathit{\text{ij}}}^{(k)},i=1,\cdots ,n,j=1,\cdots ,m$, are positive constants in the maximization step for F. Denote a = (a₁, ⋯, a_m)′. Note that the last term in (8) is not a function of p, so the part in the expected log-likelihood that involves p is

$$f(\mathit{p})\equiv -{\mathit{a}}^T\mathit{p}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{X}_{\mathit{\text{ij}}}^{(k)}\text{log}\left[1-\text{exp}(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{p}_j)\right],}}$$

with the constraint that ${\displaystyle {\sum }_{j=1}^m{p}_j=1}$ and 0 ≤ p_j ≤ 1 j = 1, ⋯, m. Because f(p) is strictly concave in p, the maximization of f becomes a concave optimization problem with constraints:

$$\text{max}f(\mathit{p})\hspace{1em}\text{subject} \text{to}{\displaystyle \sum _{j=1}^m{p}_j=1,\text{and}}{p}_j\ge 0,\hspace{1em}\text{for}j=1,\cdots ,m.$$ (9)

The first-order partial derivative of f with respect to p_j is given by

$${\dot{f}}_j(\mathit{p})=\frac{\partial }{\partial p_j}f(\mathit{p})=-a_j+{\displaystyle \sum _{i=1}^n\frac{X_{\mathit{\text{ij}}}^{(k)}{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}}{\text{exp}(e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{p}_j)-1}\hspace{1em}\text{for}j=1,\cdots ,m.}$$

The second-order partial derivative of f with respect to p_j is given by

$${\ddot{f}}_j(\mathit{p})=\frac{{\partial }^2}{\partial p_j^2}f(\mathit{p})=-{\displaystyle \sum _{i=1}^n\frac{X_{\mathit{\text{ij}}}^{(k)}{e}^{2\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\text{exp}(e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{p}_j)}{{(\text{exp}(e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{p}_j)-1)}^2}\hspace{1em}\text{for}j=1,\cdots ,m.}$$

The second-order partial derivative of f with respect to p_j and p_j′ is zero for j ≠ j′, j, j′ = 1, ⋯, m, i.e., ∂²/∂p_jp_j′f(p) = 0. The Hessian matrix ∇² f is thus a diagonal matrix, which we will exploit to derive a simple and efficient algorithm.

First we characterize the optimal solution of the concave function with the Lagrangian function. Let ν and τ_j, j = 1, ⋯, m be the Lagrange multipliers for the equality constraint and the inequality constraint, respectively. Let τ = (τ₁, ⋯, τ_m) and 1 = (1, ⋯, 1)^T. The Lagrange function with parameters τ and ν for the constrained maximization problem (9) is Γ(p, τ, ν) = f(p) + τ^T p + ν(1 − 1^T p). For a concave optimization, the necessary and sufficient conditions for a point p* to be the optimal solution are the Karush-Kuhn-Tucker (KKT) conditions (Boyd and Vandenberghe, 2004, page 243–244). Specifically, a point p* in [0, 1]^m, ${\mathit{\tau }}^{*}=({\tau }_1^{*},\cdots ,{\tau }_m^{*})$ in ℝ^m and ν* in ℝ is an optimal solution if and only if

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=1}^m{p}_j^{*}=1,}& p_j^{*}\ge 0, {\tau }_j^{*}\ge 0, {\tau }_j^{*}{p}_j^{*}=0,\hfill \\ \hfill {\dot{f}}_j({\mathit{p}}^{*})+{\tau }_j^{*}-{\nu }^{*}=0,& j=1,\cdots ,m.\hfill \end{array}$$ (10)

The maximization problem now is equivalent to solving the KKT conditions to find the solution (p*, τ*, ν*) from (10). The nonlinear equations in (10) have a simple form because of the diagonal Hessian matrix. Eliminating ${\tau }_j^{*}$ from these equations, the KKT conditions become

$${\displaystyle \sum _{j=1}^m{p}_j^{*}=1, p_j^{*}\ge 0, {\nu }^{*}\ge {\dot{f}}_j({\mathit{p}}^{*})},\hspace{1em}\left[{\nu }^{*}-{\dot{f}}_j({\mathit{p}}^{*})\right]p_j^{*}=0,j=1,\cdots ,m.$$

If $p_j^{*}=0$, then ḟ_j(p*) = ∞, which is impossible by the second inequality in the above display. Thus, $p_j^{*}>0$, and the maximizers p* and ν* must satisfy:

$${\dot{f}}_j({\mathit{p}}^{*})-{\nu }^{*}=0, {\displaystyle \sum _{j=1}^m{p}_j^{*}=1, \text{and} p_j^{*}>0,\hspace{1em}j=1,\cdots ,m.}$$

This implies that $p_j^{*}$ must be less than 1 because of the constraint ${\displaystyle {\sum }_{j=1}^m{p}_j^{*}=1}$. The KKT conditions are the necessary and sufficient conditions for the maximizers to satisfy our constrained convex maximization. The sufficient condition suggests that the initial values start from the “interior”, i.e., 0 < p_j < 1 for each j. The solutions p* and ν* are found directly from the equations for the equality constraint, while the interior-point method forces the inequality constraints $0<p_j^{*}<1,j=1,\cdots ,m$. The necessary KKT conditions infer that the interior point constraints continue to hold strictly for each ECM iteration.

3.4. Maximization Step for F: Self-Consistent Algorithm

We now describe the details of the algorithm for the maximization step of (9) using the primal-dual interior-point method, which avoids using a generic computer maximizer. The key step is to apply Newton’s method to solve the nonlinear equations (10) for the modified KKT conditions with a scalar parameter η > 0 that controls the inequality constraints. Specifically, Newton’s method approximates the nonlinear equations by the Taylor’s expansion and solves the following equations for the Newton steps (Δp, Δτ, Δν):

$$\left[\begin{array}{ccc}{\nabla }^{2}f(\mathit{p})& \mathit{I}& -\mathbf{1}\\ \text{diag}(\mathit{\tau })& \text{diag}(\mathit{p})& 0\\ -{\mathbf{1}}^T& 0& 0\end{array}\right] \left[\begin{array}{c}\mathrm{\Delta }\mathit{p}\\ \mathrm{\Delta }\mathit{\tau }\\ \mathrm{\Delta }\nu \end{array}\right]=-\left[\begin{array}{c}\nabla f(\mathit{p})+\text{diag}(\mathit{\tau })-\nu \mathbf{1}\\ \text{diag}(\mathit{\tau })p-(\mathbf{1}/\eta )\mathbf{1}\\ 0\end{array}\right],$$ (11)

where ∇²f(p) is the Hessian Matrix, diag(p) is the diagonal matrix with diagonal entries p₁, ⋯, p_m, I is the identity matrix, and 1 is the vector with all components one (Boyd and Vandenberghe, 2004, page 610).

We can solve (11) explicitly for (Δp, Δτ, Δν) because the Hessian matrix ∇² f is diagonal

$${\ddot{f}}_j(\mathit{p})\mathrm{\Delta }{p}_j+\mathrm{\Delta }{\tau }_j-\mathrm{\Delta }\nu =-\left({\dot{f}}_j(\mathit{p})+{\tau }_j-\nu \right), j=1,\cdots ,m$$ (12)

$${\tau }_j\mathrm{\Delta }{p}_j+\mathrm{\Delta }{\tau }_j{p}_j=-({\tau }_j{p}_j-1/\eta ), j=1,\cdots ,m$$ (13)

$${\displaystyle \sum _{j=1}^m\mathrm{\Delta }{p}_j={\displaystyle \sum _{j=1}^m{p}_j-1=0.}}$$ (14)

Denote ${\tau }_j^{+}={\tau }_j+\mathrm{\Delta }{\tau }_j\text{for}j=1,\cdots ,m$, and ν⁺ = ν + Δν. Equation (12) gives

$${\tau }_j^{+}={\nu }^{+}-{\ddot{f}}_j(\mathit{p})\mathrm{\Delta }{p}_j-{\dot{f}}_j(\mathit{p}).$$ (15)

Equation (13) gives ${\tau }_j\mathrm{\Delta }{p}_j=-{\tau }_j^{+}{p}_j+1/\eta$. Plugging (15) into the equation, we get

$$\left[{\tau }_i-p_j{\ddot{f}}_j(\mathit{p})\right]\mathrm{\Delta }{p}_j=-p_j{\nu }^{+}+p_j{\dot{f}}_j(\mathit{p})+1/\eta .$$

When τ_j − p_j f̈(p) ≠ 0, we have

$$\mathrm{\Delta }{p}_j=\frac{-p_j{\nu }^{+}+p_j{\dot{f}}_j(\mathit{p})+1/\eta }{{\tau }_j-p_j{\ddot{f}}_j(\mathit{p})}.$$ (16)

Using equation (14),

$${\displaystyle \sum _{j=1}^m\frac{p_j\left[{\dot{f}}_j(\mathit{p})-{\nu }^{+}\right]+1/\eta }{{\tau }_j-p_j{\ddot{f}}_j(\mathit{p})}=0.}$$

This gives

$${\nu }^{+}=\frac{{\displaystyle {\sum }_{j=1}^m\left[\left(1/\eta +p_j{\dot{f}}_j(\mathit{p})\right)/\left({\tau }_j-p_j{\ddot{f}}_j(\mathit{p})\right)\right]}}{{\displaystyle {\sum }_{j=1}^m\left[p_j/\left({\tau }_j-p_j{\ddot{f}}_j(\mathit{p})\right)\right]}},$$

provided that the denominator is not zero. The Newton step Δp_j is then calculated by (16). After calculating ${\tau }_j^{+}$ by (15), we obtain the Newton steps Δν = ν⁺ − ν and $\mathrm{\Delta }{\tau }_j={\tau }_j^{+}-{\tau }_j$. Newton’s method is an iteration procedure. Given the current iteration (p, τ, ν), the next iteration is determined by

$$p_j\leftarrow p_j+\psi \mathrm{\Delta }{p}_j, {\tau }_j\leftarrow {\tau }_j+\psi \mathrm{\Delta }{\tau }_j, \nu \leftarrow \nu +\psi \mathrm{\Delta }\nu ,$$ (17)

where ψ is calculated by a standard backtracking line search, which further controls the inequality constraints (supplemental materials available online).

Equations (17), similar in the spirit to the self-consistent algorithm of Turnbull (1976), are explicit and simple self-updating equations. Equation (15) and Equation (16) provide accurate calculations for the Newton step (Δp, Δτ, Δν). Another computational advantage of the algorithm is that it provides a numerically stable solution to the maximization problem, even if the dimension of p is large.

3.5. Summary of the Iterative Algorithm for MLE

We now summarize the algorithm that combines the ECM algorithm with the primaldual interior-point method for obtaining the MLE for the cure model with interval-censored data:

1. Take a random initial value θ⁽⁰⁾ and a random initial value p⁽⁰⁾ that satisfies ${\displaystyle {\sum }_{j=1}^m{p}_j^{(0)}=1\text{and}{p}_j^{(0)}>0}$

2. CM1: Obtain θ^(k+1) by maximizing l^(k)(θ, p^(k)) with respect to θ,

   $$l^{(k)}(\mathit{\theta },\mathit{p})={\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^m\left[-c_{\mathit{\text{ij}}}^{(k)}{p}_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}+X_{\mathit{\text{ij}}}^{(k)}\text{log}\left(1-\text{exp}(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i})\right)\right]}-X_{i,m+1}^{(k)}{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\right\},}$$

   where for i = 1, ⋯, n, $c_{\mathit{\text{ij}}}^{(k)}={\displaystyle {\sum }_{j\prime =1}^m{X}_{\mathit{\text{ij}}\prime }^{(k)}1(s_j\le s_{j\prime -1})}$,

   $$\begin{array}{cc}\hfill {\gamma }_{\mathit{\text{ij}}}(\mathit{\theta },\mathit{p})& =S_{{\mathit{Z}}_i}(s_j)\left[1-\text{exp}\left(-p_j{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\right)\right],\hspace{1em}j=1,\cdots ,m,\hfill \\ \hfill {\gamma }_{i,m+1}(\mathit{\theta },\mathit{p})& =\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}\right),\hfill \\ \hfill S_{{\mathit{Z}}_i}(s_j)& =\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}{\displaystyle \sum _{j\prime =0}^{j-1}{p}_{j^{\prime }}}\right),\hspace{1em}j=1,\cdots ,m,\hfill \\ \hfill X_{\mathit{\text{ij}}}^{(k)}& =\frac{{\delta }_{\mathit{\text{ij}}}{\gamma }_{\mathit{\text{ij}}}({\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)})}{{\displaystyle {\sum }_{j\prime =1}^m{\delta }_{\mathit{\text{ij}}\prime }{\gamma }_{\mathit{\text{ij}}\prime }({\mathit{\theta }}^{(k)},{\mathit{p}}^{(k)})}},\hspace{1em}j=1,\cdots ,m+1.\hfill \end{array}$$
3. CM2 (obtain p^(k+1) by the primal-dual interior method): given θ^(k+1), define $b_i^{(k+1)}=\text{exp}({\tilde{\mathit{Z}}}_i^{\prime }{\mathit{\theta }}^{(k+1)})$ and update for j = 1, ⋯, m,

   $$X_{\mathit{\text{ij}}}^{(k+1)}=\frac{{\delta }_{\mathit{\text{ij}}}{\gamma }_{\mathit{\text{ij}}}({\mathit{\theta }}^{(k+1)},{\mathit{p}}^{(k)})}{{\displaystyle {\sum }_{j\prime =1}^m{\delta }_{\mathit{\text{ij}}\prime }{\gamma }_{\mathit{\text{ij}}\prime }({\mathit{\theta }}^{(k+1)},{\mathit{p}}^{(k)})}}.$$
   Start with the initial value p̃ = p^(k); choose σ > 1 and τ = (τs, ⋯, τ_m) where τ_j > 0. Repeat the following to update p̃ until convergence to get p^(k+1):

   1. Determine η = σ/ξ̂, where $\widehat{\mathrm{\xi }}={\displaystyle {\sum }_{j=1}^m{\tilde{p}}_j{\tau }_j/m}$.
   2. Evaluate ${\dot{f}}_j(\tilde{\mathit{p}})={\displaystyle {\sum }_{i=1}^n{b}_i^{(k+1)}\left[\frac{X_{\mathit{\text{ij}}}^{(k)}}{\text{exp}\left(b_i^{(k+1)}{\tilde{p}}_j\right)-1}-{\displaystyle {\sum }_{j\prime =1}^m{X}_{\mathit{\text{ij}}\prime }^{(k=1)}1(s_j\le s_{j\prime -1})}\right],}$

      $$\begin{array}{cc}\hfill {\ddot{f}}_j(\tilde{\mathit{p}})& =-{\displaystyle \sum _{i=1}^n\frac{X_{\mathit{\text{ij}}}^{(k+1)}\text{exp}(2{\tilde{\mathit{Z}}}_i^{\prime }{\mathit{\theta }}^{(k+1)}\text{exp}(b_i^{(k+1)}{\tilde{p}}_j)}{{(\text{exp}(b_i^{(k+1)}{\tilde{p}}_j)-1)}^2},}\hfill \\ \hfill {\nu }^{+}& =\frac{{\displaystyle {\sum }_{j=1}^m\left[(1/\eta +{\tilde{p}}_j{\dot{f}}_j(\tilde{\mathit{p}}))/\left({\tau }_j-{\tilde{p}}_j{\ddot{f}}_j(\tilde{\mathit{p}})\right)\right]}}{{\displaystyle {\sum }_{j=1}^m\left[{\tilde{p}}_j/\left({\tau }_j^{(k)}-{\tilde{p}}_j{\ddot{f}}_j(\tilde{\mathit{p}})\right)\right]}},\hfill \\ \hfill \mathrm{\Delta }{p}_j& =\frac{{\tilde{p}}_j\left({\dot{f}}_j(\tilde{\mathit{p}})-{\nu }^{+}\right)+1/\eta }{{\tau }_j-{\tilde{p}}_j{\ddot{f}}_j(\tilde{\mathit{p}})},\hfill \\ \hfill {\tau }_j^{+}& ={\nu }^{+}-{\ddot{f}}_j(\tilde{\mathit{p}})\mathrm{\Delta }{p}_j-{\dot{f}}_j(\tilde{\mathit{p}}).\hfill \end{array}$$
   3. Update p̃, τ and ν by (17) with the standard backtracking line search as described in supplemental materials available online.

4. Repeat steps 2–3 until ‖θ^(k+1) − θ^(k)‖ + ‖p^(k+1) − p^(k)‖ < ∊₁ and the expected log-likelihood converges for a pre-specified small ∊₁ > 0.

Note that the convergence of the algorithm can be established by the general results for the constrained ECM algorithms that have been shown in Meng and Rubin (1993) and Nettleton (1999); see also Little and Rubin (2002, Theorem 8.1, page 173).

4. HELLINGER CONSISTENCY OF MLE

The technical challenge for studying the strong consistency of the MLE (θ̂_n, F̂_n) for the proposed cure model comes from interval-censored data, for which a classical approach via the Kullback-Leibler information cannot be easily applied. Instead, we prove the strong consistency of (θ̂_n, F̂_n) to the true values θ₀ and F₀ under the Hellinger distance, which provides a global consistency. The Hellinger distance is an L₂-distance between the square roots of two probability densities q₁ and q₂,

$$h(q_1,q_2)={\left(\frac{1}{2}{\displaystyle \int {(\sqrt{q_1}-\sqrt{q_2})}^{2}d\nu }\right)}^{1/2}={\left(1-{\displaystyle \int \sqrt{q_1{q}_2}d\nu }\right)}^{1/2},$$

which does not depend on the dominating measure ν. This is a true distance that satisfies h(q₁, q₂) ≤ 1 and h(q₁, q₂) = 0 if and only if q₁ = q₂ a.e. ν. For the nonparametric estimation for interval-censored data, van der Vaart and Wellner (2000) proved the strong consistency of MLE under the Hellinger distance. We extend their method to the semiparametric MLE under the cure model for a general case of interval-censored data, for which the proof is largely based on the theory of modern empirical processes (van der Vaart and Wellner, 1996, Chapter 2.4).

We first describe the setup of the general case of interval-censored data, which is similar to these described by Schick and Yu (2000) and van der Vaart and Wellner (2000), but with a modification to allow for the possibility of cure. This setup is necessary in order to take into account of the randomness of the event inspection times, but it leads to the same likelihood function (2), for which we have developed a computationally efficient algorithm for the MLE (θ̂_n, F̂_n).

Let K be a positive random integer that denotes the number of inspection times for one person, and Y_K = {Y_K,1, ⋯, Y_K,K} denote the inspection times for the event of interest, where Y_K,1 < ⋯ < Y_K,K. In practice, it is natural to assume E₀(K) < ∞. The random observation times for one person is a triangular array Y = {Y_k,j : j = 1, ⋯, k, k = 1, 2, ⋯ }, where k is the realization of K. Let Y_k = (Y_k,1, ⋯, Y_k,k) be the k-th row of the array Y with the realization denoted by y_k = (y_k,1, ⋯, y_k,k).

The event time T is only known to have occurred in one of the intervals [Y_K,j−1, Y_K,j), j = 1, ⋯, K, or [Y_K,K, Y_K,K+1], where Y_K,0 ≡ 0 and Y_K,K+1 ≡ ∞. We denote Λ_k = (Λ_k,1, ⋯, Λ_k,k+1), where Λ_k,j = 1_{[Yk,j−1,Yk,j)}(T) for j = 1, ⋯, k, and Λ_k,k+1 = 1_{[Yk,k,Yk,k+1]}(T), with the realization denoted by λ_k = (λ_k,1, ⋯, λ_k,k+1).

We now formulate the likelihood under this setup. Assume that conditional on Z, (K, Y) is independent of the event time T. We also make the noninformative inspection assumption that the distribution of (K, Y_K, Z) dose not depend on the event time T and the parameters of interest θ and F. Given Z, the conditional survival function of T follows cure model (1). Conditional on (K, Y_K) and Z, the random vector Λ_k has a multinomial distribution, i.e., (Λ_k|K, Y_K, Z) ~ Multinomial_K+1 (1, ΔS_K(Z)), where the vector

$$\mathrm{\Delta }{S}_K(\mathit{Z})\equiv (1-S(Y_{K,1}|\mathit{Z}),\cdots ,S(Y_{K,K-1}|\mathit{Z})-S(Y_{K,K}|\mathit{Z}),S(Y_{K,K}|\mathit{Z})).$$

Let V = (K, Λ_k, Y_K, Z) with the realization denoted by υ = (k, λ_k, y_k, z). Denote z̃^T = (1, z^T). The distribution of V has a version of density dP_V / dµ with respect to a dominating measure µ determined by the joint distribution of (K, Y_K, Z), which does not depend on the parameters of interest θ and F by the non-informative inspection assumption. A version of density of the distribution of V , which is the likelihood function for one observation υ that we will use, is thus given by

$$\begin{array}{c}{p}_{\mathit{\theta },F}(\mathit{\upsilon })={\displaystyle \sum _{j=1}^k{\lambda }_{k,j}\left[\text{exp}\left(-e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}F(y_{k,j-1})\right)-\text{exp}\left(-e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}F(y_{k,j})\right)\right]}\hfill \\ \hfill +{\lambda }_{k,k+1}\left[\text{exp}\left(-e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}F(y_{k,k})\right)\right].\end{array}$$ (18)

The data are n i.i.d. V ₁, ⋯, V_n copies of V , where ${\mathit{V}}_i=(K_i,{\mathrm{\Lambda }}_{K_i}^{(i)},Y_{K_i}^{(i)},{\mathit{Z}}_i)$, i = 1, ⋯, n. Define by ${\mathrm{\mathbb{P}}}_{n}g=n^{-1}{\displaystyle {\sum }_{i=1}^{n}g({\mathit{V}}_i)}$ the empirical distribution for a measurable real function g on the sample space 𝒱. The log-likelihood function for (θ, F) of Ṽ = (V ₁, ⋯, V_n) is

$$\begin{array}{c}\frac{1}{n}{l}_n(\mathit{\theta },F|\tilde{\mathit{V}})\equiv {\mathrm{\mathbb{P}}}_n(l_{\mathit{\theta },F}(\mathit{V}))=\frac{1}{n}{\displaystyle \sum _{i=1}^n\{{\displaystyle \sum _{j=1}^{K_i}{\mathrm{\Lambda }}_{K_i,j}^{(i)}\text{log}[\text{exp}(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(Y_{K_i,j-1}^{(i)}))}}\hfill \\ \hfill -\text{exp}\left(-e^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(Y_{K_i,j}^{(i)})\right)]-{\mathrm{\Lambda }}_{K_i,K_i}^{(i)}{e}^{\mathit{\theta }\prime {\tilde{\mathit{Z}}}_i}F(Y_{K_i,K_i}^{(i)})\},\end{array}$$ (19)

where

$$\begin{array}{c}{l}_{\mathit{\theta },F}(\mathit{V})={\displaystyle \sum _{j=1}^K{\mathrm{\Lambda }}_{K,j}\text{log}\left[\text{exp}\left(-e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}F(Y_{K,j-1})\right)-\text{exp}\left(-e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}F(Y_{K,j})\right)\right]}\hfill \\ \hfill -{\mathrm{\Lambda }}_{K,K+1}F(Y_{K,K})e^{\mathit{\theta }\prime \tilde{\mathit{Z}}}.\end{array}$$

The log-likelihood function (19) is same as the logarithm of the original likelihood function (2) by noting that ${\mathrm{\Lambda }}_{K_i,j}^{(i)}=1\{Y_{K_i,j-1}\le T_i<Y_{K_i,j}\},j=1,\cdots ,K_i,\text{and}{\mathrm{\Lambda }}_{K_i,K_i+1}^{(i)}=1\{Y_{K_i,K_i}\le T_i\le \mathrm{\infty }\}$. Therefore, L_i = Y_Ki,j−1 and R_i = Y_Ki,j if Y_Ki,j−1 ≤ T_i < Y_Ki,j, and if T_i ≥ Y_Ki,Ki, L_i = Y_Ki,Ki and R_i = ∞. This setup is flexible enough to allow a “data-generating” mechanism for the interval-censoring data [L_i, R_i], where the observation stops after a random number K_i of inspections. There is no need to make specific distribution assumptions about the inspection process. This setup is also convenient for the technical proof of the Hellinger consistency.

We will work with the log-likelihood function (19) to prove the Hellinger consistency, and need the following regularity conditions:

• C1. Parameter θ is restricted in a compact set Θ in ℝ^d+1, and the baseline distribution function F is in the set ℬ of all sub-distribution functions on (0, ∞).

• C2. E₀(‖Z‖₂) < ∞ for the Euclidean norm ‖ · ‖₂ in ℝ^p. For the true parameter ${\mathit{\theta }}_0,E(\text{exp}(e^{|{\mathit{\theta }}_0^{\prime }\tilde{\mathit{Z}}|}))<\mathrm{\infty }$.

• C3. The true parameter function F₀ is strictly increasing, and satisfies

  $$E_0\left\{\frac{1}{{\text{min}}_{j=1,\dots ,K}{(F_0(Y_{K,j})-F_0(Y_{K,j-1}))}^2}|K\right\}<\mathrm{\infty }.$$

Condition C3 is a technical condition for preventing E₀(1/p_θ0,F0) from escaping to infinity. It regulates the variability of the inspection process {Y_K,1, ⋯, Y_K,K}. The following theorem summarizes the strong consistency property of (θ̂_n, F̂_n). The detail of the technical proofs is provided in Supplemental Materials.

Theorem 1

Under the regularity conditions C1–C3, the maximum likelihood estimate θ̂_n and F̂_n satisfies

$$h(p_{{\widehat{\mathit{\theta }}}_n,{\widehat{F}}_n},p_{{\mathit{\theta }}_0,F_0}){\to }_{a.s.}0.$$

5. NUMERICAL STUDIES

5.1. Simulation Study

To examine the empirical properties of the proposed method, we perform a simulation study. The event time T is generated under the cure model (1) for given Z,

$$S(t|\mathit{Z})=\text{exp}\left(-e^{{\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z}}{F}_0(t)\right).$$

There is a connection between the cure model (1) and the mixture cure model as pointed out by Chen et al. (1999). The overall survival function can be written in the form of the mixture cure model:

$$S(t|\mathit{Z})=\mathrm{\pi }(\mathit{Z})+(1-\mathrm{\pi }(\mathit{Z}))S^{*}(t|\mathit{Z}),$$

where $\mathrm{\pi }(\mathit{Z})=\text{exp}[-\text{exp}({\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z})]$ is the covariate-specific probability of cure, and

$$S^{*}(t|\mathit{Z})=\frac{\text{exp}(-e^{{\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z}}{F}_0(t))-\text{exp}(-e^{{\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z}})}{1-\text{exp}(-e^{{\alpha }_0+{\mathit{\beta }}_0^{\prime }\mathit{Z}})}.$$

The conditional survival function S* is a proper survival function.

To simulate T under (1), we consider a setting with one covariate Z, which has a uniform distribution on (−1:0, 1:0). The first step is to generate a random variate distributed as Bernoulli with π(Z) for a given single covariate Z. If it is 1, then T = ∞. If it is 0, then generate a random variate T* distributed as the proper survival function S*(t|Z). To generate T* ~ S*(t|Z), we apply the accept-reject method for simulating the random variate (Devroye, 1986, page 40–65). For simplicity, we choose the baseline distribution function F₀(t) = 1 − exp(−t).

The sample size is chosen to be 50, 100 or 200. The true value for β₀ is chosen to be 0.0, 0.5 or 1.0. When β₀ = 0.0, the probability of cure is exp(−e^α0). The value of α₀ is chosen to be either 0.0 or 1.0, which corresponds to a baseline cure rate of either 0.37 or 0.07, respectively. For small sample sizes, care has been taken to ensure that there is at least one cured patient in the simulated dataset. The examination times are generated independent of Z and T, from a homogeneous Poisson process. The inter-examination times are independent and identically distributed as exponential with mean ζ of either 1/5 year or 1/2 year, corresponding to short or long inter-examinations, respectively. The length of study is either 3 years for short inter-examination or 5 years for long inter-examination. The simulation replicates are 1,000 for each scenario.

The results of the Monte Carlo simulations are summarized in Table 1, including the bias, the empirical estimate of the mean squared error (MSE) and its average standard error. The biases of estimates for α and β are very small even for a small sample size, indicating that the algorithm performs surprisingly well. The empirical estimates for the standard error, as well as the mean squared error, decrease with the sample sizes. The MSE of the estimator under the long inter-examination time is slightly higher than those under the short inter-examination time.

Table 1.

Summary of the simulation results including bias and mean squared error (MSE) for the MLE estimator α̂ and β̂, where ζ is the mean inter-examination time, n is the sample size, and the true values are α₀ and β₀.

			ζ = 0.2				ζ = 0.5
			α̂		β̂		α̂		β̂
n	α0	β0	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
50	0.0	0.0	−0.007	0.043	0.010	0.113	0.023	0.042	−0.012	0.122
		0.5	0.002	0.040	0.032	0.120	0.036	0.043	0.044	0.133
		1.0	−0.003	0.043	0.042	0.136	0.052	0.055	0.133	0.174
	1.0	0.0	0.031	0.040	0.004	0.073	0.087	0.046	−0.002	0.125
		0.5	0.042	0.042	0.021	0.092	0.110	0.055	0.113	0.152
		1.0	0.030	0.048	0.037	0.093	0.116	0.069	0.165	0.151
100	0.0	0.0	−0.009	0.019	0.011	0.053	0.023	0.019	−0.014	0.058
		0.5	0.005	0.020	0.011	0.057	0.027	0.020	0.038	0.063
		1.0	0.004	0.019	0.021	0.056	0.041	0.026	0.103	0.082
	1.0	0.0	0.018	0.022	−0.007	0.034	0.067	0.023	−0.012	0.058
		0.5	0.021	0.019	0.012	0.038	0.078	0.026	0.089	0.086
		1.0	0.012	0.022	0.020	0.043	0.070	0.024	0.098	0.056
200	0.0	0.0	−0.006	0.009	0.004	0.025	0.024	0.010	−0.003	0.028
		0.5	0.002	0.009	0.007	0.027	0.026	0.010	0.034	0.032
		1.0	0.001	0.011	0.011	0.028	0.042	0.013	0.085	0.045
	1.0	0.0	0.003	0.010	0.002	0.017	0.054	0.012	−0.028	0.026
		0.5	0.008	0.009	0.006	0.018	0.066	0.014	0.074	0.057
		1.0	0.005	0.010	0.009	0.020	0.053	0.011	0.061	0.023

NOTE: MSE was the empirical mean-squared error. The average standard errors of MSE for (α̂, β̂) were (0.036, 0.087) when ζ = 0.2, and were (0.048, 0.128) when ζ = 0.5.

5.2. Data Analysis

The proposed method was motivated by the medical study for patients with clinically localized prostate cancer, who were followed and monitored for biochemical recurrence of cancer after undergoing radical prostatectomy. As a widely used surgical procedure, radical prostatectomy takes away the entire prostate gland and surrounding tissue to remove all tumor cells, leading to a very high cure rate for early prostate cancer (Kufe et al., 2003, Chapter 111). Although no cells should remain to produce prostate-specific antigen (PSA), clinical studies have shown that about 20% to 30% of these patients could still experience biochemical recurrence of cancer, defined as a detectable serum PSA level (≥ 0.1 ng/mL) after surgery. Clinical studies have also shown that the biochemical recurrence of cancer often occurs within 3 years after surgery, which is a much earlier event than the clinical recurrence of cancer (Dillioglugil et al., 1997; Pound et al., 1999). A patient who has remained free of serum PSA three years after his surgery is generally considered to be cured of biochemical recurrence of prostate cancer. It is therefore important to know what preoperative clinical characteristics might be prognostic for the rate of cure for biochemical recurrence and how long it is likely to occur after surgery.

For this purpose, we obtained the clinical data of 260 men who underwent radical prostatectomy for clinically localized prostate cancer performed by a single surgeon at an academic hospital in Houston, Texas. The average age for the men at the operation was 59.5 (median age 59). After the operation, these men were followed up periodically for serum PSA level examination for about every 3 months. All patients were alive at their last follow-up. The longest follow-up duration s_m+1 was 4.1 years, and all biochemical recurrences were observed within r_m = 3.3 years after surgery. This indicated that the patients’ follow-up times were adequate for the analysis of the cure rate for biochemical recurrence. The exact time of biochemical recurrence was only known to have occurred between the previous examination and the latest examination for a patient. The possible prognostic factors for biochemical recurrence included the following: pathologic stage at surgery (T2, clinically organ-confined; T3, locally advanced), preoperative PSA level, Gleason score, and positive surgical margins (PSM). The preoperative PSA level was logarithmically transformed. The Gleason score graded histologically the prostate tumor cells, ranging from 2 to 10 (the higher the worse). We classified the Gleason score into 2 categories: less or equal to 7, and above 7(the baseline). Positive surgical margins (PSM), defined as the presence of cancer cells at the inked margin of a resected tumor specimen, might indicate incomplete excision of tumor, but it was not always clear in the medical literature whether PSM was associated with biochemical recurrence. Of note, being cured of biochemical recurrence is different from being cured of prostate cancer, which may be confounded with over-diagnosis of prostate cancer.

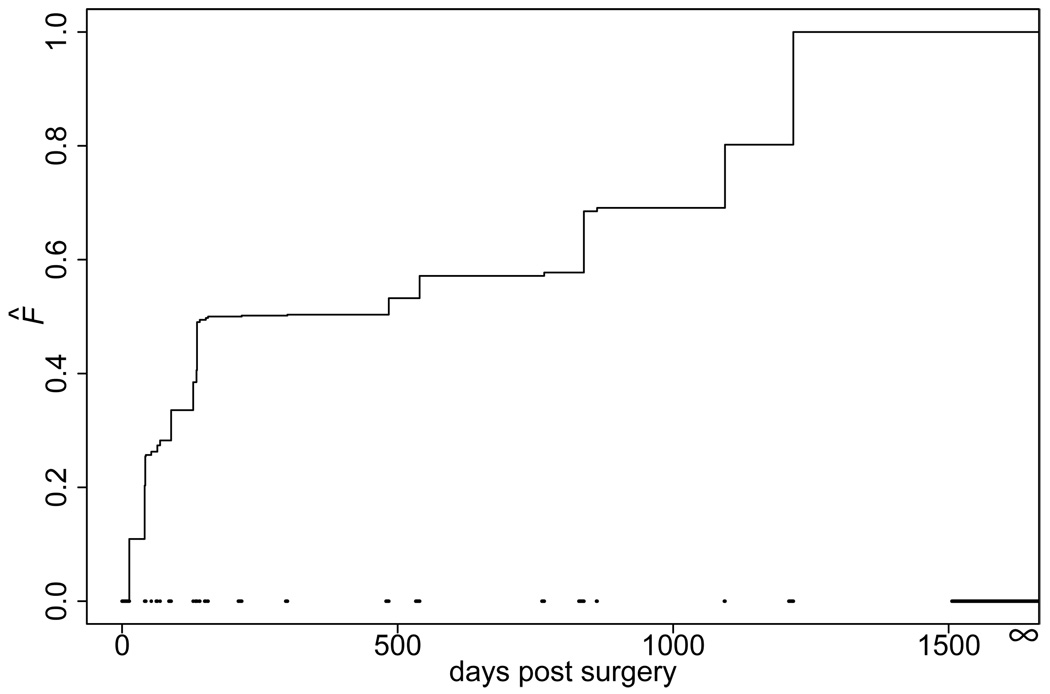
The estimated covariate coefficients were shown in Table 2. The estimated baseline function F̂ was plotted in Figure 2. For computational convenience, we used the nonparametric bootstrap method to estimate the standard errors, where the replicates of the bootstrap samples were 1,000. The intercept, stage T2, and Gleason score ≤ 7 in the regression model were not significantly different from zero, but their magnitude were negative, indicating an increased cure rate (≈ 66.3%) for patients with the following clinical characteristics: tumor of stage T2, preoperative PSA level 1.0, Gleason score ≤ 7, and a negative surgical margin. Only the preoperative PSA level was significantly associated with the cure of biochemical recurrence at the 0.05 level. The positive estimated coefficient indicated a lower preoperative PSA level would lead to a higher probability of cure.

Table 2.

Estimates and standard error (se) for analyzing the biochemical recurrence study.

	Intercept	Stage T2	log PSA level	Gleason ≤ 7	PSM
estimates	−0.34	−0.24	0.62	−0.31	0.06
bootstrap se	0.41	0.74	0.29	0.33	0.37

PSM: Positive surgical margins.

Figure 2.

NPMLE of the function F̂. The dashed lines at the bottom are the non-overlapping intervals (s_j, r_j] for j = 1, ⋯, m + 1.

6. DISCUSSION

We have studied the semiparametric MLE for a non-mixture cure model for interval-censored data. Besides its attractive properties and biological interpretation as explained by Tsodikov (1998) and Chen, Ibrahim and Sinha (1999), one advantage of the non-mixture cure model for interval-censored data is the parsimonious model of the covariate effects on both cure rate and time to event. This is especially appealing when the primary goal of a study is to evaluate risk factors for the cure rate. In addition, the proposed semiparametric non-mixture cure model S(t/Z) = exp(−ϕ(θ′Z̃)F(t)) is flexible enough to allow a general function ϕ(·) to replace exp(·) in the regression part. Our algorithm can be easily modified for the general function ϕ as long as it is nonnegative and convex. It is important to assess the goodness-of-fit for the posited model (1), perhaps based on the likelihood function developed herein. Another obvious extension within the regression framework is to allow for time-dependent covariates, which may be useful for checking the proportionality assumption in model (1). Although it will not be conceptually difficult to develop the estimators, studying their properties requires substantial effort.

Interval-censored data provides unique opportunity and challenge for analyzing the cure rate in the medical studies. We developed the likelihood function through the classic equivalence class approach of Turnbull (1976). To estimate cure rate, the likelihood function requires that at least one event-free subject be followed longer than r_m. In contrast to the mixture cure model, the definition of cure fraction for the non-mixture cure model is unchanged even in the case of insufficient follow-up. However, for sound data analysis, one should always consult with clinical investigators to assess whether the value of r_m in a given data is appropriate for the scientific context.

Another major contribution in this work for interval-censored data is the development of a computational algorithm that incorporated some modern optimization techniques with the EM method for solving MLE. The maximization step is a constrained optimization that requires the sophisticated interior-point method to keep searching in the restricted parameter subspace. Combined with the theoretically sound primal-dual method, our algorithm provides a computationally robust solution for the nonparametric estimation of the function F. We further worked out an efficient and numerically stable algorithm for the M-step for F, which is self-consistency in the sense of Turnbull (1976). Our experience is that the algorithm converges very quickly in each M-step even when the dimension of p is large, although the convergence for the entire ECM iterations still needs extra computation time.

The assumption of an independent and non-informative inspection process is for the consistency proof. That assumption is, however, likely satisfied in our data example. This is because biochemical recurrence after radical prostatectomy has been shown to occur much earlier than symptomatic clinical recurrence (Pound et al., 1999). Therefore, it is unlikely that the inspection process would be altered among the asymptomatic patients. The asymptotic normality and efficiency of n^½(θ̂_n − θ₀) may be obtained by deriving the efficient score function of θ while treating F as the nuisance function, where the detail will be reported elsewhere. We conjecture that the rate of convergence of θ̂_n is n^−½ and that of F̂_n is n^−1/3. It is difficult to obtain the asymptotic distribution for n^1/3(F̂_n − F₀), while the asymptotic normality of n^½(θ̂_n − θ₀) is relatively easy to prove by modifying the empirical process techniques for the case-2 interval-censored data as in the work of van de Geer (2000, page 228–230). The nonparametric bootstrap is a valid approach to calculating the standard error for θ̂_n. Alternatively, the asymptotic variance-covariance matrix of estimator θ̂_n and F̂_n may be estimated by the supplemented ECM (S-ECM) algorithm of van Dyk et al. (1995), which is a computational byproduct of the ECM algorithm.

Supplementary Material

supplement materials. SUPPLEMENTAL MATERIALS.

Line Search for Primal-dual Interior-point Algorithm: A brief review of the line-search procedure for primal-dual interior-point algorithm as in Boyd and Vandenberghe (2004, Chapter 11).

Proof of Hellinger consistency: Technical proof of Theorem 1.