Self-organization of grafted polyelectrolyte layers via the coupling of chemical equilibrium and physical interactions

Abstract

The competition between chemical equilibrium, for example protonation, and physical interactions determines the molecular organization and functionality of biological and synthetic systems. Charge regulation by displacement of acid-base equilibrium induced by changes in the local environment provides a feedback mechanism that controls the balance between electrostatic, van der Waals, steric interactions and molecular organization. Which strategies do responsive systems follow to globally optimize chemical equilibrium and physical interactions? We address this question by theoretically studying model layers of end-grafted polyacids. These layers spontaneously form self-assembled aggregates, presenting domains of controlled local pH and whose morphologies can be manipulated by the composition of the solution in contact with the film. Charge regulation stabilizes micellar domains over a wide range of pH by reducing the local charge in the aggregate at the cost of chemical free energy and gaining in hydrophobic interactions. This balance determines the boundaries between different aggregate morphologies. We show that a qualitatively new form of organization arises from the coupling between physical interactions and protonation equilibrium. This optimization strategy presents itself with polyelectrolytes coexisting in two different and well-defined protonation states. Our results underline the need of considering the coupling between chemical equilibrium and physical interactions due to their highly nonadditive behavior. The predictions provide guidelines for the creation of responsive polymer layers presenting self-organized patterns with functional properties and they give insights for the understanding of competing interactions in highly inhomogeneous and constrained environments such as those relevant in nanotechnology and those responsible for biological cells function.

The competition between physical interactions and chemical equilibrium is a challenging problem in physics, chemistry, and biology. A ubiquitous example of this competition in synthetic and life systems is the control of the charge state by protonation that regulates enzymatic activity (1), switches ion-conductivity in biological (2) and synthetic channels (3), induces self-assembly (4–7), and determines the properties of technologically important polyelectrolyte layers (8, 9). These processes occur in confined inhomogeneous environments, where molecular organization is restricted and competition among interactions is augmented. The optimization of charge state by protonation depends not only on the solution pH but also on the local environment (10, 11). Therefore, it is imperative to understand whether the molecular organization is determined by the independent optimization of the acid-base equilibrium and the physical interactions, or if there are phenomena that arise exclusively from their coupling. This understanding is particularly relevant today given the large number of systems explored at the nanoscale where it is observed that confinement plays a key role in regulating interactions. It is also relevant for biological systems where the environment around active sites controls the biological activity and confinement arises from compartmentalization and molecular crowding. For instance, the acid-sensing ion channels are gated by the protonation/deprotonation of sensing regions (2). However, the apparent pKas of the acid-base sensing groups are likely to be affected by the large conformational changes during channel gating and, therefore, a coupling must exist between the protonation equilibrium and channel conformation. Important insights about the underlying mechanisms in this and other important phenomena in responsive materials, self-assembly, and subcellular biology function can be obtained from the coupled treatment of physical interactions and chemical equilibria.

This work addresses the coupling between acid-base equilibrium and several physical interactions in a confined environment. We analyze a simple and highly responsive model system that consists of a layer of weak hydrophobic polyacids end-tethered to a surface. Grafted hydrophobic polymers tend to form domains because their chemical attachment to the surface does not enable macrophase separation; i.e., the chain molecules lack translational degrees of freedom. This effect has been observed in a variety of experimental realizations (4, 12–17) and several applications for this interesting property have been devised that include nanopatterning (14), motion of nano-objects (15), and surfaces with switchable ionic permeability (4), redox activity (16), or friction properties (18). For grafted layers of weak polyacids like poly(methacrylic acid) or poly(vinyl pyridine), the attractions between polymer segments compete with the electrostatic repulsions that are regulated by the acid-base equilibrium. These responsive layers have received a lot of attention lately due to their potential technological applications (8). Moreover, it has been shown that they can be used to mimic biological function, for example the modification of a single nanopore with protonable brushes displays pH-gated ion conductivity in analogy to some biological ion-channels (3). It is important to understand how the balance between chemical and physical interactions drives the organization of these systems and how this process differs between uncharged polymers, polyions without the ability to regulate charge, and polyelectrolytes bearing weak acid-base groups.

We present here a study of the morphological phase behavior of end-grafted polyacids. In particular, we show that the coupling between chemical equilibrium (charge regulation), van der Waals interactions, and electrostatic forces leads to qualitatively different results than charged systems without regulation, including phases not previously observed or predicted. The theoretical approach that we use is a generalization of a previously reported molecular theory (19, 20), originally applied assuming one dimensional inhomogeneities (1D), generalized, and applied here to treat systems that are inhomogeneous in all three spatial dimensions (3D). The molecular theory was found to quantitatively predict the structure of non-aggregated, end-grafted polyelectrolytes as compared with experimental observations (21) and computer simulations (22) for many different conditions. Furthermore, the theory was shown to provide quantitative predictions for the thermodynamics and structure of thin films with coupling of redox and acid-base equilibrium with molecular organization (23). Thus, we are confident that the results presented here are reliable. The details of the theory are presented in the Methods section and in SI Text.

Results and Discussion

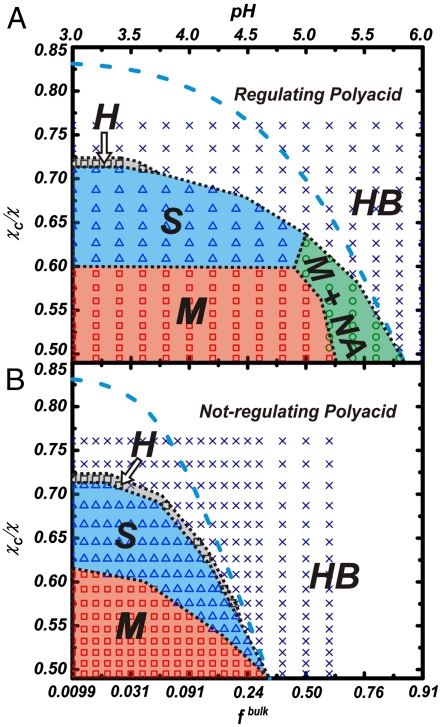
In Fig. 1A we show the predictions for the morphological phase diagram of a charge regulating polyacid as a function of bulk pH and χ_c/χ, this quantity is a measure of the hydrophobicity of the backbone^† (higher χ_c/χ corresponds to less hydrophobic polymer, SI Text) for fixed surface coverage and solution ionic strength (C_salt). The predictions show that the structure of the domains depends on both χ_c/χ and the bulk pH and that, for the conditions under study, there are five different regimes. Our prediction is that size, shape, and internal structure of domains in polyelectrolyte grafted films can be switched in water by simply changing solution pH or ionic strength, creating responsive and easily reversible surfaces. This is in addition to the control designed variables, available for both weak polyacids and uncharged polymers, such as grafting density (12, 22) or chain length (14, 22).

Fig. 1.

Morphology diagrams for regulating (A) and not-regulating (B) polyacid layers. The plane shown corresponds to bulk pH as a function of the effective hydrophobicity of the backbone as measured by the vdW attraction parameter χ_c/χ (higher χ_c/χ corresponds to weaker interactions and better solvent quality). The fraction of charged groups in the non-regulating polyelectrolyte is fixed for a given pH to that of the isolated acid group in the bulk, f^bulk = 1/(1 + [H⁺]^bulk/K_a). Each symbol is obtained by solving the 3D theory for a given set of experimentally controlled variables. Different symbols and uppercase letters indicate the resulting morphologies: M (Squares), micelles; S (Triangles), stripes; H (Circles), holes; HB (Crosses), homogeneous brush and M + NA (rhomboids): micelles plus extended chains coexistence. The Blue Dashed Line is the onset of stability of the homogeneous brush predicted by the 1D molecular theory (19). Dotted Black Lines are guides to the eye. N_P/A = 0.111 chains/nm², n(segments per chain) = 50, l = 0.35 nm (polymer segment length), C_salt = 0.1 M, and pK_a = 5.0 were used in the calculations.

It is important at this point to emphasize that the transitions between different morphologies are not true thermodynamic phase transitions but rather they represent an aggregation processes similar to micellization (24), with the additional constrain that the grafted polymers lack translational degrees of freedom. The derivatives of the free energy are continuous in the thermodynamic plane χ_c/χ-pH shown in Fig. 1. Therefore, Fig. 1 shows morphological diagrams where the lines dividing the different types of domains are not coexisting or phase transitions, but they represent shape transformations, as in surfactant micellar systems (24). The important difference with solution self-assembly, however, is that the chemical potential of all the grafted molecules is not the same because the polymers lack translational degrees of freedom. Therefore, constant polymer chemical potential is not a necessary thermodynamic equilibrium condition.

The morphologies predicted in the phase diagram of Fig. 1 are presented in Fig. 2. In the homogeneous brush structure (HB), the polymer chains are stretched out of the surface and all the molecules are equivalent. The micelles (M) are hemispherical aggregates, and the stripes (S) are infinity long parallel aggregates. In the last two morphologies, the regions between aggregates do not show any finite density of polymers. There is also a regime with solvent-filled holes (H) defects. These four different structures have been previously predicted (14, 22, 25–29) and observed (4, 12, 14, 17) in a variety of grafted systems. The region denoted as M + NA corresponds to micelles together with highly stretched individual polymers and has never been observed before. For a surface coverage larger than the one presented here, we also found stripes coexisting with individual stretched chains between the S and HB phases.

Fig. 2.

Typical examples of the predicted morphologies. (A) Polymer volume fraction (density) color maps. Upper maps for HB, M, and M + NA regimes are cut along a plane parallel to the surface (z = 2 nm, marked with Dotted White Lines on the Lower Graphs). Lower Maps are cuts along a plane perpendicular to the surface as marked with Dotted White Lines in the Upper Graphs. Only the planes parallel to the surface are shown for H and S. (B) Isodensity surfaces with constant volume fraction 〈ϕ_P(r)〉 = 0.15. The same color scale (on Upper Left) was used in all figures. The calculation box is periodic in the xy plane and contains 64 different chains arranged in a hexagonal lattice as marked by the Blue Dots that represent the grafting points.

Fig. 1B shows the predicted phase diagram under the same conditions as Fig. 1A, but assuming that the acid groups do not have the ability to regulate their charge depending on the environment, but rather the fraction of charged groups in the polyacid is given by the bulk pH; that is, the fraction of charge f^bulk = 1/(1 + [H⁺]^bulk/K_a) is independent of position and local environment. The inability of the system to regulate its charge through shifts in the acid-base equilibrium results in a phase diagram that presents less morphological regimes and different boundaries between regimes than the fully optimized and regulating system. Comparing the phase diagrams in Fig. 1A and B demonstrates that the lack of explicit inclusion of charge regulation by acid-base equilibrium coupled with the other interactions in the system provides the wrong qualitative and quantitative description of the system. This is one of the most important conclusions of the present work. The dramatic differences between the regulating and nonregulating systems can be understood from the physical origin of the driving forces for domain formation.

The physical driving forces for the formation of different structures are best understood by starting at low pH. In this limit the charges on the polymers are very small and play no role in the formation of the aggregates. As the hydrophobicity of the backbone increases (lower χ_c/χ) the polymer segments tend to avoid the solvent and below the χ_c would like to phase separate into two macroscopic phases, one rich in polymer and the other almost pure solvent (30). The polymers chains are grafted to the surface and the lack of translations prevents macrophase separation. Thus, the system microphase separates into domains. The size of the domains is determined by the interplay between the bulk free energy of having large number of segments in polymer-rich regions and the surface tension associated with the polymer-rich and solvent-rich interfaces with the constraint that the polymer chains are end-grafted to the surface (29). We find that the core of the micelles in the M region have a diameter around 8.5 nm, whereas the length of the fully stretched chain is 15 nm. The size of the micelle represents the compromise between stretching a small part of the chain, while having a compact core to optimize polymer-polymer attractions. The constraint of having grafted chain ends results in a micelle diameter that is similar to the stripe width (Fig. 2). The stripes are the preferred morphology at lower hydrophobicity because they have a lower volume fraction and, thus, the chains increase their conformational entropy by reducing their confinement. As the hydrophobicity increases the chains prefer a more compact core and, for the given surface coverage, the optimal geometry is micellar. The physical competition that drives aggregate formation in grafted polymers in poor solvents is between the attractions between the polymers and their confinement due to grafting. The uncharged micelles resulting from this competition has been called octopus micelles, due to the presence of the stretched legs and high density core (29). Interestingly, whereas the structures formed are similar to those found in modulated phases (31, 32), in grafted chains the local segregation is not due to the competition between short and long range interactions but to the relatively short-range hydrophobic attractions and the lack of lateral mobility.

Now we concentrate on the role of charge and charge regulation in modifying those structures. The nonregulating polymers show micelles to stripes to holes morphological transitions by changing either the hydrophobicity or the pH. The boundaries show that the only role of the charge is to change the effective quality of the solvent. Actually, if the phase diagram is shown in a linear scale on f^bulk, the boundaries between the different structures in Fig 1B are linear (SI Text).

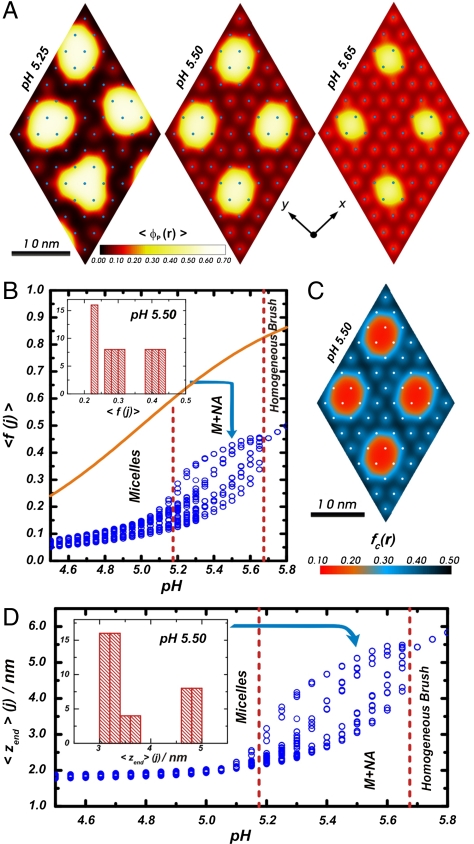
The regulating polymers, on the other hand, show richer morphological possibilities, the presence of aggregates is found in a larger region of the χ_c/χ-pH plane and the transitions occur under different conditions. The two most important differences being that the stripes to micelle transformation (and to a lesser extent the stripes to hole transition) is independent of the bulk pH and the presence of the M + NA morphology. The qualitative difference in the M to S transformation between regulating and nonregulating polymers is due to the ability of polymers to change their charge to optimize the conditions. Thus, there is a competition between the tendency to have a large local polymer concentration (hydrophobicity) and the electrostatic repulsions that arise from the charges on the polymer. For bulk 3 < pH < 5 the charge in the regulating polyacids is very low (Fig. 3B) and it remains almost constant. Fig. 3B shows the pH dependence of the average fraction of charge for each chain, 〈f(j)〉, where the index j denotes the chain. In the region where the compact micelles exist, pH < 5.1, the average fraction of charged groups per chain has a narrow but finite spread. The reason for the variation of 〈f(j)〉 at pH < 5.1 is that the polymers on the edge of the micelle have a larger fraction of charged groups than those in the interior of the aggregate. The values of 〈f(j)〉 in this region are much lower than what would be expected from the bulk pH and the pK_a of the isolated segments (Orange Line). The polymers lower their fraction of charged segments to reduce the electrostatic repulsions arising from the high polymer density inside the compact micellar structures (that are optimal due to the hydrophobicity of the backbone, Fig. 2), even at the chemical free energy cost of shifting the acid-base equilibrium. Thus, in this regime the gain in hydrophobic attractions and the lowering of the electrostatic repulsions through charge regulation, dominate at the cost of the acid-base chemical free energy. At pH ≈ 5.1, the chemical free energy cost of shifting the acid-base equilibrium to the uncharged species is too large. Thus, the system finds a different way to optimize the hydrophobic attractions, the chemical free energy, and the electrostatic repulsions through the formation of M + NA, mixtures of micelles with stretched chains.

Fig. 3.

Molecular organization in the micelles and non-aggregated chains coexistence regime. (A) Polymer volume fraction color maps along a plane parallel to the surface (z = 2.0 nm) for the M + NA morphology at different bulk pHs. (B). Average fraction of charged groups per chain j as a function of solution pH. There is one symbol per chain, i.e., for each bulk pH there are 64 symbols. The Orange Solid Line represents the dissociation fraction for an isolated acid group in the bulk isotropic solution. 〈f(j)〉 is defined as an average of the fraction of charged groups over all segments and conformations, i.e.:

where P_P(α,j) is the probability that polymer j is found in conformation α; f_c(r) is the fraction of charged groups at r and n(r,α,j) is the number of polymer segments that polymer j in conformation α has at r. (C) Color map for the local fraction of charged groups, f_c(r) along a plane parallel to the surface at z = 2.0 nm for pH 5.50 (corresponding to the middle case in A). (D) Average free-end z-position as a function of solution pH. 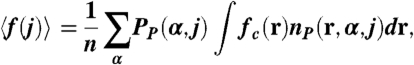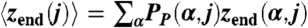, where z_end(α,j) is the height (z-position) of the free-end segment of polymer j in conformation α. In B and D, Vertical Red Lines delimitate pH regions corresponding to different morphologies. Insets show histograms for pH 5.50. For all cases, the calculation corresponds to: χ_c/χ = 0.53, n = 50, N_P/A = 0.111 chains/nm², C_salt = 0.1 M, and pK_a = 5.0.

The ability of the polymer chains to keep their charge constant over a large range of pHs explains the large differences in the morphology diagrams between the nonregulating polymers and the polyacids (Fig. 1). Changing of pH in the nonregulating polymer automatically results in a large increase in the electrostatic repulsions, making the aggregates less stable. The large changes due to regulation demonstrate the importance of coupling the chemical equilibrium to the other interactions because in experimental systems regulation is always present.

The understanding of the M + NA morphology can be obtained by analyzing the transition from micelles to the homogeneous phase by varying the bulk pH. The density maps in Fig. 3A show that the fraction of aggregated chains and the size of the micellar aggregates depends on the bulk pH, providing a continuous transformation between M and HB regimes and revealing coexistence between nanophases^‡. As the bulk pH increases over pH ≈ 5.1, the chemical free energy cost of uncharging the acid groups increases and the system has to balance the competition between electrostatic and hydrophobic interactions. The region of M + NA (5.18 ≤ pH ≤ 5.68) shows a binodal 〈f(j)〉 distribution (Fig. 3B) because these interactions are optimized by a separation into two types of morphologies with different state of charge. Comparison of the maps of the fraction of dissociated acid groups (Fig. 3C) with those of polymer volume fraction (Fig. 3A) for pH 5.5, shows that the chains in micellar aggregates are less charged than the non-aggregated molecules. For pH > 5.7, the electrostatic repulsion gains over the hydrophobic interaction, and all the polymers become completely equivalent. Thus, a symmetric homogeneous brush is obtained. Fig. 3D shows that the pH dependence of the average height of the free-end of each of the chains in the system, 〈z_end(j)〉 (Fig. 3) is similar to that of 〈f(j)〉. For pH < 5.1, all the grafted chains have a similar and small height due to the compact nature of the spherical micelles. In the M + NA region, some chains form micelles with low fraction of charged groups, short 〈z_end(j)〉 and high local volume fraction, and the other chains are highly stretched and have a larger fraction of charged segments.

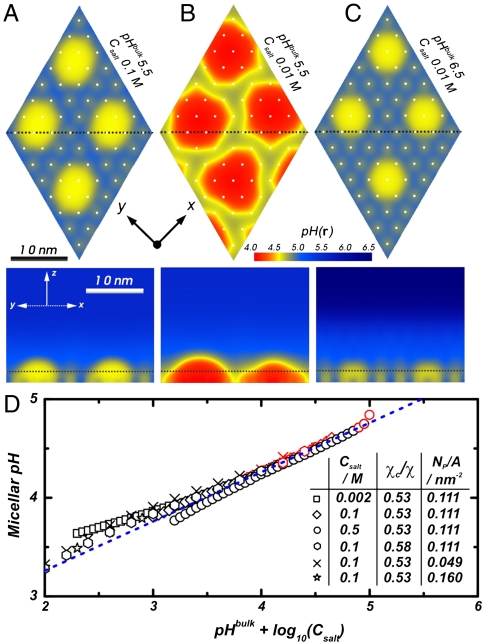
Local environments within aggregates are inhomogeneous and very different from those of the bulk solution. Fig. 4A and B display color maps of local pH (defined as - log ₁₀([H⁺(r)])) in the M and M + NA regions, respectively, for two different C_salt and a fixed solution pH. The local pH reflects the shape of the aggregates and presents large gradients in all directions. It increases about a half unit when going from the interior of the aggregates to the surface regions without polymers and around 1 (C_salt = 0.1 M) and 1.5 (C_salt = 0.01) units when moving away from the surface 10 nm in the normal direction. The reduction in salt concentration results in an increase of the strength and range of the electrostatic repulsions and, thus, one would expect the system to move in the direction of the homogeneous phase of highly stretched chains. However, the predictions show exactly the opposite, namely more compact aggregates are observed for C_salt = 0.01 M (M regime) than for C_salt = 0.1 M (M + NA regime). That is, the chemical equilibrium is shifted toward the side of the uncharged polymers (lower local pH in Fig. 3B) to reduce the electrostatic repulsions. Thus, the hydrophobicity of the backbone becomes the dominant effect.

Fig. 4.

Effect of solution composition on local pH. (A–C) Local pH color maps along a plane parallel to the surface at z = 2.0 nm (Above) and perpendicular to the surface (Below) for different bulk pHs and C_salt as noted in each figure. The intersections between parallel and perpendicular planes are shown with Black Dashed Lines and the grafting points are shown with White Dots, the calculations correspond to: χ_c/χ = 0.53, n = 50, and N_P/A = 0.111 chains/nm². (D) Local pH inside regulating polyacid micellar aggregates as a function of the relevant positive ions bulk concentrations (see text). Black and Red Symbols correspond to M and M + NA morphologies, resp. The Dashed Blue Line has a slope of ½. For all cases, pK_a = 5.0.

Fig. 4A and C show two systems at different bulk pH and C_salt. Therefore, they present different gradients and different overall optimization. However, the local pH within the micelles is the same in the two cases. We show in Fig. 4D that a universal behavior exists for the pH in the interior of the micelles as a function of bulk pH + log ₁₀ (C_salt) (which is the natural variable due to the Donnan partition), both in M and M + NA regimes. The plot shows a slope of ∼1/2, in agreement with a simple analysis including charge regulation (SI Text). This interesting buffering effect can be used to control local pH within nanometric length scales for many different bulk solution conditions.

To summarize, we analyzed the self-organization strategies of a model layer of end-grafted weak polyacids with competing chemical equilibrium, physical interactions, and conformational degrees of freedom. Charge regulation yields an unexpected mechanism of optimization by the formation of two domains with chains in different and well-defined structures and protonation states. The importance of this work is twofold. First, we propose patterning by self-assembly controlled by the proper choice of solution pH and salt concentration. We also predict the formation of domains of local pH and of chemical environment, in addition to the control over polymer morphology. These nanodomains may be used to selectively bind specific molecules from solution (e.g., metallic cations in charged regions) or to achieve spatial control over pH-dependent chemical reactions (like precipitations or enzymatic transformations), opening the door to functional surfaces with patterns of tailored chemical activity. A theoretical guide is important because it enables the fundamental understanding and it provides specific guidelines for experimental design. The second important conclusion is the relevance of the (usually neglected) coupling between chemical equilibrium and physical interactions. This coupling is essential to model and analyze responsive soft materials and to understand the dependence of chemical or biological activity on the local molecular environment, for example enzymatic activity in the vicinity of membranes where the local pH changes due to the presence of charge head-groups and polysaccharides (1). We demonstrate here that a different intuition is required to understand the properties of systems with competing physical interactions and chemical equilibrium because they present strongly nonadditive effects.

Methods

The 3D molecular theory explicitly considers the shape, size, conformation, charge, and charge distribution of all the molecular species in the system. The physical interactions considered include van der Walls attractions, steric repulsions, and electrostatic interactions. The chemical equilibrium is treated by allowing the monomers of the polymers (acid groups) to be in either protonated or non-protonated states. The basic idea of the theory is to write the free energy of the system as a functional of the distribution of the different molecular species, the probabilities of the different polymer conformations at each grafting point, and the fraction of charged and uncharged groups in the polyacids. The free energy functional is explicitly written in SI Text with a thorough description of the minimization procedure and how the calculations are carried out. We write the free energy, F, as F = -TS_mix - TS_conf + E_vdw + E_rep + E_elec + F_chem, where T is the temperature and the terms represent: S_mix is the mixing (translation) entropy of the mobile species, i.e., cations, anions, water, hydroxyl ions, and protons; S_conf is the conformational entropy of the grafted polymer chains; E_vdw represents the attractive van der Waals interactions that measures the hydrophobicity of the polymer backbone; E_rep is the steric repulsive interactions between all the molecular species; E_elec is the total electrostatic energy; and F_chem represents the free energy associated with the acid-base chemical equilibrium, i.e., the free energy cost associated with protonation and deprotonation of the acid groups. The coupling between the different contributions to the free energy arises from the fact that the density profiles and interaction fields that minimize the free energy appear in different terms and, therefore, their optimization results from the minimal total free energy. The technical details as well as the functional form of each term are shown in SI Text.