Principles of conduction and hydrophobic gating in K⁺ channels

Abstract

We present the first atomic-resolution observations of permeation and gating in a K⁺ channel, based on molecular dynamics simulations of the Kv1.2 pore domain. Analysis of hundreds of simulated permeation events revealed a detailed conduction mechanism, resembling the Hodgkin–Keynes “knock-on” model, in which translocation of two selectivity filter–bound ions is driven by a third ion; formation of this knock-on intermediate is rate determining. In addition, at reverse or zero voltages, we observed pore closure by a novel “hydrophobic gating” mechanism: A dewetting transition of the hydrophobic pore cavity—fastest when K⁺ was not bound in selectivity filter sites nearest the cavity—caused the open, conducting pore to collapse into a closed, nonconducting conformation. Such pore closure corroborates the idea that voltage sensors can act to prevent pore collapse into the intrinsically more stable, closed conformation, and it further suggests that molecular-scale dewetting facilitates a specific biological function: K⁺ channel gating. Existing experimental data support our hypothesis that hydrophobic gating may be a fundamental principle underlying the gating of voltage-sensitive K⁺ channels. We suggest that hydrophobic gating explains, in part, why diverse ion channels conserve hydrophobic pore cavities, and we speculate that modulation of cavity hydration could enable structural determination of both open and closed channels.

Electrophysiological, structural, and computational studies have provided a wealth of insight into the mechanisms underlying conductance and gating—how ionic current is switched on and off—by ion channels, most notably potassium (K⁺) channels. Key questions nonetheless remain about how channels perform these functions (1–8). X-ray structures and experimental measurements of ion binding and conduction (3, 8–10), as well as computer simulations (6, 7), have suggested that K⁺ ions and copermeating water molecules move in concert, single file, through the ion-selective region of K⁺ channels—the so-called selectivity filter (SF; Fig. 1A). Gating involves significant protein conformational changes as the pore domain opens and closes (5, 11).

Fig. 1.

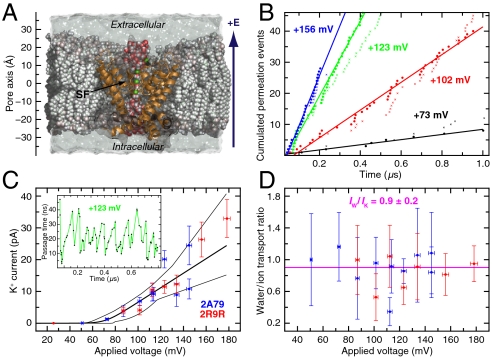
Quantitative analysis of Kv1.2 conductance. (A) Lipid-embedded rat Kv1.2 pore domain bathed in 0.6 M KCl. (B) Ion (•) and water (×) permeation events vs. time at selected voltages; linear fits to the ion permeation events are shown. (C) I_K–V relationship. Given the voltage lag, I_K, determined from the mean waiting time between consecutive permeation events, was fit to the relationship (26, 27) I_K = a(V - V^′)/{1 - exp[-b(V - V^′)]} [thick curve; thin curves, 67% confidence intervals; data from simulations of Protein Data Bank entries 2A79 (Blue) and 2R9R (Red)]. The pore conductance was derived from the linear region; errors were estimated by Monte Carlo sampling. (Inset) Ion passage time through SF vs. time (+123 mV). (D) H₂O/K⁺ transport ratio as a function of V; average is shown in pink, and individual errors were determined by propagation of I_K and I_W errors. Color coding as in (C). See SI Text and Figs. S1 and S2 for additional details.

The widely accepted view of permeation across K⁺ channels follows Hodgkin and Keynes’s knock-on model (12), in which conduction is driven by an incoming ion that “knocks on” ion(s) already bound within the SF (7, 8, 12). Attempts to define further the mechanistic details of K⁺ ion permeation from ionic current measurements have confronted a major challenge, however, in that recording the positions of individual ions as they permeate the channel has not been possible. Thus, a conduction mechanism derived from the dynamics of the individual ions as they permeate a selective ion channel has remained elusive.

Gating of voltage-sensitive channels, i.e., pore opening and closing, involves voltage-sensing domain motions that trigger conformational changes of the S4–S5 linker and the S5 and S6 helices (13). It is less widely appreciated that gating also has a component sensitive to the osmolarity of the bulk surroundings (14): the open probability (and/or single-channel conductance) of squid axon K⁺ channels is reduced under hyperosmotic stress, whereas hypoosmotic stress has the opposite effect (15). Although an interpretative framework that ties these observations to protein conformational changes has been lacking, Zimmerberg et al. demonstrated convincingly that this gating component involves depletion of water from the protein (15). We suspect that this phenomenon represents a molecular-scale dewetting transition of water confined within the hydrophobic pore cavity (16). At the single-molecule level, dewetting transitions in hydrophobic confinements (17) have not been observed experimentally, while simulations have focused primarily on small model systems (18–20). Several studies have, nonetheless, suggested a connection between dewetting and gating in MscS and nAchR channels (21, 22), underscoring the potential relevance of molecular-scale dewetting transitions to a specific biological function—namely, channel gating.

Using all-atom molecular dynamics (MD) simulations, we simulated ion permeation through a K⁺ channel, the pore domain of rat Kv1.2, on a microsecond timescale, thus providing direct characterization of single-channel conduction based on permeation of individual K⁺ ions (Fig. 1). In support of Hodgkin and Keynes’s ideas, we found that permeation proceeded with two SF-bound ions awaiting knock-on from a third, incoming ion that drives conduction. From the dynamics of the permeating ions, we propose an overall conduction mechanism that allows us to directly deduce the rate-determining and voltage-dependent step.

Under reverse voltages, we observed—in the absence of the voltage sensors—transition of the open, conducting pore into a closed, nonconducting conformation. Pore closure involved molecular-scale dehydration: Water confined within the hydrophobic cavity of the pore underwent density fluctuations, resulting in complete (cooperative) dewetting and hydrophobic collapse of the cavity; concurrent rearrangements of two key helical residues locked the channel in a closed state. These observations demonstrate that molecular-scale dewetting may be a key mechanistic element of a biological function—channel gating—and provide a functional explanation for conservation of hydrophobic cavities in voltage-gated ion channels. Our results suggest that the voltage sensors may act to prevent collapse of the pore into its intrinsically more stable closed state (23). Because hydrophobic cavities are conserved structural motifs in voltage-gated K⁺, Na⁺, and Ca²⁺ ion channels (24), hydrophobic gating may be a common component in their overall gating mechanism.

Results

Permeation.

From our MD simulations, we directly recorded ion permeation through the pore domain of the rat Kv1.2 voltage-sensitive K⁺ channel (Fig. 1) (4, 5) at experimentally accessible (depolarizing, positive) voltages (V; 0 < V < +180 mV, SI Methods). The homotetrameric pore domain—S5, S6, and S4–S5 linker helices retained, voltage sensor (helices S1–S4) and T1 domain removed—was embedded in a lipid membrane at a temperature of 310 K and bathed in 0.6 M KCl, a concentration at which K⁺ conduction is saturated (25).

In the physiologically dominant K⁺-transport direction (intracellular to extracellular, Fig. 1A), we observed, on a microsecond timescale, between 10 and 100 K⁺ ion permeation events at each applied voltage and, on aggregate, passage of over 500 ions (Table S1). The cumulative number of complete permeation events was found to increase linearly with time (Fig. 1B). The current-voltage (I_K–V) relationship (26, 27) is shown in Fig. 1C. Ions were observed to move in concert through the SF in single file (Movie S1 and Movie S2). The passage times (τ_p) required for successive ions to cross the SF were thus correlated with one another (Fig. 1C, Inset). The time for individual ions to pass through the SF varied; for example, at +123 mV, the times varied between ∼1 and ∼47 ns. The passage times across the water-filled, intracellular-facing pore cavity, ≤ 1 ns, were 30- to 700-fold shorter. Because at 0.6 M KCl the cavity was nearly always occupied by K⁺, the passage time across the full pore was essentially equal to the passage time across the SF alone.

We analyzed the mean waiting time (τ_w) between two consecutive complete permeation events as a function of V. From the mean waiting time τ_w, we determined the current—voltage (I_K–V) relationship (Fig. 1C). In the linear region (V > +51 mV), the single-channel conductance was determined to be γ_k = 233 ± 33 pS. From our recorded K⁺ ion and water molecule permeation events (Fig. 1B and Table S1), we measured the transport ratio for those moieties that permeated directly through the SF, excluding mechanistically irrelevant, yet experimentally indistinguishable, permeation events that occurred elsewhere through the protein or the membrane. We measured I_W/I_K = 0.9 ± 0.2, essentially independent of V (Fig. 1D).

Conduction Mechanism.

We found that ions and water molecules were predominantly bound in an alternating manner in the four internal SF sites S1–S4 (Fig. 2 A and B). The SF also has three peripheral sites, S0 (extracellular), and S5 and S6 (intracellular) (2–5, 7). In contrast to existing data (3–5, 7–9, 28), we found that ions and water molecules favored distinct sites, even at 0 mV: K⁺ preferred S2 and S4 over S1 and S3, whereas water molecules exhibited the opposite preference.

Fig. 2.

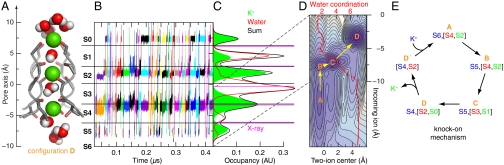
Knock-on mechanism of conduction through the selectivity filter. (A) K⁺ ions (Green) and water molecules (Red/White) are bound at SF sites S0-S6 (residues 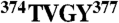, Gray/Red). Internal SF sites S1–S4 are defined by the ion-coordinating carbonyl groups and the hydroxyl group of Thr374. (B) Representative (+123 mV) positions of individual permeating ions (varying colors) vs. time. After entering the SF from S5, ions favor S4, S2, and S0 over S3 and S1. (C) Kinetic histograms of permeating ions (Green, filled) and H₂O (Red) occupancy calculated from the data in (B); AU, arbitrary units. Black (simulation) and magenta (crystal structures) lines mark the SF oxygen atom mean positions. (D) Potential of mean force (0.5 kcal/mol contours) of the multi-ion SF configurations in (B) (in cases of four-ion SF occupancy, the three SF ions with the lowest z coordinate were selected); the vertical and horizontal axes are the position of the incoming ion and the mean position of the two ions above it. The potential of mean force minima represent the four predominant three-ion configurations, denoted A–D in (E); configuration D is shown in (A). Arrows indicate transitions between the three-ion configurations. Overlay (D): Average ion-water coordination number (for simulations at depolarizing voltages). (E) Ion permeation by the knock-on mechanism. Presence of both two- (D^′) and three-ion (A–D) configurations leads to the observed kinetic occupancy, O_K ∼ 2.4. See SI Text for details.

As shown in Fig. 2B, ions moved from the intracellular to the extracellular side of the SF by consecutively occupying the following sites: [S4,S2]→[S3,S1]→[S2,S0]. The ion translocations were almost entirely unidirectional in the outward direction. The total K⁺ contribution to the occupancy histogram (Fig. 2C)—that is, the average kinetic occupancy of the SF—was measured at O_K ∼ 2.4, implying the presence of a third, incoming ion that is involved in transport. Single-file ion permeation as enforced by the SF implies that the passage and waiting times are related by τ_p = O_Kτ_w; computation of O_K from these waiting times also yielded 2.4 ± 0.1. Focusing on three-ion configurations, we represented these as a two-dimensional potential of mean force, U = -RT ln p(z_i,z_jk), where the probability of observing a given three-ion state, p(z_i,z_jk), is a function of the position of the third ion entering the SF, z_i, and the mean position of the two ions already in the SF, z_jk (7). From such a representation of our data (Fig. 2D and Fig. S3), we identified four minima corresponding to four predominant three-ion “states,” denoted A–D in Fig. 2E. We found that permeation of a single ion included transitions between the three-ion states: A → B → C → D (Fig. 2D, Movie S1 and Movie S2) (7, 8, 12).

Our simulations directly demonstrate a conduction mechanism in the spirit of the knock-on mechanism proposed in 1955 by Hodgkin and Keynes (12), whereas a vacancy type diffusion mechanism is not supported by our data (12, 29). Formation of the knock-on intermediate B (ions present in S5,[S4,S2]) is central. Upon binding, the incoming ion in S5 causes the two internal ions [S4,S2] to leave their otherwise preferred positions to form C (S5,[S3,S1]) and then, quickly, D (S4,[S2,S0]). The D → A transition involves the exit of the permeating ion from S0 and recruitment of a new ion into the intracellular cavity. To close the conduction cycle, this incoming ion must ultimately be partially dehydrated and bound at S5, typically with one water molecule positioned between it and the ion in S4. This step regenerates the knock-on intermediate B (Fig. 2E). Analysis (Fig. S4) showed that knock-on intermediate B was short-lived relative to the time taken to generate it, and that state C was also short-lived; ions in C were in their least favored internal positions, [S3,S1] (Fig. 2C). Whereas ion recruitment into the cavity is fast (< 1 ns) and only weakly field dependent, generation of the precise ion–water arrangement found in intermediate B is the rate-limiting step and also the step that depends most strongly on the applied voltage.

Gating.

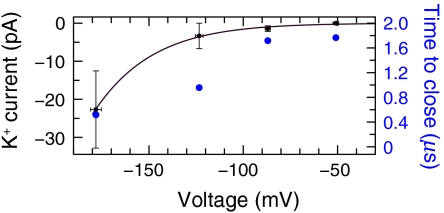
We consistently observed ionic conduction cessation and pore closure at reverse (hyperpolarizing, negative) voltages and at 0 mV (Fig. 3, Figs. S5 and S6, Table S1, and Movie S3, Movie S4, Movie S5, and Movie S6). The time before pore closure ranged from 100 ns to more than 1 μs; at negative voltages, the closure time correlated inversely with the magnitude of the applied voltage (Fig. 3 and Figs. S5). At 0 mV, the closure time was the shortest (∼100 ns). Experimentally, intact Kv1.2, with voltage sensors retained, closes on a millisecond timescale (1, 13); the timescale for closure of the isolated pore domain is unknown. (No closure occurred in a control simulation of intact Kv1.2 [0 mV, 1.7 μs], nor did the closed pore domain spontaneously reopen; Table S1.) The results presented here are direct observations both of the transition from the open, conducting pore to a nonsymmetrical closed, nonconducting pore and of the closed conformation itself, for which no experimental structure has yet been determined.

Fig. 3.

Transient K⁺ conduction and pore closure at hyperpolarizing voltages. K⁺ current (left ordinate) and time to pore closure (right ordinate) are plotted vs. V. At 0 mV, the time to pore closure was ∼100 ns.

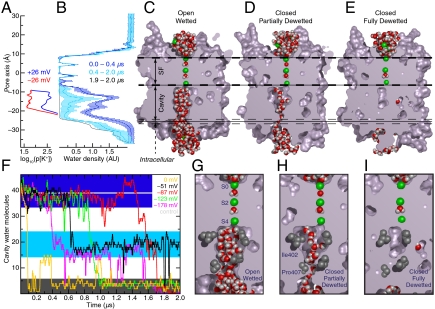
Pore closure was accompanied by dehydration of the inherently hydrophobic cavity (Fig. 4). Negative voltages (V ≤ -26 mV) depleted K⁺ ions from the cavity, leaving it temporarily occupied only by water, whereas positive voltages (V≥+26 mV) ensured steady cavity occupancy by water molecules and hydrated ions (Fig. 4A and Fig. S5). The water-vapor equilibrium of water confined within the now ion-depleted hydrophobic cavity shifted toward the vapor state (17), and pressure and density fluctuations in contiguous bulk water facilitated essentially complete dehydration—a dewetting transition—of the cavity (Fig. 4 B–F).

Fig. 4.

Gating by dewetting of the intracellular cavity at hyperpolarizing voltages. (A) Probability of observing a K⁺ ion at a given position within the cavity at positive (Blue) and negative (Red) voltages of ± 26 mV; application of these voltages resulted in neither K⁺ permeation nor pore closure. (B) Water density profiles (-178 mV) through the pore averaged over the indicated times. The density fluctuations (bars, one SD) that accompany dewetting (0.4–2.0 μs) are pronounced relative to initial fluctuations with the pore open (0–0.4 μs); after closure (1.9–2.0 μs), the cavity is essentially water free. (C–E) Cavity dewetting (-123 mV) illustrated by slices through the pore, showing wetted (open, conducting), partially dewetted (single file), and dewetted (closed, nonconducting) pore states. (F) Water occupancy inside the cavity vs. time at five pore-closing voltages; each color represents a different voltage. In a 1-μs control simulation of intact Kv1.2 at 0 mV, the pore did not close and the occupancy remained constant at 38.8 ± 1.9 (horizontal gray line; see SI Text). (G–I) Magnification of (C–E) showing the pore constrictions at Ile402 and Pro407.

The water density within the Kv1.2 cavity was initially similar to that of bulk water. As closure proceeded, the water density fluctuated dramatically on a timescale of hundreds of nanoseconds (Fig. 4B), and the cavity partially or fully emptied in a cooperative transition (Fig. 4F). At the three most hyperpolarizing voltages, the cavity completely emptied and the pore fully closed on a microsecond timescale (Fig. 4 C–I and Movie S3). At the smallest negative voltage that resulted in pore closure (-51 mV), the cavity did frequent the completely dewetted state, but ended, after 2 μs, in a partially dewetted state.

The partially dewetted state was an intermediate observed during all pore closures (Fig. 4 D, F, and H). This state is characterized by a cavity hydration level midway between the completely wetted, open cavity and the completely dewetted, closed cavity. In the partially dewetted state, a single file of water molecules formed across the tightest pore constriction, the conserved Pro405-Val406-Pro407 motif (“PxP,” “PVP” in Kv1.2; Fig. 4H, Figs. S6 and S7, and Movie S4). A single file is insufficient to facilitate ion passage through this constriction, where at most two water molecules can coordinate the ion along the pore axis (in bulk water, six to eight water molecules coordinate one K⁺); this deficit of coordinating water molecules cannot be compensated by favorable interactions with the protein. Thus, even the partially dewetted state is effectively closed.

Conformational Changes.

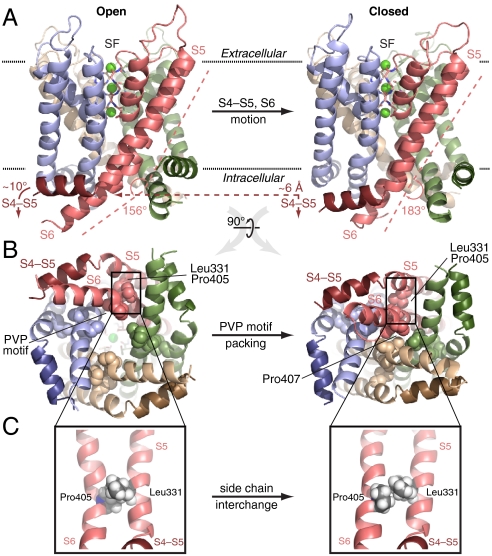
Pore closure following cavity dewetting involved pronounced conformational changes of the S5 and S6 helices, the S4-S5 linker helix, and the cavity-lining hydrophobic residues. Rearrangements of two key helix residues, Pro405 (S6) and Leu331 (S5), ultimately locked the channel in a closed conformation (Fig. 5, Fig. S7, and Movie S5). The S4-S5 linker moved toward the intracellular side by less than a helix diameter (Fig. 5A). The changes we observed support a previously hypothesized electromechanical linkage between voltage sensor motion and conformational changes of the pore domain (4, 5). Apparently, only modest (∼6 Å) linker displacements accompany larger pore conformational changes; because the voltage sensors were absent, the observed pore closure was exclusively driven by cavity dewetting and not triggered by the linker displacement.

Fig. 5.

Kv1.2 gating is asymmetric. Open (Left; 0.7 μs) and closed (Right; 1.2 μs) conformations of the pore (-123 mV); each subunit is colored distinctly (S4-S5 linker helices darker), and K⁺ ions (Green) in the SF (Sticks) are also shown. (A) Side view of the transmembrane region. Upon closure, the S4-S5 linker moves ∼6 Å toward the intracellular space and helix S6 straightens at the PVP motif (kink angle defined by S6 residues 385–405 and 406–419). (B) Closure viewed from the intracellular side. Tight packing of PVP motifs (Spheres) from diagonally opposed subunits (Pink and Tan) pinches off the cavity, especially at Pro407. (C) Enlarged view of S5 and S6. Exchange of the Leu331 and Pro405 side chains locks S6 in place.

We found that helix S6 straightened at the PVP motif, a motif present in many K⁺ channels and that has been demonstrated to be critical to channel gating (30). Straightening typically involved two of the four subunits, thereby allowing opposite PVP motifs to approach each other (Fig. 5A and B); in some cases, motion of even a single subunit was sufficient to form an ion-impermeable constriction. At negative voltages, the tightest constriction consistently developed at Pro407 (the second PVP motif Pro residue): opposite Pro407 C_α atoms were ∼13 Å apart in the open pore but only ∼5 Å apart in the closed pore. As S6 straightened, the tightly packed side chains of Pro405 and Leu331 (in helix S5 of the same subunit) exchanged positions, locking S6 into a straight conformation (Fig. 5C, Fig. S7, and Movie S6). At 0 mV, a tight constriction also developed at Ile402.

Discussion

Permeation.

The single-channel conductance, γ_K = 233 ± 33 pS, obtained from the linear part of our I_K–V curve (Fig. 1C, V > +51 mV), lies within threefold of the experimental value of 83 pS [intact Shaker, conductance ∼ 45 pS at 295 K, 0.6 M KCl (25); temperature-corrected assuming that γ_K increases ∼1.5-fold per 10 K of temperature difference [], i.e., Q₁₀ = 1.5, 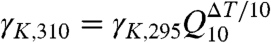(31); also, lack of the T1 domain in the simulation may lead to decreased access resistance]. The unexpected absence of current at |V| < +51 mV (Fig. 1C) suggests that an unidentified energetic barrier to conduction may be present at low voltages. This barrier may result from a force field artifact (e.g., lack of polarizability) or the absence of the voltage sensors, which could alter fluctuations of the SF that influence permeation or change the electrostatic potential (barrier) across the pore.

Macroscopic measurements in different K⁺ channels have suggested that about one water molecule, on average, is cotransported with each ion (32, 33), and a generic H₂O/K⁺ transport ratio of unity has been widely assumed. Our measurement of I_W/I_K = 0.9 ± 0.2 agrees well with experiment and suggests that this aspect of the conduction mechanism is invariant across the K⁺ channel family. The satisfactory agreement between the values for ion and water transport obtained in experiments and in our simulations suggests overall that our results can be used to provide further insight into the mechanistic details of ion permeation.

Our kinetically derived results for the Kv1.2 pore (Fig. 2D) conform to earlier thermodynamics-based proposals for KcsA (7, 8), namely, that four states are central to the conduction process. Direct recording of the individual ion positions during permeation permitted us to extend these proposals by directly identifying a minimal conduction cycle in which the rate-determining step is dehydration of a third, incoming K⁺ ion (Fig. 2E). Specifically, permeation occurs when two SF-bound ions are “knocked-on” by the incoming ion. In line with Hodgkin and Keynes’s measured flux exponent of O_K ∼ 2.5 (12), corresponding to the average SF kinetic ion occupancy, we measured O_K ∼ 2.4 from our simulations, indicating the mandatory presence of a third ion for transport. Beyond Hodgkin and Keynes’s interpretation of their own measurements, we find that formation of this knock-on intermediate is indeed the rate-determining—and the most voltage-dependent—step in K⁺ channel conduction.

Although existing crystallographic data indicate that the ion occupancy of the SF is largely uniform (8, 9), we found that ions and water molecules favored distinct SF sites: K⁺ preferred S2 and S4 over S1 and S3, whereas water molecules exhibited the opposite preference. The distinct site preferences we observed may reflect the differing coordination requirements of water molecules and K⁺ ions. Prior analysis of ion permeation through KcsA suggested that uniform ion occupancy in the SF is a prerequisite for high throughput by the knock-on mechanism (8). That model did, however, include the possibility of a nonuniform ion distribution across the SF without dramatically decreasing overall flux. Our analysis indicates that K⁺ conduction by the knock-on mechanism may proceed through an SF that is not necessarily uniformly occupied (Fig. 2 B and C).

Gating.

We directly observed the transition between an open, conducting pore of a voltage-sensitive K⁺ channel and a closed, nonconducting conformation. In the absence of the voltage sensors, this transition occurred within a few microseconds by dehydration and concurrent hydrophobic collapse of the water-filled pore cavity. Molecular-scale dewetting transitions in proteins have not been captured experimentally, but only by MD simulations of small model systems (18–20); extremely rapid dewetting was also observed in short (< 20 ns) simulations of the (closed) MscS mechanosensitive channel (21). Our observations of pore closure represent conclusive demonstration of molecular-scale dewetting in the context of a specific biological function—gating of an ion channel.

In addition to the commonly appreciated voltage-sensitive component, an additional component sensitive to osmotic pressure is likely an inherent part of (voltage-sensitive) ion channel gating (14, 34). We have identified here the source of this osmotically sensitive gating component in K⁺ channels—molecular-scale dewetting—with a hydrophobic gating mechanism. Osmotic sensitivity has been observed experimentally for K⁺ channels: Subjecting squid axon voltage-gated K⁺ channels to a uniform hyperosmotic stress reduced the open probability (and/or the single-channel conductance), whereas a hypoosmotic stress had the opposite effect (15). Similar observations were made for crayfish voltage-gated Na⁺ channels (35). The concurrent gating volume change or, equivalently, the number of water molecules evacuating the squid K⁺ channel—presumably the cavity—upon the conformational change was measured to be 40–50 water molecules, identical to the reduction in the cavity water occupancy we found upon channel closure (Fig. 4F).

Extensive electrophysiological data further support our proposal that hydrophobic gating and the conformational transition leading to a closed pore are elements of the overall gating mechanism in Shaker-family K⁺ channels. First, the narrowest constriction formed at the PVP motif. Accessibility experiments in Shaker revealed that Val406 (Kv1.2 numbering is used in the following) in the PVP motif is 10³–10⁵ times more accessible in the open state than in the closed state. Conversely, Val410, three residues below the PVP constriction, has nearly invariant high accessibility (36). Second, gating requires the S6 proline residues, as shown by Kv1.5 mutagenesis studies, although their exact locations are not critical (30).

Third, alteration of cavity hydrophobicity shifts the open/closed equilibrium (15, 37–42). Substitution of Shaker Pro407 by hydrophilic residues (for example, Pro407Asp) yields constitutively open channels, whereas hydrophobic mutants, such as Val410Trp, are constitutively closed. The Pro407Asp/Val410Trp double mutant control, which exhibits near-normal gating, indicates that all of these mutants (37, 38), as well as a Kv2.1-like Kv1.1 mutant (PVP → PIP) (39), alter the open/closed equilibrium by modifying the hydrophobicity of the cavity. The Shaker Ile402Cys mutation also slows channel closure, as seen by increased open-channel activity on hyperpolarization (40). Likewise, relative to K⁺, Rb⁺ and Cs⁺ have longer pore residence times and slow channel closure (41). Presumably these ions favor peripheral SF sites S5 and S6, given their preference for SF sites S1 and S3 relative to K⁺ (see also Fig. 2C) (8, 9), thereby keeping the cavity more hydrated (42).

The hydrophobic gating hypothesis is in accord with the open-channel blocking properties of tetraethylammonium (TEA). Intracellular TEA blockade typically prevents K⁺ channel closure (43). In the Shaker Ile402Cys mutant, however, TEA can be trapped inside the closed cavity. The increased polarity and larger volume of the cavity in this mutant enables trapping of the hydrophobic TEA cation. The ability of hydrophobic (organic) cations to modulate the open vs. closed equilibrium is exquisitely sensitive to minor variations in channel sequence and the molecular details of the blocker itself [e.g., TEA is trapped in the closed cavity of Shaker Ile402Cys, but hydrophilic N-methylglucamine cannot be trapped within the closed cavity (42)].

Consistent with these experimental data, we observed the fastest dewetting transition and pore closure time (∼100 ns) at 0 mV. At this voltage, K⁺ populated only site S4, not sites S5 or S6, at the SF-cavity boundary, which allowed the four Ile402 residues to snap into a tight hydrophobic constriction at the SF intracellular entrance. This constriction reinforced the overall cavity hydrophobic confinement, thereby accelerating the dewetting transition relative to the negative voltages (V ≤ -26 mV). Due to the applied negative potential, K⁺ ions were frequently forced into S5 and S6; the significant population of K⁺ in these sites prevented formation of the Ile402 constriction. At -26 mV, occasional K⁺ entry from the intracellular side into the cavity further ensured cavity hydration, delaying the closure time to beyond 2 μs (Fig. S5). (Because pore closure depends on the cavity electrostatics, the precise voltage where closure is fastest—here, coincidentally, 0 mV—is likely sensitive to the membrane dipolar potential, K⁺ concentration, and [absent] voltage sensors.) Crystal structures of Gly77d-Ala KcsA (44) and MlotiK1 (45) in their closed states reveal ion-depleted cavities, presumably due to a hydrophobic constriction similar to that formed by Kv1.2 Ile402 (e.g., KcsA Phe103).

Fourth, whereas most Shaker S5 and S6 alanine mutants exhibit simple, quantitative differences in gating behavior, a few mutants exhibit strikingly abnormal, multiphasic I–V curves. Abnormal mutants include Leu331Ala, Val406Ala, and Val410Ala (23). Notably, the Leu331Ala mutation, as well as separate results on a Pro405Ala mutant (46), suggests that the Leu331-Pro405 interlock (Fig. 5C) is critical for stabilizing the closed state.

Perspectives.

Hydrophobic gating is, we believe, closely linked to channel rectification. Channels with small hydrophobic cavities exhibit decreased or no inward conduction; at negative voltages they outwardly rectify, precisely because their small cavities are prone to undergo dewetting leading to pore closure. KcsA, which possesses a relatively small (Kv1.2-like) hydrophobic cavity, exhibits such outward rectification (47). By contrast, MthK and BK, two high-conductance, Ca²⁺-activated K⁺ channels that possess larger hydrophobic cavities, do not exhibit outward rectification, suggesting that these channels are less prone to undergo dewetting and pore closure (48, 49). Inward rectifying K⁺ channels such as Kir2.2 (50) possess small cavities, similar to KcsA or Kv1.2, but their more hydrophilic cavity lining (e.g., Ile402 substituted by Asp or Asn; Fig. S8) mitigates dewetting, which presumably helps maintain inward conduction through an open pore. It is particularly noteworthy that the Pro407Asp mutation in Shaker significantly weakens the outward rectification and makes the channel inward rectifying (37). Similarly, the presence of cavity-lining glycine residues in leak (K_2P) channels increases cavity size and decreases cavity hydrophobicity, leading to the unusual constitutive conduction properties of these channels (51). Point mutations or experimental conditions that favor cavity dewetting may thus be useful for obtaining future crystal structures of voltage-sensitive channels in closed conformations.

Beyond electromechanical linkages (4, 5, 13), voltage sensor repositioning in response to membrane potential changes may further adjust the open/closed channel equilibrium by tuning the electrostatic potential—and, consequently, the water stability—within the cavity. In particular, our results suggest that the sensors minimize the risk of cavity collapse; Yifrach and MacKinnon similarly proposed, on the basis of mutational data, that the natural state of the pore is closed and that the voltage sensors must exert work on the pore to open it (23).

We suggest that hydrophobic gating—which furnishes a functional argument for the not fully understood conservation of cavity hydrophobicity—is a central component of the overall gating mechanism of many ion channels (Fig. S8). Although the details may vary, hydrophobic gating is a mechanism that likely operates in several K⁺, Na⁺, and Ca²⁺ channels (24), and perhaps in other ion channels as well (21, 22, 52, 53).

Methods

Simulations were performed using Desmond (54) with the CHARMM27 force field (with backbone potential [CMAP] correction and TIP3P water model) (55, 56) and were analyzed using HiMach (57). The ionic current was driven by application (54) of a constant electric field, E, across the simulation box, a method known to mimic accurately a voltage clamp experiment (58). To obtain the applied voltage, V, from E, we assumed that the entire potential drop occurs across the SF (6, 59); this implies V = EΔz, where Δz = 13.4 ± 0.2 Å is the distance between Thr374∶O_γ and Tyr377∶O, averaged over all simulations at depolarizing voltages. All simulations were performed at experimentally accessible voltages, -180 < V < +180 mV. Throughout, error bars and “±” represent SEM. For additional methods, see SI Text.