Coherent and incoherent inference in phylogeography and human evolution

Abstract

A hypothesis is nested within a more general hypothesis when it is a special case of the more general hypothesis. Composite hypotheses consist of more than one component, and in many cases different composite hypotheses can share some but not all of these components and hence are overlapping. In statistics, coherent measures of fit of nested and overlapping composite hypotheses are technically those measures that are consistent with the constraints of formal logic. For example, the probability of the nested special case must be less than or equal to the probability of the general model within which the special case is nested. Any statistic that assigns greater probability to the special case is said to be incoherent. An example of incoherence is shown in human evolution, for which the approximate Bayesian computation (ABC) method assigned a probability to a model of human evolution that was a thousand-fold larger than a more general model within which the first model was fully nested. Possible causes of this incoherence are identified, and corrections and restrictions are suggested to make ABC and similar methods coherent. Another coalescent-based method, nested clade phylogeographic analysis, is coherent and also allows the testing of individual components of composite hypotheses, another attribute lacking in ABC and other coalescent-simulation approaches. Incoherence is a highly undesirable property because it means that the inference is mathematically incorrect and formally illogical, and the published incoherent inferences on human evolution that favor the out-of-Africa replacement hypothesis have no statistical or logical validity.

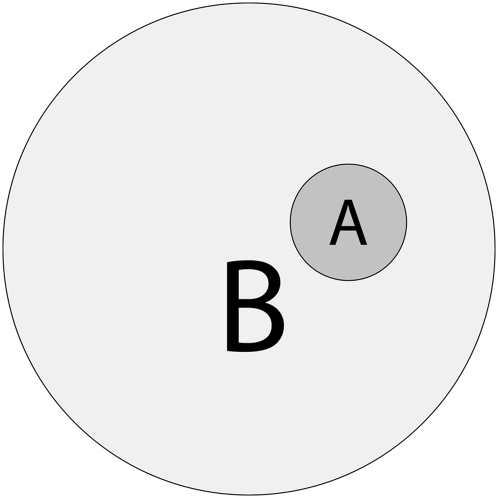
Coherence is an important statistical property when comparing nested or composite models (1, 2). Coherence means that the statistics or probabilities used to measure the goodness of fit of the models obey the constraints imposed by formal logic. For example, consider comparing two models, A and B, such that model A is fully nested within model B, as shown by the Venn diagram in Fig. 1. From elementary probability theory and Boolean logic, the probabilities of A and B must satisfy the constraint that Probability(A) ≤ Probability(B) because all observations that support model A also support model B, A being is a special case of model B; however, some observations can support model B but not model A. Any goodness-of-fit statistic or posterior probabilities on models A and B that are consistent with this logical constraint are coherent, and any statistics or posterior probabilities that can violate this logical constraint are incoherent. Another example involves partially overlapping models. Let {M₁,…,M_n} be a set of models such that at least one pair, say M_j and M_k, is overlapping; that is, Probability(M_j and M_k) > 0. Then, the probability of at least one of the M_is being true is less than the sum of the probabilities of each M_i. This situation arises because the probabilities of the intersections of the overlapping hypotheses must be subtracted from the sum to yield the true probability of at least one hypothesis being true. Any goodness-of-fit statistics or posterior probabilities on the set {M₁,…,M_n} that are consistent with this logical constraint are coherent, and any statistics or posterior probabilities that can violate this logical constraint are incoherent. Incoherent inference is formally illogical inference and represents a mathematical error.

Fig. 1.

Venn diagram of two hypotheses, A and B, such that hypothesis A is fully nested (a proper logical subset) within hypothesis B.

Intraspecific phylogeography is the investigation of the evolutionary history of populations within a species over space and time. This field entered its modern era with the pioneering work of Avise and coworkers (3, 4), who made qualitative inference from a visual overlay of an evolutionary tree of the haplotypes observed in a genomic region upon a geographical map of the sampling locations. As the field matured, there was a general recognition that the inferences being made were subject to various sources of error, so the next phase in the development of intraspecific phylogeography was to integrate statistics into the inference structure. One of the first statistical phylogeographic methods was nested clade phylogeographic analysis (NCPA) (5), which has been extended to analyze multilocus data (6–8). NCPA uses realized coalescent processes as estimated through haplotype trees as the basis of statistical inference. Alternative statistical approaches to phylogeography have been developed through coalescent simulations of specific phylogeographic models for both hypothesis testing and parameter estimation (9, 10). NCPA and simulation approaches are not mutually exclusive, because both can be used in a synergistic fashion to produce deeper phylogeographic insight than possible with either approach alone (11). I show in this paper that some coalescent-simulation methods are incoherent and therefore have only limited utility in hypothesis testing but still can be used in a synergistic fashion with NCPA. Potential causes of this incoherence are discussed, and some corrections are proposed. Coherent inference is possible through NCPA, and a contrast of coherent and incoherent inference pertaining to human evolution is presented.

An Example of Incoherent Inference

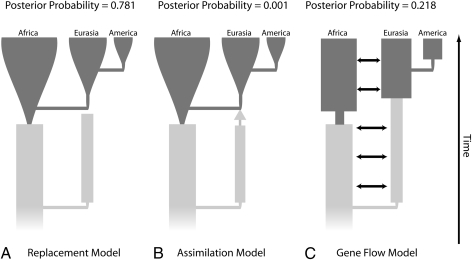
Recent reviews and defenses of the coalescent-simulation approach (10, 12) cite the analysis of Fagundes et al. (13) as an exemplar of statistical phylogeographic inference. That paper uses the popular coalescent-simulation technique of approximate Bayesian computation (ABC) (14) that is presented as allowing statistical comparisons among complex phylogeographic models. In particular, ABC assigns posterior probabilities, given the data, to a finite set of simulated a priori models. These posterior probabilities are supposed to measure the probability of a model being true given that one of the simulated models is true. Fig. 2 is a simplified version of figure 1 in Fagundes et al. (13) that shows the three models of human evolution to which those authors assigned posterior probabilities, along with those probabilities.

Fig. 2.

(A–C) Three models of human evolution and their posterior probabilities as calculated by the ABC method (13). For all models, dark gray represents modern human populations, and lighter gray represents archaic populations. Differences in width of the gray areas indicate differences in population size over time. The single arrow in B indicates the possibility of a genetic contribution by archaic Eurasian populations to modern populations via admixture with the population expanding out of Africa. The double-headed arrows in C indicate gene flow between African and Eurasian populations.

Of particular interest are models A (Fig. 2A) and B (Fig. 2B). Model A is the out-of-Africa replacement model, which posits that an expanding African population completely replaced Eurasian populations with no admixture. Model B is the assimilation model that allows potential admixture between the expanding African population and the Eurasian populations. The degree of admixture is measured by a parameter M that can vary from zero (no genetic input from archaic Eurasians) to 1 (no genetic input from the expanding African population into Eurasians). M measures the strength of the arrow shown in Fig. 2B. As Fagundes et al. (13) note, the replacement model is a special case of the assimilation model with M = 0. Fagundes et al. (13) assigned a posterior probability of 0.781 to model A, the special case with M = 0, and a posterior probability of 0.001 to model B, the general case that includes model A. It is mathematically and logically impossible for model A to have a greater probability than model B (Fig. 1). As this example clearly demonstrates, ABC is incoherent.

Note that in this case the incoherence is not some minor numerical deviation that could be attributable to an approxima-tion or rounding error. Model A is three orders of magnitude more likely than the general case model B (Fig. 2). Moreover, as is shown in the next section, the central equation of ABC is inherently incoherent for three separate reasons, two of which are applicable in every case that deals with logically overlapping hypotheses. Hence, the incoherence in this example is not a case-specific computational error but rather arises from a mathematical error in the ABC algorithm.

Causes of Incoherent Inference with ABC

There are many mathematical flaws in the ABC procedure (15), and some of them can lead to incoherent inference. The general form of the ABC equation used to estimate the posterior probability, P, for hypothesis i (H_i) given the vector of observed summary statistics, S*, and given that one of the n simulated a priori hypotheses (set H) is true, is (see equation 9 in ref. 14 or the equation in the supplementary text of ref. 13)

where Π_i is the prior probability of hypothesis i, and G_i is a goodness-of-fit measure based on a normalized difference of the vector of expected (simulated) summary statistics S_i under model i minus the vector of observed statistics S*, but using only those points that also satisfy where δ is a prespecified tolerance parameter. The goodness-of-fit measure is designed to achieve its maximum value when S_i = S*.

One flaw in Eq. 1 is that the goodness-of-fit measures often are not adjusted for the dimensionality of the data or the models. For continuous data, the dimensionality of the data is the number of effectively independent observations. For categorical data, the dimensionality is the number of mathematically unconstrained categories. The dimensionality of the model is the effective number of mathematically unconstrained parameters. It has long been known that raw goodness-of-fit statistics must be adjusted for dimensionality to avoid false and incoherent inference (16–18). For example, suppose in a plant population 50% of the plants had white flowers and 50% had red flowers. Let hypothesis 1 be that this color polymorphism is the result of a single autosomal locus with two alleles, w and r, such that white is recessive, and that the population is randomly mating. The estimated frequency of the w allele under this random-mating model is 1/√2, and the expected phenotype frequencies are 50% white, 50% red—a perfect fit to the data. Now consider hypothesis 2 that assumes that red is the recessive phenotype in a random-mating population. Now, the estimated frequency of the r allele is 1/√2, and the expected phenotype frequencies are 50% white, 50% red—another perfect fit. Now consider a third hypothesis that the population is self-mating with all individuals being homozygous. The estimate of the w or r allele frequencies are 1/2 under this model, and the expected phenotype frequencies under this model are 50% white, 50% red—yet another perfect fit. Three contradictory models all have perfect fits. Obviously, goodness of fit alone is insufficient for valid statistical inference. The problem here is one of dimensionality; the data have a dimensionality of one (a single independent phenotypic class), and all three models have a dimensionality of one (a single independent allele frequency parameter), so the difference between the dimensionality of the data and the dimensionality of the model (degrees of freedom) is zero. The zero degrees of freedom indicate that the perfect fits of these three contradictory models are without any biological or statistical significance whatsoever.

Now consider a case of two models, A and B, that differ in dimensionality. Suppose the χ² statistic for model A is 10 and for B is 5. Given that the χ² statistic decreases in value with increasing goodness of fit, then the raw χ² statistics indicate that model B fits the data better than model A. However, suppose that the degrees of freedom of A are five and the degrees of freedom of B are one. When the χ² statistics are adjusted for the degrees of freedom, the probability assigned to model B is 0.025 and that for model A is 0.075. Hence, using the standard 5% level of significance, model A is accepted, and model B is rejected, the opposite inference from the unadjusted goodness-of-fit statistics. The ABC method in Fagundes et al. (13) uses goodness-of-fit measures that are not adjusted for the dimensionalities of the data or the models, and this condition alone can cause incoherence. Part of the problem in adjusting for dimensionality in simulations is that the dimensionality in complex simulations often is not clear. For example, from table S7 in ref. 13, the assimilation model has four additional parameters relative to the replacement model. However, if only one of these parameters (M) takes on the value of zero, then the assimilation model collapses into the replacement model. The other three parameters are meaningful only when conditioned on M > 0. The difference in dimensionality between these two models is somewhere between one and four, but the exact value is difficult to calculate because of the conditional dependencies among the parameters. Nonetheless, difficulty in calculating dimensionality does not justify ignoring it.

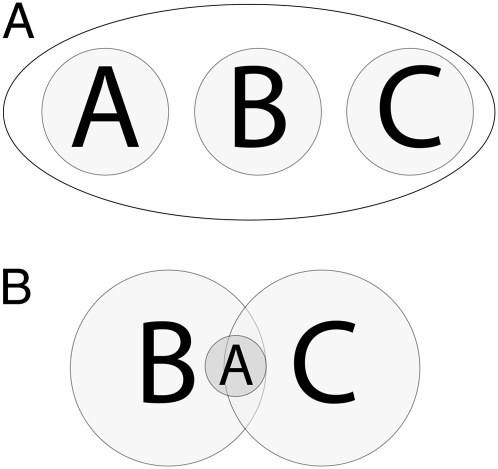
A second flaw in Eq. 1 is the denominator. Simulation techniques assess the relative fit of a finite number of prespecified, but rarely exhaustive, phylogeographic models. To obtain the relative fit of a specific model, it is mathematically required to condition on the event that one of the simulated models is true. The denominator in Eq. 1 is supposed to be proportional to the probability that one of the models in H, the set of all simulated models, is true; logically, this denominator should be proportional to the probability of the union of all n models. Note that the denominator in Eq. 1 is a simple sum over all n models. From elementary probability theory, the probability of the union of several events is the sum of the probabilities of the individual events if and only if all the events are nonoverlapping and mutually exclusive. An example of mutually exclusive models is illustrated in a Venn diagram for a three-model case in Fig. 3A. Fig. 3B shows the logical relationships of the three models simulated by Fagundes et al. (13). As noted above, the replacement model A is a proper subset of the assimilation model B. The third model C is a composite model that shares many components with models A and B, as shown by the extensive sharing of parameters and prior distributions given in table S7 from ref. 13. Hence, model C overlaps with models A and B, as shown in Fig. 3B. Using elementary probability theory, the probability of the union of these three models is

Fig. 3.

The logical union of three models. A shows the set that contains the union of three nonoverlapping, mutually exclusive hypotheses. B shows the union of the three models of human evolution given in Fig. 2.

Thus, the denominator in Eq. 1 is mathematically and logically incorrect when applied to the models simulated by Fagundes et al. (13). ABC uses Eq. 1for all cases, regardless of the logical relationship of the hypotheses being simulated. Because the models that are simulated vary from case to case on an ad hoc basis, there can be no universal denominator for Eq. 1. The denominator in Eq. 1 is mathematically wrong and incoherent because a simple sum always violates the constraints of logic when logically overlapping models are tested.

The third flaw in Eq. 1 concerns the prior distribution defined by the Π_is. Fagundes et al. (13) assigned a prior probability of one third to each of these three models. Given that the replacement model is fully nested within the assimilation model, Π(replacement) equals Π(assimilation) equals one third if and only if the prior assigns the probability of one third to the subset of the assimilation model with M = 0 and assigns a prior probability of zero to the subset of the assimilation model with M > 0. Hence, the possibility of favoring M > 0 is eliminated by assumption in their analysis. Worse, they treat the Π_is as mutually exclusive and exhaustive events such that they sum to one. However, from Eq. 2, the sum of these three probabilities must be less than two thirds; otherwise the constraints of logic are violated. Thus, the prior probabilities used in the very first step of their Bayesian analysis are incoherent.

ABC is used for parameter estimation in addition to hypothesis testing, and another source of incoherence is suggested from the internal discrepancy between the posterior probabilities generated by ABC and the parameter estimates obtained by ABC found in ref. 13. Consider again models A and B in Fig. 2. The posterior probabilities given in Fig. 2 are incoherent, but for the sake of argument, let us suppose they are true. In that case, the optimal estimate of M under model B should be M = 0. If ABC had estimated M as zero, the goodness of fit of model B would be identical to that of model A, and the inference would have been coherent. Instead, ABC converged to an “optimal” estimate of M that was small but significantly different from zero.

There are three explanations for this internal inconsistency. The first is that the posterior probabilities are correct, but the estimation algorithm is flawed. This explanation is formally illogical. The posterior probabilities given by Eq. 1 explicitly depend upon the “optimal” parameter estimates, therefore, if the estimation procedure is flawed, so are the posterior probabilities.

The second explanation is that the posterior probabilities of the models are incorrect (as already shown), but the estimation procedure of ABC is correct. This possibility may be possible because the estimation algorithm does not depend upon the incoherent denominator or priors used in Eq. 1. If the estimation algorithm is correct, the estimate of M is truly greater than zero, despite other assumptions in their simulation that strongly bias the estimate of M downward (15). The estimation algorithm of ABC also generates posterior probabilities for the parameters under a specific model, and the posterior distribution of M under the assimilation model provides another method of evaluating the replacement model. Fagundes et al. (13) report that the 95% highest posterior density for their estimate of M does not overlap zero despite their strong biases toward smaller values of M. Because only the lower tail of the posterior distribution of M would include M = 0, the posterior probability of replacement (M = 0) is ≤0.025, whereas the posterior probability of admixture (M > 0) is ≥0.975, so the posterior probabilities of M reject the replacement model in favor of the admixture model. Hence, the posterior probabilities generated by ABC from Eq. 1 directly contradict the posterior probabilities generated by the ABC estimation algorithm.

The third possibility is that both the posterior probabilities and the estimation algorithm of ABC are incorrect. Although the estimation algorithm does not suffer from all the errors contained in Eq. 1, it also has serious problems (15). In addition, Fagundes et al. (13) argue that the discrepancy arises because the estimation algorithm is sensitive to the prior. The prior used on M was a uniform prior over the interval [0,1] (13), which defines the entire range of possible values for M. Such a flat prior typically is invoked in Bayesian inference to reflect ignorance of the value of the parameter to be estimated. In a well-constructed Bayesian procedure, such flat priors should be quickly overwhelmed by the data in generating the posterior distributions (see the statistical appendix in ref. 19). However, Fagundes et al. (13) argue that a flat prior of ignorance so overwhelmed the data that the Bayesian procedure could come close to but could not find a solution (M = 0) that they claimed was 1,000-fold better than their final estimator (M > 0). An optimal Bayesian procedure should not show extreme sensitivity to a prior of ignorance (2, 20). Thus, if one accepts the explanation of Fagundes et al. (13), ABC is a deeply flawed Bayesian procedure in which ignorance overwhelms data to create massive incoherence.

Incoherent Inference in Coalescent-Simulation Approaches to Phylogeography and Its Possible Corrections

The ABC method is not the only incoherent method used with coalescent simulations for phylogeographic inference. For example, Bayes factors frequently are combined with coalescent simulations for phylogeographic inference (21–23), but Bayes factors are known to be incoherent (2) and highly sensitive to priors (24). Recent reviews (9, 10) of how coalescent simulations are used for statistical phylogeographic inference reveal that the problem of calculating the dimensionalities of the data and the simulated hypotheses often is ignored. Also, these reviews show that simulated hypotheses are often treated as mutually exclusive alternatives regardless of their actual logical relationships. Any coalescent-simulation procedure that does not adjust for dimensionality and ignores the logical relationships among the simulated hypotheses is capable of producing incoherent inference.

The coalescent-simulation approaches are applicable in some situations. For example, Bayes factors are appropriate when testing a model versus its logical complement (e.g., population subdivision versus panmixia). ABC could be extended to nested and composite hypotheses if the denominator in Eq. 1 and the priors were defined in a manner consistent with their logical relationships. To meet this requirement, the denominator in Eq. 1 would have to be redefined for every set of models to be compared. Composite hypotheses could be tested only if their intersections in probability space were calculated, and this calculation will be extremely difficult for complex models with multiple parameters. The goodness-of-fit measures used in ABC also would have to be corrected for dimensionality. Calculation of the dimensionality of complex models with multiple interacting parameters is not simple but could be done in a manner similar to that proposed by Cheverud (25), which would involve preliminary simulations followed by an eigenvalue analysis.

Some of the previously identified (15) problems in the parameter estimation portion of ABC are easily avoided by limiting the summary statistics to Euclidian measures, orthogonalizing the summary statistics before searching for the optimal fit, investigating robustness to the tolerance parameter instead of using a single set of heuristic guidelines for all sample sizes and geographical coverages, incorporating the sampling error of the observed statistics S*, and calculating dimensionalities of all models tested to avoid irrelevant and overdetermined models (recall the flower color example given above). The additional problem of sensitivity to priors of ignorance (13) needs to be investigated thoroughly.

Coherent Inference

One well-established method for the coherent testing of nested hypotheses is the likelihood ratio test (16, 26). Log-likelihood ratio tests are always greater than or equal to zero because the likelihood of the more general hypothesis is greater than or equal to the likelihood of the nested (null) hypothesis, as demanded by coherence. If the null hypothesis is true, then the likelihood of the nested hypothesis should be close to that of the more general hypothesis (but never greater, because that condition would be incoherent), resulting in a small-valued test statistic. Hence, the coherent log-likelihood ratio statistic tests whether the likelihood of the more general model is significantly greater than the likelihood of the nested null hypothesis under the assumption that the null hypothesis is true. If the general hypothesis has a likelihood that is significantly greater than that of the nested null hypothesis, then the null hypothesis is rejected.

NCPA is a coalescent-based testing approach that uses a combination of simulated permutation testing of null models and coherent log-likelihood ratio tests on nested hypotheses. The likelihood ratio test framework of NCPA is flexible and can also be used to test explicit a priori hypotheses. For example, the a priori out-of-Africa replacement hypothesis was tested in NCPA using log-likelihood ratio tests (27–29). The replacement model is treated explicitly as a nested hypothesis within the more general model that allows admixture and gene flow. All dimensionalities are calculated, so the degrees of freedom are known to be 17. The resulting log-likelihood ratio test had a value of 118.18, which, when adjusted for the 17 degrees of freedom, leads to the probability of the null hypothesis of replacement being true given the data of less than 10⁻¹⁷. This probability represents an extremely strong falsification of the replacement hypothesis.

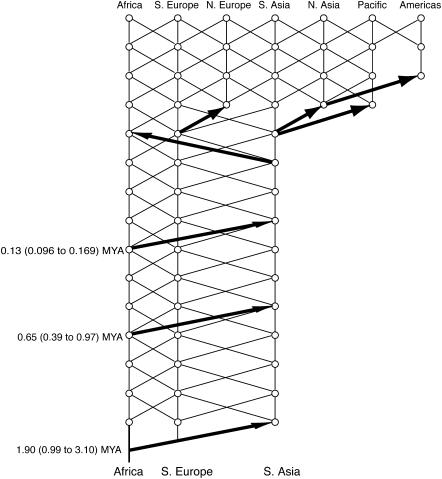
NCPA also is appropriate for coherent inference about composite hypotheses. Unlike coalescent-simulation approaches, NCPA does not require any prespecified models; rather, the overall model emerges from falsification of null hypotheses concerning each component. For example, consider the composite model of human evolution shown in Fig. 4 that was produced by NCPA (27–29). Fig. 4 shows three out-of-Africa expansion events because the null hypotheses of one or two out-of-Africa expansion events are rejected by likelihood ratio tests. This rejection does not mean that NCPA proves that there were exactly three expansion events out of Africa; rather, at least three events occurred, and there currently is no significant statistical evidence for more than three. The middle expansion in Fig. 4 is well corroborated by fossil, archaeological, and paleoclimatic data (29), so the middle Acheulean expansion should not be left out of any model of human evolution.

Fig. 4.

The model of human evolution based on the falsification of null hypotheses under NCPA. The thick black arrows indicate major events in population range expansion. The trellis indicates gene flow. The dating and 95% confidence intervals for the three major out-of-Africa expansions are based solely on the molecular genetic data. Further details are in refs. 27–29.

Fig. 4 also shows that the middle and most recent expansion events did not break the lines of genetic continuity in Eurasia; that is, neither of these out-of-Africa expansion events were total Eurasian-replacement events because the null hypothesis of total replacement was rejected by likelihood ratio tests (27, 28). Similarly, a trellis is shown interconnecting the African and Eurasian populations between the first and last out-of-Africa expansion events. This trellis signifies the inference of gene flow constrained by isolation by distance between Eurasian and African populations throughout the Pleistocene. Once again, this component of the model is supported by the strong rejection of the null hypothesis of no gene flow between Africans and Eurasians throughout the Pleistocene [log-likelihood ratio test = 72.39 with 18 degrees of freedom, P < 10⁻⁸, for the time range of 0.13–1.9 Mya, the molecular dates of the first and third expansion (30) and the log-likelihood ratio test = 30.02 with 18 degrees of freedom, P = 0.0094, for the narrower time range of 0.08–0.64 Mya (15), the narrowest time range suggested in ref. 13]. Similarly, every component of the model of human evolution shown in Fig. 4 has explicit statistical support based on rejecting null hypotheses with coherent tests of well-defined dimensionality.

Discussion

A statistical test can have many properties, such as power or false-positive rates. Such properties refer to the optimality of the test, but incoherence goes to the very core of the mathematical validity of the test. An incoherent statistic is a mathematical error and nothing more. For example, the fundamental equation of ABC, Eq. 1, is mathematically incorrect in every instance when two or more of the models being compared have any degree of logical overlap. Therefore any result derived from Eq. 1 is a mathematical error when dealing with logically overlapping hypotheses, even when the resulting posterior probabilities superficially obey the constraints of logic. For example, suppose A is nested within B, and that Eq. 1 yields P(A) equal to or less than P(B), a result which is superficially coherent. Because the denominator of Eq. 1 is mathematically wrong in this case, both P(A) and P(B) are wrong also. A single example of incoherence demonstrates that the equations being used are mathematically incorrect, and there can be no confidence in the validity of any result derived from these equations when dealing with logically overlapping hypotheses, even if coherence is superficially satisfied. Hence, incoherent methods, such as ABC, Bayes factors, or any simulation approach that treats all hypotheses as mutually exclusive should never be used with logically overlapping hypotheses. Previously published inferences based on incoherent probabilities, such as favoring the replacement hypothesis of human evolution (13), have no scientific or logical validity and are merely mathematical errors. Of course, one always can restrict incoherent methods such as ABC to simple, mutually exclusive hypotheses. However, such simple hypotheses (e.g., population subdivision versus no subdivision) often can be tested with standard statistical tests that do not require extensive computer simulations. The main rationale for using extensive computer simulations is to model more complex, composite hypotheses in which some degree of logical overlap is the norm, not the exception. For example, all phylogeographic models of human evolution in the recent literature show logical overlap (29). Hence, incoherent methods such as ABC cannot be used in a mathematically valid way to test any of the models of human evolution but rather must be restricted to the most simple and trivial phylogeographic hypotheses. Simply put, incoherent statistics produce formally illogical results, and scientific inference should, first and foremost, be logical.

There are other issues of fundamental logic relating to phylogeographic inference. First, the logical basis of inference in NCPA is based on falsifying null hypotheses, whereas coalescent-simulation approaches assign probabilities of truth or goodness-of-fit statistics to a finite set of nonexhaustive phylogeographic models under the assumption that one of the models in the set is true. As a result, the strong falsification of the replacement model of human evolution by NCPA is not logically incompatible with replacement having the highest probability of being “true” in the ABC analysis. Even a coherent inference scheme of relative fit can give a high probability of “truth” to a false hypothesis if all the hypotheses in the inference set are false. In this regard, any model of human evolution that does not have the Acheulean expansion or gene flow between Pleistocene human populations has been falsified (29), so all three models in ref. 13 have been falsified. Hence, the high probability of “truth” for replacement relative to three falsified hypotheses is logically compatible with the strong falsification of replacement as a null hypothesis by the coherent NCPA. Moreover, if the estimation component of ABC is correct, then the work of Fagundes et al. (13) also falsifies the replacement hypothesis and is therefore consistent with the coherent falsification of replacement by NCPA.

Because coalescent-simulation approaches can give high probabilities of truth to false hypotheses, they can generate false positives. The only way to protect against such false positives is to make sure that the true model is in the simulated set—an unrealistic demand. Consequently, the false-positive rate of coalescent-simulation approaches is logically unknowable and therefore is uncorrectable. In contrast, the multilocus cross-validation procedure of NCPA is effective in reducing false positives to below nominal levels as shown both by test cases of actual data and computer simulation (31).

Another major issue in logic is the treatment of composite hypotheses. Because coalescent-simulation approaches assign a single posterior probability or goodness-of-fit statistic to each composite model as a whole, it is logically impossible to make inference about any single component. For example, Fagundes et al. (13) argued against admixture on the basis of a single (incoherent) probability assigned to the assimilation model as a whole. Fig. 2 shows that the assimilation model also assumed total genetic isolation between human populations in Africa and Eurasia throughout the Pleistocene. This assumed isolation is irrelevant to the goodness of fit of the replacement model because the Eurasian population makes no genetic contribution to living humans under replacement, but it does affect the goodness of fit statistics of the assimilation model when M > 0. Because NCPA gives explicit statistical support to each component of a composite model, NCPA makes it clear that the assumption of total Pleistocene isolation is false (P < 10⁻⁸), and the null hypothesis that M = 0 is strongly falsified (P < 10⁻¹⁷), leaving only the alternative that M > 0 (15). Thus, the component of the assimilation model in Fig. 2B that is wrong is the assumed Pleistocene isolation between Africa and Eurasia and not the presence of admixture. The inference in ref. 13 that the low probability assigned to the assimilation model was caused solely by admixture has no logical basis, even if the probability had been coherent. As this example shows, NCPA allows logical inference on specific components of a composite model, but coalescent simulation does not.

NCPA is superior to coalescent simulations for phylogeographic hypothesis testing because it is coherent, is based on falsification rather than on relative fit, can logically control for false positives, and can decompose composite hypotheses (the norm in phylogeography) in a logical fashion. However, NCPA has some serious limitations. Unlike ABC and other coalescent-simulation approaches, NCPA does not estimate parameter values other than times of past phylogeographic events. Moreover, NCPA requires genomic regions that have had little to no recombination such that haplotype trees can be reliably estimated (with quantifiable error). Evolutionary history is written most clearly in such genomic regions, but other types of genetic data certainly do contain historic information and cannot be used by NCPA. Once hypotheses have been generated by coherent NCPA, coalescent-simulation approaches can be used for parameter estimation and for evaluating the compatibility of data sets other than haplotype trees with the hypotheses generated by NCPA (11). In this manner, NCPA and coalescent-simulation approaches should be regarded as complementary and synergistic approaches that both have a legitimate role in an integrated, phylogeographic inference scheme.