Joint estimation of DNA copy number from multiple platforms

Abstract

Motivation: DNA copy number variants (CNVs) are gains and losses of segments of chromosomes, and comprise an important class of genetic variation. Recently, various microarray hybridization-based techniques have been developed for high-throughput measurement of DNA copy number. In many studies, multiple technical platforms or different versions of the same platform were used to interrogate the same samples; and it became necessary to pool information across these multiple sources to derive a consensus molecular profile for each sample. An integrated analysis is expected to maximize resolution and accuracy, yet currently there is no well-formulated statistical method to address the between-platform differences in probe coverage, assay methods, sensitivity and analytical complexity.

Results: The conventional approach is to apply one of the CNV detection (‘segmentation’) algorithms to search for DNA segments of altered signal intensity. The results from multiple platforms are combined after segmentation. Here we propose a new method, Multi-Platform Circular Binary Segmentation (MPCBS), which pools statistical evidence across platforms during segmentation, and does not require pre-standardization of different data sources. It involves a weighted sum of t-statistics, which arises naturally from the generalized log-likelihood ratio of a multi-platform model. We show by comparing the integrated analysis of Affymetrix and Illumina SNP array data with Agilent and fosmid clone end-sequencing results on eight HapMap samples that MPCBS achieves improved spatial resolution, detection power and provides a natural consensus across platforms. We also apply the new method to analyze multi-platform data for tumor samples.

Availability: The R package for MPCBS is registered on R-Forge (http://r-forge.r-project.org/) under project name MPCBS.

Contact: nzhang@stanford.edu; junzli@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In recent years, more and more genetic studies have relied on collecting genome-scale data on DNA variants. With the rapid influx of large datasets came the increasingly common problem of data integration when multiple technical platforms (or different versions of the same platform) were used to interrogate the same biological samples. For example, The Cancer Genome Atlas (TCGA) project, an NIH-funded initiative to characterize DNA, RNA and epigenetic abnormalities in tumors, has adopted three independent platforms for studying DNA copy number variants (CNVs) in its pilot phase: Affymetrix SNP 6.0 arrays, Illumina HumanHap 550K SNP arrays and Agilent CGH 244K arrays. The conventional approach for analyzing these data is to apply one of the CNV detection (‘segmentation’) algorithms to search for genomic intervals of altered signal intensity using data from each platform separately. The segmentation results from three platforms are then combined. However, when the platforms disagree on the calling of a CNV, it is difficult to decide what the consensus should be. Furthermore, the reported DNA copy numbers (i.e. the location and magnitude of the changes) are often different in different platforms. At the fundamental level, the three platforms represent three distinct marker panels and different molecular assay methods:

• Illumina arrays produce allele-specific data, Agilent arrays produce only the total intensity, whereas Affymetrix arrays have both allele-resolved SNP probes and invariant CNV probes, thus effectively containing two sub-platforms.

• Agilent arrays produce two-color ratio data in a test/reference format, whereas the other two measure each sample independently.

• In regions of high-fold amplification, Illumina and Affymetrix tend to have more pronounced signal saturation. In fact, all three platforms estimate the true levels of copy number change with different scaling factors, which may be non-linear and may vary across chromosomes or samples (Bengtsson et al., 2009).

• The three methods produce data values with distinct noise characteristics, with different proportions of low-quality SNPs and distinct local signal trends that are partly due to the sample amplification procedures used.

• For some, such as the Illumina data, the default normalization procedure is not tailored to copy number analysis.

In short, each platform has its advantages and disadvantages, but together they produce a more detailed genome-wide survey for each sample. If the datasets from the three platforms are separately segmented, it is difficult to combine their respective segment summaries because, for the same underlying event, they will report different magnitudes, with different boundaries and different degrees of uncertainty. An integrated analysis, where information from all platforms are used at the same time to detect CNVs and to estimate the levels of change, is expected to maximize resolution and accuracy. Currently, however, there is no well-formulated statistical method to address the between-platform differences in probe coverage, sensitivity and analytical complexity. Simply combining the three data series into a single dataset without proper normalization will not yield better segmentation results, because when the underlying true copy number is not known, it is difficult to determine how to normalize across platforms given the uneven coverage between the platforms at any genomic region.

In order to tackle the increasingly common problem of data integration across multiple sources, we propose a new method based on a simple multi-platform change-point model. The model extends existing approaches for detecting change-points in a single sequence (Zacks, 1983) to the problem of detecting coupled changes in multiple sequences with differing noise and signal intensities. The model gives rise to an efficient algorithm, Multi-Platform Circular Binary Segmentation (MPCBS), which relies on a weighted sum of t-statistics to scan for copy number changes. MPCBS sums statistical evidence across platforms with proper scaling, and does not require a pre-standardization of different data sources. The statistics are derived through maximizing the likelihood of the multi-platform model, with the dimension of the model (i.e. the number of segments) chosen by maximizing a generalized form of the modified Bayes information criterion (BIC) proposed in Zhang and Siegmund (2007). Platform-specific quantities, such as noise variances and response ratios, are also estimated by our method. Importantly, the method provides a single, platform-free consensus profile for each sample for downstream analyses.

2 MULTI-PLATFORM MODEL AND METHODS OVERVIEW

Let the platforms be indexed by k = 1,…, K, with K being the total number of platforms. We observe total intensity data y_k = y_k1,…, y_knk for the n_k SNPs/clones on the k-th platform, which have ordered locations (t_k1,…, t_knk) along a chromosome. We assume that for each platform, the data have been normalized to be centered at 0 for ‘normal’ copy number and to have Gaussian (or near-Gaussian) noise. Actual data must be transformed with missing values imputed, sometimes with extreme outliers truncated in order to approximate Gaussian noise. In some studies, the ‘normal’ diploid state of the genome is difficult to determine, such as when an entire chromosome has been amplified. When this occurs, other types of information, such as allelic ratios from SNP arrays, or intensity ratios from two-color array comparative genomic hybridization (aCGH) experiments, will be needed to help assign the correct absolute copy number to each segment. Such complications are expected to affect all platforms. Here, we deal with the integration of multiple platforms in detecting changes in CNV and only need to assume that the baseline ‘normal’ state is shared in common across platforms.

The fact that all {y_k : k = 1,…, K} are assaying the same biological sample implies that at any genomic location t there is only one true underlying copy number μ_t for all platforms. We define the observed intensity level for the i-th probe of the k-th platform as consisting of a signal f_k(μ_tk,i) plus a noise term that has platform-specific variance σ²_k. Specifically, we assume the following model for the data:

(1)

where the noise term ϵ_k,i are independently distributed N(0, σ²_k). We call f_k(·), which quantifies the dependence of the observed intensity on the underlying copy number, the response function of platform k.

We model the true copy number as a piecewise constant function, i.e. constant within a segment, and yet may change to a different level at a ‘change-point’. For a chromosome of length T, we assume that there exists a series of change-points 0 = τ₀ < τ₁ < ··· < τ_m < T such that within each interval,

(2)

The magnitude parameters θ = (θ₀,…, θ_m) and change-points τ = (τ₁,…, τ_m) are all unknown and, like the response functions, must be estimated from the data.

For this article, we assume that the response function is linear, i.e. f_k(μ) = r_kμ. The parameter r_k, which we call the response ratio, describes the ratio between the change in observed intensity for platform k and the underlying copy number. The linearity assumption allows for simple and intuitive test statistics and fast scanning algorithms.

While the linearity assumption is an oversimplified ideal situation, empirically the platform response functions are often observed to be approximately linear for low-amplitude changes. Response functions are usually non-linear for high-amplitude changes due to saturation effects. However, the high-amplitude changes usually have high statistical significance and are relatively less affected by this simplification in modeling. The main purpose of our method is to boost power for the low amplitude, statistically borderline cases through multi-platform integration.

When the platform-specific response ratios r_k are known, the breakpoints τ and true copy numbers θ can be estimated through a likelihood-based recursive segmentation procedure that builds on the conceptual foundations of Olshen et al. (2004) and Vostrikova (1981), which we describe in Section 3.1. Conversely, when τ and θ are given, f_k can also be easily estimated using the procedures described in Section 3.4. Since both are usually unknown, we propose the iterative procedure described in Section 3.5.

3 METHODS

3.1 Pooling evidence by weighted t-statistics

First, consider the case where the goal is to test whether there is a CNV at a window from s to t. Under the null hypothesis that there is no CNV, the data within this region should have baseline mean f_k(0) = 0, i.e.

(3)

If there is a gain (or loss) of magnitude μ, each platform should respond with signal f_k(μ) = r_kμ. The signal is a mean shift in a common direction for all platforms, with the observed magnitude of shift being r_kμ for platform k, i.e.

(4)

Since the likelihood ratio statistic maximizes the power over all statistical tests for this model, we will use the likelihood-based framework to test this hypothesis. Let n_k(s, t) = |{i : t_k,i ∈ (s, t]}| be the number of probes from the k-th platform that falls within the interval (s, t]. Let 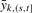denote the mean intensity of probes that map within (s, t]. It can be shown (Supplementary Material) that under this formulation, the generalized log likelihood ratio statistic is a weighted sum of platform-specific terms:

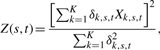(5)

where

(6)

is the t-statistic for testing for a change in segment (s, t) using the data from platform k. The weights

(7)

are proportional to the response ratio r_k, the square root of the number of probes from that platform that fall into [s, t), and the inverse of the estimated error SD 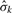. When there is only one platform, the statistic (5) is equivalent to the chi-square statistic used in the Circular Binary Segmentation (CBS) algorithm of Olshen et al. (2004). Theoretical properties of scans using (6) and related statistics for a single platform were studied by Siegmund (2007) and James et al. (1987). Usually σ_k is unknown and must be estimated from the data as well, and we replace it with an estimate 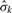in (6) and (7). In the simplest case, we assume a common variance for all probes of a given platform. The estimate of error standard deviation (SD) from platform k, 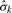, can be obtained from the residuals after subtracting the mean within each segment. The number of data points used to estimate σ is very large and thus 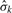is very precise and for all practical purposes can be treated as a known quantity. In situations where σ_k is dependent on the underlying copy number or differs between genomic regions, a generalized likelihood ratio statistic similar to (5) can also be computed.

Note that the statistic (5), which we call the weighted t-statistic, is different from the sum of chi-square (SC) statistic proposed in Zhang et al. (2009) for multi-sample segmentation, where each sample comes from a different biological source assayed on the same experimental platform. The statistic used in Zhang et al. (2009) is the SC from N samples,

(8)

Intuitively, one may be tempted to extend the above formula to the multi-platform case by proposing a weighted form (SWC)

(9)

that does not treat all platforms equally. However, this approach has the drawback that it does not reward agreement between platforms. When pooling data across samples, independent biological specimens are not expected to carry the same CNV, and often both deletions and amplifications can be observed between the samples at the same genome location. Thus, the statistic (8) is intuitively correct in not ‘rewarding’ agreement in direction of change between samples. For pooling data across platforms, however, the underlying CNV is the same, and the statistic in (5) correctly rewards agreement and penalizes disagreement. For example, consider the case of K = 2, where (5) simplifies to (δ₁²X₁² + δ₂²X₂² + 2δ₁δ₂X₁X₁)/2. If the signs of X₁ and X₂ agree, this statistic is always larger than (8), while if the signs disagree, it is smaller. This makes the weighted t-statistic more suitable for pooling evidence across multiple samples that come from the same biological source.

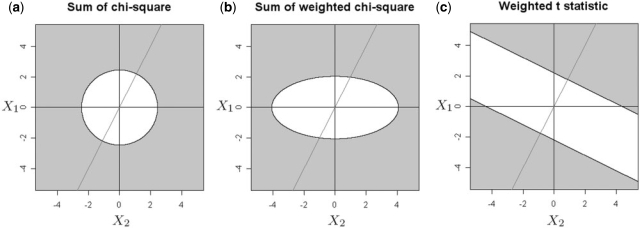
The difference between the three statistics is shown graphically in Figure 1 for the simple case of two platforms with the response ratio of the second platform being twice that of the first platform. Note that all three statistics are functions of X = (X₁, X₂), which, assuming that σ_k = 1, is bivariate Gaussian with mean 0 and identity covariance matrix under the null hypothesis. Figure 1a–c show in gray the region in the (X₁, X₂) plane where the null hypothesis will be rejected. That is, X needs to fall into the gray region to make a CNV call. For example, in Figure 1a, which depicts the situation in (8), the gray region is {X : Z^SC(X) > t^SC_α}, where t^SC_α is a threshold chosen for the test to have significance level α. In Figure 1b, which depicts the situation in (9), the weights δ₂/δ₁ = 2 favor evidence from X₂ over evidence from X₁, giving an elliptical boundary. In Figure 1c, which depicts the situation in (5), the boundary of the rejection boundary is {X : δ′X > t_α}, which is perpendicular to the vector δ₂/δ₁. Importantly, note that Figure 1c rewards agreement between the two platforms, while Figure 1a and b treat all quadrants of the plane equally. The statistic (5, Fig. 1c) also allows one platform to dominate the others: In the case where the directions disagree, e.g. in the upper-left or lower-right quandrants, the consensus can still be made according to the dominant platform.

Fig. 1.

Comparison of the null hypothesis rejection regions between the SC statistic (8) (a), the weighted SC statistic (9) (b) and the weighted t-statistic (5) (c) on K = 2 platforms. In all figures, the axes are the magnitudes of the X variables (6) for platforms 1 and 2. A significance level of 0.05 is used to determine the decision boundaries of all three statistics. For (b) and (c), weights of δ₁ = 1, δ₂ = 2 are used. The oblique line shows the direction of the weight vector δ = (δ₁, δ₂).

3.2 Recursive segmentation procedure

In the previous section, we described the statistic used to test whether a specific interval [s, t) constitutes a CNV. In reality, there can be multiple change-points in a chromosome's copy number. To detect all change-points, we adopted an extension to the recursive binary segmentation framework (Olshen et al., 2004; Vostrikova, 1981; Zhang and Siegmund, 2007). Vostrikova (1981) proved the consistency of binary segmentation algorithms. Olshen et al. (2004) proposed an improvement, called CBS, which works better in detecting small intervals of change in the middle of long regions. Zhang and Siegmund (2007) proposed a BIC criterion for deciding the number of segments. Both Olshen et al. (2004) and Zhang and Siegmund (2007) showed that these types of procedures work well on DNA copy number data. Two independent comparative reviews by Willenbrock and Fridlyand (2005) and Lai et al. (2005) concluded that the CBS algorithm of Olshen et al. (2004) is one of the best performing single-platform segmentation methods. This motivated us to extend CBS to the case of multiple platforms.

The MPCBS algorithm will be described in detail in the Supplementary Material. Here, we give an intuitive overview using the following notation: Let ℛ be an ordered set of segments {(i, j) : 0 < i < j < T}, and 𝒵 be the corresponding likelihood ratio statistics. Let M be the maximum number of change-points tolerated, which is usually determined by computational resources.

The algorithm proceeds as follows: S_k is the list of estimated change-points in the k-th iteration, which is initialized to contain only {0, T}. The entire dataset is scanned for the window [s*, t*) that maximizes Z(s, t), that is, where the evidence for a change is the strongest. This window is added to S_k. Then, the region (i) to the left of s*, (ii) between s* and t* and (iii) to the right of t* are each scanned for a sub-segment that maximizes Z(s, t), these maximum values are called Z_L, Z_C and Z_R, respectively. The corresponding locations of the maximum are R_L, R_C and R_R. These are kept in the ordered lists 𝒵 and ℛ. At each iteration k of the algorithm, the region whose maximum weighted t-statistic is the largest, i.e. i* = argmax_i 𝒵[i], is determined. The change-points from that region which achieve this maximum, i.e. (s*, t*) = ℛ[i*], are added to S_k. Since s*, t* splits a previously contiguous region into three regions, 𝒵 and ℛ must be updated to include the maximal z-values and maximizing change-points for the new regions to the left, center and right of the new change points. This process is repeated until S_k has at least M change−points in addition to {0, T}. Finally, the modified BIC criterion described in the next section is used to determine a best estimate of the number of change-points and the final segmentation. The modified BIC is a theoretically proven method for estimating the true number of change-points based on asymptotic approximations to posterior model probabilities. It is an off-the-shelf method that automatically determines the trade-off between false positive and false negative rates. For users who wish to detect CNV using more or less stringent stopping rules, the software MPCBS allows the option of a user-tunable z-score threshold for deciding the fineness of the segmentation.

3.3 Estimating the number of segments

To estimate the number of change-points, we use a modified form of the classic BIC criterion that extends the approach of Zhang and Siegmund (2007). In Zhang and Siegmund (2007), it was shown that the modified BIC, when used on top of the CBS procedure of Olshen et al. (2004), improves its performance for DNA copy number data.

To describe the extension of Zhang and Siegmund (2007) to the case of multiple platforms, we first define several quantities. For a given genome position t, let n_k(t)=|{i : t_k,i<t}| be the number of probes in the region [0, t) for platform k. Let

be the sum of the intensities of all probes in this region. For a given set of estimated change-points 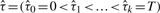, let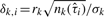

and

X_k,i is the t-statistic for testing that the change in mean at 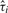is not zero. 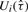is a weighted sum of X_k,i, just as (5) is a weighted sum of (6). Let N be the total number of distinct values in {t_k,i : 1≤k≤K, 1≤i≤n_k}, that is, the number of different probe locations from all K platforms. For any natural number n, n! denotes the factorial of n. It is possible to show using arguments similar to Zhang and Siegmund (2007) that

(10)

is asymptotically within an O_p(1) error term of the Bayes factor for comparing the model with k change-points versus the null model. The number of change-points should be selected to maximize (10), which we call the modified BIC.

The first term of the modified BIC is the maximized likelihood, and is thus the same as the first term of the classic BIC criterion. The second and third terms are penalties that increase with the number of change-points. The second term penalizes the θ parameters by summing up the logarithm of the effective sample size for estimating each θ_i. The third term is the logarithm of the total number of ways to select m change-points from N possible values, which penalizes the change-point parameters τ.

3.4 Estimating the platform-specific response ratio

In this section, we discuss the situation where the segmentation is known, and we would like to estimate the platform-specific response ratios r = (r₁,…, r_K), the baseline levels α = (α₁,…, α_K) and the underlying copy numbers θ = (θ₁,…, θ_m). For each 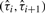, the data from platform k that fall within the segment can be used to obtain an estimate of f_k(θ_i):

(11)

For each i and k, 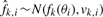, where 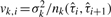is proportional to the noise variance of the k-th platform and inversely proportional to the number of probes in that platform that lies in the i-th segment. Thus, the negative log-likelihood of the data is

(12)

where α_k is a platform specific shift. The unknown parameter vectors r and θ should be chosen to minimize the above weighted sum of squares.

If the variances v_k,i were identical across i and k, r and θ can be estimated through the singular value decomposition of the matrix F=(f_i,k) or through a robust approach such as median polish. This model would then be similar to those proposed in Irizarry et al. (2003) and Li and Wong (2001) for model-based probe set summary of Affymetrix Genechip data. However, the differences in variances should not be ignored, because segments with less data, for which we are less sure of the mean estimate, should be down-weighted. Similarly, platforms with higher noise variance should also be down-weighted compared with platforms with smaller noise.

There are many ways to modify existing approaches to minimize (12). We take the following simple iterative approach: note that for any fixed value of r, the corresponding minimizer 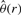can be found through a weighted least squares regression. The same is true if we minimize with respect to r when the value of θ is held fixed. Thus, joint optimization of r and θ is achieved through a simple block update procedure which we detail in the Supplementary Material.

3.5 Iterative joint estimation

Sections 3.1–3.3 detail a method for segmenting the data when the platform-specific signal response functions are known. Then, Section 3.4 describe a method for estimating the response functions with the segmentation given. In most cases both the segmentation and the response functions are unknown. The following algorithm is an iterative procedure that jointly estimates both quantities from the data.

Algorithm: Multi-platform joint segmentation

Fix stopping threshold ϵ. Initialize f_k⁽⁰⁾(μ) = μ for k = 1,…, K. Set i ← 0.

1. Estimate the segmentation τ⁽ⁱ⁾ using MPCBS assuming response functions f⁽ⁱ⁾.

2. Estimate f⁽ⁱ⁺¹⁾ as described in Section 3.4 assuming the segmentation τ⁽ⁱ⁾.

3. If ‖f⁽ⁱ⁺¹⁾−f⁽ⁱ⁾‖<ϵ, exit loop and report:

   

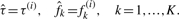
Otherwise, set i ← i + 1, and iterate.

In this algorithm, f_k⁽ⁱ⁾ and τ⁽ⁱ⁾ are, respectively, the response functions and the segmentation estimated in the i-th iteration. The response functions are initialized to be equal in all platforms, a setting which in most cases already gives a decent segmentation. After the first iteration, the estimated segmentation can be used to obtain a more accurate estimate of the response functions, which can then be used to improve the segmentation. In all of our computations we simply set the stopping parameter ϵ = 0.01. The estimates of f_k stabilized within a few iterations for all of the HapMap samples analyzed in Section 4.1.

4 RESULTS

4.1 Comparison with single platform CBS by using HapMap data

We applied our approach to the eight HapMap samples analyzed in Kidd et al. (2008) using fosmid clone end-sequencing. In addition, we also analyzed the reference genotype data for the same eight samples from an Agilent platform with over 5000 common copy number variants (Conrad et al., 2009). We combined the fosmid and Agilent datasets and collectively referred to them as reference CNVs. The same HapMap samples have both been analyzed by Illumina 1M Duo and Affymetrix 6.0 genotyping chips. We used MPCBS to combine the two platforms in making joint CNV calls, and compared these calls with those made by running CBS on each individual platform separately. We also compared MPCBS results with the union of CBS calls made on both platforms, as well as the intersection of CBS calls made on both platforms. Details of data source and normalization are described in the Supplementary Material. For CBS analysis, we show results using a range of P-values from 0.0001 to 0.1. For MPCBS, we show results using both the modified BIC-based stopping criterion described in this article, as well as a range of z-score thresholds from 4.5 to 9. We assessed performance by computing, for each method and stopping threshold, the fraction of calls made by the method that is also reported in Kidd et al. (2008) or Conrad et al. (2009) (precision), and the fraction of CNVs reported in these two references that were also detected by the method (recall).

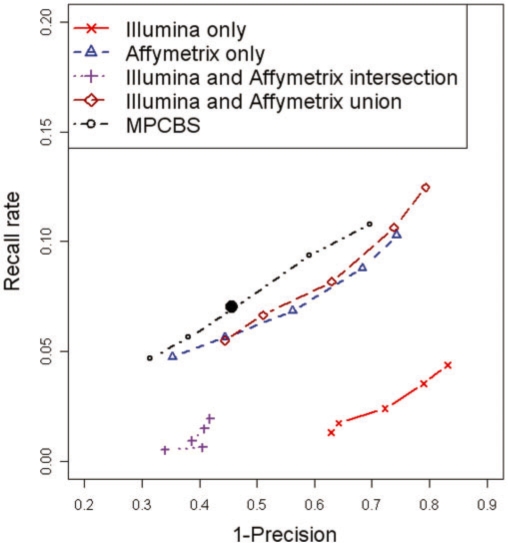
When the fosmid and Agilent platforms detect a CNV, the boundaries of the CNV are not precisely defined. We therefore defined concordance to be any overlap between a CNV called by CBS/MPCBS and a reference CNV. When multiple calls made by CBS/MPCBS overlapped with the same reference CNV, only one of them was counted as concordant. This guarded against over-segmented CNV regions. This criteria of overlap can be made more or less stringent, but as long as it is applied consistently in the comparison between CBS and MPCBS, the conclusion made would be unbiased. Figure 2 shows the curves of 1-precision versus recall. We see from these results that concordance with reference is low across all methods. The low concordance with fosmid-detected CNVs has also been reported previously, see for example, Cooper et al. (2008) and McCarroll et al. (2008). Importantly, at comparable levels of precision, MPCBS gives higher recall rates than either Affymetrix or Illumina does alone, and higher recall rates than combining calls from the two platforms by intersection or union. In general, Affymetrix discovers many more segments than Illumina, with many more concordant calls, likely due to having more probes than the Illumina chip.

Fig. 2.

Precision–recall curve for detection of CNVs in eight HapMap samples. The methods being compared are (I) CBS on Illumina platform only, (II) CBS on Affymetrix platform only, intersection of (I) and (II), union of (I) and (II) and MPCBS jointly on Illumina and Affymetrix. The solid black dot is the result given by MPCBS using the modified BIC stopping criterion. The horizontal axis is the fraction of calls made by the given method that fails to overlap with a reference CNV (1−precision). The vertical axis is the fraction of all reference CNVs that are discovered by the given method (recall). The curves are obtained by varying the stopping thresholds of CBS and MPCBS.

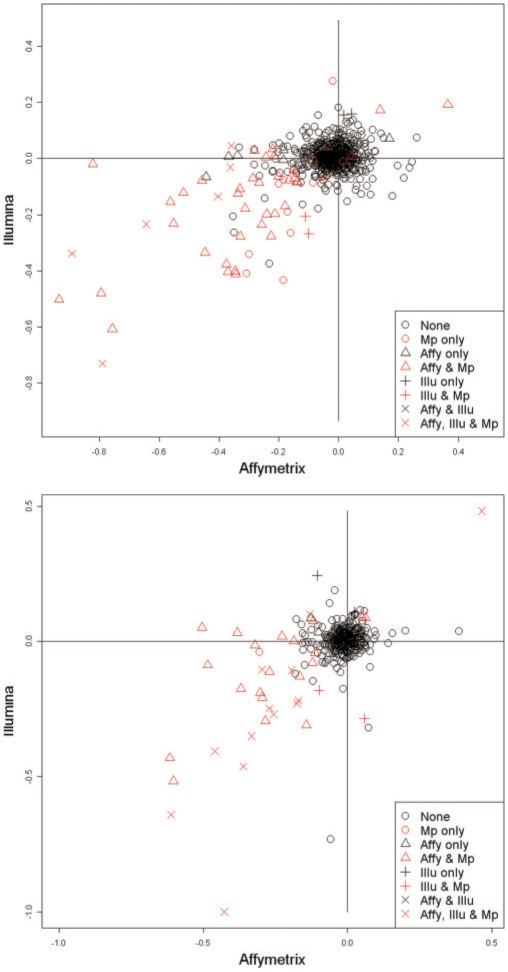
Is the low concordance between Affymetrix, Illumina and reference CNVs due to inherent disagreement in the raw data, or low sensitivity or specificity of the statistical method? To investigate this issue, for each reference CNV, we computed the mean intensity of the Affymetrix or Illumina probes mapping within each reference CNV. We would expect that if the absolute change in mean probe intensity is high for a given platform, and if the segment spans a sufficient number of probes, the CNV is more likely to be also called by that platform. Alternatively, if the mean probe intensity within the reference CNV is indistinguishable from baseline, it would be missed by that platform. Figure 3 shows the Affymetrix versus Illumina mean intensity plot for two of the eight samples. Each point corresponds to a reference CNV. The points colored in red are reference CNVs also detected by MPCBS, i.e. overlapping one of the CNVs called by MPCBS. The shapes of the points reflect whether they are detected by single platform CBS in none of the individual platforms alone, in only Affymetrix, in only Illumina or in both Affymetrix and Illumina. Most of the reference CNVs do not have a shift in intensity in any platform, suggesting that the microarray-based assays are noisy and prone to cross-hybridization, especially in repetitive regions or regions with complex rearrangements (Cooper et al., 2008). By combining information from the Affymetrix and Illumina platforms, MPCBS is able to make calls that were not identified in either platform alone.

Fig. 3.

Mean probe intensities within reference CNV calls for Affymetrix versus for Illumina in samples NA18956 and NA12878. The points are colored and shaped based on the combination of Affymetrix (Affy), Illumina (Illu), and MPCBS (Mp) that detected them.

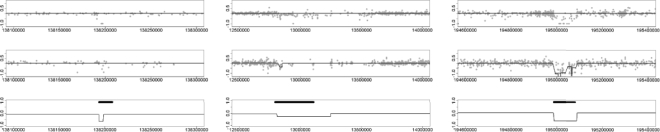
Figure 4 shows three examples of CNV calls made by multiplatform CBS that are missed by one or both of the individual platforms. In the left panel, the detected CNV region contains too few probes and is thus missed by CBS on both Affymetrix and Illumina platforms alone. However, by pooling the information from both platforms, MPCBS is able to make a call. Similarly, in the middle panel, neither platform alone has strong signal, but with pooled evidence the MPCBS call has good agreement with the reference. The right panel shows that CBS has the tendency to over-segment CNV regions. The problem is mitigated in MPCBS coupled with the modified BIC stopping criterion.

Fig. 4.

Examples of regions detected by MPCBS. For each panel, the top plot shows the Illumina data with CBS fit, the middle plot shows the Affymetrix data with CBS fit and the bottom plot shows the MPCBS consensus estimate along with thick horizontal lines depicting the reference CNV call. In all plots, the horizontal axis is probe location in the unit of base pairs, and the vertical axis is the data intensity for the given platform or the consensus intensity estimate θ in the case of MPCBS.

4.2 TCGA cancer data

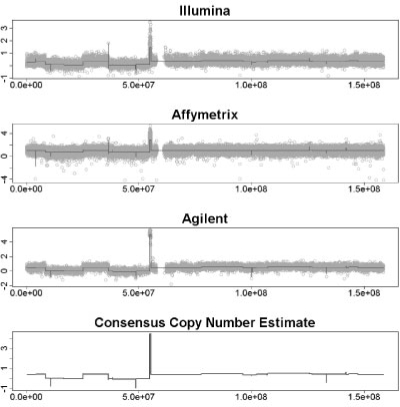
To provide an example of application to somatic CNVs, we analyze a dataset from TCGA samples. Intensity data from three platforms, Illumina 550 K, Affymetrix 6.0 and Agilent 244K were downloaded from TCGA data portal. The segmentation result for CBS and MPCBS on chromosome 7 of the data is shown in Figure 5. The top three panels show the results for the standard approach, which is to call CNVs for each platform separately. But to integrate the three CBS datasets one is faced with the difficulty that for a true underlying CNV, the three segmentation summaries may not have all detected the CNV, and even when they do, they will report different magnitudes, different boundaries and different degrees of uncertainty. The MPCBS result in the bottom panel provides a natural consensus estimate without the problem of having to decide how to integrate the three CBS segmentation results. While MPCBS provides a single combined estimate, it remains a statistically constructed best possible summary, and cannot be automatically taken as evidence of technical replication. We emphasize that crucial results in specific regions still require careful validation in further experiments.

Fig. 5.

Result of MPCBS on a TCGA sample. The top three plots show Illumina, Affymetrix, and Agilent data with CBS fit. Bottom panel shows multi-platform consensus. For all plots, the horizontal axis is probe location in base pairs, and the vertical axis is the data intensity for the given platform or the consensus intensity estimate θ in the case of MPCBS.

4.3 Computing time

The computation was done on a 1.6 GHz Intel Core 2 Duo processor. In the analysis of this example region, which contains 30 170 Illumina probes, 98 993 Affymetrix probes and 13 241 Agilent probes, MPCBS took 122 s for each iteration of steps 1–3 in Section 3.5. The algorithm converged in two iterations. Extrapolating to the full dataset consisting of ∼2 million Affymetrix probes, > 1 million Illumina probes and 240K Agilent probes, the computing time is on the order of 1 CPU-hour per sample, and fluctuates according to the number of CNVs detected. In general, computing time scales with the number of samples linearly, and with the number of probes N as Nlog N. We have implemented additional speed-up algorithms that are documented in the R package.

5 DISCUSSION

We have proposed a model for the joint analysis of DNA copy number data coming from multiple experimental platforms. Under simplifying assumptions, the maximum likelihood framework can lead to an easily interpretable statistic and a computationally tractable algorithm for combining evidence across platforms during segmentation. By comparing with Agilent and fosmid clone end-sequencing data on eight HapMap samples, we showed that MPCBS gives more accurate copy number calls, as compared with a simple intersection or union of the calls made by CBS separately on each platform. This method has also been applied to TCGA data, where it provides consensus copy number estimates that provide a natural summary of data from Affymetrix, Illumina and Agilent platforms.

A main feature of MPCBS is that it combines scan statistics from multiple platforms in a weighted fashion, thus without requiring pre-standardization across different data sources. For a given underlying copy number change, platform A may report a higher level of absolute change in signal intensity than platform B, but if A also shows a higher level of noise, or fewer probes in the genomic region in question, the scan statistics of A may not be larger than those of B because such statistics are scaled appropriately within each platform before being combined in MPCBS. However, careful normalization and standardization across platforms are still desirable when running MPCBS. This is because while segmentation per se is not sensitive to absolute signals of different platforms, the mean level of change reported by MPCBS can still be sensitive to the scale of different platforms. Recently, Bengtsson et al. (2009) proposed a joint normalization method for bringing different platforms to the same scale and for addressing the issue of non-linear scaling between platforms. While the method of Bengtsson et al. is not concerned with joint segmentation, it can be coupled to MPCBS so that the mean level of copy number change reported by MPCBS is an even better approximation of the consensus level of change. We expect that the segmentation result will alter slightly when using data preprocessed by the method of Bengtsson et al. mainly because the current version of MPCBS has not considered non-linear response functions. In short, we recommend pre-standardization of the scale of copy number changes across platforms before running MPCBS. This would have little impact on segmentation but may improve the mean copy number change reported.

MPCBS can be applied also to the situation when a biological sample is assayed multiple times on the same experimental platform. In our general specification of the model (2.1), we allow the SNPs/clones from different assays to overlap. When the same platform is used for repeated assays of the same sample, model (2.1) and the MPCBS algorithm still apply without modification. This does not assume that technical replicates using the same platform have the same signal response curves, as there may be differential quality in replicates due to differing handling and hybridization conditions. However, the user can have the option of constraining the response ratios to 1 if the samples have already been preprocessed, e.g. using the method of Bengtsson et al. (2009) to equalize the signal magnitudes.