Globally, unrelated protein sequences appear random

Abstract

Motivation: To test whether protein folding constraints and secondary structure sequence preferences significantly reduce the space of amino acid words in proteins, we compared the frequencies of four- and five-amino acid word clumps (independent words) in proteins to the frequencies predicted by four random sequence models.

Results: While the human proteome has many overrepresented word clumps, these words come from large protein families with biased compositions (e.g. Zn-fingers). In contrast, in a non-redundant sample of Pfam-AB, only 1% of four-amino acid word clumps (4.7% of 5mer words) are 2-fold overrepresented compared with our simplest random model [MC(0)], and 0.1% (4mers) to 0.5% (5mers) are 2-fold overrepresented compared with a window-shuffled random model. Using a false discovery rate q-value analysis, the number of exceptional four- or five-letter words in real proteins is similar to the number found when comparing words from one random model to another. Consensus overrepresented words are not enriched in conserved regions of proteins, but four-letter words are enriched 1.18- to 1.56-fold in α-helical secondary structures (but not β-strands). Five-residue consensus exceptional words are enriched for α-helix 1.43- to 1.61-fold. Protein word preferences in regular secondary structure do not appear to significantly restrict the use of sequence words in unrelated proteins, although the consensus exceptional words have a secondary structure bias for α-helix. Globally, words in protein sequences appear to be under very few constraints; for the most part, they appear to be random.

Contact: wrp@virginia.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

We are interested in exploring the extent to which protein structural constraints and secondary structure sequence preferences restrict the space of possible protein sequences. The remarkable ability of sequence similarity searching, and local similarity statistics, to identify proteins that share similar structures, even when those proteins share <25% protein sequence identity, reflects the observation that real unrelated protein sequences have similarity scores that are indistinguishable from random protein sequences (Brenner et al., 1998; Pearson and Sierk, 2005). Thus, proteins that share more similarity than expected by chance can reliably be inferred to be homologous. Moreover, from a sequence similarity perspective, real unrelated proteins are indistinguishable from random synthetic protein sequences.

However, sequence similarity involves the comparison of two complete proteins; in real protein sequences, short amino acid words from a modest number of structural types may provide substantial constraints. For example, while there are 20²⁰⁰ possible proteins of length 200, one could imagine these proteins to be comprised of 10⁵⁰ combinations of four-amino acid words from 10 different structural types. While the latter number is very large, so that a protein structural alphabet might not constrain sequence similarity scores enough to make them appear non-random, it is more than 10²⁰⁰ times smaller than the former. Here, we search for restrictions on the space of protein sequences that can be used to build real proteins by counting four- and five-residue words in non-redundant sets of proteins.

Our approach, identifying constraints on global amino acid choice in proteins, is very different from the more traditional goal of associating sequence preferences with amino acid secondary structure (Chou and Fasman, 1974; Rost and Sander, 1993). Amino acid preferences in secondary structure, when coupled with data from aligned homologous sequences, can yield accurate (>70% Q₃) secondary structure predictions (Jones, 1999; McLysaght, 2005; Pollastri et al., 2002; Rost, 2001). However, it is unclear whether these secondary structure preferences restrict amino acid word choice across the entire protein. Put another way, do secondary structure word preferences drive protein word composition? or are protein sequence word choices relatively unrestricted, so that the local word choices drive the secondary structure, rather than vice-versa? Here, we focus on sequence constraints in unrelated proteins with dissimilar structures; within a protein family, there are strong evolutionary constraints on protein word choice that reflect evolutionary history in addition to structural constraints.

If secondary structure word preference drives protein word composition, real protein sequences should prefer structurally favored amino acid words, and these preferences should distinguish real proteins from models of random proteins. For example, the engrailed homeodomain from Drosophila melanogaster folds rapidly in a hierarchical manner by the diffusion–collision of partially formed secondary structural elements (Mayor et al., 2003). Here, folding information should be encoded locally in the sequence, since secondary structure must form first with only local interactions (Baldwin and Rose, 1999; Karplus and Weaver, 1994). Proteins that fold by the hierarchical diffusion–collision process should show local sequence constraints.

Conversely, if protein folding constraints are local in the structure, but distant in the sequence, then real protein sequences might be largely indistinguishable from random sequences. Proteins that fold by nucleation–condensation, with the concurrent acquisition of secondary and tertiary structure (Fersht, 1995), should appear more random. Chymotrypsin inhibitor 2 (CI2) shows 2-state folding kinetics and is proposed to fold by a global process; a mostly denatured unfolded chain quickly folds to its native conformation with secondary and tertiary structure forming concomitantly (Jackson and Fersht, 1991). These proteins should not have strong local sequence constraints, since the folding nucleus is diffuse and requires contacts from many sequence distant amino acid residues.

Here, we present a rigorous survey of a large non-redundant domain library using four- and five-residue words at regular spacings that span 4–13 amino acids and 5–17 residues, respectively. We find that most protein words are well described by random sequence models, suggesting that there are no strong constraints limiting the space of amino acid words in protein sequences.

The hypothesis that proteins are largely random is not new. Ptitsyn and Volkenstein (1986) argued that proteins ‘mainly represent memorized random sequences while biological evolution reduces to the editing these random sequences’, and the high information content of protein sequences seen with Shannon entropy analysis (Crooks and Brenner, 2004; Weiss et al., 2000) supports the random model.

We extend previous studies by comparing the observed word clump counts to those estimated from four different random models of protein sequences: Bernoulli [MC(0)], Markov chain order 1 [MC(1)], shuffled and 10-residue segment window shuffled (win10-shuffled). We then assign a statistical significance to each non-overlapping word and use false positive discovery rate (FDR; q-value) analysis to select statistically significant exceptional words (Reinert et al., 2000; Storey and Tibshirani, 2003). We present the first list of statistically exceptional words, mapped onto a non-redundant set of protein structures. We find that, on the whole, protein words are largely random; there are few statistically exceptional words and their deviation from random expectation is small. Overrepresented four-amino acid words are no more evolutionarily conserved than random, but overrepresented four- and five-residue words do show a preference for α-helical secondary structure.

2 MATERIALS AND METHODS

2.1 Non-redundant library construction

A non-redundant library of protein domains was built using Pfam version 21.0 domain boundaries (Sonnhammer et al., 1997). A single random representative from each PfamA family or clan produced 7510 domains; 186 970 non-redundant PfamB domain representatives were chosen. The PfamA and PfamB domains were combined and clustered (single-linkage) to remove related sequences using an E-value threshold ≤0.001 from a Smith–Waterman all-versus-all comparison (ssearch34 with blosum62 on seg-ed sequences). The longest domain from each cluster was selected to give the final non-redundant library of 7431 PfamA and 178 101 PfamB domains with a cumulative length of 19.6 million residues (18.2 after seg.)

A library of PfamA domains with known conservation (entropy) profiles was created from PfamA as described above, with 1.37 million residues (1.29 after seg). Sequences from non-redundant representative domains were aligned to its corresponding hidden Markov models (HMMs) using hmmpfam version 2.3.2 (Eddy, 1998). The match state entropy in half-bits for each position was calculated using the null and match state emission scores from the corresponding HMM, and the Shannon entropy H(X_i) for each match position X_i within the HMM was calculated. The entropy per position was converted into half bits and rounded down so that each position in a match emission state gets an integer score between 0 and 8. At a position that is invariant, the entropy will be zero, but the lowest observed entropy is 1 half bit. Positions in the HMM that have no amino acid preference have a score of 8.

To examine word preferences in protein secondary structures, we constructed a dataset containing one randomly selected sequence from each topology class in cath v3.1.0 (Orengo et al., 1997), producing a library of 1084 distinct topolog sequences with a total of 155 950 amino acids (151 327 after seg). The amino acid sequence and secondary structure assignments were taken from the CATH supplied DSSP files available from http://www.cathdb.info/staticdata/v3_1_0/domdssp/. The 8-state DSSP secondary structure assignments were assigned to 3-states by one of two methods: (i) H to H; E to E, all others to L or (2) H, G and I to H; E and B to E; all others to L. The data presented here are exclusively from the second assignment method although both assignments gave similar results.

2.2 Counting word clumps

The simplest method for counting four-residue words in a protein simply tabulates the N − 3 words in a sequence of length N. However, overlapping word positions are not independent, e.g. in the sequence QRQRQR the second QRQR is much more probable given the first QRQR (Reinert et al., 2000). In this article, we report statistics on the number of four-amino acid word clumps, or non-overlapping words. A clump is an island of potentially overlapping words (Reinert et al., 2000). There is only one four-amino acid clump in QRQRQR. Within a protein sequence, if two identical four-letter words are found to overlap one another, then the clump is enlarged to contain both of the words into one clump.

To count clumps or islands in four-amino acid words built from non-adjacent residues, e.g. the residues at positions 1, 3, 5, 7 (i+2); 1, 4, 7, 10 (i+3); or 1, 5, 9, 13 (i+4), the sequences were first transformed into a new set of words using the indicated offset, and then the clumps within the words were identified. The same process is used for non-adjacent five-residue word clumps.

2.3 Random libraries and parameter estimation

Random libraries were constructed using perl version 5.8 and R version 2.4.1 (http://www.r-project.org/) scripts. Four models were used to produce random protein sequences: (1) a Bernoulli or Markov chain order 0 [MC(0)] model, which produces sequences based on the frequencies of the 20 individual amino acids; (2) a Markov chain order 1 [MC(1)] model, which produces sequences that preserve di-peptide frequencies; (3) sequences produced by shuffling real protein sequences uniformly across the length of each sequence; (4) sequences produced by shuffling real protein sequences locally within a 10-letter window (win10-shuffled). Models (3) and (4) differ from (1) and (2) by preserving the sequence composition bias present in individual protein sequences. For a hypothetical 100 000 sequence library, model (3) can be thought of as 100 000 approximate instances of model (1), where the composition of the individual protein is used to produce the amino acid frequencies. Model (4) produces random sequences that reproduce both individual sequence composition bias and internal domain composition bias. Thus, model (4) is expected to have statistical properties that are most similar to real protein sequences. For five-residue word counts from a 10-letter alphabet (Murphy et al., 2000), residues were mapped and 10-letter frequencies [MC(0)] or 10²-di-peptide frequencies [MC(1)] were used. The expected clump count used for probability calculations was estimated from the mean clump counts from 100 replicate random libraries.

2.4 Statistical significance and q-value analysis

Given a set of word counts from real proteins, we ask whether individual word frequencies differ significantly from four random models. Exact algorithms are too slow to calculate P-values for all four- or five-residue words (Nuel, 2006), so we estimated word probabilities using either a Poisson distribution, for words with an estimated expected clump count N ≤ 50, or a Normal distribution (N > 50). Mean clump counts were estimated from random libraries and used for the Poisson λ and Normal mean parameter. The Normal distribution standard deviation (SD) was estimated from 100 replicate random libraries. Each observed word's P-value is then taken from a two-tailed test using the Poisson or Normal distribution.

The q-value analysis was used to estimate the inclusion of likely false positives into a pool of exceptional words. R version 2.4.1 with the package qvalue version 1.1 was used to assign a q-value to each word when given the above set of words with their associated P-values (Storey and Tibshirani, 2003). Briefly, each word w was ordered by its P-value and, iteratively, words w with the lowest P-value were placed into the statistically exceptional pool of words as long as the word has a q-value less than the predetermined cutoff. The q-value estimates the false positive rate when including that word in the significant pool. We used a q-value cutoff <0.03 for labeling words statistically exceptional. Based on this cutoff, the final pool of exceptional words should contain <3% false positives.

3 RESULTS

3.1 Four- and five-residue words from non-redundant protein libraries appear random

To explore restrictions on protein words, we tabulated the number of four-residue words found in Human-RefSeq proteins and compared them with words produced by four random models: Bernoulli or MC(0), MC(1), shuffled and win10-shuffled (Section 2). A comparison of Human-RefSeq proteins with a random Markov chain order 1 [MC(1)] model that preserves the di-peptide observed frequencies is shown in Figure 1. Although we refer to amino acid words throughout this article, we actually tabulated the number of independent four- or five-residue word clumps, rather than every four- or five-residue word, in a sequence. Amino acid clumps are non-overlapping words; the sequence QYEKQQQQQPDKQFKE has two overlapping instances of QQQQ but only one clump (Reinert et al., 2000, see Section 2). The sequence QRSTQRSTQRST contains nine four-residue words and also nine four-residue clumps, because even though the sequence is repetitive, there are no overlapping repeats. We report clump counts, rather than word counts, because the residue positions within overlapping words are not independent. The Poisson distribution describes clump counts in sequences produced by Markov model (Reinert et al., 2000). The Poisson distribution accurately estimates clump counts less than 50 (larger counts can be estimated using the Normal distribution). While there are ∼14.6 million residues in the Human-RefSeq protein set, the median expected clump size is ∼56 (Fig. 1), so almost half of the Human-RefSeq clump counts, and one-third of the Pfam-AB counts, are estimated using the Poisson distribution.

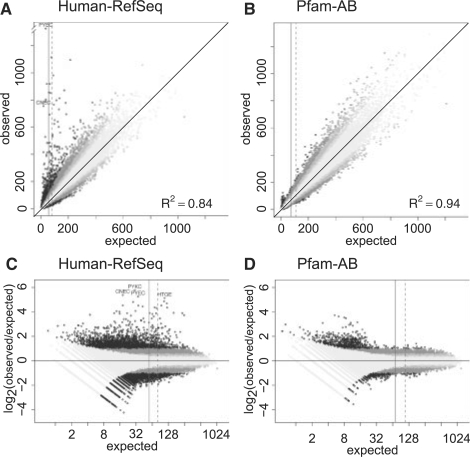
Fig. 1.

Non-redundant protein sequences are well described by a random MC(1) model. Four-letter word clump counts from Human-RefSeq (A, C) or non-redundant Pfam-AB (B, D) sequences are compared with average four-residue word clump counts from the corresponding MC(1) model. Low-complexity regions were removed from the sequences with seg. Observed and expected counts, and the corresponding R² value, are plotted directly in (A, B); the log₂ ratio of the observed to expected counts is displayed in (C, D). Eleven points with counts greater than 1328 are omitted. The identities of some of the most overrepresented Human-RefSeq words are shown. The median expected clump counts (solid vertical line) are 56 (Human-RefSeq) and 72 (Pfam-AB). The mean expected clump counts (dashed line) are 81 (Human-RefSeq) and 109 (Pfam-AB). Clumps that are statistically significantly over- or underrepresented, as calculated using the q-value analysis, are shown with shades of gray, ranging from darkest for words 2-fold overrepresented or 0.5-fold underrepresented, to the lightest, where the deviation is ≤1.25 or >0.8.

The size of our datasets (14.6 million for Human-RefSeq, 18.2 million for Pfam-AB) prevents us from examining longer protein word clumps using a 20-letter alphabet. There are only 160 000 words of length 4, but 3.2 million possible words of length 5, which reduces the median clump size for Pfam-AB from 72 to 3. Clump counts are Poisson distributed (Reinert et al., 2000), so a four-residue word must be present 1.33 times expected at a median of 72 clumps to be significantly overrepresented.¹ To examine five-residue words, we used a reduced structural alphabet comprised of 10 letters: LMIV-C-A-G-ST-P-FYW-EDNQ-KR-H (Murphy et al., 2000). There are 100 000 possible five-residue words in this alphabet, but the 10-letter mapping concentrates LMIV into one letter and EDNQ into another, so the dynamic range in abundance is much greater than that found for the 20-letter alphabet. As a result, the median clump size for five-residue words is 40.

In the Human-RefSeq protein set and other comprehensive protein databases, a well-recognized difference between real and random sequences is low-complexity regions minus regions of proteins, where the local amino acid composition is restricted. The sequences in Figure 1 were scanned with seg to remove low-complexity sequences (Federhen, 1993). seg reduces, but does not eliminate completely the overabundance of observed low-complexity words within both Human-RefSeq and Pfam-AB (Supplementary Material). Qualitatively, there is good agreement between real word frequencies and those produced by the random MC(1) model for Human-RefSeq with R² values of 0.84 (slope 1.01) after seg. An R² value of 0.84 implies that a random MC(1) model accounts for 84% of the variance within the observed word clump counts in Human-RefSeq.

A less well-recognized difference between comprehensive real protein datasets and random protein sequences is evolutionary redundancy—proteins that are similar because they share a common ancestor. Human-RefSeq proteins have a large number of word clumps that differ significantly from random and are more than 2-fold overrepresented (Fig. 1C, dark symbols); indeed HGTE, PYEC, PYKC and CNEC are present in Human-RefSeq proteins 2⁵ or 32 times more often than expected. These overrepresented words are commonly found in related Human zinc finger proteins, one of the largest protein families in the Human genome with more than 500 members.

To investigate how evolutionary redundancy influences word counts, we constructed a non-redundant library of protein from 7431 PfamA and 178 101 PfamB domains (version 21, see Section 2). Again low-complexity regions, ∼7.1% of the library, were removed with seg. The R² value for the correlation of the Pfam-AB four-residue word clump counts to the estimated expected number from a MC(1) model is 0.94 (with a slope of 1.00, Fig. 1B). To put this in perspective, the R² for the correlation of sets of proteins produced with different random models ranges from ∼0.95 [Bernoulli versus MC(1), shuffled or window-shuffled] to 0.98 (shuffled versus window-shuffled; in each case the slope was ∼1.0), and the R² for the Pfam-AB word counts against different random models ranges from 0.90 [an MC(0) model based on individual amino acid frequencies, slope 1.02] to 0.95 (shuffled or window-shuffled models, slope 1.0, Table 1). Thus, word frequencies in real proteins are almost entirely explained by amino acid composition.

Table 1.

Overrepresented four-residue exceptional words under different random models

Model and spacing	Overrepresented exceptional wordsa
	1up2	1up3	1up5
	>2	>1.50	>1.25
Bernoulli, MC(0)
(R2 0.90) i+1	1822 (1.1)	7519 (4.7)	17197 (10.7)
MC(1)
(R2 0.94) i+1	742 (0.5)	3240 (2.0)	10006 (6.3)
shuffled
(R2 0.93) i+1	312 (0.2)	2952 (1.8)	10613 (6.6)
win10-shuffled
(R2 0.95) i+1	167 (0.1)	1676 (1.0)	6463 (4.0)
Consensus (3 of 4)
i+1	209 (0.1)	1538 (1.0)	6350 (4.0)
i+2	73 (0.0)	1079 (0.7)	4371 (2.7)
i+3	252 (0.2)	459 (0.3)	1476 (0.9)
i+4	16 (0.0)	113 (0.1)	874 (0.5)
Consensusb (2 of 3)
i+1	295 (0.2)	2543 (1.6)	9351 (5.8)
i+2	76 (0.0)	1259 (0.8)	5034 (3.1)
i+3	252 (0.2)	472 (0.3)	1604 (1.0)
i+4	16 (0.0)	117 (0.1)	932 (0.6)

^aNumber and fraction of exceptional words in parentheses.

^bExcluding MC(1).

Moreover, the 2-fold overrepresented Pfam-AB-seg clumps in Figure 1D are not overrepresented because they are frequent in real proteins, as might be expected for words that play an important structural role; they are overrepresented because the words are infrequent in the random protein set. Of the 742 statistically exceptional words that are 2-fold overrepresented in Figure 1D and Table 1, only 51 have counts greater than the median expected count. In contrast, when Pfam-AB-seg counts are compared with the win10-shuffled values, 44 of the 167 clumps that are 2-fold overrepresented by q-value analysis are larger than the median expected count. This suggests that the apparent number of over- or underrepresentation clumps may reflect shortcomings in the random models, rather than structural constraints. The two purely mathematical models [MC(0) and MC(1)] do not account for variation in amino acid composition among protein classes; the two shuffled models capture differences in amino acid composition and thus can produce more accurate clump counts for combinations of rare amino acids, which in turn reduces the number of exceptional words.

The strong agreement between Pfam-AB word counts and the random models confirms that much of the excess variation in the Human-RefSeq protein set reflects the word preferences of the largest protein families; when homologous proteins are removed from the library, most of the difference between the counts of real and random words disappears. When each protein family is represented only once, the correlation of non-redundant Pfam-AB word counts to random proteins that preserve di-peptide frequencies is very similar to the correlation among different random models, and it is almost impossible to distinguish real protein words from random protein words. Thus, structural constraints on protein sequences appear to place very little restriction on the space of possible proteins.

3.2 Exceptional words at q-value cutoff of 0.03

Although Pfam-AB word counts are generally well described by the random MC(1) model, some of the discrepancy between the random models and Pfam-AB counts may reflect structural constraints. To identify words within seg-Pfam-AB that are not well described by the random models, each four- or five-residue word was assigned a probability (P-value, see Section 2). An FDR approach using a q-value cutoff of 0.03 was used to identify exceptional words for further analysis (Storey and Tibshirani, 2003).

q-value FDR analysis is used to analyze large datasets when the goal is to limit the number of false positives found across the entire set of results, in contrast with the more conservative family-wide error rate analysis, typically implemented with a Bonferroni correction, which limits the likelihood of error for each individual member of the dataset (Benjamini and Hochberg, 1995). We can think of our analysis of four-residue clumps as 160 000 tests, where in each test we ask whether the number of Pfam-AB words is different from that expected by chance. Using the Bonferroni correction, the expected number of times a word should occur by chance is simply its random probability P() times the number of tests, 160 000. For the seg-scanned Pfam-AB data, there are 3082 four-residue words with a P() < 6.3 × 10⁻⁸ based on the random MC(1) model, corresponding to an E-value <0.01. The Bonferroni correction attempts to ensure that the odds of any of the 160 000 words being classified as significantly different from random is <0.01. But, because it is a very strict criterion, the Bonferroni correction reduces the power of the analysis; amino acid words that are significantly over- or underrepresented in the dataset as a whole may be missed. To improve sensitivity, we use a q-value approach that calculates a value based on the discrepancy between the observed probabilities and those expected from a random data set. For the Pfam-AB-seg data (four-residue words), there are 23 594 words with P() < 0.007, a value where we would expect that less than 0.03 of the 23 594 words, or 708, are false positives, i.e. words that are no more or less frequent than expected by chance. For five-residue words from the 10-letter structural alphabet, 17 686 (17.7%) are significantly over- or underrepresented at P() < 0.008 or q() < 0.03. The remaining ∼97% of those words have counts that are significantly different from the chance expectation. These numbers are much higher than the Bonferroni value, because we are allowing false positives to occur across the entire dataset.

The false discovery rate approach is potentially more sensitive, but it can assign words to the exceptional class when the difference between observed and expected counts is very small. To highlight the most over- and underrepresented exceptional words, we grouped exceptional words from Pfam-AB based on their deviation from estimated expected occurrence. The ‘1up2’ category contains words observed twice as often as expected; for every two counts, one is in excess of the expected number from the random model. Similarly, ‘1dn2’ contains words present <50% as frequently as expected; here, for every two expected word counts, one occurrence is missing from Pfam-AB. Figure 2 shows the fraction of all over- and underrepresented words, shading the most over- and underrepresented groupings and including broad groupings that include ∼75% of the exceptional words (>1.25, 1up5; <0.8, 1dn5). For four-residue clumps, the number of exceptional words compared with the MC(1) model in the 1dn2 and 1up2 categories is small, with 1102 (742 + 360) from Pfam-AB-seg accounting for <1% of the total 160 000 possible words.

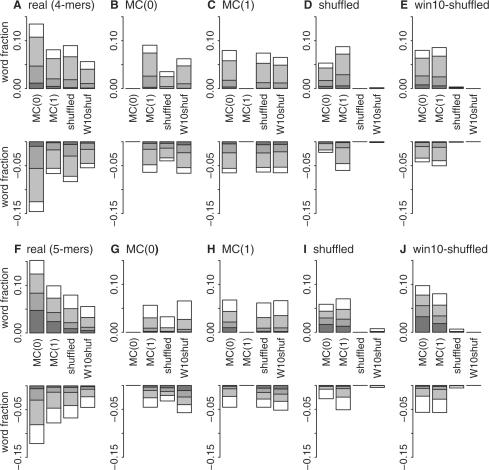
Fig. 2.

Over/underabundance of real Pfam-AB and synthetic words versus random models. Alternate estimates of exceptional four-letter (A–E) and five-letter (F–J) word clump counts from q-value analysis of Pfam-AB-seg Real (A, F), MC(0) (B, G), MC(1) (C, H), shuffled (D, I) and win10-shuffled (E, J) libraries based on four random models: MC(0), MC(1), shuffled and win10-shuffled (W10shuf) are shown. Overrepresented words are shown as positive fractions; underrepresented words are negative fractions. Shading denotes the magnitude of the over- or underrepresentation with respect to the corresponding random model; dark gray, >2.0 (1up2) or <0.5 (1dn2); gray, >1.5 (1up3) or <0.67 (1dn3); light gray, >1.25 (1up5) or <0.8 (1dn5); and white, exceptional words between 0.8- and 1.25-fold of the expected value.

The counts of exceptional words summarized in Figure 2 and Tables 1 and 2 may reflect structural constraints, but alternatively they may simply reflect shortcomings in our random models. Different random models produce slightly different word distributions, and the very sensitive q-value analysis detects significant differences in these distributions (Fig. 2). Thus, shuffled sequences produce word counts that are significantly different from purely mathematical models (Fig. 2B, C, F and G) and vice-versa (Fig. 2D, E, H and I). Only when a random model is compared with itself are there no exceptional words, though the two shuffled models also produce very few exceptional words when compared with each other. Not only do the different random models produce number of exceptional words that are similar to the numbers produced by real proteins, they also produce exceptional words with similar abundances (1up2, 1up5, etc.).

Table 2.

Overrepresented five-residue exceptional words under different random models

Model and spacing	Overrepresented exceptional words
	1up2	1up3	1up5
	>2	>1.50	>1.25
Bernoulli, MC(0)
(R2 0.95) i+1	4724 (4.7)	8352 (8.4)	12372 (12.4)
MC(1)
(R2 0.96) i+1	2369 (2.4)	4287 (4.3)	7303 (7.3)
shuffled
(R2 0.96) i+1	897 (0.9)	2144 (2.1)	5093 (5.1)
win10-shuffled
(R2 0.97) i+1	484 (0.5)	1196 (1.2)	3252 (3.3)
Consensus (3 of 4)
i+1	761 (0.8)	1641 (1.6)	3688 (3.7)
i+2	231 (0.2)	649 (0.6)	1864 (1.9)
i+3	448 (0.4)	632 (0.6)	950 (0.9)
i+4	64 (0.1)	138 (0.1)	398 (0.4)
Consensus (2 of 3)
i+1	896 (0.9)	2103 (2.1)	4875 (4.9)
i+2	239 (0.2)	710 (0.7)	2160 (2.2)
i+3	451 (0.5)	637 (0.6)	1020 (1.0)
i+4	66 (0.1)	144 (0.1)	419 (0.4)

One way to judge the significance of the number of exceptional words in real proteins is to compare this number with the number of exceptional words in random proteins across different random models (Fig. 2). seg-scanned Pfam-AB contains 10 006 words that are overrepresented by at least 25% when compared with an MC(1) model, but only 6643 words are 25% overrepresented compared with the win-10 shuffled model (Table 1). However, when either the Bernoulli MC(0), shuffled or win-10 shuffled random protein words are compared with the MC(1) model, ∼11 000 words are 25% overrepresented. Thus, for three of the four random models, the number of 25% overrepresented words in the real Pfam-AB-seg sequences compared with the MC(1) model set is smaller than the number found in the four different random synthetic protein sets.

We may miss differences in amino acid word choice between real and random proteins because of the word lengths and residue alphabet. To improve structural sensitivity, we analyzed the non-redundant Pfam-AB database using a 10-letter structural alphabet (Murphy et al., 2000) that allows us to look at five-residue word clumps (Fig. 2F–J and Table 2). In our non-redundant CATH structure database, β-strands and coils have a median length of 4, while α-helices have a median length of 8 residues; five-residue structural alphabet words span more than half of β-strands and coils, and about one−third of α-helices.

Increasing the protein word length with a more structurally informed alphabet has very little effect on the fraction of exceptional words (Fig. 2). With the structural alphabet and five-residue words, the simplest model, Bernoulli MC(0), reports that 12.4% of the words are 25% overrepresented, slightly more than the 10.7% found with four-residue words, while the most complex model (win10-shuffled) finds that 3.3% of the words are 25% overrepresented, slightly less than the 4.0% four-residue words. Although we expect higher structural sensitivity, five-residue clump counts from a more structurally informed alphabet have very few abundant exceptional words.

Our sampling of exceptional words probably produces a mixture of words—those identified because of shortcomings of our random models and those that reflect structural constraints on proteins. To enrich the signal caused by structural constraints, we identified consensus exceptional words from the four random models. We performed Venn diagram analysis to find exceptional words shared between the different models in the 1up2, 1up3 and 1up5 groupings (data not shown). Tables 1 and 2 show the number of words that are labeled exceptional by three of the four random models, or two of three random models, excluding the (MC(1) random model, which potentially could capture some β-strand characteristics).

There are 9351 four-residue two of three model consensus words; in general, they are more abundant than PfamAB words as a whole (7611 of the words are more abundant than the median PfamAB word). A list of the 50 most common four-residue consensus exceptional words, with their relative abundance compared with the average of the three random models, and their count and frequency in our CATH structure sample, is shown in Supplementary Table 1. Similarly, there are 4875 five-residue (10-letter) two of three model words; 3741 are more abundant than the median 5mer PfamAB clump (statistics for abundant five-residue words are shown in Supplementary Table 3.)

These consensus exceptional words were examined more closely to see if they shared evolutionary constraints or structural features.

3.3 Exceptional words are not enriched in conserved positions within protein families

Our inability to detect substantial differences between real and random protein sequences might be explained by the observation that in many protein families, there are a relatively small number of highly conserved sites that are believed to play critical functional and structural roles, whereas the other positions in the protein may be relatively free to diverge (Mirny and Shakhnovich, 2001; Ptitsyn, 1998). The Pfam-A domain database provides high-quality alignments and HMMs that can be used to identify conserved regions in protein domains. However, Pfam-A is only ∼10% as large as Pfam-AB, so we could not investigate whether conserved positions within protein families contain exceptional words. Instead, we asked whether the consensus exceptional words found from Pfam-AB-seg were enriched in positions that are well conserved in protein families.

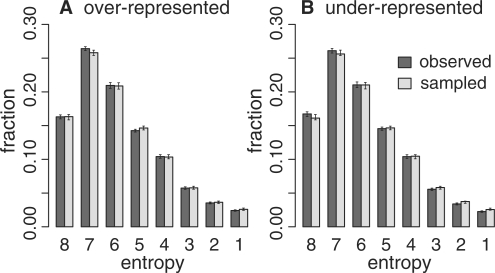
The 6350 overrepresented and 6648 underrepresented consensus three of four exceptional words were mapped onto a non-redundant library of single PfamA representatives. Based on Pfam-A HMM match states, invariant positions have an entropy score of 0; positions that show no preference for an amino acid will have about 4-bits of entropy, or an entropy half-bit score of 8. The entropy profile for consensus exceptional words is indistinguishable from the profile plotted for randomly sampled words (Fig. 3). The entropy distributions for words at the i + 2 through i + 4 spacings look similar and are not shown. The consensus exceptional words are not enriched at conserved positions within Pfam-A domains.

Fig. 3.

Conservation of consensus exceptional words. Fraction of words versus Pfam-A HMM entropy (variation) in half bits. The most conserved sites are on the right with low entropy values. (A) Consensus overrepresented exceptional words [observed, 1up5, (i + 1) spacing] compared randomly sampled words (sampled). (B) Underrepresented words. Error bars report the 95% confidence intervals obtained by 500 bootstraps of the Pfam-A library with replacement.

3.4 Overrepresented exceptional words show some preference for α-helix

Just as there are too few non-redundant Pfam-A sequences to identify statistically exceptional words, there are also too few non-redundant protein structures (our non-redundant CATH 3.1 topolog library contains only 1084 sequences and ∼155 000 residues, <1% of Pfam-AB, see Section 2) either to look for exceptional words or to identify significant differences in word use in different secondary structural elements. Of the 9351 consensus exceptional four-residue words, 6393 are found in our CATH topolog library, 3894 are found more than once, but only 1313 are found four or more times. There are 2803 consensus exceptional five-residue words; 1798 are present more than once and 960 are present four or more times. Despite the small number of structural words, we can ask whether the set of consensus exceptional words from Pfam-AB have a secondary structure preference by mapping each consensus exceptional word onto the aligned secondary structure positions.

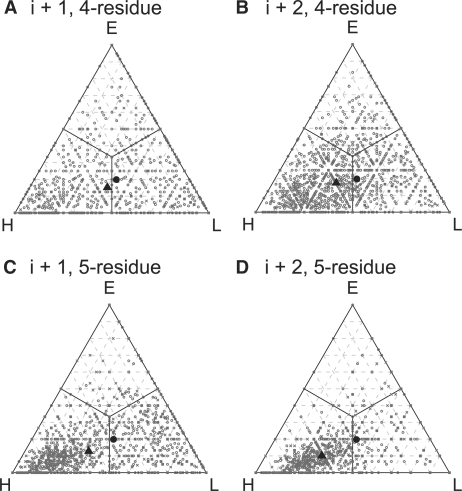
Figure 4 shows the structural biases of the two of three consensus exceptional words from i+1 to i+4; the i+2 spacing, which covers 7 (four-residue words) or 9 (five-residue words) residues, shows the strongest bias. Our non-redundant CATH library contains 38% α-helix (H), 20% extended sheet (E) and 42% loop (L). For four-residue words, i+1 words are 44.7% H, 15.1% E and 40.1% L, whereas i+2 words are 58.9% H, 11.6% E and 29.4% L. For five−residue words, i+1 words are 54.3% H, 12.8% E and 32.9% L, whereas i+2 words are 60.9% H, 10.1% E and 29.0% L. The consensus overrepresented words thus show a preference for α-helix secondary structure, with the i+2 spacing showing the largest preference. The preference for α-helix reflects the preferences of the most abundant words. Overall, for four-residue exceptional words present four or more times in CATH structures, there are ∼3.1 times more words present more frequently in α-helices than in β-strands (based on the overall composition of the CATH structures, this ratio should be 1.8); for the most abundant quartile of exceptional words in known structures, that ratio increases to 7.3-fold. Supplementary Table 1 shows the structural preferences of the 50 most abundant consensus exceptional words; Supplementary Tables 2A and 4A show the abundance and preferences of the 50 exceptional words present four or more times with the strongest α-helical bias; each of these words is present only in α-helix. Supplementary Tables 2B and 4B shows the abundance and preferences of the 50 exceptional words present four or more times with the strongest β-strand bias; here, only one word is exclusively found in β-strand; none is found in α-helix, but are frequently found in loops.

Fig. 4.

Secondary structure of consensus exceptional words. Consensus exceptional words [two of three models, excluding MC(1)] within the 1up5 category from Tables 1 and 2 were mapped onto a representative structure. Frequencies for α-helix, H; extended β-sheet, E; or random-coil, L for each exceptional word are displayed in a triplot. (A, B) Four-residue word preferences at spacings i+1 (A) and i+2 (B). (C, D) Five-residue preferences at spacings i+1 (C) and i+2 (D). A point in the middle of the plot is found equally frequently in the three secondary structures. The filled circle represents the average secondary structure in our non-redundant CATH dataset. The filled triangle shows the average secondary structure for consensus overrepresented words. Bootstrapped 95% confidence intervals are within the dimension of the symbols.

Exceptional words shared by three of four models, rather than two of three, show a slightly greater preference for α-helix (1.23−fold at i+1 and 1.57−fold at i+2 for four-residue words and 1.52-fold at i+1 and 1.63−fold at i+2 for five-residue words). If exceptional words shared by all models, rather than two of three, are used as the consensus set, then the preference for the exceptional words is further enhanced toward α-helix, but the number of exceptional words is greatly reduced (data not shown). We found no secondary structure preference (or avoidance) in underrepresented words (data not shown).

4 DISCUSSION

Despite the protein word preferences seen in different secondary structures, the landscape of four- and five-residue words in non-redundant databases is well described by random sequence models. Comparison of Pfam-AB to each of the four random models has R² values >0.9; thus >90% of the observed variance in word counts is explained by each random model. Using the more sensitive FDR analysis, statistically exceptional Pfam-AB words have counts that differ only slightly from the random models; the real-random count differences are similar in magnitude to differences seen between alternative random models. The apparent randomness of protein sequences, when taken as a whole, suggests that secondary structure word preferences do little to restrict the word composition of proteins, consistent with the model that sequence largely drives secondary structure, rather than vice-versa.

Our observation that local secondary structure preferences do not significantly restrict overall amino acid word use in protein sequences is consistent with a global process for protein folding, where secondary structures form late in the process, but it certainly does not rule out a hierarchical folding process in which secondary structures form early. What it does show is that if the folding process is hierarchical, secondary structures do not restrict sequence choice. More realistically, it seems likely that protein families fold along a spectrum from hierarchical to global, and across this spectrum, word preferences appear largely random.

Our observations may also appear inconsistent with the relatively high accuracy of secondary structure prediction algorithms, but we believe this discrepancy is more apparent than real. The current best secondary structure prediction programs achieve higher accuracy on α-helices than on β-strands (Aydin et al., 2006), consistent with the enrichment for α-helical structure found in our exceptional words. Moreover, current secondary structure prediction improves from about 70% to 80% Q₃ accuracy when evolutionary conservation is exploited; for single sequences in new folds, prediction accuracy can be even lower (Aydin et al., 2006). Secondary structure prediction accuracy on unrelated novel folds seems consistent with our observations that word structural preferences do not restrict overall protein sequence.

The small discrepancies that we find between non-redundant real protein sequences and our random models may reflect structural constraints on protein word use, or they may reflect the shortcomings of our random models. Our two mathematically based models, the MC(0) or Bernoulli model, which simply produces protein sequences with appropriate amino acid frequencies, and the MC(1) model, which also preserves di-peptide frequencies, produce protein sequences by sampling from a single average distribution of amino acid or di-peptide frequencies. These models cannot produce protein sequences with transmembrane domains, nor can they model buried hydrophobic patches. Yet our least realistic random model, MC(0) Bernoulli, suggests that only ∼1% of four-residue and 5% five-residue words are 2-fold overrepresented in Pfam-AB-seg. We also generated random sequences by shuffling real proteins; the win10-shuffle model does preserve transmembrane composition. Less than 0.2% of four-residue, and ∼0.5% of five-residue words are 2-fold overrepresented with shuffle random models. Mixtures of MC(1) models with different composition biases would certainly reduce the number of exceptional words, thus reducing the potential influence of structural constraints. In general, we do not find constraints on protein sequences that restrict protein word use in non-redundant datasets.

While most words in proteins may be unconstrained, one might expect that the most conserved positions in proteins have stronger constraints on word use. We cannot address this question directly using a 20- or 10-letter alphabet; there are too many possible protein words to accurately sample either the Pfam-A or CATH datasets. However, we can ask whether statistically exceptional words are more conserved than randomly selected words—they are not.

We can also ask whether exceptional words have secondary structure preferences; here it appears that there is a consistent preference for α-helical regions in consensus overrepresented words, particularly using five-residue words from the 10-letter structural alphabet. While the total number of consensus exceptional words is small, with <1% of the consensus exceptional words belonging to this category (Tables 1 and 2), a consistent preference is seen for words spanning from 4 (i+1, four−residue words) to 17 (i+4, five-residue words) amino acids. It is reassuring that the structural preference we find is for α-helices, since these structures involve local H-bond interactions and are expected to reflect local sequence constraints, and that the preferences become stronger as we sample longer regions, as four residue is barely enough to form an α-helix.

Our major result—that protein sequences appear to be made up of random words—conflicts with some earlier studies of amino acid preferences and oligopeptide compositions in different genomes (e.g. Pe'er et al., 2004). We believe that our analysis differs from earlier work because we examine non-redundant protein databases. Protein families have strong oligopeptide preferences that can be used to identify homologs (Wu et al., 1996). Additional genome-specific biases can be introduced by differences in amplification of low-complexity regions. Human-RefSeq proteins are redundant and biased because of low-complexity regions; the non-redundant Pfam-AB-seg dataset has few statistically exceptional words. Indeed, all the overabundant high-complexity words (TGE, HTG, YKC and CGK) from Homo sapiens given in Table II from (Pe'er et al., 2004) are found in related zinc-finger proteins. Thus, although individual genomes may have different amino acid and word compositions, we suspect that much of their phylogenetic signal based on word counts is due to genome-specific protein expansions.

Our results also stand in apparent contrast with recent success in ab initio modeling of proteins at CASP6 by Rosetta, which has been attributed to the incorporation of local sequence/structure information from protein structure fragments from the PDB (Moult, 2005; Rohl et al., 2004). However, it is important to distinguish the need to restrict protein structure search space, which Rosetta does during fragment insertion (Rohl et al., 2004), from the need to restrict protein sequence space. At the local level, different short peptides may adapt similar structures; the mapping of local sequence to local structure is redundant. Moreover, Rosetta combines both local and global approaches to predict structure. Global interactions are critical for accurate tertiary structure prediction (Rohl et al., 2004), and Rosetta refines its initial conformations using a global energy scoring function. The importance of the global energy minimization is illustrated by the Baker lab's recent success in CASP7, where they used Rosetta@home to implement a global all-atom refinement (Das et al., 2007; Jauch et al., 2007). Here, for each target sequence, ab initio predictions used a remarkable ∼500 000 CPU hours that yielded some 10⁵ −10⁶ conformations from which the best five were selected (Das et al., 2007). Rosetta@home clearly surpassed the automated Robetta server that utilized the same fragment insertion protocols, but lacked the all-atom refinement (Das et al., 2007). Although current protein structure data can effectively restrict structural search space, it need not follow that sequence space is significantly restricted.

5 CONCLUSION

The small number of exceptional words and their modest overabundance suggest that secondary structure constraints do not strongly bias protein sequences as a whole. Globally, protein sequences have very few local sequence constraints; it is very difficult to distinguish real from random sequences.

Funding: National Library of Medicine (grant LM04969).

Conflict of Interest: none declared.