Abstract
Background
Segmental duplication is widely held to be an important mode of genome growth and evolution. Yet how this would affect the global structure of genomes has been little discussed.
Methods/Principal Findings
Here, we show that equivalent length, or  , a quantity determined by the variance of fluctuating part of the distribution of the
, a quantity determined by the variance of fluctuating part of the distribution of the  -mer frequencies in a genome, characterizes the latter's global structure. We computed the
-mer frequencies in a genome, characterizes the latter's global structure. We computed the  s of 865 complete chromosomes and found that they have nearly universal but (
s of 865 complete chromosomes and found that they have nearly universal but ( -dependent) values. The differences among the
-dependent) values. The differences among the  of a chromosome and those of its coding and non-coding parts were found to be slight.
of a chromosome and those of its coding and non-coding parts were found to be slight.
Conclusions
We verified that these non-trivial results are natural consequences of a genome growth model characterized by random segmental duplication and random point mutation, but not of any model whose dominant growth mechanism is not segmental duplication. Our study also indicates that genomes have a nearly universal cumulative “point” mutation density of about 0.73 mutations per site that is compatible with the relatively low mutation rates of (1 5)
5) 10
10 /site/Mya previously determined by sequence comparison for the human and E. coli genomes.
/site/Mya previously determined by sequence comparison for the human and E. coli genomes.
Introduction
Evolution has many facets, and one that is particularly accessible to quantitative analysis is the evolution of genomic sequences. In particular, the study of point mutations (here used in the sense that includes relatively small insertions and deletions, or indels) on genes has led to deep understandings of many aspects of genome evolution [1], [2]. Point mutation however cannot be the main force driving genome growth, because it does not give rise to gene duplication [3]–[8], and because the pace of evolution based on point mutation alone would be too slow. Gene duplication is a product of segmental duplication (SD). In fact, genomes are replete with vestiges of duplication [9]–[11], not only in the form of homologous genes, but also as transposons [12]–[14], pseudogenes [15]–[18], and many other types of coding and non-coding repeats [19]–[22]. There is also evidence of large-scale genomic rearrangements [23]–[27] and whole genome duplications [3], [28]–[30]. This has led to the generally held view that SD is an important mode of genome growth and evolution.
If products of SD are so prevalent in genomes, we expect the SD's in a genome, collectively, to leave a large imprint on the global structure of its host, one that is detectable using means not relying on sequence alignment, which in any case is not suitable for global studies. One may reasonably expect a study to understand the formation of such an imprint to yield useful insights into the global pattern of genome growth and evolution, yet no such effort has been made.
Here, we study the statistical properties of genomes by analyzing the distribution of the frequency of occurrence, or FD, of  -letter words, or
-letter words, or  -mers, in the sequence. Although genomic FDs have been much studied before [31]–[36], the method and focus of the present study are both distinct from all previous studies. A novel approach we use, crucial to our ability to extract results presented here, is the separation of the contributions to the variance from the fluctuating part of an FD (FFD), and the non-fluctuaing part (NFFD). We show that NFFD is entirely understood; it carries no statistical information other than the base composition of a sequence. A genomic sequence and its matching random sequence have essentially the same NFFD. The contribution from NFFD overwhelmingly dominates the variance (of an FD) of a random sequence in all cases and dominates the variance of a genome except when its base composition is approximately even. As a consequence, if the separation mentioned above is not carried out, then it is sometimes easy to distinguish genomic from random sequences and sometimes not, a situation that has confounded many previous studies. We will demonstrate that the very special characteristics of genomic FFDs sharply distinguishes them from their random counterparts under all circumstances.
-mers, in the sequence. Although genomic FDs have been much studied before [31]–[36], the method and focus of the present study are both distinct from all previous studies. A novel approach we use, crucial to our ability to extract results presented here, is the separation of the contributions to the variance from the fluctuating part of an FD (FFD), and the non-fluctuaing part (NFFD). We show that NFFD is entirely understood; it carries no statistical information other than the base composition of a sequence. A genomic sequence and its matching random sequence have essentially the same NFFD. The contribution from NFFD overwhelmingly dominates the variance (of an FD) of a random sequence in all cases and dominates the variance of a genome except when its base composition is approximately even. As a consequence, if the separation mentioned above is not carried out, then it is sometimes easy to distinguish genomic from random sequences and sometimes not, a situation that has confounded many previous studies. We will demonstrate that the very special characteristics of genomic FFDs sharply distinguishes them from their random counterparts under all circumstances.
In this study we used the FFD to define the equivalent lengths ( 's; one for each
's; one for each  ) of a sequence and discovered a universality in these quantities. We then identify these
) of a sequence and discovered a universality in these quantities. We then identify these  's and their small values, as a clear and distinct global imprints of genome growth and evolution. (The
's and their small values, as a clear and distinct global imprints of genome growth and evolution. (The  of a sequence is inversely proportional to the FFD part of the variance and is defined such that the
of a sequence is inversely proportional to the FFD part of the variance and is defined such that the  of a random sequence is its own true length. Therefore, a sequence whose equivalent length is
of a random sequence is its own true length. Therefore, a sequence whose equivalent length is  has the characteristic randomness of a random sequence of length
has the characteristic randomness of a random sequence of length  .) We computed the
.) We computed the  of about 900 complete chromosomes, all the complete sequences at the time of download from GenBank, for
of about 900 complete chromosomes, all the complete sequences at the time of download from GenBank, for  = 2 to 10, and found some unexpected and useful results: Roughly, the complete set of about 7400
= 2 to 10, and found some unexpected and useful results: Roughly, the complete set of about 7400  -dependent whole-chromosome
-dependent whole-chromosome  's is well represented by the universal formula
's is well represented by the universal formula  (
( ) =
) = 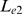
 where
where  b (base pair) and
b (base pair) and  = 0.92. The formula means that, for the smaller
= 0.92. The formula means that, for the smaller  's, the universal genomic
's, the universal genomic  is only a small fraction of the genome length even for the shortest genomes. Another unexpected result is the small difference between the
is only a small fraction of the genome length even for the shortest genomes. Another unexpected result is the small difference between the  's of coding and non-coding parts. In our successful attempt to describe these results in a simple genome growth model driven by random segmental duplication, we obtained a universal cumulative point mutation density of
's of coding and non-coding parts. In our successful attempt to describe these results in a simple genome growth model driven by random segmental duplication, we obtained a universal cumulative point mutation density of  = 0.73
= 0.73 0.07/site for genomes. This value is compatible with the relatively low mutation rates previously determined by sequence comparison for the human and E. coli genomes [37]–[39].
0.07/site for genomes. This value is compatible with the relatively low mutation rates previously determined by sequence comparison for the human and E. coli genomes [37]–[39].
Results
Only FFD contains non-trivial information
A key to our approach to the analysis of genomic sequences is the decomposition of  –
–  is the coefficient of variation of an FD – into FFD and NFFD components (Methods). This is illustrated in Fig. 1, which shows the values of
is the coefficient of variation of an FD – into FFD and NFFD components (Methods). This is illustrated in Fig. 1, which shows the values of  for 2-mers; results for other
for 2-mers; results for other  's are similar. The full
's are similar. The full  of genomic sequences (Fig. 1(a)) differs from that of their matching random sequences (Fig. 1(b)) clearly only when
of genomic sequences (Fig. 1(a)) differs from that of their matching random sequences (Fig. 1(b)) clearly only when 


 0.1, where
0.1, where  is the fractional A/T-content. (A genome and its matching random sequence have the same length and base composition.) The situation becomes much clearer when
is the fractional A/T-content. (A genome and its matching random sequence have the same length and base composition.) The situation becomes much clearer when  is decomposed into its FFD and NFFD parts,
is decomposed into its FFD and NFFD parts,  and
and  , respectively. While the values of
, respectively. While the values of  for the two type of sequences are almost indistinguishable ((red) triangles, Fig. 1(c,d); the two “volcano” curves are identical, being both given by the theoretical prediction, Eq. (12)), the values of
for the two type of sequences are almost indistinguishable ((red) triangles, Fig. 1(c,d); the two “volcano” curves are identical, being both given by the theoretical prediction, Eq. (12)), the values of  for genomes and random sequences are drastically different ((blue) bullets, Fig. 1(c,d)). The genomic
for genomes and random sequences are drastically different ((blue) bullets, Fig. 1(c,d)). The genomic  span a narrow band ranging from 0.01 to 0.1, while the random
span a narrow band ranging from 0.01 to 0.1, while the random  are several orders of magnitude smaller. In fact for random sequences the value of
are several orders of magnitude smaller. In fact for random sequences the value of  is well understood to be inversely proportional to sequence length (Eq. (13), and below). Clearly, if random sequences are used as controls to discuss the non-random properties of genomic sequences when the distinction between FFD and NFFD is not made, then it is possible that conflicting conclusions [32], [40]–[43] may be drawn.
is well understood to be inversely proportional to sequence length (Eq. (13), and below). Clearly, if random sequences are used as controls to discuss the non-random properties of genomic sequences when the distinction between FFD and NFFD is not made, then it is possible that conflicting conclusions [32], [40]–[43] may be drawn.
Figure 1. Fluctuating and non-fluctuating parts of variance.
(a) Variances of 2-mer frequency distribution of 865 complete sequences. (b) Same as (a) but for for 865 matching random sequences. Bottom: same data as in top plots, but with each variance split into non-fluctuating (triangles) and fluctuating (bullets) parts, for (c) genomes and (d) matching random sequences. The “volcanic” curves through the non-fluctuating data in (c) and (d) plot theoretical values given by Eq. (12).
Genomic  is approximately a constant of sequence length
is approximately a constant of sequence length
Throughout this paper we use  to denote generically the equivalent length of any sequence (Eq. (14), Methods), and reserve
to denote generically the equivalent length of any sequence (Eq. (14), Methods), and reserve  for denoting entire sequences such as a complete chromosomes. Fig. 2 shows
for denoting entire sequences such as a complete chromosomes. Fig. 2 shows  versus segment length
versus segment length  for segments taken from the chromosomes of four model organisms: E. coli
for segments taken from the chromosomes of four model organisms: E. coli
 ; C. elegans, Chr. (chromosome) 1; A. thaliana, Chr. 1; H. sapiens, Chr. 1, and matching random sequences. The computation is carried out only when
; C. elegans, Chr. (chromosome) 1; A. thaliana, Chr. 1; H. sapiens, Chr. 1, and matching random sequences. The computation is carried out only when  is at least four times
is at least four times  , since for shorter lengths the systematic error becomes too large. It is seen that whereas the
, since for shorter lengths the systematic error becomes too large. It is seen that whereas the 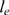 of random sequences closely tracks
of random sequences closely tracks  , as expected, the
, as expected, the  of genomic sequences quickly levels off to a saturation value
of genomic sequences quickly levels off to a saturation value  . These results for
. These results for 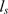
 5 kb may be summarized in terms of the scaling relation
5 kb may be summarized in terms of the scaling relation 

 . Then we have the two distinct classes
. Then we have the two distinct classes 
 1 for random sequences and
1 for random sequences and 
 0 for genomic sequences. This scaling relation is not the same as the long-range correlation and scale-invariance observed in binary analyses of long genomic sequences [44]–[46]. In Fig. 2
0 for genomic sequences. This scaling relation is not the same as the long-range correlation and scale-invariance observed in binary analyses of long genomic sequences [44]–[46]. In Fig. 2
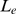 is seen not to depend strongly on organism. For small
is seen not to depend strongly on organism. For small  ,
,  is diminutive relative to genome length:
is diminutive relative to genome length:  0.35 and
0.35 and  1.0 kb when
1.0 kb when  = 2 and 4, respectively, growing to
= 2 and 4, respectively, growing to  600 kb when
600 kb when  = 10. Within a genome, the apparent invariance of
= 10. Within a genome, the apparent invariance of 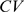 (not
(not  ) with respect to segment length was noted in [47]–[49] and the relation between Shannon information and a quantity similar to
) with respect to segment length was noted in [47]–[49] and the relation between Shannon information and a quantity similar to  was discussed in [50].
was discussed in [50].
Figure 2. Segmental equivalent lengths from four model organisms.
Equivalent length  versus sequence length
versus sequence length  for genomic (hollow symbols) and matching random (solid symbols) sequences. Genomic segments are from E. coli (
for genomic (hollow symbols) and matching random (solid symbols) sequences. Genomic segments are from E. coli ( ), worm (C. elegans (chromosome) I,
), worm (C. elegans (chromosome) I,  ), mustard (A. thaliana I,
), mustard (A. thaliana I,  ), and human (H. sapiens I,
), and human (H. sapiens I,  ). Each
). Each  in the form of mean
in the form of mean SD is averaged over the maximum number of non-overlapping segments (of length
SD is averaged over the maximum number of non-overlapping segments (of length 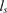 ) in the chromosome or, if the chromosome is longer than 20
) in the chromosome or, if the chromosome is longer than 20 , 20 randomly selected segments.
, 20 randomly selected segments.
Whole chromosomes have nearly universal 
A list of the 865 complete chromosomes studied here is given in Table S1, and a list of  's,
's,  = 2 to 10, for the chromosomes is give in Table S2. Fig. 3 shows
= 2 to 10, for the chromosomes is give in Table S2. Fig. 3 shows  , as a function of
, as a function of  (top panels) and chromosome length
(top panels) and chromosome length  (bottom panels), computed from the complete chromosomes for even
(bottom panels), computed from the complete chromosomes for even  's up to
's up to  = 10. Table 1 gives the
= 10. Table 1 gives the  ,
,  = 2 to 10, of chromosomes of seven model organisms. It is seen that
= 2 to 10, of chromosomes of seven model organisms. It is seen that  has a clear dependence on
has a clear dependence on  , is essentially independent of sequence length, and has a weak dependence on
, is essentially independent of sequence length, and has a weak dependence on 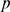 . Fig. 4 gives
. Fig. 4 gives  for odd
for odd  's averaged over categories of organisms and over chromosomes in model organisms (for more detailed results see Table S3). The
's averaged over categories of organisms and over chromosomes in model organisms (for more detailed results see Table S3). The  = 5 data reconfirms the absence in
= 5 data reconfirms the absence in  of a systematic dependence on chromosome length (similarly for other
of a systematic dependence on chromosome length (similarly for other  's). In the
's). In the  = 3 and 7 plots
= 3 and 7 plots  's are given separately for the whole chromosome, and genic (gn), and inter-genic (ig), exon (ex) and intron (in, when applicable) concatenates (Methods). The unicellulars are seen to have the largest variation in
's are given separately for the whole chromosome, and genic (gn), and inter-genic (ig), exon (ex) and intron (in, when applicable) concatenates (Methods). The unicellulars are seen to have the largest variation in  , especially for the ig and in regions. This partly reflects the fact that this category includes two phylogenetically remote groups, protists and fungi. In contrast, the relatively small variation in the vertebrate
, especially for the ig and in regions. This partly reflects the fact that this category includes two phylogenetically remote groups, protists and fungi. In contrast, the relatively small variation in the vertebrate  reflects the fact that, compared to organisms in other categories, vertebrates are phylogenetically very close. Two examples in opposite extremes are shown in the bottom panel of Fig. 4 (
reflects the fact that, compared to organisms in other categories, vertebrates are phylogenetically very close. Two examples in opposite extremes are shown in the bottom panel of Fig. 4 ( = 7): the malaria causing parasite P. falciparum with especially small
= 7): the malaria causing parasite P. falciparum with especially small  's, and the fungus S. pombe with relatively large
's, and the fungus S. pombe with relatively large  's. This indicates that the chromosomes of P. falciparum and S. pombe are much less and much more random, respectively, than the genomic norm. Although such inter-category, inter-species and inter-regional differences are significant, they pale when compared with the difference between
's. This indicates that the chromosomes of P. falciparum and S. pombe are much less and much more random, respectively, than the genomic norm. Although such inter-category, inter-species and inter-regional differences are significant, they pale when compared with the difference between  and true chromosome lengths. Table 2 lists
and true chromosome lengths. Table 2 lists  ,
,  = 2, 5, 7 and 10, averaged over all 865 sequences, for whole chromosome and the four types of concatenates.
= 2, 5, 7 and 10, averaged over all 865 sequences, for whole chromosome and the four types of concatenates.
Figure 3. Chromosomal equivalent length ( ) versus
) versus  and
and  .
.
Top panels:  versus
versus  ; bottom panels:
; bottom panels:  versus
versus  . Each piece of data gives the
. Each piece of data gives the  from a complete chromosome:
from a complete chromosome: 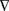 (red),
(red),  = 2;
= 2;  (gray),
(gray), 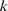 = 4;
= 4;  (blue),
(blue),  = 6,
= 6,  (green),
(green),  = 8,
= 8,  (orange),
(orange),  = 10. Lines in top-left panel represent the “universality class”
= 10. Lines in top-left panel represent the “universality class”  (
(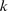 ;
; ) (Eq. (1)). The right panels show the collapse of genomic data to around unity when the genomic
) (Eq. (1)). The right panels show the collapse of genomic data to around unity when the genomic  is divided by
is divided by  (
( ;
;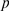 ).
).
Table 1. Genomic equivalent lengths for model organisms.
 (kb) (kb)
|
|||||||||
Organism 

|
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
H. sapiens (24)
|
.188 .021 .021 |
.448 .046 .046 |
1.22 .13 .13 |
3.39 .41 .41 |
9.34 1.36 1.36 |
23.8 4.4 4.4 |
53.9 12.6 12.6 |
103 29 29 |
170 54 54 |
H. sapiens (gn; 43.2%)
|
.185 .022 .022 |
.440 .048 .048 |
1.20 .14 .14 |
3.31 .42 .42 |
9.02 1.33 1.33 |
22.4 4.0 4.0 |
49.2 10.9 10.9 |
90.5 23.7 23.7 |
144 42 42 |
H. sapiens (ig; 63.6%)
|
.190 .021 .021 |
.452 .045 .045 |
1.24 .13 .13 |
3.44 .41 .41 |
9.51 1.36 1.36 |
24.5 4.5 4.5 |
56.6 13.4 13.4 |
111 32 32 |
186 61 61 |
H. sapiens (ex; 2.1%)
|
.171 .019 .019 |
.412 .042 .042 |
1.12 .12 .12 |
3.07 .39 .39 |
8.21 1.26 1.26 |
19.9 3.8 3.8 |
41.9 10.3 10.3 |
72.2 21.6 21.6 |
117 22 22 |
H. sapiens (in; 37%)
|
.182 .020 .020 |
.434 .043 .043 |
1.18 .13 .13 |
3.26 .40 .40 |
8.84 1.34 1.34 |
21.9 4.2 4.2 |
47.7 11.5 11.5 |
87.2 24.9 24.9 |
139 45 45 |
A. thaliana (5)
|
.373 .005 .005 |
.871 .013 .013 |
2.20 .04 .04 |
5.89 .10 .10 |
16.0 .3 .3 |
42.1 .8 .8 |
109 2 2 |
273 7 7 |
642 20 20 |
A. thaliana (gn; 55.8%)
|
.333 .004 .004 |
.822 .011 .011 |
2.06 .03 .03 |
5.57 .08 .08 |
15.9 .2 .2 |
44.9 .7 .7 |
129 2 2 |
367 6 6 |
981 22 22 |
A. thaliana (ig; 44.1%)
|
.394 .007 .007 |
.798 .014 .014 |
1.94 .04 .04 |
4.95 .10 .10 |
12.3 .2 .2 |
28.9 .6 .6 |
66.1 1.5 1.5 |
144 4 4 |
296 12 12 |
A. thaliana (ex; 32.9%)
|
.288 .003 .003 |
.715 .007 .007 |
1.75 .02 .02 |
4.72 .05 .05 |
13.6 .1 .1 |
38.9 .4 .4 |
113 2 2 |
326 7 7 |
865 35 35 |
A. thaliana (in; 16.1%)
|
.350 .003 .003 |
.752 .006 .006 |
1.80 .02 .02 |
4.42 .04 .04 |
11.1 .1 .1 |
27.3 .4 .4 |
68.1 1.0 1.0 |
167 3 3 |
400 1 1 |
 (4) (4)
|
.409 .142 .142 |
.957 .213 .213 |
2.54 .46 .46 |
6.90 1.17 1.17 |
18.7 3.2 3.2 |
48.2 9.5 9.5 |
117 31 31 |
268 102 102 |
676 294 294 |
 (gn; 56.4%) (gn; 56.4%)
|
.432 .108 .108 |
1.02 .15 .15 |
2.71 .30 .30 |
7.35 .85 .85 |
20.0 2.8 2.8 |
51.6 9.9 9.9 |
127 35 35 |
326 120 120 |
756 321 321 |
 (ig; 43.5%) (ig; 43.5%)
|
.392 .194 .194 |
.882 .305 .305 |
2.30 .66 .66 |
6.15 1.57 1.57 |
16.1 3.3 3.3 |
39.4 7.5 7.5 |
90.0 28.1 28.1 |
235 87 87 |
536 231 231 |
 (ex; 23.9%) (ex; 23.9%)
|
.478 .023 .023 |
1.16 .09 .09 |
2.82 .41 .41 |
7.55 1.39 1.39 |
21.0 4.2 4.2 |
55.6 10.7 10.7 |
140 29 29 |
377 111 111 |
907 324 324 |
 (in; 34.8%) (in; 34.8%)
|
.378 .145 .145 |
.833 .168 .168 |
2.15 .30 .30 |
5.65 .73 .73 |
14.8 2.3 2.3 |
36.2 7.9 7.9 |
84.0 26.2 26.2 |
207 79 79 |
458 198 198 |
C. elegans (6)
|
.119 .012 .012 |
.258 .032 .032 |
.624 .089 .089 |
1.63 .26 .26 |
4.46 .78 .78 |
12.6 2.3 2.3 |
35.5 6.9 6.9 |
98.8 21.0 21.0 |
264 63 63 |
C. elegans (gn; 58.6%)
|
.126 .017 .017 |
.284 .047 .047 |
.697 .135 .135 |
1.83 .40 .40 |
5.06 1.21 1.21 |
14.3 3.7 3.7 |
40.8 11.1 11.1 |
114 34 34 |
306 99 99 |
C. elegans (ig; 41.3%)
|
.109 .009 .009 |
.226 .022 .022 |
.539 .061 .061 |
1.39 .18 .18 |
3.78 .51 .51 |
10.5 1.5 1.5 |
29.3 4.5 4.5 |
79.5 13.6 13.6 |
202 41 41 |
C. elegans (ex; 27.5%)
|
.184 .010 .010 |
.483 .025 .025 |
1.28 .07 .07 |
3.64 .23 .23 |
10.9 .7 .7 |
33.2 2.4 2.4 |
102 8 8 |
306 25 25 |
822 58 58 |
C. elegans (in; 32.3%)
|
.085 .015 .015 |
.169 .037 .037 |
.382 .096 .096 |
.939 .265 .265 |
2.44 .73 .73 |
6.52 1.99 1.99 |
17.4 5.3 5.3 |
45.4 14.1 14.1 |
113 37 37 |
S. pombe (3)
|
.362 .010 .010 |
.894 .030 .030 |
2.41 .09 .09 |
6.74 .28 .28 |
19.2 .9 .9 |
54.6 3.0 3.0 |
153 11 11 |
402 39 39 |
1013 39 39 |
S. pombe (gn; 57.8%)
|
.339 .002 .002 |
.880 .006 .006 |
2.38 .01 .01 |
6.82 .05 .05 |
20.2 .2 .2 |
59.6 .8 .8 |
173 6 6 |
455 42 42 |
— |
S. pombe (ig; 42.1%)
|
.364 .019 .019 |
.812 .045 .045 |
2.08 .12 .12 |
5.31 .32 .32 |
13.5 .8 .8 |
33.6 2.1 2.1 |
81.7 5.8 5.8 |
187 16 16 |
— |
S. pombe (ex; 53.9%)
|
.357 .007 .007 |
.889 .018 .018 |
2.40 .06 .06 |
6.73 .18 .18 |
19.2 .6 .6 |
54.4 2.3 2.3 |
149 10 10 |
374 42 42 |
— |
S. pombe (in; 3%)
|
.361 .007 .007 |
.898 .017 .017 |
2.41 .06 .06 |
6.53 .14 .14 |
17.0 .4 .4 |
38.2 3.1 3.1 |
— | — | — |
 (14) (14)
|
1.40 .20 .20 |
.287 .019 .019 |
.376 .023 .023 |
.512 .036 .036 |
.729 .059 .059 |
.998 .089 .089 |
1.34 .13 .13 |
1.73 .19 .19 |
— |
 (gn; 56%) (gn; 56%)
|
.595 .118 .118 |
.659 .085 .085 |
1.02 .12 .12 |
1.86 .29 .29 |
3.59 .74 .74 |
6.73 1.86 1.86 |
12.3 4.3 4.3 |
16.3 10.4 10.4 |
— |
 (ig; 44%) (ig; 44%)
|
.665 .108 .108 |
.111 .017 .017 |
.130 .017 .017 |
.162 .022 .022 |
.212 .031 .031 |
.276 .042 .042 |
.357 .057 .057 |
.398 .032 .032 |
— |
 (ex; 53%) (ex; 53%)
|
.515 .058 .058 |
.717 .060 .060 |
1.12 .07 .07 |
2.10 .11 .11 |
4.21 .23 .23 |
8.30 .56 .56 |
16.0 1.3 1.3 |
32.0 1.6 1.6 |
— |
 (in; 5.7%) (in; 5.7%)
|
.163 .019 .019 |
.052 .002 .002 |
.064 .003 .003 |
.076 .003 .003 |
.095 .004 .004 |
.116 .003 .003 |
— | — | — |
E. coli (1)
|
.373 | .729 | 1.74 | 4.52 | 12.6 | 37.0 | 111 | 328 | 879 |
E. coli (gn; 88.7%)
|
.346 | .656 | 1.56 | 4.05 | 11.3 | 33.0 | 98.9 | 292 | — |
E. coli (ig; 11.2%)
|
.553 | 1.22 | 2.60 | 6.33 | 16.0 | 39.3 | 83.9 | — | — |
 ,
,  = 2 to 10, of chromosomes of model organisms. The
= 2 to 10, of chromosomes of model organisms. The  's given are mean
's given are mean SD averaged over chromosomes of the organism, except for the single chromosome E. coli. See Table S2 for list of all computed
SD averaged over chromosomes of the organism, except for the single chromosome E. coli. See Table S2 for list of all computed  's. (
's. ( ) Number in parentheses indicates total number of complete chromosomes in organism. (
) Number in parentheses indicates total number of complete chromosomes in organism. ( ) Abbreviations: gn, gene; gn, intergenic; ex, exon; in, intron. Percentage given indicates portion of complete sequence. “N-runs” or gaps in sequences are not counted. (
) Abbreviations: gn, gene; gn, intergenic; ex, exon; in, intron. Percentage given indicates portion of complete sequence. “N-runs” or gaps in sequences are not counted. ( ) Ex and in segments selected as given by Genbank; sum of percentages for ex and in may be less than or exceed that of gn due to incomplete or duplicated segments. (
) Ex and in segments selected as given by Genbank; sum of percentages for ex and in may be less than or exceed that of gn due to incomplete or duplicated segments. ( )
)  (
( ) computed only if category has more than one sequence whose length exceeds
) computed only if category has more than one sequence whose length exceeds  .
.
Figure 4. Averaged equivalent lengths for complete chromosomes and concatenates.
The concatenates are: “gene” (gn in main text), coding regions; “intergene” (ig), non-coding or intergenic regions; “exon” (ex), exons in gn (for eukaryotes); “intron” (in), introns in gn. Top left,  (
( = 3) averaged over phylogenetic categories (Uni, unicellulars; Pla, plants; Ins, insects; Ver, vertebrayes; Pro, prokaryotes); top right,
= 3) averaged over phylogenetic categories (Uni, unicellulars; Pla, plants; Ins, insects; Ver, vertebrayes; Pro, prokaryotes); top right,  (
( = 5) versus chromosome length average over categories; bottom,
= 5) versus chromosome length average over categories; bottom,  (
( = 7) for seven model organisms averaged over chromosomes. Boxes indicate data in the 10, 25, 50, 75 and 90% range.
= 7) for seven model organisms averaged over chromosomes. Boxes indicate data in the 10, 25, 50, 75 and 90% range.
Table 2. Average genomic equivalent lengths.
 (kb) (kb) |
||||
| Category | ( = ) 2 = ) 2 |
5 | 7 | 10 |
| All |

|

|

|

|
| gn (41.8%) |

|

|

|

|
| ig (59.6%) |

|

|

|

|
| ex (3.3%) |

|

|

|

|
| in (31.8%) |

|

|

|

|
 ( ( = 0.5) = 0.5) |

|

|

|

|
| RSD model |

|
|

|

|
 ,
,  = 2, 5, 7 and 10, averaged over 865 chromosomes. Total sequences length is about 2.2
= 2, 5, 7 and 10, averaged over 865 chromosomes. Total sequences length is about 2.2 10
10 bases. Abbreviations: All, complete chromosome; gn, genes; ig, intergenic; ex, exons; in, introns. Percentage given indicates portion of complete sequence.
bases. Abbreviations: All, complete chromosome; gn, genes; ig, intergenic; ex, exons; in, introns. Percentage given indicates portion of complete sequence.  is defined in Eq. (1) and RSD results are averaged over 200 model sequences. See Table S4 for
is defined in Eq. (1) and RSD results are averaged over 200 model sequences. See Table S4 for  of other
of other  values.
values.
Summary of genomic data
We summarize the trends of genomic data: (a)  increases with
increases with  . (b) For given
. (b) For given  ,
,  has no systematic dependence on
has no systematic dependence on  and has a weak dependence on
and has a weak dependence on  . (c) For given
. (c) For given  ,
,  for different organisms are of the same order of magnitude. (d) Within a genome,
for different organisms are of the same order of magnitude. (d) Within a genome,  differs little among chromosomes. (e) There is remarkable agreement between the gn and ex data sets. (f) There is not a significant difference between the
differs little among chromosomes. (e) There is remarkable agreement between the gn and ex data sets. (f) There is not a significant difference between the  's for coding (
's for coding ( and
and  ) and non-coding (
) and non-coding ( and
and  ) regions, and the agreement between the two regions improves when that fact that coding regions tend to be GC-rich is taken into account (Text S1 and Fig. S1). We remark that in splicing the
) regions, and the agreement between the two regions improves when that fact that coding regions tend to be GC-rich is taken into account (Text S1 and Fig. S1). We remark that in splicing the  concatenate genes in positive and negative orientations from a
concatenate genes in positive and negative orientations from a  strand of DNA are concatenated, without inverting the negatively oriented genes (Methods). Similarly for the
strand of DNA are concatenated, without inverting the negatively oriented genes (Methods). Similarly for the  concatenate.
concatenate.
Discussion
Universal 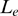 is not a result of inter-chromome similarity in
is not a result of inter-chromome similarity in  -mer-content
-mer-content
Fig. 5 shows intra-chromosome  -mer-content similarity plots (Methods) for six representative chromosomes. In the plots, a small value of
-mer-content similarity plots (Methods) for six representative chromosomes. In the plots, a small value of  (
( 0.2, black-blue) indicates high degree of similarity, and a large value (
0.2, black-blue) indicates high degree of similarity, and a large value ( 1, cyan to red) indicates the opposite. A general trend is that local
1, cyan to red) indicates the opposite. A general trend is that local  -mer-content within a chromosome is fairly homogeneous [51], [52] on a scale as small as 50 kb. When
-mer-content within a chromosome is fairly homogeneous [51], [52] on a scale as small as 50 kb. When  -mer-contents of coding and non-coding parts show a significant difference, as is seen in the case of P. falciparum, M. stadtmanae, and E. coli, it is mainly caused by the gn part being substantially richer in GC content than the
-mer-contents of coding and non-coding parts show a significant difference, as is seen in the case of P. falciparum, M. stadtmanae, and E. coli, it is mainly caused by the gn part being substantially richer in GC content than the  part (Table 3). Nevertheless, because
part (Table 3). Nevertheless, because 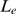 is defined such that first-order dependence in base composition is removed, within a chromosome the
is defined such that first-order dependence in base composition is removed, within a chromosome the  's for the
's for the  and
and  parts and for the whole chromosome generally have similar values (Table S3,
parts and for the whole chromosome generally have similar values (Table S3,  ).
).
Figure 5. Intra-chromosomes similarity plots.
Plots are for  = 2 (Methods). Sliding window has width 25 kb and slide 10 kb; pixel size is 10 kb by 10 kb. In each plot, the coordinates for the upper-left triangle are sites along the chromosome (chr), and those for the lower-right triangle are along a concatenate composed of gene (gn, left side) and intergene (ig, right side) parts. In effect, the upper-left triangle shows chr-chr similarity, and the lower-right triangle shows gn-gn (lower-left sub-triangle), ig-ig (upper-right sub-triangle), and gn-ig (rectangular) similarities in three separate regions. The lengths of the gn and ig parts are given in Table 3.
= 2 (Methods). Sliding window has width 25 kb and slide 10 kb; pixel size is 10 kb by 10 kb. In each plot, the coordinates for the upper-left triangle are sites along the chromosome (chr), and those for the lower-right triangle are along a concatenate composed of gene (gn, left side) and intergene (ig, right side) parts. In effect, the upper-left triangle shows chr-chr similarity, and the lower-right triangle shows gn-gn (lower-left sub-triangle), ig-ig (upper-right sub-triangle), and gn-ig (rectangular) similarities in three separate regions. The lengths of the gn and ig parts are given in Table 3.
Table 3. Intra-chromosome similarity indexes.
Length (Mb)/
|
Average 
|
||||||
| Organism | chr | gn | ig | chr-chr | gn-gn | ig-ig | gn-ig |
| S. pombe Chr. 1 | 2.45/0.64 | 1.40/0.61 | 1.05/0.69 | 0.648 | 0.569 | 0.615 | 0.647 |
| E. cuniculi (genome) | 2.50/0.53 | 2.15/0.53 | 0.35/0.55 | 0.527 | 0.481 | 0.450 | 0.666 |
| P. falciparum Chr. 13 | 2.73/0.82 | 1.55/0.79 | 1.18/0.87 | 0.801 | 0.742 | 0.641 | 2.11 |
| M. stadtmanae | 1.77/0.73 | 1.51/0.71 | 0.26/0.83 | 0.805 | 0.782 | 0.757 | 2.52 |
| S. glossinidius morsitans | 4.17/0.46 | 2.15/0.44 | 2.02/0.47 | 0.638 | 0.510 | 0.635 | 0.729 |
| E. coli K12 | 4.64/0.50 | 4.12/0.49 | 0.52/0.58 | 0.517 | 0.481 | 0.548 | 1.63 |
Compositions and average regional similarity indexes of sequences shown in Fig. 6; chr, chromosome; gn, gene; ig, intergenic.
Fig. 6 compares the intra-E. coli plot with inter-chromosome plots of E. coli versus seven other organisms whose phylogenetic distances to E. coli range from close to remote. The approximate monochromaticity of each plot reconfirms our previous observation that  -mer-content within a chromosome has a high degree of homogeneity (on a scale of 100 kb). We see close correlation between phyogenetic distance and the shades (colors) of the seven inter-chromosome plots. Fig. 7 gives the mean
-mer-content within a chromosome has a high degree of homogeneity (on a scale of 100 kb). We see close correlation between phyogenetic distance and the shades (colors) of the seven inter-chromosome plots. Fig. 7 gives the mean  for the plots and P-values from Student t-tests for the null assumption that the inter-chromosome plots are the same as the intra- E. coli plot. These results verify that the observed near universal value in
for the plots and P-values from Student t-tests for the null assumption that the inter-chromosome plots are the same as the intra- E. coli plot. These results verify that the observed near universal value in 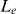 is not cause by similarity in
is not cause by similarity in  -mer-content among chromosomes.
-mer-content among chromosomes.
Figure 6. Intra- E. coli and inter-chromosome similarity plots.
The plots are those of E. coli chromosome  the chromosomes of, left to right and top to bottom, E. coli, E. coli UT189, Salmonella, the delta-proteobacteria S. aciditrophicus, the cyanobacteria Synechocystis, the archaea P. aerophilum, chromosome 5 of the fungus A. fumigatus, and the first 4.5 Mb segment from chromosome 1 of H. sapiens. Coordinates are sites along the sequence. Sliding window width is 100 kb and slide is 25 kb, pixel size is 25 kb by 25 kb.
the chromosomes of, left to right and top to bottom, E. coli, E. coli UT189, Salmonella, the delta-proteobacteria S. aciditrophicus, the cyanobacteria Synechocystis, the archaea P. aerophilum, chromosome 5 of the fungus A. fumigatus, and the first 4.5 Mb segment from chromosome 1 of H. sapiens. Coordinates are sites along the sequence. Sliding window width is 100 kb and slide is 25 kb, pixel size is 25 kb by 25 kb.
Figure 7. Comparison of inter-chromosome similarity matrices.
Mean values and SD of the eight  -plots (of
-plots (of  -matrices) shown in Fig. 6 and P-values for the null assumption that the 2nd to 7th cases are the same as the 1st case.
-matrices) shown in Fig. 6 and P-values for the null assumption that the 2nd to 7th cases are the same as the 1st case.
As an aside, we note that in Fig. 6 the plot for S. pombe indicates a  100 kb ig segment around the 1.1 Mb site has extraordinary low similarity with respect to all other regions of the chromosome. This could be the result of a non-genic horizontal/lateral transfer [53], [54] and suggests that similarity plots may be useful for locating such events.
100 kb ig segment around the 1.1 Mb site has extraordinary low similarity with respect to all other regions of the chromosome. This could be the result of a non-genic horizontal/lateral transfer [53], [54] and suggests that similarity plots may be useful for locating such events.
A universal formula for 
The 7360 pieces of data in the “All” set in Table 2 is well represented by the empirical formula,
| (1) |
| (2) |
where  = 0.92,
= 0.92,  b, and
b, and  = 0.50
= 0.50 0.05. The central values of the formula are shown as solid lines in Fig. 3 and listed as the entries in the row labeled
0.05. The central values of the formula are shown as solid lines in Fig. 3 and listed as the entries in the row labeled  in Table 2. The denominator in Eq. (2) represents the residual
in Table 2. The denominator in Eq. (2) represents the residual  -dependence indicated in the data in Fig. 3; it works well even for chromosomes with large
-dependence indicated in the data in Fig. 3; it works well even for chromosomes with large 
 0.5
0.5 (Table S4,
(Table S4,  ). For the vast majority of genomic
). For the vast majority of genomic  's,
's, 

 (
( /
/ (Text S1) is less than 1 (Fig. S2) and, averaged over the 7360 pieces of data in the “All” set,
(Text S1) is less than 1 (Fig. S2) and, averaged over the 7360 pieces of data in the “All” set,  = 0.43. This means that on average the genomic
= 0.43. This means that on average the genomic  is within a factor of two of
is within a factor of two of  . In recognizing that genomes as a category exhibit such a non-trivial common feature which is itself the manifest of an underlying but yet undetermined cause, we say genomes belong to a universality class. It is realized that Eq. (1) cannot be extended to
. In recognizing that genomes as a category exhibit such a non-trivial common feature which is itself the manifest of an underlying but yet undetermined cause, we say genomes belong to a universality class. It is realized that Eq. (1) cannot be extended to  much greater than 10 (and not even to 10 for some of the smaller chromosomes), because a meaningful value for
much greater than 10 (and not even to 10 for some of the smaller chromosomes), because a meaningful value for  may be extracted only when a sequence is at least
may be extracted only when a sequence is at least  bases long.
bases long.
A universal formula for the standard deviation from the fluctuating part in  -mer frequency
-mer frequency
The short genomic  (relative to actual chromosome length) is a direct consequence of the genomic
(relative to actual chromosome length) is a direct consequence of the genomic  being much larger than its random-sequence counterpart. If we approximate
being much larger than its random-sequence counterpart. If we approximate 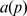 in Eq. (1) by
in Eq. (1) by  and approximate the factor
and approximate the factor  in Eq. (14) (Methods) by unity, then through Eq. (14) we convert Eq. (1) to a universal formula for the
in Eq. (14) (Methods) by unity, then through Eq. (14) we convert Eq. (1) to a universal formula for the  -set-averaged standard deviation for the
-set-averaged standard deviation for the  -mer FFD:
-mer FFD:
| (3) |
where  is the sequence length. The formula is meant to be applicable so long as
is the sequence length. The formula is meant to be applicable so long as  is several times greater than
is several times greater than  . For sequences with
. For sequences with 
 0.5,
0.5,  reduces to the usual variance. Note that for random sequences
reduces to the usual variance. Note that for random sequences 

 . Since
. Since  is large, genomic
is large, genomic  can be orders of magnitude greater than its random counterpart. For instance, for the 4.6 Mb chromosome, the
can be orders of magnitude greater than its random counterpart. For instance, for the 4.6 Mb chromosome, the  = 4 values for
= 4 values for  given by Eq. (3), the actual chromosome (
given by Eq. (3), the actual chromosome ( -averaged), and a random sequence are 6440 b, 6230 b, and 134 b, respectively, and for the 228 Mb human chromosome 1, the corresponding values are 319,000 b, 380,000 b, and 943 b, respectively. To give statistical meaning to such differences, Table 4 examines universal genomes of various lengths and gives the fractions of 2-mers and 9-mers (in the genomes) whose frequencies have P-values that are less than P
-averaged), and a random sequence are 6440 b, 6230 b, and 134 b, respectively, and for the 228 Mb human chromosome 1, the corresponding values are 319,000 b, 380,000 b, and 943 b, respectively. To give statistical meaning to such differences, Table 4 examines universal genomes of various lengths and gives the fractions of 2-mers and 9-mers (in the genomes) whose frequencies have P-values that are less than P – the P-value corresponding to
– the P-value corresponding to  standard deviations away from the expected frequency in a random sequence – for
standard deviations away from the expected frequency in a random sequence – for  = 3, 6, and 8, respectively. Because
= 3, 6, and 8, respectively. Because 

 , the fraction increases with decreasing
, the fraction increases with decreasing  and increasing
and increasing  (for a given
(for a given  ). For instance, for a sequence 4.6 Mb long (length of E. coli chromosome), fourteen of the sixteen 2-mers have P
). For instance, for a sequence 4.6 Mb long (length of E. coli chromosome), fourteen of the sixteen 2-mers have P P
P ( = 1.3
( = 1.3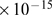 ), whereas only 26,000 of the 262,144 9-mers are so. In comparison, for a sequence 226 Mb long (length of human chromosome 1), all sixteen 2-mers and 213,000 of the 9-mers are so.
), whereas only 26,000 of the 262,144 9-mers are so. In comparison, for a sequence 226 Mb long (length of human chromosome 1), all sixteen 2-mers and 213,000 of the 9-mers are so.
Table 4. P-values for  -mer distribution in universality class.
-mer distribution in universality class.
Fraction of  -mers whose P-value is less than P -mers whose P-value is less than P , P , P , or P , or P
| ||||||
 = 2 ( = 2 ( = 310 b) = 310 b) |
 = 9 ( = 9 ( = 194 kb) = 194 kb) |
|||||
| Length (Mb) | P P P
|
P P P
|
P P P
|
P P P
|
P P P
|
P P P
|
| 0.8 | 0.953 | 0.906 | 0.875 | 0.139 | 0.0031 | 0.0001 |
| 4.6 | 0.980 | 0.960 | 0.955 | 0.538 | 0.418 | 0.100 |
| 30 | 0.992 | 0.985 | 0.979 | 0.809 | 0.628 | 0.519 |
| 226 | 0.997 | 0.994 | 0.992 | 0.930 | 0.860 | 0.815 |
P-values for  -mer distribution given by Eq. (1) (at
-mer distribution given by Eq. (1) (at  = 0.5). Null theory assumes genomes are random sequences. The P-values P
= 0.5). Null theory assumes genomes are random sequences. The P-values P = 2.7
= 2.7 , P
, P = 2.0
= 2.0 , and P
, and P = 1.3
= 1.3 correspond to
correspond to  -values of three, six and eight, respectively.
-values of three, six and eight, respectively.
Segmental duplication shortens 
We now discuss probable causes for the formation of the universality class. We first list some general properties of the ratio  of
of  to the sequence length
to the sequence length 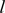 : if the sequence is (nearly) random then
: if the sequence is (nearly) random then  ( =
( =  /
/ )
) 1; if it is far less random than a random sequence of length
1; if it is far less random than a random sequence of length  then
then 
 1; if it is essentially ordered then
1; if it is essentially ordered then 
 0; if it is the
0; if it is the  -fold replication of a random sequence, then
-fold replication of a random sequence, then 
 1/
1/ . We illustrate how segmental duplication can cause a sequence to have
. We illustrate how segmental duplication can cause a sequence to have  much less then one, by considering the effect of a generalization of the operation of replication on
much less then one, by considering the effect of a generalization of the operation of replication on  . To be specific we label XY a concatenate composed of X and Y. If Y is a coarse-grained rearrangement of X, then, provided the scale of the rearrangements is not too small,
. To be specific we label XY a concatenate composed of X and Y. If Y is a coarse-grained rearrangement of X, then, provided the scale of the rearrangements is not too small,  (X)
(X)
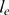 (Y) and concatenating X and Y is similar to doubling X by replication, hence
(Y) and concatenating X and Y is similar to doubling X by replication, hence  (XY) will be nearly equal to
(XY) will be nearly equal to  (X).
(X).
In general, if the  -mer-contents of X and Y are similar, then (provided the sequences are sufficiently long) we expect
-mer-contents of X and Y are similar, then (provided the sequences are sufficiently long) we expect  (XY)
(XY)
 (X)
(X)
 (Y). Conversely, if the
(Y). Conversely, if the  -mer-contents of X and Y are significantly different, then we expect
-mer-contents of X and Y are significantly different, then we expect  (XY)
(XY)
 (
( (X),
(X),  (Y)) (see Text S1 for an expanded discussion, including formulas given in Table S5). Results for testing these simple rules with real sequences are shown in Table 5. We expect agreement with theory to improve with increasing sequence length (
(Y)) (see Text S1 for an expanded discussion, including formulas given in Table S5). Results for testing these simple rules with real sequences are shown in Table 5. We expect agreement with theory to improve with increasing sequence length ( ). The first two rows of results in Table 5 verify that for random sequence
). The first two rows of results in Table 5 verify that for random sequence  is always close to one, or
is always close to one, or 

 . The results for AA
. The results for AA and BB
and BB show that concatenating two equal-length segments from the same chromosome is indeed like doubling a sequence by replication. Chromosomes labeled C
show that concatenating two equal-length segments from the same chromosome is indeed like doubling a sequence by replication. Chromosomes labeled C have
have  -mer-contents relatively more similar to A (Figs. 4 and 5), therefore
-mer-contents relatively more similar to A (Figs. 4 and 5), therefore  (AC
(AC )
)
 (AA
(AA )
)
 (A) as expected. Chromosomes labeled D
(A) as expected. Chromosomes labeled D and B have
and B have  -mer-contents more dissimilar to A, therefore
-mer-contents more dissimilar to A, therefore  (AX)
(AX)
 (
( (A),
(A),  (X)). The case of AD
(X)). The case of AD , where D
, where D is H. sapiens chr. 1, is not an exception to the rule even for
is H. sapiens chr. 1, is not an exception to the rule even for  = 2, because
= 2, because  (D
(D )
)
 (A). In the bottom portion of Table 5 the approximate relation
(A). In the bottom portion of Table 5 the approximate relation 


 (Table S5;
(Table S5;  is the equivalent length of the genomic portion and
is the equivalent length of the genomic portion and  is the ratio of the length of the concatenate to the that of the genomic portion) is seen to hold:
is the ratio of the length of the concatenate to the that of the genomic portion) is seen to hold: 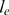 (RX)
(RX) 4
4 (X) (X being A or B),
(X) (X being A or B),  (RAB)
(RAB) 2.3
2.3 (AB), and
(AB), and  (RR'X)
(RR'X) 9
9 (X).
(X).
Table 5. Equivalent lengths of composite sequences.

|
||||
 = 2 = 2 |
 = 6 = 6 |
|||
| Sequence |
 = 50 = 50 |
 = 200 = 200 |
 = 50 = 50 |
 = 200 = 200 |
| R | 47.5 28.2 28.2 |
154 126 126 |
48.6 1.5 1.5 |
192 5 5 |
RR
|
37.0 16.2 16.2 |
124 46 46 |
48.2 1.2 1.2 |
197 5 5 |
| A | .348 .037 .037 |
.360 .033 .033 |
9.55 .69 .69 |
11.7 .7 .7 |
AA
|
.357 .046 .046 |
.352 .023 .023 |
9.88 1.07 1.07 |
11.1 .7 .7 |
AC
|
.351 .061 .061 |
.361 .021 .021 |
9.37 1.01 1.01 |
11.5 .6 .6 |
AC
|
.354 .043 .043 |
.384 .045 .045 |
9.18 .83 .83 |
11.6 .9 .9 |
AC
|
.359 .051 .051 |
.371 .034 .034 |
11.0 .9 .9 |
14.2 1.5 1.5 |
AD
|
.411 .044 .044 |
.423 .024 .024 |
11.8 .9 .9 |
14.3 .6 .6 |
AD
|
.942 .275 .275 |
1.05 .09 .09 |
14.9 1.4 1.4 |
20.4 1.1 1.1 |
AD
|
.598 .104 .104 |
.613 .052 .052 |
17.9 1.6 1.6 |
24.0 1.6 1.6 |
AD
|
.324 .052 .052 |
.383 .055 .055 |
11.2 1.9 1.9 |
16.9 1.9 1.9 |
| B | .124 .029 .029 |
.166 .099 .099 |
5.17 .68 .68 |
6.54 2.00 2.00 |
BB
|
.232 .155 .155 |
.258 .183 .183 |
6.16 1.94 1.94 |
7.54 2.30 2.30 |
| AB | .463 .241 .241 |
.502 .263 .263 |
11.2 1.9 1.9 |
15.2 3.5 3.5 |
| RA | 1.19 .09 .09 |
1.34 .20 .20 |
22.6 1.2 1.2 |
38.5 3.0 3.0 |
| RB | .575 .321 .321 |
.754 .637 .637 |
15.6 4.2 4.2 |
23.3 8.5 8.5 |
| RAB | .873 .424 .424 |
1.10 .49 .49 |
18.4 3.2 3.2 |
31.3 6.0 6.0 |
RR A A |
2.63 .66 .66 |
3.16 .30 .30 |
31.5 2.1 2.1 |
72.2 6.8 6.8 |
RR B B |
1.03 .62 .62 |
1.37 .70 .70 |
22.9 4.5 4.5 |
44.7 14.3 14.3 |
Equivalent lengths  of composite sequences of total length
of composite sequences of total length  (in kb). The composite XY is the concatenation of two equal-length components X and Y. Similarly for the composite XYZ. A and A
(in kb). The composite XY is the concatenation of two equal-length components X and Y. Similarly for the composite XYZ. A and A are segments from E. coli, and B and B
are segments from E. coli, and B and B are from C. tetani (2.80 Mb,
are from C. tetani (2.80 Mb,  = 0.70). C
= 0.70). C and D
and D , are the seven “other” chromosomes in Fig. 6, in the order given there. R and R
, are the seven “other” chromosomes in Fig. 6, in the order given there. R and R are
are  = 0.5 random sequences. Results are averaged over 10 samples in all cases.
= 0.5 random sequences. Results are averaged over 10 samples in all cases.
Artificial sequences generated by RSD growth model exhibit universal 
We show that a very simple growth model, the minimum random segmental duplication (RSD) model [49] (Methods; Text S1)), generates chromosome-length sequences that have  's very close to the universal
's very close to the universal  given by Eq. (1). In the model, simple segmental duplication (SD) serves to represent the numerous modes of DNA copying processes known to occur in genomes [9]–[11], [55], [56], and point mutation represents all small non-duplicating events. We consider random events because it is the simplest assumption and because it generates sequences with a reasonable degree of homogeneity [51], [52]. (It is known that genomes have long-range correlations that require tandem SDs to generate [46], [57]. Since tandem duplications do not effect
given by Eq. (1). In the model, simple segmental duplication (SD) serves to represent the numerous modes of DNA copying processes known to occur in genomes [9]–[11], [55], [56], and point mutation represents all small non-duplicating events. We consider random events because it is the simplest assumption and because it generates sequences with a reasonable degree of homogeneity [51], [52]. (It is known that genomes have long-range correlations that require tandem SDs to generate [46], [57]. Since tandem duplications do not effect  , for simplicity they are not given special treatment in this study.) The three parameters of the model are
, for simplicity they are not given special treatment in this study.) The three parameters of the model are 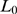 (initial length),
(initial length), 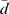 (average duplicated segment length), and
(average duplicated segment length), and  (cumulative point mutation per-base density) (Methods.
(cumulative point mutation per-base density) (Methods.  generated by the model is insensitive to sequence length provided it is longer than 0.5 Mb, allows a generous range in
generated by the model is insensitive to sequence length provided it is longer than 0.5 Mb, allows a generous range in 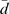 and a tighter range in
and a tighter range in  , and is highly sensitive to
, and is highly sensitive to  (Fig. S3,
(Fig. S3,  ). (Because RSD will at least initially cause
). (Because RSD will at least initially cause  to be longer than
to be longer than  and because
and because  (
( = 2)
= 2) 300 b,
300 b,  must be significantly less than 300 b.) Fig. 8 shows that, at
must be significantly less than 300 b.) Fig. 8 shows that, at  = 64, the model admits a basin of good values delimited by
= 64, the model admits a basin of good values delimited by 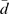 = 120 to 5000 and
= 120 to 5000 and  = 0.65 to 0.80.
= 0.65 to 0.80.  's of model sequences obtained using the “best set” of parameters
's of model sequences obtained using the “best set” of parameters  = 64,
= 64, 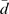 = 1000, and
= 1000, and  = 0.73 are shown in the right panel in Fig. 8, where the lines represent the universality class
= 0.73 are shown in the right panel in Fig. 8, where the lines represent the universality class  (Eq. (1)). The
(Eq. (1)). The  for these
for these  's is 0.18 and implies that on average, the model
's is 0.18 and implies that on average, the model  and
and  agree to within a factor of 1.6. This small
agree to within a factor of 1.6. This small  can easily be increased to match that of the genomic data (
can easily be increased to match that of the genomic data ( = 0.43) by using model parameters that cover suitable ranges of values centered around the best values.
= 0.43) by using model parameters that cover suitable ranges of values centered around the best values.
Figure 8. Results from minimal RSD model.
Left: Equi- contour on the
contour on the  -
- plane, with
plane, with  = 64 (bases). Right:
= 64 (bases). Right:  ,
, 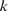 = 2, 4, 6, 8, 10 from 200 model sequences of length 2 Mb generated using the “best set” of parameters
= 2, 4, 6, 8, 10 from 200 model sequences of length 2 Mb generated using the “best set” of parameters  = 64,
= 64,  = 1000 (b) and
= 1000 (b) and  = 0.73 (b
= 0.73 (b ). Lines in right panel are
). Lines in right panel are  (Eq. (1)).
(Eq. (1)).
The range of  within the basin of good values seems biologically realistic, for it is consistent with the range of the characteristic lengths of genes. The isolated basin near
within the basin of good values seems biologically realistic, for it is consistent with the range of the characteristic lengths of genes. The isolated basin near 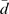 = 30,
= 30,  = 0.3 allows copious duplication of regulatory sequences, including microRNAs [58], that are much shorter than genes. The considerable size of the main basin implies that it is easily accessible in an evolutionary selective process. On the other hand, that
= 0.3 allows copious duplication of regulatory sequences, including microRNAs [58], that are much shorter than genes. The considerable size of the main basin implies that it is easily accessible in an evolutionary selective process. On the other hand, that  increases sharply outside the basin of good values demonstrates that even in the context of the RSD model it is very easy to generate sequences that are far outside the universality class.
increases sharply outside the basin of good values demonstrates that even in the context of the RSD model it is very easy to generate sequences that are far outside the universality class.
Rates of genome growth and duplication
The parameters of the RSD model are compatible with rates of genome growth and duplication determined using sequence comparison [37]–[39]. In a model where a genome grows at a constant per-time rate  , we have
, we have  =
=  where
where  is the length of the genome at time
is the length of the genome at time  (Eq. (16), Methods). For human we can take
(Eq. (16), Methods). For human we can take  to be the current time because the human genome has grown 15% to 20% in the last 50 Mya (10
to be the current time because the human genome has grown 15% to 20% in the last 50 Mya (10 years) [39]. The ancestors of eubacteria and archaea-eukaria diverged
years) [39]. The ancestors of eubacteria and archaea-eukaria diverged  3.4 Gya (10
3.4 Gya (10 years) ago [59]–[61]), and before that proto-genomes most likely evolved as communities [62]–[64], and hence had a different growth regime than later times. The smallest bacterial genome is about 0.2 Mb; we take
years) ago [59]–[61]), and before that proto-genomes most likely evolved as communities [62]–[64], and hence had a different growth regime than later times. The smallest bacterial genome is about 0.2 Mb; we take  to be from 0.05 to 0.2 Mb and
to be from 0.05 to 0.2 Mb and  = 3 Gb. Then
= 3 Gb. Then  = 2.7
= 2.7 3.7/Mya. These rates imply the human genome grew 14
3.7/Mya. These rates imply the human genome grew 14 20% in the last 50 Mya, in agreement with [39]. If we assume the growth is purely SD and take the length of duplicated segment
20% in the last 50 Mya, in agreement with [39]. If we assume the growth is purely SD and take the length of duplicated segment 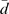 to be 500 b to 2 kb, then the rate of SD events is
to be 500 b to 2 kb, then the rate of SD events is  =
=  = 1.4
= 1.4 7.4/Mb/Mya. These values are comparable to the estimates of 3.9/Mb/Mya (from animal gene duplication rate of
7.4/Mb/Mya. These values are comparable to the estimates of 3.9/Mb/Mya (from animal gene duplication rate of  0.01 per gene per Mya [6] and human coding region
0.01 per gene per Mya [6] and human coding region  3% of genome), and 2.8/Mb/Mya (from human retrotransposition event rate [39]).
3% of genome), and 2.8/Mb/Mya (from human retrotransposition event rate [39]).
Cumulative mutation density and mutation rates
The parameter  in the RSD model, the cumulative point mutation density, is related to the (per-site per-time) rate density
in the RSD model, the cumulative point mutation density, is related to the (per-site per-time) rate density  of “point mutations” – including small deletion and insertion but excluding SD – by
of “point mutations” – including small deletion and insertion but excluding SD – by 

 (Eq. (19), Methods). If we take the best value
(Eq. (19), Methods). If we take the best value  = 0.73 from the RSD model then
= 0.73 from the RSD model then  = 0.98
= 0.98 1.4
1.4 10
10 /site/Mya. This agrees well with the value
/site/Mya. This agrees well with the value 
 1
1 10
10 /site/Mya [37]–[39] determined by sequence comparison.
/site/Mya [37]–[39] determined by sequence comparison.
We cannot assume the E. coli genome is still growing, as the human genome appears to be. Instead, like most bacteria E. coli probably acquired its full length in antiquity, not too long after ancestors of eubacteria and archaea-eukaria diverged [61]. If we assume E. coli acquired its current length of 4.6 Mb about 0.4 to 0.6 Gya after that, then with  as before, we have
as before, we have  = 5.4
= 5.4 11/Mya, and
11/Mya, and 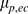 = 2.0
= 2.0 4.0
4.0 10
10 /site/Mya. Fortuitously or perhaps this range of rates represent an equilibrium value, it is compatible with the sequence-comparison E. coli rate of
/site/Mya. Fortuitously or perhaps this range of rates represent an equilibrium value, it is compatible with the sequence-comparison E. coli rate of 
 5
5 10
10 /site/Mya based on mutations that (putatively) occurred in the last 0.5 Gya or less [37], [38]. There is some evidence that natural selection does cause genomes to have a relatively low and stable mutation rate. For instance, laboratory measured spontaneous mutation rates of E. coli
[65], C. elegans
[65], [66], and
/site/Mya based on mutations that (putatively) occurred in the last 0.5 Gya or less [37], [38]. There is some evidence that natural selection does cause genomes to have a relatively low and stable mutation rate. For instance, laboratory measured spontaneous mutation rates of E. coli
[65], C. elegans
[65], [66], and  [65], [67] tend to be two or three orders of magnitudes higher than the characteristic rates of
[65], [67] tend to be two or three orders of magnitudes higher than the characteristic rates of  0.001/site/Mya of wild types.
0.001/site/Mya of wild types.
Presumably the same selective force is what causes the  's, hence the cumulative mutation density
's, hence the cumulative mutation density  , of coding and non-coding regions of a chromosome to be nearly equal. Such a force must be acting for otherwise we expect non-coding regions to have a significantly higher
, of coding and non-coding regions of a chromosome to be nearly equal. Such a force must be acting for otherwise we expect non-coding regions to have a significantly higher  , which is not the case.
, which is not the case.
Materials and Methods
Complete genome sequences
A total of 865 complete chromosomes were downloaded from the genome database [68] on 2006/10/01. The set is composed of 467 prokaryotic chromosomes (435 eubacteria and 32 archaea) and 398 chromosomes from 28 eukaryotes including: 12 unicellulars (A. fumigatus (8 chromosomes), C. albicans (1), C. glabrata (13), C. neoformans (14), D. hansenii (7), E. cuniculi (11), E. gossypii (7), Kluyveromyces lactis (6), S. cerevisiae (16), S. pombe (3), Y. lipolytica (6), P. falciparum (14)), 5 insects (A. gambiae (3), A. mellifera (16), C. elegans (6), D. melanogaster (4), T. casteneum (10)), 2 plants (A. thaliana (5), O. sativa (12), 9 vertebrates (B. taurus (30), C. familiaris (39), D. rerio (25), G. gallus (30), H. sapiens (24), M. multatta (21), M. musculus (21), P. troglodytes (25), R. norvegicus (21)). The complete list of sequences, their accession numbers, lengths and other properties relevant to this study are given in Table S1.
Partition of  -mers into
-mers into  -sets
-sets
We always speak of single-stranded sequences. We refer to a  -base nucleic word as a
-base nucleic word as a  -mer and denote the set of all
-mer and denote the set of all 

 types of
types of  -mers by
-mers by  . Given a sequence, we count the frequency of occurrence (or frequency)
. Given a sequence, we count the frequency of occurrence (or frequency)  of each
of each  -mer-type
-mer-type  in
in  using an overlapping sliding window of width
using an overlapping sliding window of width  and slide one [36]. Then the sum of the frequencies is
and slide one [36]. Then the sum of the frequencies is 
 =
=  −
− +1, here approximate by
+1, here approximate by  , and the mean frequency is
, and the mean frequency is  =
=  . Let the fractional AT- and CG-content of a sequence be
. Let the fractional AT- and CG-content of a sequence be  and
and  = 1−
= 1− , respectively. We say a sequence has an even-base composition when
, respectively. We say a sequence has an even-base composition when  is equal to or very close to 0.5, otherwise it has biased base composition. Owing to Chargaff's second parity rule [69]
is equal to or very close to 0.5, otherwise it has biased base composition. Owing to Chargaff's second parity rule [69]
 is an accurate and efficient classifier of base composition for statistical analysis. The
is an accurate and efficient classifier of base composition for statistical analysis. The  -mers in a sequence are naturally partitioned into
-mers in a sequence are naturally partitioned into  +1 “
+1 “ -sets”,
-sets”,  ,
,  = 0,1,
= 0,1,
 , where each
, where each  -mer in
-mer in  has
has  and only
and only  AT's;
AT's;  . For example, in the case of
. For example, in the case of  = 2,
= 2,  is the set {CC, CG, GC, GG};
is the set {CC, CG, GC, GG};  is the set {CA, CT, GA, GT, AC, AG, TC, TG}; and
is the set {CA, CT, GA, GT, AC, AG, TC, TG}; and  is the set {AA AT, TA, TT}. The the number of types of
is the set {AA AT, TA, TT}. The the number of types of  -mers in
-mers in  is
is  , which satisfies the sum-rule
, which satisfies the sum-rule 
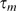 =
=  =
=  . These relations derive from the binomial expansion (for given
. These relations derive from the binomial expansion (for given  )
)
| (4) |
Let  =
= 
 be the sum frequency of the
be the sum frequency of the 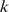 -mers in
-mers in  . Then
. Then 
 =
=  and the mean frequency of the
and the mean frequency of the  -mers in
-mers in 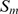 is
is 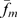 =
=  . The large-
. The large- limit of
limit of  for a random sequence,
for a random sequence,  , is obtained from the binomial expansion
, is obtained from the binomial expansion
| (5) |
That is,
| (6) |
Depending on  ,
,  can vary widely, all collapsing to
can vary widely, all collapsing to  when
when  = 0.5. Eq. (6) not only provides an highly accurate estimate of the value of
= 0.5. Eq. (6) not only provides an highly accurate estimate of the value of  for genome-size random sequences, it also gives a reasonable estimate for genomic
for genome-size random sequences, it also gives a reasonable estimate for genomic  (Table 6).
(Table 6).
Table 6. Average frequency of occurrence ( ) of 5-mers in
) of 5-mers in 
 0.5 and
0.5 and 
 0.7 sequence.
0.7 sequence.

|
||||||
| Sequence | ( = ) 0 = ) 0 |
1 | 2 | 3 | 4 | 5 |

|
||||||
| E. coli | 2509 | 2245 | 1877 | 1760 | 1944 | 2656 |
| Random | 2101 | 2044 | 1987 | 1922 | 1857 | 1795 |
 Random Random
|
2114 | 2048 | 1983 | 1920 | 1860 | 1801 |

|
||||||
| C. acetobutylicum | 154 | 397 | 918 | 1951 | 4272 | 10300 |
| Random | 176 | 394 | 882 | 1970 | 4400 | 9832 |
 Random Random
|
176 | 393 | 880 | 1968 | 4402 | 9845 |
All sequences normalized to a length of 2 Mb;  = 2
= 2 10
10 /4
/4 = 1953. Random means matching random sequence, or sequence obtained by scrambling the genome.
= 1953. Random means matching random sequence, or sequence obtained by scrambling the genome.  Values of
Values of  given by Eq. (6).
given by Eq. (6).
Fluctuation in occurrence frequency
The coefficient of variation of the frequency distribution is  =
=  , where
, where  is the standard deviation. For random events of equal probability, here translated to
is the standard deviation. For random events of equal probability, here translated to  -mer frequencies of a (long) random sequence with even-base composition, the distribution is Poisson and
-mer frequencies of a (long) random sequence with even-base composition, the distribution is Poisson and  =
=  , hence
, hence  =
=  =
=  , which tends to zero in the large-
, which tends to zero in the large- limit. This no longer holds when the random sequence has a biased base composition. As controls we consider random sequences that match genomes, namely those whose lengths and base compositions are the same as their genomic counterparts. In particular, such sequences obey Chargaff's second parity rule [69] in that their A and T, and C and G, separately have nearly equal probabilities. For any sequence whose
limit. This no longer holds when the random sequence has a biased base composition. As controls we consider random sequences that match genomes, namely those whose lengths and base compositions are the same as their genomic counterparts. In particular, such sequences obey Chargaff's second parity rule [69] in that their A and T, and C and G, separately have nearly equal probabilities. For any sequence whose  -mers are partitioned into
-mers are partitioned into  -sets, using a generalization of the parallel axis theorem, we write as follows:
-sets, using a generalization of the parallel axis theorem, we write as follows:
 |
(7) |
The second term vanishes upon summing over  , so
, so  is composed of two parts,
is composed of two parts,
| (8) |
a non-fluctuating part determined by average frequencies  and
and  ,
,
| (9) |
and a fluctuating part determined by the fluctuation of  (in an
(in an  -set) around an average frequency,
-set) around an average frequency,
| (10) |
Thus,
| (11) |
The non-fluctuating, or “non-statistical”, part,  , has a well-defined value in the large-
, has a well-defined value in the large- limit, obtained by replacing
limit, obtained by replacing  by
by  in Eq. (9):
in Eq. (9):
 |
(12) |
which has a strong dependence on  and vanishes
and vanishes  = 0.5. Because genomes are large,
= 0.5. Because genomes are large, 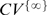 gives an accurate description of
gives an accurate description of  for genome-size random sequences; it also happens to do almost as well for genome (Fig. 1). Owing to the existence of this term, the
for genome-size random sequences; it also happens to do almost as well for genome (Fig. 1). Owing to the existence of this term, the  for a genomic sequence may be much greater than that of its matching random sequence (when
for a genomic sequence may be much greater than that of its matching random sequence (when 
 0.5; see, e.g., Fig. 9 (A)), or quite similar (when
0.5; see, e.g., Fig. 9 (A)), or quite similar (when  differs significantly from 0.5; see, e.g., Fig. 9 (B)). Because
differs significantly from 0.5; see, e.g., Fig. 9 (B)). Because  hardly depends on the distribution of the
hardly depends on the distribution of the  -mers, it should be considered a background in
-mers, it should be considered a background in  in relation to the signal which is
in relation to the signal which is  .
.
Figure 9. Frequency distributions of 5-mers.
Frequency occurrence distributions, or spectra, of 5-mers from the genomes of two prokaryotes, (A) E. coli (with (A+T) content 
 0.5) and (B) C. acetobutylicum (
0.5) and (B) C. acetobutylicum (
 0.7), normalized to a sequence length of 2 Mb. Abscissa give occurrence frequency and ordinates give number of 5-mers averaged, for better viewing, over a range of 21 frequencies to reduce fluctuation. The black, green and red curves represent spectra of the complete genomes, the randomized genome sequences and sequences generated in a model (see text), respectively. (C) Details of the m = 2 subspectra from (B).
0.7), normalized to a sequence length of 2 Mb. Abscissa give occurrence frequency and ordinates give number of 5-mers averaged, for better viewing, over a range of 21 frequencies to reduce fluctuation. The black, green and red curves represent spectra of the complete genomes, the randomized genome sequences and sequences generated in a model (see text), respectively. (C) Details of the m = 2 subspectra from (B).
For a random sequence, the frequency distribution in the subset  is nearly Poisson, hence
is nearly Poisson, hence 

 in the large-
in the large- limit. Therefore, from Eq. (10),
limit. Therefore, from Eq. (10),
 |
(13) |
which is exactly the limit expected of  for an even-base (
for an even-base ( = 0.5) random sequence. In other words, for random sequences
= 0.5) random sequence. In other words, for random sequences  , but not
, but not  , has the correct large-
, has the correct large- limit expected of a random system. The right-hand-side does not depend on
limit expected of a random system. The right-hand-side does not depend on  , which is a reflection of the fact that for genome as well as random sequences,
, which is a reflection of the fact that for genome as well as random sequences,  has at most a weak
has at most a weak  -dependence; the main
-dependence; the main  -dependence having been removed when
-dependence having been removed when  is subtracted from
is subtracted from  . Because (for random sequences)
. Because (for random sequences)  decreases with increasing
decreases with increasing  but
but  does not, there is a crossover value of
does not, there is a crossover value of  beyond which
beyond which  becomes the leading term in
becomes the leading term in  (when
(when 
 0.5). When
0.5). When  = 0.7, this crossover value is 42, 316 and 2851 (bases) for
= 0.7, this crossover value is 42, 316 and 2851 (bases) for  = 2, 4, and 6, respectively, which are orders of magnitudes shorter than even the smallest chromosomes. To summarize, if one wants to compare the statistical properties in the frequency distributions of
= 2, 4, and 6, respectively, which are orders of magnitudes shorter than even the smallest chromosomes. To summarize, if one wants to compare the statistical properties in the frequency distributions of  -mers in the genomic and random sequence, one must use
-mers in the genomic and random sequence, one must use  , not
, not  .
.
Two examples: E. coli and C. acetobutylicum
We explain the formulation presented in the last two sections by presenting results of distributions, or spectra, of frequency of 5-mers (as an example), and values of quantities such as  ,
,  , and
, and  for two genomes with very different base compositions: E. coli (
for two genomes with very different base compositions: E. coli ( = 0.492) and C. acetobutylicum (
= 0.492) and C. acetobutylicum ( = 0.691). Here, a spectrum is the number of
= 0.691). Here, a spectrum is the number of  -mers plotted against occurrence frequency. The spectra for the two genomes are shown as black curves in panels (A) and (B) of Fig. 9. The solid green curves characterized by narrow peaks are the spectra for random sequences obtained by scrambling the genomes. (The red curves are for sequences generated in the RSD model, see text.) In (A) the mean frequency of both spectra is
-mers plotted against occurrence frequency. The spectra for the two genomes are shown as black curves in panels (A) and (B) of Fig. 9. The solid green curves characterized by narrow peaks are the spectra for random sequences obtained by scrambling the genomes. (The red curves are for sequences generated in the RSD model, see text.) In (A) the mean frequency of both spectra is  = 2
= 2 10
10 /4
/4 = 1953. However, the genomic spectrum is seen to be much broader then the random-sequence spectrum, indicating that whereas in the random sequence frequencies (
= 1953. However, the genomic spectrum is seen to be much broader then the random-sequence spectrum, indicating that whereas in the random sequence frequencies ( ) of individual 5-mers deviate little from the mean (
) of individual 5-mers deviate little from the mean ( ), in the genomic sequence that is not the case; frequencies of individual 5-mers fluctuate widely around the mean. Drastically different from (A), the overall widths of genome and random-sequence spectra in (B) are similar. Instead of having a single peak, the random-sequence spectrum is composed of six widely spread narrow subspectra whose peaks are near the theoretical mean frequencies (for
), in the genomic sequence that is not the case; frequencies of individual 5-mers fluctuate widely around the mean. Drastically different from (A), the overall widths of genome and random-sequence spectra in (B) are similar. Instead of having a single peak, the random-sequence spectrum is composed of six widely spread narrow subspectra whose peaks are near the theoretical mean frequencies (for  = 0.7) of the
= 0.7) of the  -sets,
-sets, 
 152, 354, 827, 1930, 4500, 10500, for
152, 354, 827, 1930, 4500, 10500, for  = 0 to 5, respectively. Eq. (6) shows that these mean values are determined by
= 0 to 5, respectively. Eq. (6) shows that these mean values are determined by  and the base composition of the sequence, or
and the base composition of the sequence, or  , and does not depend on the fluctuation of frequencies of
, and does not depend on the fluctuation of frequencies of  -specific 5-mers. (B) and (C) in Fig. 9 show that in the random sequence frequency fluctuation within an
-specific 5-mers. (B) and (C) in Fig. 9 show that in the random sequence frequency fluctuation within an  -set is again small. In contrast, and just as in (A), frequency fluctuations of
-set is again small. In contrast, and just as in (A), frequency fluctuations of  specific 5-mers in the genomic sequence are large (Fig. 9 (C) and Fig. 10
[70]).
specific 5-mers in the genomic sequence are large (Fig. 9 (C) and Fig. 10
[70]).
Figure 10. Frequency distributions of 5-mers in  -sets.
-sets.
Details of  = 5,
= 5,  -specific subspectra from the C. acetobutylicum genome (broken green curves) and matching random sequence (solid green curves); black curve is the same as in (B) Fig. 9. The five narrow subspectra peak (approximately) at
-specific subspectra from the C. acetobutylicum genome (broken green curves) and matching random sequence (solid green curves); black curve is the same as in (B) Fig. 9. The five narrow subspectra peak (approximately) at  ,
,  = 0 to 4, or at 152, 354, 827, 1939, 4500, respectively; the
= 0 to 4, or at 152, 354, 827, 1939, 4500, respectively; the  = 5 peak at 10500 is off scale (see Fig. 9 (B)).
= 5 peak at 10500 is off scale (see Fig. 9 (B)).
Table 6 shows that  gives a very accurate estimate of
gives a very accurate estimate of  for random sequences and a fair one for genomic sequences. In the
for random sequences and a fair one for genomic sequences. In the  = 0.492 case, the relation
= 0.492 case, the relation 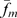

 for all the
for all the  's explains the narrowness of the random spectrum in Fig. 9 (A): like its counterpart in (B), it is also composed of six subspectra, but unlike (B) whose subspectra are spread widely, now the subspectra are superimposed. Table 7 highlight important aspects of our formulation: (i)
's explains the narrowness of the random spectrum in Fig. 9 (A): like its counterpart in (B), it is also composed of six subspectra, but unlike (B) whose subspectra are spread widely, now the subspectra are superimposed. Table 7 highlight important aspects of our formulation: (i)  has a strong dependence on
has a strong dependence on  but not on whether a sequence is genomic or random; (ii)
but not on whether a sequence is genomic or random; (ii)  gives an excellent estimate of
gives an excellent estimate of  for random sequences, and a fair estimate for genomes; (iii)
for random sequences, and a fair estimate for genomes; (iii)  depends weakly on
depends weakly on  but strongly on whether a sequence is genomic (relative large value) or random (several orders of magnitude smaller, and much smaller than
but strongly on whether a sequence is genomic (relative large value) or random (several orders of magnitude smaller, and much smaller than  except when
except when 
 0.5). (iv) For random sequences Eq. (13) is a fairly accurate relation.
0.5). (iv) For random sequences Eq. (13) is a fairly accurate relation.
Table 7. Values of  's from 5-mers in
's from 5-mers in 
 0.5 and
0.5 and 
 0.7 sequences.
0.7 sequences.
 (in units of 10 (in units of 10 ) ) |

|

|

|
||||||
| Sequence | ( = ) 0 = ) 0 |
1 | 2 | 3 | 4 | 5 | |||

|
|||||||||
| E. coli | 144 | 141 | 74.2 | 58.4 | 66.4 | 83.7 | 0.212 | 0.013 |

|
| Random | .174 | 0.203 | 0.185 | 0.177 | 0.144 | 0.110 | 4.6 10 10
|
0.0012 | 0.0013 |

|
|||||||||
| C. acetobutylicum | 0.60 | 6.95 | 26.1 | 65.4 | 97.1 | 336 | 0.145 | 1.00 |

|
| Random | 0.011 | 0.038 | 0.102 | 0.218 | 0.500 | 1.24 | 5.8 10 10
|
0.969 | 0.976 |
All sequences normalized to a length of 2 Mb; for  = 5,
= 5,  = 1953,
= 1953,  = 1024, and
= 1024, and 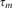 = 32, 160, 320, 160, 32, for
= 32, 160, 320, 160, 32, for  = 0 to 5.
= 0 to 5.
Equivalent length
The  -mers equivalent length of a sequence is defined as
-mers equivalent length of a sequence is defined as
| (14) |
where  is given by the frequency distribution of
is given by the frequency distribution of  -mers. Recalling that for a random sequence
-mers. Recalling that for a random sequence  is inversely proportional sequence length (Eq. (13)), we see that
is inversely proportional sequence length (Eq. (13)), we see that  is the length of a random sequence whose
is the length of a random sequence whose  has the same value as that of the genome. The empirical factor
has the same value as that of the genome. The empirical factor  = 1−
= 1− , instead of the theoretical binomial factor 1
, instead of the theoretical binomial factor 1
 , is used to ensure that for a random sequence, regardless of base composition,
, is used to ensure that for a random sequence, regardless of base composition,  approximates the true sequence length with a high degree of accuracy. With the signal term
approximates the true sequence length with a high degree of accuracy. With the signal term  included but the strongly
included but the strongly  -dependence background term
-dependence background term  excluded in its definition,
excluded in its definition,  is expected to have at most a weak
is expected to have at most a weak  -dependence. That is,
-dependence. That is,  is a quantity with which we can compare on the same footing genomes with widely disparate base compositions.
is a quantity with which we can compare on the same footing genomes with widely disparate base compositions.
Genic, non-genic, exon, and intron concatenates
These various concatenates are formed by splicing corresponding sections from a single strand of the DNA sequence and them stitching the sections together in the order and orientation they appear in the sequence. In particular, the genic and exon concatenates include genetic codes in positive and negative orientations.
Similarity index and similarity matrix
Given a pair of equal-length sequences  and
and  , the similarity index
, the similarity index  for the pair is defined as
for the pair is defined as
| (15) |
where  is an
is an  -set and
-set and  is the variance of the frequency of the
is the variance of the frequency of the  -mers in
-mers in  . The pair are similar (in
. The pair are similar (in  -mer-content) when
-mer-content) when 
 1, are (considered to be) identical when
1, are (considered to be) identical when  = 0, and are highly dissimilar when
= 0, and are highly dissimilar when 
 1. If we divide
1. If we divide  and
and  into (possibly overlapping) segments {
into (possibly overlapping) segments { ,
, ,
, } and {
} and {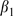 ,
, ,
, }, respectively, then we call the matrix whose element (
}, respectively, then we call the matrix whose element ( ,
, ) is valued
) is valued  a similarity matrix. In Fig. 6, similarity matrices are displayed as similarity plots by color coding elements of similarity matrices.
a similarity matrix. In Fig. 6, similarity matrices are displayed as similarity plots by color coding elements of similarity matrices.
Minimum RSD model for genome growth
We denote by  the designated length of a sequence and
the designated length of a sequence and  the designated AT-fraction of the sequence. We call the pair (
the designated AT-fraction of the sequence. We call the pair ( ,
,  ) the profile of a sequence; in our model, the two profiles (
) the profile of a sequence; in our model, the two profiles ( ,
,  ) and (
) and ( , 1−
, 1− ) are mathematically equivalent. By a growth model we mean a computer algorithm for generating, from an initial sequence, a target sequence that has a given profile and other specific genome-like attributes. Ours is a model of random segmental duplication (RSD) [49] in which the three main steps are: (i) randomly select a site from the sequence, (ii) from that site cull a segment of random length (but from a given length distribution) for duplication; (iii) reinsert the duplicated segment into the sequence at a (second) randomly selected site. The model has three explicit parameters:
) are mathematically equivalent. By a growth model we mean a computer algorithm for generating, from an initial sequence, a target sequence that has a given profile and other specific genome-like attributes. Ours is a model of random segmental duplication (RSD) [49] in which the three main steps are: (i) randomly select a site from the sequence, (ii) from that site cull a segment of random length (but from a given length distribution) for duplication; (iii) reinsert the duplicated segment into the sequence at a (second) randomly selected site. The model has three explicit parameters:  , the initial sequence length;
, the initial sequence length; 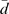 , the average length of duplicated segments;
, the average length of duplicated segments;  , the cumulative point mutation density (replacement only), or number of mutations per site. The generation of a model sequence involves three steps: selection of initial sequence, growth by RSD, point mutations. An initial sequence (of length
, the cumulative point mutation density (replacement only), or number of mutations per site. The generation of a model sequence involves three steps: selection of initial sequence, growth by RSD, point mutations. An initial sequence (of length  ) is chosen such that it has a target value
) is chosen such that it has a target value  but is otherwise random. The lengths
but is otherwise random. The lengths  of the duplicated segments are selected with uniform probability within the range 1 to 2
of the duplicated segments are selected with uniform probability within the range 1 to 2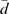 , unless the current length of the genome
, unless the current length of the genome  is less than 2
is less than 2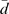 , in which case
, in which case  is selected from within the range 1 to
is selected from within the range 1 to  . Growth is stopped when the length of the sequence exceeds the target length for the first time. Point mutations have a base bias defined by
. Growth is stopped when the length of the sequence exceeds the target length for the first time. Point mutations have a base bias defined by  and are administered after the growth is complete. That is, the administration of point mutations on the sequence is not meant to emulate point mutations suffered by a genome during its growth. Rather,
and are administered after the growth is complete. That is, the administration of point mutations on the sequence is not meant to emulate point mutations suffered by a genome during its growth. Rather,  is meant to indicate the average cumulative number of point mutations per site experience by the genome throughout its life. Because RSD causes drifts in base composition, the profile of the generated sequence will have a profile that is a close approximation of, but not exactly equal to, the target profile.
is meant to indicate the average cumulative number of point mutations per site experience by the genome throughout its life. Because RSD causes drifts in base composition, the profile of the generated sequence will have a profile that is a close approximation of, but not exactly equal to, the target profile.
Mutation rates
We derive formulas for computing the rate density, or per site rate, of duplication events,  , and the rate density of “point mutation” – including small deletion and insertion but excluding SD – events,
, and the rate density of “point mutation” – including small deletion and insertion but excluding SD – events,  . If the genome grows from time
. If the genome grows from time  to time
to time  at a rate proportional to its length
at a rate proportional to its length  , that is,
, that is,  =
=  where
where  is the event rate (number of events per unit of time), then
is the event rate (number of events per unit of time), then
| (16) |
If the grow is purely by SD and the average length of the duplicated segment is 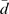 , then
, then
| (17) |
If  is the cumulative number of point mutations, then
is the cumulative number of point mutations, then  =
=  . In SD dominated growth, the effect of point mutation on the overall length of a genome is negligible, so integrating the relation yields
. In SD dominated growth, the effect of point mutation on the overall length of a genome is negligible, so integrating the relation yields
| (18) |
For any  such that
such that 

 ,
,  =
=  . The cumulative mutation sites is greater than
. The cumulative mutation sites is greater than  because mutation sites are copied during SD. The number of copied mutation sites satisfy
because mutation sites are copied during SD. The number of copied mutation sites satisfy  =
= 

 (for large
(for large  ). Therefore
). Therefore 

 , that is, the cumulative number of mutated sites is twice
, that is, the cumulative number of mutated sites is twice  . At full genome length
. At full genome length  , this number is
, this number is  , hence
, hence
| (19) |
Supporting Information
Category Le for coding and non-coding parts. Averages of p (fractional A/T-content) and Le for k = 7 (situations for other ks are similar) for the coding parts (solid symbols; ex for eukaryotes and gn for prokaryotes) and non-coding parts (hollow symbols; in for eukaryotes and ig for prokaryotes) of chromosomes. Symbols for categories are: vertebrates, red (square); unicellulars, blue (triangle-up); insects, orange (triangle-down); plants, green; prokaryotes, gray (bullet/circle). Numeral indicates number of chromosomes in each category. The curve represents Le for the universality class: Le{uc}(k; p).
(0.26 MB TIF)
Distributions of χ2 versus L and p. Each symbol gives the χ2 for one chromosomal Le. Top panels, for genic (gn) and exon (ex) concatenates. Bottom panels, for intergenic (ig) and intron (in) concatenates. Symbols, with color, number of data in group, and number of data whose χ2 is less than 10−3 given in brackets, stand for: diamond, gn (blue; 7100; 229); square, ex (red; 2844, 95); triangle-down, ig (green; 6377, 270); triangle-up, in (orange; 2960, 104).
(0.77 MB TIF)
Results from minimal RSD model. Top-left: Equi-χ2 contour as function of r and d, with L0 = 64 (bases); length (L) of generated model sequence is 2 Mb and only Le(k) results for k = 7 are used. Top-right: Le(k), k = 2, 4, 6, 8, 10 from 200 model sequences generated using the “best” parameters L0 = 64, <d> = 1000 (b) and r = 0.73 (cumulative point mutations per base). The lines are Le{uc}(k; p) that represent the universality class given in the main text. The χ2 for the model sequences is 0.18. Bottom-left: χ2 versus L0 (otherwise best parameters); model sequences have L = 2 Mb and p = 0.5. Bottom-right: Le versus L, for a p = 0.5 model sequence generated using the best parameters.
(1.17 MB TIF)
List of complete sequences included in the study (20 pp).
(0.13 MB PDF)
Equivalent lengths of complete sequences (100 pp).
(0.36 MB PDF)
Le(k), k = 2 to 10, averaged over categories of organisms.
(0.06 MB PDF)
Le of sequences with highly biased compositions.
(0.06 MB PDF)
Effect of replication and segmental duplication on le.
(0.04 MB PDF)
(0.07 MB PDF)
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was funded by the National Science Council (ROC) (http://web1.nsc.gov.tw/mp.aspx?mp=7), Cathay General Hospital (http://www.cgh.org.tw/en/index.html), National Central University (http://www.ncu.edu.tw/e_web/index.php). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Nei M, Li WH. Mathematical model for studying genetic variation in terms of restriction endonucleases. Proc Natl Acad Sci U S A. 1979;76:5269–5273. doi: 10.1073/pnas.76.10.5269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li WH. Molecular Evolution. Sunderland, , MA.: Sinauer Associates; 1997. [Google Scholar]
- 3.Ohno S. Evolution by Gene Duplication. Berlin.: Springer-Verlag; 1970. [Google Scholar]
- 4.Hansche PE, Beres V, Lange P. Gene duplication in Saccharomyces cerevisiae. Genetics. 1978;88:673–687. [PMC free article] [PubMed] [Google Scholar]
- 5.Yamanaka K, Fang L, Inouye M. The CSPA family in Escherichia coli: multiple gene duplication for stress adaptation. Mol Microbiol. 1998;27(2):247–255. doi: 10.1046/j.1365-2958.1998.00683.x. [DOI] [PubMed] [Google Scholar]
- 6.Lynch M, Conery JS. The evolutionary fate and consequences of duplicate genes. Science. 2000;290:1151–1155. doi: 10.1126/science.290.5494.1151. [DOI] [PubMed] [Google Scholar]
- 7.Gu Z, Steinmetz LM, Gu X, Scharfe C, Davis RW, et al. Role of duplicate genes in genetic robustness against null mutations. Nature. 2003;421:63–66. doi: 10.1038/nature01198. [DOI] [PubMed] [Google Scholar]
- 8.Zhang J. Evolution by gene duplication: an update. Trends Ecol Evol. 2003;18(6):292–298. [Google Scholar]
- 9.Lewin B. Genes VII. Oxford Univ Press; 2000. pp. 89–115. [Google Scholar]
- 10.Lander ES, Linton LM, Birren B, Nusbaum C, Zody MC, et al. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- 11.Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
- 12.Kleckner N. Transposable elements in prokaryotes. Ann Rev Genet. 1981;15:341–404. doi: 10.1146/annurev.ge.15.120181.002013. [DOI] [PubMed] [Google Scholar]
- 13.Castilho BA, Olfson P, Casadaban MJ. Plasmid insertion mutagenesis and lac gene fusion with mini-mu bacteriophage transposons. J Bacteriol. 1984;158(2):488–495. doi: 10.1128/jb.158.2.488-495.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Levis RW, Ganesan R, Houtchens K, Tolar LA, Sheen FM. Transposons in place of telomeric repeats at a Drosophila telomere. Cell. 1993;75(6):1083–1093. doi: 10.1016/0092-8674(93)90318-k. [DOI] [PubMed] [Google Scholar]
- 15.Li WH, Gojobori T, Nei M. Pseudogenes as a paradigm of neutral evolution. Nature. 1981;292:237–239. doi: 10.1038/292237a0. [DOI] [PubMed] [Google Scholar]
- 16.Vanin EF. Processed pseudogenes: Characteristics and evolution. Annu Rev Genet. 1985;19:253–272. doi: 10.1146/annurev.ge.19.120185.001345. [DOI] [PubMed] [Google Scholar]
- 17.Weiner AM, Deininger PL, Efstratiadis A. Nonviral retroposons: genes, pseudogenes, and trans- posable elements generated by the reverse flow of genetic information. Annu Rev Biochem. 1986;55:631–661. doi: 10.1146/annurev.bi.55.070186.003215. [DOI] [PubMed] [Google Scholar]
- 18.Bensasson D, Zhang DX, Hartl DL, Hewitt GM. Mitochondrial pseudogenes: evolution's misplaced witnesses. Trends Ecol Evol. 2001;16(6):314–321. doi: 10.1016/s0169-5347(01)02151-6. [DOI] [PubMed] [Google Scholar]
- 19.McGrath JM, Jancso MM, Pichersky E. Duplicate sequences with a similarity to expressed genes in the genome of Arabidopsis thaliana. Theor Appl Genet. 1993;86:880–888. doi: 10.1007/BF00212616. [DOI] [PubMed] [Google Scholar]
- 20.Bailey JA, Yavor AM, Massa HF, Trask BJ, Eichler EE. Segmental duplications: Organization and impact within the current human genome project assembly. Genome Res. 2001;11:1005–1017. doi: 10.1101/gr.187101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bailey JA, Gu Z, Clark RA, Reinert K, Samonte RV, et al. Recent segmental duplications in the human genome. Science. 2002;297:1003–1007. doi: 10.1126/science.1072047. [DOI] [PubMed] [Google Scholar]
- 22.Sharp AJ, Locke DP, McGrath SD, Cheng Z, Bailey JA, et al. Segmental duplications and copy-number variation in the human genome. Am J Human Genet. 2005;77:78–88. doi: 10.1086/431652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gaut BS, Doebley JF. DNA sequence evidence for the segmental allotetraploid origin of maize. Proc Natl Acad Sci U S A. 1997;94:6809–6814. doi: 10.1073/pnas.94.13.6809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gale MD, Devos KM. Comparative genetics in the grasses. Proc Natl Acad Sci U S A. 1998;95:1971–1974. doi: 10.1073/pnas.95.5.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mochizuki K, Fine NA, Fujisawa T, Gorovsky MA. Analysis of a piwi-related gene implicates small RNAs in genome rearrangement in Tetrahymena. Cell. 2002;110:689–699. doi: 10.1016/s0092-8674(02)00909-1. [DOI] [PubMed] [Google Scholar]
- 26.Coghlan A, Wolfe KH. Fourfold faster rate of genome rearrangement in nematodes than in Drosophila. Genome Res. 2002;12:857–867. doi: 10.1101/gr.172702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pevzner P, Tesler G. Genome rearrangements in mammalian evolution: Lessons from human and mouse genomes. Genome Res. 2003;13:37–45. doi: 10.1101/gr.757503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Grant D, Cregan P, Shoemaker RC. Genome organization in dicots: Genome duplication in Arabidopsis and synteny between soybean and Arabidopsis. Proc Natl Acad Sci U S A. 2000;97:4168–4173. doi: 10.1073/pnas.070430597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spring J. Genome duplication strikes back. Nat Genet. 2002;31:128–129. doi: 10.1038/ng0602-128. [DOI] [PubMed] [Google Scholar]
- 30.Kellis M, Birren BW, Lander ES. Proof and evolutionary analysis of ancient genome dupli- cation in the yeast Saccharomyces cerevisiae. Nature. 2004;428:617–624. doi: 10.1038/nature02424. [DOI] [PubMed] [Google Scholar]
- 31.Peng CK, Buldyrev SV, Goldberg AL, Havlin S, Simons M, et al. Finite-size effects on long-range correlations: Implications for analyzing DNA sequences. Phys Rev E. 1993;47:3730–3733. doi: 10.1103/physreve.47.3730. [DOI] [PubMed] [Google Scholar]
- 32.Mantegna RN, Buldyrev SV, Goldberger AL, Havlin S, Peng CK, et al. Linguistic features of noncoding DNA sequences. Phys Rev Lett. 1994;73:3169–3172. doi: 10.1103/PhysRevLett.73.3169. [DOI] [PubMed] [Google Scholar]
- 33.Forsdyke D. Relative roles of primary sequence and (G+C)% in determining the hierarchy of frequencies of complementary trinucleotide pairs in DNAs of different species. J Mol Evol. 1995;41:573–581. doi: 10.1007/BF00175815. [DOI] [PubMed] [Google Scholar]
- 34.Karlin S, Mrazek J. Compositional differences within and between eukaryotic genomes. Proc Natl Acad Sci U S A. 1997;94:10227–10232. doi: 10.1073/pnas.94.19.10227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Deschavanne PJ, Giron A, Vilain J, Fagot G, Fertil B. Genomic signature: characterization and classiffication of species assessed by chaos game representation of sequences. Mol Biol Evol. 1999;16(10):1391–1399. doi: 10.1093/oxfordjournals.molbev.a026048. [DOI] [PubMed] [Google Scholar]
- 36.Hao BL, Lee HC, Zhang SY. Fractals related to long DNA sequences and complete genomes. Chaos, Solitons and Fractals. 2000;11:825–836. [Google Scholar]
- 37.Ochman H, Elwyn S, Moran NA. Calibrating bacterial evolution. Proc Natl Acad Sci U S A. 1999;96:12638–12643. doi: 10.1073/pnas.96.22.12638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nachman MW, Crowell SL. Estimate of the mutation rate per nucleotide in humans. Genetics. 2000;156:297–304. doi: 10.1093/genetics/156.1.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liu G, Program NCS, Zhao S, Bailey JA, Sahinalp SC, et al. Analysis of primate genomic variation reveals a repeat-driven expansion of the human genome. Genome Res. 2003;13:358–368. doi: 10.1101/gr.923303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Voss RF. Comment on “Linguistic features of noncoding DNA sequences”. Phys Rev Lett. 1996;76:1978. doi: 10.1103/PhysRevLett.76.1978. [DOI] [PubMed] [Google Scholar]
- 41.Bonhoeffer S, Herz AV, Boerlijst MC, Nee S, Nowak MA, et al. No signs of hidden language in noncoding DNA. Phys Rev Lett. 1996;76:1977. doi: 10.1103/PhysRevLett.76.1977. [DOI] [PubMed] [Google Scholar]
- 42.Israeloff NE, Kagalenko M, Chan K. Can Zipf distinguish language from noise in noncoding DNA? Phys Rev Lett. 1996;76:1976. doi: 10.1103/PhysRevLett.76.1976. [DOI] [PubMed] [Google Scholar]
- 43.Mantegna RN, Buldyrev SV, Goldberger AL, Halvin S, Peng CK, et al. Mantegna et al. reply:. Phys Rev Lett. 1996;76:1979–1981. doi: 10.1103/PhysRevLett.76.1979. [DOI] [PubMed] [Google Scholar]
- 44.Peng CK, Buldyrev SV, Havlin S, Simons M, Stanley HE, et al. Mosaic organization of DNA nucleotides. Phys Rev E. 1994;49:1685–1689. doi: 10.1103/physreve.49.1685. [DOI] [PubMed] [Google Scholar]
- 45.Bernaola-Galvffan P, Carpena P, Roman-Roldan R, Oliver JL. Study of statistical correlations in DNA sequences. Gene. 2002;300:105–115. doi: 10.1016/s0378-1119(02)01037-5. [DOI] [PubMed] [Google Scholar]
- 46.Messer PW, Arndt PF, Lassig M. Solvable sequence evolution models and genomic correlations. Phys Rev Lett. 2005;94:138103. doi: 10.1103/PhysRevLett.94.138103. [DOI] [PubMed] [Google Scholar]
- 47.Fickett JW, Torney DC, Wolf DR. Base compositional structure of genomes. Genomics. 1992;13:1056–1064. doi: 10.1016/0888-7543(92)90019-o. [DOI] [PubMed] [Google Scholar]
- 48.Xie HM, Hao BL. Visualization of k-tuple distribution in procaryote complete genomes and their randomized counterparts. Proceedings of the IEEE Computer Society Bioinformatics Conference. 2002:31–42. [PubMed] [Google Scholar]
- 49.Hsieh LC, Luo LF, Lee HC. Genomes are large systems with small-system statistics: Seg- mental duplication in the growth of microbial chromosomes. AAPPS Bulletin. 2003;13:22–27. [Google Scholar]
- 50.Chen TY, Hsieh LC, Lee HC. Shannon information and self-similarity in complete chromosomes. Comput Phys Commun. 2005;169:218–221. [Google Scholar]
- 51.Zhou F, Olman V, Xu Y. Barcodes for genomes and applications. BMC Bioinformatics. 2008;9:546. doi: 10.1186/1471-2105-9-546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kong SG, Chen HD, Fan WL, Wigger J, Torda AE, et al. Quantitative measure of random- ness and order for complete genomes. Phys Rev E. 2009;79:061911. doi: 10.1103/PhysRevE.79.061911. [DOI] [PubMed] [Google Scholar]
- 53.Bapteste E, Boucher Y, Leigh J, Doolittle WF. Phylogenetic reconstruction and lateral gene transfer. Trends Microbiol. 2004;12:406–411. doi: 10.1016/j.tim.2004.07.002. [DOI] [PubMed] [Google Scholar]
- 54.Delsuc F, Brinkmann H, Philippe H. Phylogenomics and the reconstruction of the tree of life. Nat Rev Genet. 2005;6:361–375. doi: 10.1038/nrg1603. [DOI] [PubMed] [Google Scholar]
- 55.Lynch M, Conery JS. The origins of genome complexity. Science. 2003;302:1401–1404. doi: 10.1126/science.1089370. [DOI] [PubMed] [Google Scholar]
- 56.Coghlan A, Eichler EE, Oliver SG, Paterson AH, Stein L. Chromosome evolution in eukaryotes: a multi-kingdom perspective. Trends Genet. 2005;21:673–682. doi: 10.1016/j.tig.2005.09.009. [DOI] [PubMed] [Google Scholar]
- 57.Messer PW, Bundschuh R, Vingron M, Arndt PF. Effects of long-range correlations in DNA on sequence alignment score statistics. J Comput Biol. 2007;14:655–668. doi: 10.1089/cmb.2007.R008. [DOI] [PubMed] [Google Scholar]
- 58.Bartel DP. Micrornas: Genomics, biogenesis, mechanism, and function. Bioinformatics. 2004;116:281–297. doi: 10.1016/s0092-8674(04)00045-5. [DOI] [PubMed] [Google Scholar]
- 59.Doolittle WF. Fun with genealogy. Proc Natl Acad Sci U S A. 1997;94:12751–12753. doi: 10.1073/pnas.94.24.12751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Feng DF, Cho G, Doolittle RF. Determining divergence times with a protein clock: Update and reevaluation. Proc Natl Acad Sci U S A. 1997;94:13028–13033. doi: 10.1073/pnas.94.24.13028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hedges SB. The origin and evolution of model organisms. Nat Rev Genet. 2002;3:838–849. doi: 10.1038/nrg929. [DOI] [PubMed] [Google Scholar]
- 62.Woese CR. The universal ancestor. Proc Natl Acad Sci U S A. 1998;95:6854–6859. doi: 10.1073/pnas.95.12.6854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Woese CR. On the evolution of cells. Proc Natl Acad Sci U S A. 2002;99:8742–8747. doi: 10.1073/pnas.132266999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Glansdorff N, Xu Y, Labedan B. The last universal common ancestor: emergence, constitution and genetic legacy of an elusive forerunner. Biol Direct. 2008;3:29. doi: 10.1186/1745-6150-3-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Drake JW, Charlesworth B, Charlesworth D, Crow JF. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Denver DR, Morris K, Lynch M, Thomas WK. High mutation rate and predominance of insertions in the Caenorhabditis elegans nuclear genome. Nature. 2004;430:679–682. doi: 10.1038/nature02697. [DOI] [PubMed] [Google Scholar]
- 67.Haag-Liautard C, Dorris M, Maside X, Macaskill S, Halligan DL, et al. Direct estimation of per nucleotide and genomic deleterious mutation rates in Drosophila. Nature. 2007;445:82–85. doi: 10.1038/nature05388. [DOI] [PubMed] [Google Scholar]
- 68.GenBank The genbank genome database. 2009. URL http://www.ncbi.nlm.nih.gov/sites/entrez?db=genome.
- 69.Rudner R, Karkas JD, Chargaff E. Separation of B. subtilis DNA into complementary strands. iii. direct analysis. Proc Natl Acad Sci U S A. 1968;60:921–922. doi: 10.1073/pnas.60.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Chen HD, Chang CH, Hsieh LC, Lee HC. Divergence and Shannon information in genomes. Phys Rev Lett. 2005;94:178103. doi: 10.1103/PhysRevLett.94.178103. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Category Le for coding and non-coding parts. Averages of p (fractional A/T-content) and Le for k = 7 (situations for other ks are similar) for the coding parts (solid symbols; ex for eukaryotes and gn for prokaryotes) and non-coding parts (hollow symbols; in for eukaryotes and ig for prokaryotes) of chromosomes. Symbols for categories are: vertebrates, red (square); unicellulars, blue (triangle-up); insects, orange (triangle-down); plants, green; prokaryotes, gray (bullet/circle). Numeral indicates number of chromosomes in each category. The curve represents Le for the universality class: Le{uc}(k; p).
(0.26 MB TIF)
Distributions of χ2 versus L and p. Each symbol gives the χ2 for one chromosomal Le. Top panels, for genic (gn) and exon (ex) concatenates. Bottom panels, for intergenic (ig) and intron (in) concatenates. Symbols, with color, number of data in group, and number of data whose χ2 is less than 10−3 given in brackets, stand for: diamond, gn (blue; 7100; 229); square, ex (red; 2844, 95); triangle-down, ig (green; 6377, 270); triangle-up, in (orange; 2960, 104).
(0.77 MB TIF)
Results from minimal RSD model. Top-left: Equi-χ2 contour as function of r and d, with L0 = 64 (bases); length (L) of generated model sequence is 2 Mb and only Le(k) results for k = 7 are used. Top-right: Le(k), k = 2, 4, 6, 8, 10 from 200 model sequences generated using the “best” parameters L0 = 64, <d> = 1000 (b) and r = 0.73 (cumulative point mutations per base). The lines are Le{uc}(k; p) that represent the universality class given in the main text. The χ2 for the model sequences is 0.18. Bottom-left: χ2 versus L0 (otherwise best parameters); model sequences have L = 2 Mb and p = 0.5. Bottom-right: Le versus L, for a p = 0.5 model sequence generated using the best parameters.
(1.17 MB TIF)
List of complete sequences included in the study (20 pp).
(0.13 MB PDF)
Equivalent lengths of complete sequences (100 pp).
(0.36 MB PDF)
Le(k), k = 2 to 10, averaged over categories of organisms.
(0.06 MB PDF)
Le of sequences with highly biased compositions.
(0.06 MB PDF)
Effect of replication and segmental duplication on le.
(0.04 MB PDF)
(0.07 MB PDF)












