Differentiation of Cognitive Abilities across the Lifespan

Abstract

Existing representations of cognitive ability structure are exclusively based on linear patterns of interrelations. However, a number of developmental and cognitive theories predict that abilities are differentially related across ages (age differentiation-dedifferentiation) and across levels of functioning (ability differentiation). Nonlinear factor analytic models were applied to multivariate cognitive ability data from 6,273 individuals, ages 4 to 101 years, who were selected to be nationally representative of the United States population. Results consistently supported ability differentiation, but were less clear with respect to age differentiation-dedifferentiation. Little evidence for age modification of ability differentiation was found. These findings are particularly informative about the nature of individual differences in cognition, and the developmental course of cognitive ability level and structure.

Differentiation of Cognitive Abilities across the Lifespan

In the first of a series of empirical and methodological undertakings to evaluate whether “the abilities commonly taken to be ‘intellectual’ had any correlation with each other” (Spearman, 1930, p. 322), Charles Spearman (1904) made the observation that many diverse measures of cognitive performance were indeed positively interrelated. This lead him to develop a “two factor” theory of intelligence, in which he proposed that a given individual’s level of performance on a given cognitive task was determined by a general ability (“g”) that could be diversely applied to many sorts of cognitive tasks, and one of many specific abilities (“s”) that could only be applied to the task in question. This theory was supported by Spearman’s demonstration that the correlations observed among a number of cognitive tests could be closely approximated from a model in which every test was assumed to be related to an unobserved common “g” factor. Elaborations of this method have come to be termed common factor analysis.

Over the hundred years since Spearman’s original (1904) work, factor analyses have continued to be applied to correlation/covariance matrices from cognitive test batteries. Based on such works, it is now clear that sets of cognitive tests tend to cluster into several “broad” ability factors, including what might be described as processing speed, episodic memory, visual-spatial thinking, fluid reasoning, and comprehension knowledge (i.e. crystallized intelligence). The interrelations among these broad abilities can in turn be accounted for by a higher order common factor that is statistically analogous to Spearman’s original conception of general intelligence. Such a contemporary representation of cognitive ability structure was termed the Three Stratum Theory by Carroll (1993), referring to fairly specific factors at the first stratum, broad abilities at the second stratum, and a general factor at the third stratum. This theory is largely based on, and very similar to, the Horn-Cattell theory of fluid and crystallized intelligence (Cattell, 1941; Cattell, 1987; Horn, 1965) which, in addition to fluid intelligence and crystallized intelligence, includes factors such as visualization, retrieval, and cognitive speed. Because such theories presume more specific factors nested within more general factors, they are generally termed hierarchical.

Contemporary hierarchical representations of cognitive abilities are supported by a number of basic findings: 1) patterns of convergent validity (high covariation among measures of the same factor), discriminant validity (more moderate covariation among measures of different factors), and face validity (measures designed to indicate a particular factor often do so); 2) differential patterns of relations of the various abilities with various external variables, including school and job performance, educational attainment, personality, and demographic indicators (e.g. Gottfredson, 2003; McGrew, 2009); 3) quantitative genetic estimates of heritability and environmentality specific to the various abilities (e.g. Petrill, 1997); 4) differential patterns of relations between the various abilities and neuroanatomical/neurobiological indices (e.g. Colom et al, in press); and 5) ability-specific developmental trajectories across both childhood and adulthood (presumably biologically-based abilities tend to grow in childhood, peak at late-adolescence/early adulthood, and decline into later adulthood; knowledge-based abilities tend to grow until mid-to-late adulthood and either stabilize or decline thereafter; Li, Lindenberger, Hommel, Aschersleben, Prinz, & Baltes, 2004; McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002; McGrew & Woodcock, 2001).

This final line of evidence is of particular relevance to the current investigation. The enterprise of cognitive developmental research is concerned with the striking changes in the quality and extent of cognitive performance as children grow and adults mature. For example, the effect size of increasing age on declining speed of information processing in adults has been listed among the largest effects in all of behavioral research (uncorrected meta-analytic estimated bivariate correlation = −.52; Meyer et al., 2001). Given that levels of cognitive performance differ so dramatically as functions of chronological age, it is very possible that the structural organization of cognitive abilities differs with age as well. A related possibility is that the structural organization of cognitive abilities differs with ability level. These two hypotheses have been the topic of much theoretical speculation for quite some time.

In fact, it was Spearman (1927; see Deary and Pagliari, 1990) who was the first researcher to propose that the relations among cognitive abilities may not be constant, but rather a diminishing function of ability level (what he called “the law of diminishing returns”). He reasoned that at low ability levels, a scarcity of domain general resources constrains multiple modes of cognitive functioning, but that at high ability levels, cognitive functioning is instead constrained by the levels of domain-specific resources. He supported this hypothesis by demonstrating that the mean correlation among 12 ability tests in 78 normal children was .466, but in 22 “defective” children was .782. Here this hypothesis is referred to as the ability differentiation hypothesis.

Referring to others’ works, Spearman (1904, 1927) also speculated that the magnitudes of ability relations may differ according to age. It was Garrett (1938; 1946) who introduced the age differentiation hypothesis, that with child development “an amorphous general ability” gradually breaks down “into a group of fairly distinct aptitudes” (Garrett, 1946, p. 375). Elaborating on this hypothesis to include both child development and adult aging, Balinsky (1941, p. 227) argued for a “greater specialization up to a certain point, followed by a later reintegration of the various abilities into a flexible whole.” This hypothesis, which has come to be termed the age differentiation-dedifferentiation hypothesis, was supported by Balinsky’s finding that a single common factor accounted for a decreasing amount of variance in the Wechsler-Bellevue test battery with older childhood age groups and an increasing amount variance with older adult age groups.

Lienert and Crott (1964) noted that age and ability based differentiation/dedifferentiation may not be independent phenomena. Because cognitive abilities are known to increase with childhood age and decrease with adult age, they explained that age differentiation-dedifferentiation could potentially be explained by ability differentiation. Nevertheless, the two hypotheses have often been examined independently of one another.

As will be discussed subsequently, the two somewhat separate bodies of literature on the topics tend to support ability differentiation, but are much more mixed with respect to age differentiation-dedifferentiation. Extant studies, however, have been typified by a number of shortcomings, outlined briefly below.

1. Past studies of age differentiation have primarily been isolated to segments of childhood or adulthood, and past studies of ability differentiation have primarily been isolated to samples containing even narrower age ranges. Given that the age differentiation-dedifferentiation hypothesis posits a specific pattern of shifts in ability interrelations across the lifespan, it is advantageous to examine it in lifespan samples. Moreover, the investigation of ability differentiation in age-heterogeneous samples would allow for inquiry as to whether it is a developmentally emergent phenomenon.

2. No study has estimated models that simultaneously allow for both age and ability differentiation. This is particularly important given that a single mechanism might be responsible for both phenomena.

3. Although it is well recognized that the hypotheses are inherently nonlinear, previous studies have been based on comparisons of linear relations across subgroups. Moreover, the arbitrary division of continuous variables (i.e. age and ability level) for the purpose of subgroup classification is marked by selection effects that threaten the validity of cross-group comparisons.

4. Although the assumption of interval measurement is a requisite for the comparisons of relational magnitudes, previous studies have not paid sufficient attention to the measurement properties of the tests employed.

In this article, the above shortcomings are discussed and nonlinear factor analysis of carefully scaled data is offered as a preferable alternative to other recently applied methodologies. Results of such an application to a large nationally representative lifespan sample of individuals, measured on a broad array of well-established cognitive abilities, are reported. First, recent theories and examinations of ability differentiation and age differentiation-dedifferentiation are reviewed. For more comprehensive reviews of older studies, see Deary, Egan, Gibson, Austin, Brand, & Kellaghan (1996) and Reinert (1970).

Ability Differentiation: Recent Theory and Research

Several cognitive theories have been invoked to explain ability differentiation. Anderson’s (1992; c.f. Anderson, 2001) theory of minimal cognitive architecture is perhaps the theory that is most explicit in postulating a mechanism that would lead to such a pattern. It suggests that independent cognitive algorithms differentially contribute to various domains of intellectual performance, but that because the complexity of each of these algorithms is constrained by a single basic processing mechanism, performance across different domains is correlated. Among people for whom the basic processing mechanism is more efficient (i.e. faster), the independent algorithms are less constrained, and performance levels across disparate domains become less correlated. This view bears resemblance to that of Spearman (1927), who argued that general intelligence can be conceptualized as fuel for engines that perform task-specific functions, reasoning that constant increments in fuel only result in diminishing increments in engine efficiency. Detterman and Daniel (1989) have similarly reasoned that if “central processes are deficient, they limit the efficiency of all other processes in the system. So all processes in subjects with deficits tend to operate at the same uniform level. However, subjects without deficits show much more variability across processes because they do not have deficits in important central processes.”

Ability differentiation has conventionally been examined by dividing samples into high and low ability groups, and comparing the magnitudes of correlations or the proportion of variance accounted for by a common factor, across the groups. Detterman and Daniel (1989), for example, compared the average cognitive ability test intercorrelations in mentally retarded versus college students, and low versus high IQ high school students and found substantially lower intercorrelations in the mentally retarded/low IQ groups than in the college/high IQ groups. They similarly divided the standardization samples from the WAIS-R and WISC-R into 5 ability groups, and found that the average subtest intercorrelations decreased from about .7 in the lowest ability groups (IQ equivalent less than 78) to about .4 in the highest ability groups (IQ equivalent greater than 122).

Using a novel method to create similarly distributed subsamples of low and high age and ability individuals from a parent sample of 10,500 school children (ages 14–17), Deary et al. (1996) found that the first principle component accounted for a greater percentage of variance (about 2% more) in low ability groups than in high ability groups, but accounted for a similar percentage of variance in younger and older adolescent age groups. Abad, Colom, Juan-Espinosa, & García (2003) applied this method to 3,430 university applicants, and 823 adults (ages 20–54) composing the Spanish standardization sample of the WAIS-III. They found that a single common factor accounted for greater percentages of variance in low ability groups than in high ability groups (a difference of about 2% in the university applicants and about 12% in the WAIS-III sample). Kane, Oakland, and Brand (2006) applied this method to the standardization sample of the WJ-R (N=6,359, ages 2–95 years) and found that a single common factor accounted for 52% of the variance in test scores in the low ability group and 29% of the variance in test scores in the high ability group. In an examination of the KABC-II (N =2,375, ages 6–18 years) Reynolds and Keith (2007) fit a number of hierarchical ability models with confirmatory factor analysis, and found that a higher order common factor accounted for about 10% more variance per variable in the low ability group than in the high ability group. One notable study not supportive of ability differentiation was a sophisticated set of analyses by Nesselroade and Thompson (1995). A series of nested linear factor models were compared across high and low ability groups of adult twins (ages 49 to 92 years), with only 1 twin from each pair per analysis, and the co-twin in a second set of cross-validation analyses. Results indicated that both the number of factors and the magnitudes of their loadings were invariant across ability groups.

Only one study seems to have implemented nonlinear models to examine either of the differentiation hypotheses. Der and Deary (2003) used polynomial regressions to predict scores on a test of reasoning from simple and complex reaction times. Whereas a linear model adequately described the relation between reasoning and complex reaction time, a quadratic model was incrementally descriptive of the relation between reasoning and simple reaction time in the direction predicted by the ability differentiation hypothesis.

Age Differentiation-Dedifferentiation: Recent Theory and Research

A number of recent cognitive developmental and aging theories have made specific predictions supportive of age differentiation-dedifferentiation. Cattell’s (1987) investment theory proposes that individuals begin life with a single general (fluid) ability that through experience and development is invested in the formulation and elaboration of knowledge-based (crystallized) abilities. As environmental and non-cognitive (e.g. interest, motivation) influences on knowledge acquisition accumulate with age, and as cognitive functions become automatized, fluid and crystallized abilities increase in their relational independence. A number of researchers (Baltes & Lindenberger, 1997; Li et al., 2004; Lövdén, Ghisletta, & Lindenberger, 2004) have expanded upon this hypothesis. They have proposed that during childhood, heterogeneous contributions to development and learning result in increases in ability levels and associated increases in ability independence, whereas during adulthood, more global biological constraints result in broad declines in ability levels and associated increases in ability interrelations. Li and colleagues (Li & Lindenberger, 1999; Li, Lindenberger, & Sikstrom, 2001) have proposed that such aging related biological constraints may be attributable to decreases in neurotransmission that result in increased noise in information processing. When such constraints are simulated with computational models, the results are decreases in cognitive performance, increases in cognitive performance variability, and increases in the relations among cognitive abilities. These emphases on the age-based operation of broad constraints bear theoretical similarity to the cognitive theories described above (see Tucker-Drob & Salthouse, 2008, for a discussion and review).

A separate area of empirically based developmental theory predicts patterns inconsistent with the age differentiation-dedifferentition hypothesis. A number of behavioral genetic investigations have established that the proportion of individual differences in cognitive performance that can be attributed to genetic sources increases monotonically across the childhood and adult lifespan. These findings have been described as “among the most striking and strongly substantiated findings of behavioral genetics in recent years” (Jensen, 1998, p. 179). It has been proposed (e.g. Dickens, unpublished manuscript; Dickens and Flynn, 2001; Scarr & McCartney, 1983) that these findings result from individuals self-selecting into environments that are compatible with their ability levels, and which proportionally amplify their many abilities. The notion that multiple sources of individual variation dynamically interact to produce increasing intercorrelations with childhood age has also been proposed by van der Maas, Dolan, Grasman, Wicherts, Huizenga, & Raijmakers (2006) in their theoretical model of the “positive manifold of intelligence by mutualism.” Therefore, to the extent that broad and dynamic determinants of cognitive abilities (including the self selection into environments that proportionally amplify cognitive abilities) operate across the lifespan, one would expect that the relations among cognitive abilities might increase concomitantly.

Similar to examinations of ability differentiation, age differentiation-dedifferentiation has conventionally been examined by contrasting correlations, or the proportion of variance accounted for by a common factor, across age groups.

Some of the most recent support of age differentiation-dedifferentiation comes from Li et al. (2004) who divided a population based sample of 291 individuals into six age groups ranging from 6 to 89 years of age and found that the correlations between fluid and crystallized intelligence in the adolescent, young adult, and middle adult groups were smaller in magnitude than the correlations in the young children and two older adult groups, and that a similar trend was present in the percentage of variance in cognitive and intellectual measures explained by the first principal component. De Frias, Lövdén, Lindenberger, and Nilsson (2007) compared covariances among levels of cognitive ability measures across 5 cohorts of individuals (aged 35–80) and found evidence for age-related increases in ability interrelations beginning after about 65 years of age, reasoning that this is the age range in which broad and severe determinants of cognitive decline begin to dominate.

Others have been unable to support age differentiation-dedifferentiation. In a sample of 2,087 adults (ages 65 and older) Anstey, Hofer, & Luszcz (2003) examined differences in intercorrelations among Verbal, memory, Vision, & Hearing factors across low, middle, and high ability groups, young-old, mid-old, and old-old age groups, and across 8 years of longitudinal change (791 participants retained). They found some evidence for ability differentiation but little evidence for age-dedifferentiation. Analyzing data from the WJ-R (N=2,201), Bickley, Keith, & Wolfle (1995) found that neither the intercorrelations among subtests, nor the hierarchical factor structure, differed significantly across 8 age groups ranging from 6 to 79 years of age. Juan-Espinosa, García, Escorial, Rebollo, Colom, & Abad (2000), examined the Italian, Spanish, and American standardization samples of the WPPSI and the WISC-R in 17 age groups ranging from 4 to 16 years of age and found no evidence for systematic age-related differences in the percent of variance accounted for by a single factor, or in the average inter-test correlation. In a similar investigation of adults, Juan-Espinosa, García, Escorial, Rebollo, Colom, & Abad (2002) divided the Spanish standardization sample of the WAIS-III (N=1,369) into six age groups ranging from 16 to 94, and after correcting for group differences in ability range found no evidence for systematic age-related differences in the percentage of variance accounted for by a common factor. Using Deary et al.’s (1996) method to sample similarly distributed young and old subsamples from two parent populations of N=6,980 (ages 12–16) and N=11,448 (ages 15–24) Hartmann (2006) found no evidence for differences in the average magnitude of test intercorrelations, or percent of variance accounted for by the first principal component or single common factor, across age groups. These patterns of results unsupportive of age differentiation-dedifferentiation Juan-Espinosa et al. (2002, p. 407), to provide an anatomical metaphor in concluding that “basic structure does not change at all, although, like the human bones, the cognitive abilities grow up and decline at different periods of life.”

Age Modification of Ability Differentiation

Facon (2006) investigated the unique hypothesis that ability-differentiation may not be an age-invariant phenomenon, but rather emerges with childhood development. Facon split the French standardization sample of the WISC-III into 3 age groups ranging from 7 to 15 years, and split the age group into low and high ability groups. He found that the strength of the relations among subtests, as indexed by the median intercorrelation differed more greatly between low and high ability groups for older ability group pairs. Facon (2004), examined the same hypothesis in 4 to 9 year olds (N=574), in comparing subtest intercorrelation matrices across low and high ability groups, and because he did not find evidence for ability differentiation, concluded that the phenomenon must emerge later in development. Arden and Plomin (2007) have made similar speculations.

Goals of Current Investigation

Three major questions were addressed for the current project.

1. To what extent do the relations among cognitive abilities differ across the lifespan?

2. To what extent do the relations among cognitive abilities differ according to ability level?

3. Given the substantial age-related trends in cognitive ability levels, to what extent are (1) and (2) independent of one another? Moreover, to what extent does (2) differ according to age?

In the following sections, key methodological and conceptual issues are surveyed, and the analytic approach for addressing the above questions is described.

Methodological Considerations

Linear Factor Analysis and Nonlinear Factor Analysis

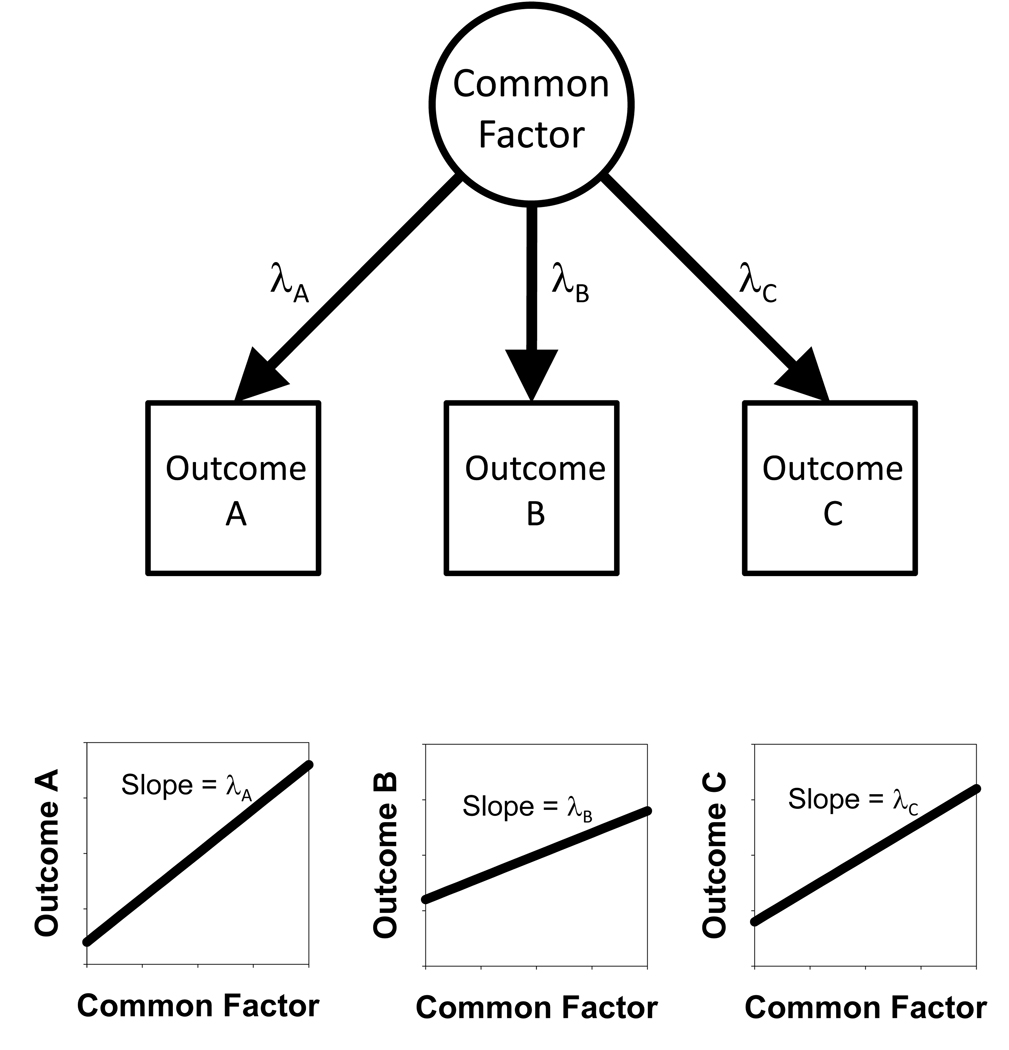
A three outcome¹ version of the conventional common factor model is depicted as a path diagram in Figure 1. In this diagram, measured outcomes are represented as squares, unobserved (theoretical) variables are represented as circles, and linear regression relationships (e.g. factor loadings) are represented as single headed arrows. This basic model, on which most existing structural representations of cognitive abilities are based, relies on the assumptions that the pattern of observed interrelations among the outcomes can be fully accounted for by their relations to an unobserved (theoretical) common factor, and that patterns of relations that the outcomes have with external variables are fully attributable to the mediation of the common factor (although these assumptions can be relaxed in some more advanced models). To the extent that more than three outcomes per factor are included, or relations with external variables are included, such models are empirically falsifiable. A further assumption of this basic model that is also amenable to empirical falsification (but which is rarely actually scrutinized) is that all relations are linear in nature. This is represented by the three plots at the bottom of Figure 1, in which it can be seen that each outcome is assumed to have a linear relation to the common factor. Put in other words, this basic model assumes that individuals’ abilities are related to their performance on a given outcome to the same extent regardless of ability level, or level of some other variable (e.g. age). It is precisely these latter assumptions that the ability differentiation and age differentiation-dedifferentiation hypotheses call into question.

Figure 1.

The conventional common factor model assumes that performance on a given outcome is a linear function of the score on the common factor. In this hypothetical factor analysis, λ_A, λ_B, and λ_C are factor loadings, which correspond to the slopes of the regressions of the outcomes on the common factor.

The typical approach that has arisen for scrutinizing the assumption of constancy of relations, particularly with respect to age and ability level, is one in which the basic factor model depicted in Figure 1 is fit to two or more groups that have been formed based on fairly arbitrary criteria (i.e. above and below a certain test score or age), and allowing the linear structural interrelations to differ across the two groups. Such an approach has been criticized on a number of grounds, including the application of a linear model to examine an inherently nonlinear hypothesis, the arbitrary nature of dividing a continuous variable into groups and the associated artifacts of such division (e.g. unequal ranges of scores), and the use of observable indices of ability level to form ability groups, when the unobservable true ability is the variable of theoretical interest. See Deary et al. (1996) for a more detailed discussion of these methodological issues.

An alternative to the multiple group approach is one that represents structural interrelations as occurring within a single group and along continuous dimensions, but in nonlinear and interactive ways (see, e.g., Bauer, 2005). Such an approach can help to diminish the above described threats that are associated with multiple group approaches. Moreover, whereas the division of samples into discrete age groups almost inevitably results in groups that also differ in ability level (and vice versa), a continuous approach can allow for a great deal of flexibility in simultaneously modeling the effects of age and ability level.

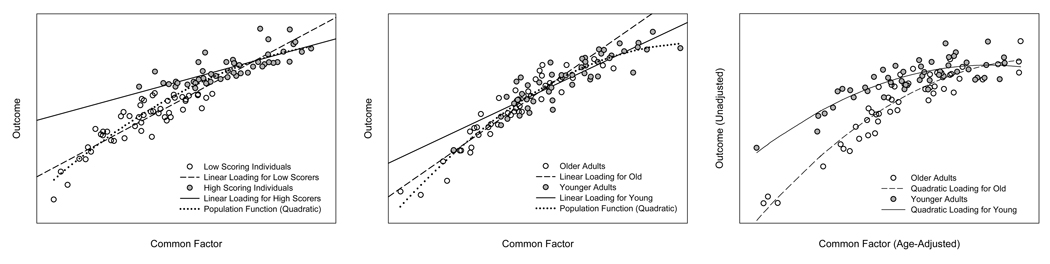
Figure 2 depicts the results of an analysis of simulated data that illustrates how nonlinear factor analytic methods can be employed in examining the differentiation hypotheses. In the left plot a single nonlinear function describes the relationship between outcome and the common factor. It can be seen that by fitting separate linear regressions to participants scoring below and above the mean on the outcome, the nonlinear relationship is approximated, but suggests lack of measurement invariance (i.e. a single model cannot adequately account for the relation in both groups). Alternatively, a single measurement invariant nonlinear model is a preferable depiction of the relationship. In the center plot a single nonlinear function again best describes the relation between the common factor and the outcome. In this case, when separate linear models are fit to young and old adult groups (assuming that old adults perform more poorly on average than young adults), the results again approximate the nonlinear relationship, and suggest lack of measurement invariance. In the right plot, the nonlinear loading is modeled separately for young and old adults, allowing for inferences to be made regarding both ability differentiation and age differentiation-dedifferentiation. The approach taken in the current study is most analogous to that depicted in the right plot, in which nonlinear loadings, and age-modification of loadings are simultaneously modeled. In the current study, however, both ability level and age are considered as continuous variables.

Figure 2.

Left: Simulated Data. Linear regressions fit to High and Low scoring individuals. Although a single (nonlinear) population function applies, a two group linear approach indicates measurement noninvariance across ability groups. Middle: Simulated Data. Linear regressions fit to old and young adult groups. Although a single (nonlinear) population function applies, a two group linear approach indicates measurement noninvariance across age groups. Right: Simulated Data. Quadratic regressions fit to old and young adult groups. Here, the observed score-true score relations differ according to both age and ability level.

The Importance of a Proper Measurement Model

In order to examine influences that may potentially modify the relational magnitudes among variables, it is important for each variable to be measured on a scale for which the distance between any two values has the same meaning as a distance of the same magnitude between any two other values. Put another way, in order for differences in relational magnitudes to be meaningfully examined, the variables should be measured on interval scales. This is because the magnitude of a relation can be conceptualized as a magnitude of change in the expected value of one variable, given a unit of change in the value of another variable. Therefore, only if it is meaningful to compare magnitudes of differences at different areas along the scales, is it meaningful to compare the magnitudes of relations at different areas along the scales.

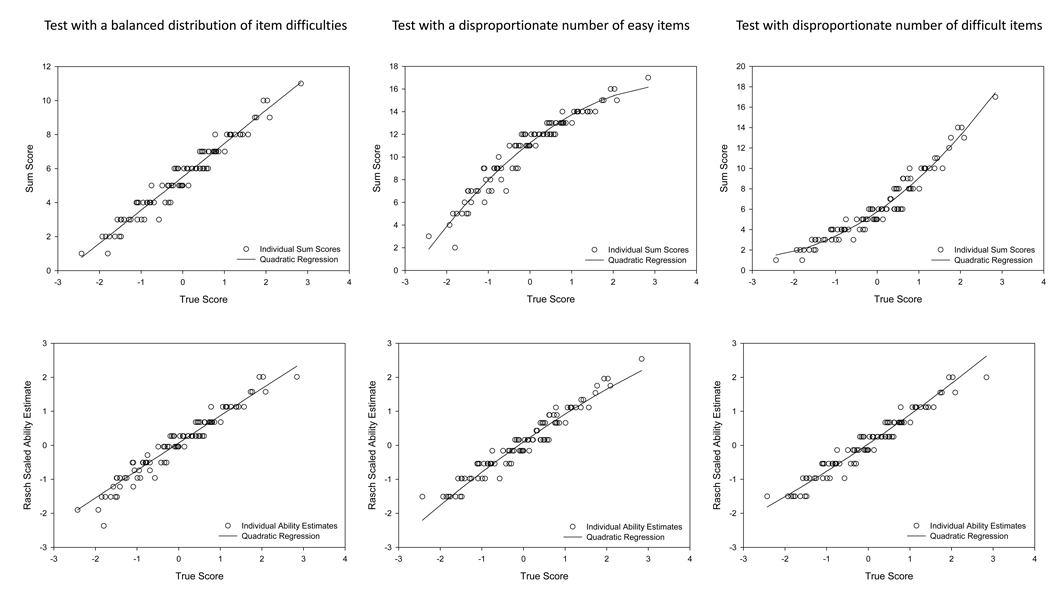
Whereas most extant examinations of the ability differentiation and age differentiation-dedifferentiation hypotheses have failed to consider the measurement properties of the instruments, the current analyses are of Rasch-scaled ability estimates, which are based on the logistic item response model, and which can be considered to have interval measurement properties. The advantage of the Rasch model is illustrated by analyses of simulated data, results of which are presented in Figure 3. The top row contains plots of sum scores (total number of items correct) as functions of the true ability scores that were generated in the simulation. The bottom row contains ability estimates obtained using an Item Response Theory, Rasch (1 parameter logistic), measurement model as functions of the true scores. The columns represent conditions in which the distribution of item difficulties is either balanced, disproportionately easy, or disproportionally difficult. It can be seen that only when the distribution of item difficulties is balanced relative to the population measured, is interval measurement is maintained such that a sum score is an appropriate indication of the true score. Moreover, by simply adding easy or difficult items to a test, the sum score loses its interval properties and can instead artifactually create an impression of ability-differentiation or even, what might be described as ability dedifferentiation (i.e. the relation between the true score and the sum score becomes nonlinear). However, by applying a Rasch measurement model to the data, interval properties are well maintained in all cases. For a more detailed discussion of the advantages of Rasch scaling to achieve interval measurement properties, see Embretson & Reise (2000).

Figure 3.

Simulated Data. The item composition of a measure can influence the quality and magnitude of its interrelations. A sum score is particularly problematic when the distribution of item difficulties does not match the distribution of person abilities. Rasch (Item Response Theory) scaling can help to reduce such biases.

Method

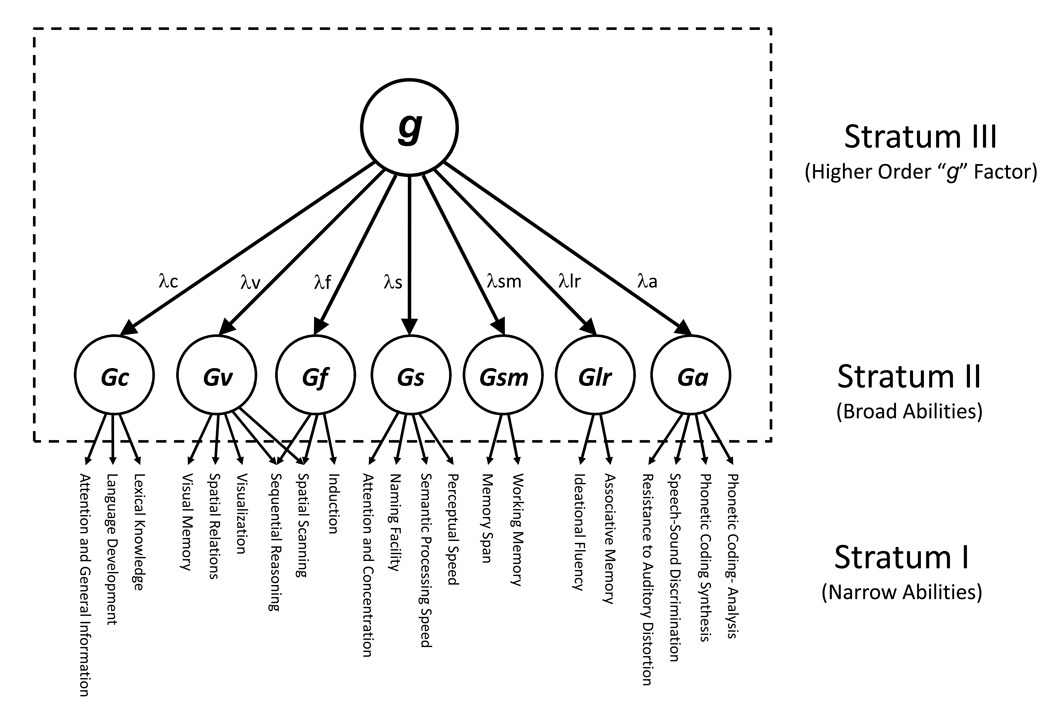
The current investigation is based on analyses of the standardization sample of the Woodcock-Johnson III (WJ-III) Tests of Cognitive Abilities (Woodcock, McGrew, & Mather, 2001). The WJ-III test battery was constructed based on an integration of Cattell’s and Horn’s theory of Fluid and Crystallized intelligence (Cattell, 1941; Cattell, 1987; Horn, 1965), and Carroll’s (1993) three-stratum theory of cognitive abilities. This integration has been termed Cattell-Horn-Carroll (CHC) theory, and is represented as a three-stratum hierarchical structure in Figure 4. The main focus of the current investigation is on the relations between the second stratum abilities and the higher order common (g) factor, as demarcated by the dashed box in the figure. The second stratum abilities are described below (adapted from McGrew & Woodcock, 2001).

Figure 4.

A graphical depiction of the theoretical structure on which the WJ-III Tests of Cognitive Abilities was based. This Horn-Cattell-Carroll Model assumes that cognitive abilities are organized in a hierarchy containing three strata, with variables in contiguous strata related to one another by way of linear factor loadings (λ’s). The current investigation focuses on (potentially nonlinear) relations between the variables thought to represent abilities at Stratum II, and a higher order g factor at Stratum III.

Comprehension-Knowledge (Gc), also termed crystallized intelligence, refers to knowledge (especially verbal knowledge) that is autobiographically acquired from a culture through experience and learning. It includes factual information, comprehension, concepts, rules, knowledge of relationships, and procedural knowledge that has become automatized.

Visual-Spatial Thinking (Gv) refers to the ability to integrate, perceive, store, recall, rotate and mentally manipulate, and reason with visual patterns and representations.

Fluid Reasoning (Gf) refers to the ability to inductively and deductively reason in novel ways, and with unfamiliar information, by identifying relations, drawing inferences, forming concepts, and identifying conjunctions and disjunctions.

Processing Speed (Gs) refers to the ability to quickly and efficiently perform cognitive tasks requiring focused attention.

Short-Term Memory (Gsm) refers to the ability to apprehend and store information in immediate awareness before it is retrieved or applied.

Long-Term Retrieval (Glr), also termed episodic memory, refers to the ability to encode information and later retrieve it. Between encoding and retrieval, the information departs from immediate awareness.

Auditory Processing (Ga) refers to the ability to integrate, synthesize, discriminate, and process auditory stimuli that may or may not be distorted or obscured.

Whereas the conventional CHC model of cognitive abilities is based on linear patterns of relations, the current investigation examines the possibility that these relations are nonlinear, such that they are functions of age and ability level. This is achieved using nonlinear factor analytic methods, in which potential age and ability level modification of common factor-broad ability relations are evaluated as empirical questions (i.e. the three questions posed earlier).

Participants

The WJ-III sample was recruited from over 100 geographically diverse communities to be nationally representative of the United States population, as indexed by the 2000 census projections (McGrew & Woodcock, 2001). Participants were selected using a stratified sampling design that controlled for census region, community size, sex, race, Hispanic vs. non-Hispanic, type of college/university (for college and university students), educational attainment (for adults), employment status (for adults), and occupation (for adults). Although this design produced samples with distributions of participants closely approximating the U.S. population, individual subject weights² were applied for all models reported here in order to obtain the most precisely representative parameter estimates possible. Note that results from models in which subject weights were not applied were very similar to those reported here.

Because recruitment was carried out separately for school-age (kindergarten through 12^th grade), college and university, and adult (nonstudent) subsamples, data from these three subsamples were analyzed separately in the current project³. The interested reader can refer to the online supplement to this paper for detailed results of a single group analysis (of data aggregated across all three subsamples). Those results were very similar to the ones reported here.

Table 1 presents key descriptive statistics for the three subsamples. Note that in order to avoid extreme influences and sparse data in some areas of the multivariate distributions (e.g. older adults who were still in college), age and grade inclusion criteria were set for each subsample (see starred cells of Table 1). Moreover, participants were only included if they had data available for at least one broad ability cluster score (described below).

Table 1.

Composition of Subsamples

Subsample	Grade at Testing (Lowest)	Grade at Testing (Highest)	Age Range (Lowest)	Age Range (Highest)	N	Mean Age
School Age	0*	12*	4	18*	4,057	11.4
College and University	13*	18	18*	27*	779	21.0
Adult	not students*		21*	101	1,437	49.2

Note: * indicates that this value was one of the criteria used to define the subsample for this project. Grade 0 corresponds to kindergarten.

Measures

Analyses are based on seven cluster scores corresponding to the seven second stratum broad abilities depicted in Figure 4. Each cluster scores is based on the average of two W-scaled tests representative of the respective ability. The W-scale is a transformation of the Rasch (1 parameter logistic) Item Response Theory model, which has been centered such that 500 corresponds to the approximate level of performance of ten year olds, and scaled to have interval properties such that at any level of functioning (a) a difference between person ability and item difficulty (ability minus difficulty) of 0 corresponds to 50% probability of success, (b) a difference between person ability and item difficulty of 10 corresponds to a 75% probability of success, and (c) a difference between person ability and item difficulty of −10 corresponds to a 25% chance of success (McGrew, Werder, & Woodcock, 1991).

The tests used to measure each ability are described in Table 2. Reliabilities of the cluster scores by age groups are provided in Table 3. The reliabilities of the cluster scores were very high for all age groups, and there was very little evidence that the reliabilities systematically differed according to age. This is important, because systematic differences in variable interrelations could be due to systematic differences in variable reliabilities, if they exist. This possibility was also considered with respect to differences in reliability by ability level. It is well known in modern test theory that ability estimates are less accurate for ability regions that are measured by fewer items. Because the WJ-III tests contain greater item representation at the middle of the scales than at the extremes, ability estimates are likely to be less accurate for extremely high and low functioning participants. It can be inferred that the findings reported in this paper were not biased by this phenomenon, as models that only included individuals scoring within one standard deviation of the sample mean’s general intellectual ability composite score (approximately the middle 68%, where items are evenly and abundantly distributed) produced very similar patterns of results as those reported here.

Table 2.

Descriptions of Measures of Broad Abilities

Broad Ability	Measure	Description
Comprehension Knowledge (Gc)	Verbal Comprehension	Name pictured objects, select synonyms and antonyms, and complete verbal analogies.
	General Information	Identify where specified objects can be found, and what specified objects are typically used for.
Visual-Spatial Thinking (Gv)	Spatial Relations	Identify the pieces needed to construct a specified shape.
	Picture Recognition	Identify previously presented pictures within a field of distracting pictures.
Fluid Reasoning (Gf)	Concept Formation	Identify, categorize, and determine rules from a complete stimulus set.
	Analysis-Synthesis	Learn and apply novel symbolic formulations to determine the missing components of puzzles.
Processing Speed (Gs)	Visual Matching	Quickly locate and circle two identical numbers in a row of numbers.
	Decision Speed	Quickly locate and circle two conceptually related pictures in a row of pictures.
Short-Term Memory (Gsm)	Numbers Reversed	Recall a series of numbers from immediate awareness in reverse sequence.
	Memory for Words	Repeat a list of unrelated words in the sequence presented.
Long-Term Retrieval (Glr)	Visual-Auditory Learning	Learn and recall pictorial representations of words.
	Retrieval Fluency	Name as many examples as possible from a specified category.
Auditory Processing (Ga)	Sound Blending	Synthesize phonetic units.
	Auditory Attention	Identify auditorily presented words in the presence of increasing intensities of background noise.

Note: Adapted from Table 4-2 of WJ-III Technical Manual (McGrew et al., 2001)

Table 3.

Estimated Reliabilities of Cluster Scores by Age Group.

Age	Gc	Gv	Gf	Gs	Gsm	Glr	Ga
4	0.92	0.89	0.95	0.93	0.93	0.88	0.94
5	0.93	0.87	0.96	0.94	0.91	0.87	0.93
6	0.92	0.76	0.96	0.95	0.88	0.87	0.88
7	0.92	0.70	0.96	0.94	0.86	0.89	0.87
8	0.93	0.77	0.95	0.92	0.87	0.87	0.86
9	0.93	0.78	0.95	0.92	0.83	0.86	0.88
10	0.94	0.80	0.94	0.92	0.88	0.87	0.88
11	0.94	0.74	0.95	0.90	0.85	0.86	0.88
12	0.94	0.80	0.95	0.91	0.87	0.88	0.89
13	0.95	0.81	0.95	0.92	0.88	0.87	0.89
14	0.96	0.84	0.96	0.92	0.91	0.90	0.91
15	0.96	0.81	0.95	0.92	0.86	0.90	0.91
16	0.95	0.79	0.95	0.91	0.87	0.88	0.89
17	0.95	0.76	0.94	0.91	0.87	0.88	0.89
18	0.95	0.82	0.94	0.93	0.87	0.87	0.91
19	0.95	0.81	0.93	0.92	0.89	0.91	0.90
20–29	0.96	0.84	0.95	0.93	0.88	0.92	0.93
30–39	0.97	0.83	0.97	0.94	0.92	0.94	0.94
40–49	0.98	0.87	0.97	0.95	0.92	0.93	0.94
50–59	0.97	0.86	0.97	0.95	0.90	0.93	0.94
60–69	0.98	0.87	0.97	0.94	0.93	0.93	0.95
70–79	0.97	0.79	0.97	0.96	0.91	0.89	0.93
80+	0.97	0.88	0.97	0.97	0.92	0.91	0.94

Note: Estimates are from Appendix B of the WJ-III Technical Manual (McGrew et al., 2001). Cluster reliability estimates are based on split-half internal consistencies for all tests except for the speeded tests, which were calculated from Rasch-based error scores.

Finally, it is possible that nonlinear trends can be artifactually produced by ceiling and floor effects of the measures. The WJ-III tests underwent a rigorous development process to ensure, among other things, that all ability levels could be sensitively measured. The success of this procedure was confirmed here, by examining histograms of each of the cluster scores. For no variable was there evidence for a disproportionate frequency of scores at the extremes of the scales, or a truncation of the distribution.

Analyses

All models were run in Mplus (Muthén & Muthén, 1998–2007) with Full Information Maximum Likelihood (FIML) estimation procedures using a numerical integration algorithm that permits estimation of interactive effects (see Appendix A for an example script). FIML is also able to accommodate missing data under the missing at random assumption (McArdle, 1994; Muthén & Muthén, 1998–2007). Given the large number of statistical comparisons, alpha values were set to .01.

Sets of stepwise models were separately applied to school-age, college and university, and adult subsamples. In these equations, [x] indicates that a term is specific to each broad ability. For example, G[x] represents the broad abilities Gc, Gv, Gf, Gs, Gsm, Glr, and Ga. Also note that υ represents ability intercepts, α₁[x] and α₂[x] represent the regression coefficients of the broad abilities on age and age squared⁴, g represents the higher order common factor, λ₁[x]-λ₄[x] represent loadings on g, and u[x] represents the (unique) component of each broad ability that is not accounted for by the other terms in the model. The subscript n denotes that a term varies between individuals. In all models, g and u[x] are allowed to have between-person variances σ²_g and σ²_u[x] respectively. To define the metric of g, σ²_g was set to 1 for all models. However, as a result of the differential recruitment procedures for the three subsamples, is likely that the school-age, college and university, and adult subsamples, differed in the magnitudes of the variation in their latent abilities⁵. Therefore, the parameters for the subsamples were likely not on comparable scales, and across subsample comparisons of parameter values should not be made. However within subsample age-comparisons are of course a main topic of inquiry.

Age was centered for each subsample by subtracting its mean, and the mean of common factor (g) was fixed to 0 for each subsample. This helped to reduce nonessential multicollinearity among the main effects, quadratic effects, and interactive effects of age and g, thus facilitating model estimation and interpretability.

Step 1

In the first step of model fitting, each ability was simultaneously predicted by linear and quadratic age trends, and linear loadings on the common factor (g). This model is equivalent to conventional (linear) common factor models. It is written as

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\alpha }}_1[x]·{\mathit{\text{age}}}_n+{\mathrm{\alpha }}_2[x]·{{\mathit{\text{age}}}_n}^2+{\mathrm{\lambda }}_1[x]·g_n+u{[x]}_n.$$ (Eq. 1)

Step 2

In the second step, two parallel models were constructed: one with the addition of terms for quadratic common factor loadings, and a second with the addition of terms for age-modification of the linear common factor loadings. The former model examines the ability differentiation hypothesis, and is written as

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\alpha }}_1[x]·{\mathit{\text{age}}}_n+{\mathrm{\alpha }}_2[x]·{{\mathit{\text{age}}}_n}^2+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_2[x]·{g_n}^2+u{[x]}_n.$$ (Eq. 2)

The latter model examines the age differentiation-dedifferentiation hypothesis, and is written as

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\alpha }}_1[x]·{\mathit{\text{age}}}_n+{\mathrm{\alpha }}_2[x]·{{\mathit{\text{age}}}_n}^2+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n·g_n+u{[x]}_n.$$ (Eq. 3)

Step 3

In the third step, quadratic common factor loadings and age-modification of the linear common factor loadings were simultaneously estimated. This model simultaneously examines both the ability differentiation and age differentiation-dedifferentiation hypotheses. It is written as

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\alpha }}_1[x]·{\text{age}}_n+{\mathrm{\alpha }}_2[x]·{{\mathit{\text{age}}}_n}^2+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_2[x]·{g_n}^2+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n·g_n+u{[x]}_n.$$ (Eq. 4)

Step 4

In a final step, terms for age-modification of the quadratic factor loadings were added. In addition to examining the ability differentiation and age differentiation-dedifferentiation hypotheses, this model examines the possibility that ability-differentiation may be modified by age (e.g. that differentiation may emerge with development). The full model is written as

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\alpha }}_1[x]·{\mathit{\text{age}}}_n+{\mathrm{\alpha }}_2[x]·{{\mathit{\text{age}}}_n}^2+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_2[x]·{g_n}^2+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n·g_n+{\mathrm{\lambda }}_4[x]·{\mathit{\text{age}}}_n·{g_n}^2+u{[x]}_n,$$ (Eq. 5)

or in expanded form as

$$\left[\begin{array}{c}\hfill G{c}_n\hfill \\ \hfill G{v}_n\hfill \\ \hfill G{f}_n\hfill \\ \hfill G{s}_n\hfill \\ \hfill G{\mathit{\text{sm}}}_n\hfill \\ \hfill G{\mathit{\text{lr}}}_n\hfill \\ \hfill G{a}_n\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \mathrm{\upsilon }\mathrm{c}\hfill \\ \hfill \mathrm{\upsilon }\mathrm{v}\hfill \\ \hfill \mathrm{\upsilon }\mathrm{f}\hfill \\ \hfill \mathrm{\upsilon }\mathrm{s}\hfill \\ \hfill \mathrm{\upsilon }\text{sm}\hfill \\ \hfill \mathrm{\upsilon }\text{lr}\hfill \\ \hfill \mathrm{\upsilon }\mathrm{a}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\mathrm{\alpha }}_1\mathrm{c}\hfill \\ \hfill {\mathrm{\alpha }}_1\mathrm{v}\hfill \\ \hfill {\mathrm{\alpha }}_1\mathrm{f}\hfill \\ \hfill {\mathrm{\alpha }}_1\mathrm{s}\hfill \\ \hfill {\mathrm{\alpha }}_1\text{sm}\hfill \\ \hfill {\mathrm{\alpha }}_1\text{lr}\hfill \\ \hfill {\mathrm{\alpha }}_1\mathrm{a}\hfill \end{array}\right]·{\mathit{\text{age}}}_n+\left[\begin{array}{c}\hfill {\mathrm{\alpha }}_2\mathrm{c}\hfill \\ \hfill {\mathrm{\alpha }}_2\mathrm{v}\hfill \\ \hfill {\mathrm{\alpha }}_2\mathrm{f}\hfill \\ \hfill {\mathrm{\alpha }}_2\mathrm{s}\hfill \\ \hfill {\mathrm{\alpha }}_2\text{sm}\hfill \\ \hfill {\mathrm{\alpha }}_2\text{lr}\hfill \\ \hfill {\mathrm{\alpha }}_2\mathrm{a}\hfill \end{array}\right]·{\mathit{\text{age}}}_n{}^2+\left[\begin{array}{c}\hfill {\mathrm{\lambda }}_1\mathrm{c}\hfill \\ \hfill {\mathrm{\lambda }}_1\mathrm{v}\hfill \\ \hfill {\mathrm{\lambda }}_1\mathrm{f}\hfill \\ \hfill {\mathrm{\lambda }}_1\mathrm{s}\hfill \\ \hfill {\mathrm{\lambda }}_1\text{sm}\hfill \\ \hfill {\mathrm{\lambda }}_1\text{lr}\hfill \\ \hfill {\mathrm{\lambda }}_1\mathrm{a}\hfill \end{array}\right]·g_n+\left[\begin{array}{c}\hfill {\mathrm{\lambda }}_2\mathrm{c}\hfill \\ \hfill {\mathrm{\lambda }}_2\mathrm{v}\hfill \\ \hfill {\mathrm{\lambda }}_2\mathrm{f}\hfill \\ \hfill {\mathrm{\lambda }}_2\mathrm{s}\hfill \\ \hfill {\mathrm{\lambda }}_2\text{sm}\hfill \\ \hfill {\mathrm{\lambda }}_2\text{lr}\hfill \\ \hfill {\mathrm{\lambda }}_2\mathrm{a}\hfill \end{array}\right]·g_n{}^2+\left[\begin{array}{c}\hfill {\mathrm{\lambda }}_3\mathrm{c}\hfill \\ \hfill {\mathrm{\lambda }}_3\mathrm{v}\hfill \\ \hfill {\mathrm{\lambda }}_3\mathrm{f}\hfill \\ \hfill {\mathrm{\lambda }}_3\mathrm{s}\hfill \\ \hfill {\mathrm{\lambda }}_3\text{sm}\hfill \\ \hfill {\mathrm{\lambda }}_3\text{lr}\hfill \\ \hfill {\mathrm{\lambda }}_3\mathrm{a}\hfill \end{array}\right]·{\mathit{\text{age}}}_n·g_n+\left[\begin{array}{c}\hfill {\mathrm{\lambda }}_4\mathrm{c}\hfill \\ \hfill {\mathrm{\lambda }}_4\mathrm{v}\hfill \\ \hfill {\mathrm{\lambda }}_4\mathrm{f}\hfill \\ \hfill {\mathrm{\lambda }}_4\mathrm{s}\hfill \\ \hfill {\mathrm{\lambda }}_4\text{sm}\hfill \\ \hfill {\mathrm{\lambda }}_4\text{lr}\hfill \\ \hfill {\mathrm{\lambda }}_4\mathrm{a}\hfill \end{array}\right]·{\mathit{\text{age}}}_n·g_n{}^2+\left[\begin{array}{c}\hfill u{c}_n\hfill \\ \hfill u{v}_n\hfill \\ \hfill u{f}_n\hfill \\ \hfill u{s}_n\hfill \\ \hfill u{\mathit{\text{sm}}}_n\hfill \\ \hfill u{\mathit{\text{lr}}}_n\hfill \\ \hfill u{a}_n\hfill \end{array}\right],$$

where G[x] represents the broad abilities, υ[x] represents ability-specific intercepts, α₁[x] represents the linear components of the age trends in each ability, α₂[x] represents the quadratic components of the age trends in each ability, λ₁[x] represents the linear influences of g on each ability, λ₂[x] represents the quadratic (nonlinear) influences of g on each ability (ability differentiation), λ₃[x] represents age modification of the linear influence of g on each ability (age differentiation), λ₄[x] represents age modification of the quadratic influence of age on each ability (age modification of ability differentiation), and u[x] represents unique ability-specific factors.

Results

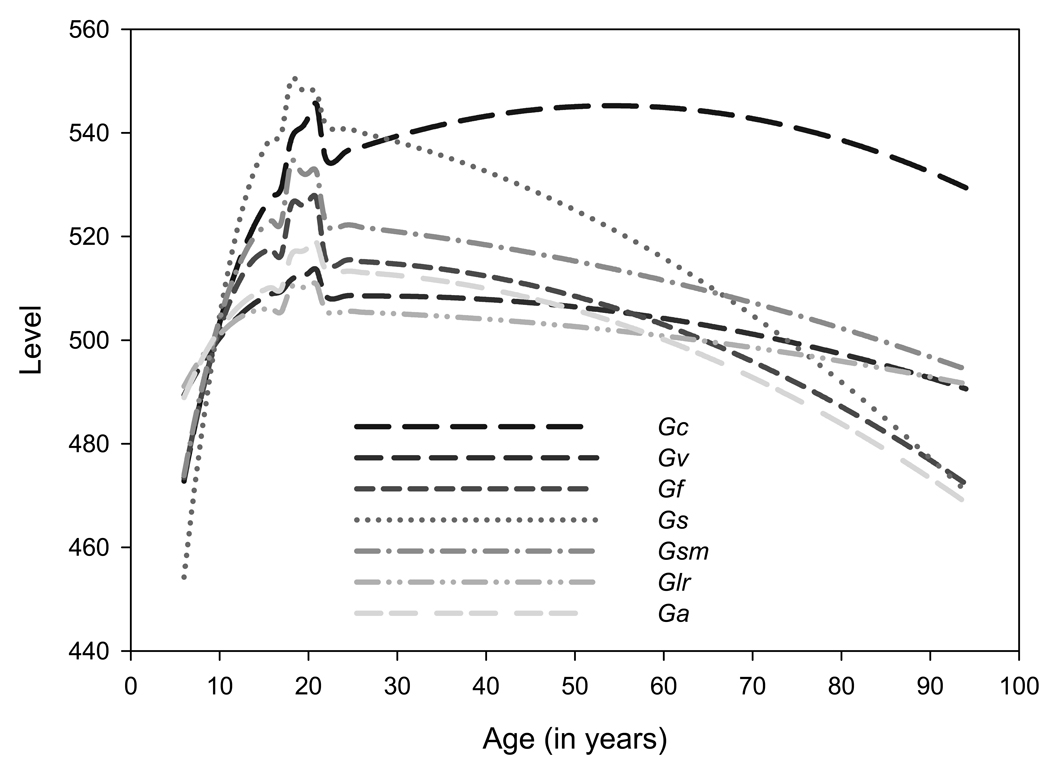
Model implied age trends in the broad factors are depicted in Figure 5. These were produced using the terms α₁[x] and α₂[x] of the full models from each group, but the parameters were very similar for each step of the model fitting. Note that because linear and quadratic trends were fit separately for the school-age, college and university, and adult subsamples, elaborate lifespan age trends were able to be captured with these fairly simple functions⁶. Such trends would ordinarily require much more complex functions (e.g. high degree polynomials, or the dual exponential model that was fit by McArdle et al., 2002) had the lifespan age trends not been modeled in three segments. The trends are consistent with those found in many cross sectional (e.g. Li et al., 2004) and longitudinal (e.g. McArdle et al., 2002) examinations of similar variables. In particular, all abilities except for Gc increase in level during childhood development, peak during late adolescence/early adulthood, and decrease in level across adulthood, whereas Gc increases in level through childhood and until middle adulthood, where it peaks and decreases thereafter. Also of prominence in Figure 5 is the positive selection of college and university participants that is often of concern in psychological research. This thorough modeling of lifespan age-trends is of particular importance for the current project, because covariational patterns can often be influenced by common (or discrepant) mean age trends in the data if they are not modeled and controlled for (see, for example, Hofer & Sliwinksi, 2001; Kalveram, 1965; Salthouse & Nesselroade, 2002).

Figure 5.

Model implied lifespan age trends in the broad abilities. These cross sectional trends are based on three models, fit to school age, college and university, and adult (nonstudent) subsamples separately. The discontinuity in the trends apparent surrounding approximately 20 years of age is likely due to the positive selection of the college and university subsample.

Comparisons of, and fit indices for, the stepwise models are reported in Table 4. For all three subgroups, stepwise model comparisons indicated that the full model fit the data best. A number of observations are particularly relevant. First, larger increments in model fits were associated with the addition of the terms corresponding to ability differentiation (λ₂[x]), whereas fairly modest increments in model fits were associated with the terms corresponding to age differentiation-dedifferentiation (λ₃[x]). In the case of the college and university subsample, increments in model fits associated with the age differentiation-dedifferentiation step were not significant, which is not surprising, given that this sample did not include a very wide age range.

Table 4.

Fit Indices and Comparisons of Stepwise Models.

	Step 1 Linear Model	Step 2 Nonlinear Model	Step 2 Age Modification Model	Step 3 Nonlinear + Age Modification Model	Step 4 Full Model
School Age Subsample
loglikelihood	−86596.069	−86548.230	−86562.504	−86513.705	−86490.469
free parameters	35	42	42	49	56
χ2 of difference		76.893	53.948	49.964	29.191
degrees of freedom of difference		7	7	7	7
AIC	173262.138	173180.459	173209.009	173125.410	173092.937
BIC	173482.925	173445.404	173473.953	173434.511	173446.197
College and University Subsample
loglikelihood	−15684.270	−15657.859	−15673.480	−15650.531	−15623.881
free parameters	35	42	42	49	56
χ2 of difference		43.655	19.477	12.505	128.125
degrees of freedom of difference		7	7	7	7
AIC	31438.539	31399.719	31430.960	31399.062	31359.762
BIC	31601.570	31595.355	31626.596	31627.305	31620.611
Adult Subsample
loglikelihood	−32692.657	−32475.035	−32648.890	−32454.102	−32433.470
free parameters	35	42	42	49	56
χ2 of difference		309.570	45.261	24.369	26.150
degrees of freedom of difference		7	7	7	7
AIC	65455.313	65034.070	65381.780	65006.205	64978.940
BIC	65639.774	65255.423	65603.133	65264.450	65274.077

Note: The nonlinear Model and the Age Modification Model were alternative models considered separately for the second step. χ² of difference and degrees of freedom of difference refer to comparisons relative to model in previous step (because the nonlinear model always fit better than the age modification model, the Step 3 – Step 2 comparison was always with respect to the nonlinear model). Comparisons in bold are significant at p<.01. Each χ² of difference was computed using model-specific scaling factors.

Although the stepwise model comparisons indicated that the addition of terms corresponding to both ability level and age modification of factor loading magnitudes significantly improved model fits, it is important to inspect the direction and statistical significance of each of the terms in order to evaluate whether the ability differentiation and age differentiation-dedifferentiation hypotheses were supported. To accept such support, the parameters should be in directions indicative of lower loadings at high ability levels, lower loadings with increasing childhood age, and higher loadings with increasing adult age. Moreover, the effects should not be isolated to a single broad ability, but should instead be statistically significant and consistent in direction for multiple abilities.

Parameter estimates from the baseline and intermediate stepwise models are reported in Table 5. It is useful to examine the parameter estimates from each of these models in turn. Because it served as the baseline model of which all other models were elaborations, the linear (Step 1) model merits particular scrutiny. It can be seen that all linear loadings (λ1) were highly significant, as none of their 99% confidence intervals included zero. The magnitudes of these linear loadings were moderate to large, all having standardized values greater than 0.50, indicating convergent validity of the common “g” factor. Moreover, the linear model fit the data from each subgroup well in absolute terms (School Age Subsample RMSEA=0.044, CFI=.0994, TLI=0.986; College and University Subsample RMSEA=0.063, CFI=0.925, TLI=0.812; Adult Subsample RMSEA=.039, CFI=.992, TLI=.980). Note that because all subsequent (nonlinear and interactive) models do not produce sample-level covariance expectations, these absolute fit indices are not available for them.

Table 5.

Key Parameter Estimates (and 99% Confidence Intervals) from Baseline and Intermediate Models.

	Linear Model		Nonlinear Model		Age Modification Model		Nonlinear + Age Modification Model
Parameter Coefficient on	λ1 g	λ1(std)	λ1 g	λ2 g2	λ1 g	λ3 age · g	λ1 g	λ2 g2	λ3 age · g
School Age Subsample
Gc	11.006 (10.290, 11.722)	0.793	10.893 (10.197, 11.588)	−1.141 (−1.61, −0.673)	11.026 (10.316, 11.735)	0.419 (0.223, 0.615)	10.904 (10.219, 11.59)	−1.127 (−1.573, −0.682)	0.422 (0.238, 0.605)
Gv	4.007 (3.540, 4.475)	0.517	4.018 (3.553, 4.483)	−0.063 (−0.433, 0.306)	3.975 (3.508, 4.443)	0.186 (0.042, 0.330)	3.987 (3.524, 4.451)	−0.044 (−0.428, 0.340)	0.187 (0.045, 0.329)
Gf	11.278 (10.624, 11.932)	0.783	11.216 (10.575, 11.856)	−0.778 (−1.208, −0.348)	11.336 (10.677, 11.996)	0.017 (−0.168, 0.201)	11.280 (10.632, 11.927)	−0.727 (−1.170, −0.284)	0.004 (−0.172, 0.180)
Gs	8.808 (7.990, 9.626)	0.557	8.713 (7.898, 9.528)	−0.818 (−1.456, −0.181)	8.788 (7.971, 9.605)	0.005 (−0.235, 0.244)	8.69 (7.878, 9.502)	−0.869 (−1.505, −0.232)	0.001 (−0.232, 0.234)
Gsm	12.241 (11.353, 13.128)	0.678	12.086 (11.205, 12.968)	−1.075 (−1.75, −0.399)	12.213 (11.323, 13.103)	0.140 (−0.093, 0.373)	12.050 (11.17, 12.930)	−1.112 (−1.797, −0.426)	0.149 (−0.075, 0.373)
Glr	3.778 (3.529, 4.027)	0.760	3.792 (3.538, 4.045)	−0.115 (−0.285, 0.054)	3.769 (3.519, 4.019)	0.038 (−0.029, 0.105)	3.775 (3.522, 4.027)	−0.132 (−0.300, 0.037)	0.041 (−0.023, 0.105)
Ga	5.653 (5.199, 6.107)	0.644	5.636 (5.181, 6.091)	−0.269 (−0.626, 0.088)	5.635 (5.178, 6.091)	0.097 (−0.042, 0.236)	5.613 (5.16, 6.067)	−0.312 (−0.674, 0.050)	0.102 (−0.035, 0.239)
College and University Subsample
Gc	9.103 (6.609, 11.596)	0.720	8.538 (6.210, 10.866)	−2.159 (−3.98, −0.337)	9.379 (6.879, 11.879)	1.075 (−0.213, 2.363)	8.715 (6.349, 11.081)	−1.964 (−3.622, −0.307)	0.666 (−0.562, 1.894)
Gv	5.478 (4.419, 6.537)	0.679	5.395 (4.301, 6.490)	−0.700 (−1.492, 0.092)	5.430 (4.377, 6.484)	0.013 (−0.406, 0.432)	5.36 (4.254, 6.466)	−0.693 (−1.527, 0.140)	−0.068 (−0.507, 0.372)
Gf	8.134 (6.672, 9.597)	0.793	7.841 (6.376, 9.305)	−1.715 (−2.939, −0.49)	8.034 (6.547, 9.521)	−0.17 (−0.892, 0.552)	7.793 (6.354, 9.231)	−1.661 (−2.819, −0.503)	−0.287 (−1.047, 0.473)
Gs	9.46 (7.254, 11.666)	0.566	9.663 (7.124, 12.202)	−0.201 (−2.021, 1.620)	9.334 (7.128, 11.540)	0.051 (−0.805, 0.907)	9.546 (7.017, 12.076)	−0.224 (−2.1, 1.653)	0.045 (−0.828, 0.918)
Gsm	9.662 (7.564, 11.759)	0.613	9.572 (7.241, 11.903)	−0.500 (−1.899, 0.900)	9.633 (7.525, 11.741)	0.320 (−0.502, 1.143)	9.575 (7.207, 11.944)	−0.412 (−1.856, 1.032)	0.265 (−0.545, 1.075)
Glr	4.065 (3.223, 4.907)	0.734	4.040 (3.165, 4.914)	−0.435 (−1.110, 0.240)	4.036 (3.181, 4.891)	0.116 (−0.227, 0.459)	3.997 (3.116, 4.878)	−0.446 (−1.134, 0.242)	0.038 (−0.327, 0.402)
Ga	5.912 (4.666, 7.159)	0.667	5.812 (4.562, 7.063)	−0.720 (−1.667, 0.226)	5.884 (4.682, 7.086)	0.534 (0.028, 1.04)	5.796 (4.586, 7.006)	−0.620 (−1.533, 0.293)	0.452 (−0.051, 0.955)
Adult Subsample
Gc	27.148 (23.325, 30.97)	0.927	25.388 (21.804, 28.973)	−7.770 (−9.529, −6.011)	25.735 (22.339, 29.132)	−0.262 (−0.418, −0.106)	24.984 (21.497, 28.471)	−7.621 (−9.318, −5.925)	−0.038 (−0.167, 0.091)
Gv	6.685 (5.502, 7.868)	0.705	6.518 (5.477, 7.559)	−0.721 (−1.552, 0.110)	6.308 (5.052, 7.564)	−0.065 (−0.119, −0.011)	6.204 (5.065, 7.342)	−0.665 (−1.534, 0.204)	−0.043 (−0.100, 0.014)
Gf	18.592 (16.483, 20.702)	0.892	17.784 (15.797, 19.772)	−3.208 (−4.421, −1.996)	18.164 (16.141, 20.187)	−0.096 (−0.194, 0.003)	17.723 (15.708, 19.737)	−3.178 (−4.396, −1.959)	−0.001 (−0.091, 0.090)
Gs	19.457 (16.262, 22.653)	0.799	17.838 (15.092, 20.584)	−4.576 (−6.665, −2.487)	18.996 (16.005, 21.987)	−0.103 (−0.274, 0.069)	17.708 (15.095, 20.321)	−4.611 (−6.646, −2.576)	−0.005 (−0.143, 0.134)
Gsm	18.562 (16.28, 20.844)	0.789	18.174 (16.078, 20.270)	−1.717 (−3.269, −0.165)	18.824 (16.589, 21.060)	0.021 (−0.093, 0.134)	18.444 (16.323, 20.564)	−1.814 (−3.319, −0.309)	0.072 (−0.035, 0.178)
Glr	6.862 (5.943, 7.781)	0.903	6.300 (5.561, 7.038)	−0.335 (−0.834, 0.164)	6.77 (5.879, 7.661)	−0.099 (−0.139, −0.060)	6.216 (5.51, 6.923)	−0.369 (−0.826, 0.089)	−0.058 (−0.091, −0.026)
Ga	11.950 (10.192, 13.707)	0.840	11.662 (10.218, 13.105)	−1.386 (−2.729, −0.044)	11.811 (10.315, 13.306)	−0.051 (−0.152, 0.049)	11.714 (10.323, 13.105)	−1.349 (−2.614, −0.083)	0.004 (−0.077, 0.086)

Note: Values in bold indicate p<.01. The λ1(std) column contains loadings that have been standardized with respect to age- and age squared- partialled variances. The linear factor solutions (both unstandardized and standardized) for the three subsamples have congruence coefficients with one another that are all greater than .97, suggesting that the solutions are very similar (Jensen, 1998). Although the parameters are not reported here, all models included the terms α₁[x] · age and α₂[x] · age² to account for the age trends in the broad abilities depicted in Figure 5.

Results from the nonlinear model include terms corresponding to ability level modification of the factor loadings (λ₂) that were negative for all abilities and statistically significant for 4 of 7 abilities in the school age subsample, 2 of 7 abilities in the college and university subsample, and 5 of 7 abilities in the adult subsample, a finding consistent with ability-differentiation. Results from the age-modification model include terms corresponding to age modification of factor loadings (λ₃) that were statistically significant for 2 of 7 abilities in the school age subsample, 1 of 7 abilities in the college and university subsample, and 3 of 7 abilities in the adult subsample. Interestingly, these significant λ₃ terms were in the directions opposite to those predicted by the age differentiation-dedifferentiation hypothesis, and instead indicate a pattern of larger factor loadings with childhood development and smaller factor loadings with adult aging. The ability differentiation hypothesis is therefore supported by these data, but the age differentiation-dedifferentiation hypothesis is not supported (instead, an age dedifferentiation-differentiation pattern seems to be evident). Similar patterns persisted when the nonlinear (λ₂) and age-modification (λ₃) terms were estimated in a single model.

Parameters from the full model for the three subsamples are reported in Table 6. It can be seen that there was very little evidence that ability differentiation was modified by age, as the corresponding terms were only significant for 2 of 7 abilities in the school age subsample (and in opposite directions to one another), 1 of 7 abilities in the college and university subsample, and 0 of 7 abilities in the adult subsample. Note that because the main effects of age were controlled for, and because age and g were centered at their means, multicollinearly was greatly reduced⁷ and the estimates for the λ₁, λ₂, and λ₃ parameters were very similar to those from the models fit in the intermediate steps (reported in Table 5). That is, the patterns of results in the full model were again consistent with ability differentiation and inconsistent with age differentiation-dedifferentiation, with some indication of an age dedifferentiation-differentiation pattern.

Table 6.

Parameter Estimates (and 99% Confidence Intervals) from Full Model.

Parameter Coefficient on	υ	α1 age	α2 age2	λ1 g	λ2 g2	λ3 age · g	λ4 age · g2	σ2u
School Age Subsample
Gc	508.884 (507.87, 509.898)	5.529 (5.31, 5.748)	−0.347 (−0.398, −0.295)	10.941 (10.241, 11.64)	−1.175 (−1.628, −0.722)	0.447 (0.255, 0.639)	−0.115 (−0.253, 0.023)	78.640 (70.246, 87.035)
Gv	502.444 (501.75, 503.138)	1.972 (1.795, 2.149)	−0.133 (−0.168, −0.098)	3.972 (3.511, 4.434)	−0.098 (−0.489, 0.294)	0.189 (0.052, 0.326)	0.001 (−0.139, 0.141)	54.893 (50.478, 59.307)
Gf	506.67 (505.676, 507.665)	4.409 (4.163, 4.655)	−0.457 (−0.514, −0.401)	11.348 (10.697, 11.998)	−0.714 (−1.136, −0.292)	0.021 (−0.157, 0.199)	−0.153 (−0.274, −0.033)	87.806 (78.986, 96.625)
Gs	513.409 (512.298, 514.521)	8.523 (8.226, 8.819)	−0.678 (−0.74, −0.616)	8.696 (7.884, 9.508)	−0.859 (−1.503, −0.215)	0.035 (−0.197, 0.268)	0.102 (−0.080, 0.284)	206.436 (191.689, 221.183)
Gsm	509.163 (507.954, 510.372)	4.928 (4.62, 5.235)	−0.436 (−0.504, −0.369)	12.043 (11.165, 12.92)	−1.127 (−1.804, −0.45)	0.193 (−0.032, 0.418)	0.071 (−0.094, 0.235)	203.517 (187.98, 219.055)
Glr	502.686 (502.316, 503.057)	1.499 (1.416, 1.583)	−0.169 (−0.188, −0.15)	3.772 (3.518, 4.026)	−0.143 (−0.311, 0.025)	0.051 (−0.015, 0.116)	0.023 (−0.026, 0.072)	11.773 (10.351, 13.194)
Ga	504.237 (503.594, 504.881)	2.121 (1.965, 2.276)	−0.193 (−0.226, −0.16)	5.63 (5.173, 6.087)	−0.342 (−0.684, 0.001)	0.124 (−0.011, 0.259)	0.119 (0.008, 0.23)	52.006 (47.671, 56.341)
College and University Subsample
Gc	545.207 (542.721, 547.693)	1.991 (1.042, 2.941)	−0.096 (−0.358, 0.166)	8.643 (6.663, 10.624)	−2.112 (−3.46, −0.764)	0.318 (−0.553, 1.189)	−1.188 (−1.807, −0.569)	92.832 (70.688, 114.977)
Gv	513.411 (511.7, 515.122)	0.425 (−0.128, 0.977)	−0.061 (−0.227, 0.105)	5.274 (4.248, 6.300)	−0.855 (−1.619, −0.091)	−0.148 (−0.555, 0.259)	−0.069 (−0.343, 0.206)	51.012 (40.346, 61.679)
Gf	526.831 (525.081, 528.581)	0.123 (−0.646, 0.893)	−0.081 (−0.295, 0.133)	8.071 (6.715, 9.427)	−1.680 (−2.631, −0.728)	−0.122 (−0.787, 0.543)	0.322 (−0.086, 0.731)	49.804 (37.141, 62.467)
Gs	547.456 (544.195, 550.717)	−0.442 (−1.568, 0.684)	0.134 (−0.204, 0.472)	9.274 (6.911, 11.636)	−0.767 (−2.441, 0.906)	0.002 (−0.814, 0.818)	0.217 (−0.334, 0.768)	289.708 (236.368, 343.048)
Gsm	532.04 (529.055, 535.025)	−0.002 (−1.154, 1.15)	0.207 (−0.121, 0.534)	9.425 (7.133, 11.718)	−0.626 (−2.008, 0.757)	0.030 (−0.841, 0.901)	−0.367 (−0.926, 0.192)	231.873 (191.473, 272.272)
Glr	510.558 (509.37, 511.747)	0.062 (−0.323, 0.446)	−0.033 (−0.153, 0.088)	4.078 (3.222, 4.934)	−0.448 (−1.019, 0.122)	0.101 (−0.215, 0.416)	−0.079 (−0.221, 0.064)	20.554 (15.768, 25.34)
Ga	518.615 (516.788, 520.443)	0.603 (−0.083, 1.29)	−0.067 (−0.234, 0.100)	5.646 (4.423, 6.868)	−0.861 (−1.821, 0.099)	0.193 (−0.43, 0.817)	−0.479 (−1.017, 0.06)	62.483 (49.917, 75.05)
Adult Subsample
Gc	544.984 (541.637, 548.33)	0.100 (−0.025, 0.225)	−0.01 (−0.016, −0.005)	24.156 (20.746, 27.566)	−7.081 (−8.9, −5.262)	−0.186 (−0.349, −0.022)	0.150 (0.039, 0.261)	121.872 (98.559, 145.185)
Gv	506.554 (505.151, 507.956)	−0.177 (−0.239, −0.116)	−0.004 (−0.006, −0.001)	6.251 (5.105, 7.398)	−0.801 (−1.741, 0.139)	−0.061 (−0.117, −0.004)	−0.012 (−0.064, 0.04)	62.185 (52.704, 71.667)
Gf	508.823 (506.066, 511.581)	−0.458 (−0.575, −0.341)	−0.008 (−0.013, −0.004)	17.338 (15.365, 19.312)	−2.982 (−4.393, −1.57)	−0.083 (−0.179, 0.013)	0.065 (−0.018, 0.147)	112.324 (93.572, 131.077)
Gs	525.738 (522.669, 528.808)	−0.823 (−0.952, −0.695)	−0.009 (−0.014, −0.004)	17.525 (14.95, 20.099)	−4.574 (−6.683, −2.465)	−0.077 (−0.228, 0.073)	0.029 (−0.095, 0.153)	291.726 (246.674, 336.777)
Gsm	515.518 (512.334, 518.702)	−0.338 (−0.466, −0.209)	−0.003 (−0.008, 0.002)	18.308 (16.206, 20.41)	−1.915 (−3.505, −0.326)	0.011 (−0.103, 0.125)	−0.002 (−0.096, 0.091)	258.337 (223.104, 293.57)
Glr	502.739 (501.826, 503.652)	−0.160 (−0.199, −0.121)	−0.002 (−0.004, −0.001)	6.184 (5.476, 6.892)	−0.361 (−0.857, 0.135)	−0.081 (−0.114, −0.049)	0.013 (−0.016, 0.042)	12.133 (9.591, 14.675)
Ga	506.209 (504.166, 508.253)	−0.480 (−0.557, −0.403)	−0.008 (−0.011, −0.005)	11.487 (10.171, 12.804)	−1.161 (−2.3, −0.023)	−0.038 (−0.118, 0.043)	0.062 (−0.007, 0.131)	77.088 (62.001, 92.174)

Note: Values in bold indicate p<.01. The full model is given by Equation 5 in the text.

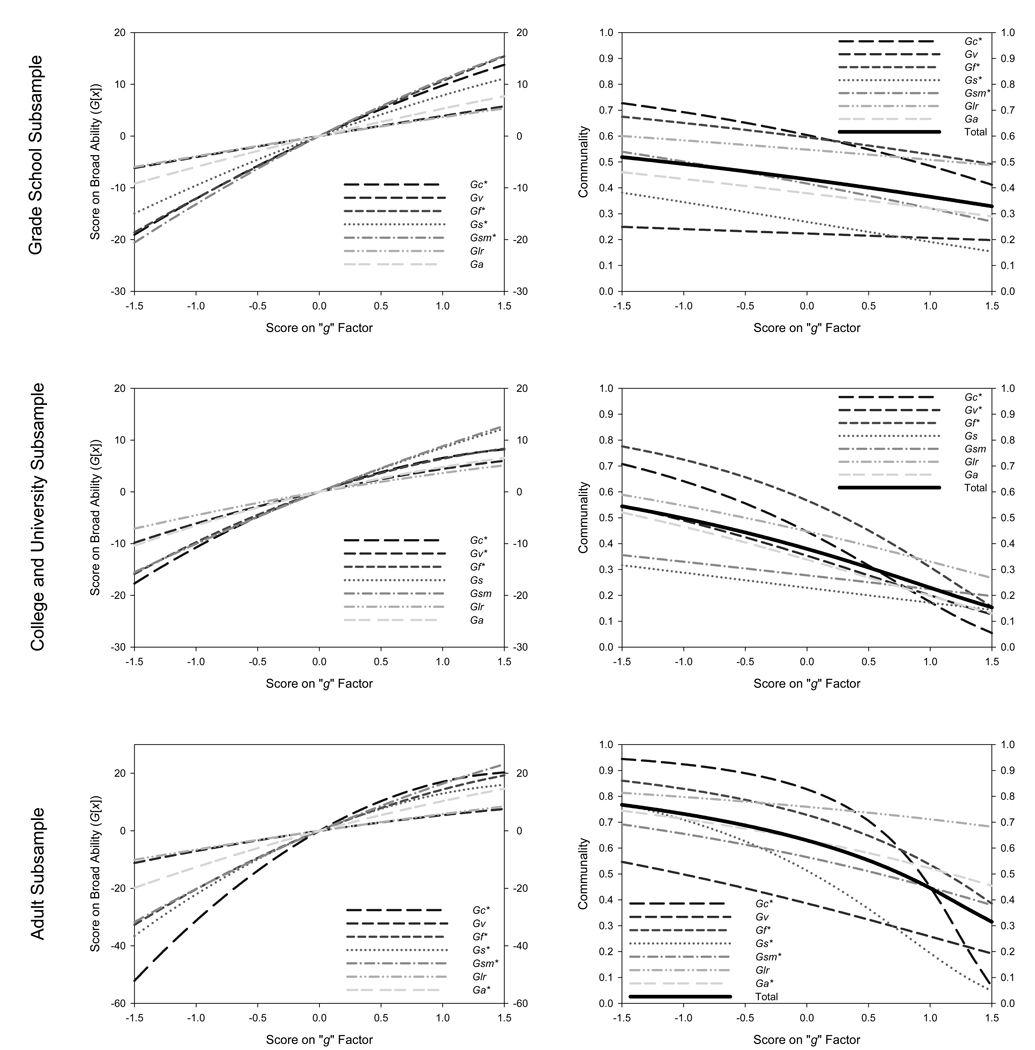
Figure 6 illustrates the findings with respect to ability differentiation in the 3 subsamples (based on parameter estimates from the full model). The left column of plots displays the model implied quadratic relations between the broad abilities and the common (g) factor. It can be seen that because the trends are concave downward, the slopes of the functions diminish with increasing ability level (note that because g is on the Z metric, the ability levels in these plots range from the 7^th percentile to the 93^rd percentile). These trends can also be expressed as communalities for the broad abilities, where communality is defined as the percentage of age-independent variance in the ability that is accounted for the common factor (see Appendix B for formulas). In the right column it can be seen that, consistent with the ability differentiation hypothesis, the communalities decrease with ability level in all cases. This is also apparent in the total proportion of standardized age-independent variance in the broad abilities that is accounted for by the common factor. Consistent with ability differentiation, this proportion differs by between approximately twenty and forty-five percentage points, in the range from the 7^th percentile to the 93^rd percentile of functioning.

Figure 6.

Model implied relations between the score on the “g” factor and each broad ability (left column), and communalities in each broad ability (right Colum), in grade school (top row), college and university (middle row), and adult (bottom row) subsamples. Communalities are based on age- and age squared- partialled variances. It can be seen that, in all panels, the “g” factor accounts for decreasing amounts of variance in the broad abilities at increasing ability levels. Total refers to the total proportion of standardized variance in all of the broad abilities accounted for by the higher order g factor. * indicates that the negative quadratic coefficient, λ₂, was significant at p<.01.

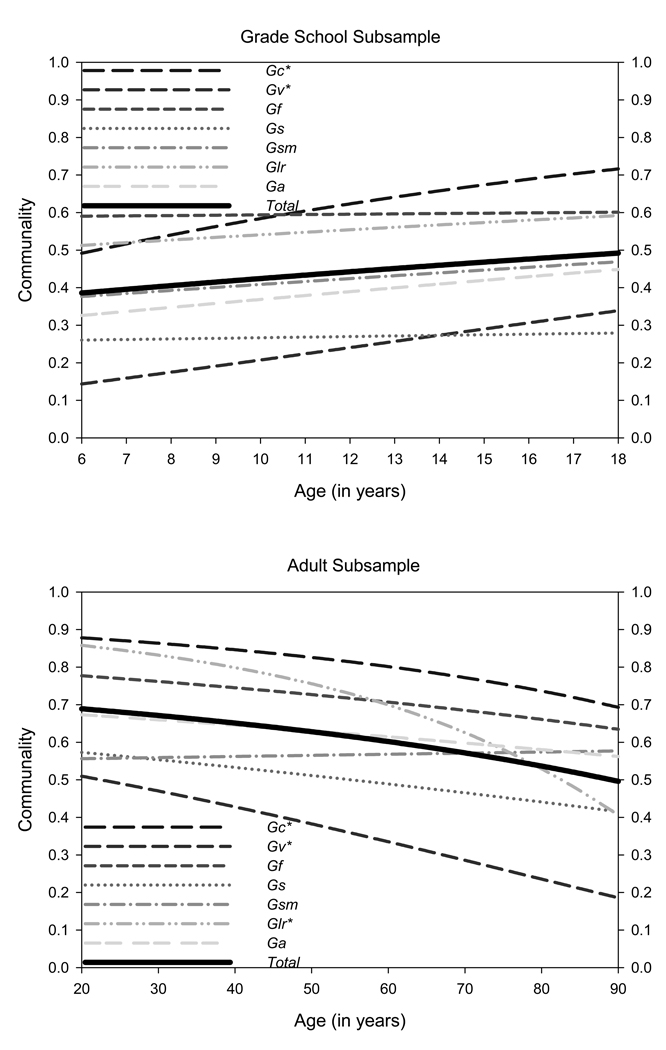
Figure 7 illustrates the findings with respect to age trends in broad ability communalities in the child and adult subsamples (based on parameter estimates from the full model). Although the trends are less apparent than those that are displayed in Figure 6, the general pattern is one of increasing communalities in childhood (significant age trends in the loadings of Gc and Gv on g), and decreasing communalities in adulthood (significant age trends in the loadings of Gc, Gv, and Glr on g).

Figure 7.

Model implied relations between age and communalities in each broad ability) in grade school (top) and adult (bottom) subsamples. Communalities are based on age- and age squared-partialled variances. Contrary to the age differentiation-dedifferentiation hypothesis, there is some evidence that communalities increase in childhood and decrease in adulthood. Total refers to the total proportion of standardized variance in all of the broad abilities accounted for by the higher order g factor. * indicates that the coefficient λ₃ was significant at p<.01.

Finally, it is of note that in addition to the models reported here, a number of higher order mediation models (examples of linear forms of which can be found in Salthouse & Ferrer-Caja, 2003, and Salthouse, 1998) were considered. Such models consider the common higher order (g) factor as a mediator of the age-related influences on each ability (ability-differentiation can therefore be conceptualized with respect to absolute ability level instead of age-controlled ability level), with direct effects from age to the individual abilities allowed as needed. These models produced very similar patterns of results to those reported here (weaker factor loadings at higher ability levels, stronger factor loadings with childhood age, and weaker factor loadings with adult age). Such models are suspect, however, as they may potentially produce nonlinear factor loading estimates as artifacts of the nonlinear age-trends that are apparent in Figure 5. These results are therefore not reported.

Discussion

Summary of Findings

The results reported here provide consistent support for the hypothesis that cognitive abilities are less related to each other at higher ability levels, and less clear support for hypotheses that cognitive abilities systematically change in their degrees of independence across the human lifespan. In fact, contrary to the conventional age differentiation-dedifferentiation hypothesis that abilities become less related with childhood development and more related with adult aging, there was partial evidence of the reverse- some factor loadings showed increases in their magnitudes with childhood age and decreases in their magnitudes with adult age.

In contrast to most previous investigations of age differentiation and ability differentiation-dedifferentiation, the current study examined age modification and ability level modification of ability relations on continuous bases, and across close to the entirety of the lifespan. This was achieved using nonlinear factor analytic methods that enabled for more flexible examinations of hypotheses that are by their very nature nonlinear. While it has been frequently acknowledged that such hypotheses are nonlinear in nature, it seems that there is only one previous examination that has used nonlinear functions to test them. Der and Deary (2003) fit polynomial regressions predicting scores on a test of reasoning from simple and complex reaction times, and found some support for a quadratic relationship between reasoning and simple reaction time in the direction predicted by the ability differentiation hypothesis.

Explanations for Ability Differentiation

Why would abilities be more independent at higher ability levels? One possible explanation might be that the components of higher order cognition and knowledge are hierarchically structured (hierarchical in this context is used somewhat differently from hierarchical factor analytic models, although a parallel likely exists), such that the diverse array of complex behaviors are the products of a more narrow range of simpler behaviors/capacities. Given that more complex behaviors can only be expressed by those with the capacity for simpler component behaviors, those operating at higher levels of functioning can specialize within a subset of a wider range of behaviors, and the profiles of these higher functioning individuals will be more heterogeneous across individuals. This proposal might be considered a form of sampling theory (Thurstone, 1938), in which lower ability individuals have a narrower pool of cognitive resources and processes on which to base their behaviors, whereas higher ability individuals have a more diverse pool of specialized resources and processes on which to base their behaviors.

Such a perspective is compatible with Spearman’s (c.f. Detterman and Daniel, 1989) conception that at lower ability levels, a scarcity of cognitive resources constrains a wide range of disparate behaviors, but that at higher ability levels, cognitive resources are profuse, and cognitive functioning is instead constrained by domain specific resources. Deary et al. (1996, p. 124) have made the similar suggestion that “intelligence is spent and invested like money: at low levels of income, increments are predictably directed toward housing, food, clothing, and the care of children. At higher levels of income spending is more differentiated: disposable income may be directed at a near-infinite range of targets. At higher levels of intelligence, ability is probably more directed by interest, motivation, and choice.”

While these related theoretical explanations are intuitively very plausible and consistent with current conceptualizations of complex thought, it is unclear why they would not result in age-related decreases in ability interrelations during childhood and age-related increases in ability relations during adulthood. Particularly, because ability differentiation was supported, and because mean ability levels increase with childhood age and decrease with adult age, one would expect age differentiation-dedifferentiation to have been supported, albeit as an epiphenomenon. One possible explanation for these paradoxical findings is that the age-related growth and decline of cognitive abilities is a socio-evolutionarily produced property of the human cognitive system that has resulted from the age-related rise and decline of cognitive demands within the environment. Given this assumption, a higher level of cognitive functioning that is achieved during later childhood does not result in excess cognitive “capital,” because of increased environmental demands for higher cognitive performance during later ages. While this hypothesis is purely speculative, it is consistent with the standard practice of assessing abilities, and diagnosing impairments, relative to individuals’ same-aged peers.

Explanations for (Lack of) Age Differentiation-Dedifferentiation

The lack of support for the conventional age differentiation-dedifferentiation hypothesis is, by itself, of important theoretical significance. A number of contemporary conceptualizations of child and adult development posit specific age-based mechanisms that should result in childhood differentiation followed by adult dedifferentiation, so much so that the age differentiation-dedifferentiation hypothesis has been referred to as “the most comprehensive proposition about lifespan changes in variability” (Lindenberger & von Oertzen, 2006, p. 303).

The work of Li, Lindenberger and colleagues (e.g. Li & Lindenberger, 1999), has suggested that diverse sources of growth during childhood lead to age-related increases in ability independence, whereas common constraints on functioning in adulthood lead to age-related decreases in ability independence. They have posited that a likely mechanism leading to such constraints is the age-based pattern of changes in the efficiency of neurotransmission (of dopamine for example) in diverse areas of the brain, and have demonstrated using computational models how such a mechanism would result in age-based differences in ability interrelations. Functional brain imaging work (e.g. Cabeza, 2002) has built upon such conceptualizations in positing that age-related decreases in the specialization of functioning in adult brains may explain both patterns of age-dedifferentiation of cognitive abilities and age-related hemispheric asymmetry reductions in brain activation patterns during performance of cognitive tasks (for an integrated discussion of these two bodies of literature, see Lindenberger & von Oertzen, 2006). If the age differentiation-dedifferentiation hypothesis continues to lack substantiation in future research, such theoretical conceptualizations will likely need to be re-examined and potentially revised.

The finding that some factor loadings increased with childhood age was somewhat unexpected and is in need of replication. While inconsistent with the above reviewed perspectives, this finding is consistent with the perspectives of Dickens (unpublished manuscript; also see Dickens & Flynn, 2001) and van der Maas et al. (2006), who posit developmental strengthening, if not emergence, of the positive relations among abilities as the result of dynamic feedback processes between individuals and environments and among the different abilities within individuals.

The finding that some factor loadings decreased with adult age was similarly unexpected and also in need of replication. While not necessarily evidence against “common cause” hypotheses (e.g. Baltes & Lindenberger, 1997) this finding is, however, consistent with the presence of “multiple co-occurring causal mechanisms” that differentially contribute to cognitive decline in different abilities (Buckner, 2004). Investigations based on longitudinal changes will likely provide distinct advantages in discriminating between the specificity versus generality of the cognitive changes that occur with development and aging (see Future Directions section).

Limitations

Measurement

One of the major strengths of the current study is that test scores were scaled using the Rasch measurement model. When the assumptions of the Rasch model are met, Rasch scaling places scores on a meaningful metric with interval properties that is largely unaffected by the distribution of item difficulties composing the measure. One major assumption, that cannot be fully tested, however, is that the items within a test all represent the same dimension of individual differences. If, alternatively, the tests actually measure different abilities at different difficulty levels, what appear to be nonlinear effects might actually be artifacts of differential representations of these different abilities at different areas of the scales. This is a limitation of both the Rasch model and sum-based scoring methods.

Age-Based Subsamples

The current study was based on separate analyses of school age, college and university, and adult subsamples (although see the online supplement to this paper for the results of an alternative approach). Comparisons related to differentiation were not made across the subsamples, only within them. Given that the age differentiation-dedifferentiation hypothesis proposes two distinct phases of ability structure transformation corresponding to child development and adult aging, this approach fit the analytical questions quite well. That is, although no direct comparisons between groups were made, there were no specific hypotheses requiring such comparisons.

Use of Polynomial Functions

There is no reason to expect polynomial (e.g. quadratic⁸) functions to be the most precise functions for characterizing the nonlinear relations of interest. Polynomial functions were advantageous for the current examination because 1) they are each composed of a linear component and deviations from a linear component (e.g. the quadratic term), allowing for direct evaluation of evidence for loadings that depart from linearity, 2) they are easily programmed in currently available factor analytic software (e.g. Mplus), and 3) they are well known for being able to closely approximate a wide variety of functions within a bounded range. Polynomials have distinct disadvantages, however, when the goal is to extrapolate beyond the range of the data. Moreover, while the quadratic (being composed of a linear and a nonlinear component) has interpretational advantages, higher order polynomials are often substantively opaque and difficult to interpret. Other functions that could be considered in future research on differentiation include the exponential, logistic, and Gompertz curves (e.g. Neale & McArdle, 2000).

Use of a Hierarchical Representation of Cognitive Ability Structure

Any structural representation of cognition is merely a model that parsimoniously approximates observable and unobservable patterns. The g factor may not be a reifiable construct, but it is a parsimonious way of representing the higher order patterns of relations among cognitive abilities. In the current paper, direct evidence was not provided for the existence of a g factor, and in fact, there are contemporary representations of cognitive ability structure (e.g. Snow, Kyllonen, & Marshelek, 1984, van der Maas et al., 2006) that do not assume a higher order g factor. Moreover, the original Horn-Cattell conceptualization of fluid and crystallized intelligence did not include a higher order g factor, and has thus sometimes been termed a “truncated hierarchy” (Jensen, 1998, p. 124). Questions regarding ability and age differentiation can potentially be addressed under such frameworks as well, and the hierarchical framework chosen here was done so mostly out of convention and ease of presentation. For a discussion of evidence for a higher order g factor see Jensen (1998).

Future Directions

Correlated Longitudinal Changes

The differentiation-dedifferentiation hypotheses are primarily based on developmental theories that posit diverse learning processes operating over child development and broad psychological constraints operating over adult aging. The arguments have been that diverse, domain specific, processes influence cognitive growth, causing abilities to be less related to one another with childhood age, and broad, domain general, processes influence cognitive decline, causing abilities to be more related to one another with adult age. Cross-sectional comparisons of different individuals at different ages, however, are only proxies for the processes that occur within individuals as they change over time (and possibly poor proxies at that). More direct tests of the domain specificity versus generality of developmental changes would be derived from examinations of the extents to which actual longitudinal cognitive changes in different cognitive domains are correlated with one another. Such questions have been partially addressed in some past work (e.g. Blaga et al., 2009; Hertzog, Dixon, Hultsch, & MacDonald, 2003; Wilson et al., 2002), and are a primary theme of my ongoing research.

Additional Modifiers

After finding that the linear relations among cognitive measures were smaller in magnitude in higher ability groups, Detterman and Daniel (1989) questioned whether “one factor analytic model [can] adequately represent high and low ability subjects simultaneously.” Here it was demonstrated that while the magnitude of structural relations among cognitive abilities indeed differs according to ability level, this phenomenon is well described by a single, albeit nonlinear, factor analytic model that applies to a broad and nationally representative range of ability levels. Such a model is also advantageous in its ability to simultaneously consider multiple modifiers of ability interrelations. A natural extension of the current project might therefore be to consider additional variables as potential modifiers in multivariate structural models of cognitive ablities.

In fact, contemporary interactive factor analytic models have recently been applied to investigations of the genetic and environmental sources of individual differences in cognitive abilities. Turkheimer, Harden, and colleagues (Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman, 2003; Harden, Turkheimer, & Lohelin, 2007) have demonstrated that cognitive abilities are more heritable at higher levels of socioeconomic status, where environmental constraints are presumably less influential, and genetic propensities (and genotype-induced self-selection into congruent environments) can become more fully actuated. Interestingly, because higher socioeconomic status is often related to higher ability levels, this phenomenon appears to be somewhat discordant with the hypothesis that heritability decreases with ability level. However, if these two separate mechanisms are simultaneously operating, they may suppress one another, and it is therefore imperative to consider them simultaneously.

Applied Research

The strong and consistent support for ability differentiation has significant implications for research on selection and human capital. One major implication concerns the use of general ability composite scores. The current findings suggest that for higher scoring individuals, general composite scores are less adequate reflections of individuals’ cognitive capabilities across diverse domains. It is well-accepted in the personnel selection literature that broad ability (domain-specific) scores are comparatively poor predictors of job performance beyond the strong predictive utility of general cognitive ability composite scores (Gottfredson, 2003; Hunter & Schmidt, 1996; Ree & Earles, 1992). However, in light of the current findings, one might expect that broad ability scores have higher predictive utility, and general ability scores have lower predictive utility, at higher ability levels. While Coward and Sackett (1990) have concluded against nonlinearity of ability-performance relationships, future investigations are likely to benefit from new methods and more diverse predictors and outcomes. In fact, very recently, Park, Lubinski, & Benbow (2007) found that the math versus verbal “tilt” of intellectually talented (top 1%) adolescents’ SAT scores was strongly predictive of literary achievement and scientific-technical innovation over approximately 25 years of development, suggesting that domain-specific capabilities are indeed very important for predicting professional performance among high ability individuals.

Conclusion

In summary, nonlinear factor analytic models were applied to carefully scaled data on seven well-established cognitive abilities measured in a large nationally representative lifespan sample of individuals. Consistent with the ability differentiation hypothesis, results indicated that a general factor accounted for a decreasing amount of (and proportion of) individual differences in the abilities at higher ability levels, suggesting that at higher ability levels more specific cognitive mechanisms may be less constrained and more prominently expressed. However, results were inconsistent with the age differentiation-dedifferentiation hypotheses that the magnitudes of ability relations decrease with childhood age and increase with adult age. There was rather some evidence to suggest that abilities become more related with childhood age, and less related with adult age. It is proposed that future examinations of age differentiation-dedifferentiation focus on the multivariate relations among individual differences in rates of longitudinal changes.

Appendix A: Example Mplus Script

TITLE:

This is an example script for the full model (Equation 5) applied to the adult subsample. Scripts for other models, including a multiple group version of this model, are available from the author upon request.

DATA:

FILE IS "wj3.dat";

VARIABLE:

NAMES ARE

Gc Gv Gf Gs Gsm Glr Ga age agesq group SUBWT;

MISSING ARE ALL (−9999);

WEIGHT IS SUBWT;

USEOBSERVATIONS ARE (group EQ 3); !Limit Analyses to Adult Group

USEVARIABLES ARE

Gc Gv Gf Gs Gsm Glr Ga age agesq;

ANALYSIS:

TYPE IS RANDOM; ALGORITHM IS INTEGRATION;

MODEL:

!Regress G[x] on age and age^2

Gc ON age agesq; !(alpha1, alpha2)

Gv ON age agesq;

Gf ON age agesq;

Gs ON age agesq;

Gsm ON age agesq;

Glr ON age agesq;

Ga ON age agesq;

!freely estimate linear components of loadings of G[x] on g

g BY Gc*; !(Lambda1)

g BY Gv*;

g BY Gf*;

g BY Gs*;

g BY Gsm*;

g BY Glr*;

g BY Ga*;

!Assign g unit variance to define its metric

g@1;

!Create Quadratic g component

gxg | g XWITH g;

!Create g by age interaction

gxA | g XWITH age;

!Create g-squared by age interaction

gxgxA | gxg XWITH age;

!Regress G[x] onto gxg, gxA, and gxgxA

Gc ON gxg gxA gxgxA; !(lambda2, lambda3, lambda4)

Gv ON gxg gxA gxgxA;

Gf ON gxg gxA gxgxA;

Gs ON gxg gxA gxgxA;

Gsm ON gxg gxA gxgxA;

Glr ON gxg gxA gxgxA;

Ga ON gxg gxA gxgxA;

OUTPUT: SAMPSTAT CINTERVAL;

Appendix B: Description of Equations for Calculating Instantaneous Communalities

In common factor analysis, communality (h²) is defined as the proportion of variance that an indicator shares with all other indicators of the factors on which it loads, or put another way, as the proportion of variance in the indicator explained by the common factors (also, generally termed R²). Communality can generally be written as:

$$h^2=\frac{\text{Shared Variance}}{\text{Shared Variance}+\text{Unique Variance}}$$ Eq. B1

A linear common factor model adhering to simple structure, such that each indicator G[x] only loads on one common factor, can be expressed as

$$G{[x]}_n=\mathrm{\upsilon }[x]+\mathrm{\lambda }[x]·g_n+u{[x]}_n,$$ Eq. B2

where the common factor g and the unique factor u[x] have variances σ²_g and σ²_u[x] respectively. υ[x] is an indicator-specific, person invariant, intercept that does not affect communality. Shared variance can be computed by squaring the slope of Equation B2 (λ[x]) and multiplying it by σ²_g, as follows

$$\text{Shared Variance}=\mathrm{\lambda }{[x]}^2·{{\mathrm{\sigma }}^2}_g.$$ Eq. B3

The communality of G[x] can then be written as

$${h^2}_{G[x]}=\frac{\mathrm{\lambda }{[x]}^2·{{\mathrm{\sigma }}^2}_g}{\mathrm{\lambda }{[x]}^2·{{\mathrm{\sigma }}^2}_g+{{\mathrm{\sigma }}^2}_{u[x]}}.$$ Eq. B4

The linear common factor model specified by Equation A2 can be expanded to include a quadratic loading, such that

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_2[x]·{g_n}^2+u{[x]}_n.$$ Eq. B5

The slope of this function can be found by taking its derivative, which is

$$G^{’}{[x]}_n={\mathrm{\lambda }}_1[x]+2·{\mathrm{\lambda }}_2[x]·g_n.$$ Eq. B6

Shared variance then becomes

$$\text{Shared Variance}={({\mathrm{\lambda }}_1[x]+2·{\mathrm{\lambda }}_2[x]·g_n)}^2·{{\mathrm{\sigma }}^2}_g,$$ Eq. B7

and the communality of G[x] becomes

$${h^2}_{G[x],g_n}=\frac{{({\mathrm{\lambda }}_1[x]+2·{\mathrm{\lambda }}_2[x]·g_n)}^2·{{\mathrm{\sigma }}^2}_g}{{({\mathrm{\lambda }}_1[x]+2·{\mathrm{\lambda }}_2[x]·g_n)}^2·{{\mathrm{\sigma }}^2}_g+{{\mathrm{\sigma }}^2}_{u[x]}},$$ Eq. B8

such that the communality is now “instantaneous” and conditional on the factor score of the individual on g. Note that the proportion of standardized variance in all of the indicators accounted for by their single common factor is the average of each individual indicator’s communality.

For an age modification model,

$$G{[x]}_n=\mathrm{\upsilon }[x]+{\mathrm{\lambda }}_1[x]·g_n+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n·g_n+u{[x]}_n,$$ Eq. B9

the instantaneous communality can be derived in a similar fashion, producing

$${h^2}_{G[x],{\mathit{\text{age}}}_n}=\frac{{({\mathrm{\lambda }}_1[x]+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n)}^2·{{\mathrm{\sigma }}^2}_g}{{({\mathrm{\lambda }}_1[x]+{\mathrm{\lambda }}_3[x]·{\mathit{\text{age}}}_n)}^2·{{\mathrm{\sigma }}^2}_g+{{\mathrm{\sigma }}^2}_{u[x]}}.$$ Eq. B10