Abstract
A dynamical biophysical model for the functioning of an epithelium is presented. This model integrates the electrical and osmotic behaviors of the epithelium, taking into account intracellular conditions. The specific tissue modeled is the human bronchial epithelium, which is of particular interest, as it is the location of the most common lethal symptoms of cystic fibrosis. The model is implemented in a modular form to facilitate future application of the code to other epithelial tissue by inputting different transporters, channels, and geometric parameters. The model includes pH regulation as an integral component of overall regulation of epithelial function, through the interdependence of pH, bicarbonate concentration, and current. The procedures for specification, the validation of the model, and parametric studies are presented using available experimental data of cultured human bronchial epithelium. Parametric studies are performed to elucidate a), the contribution of basolateral chloride channels to the short-circuit current functional form, and b), the role that regulation of basolateral potassium conductance plays in epithelial function.
Introduction
Several computational models have been published that describe the ion transport behavior of airway epithelia as distinct from osmotic effects, as recently reviewed by Warren and colleagues (1). There has also been work done to couple osmotic effects (cell volume change and transepithelial water transport) in epithelia with ionic movements (1–4). The general purpose of this article is to add to the previous work coupling to pH regulation, by creating a generalized osmoelectric pH model1 on a particular epithelial tissue of both scientific and medical interest, specifically the bronchial epithelium of the human airway. (We use the phrase “generalized osmoelectric” here to refer to water movement down an osmotic gradient that is created by ion movements, but proceeds along a separate pathway. In the literature to date, both “osmoelectric” and “electro-osmosis” are used to describe situations where water and charge movement are physically coupled and move along the same pathways.) The specific scientific purposes of this study are 1), to elucidate as well as possible the functioning of this tissue in the context of published data on ion transport mechanisms, including the effects of pH and varying Cl−, Na+, K+, and and permeability; and 2), to identify particular data that are necessary to achieve a comprehensive understanding of how ion transport gives rise to the overall functioning of the epithelium. Understanding these issues for one particular epithelium should be extendable to epithelial function in general. In medical application, the human bronchial epithelium (HBE) is chosen because it is the site of the most commonly lethal symptoms of cystic fibrosis (5).
The model described in this article is an extension of a previous version (3,4) from our laboratory. That model included only the combination of parameters necessary to maintain physiological concentrations, apical and intracellular volumes, and membrane potentials in airway epithelium. The relevant parameters were apical permeabilities for Na+ and Cl−, basolateral permeability for K+, and maximum fluxes through the sodium-potassium (NaK) pump and sodium-potassium-chloride cotransporter (NKCC).
In developing the specification of the model to HBE, particular attention is given to the cystic fibrosis transmembrane conductance regulator (CFTR) in normal and CF tissues, given its role in the disease and in regulatory function. The latter is yet to be completely understood (5). We note that this channel is also permeable to , and we introduce a model that takes into account transporters that carry and protons and evaluate intracellular pH, which is known to be involved in a variety of physiological processes.
Other improvements of the model were made based on findings reported in the literature. The basolateral membrane includes the sodium bicarbonate cotransporter (NBC) (6,7), the anion exchanger (AE), and the sodium hydrogen exchanger (NHE) (8). Cl− crosses the cell apical membrane through the CFTR even before it is stimulated (9) and also through other channels such as the calcium-activated chloride channel (10) and CLC2 (11). Cations flow through Na+-selective and cation-selective amiloride-sensitive epithelial sodium channels (ENaCs), and amiloride-insensitive cation channels (9). The CFTR is also permeable to , playing a role in apical pH regulation. Basolateral transporters contribute to the intracellular pH regulation. The catalyst carbonic anhydrase (CA) is also known to impact the flux rates of AEs and NBCs (12–14).
The version of the model introduced here adds to the previous version all of the permeation, transport, and regulatory mechanisms mentioned above, with one exception: the additional Cl− channels are merged with the CFTR into one model Cl−/ channel for the apical membrane. The reason for this is that the existing data for this tissue do not permit assignment of the relative contribution of the different Cl− channels.
Fig. 1 shows a schematic of the transport mechanism included in the model. The direction of the passive ionic transport obeys the electrochemical potential. The pump and other transporters (cotransporters and exchangers) are presented showing the direction in which their corresponding ions are most commonly carried.
Figure 1.
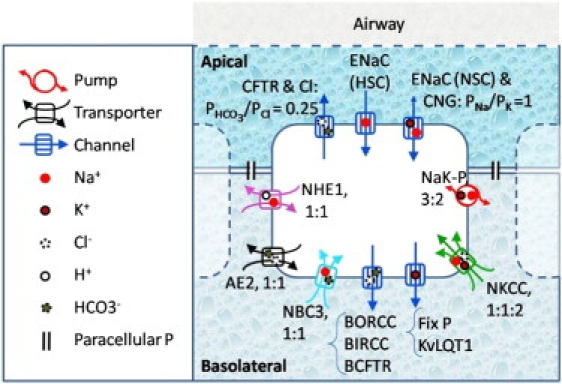
Ionic pathways taken into account in the model of HBE. Apical ion channels for Cl−, Na+, and K+ are considered, as are the basolateral Cl− and K+ channels. The basolateral NaK pump and the NKCC are reminiscent of the previous model. NHE, AE, and NBC are included in the version of the model introduced here. HSC, highly selective channel; NSC, nonselective channel; CNG, cyclic nucleotide-gated channel; NaK-P, sodium potassium pump.
In constructing computational and mathematical models, two distinct ways of using experimental data are required. The first use of experimental data is in building the model. In this stage, we refer to data to create hypotheses about how the system is organized and to decide on numerical parameters. In the second stage, we compare simulated data to experimental data to validate the model. To the extent feasible, data used for model construction should be obtained independently of data used for validation, but both sets should be obtained on precisely equivalent biological systems. However, it is not always possible to achieve this ideal. In particular, it is common practice in interpreting data from cell and tissue research to integrate observations from cells pertaining to different regions of the same organ (15–19), or to integrate knowledge about different tissues of similar functionality (6,16,20), to arrive at a comprehensive understanding of cell and tissue function. In the same manner, in constructing this model, we found it necessary to incorporate data from an airway region broader than the HBE. This extrapolation is necessary in situations where characterization of the targeted tissue region and cells is not completely available. Although some of the parameters are derived from different sections of the airway, in this article, we validate the model entirely by comparison to experimental data from the HBE.
For validation, we use experimental data from the short-circuit current (Isc) crossing HBE monolayers. We provide properties of the system not experimentally available, such as the reversal potential for each ionic species over time and apical and basolateral fluxes. The contributions of the basolateral Cl− channels (21,22) and the voltage-gated K+ channels (23,24) to the Isc are also addressed, to provide the most comprehensive information possible about how all transport mechanisms contribute to tissue function. As a direct improvement over our previous model, the version described here is able to reproduce the Isc after sequential addition of amiloride, forskolin, and bumetanide within the experimental values (16), whereas the former would predict such Isc to be ∼70% lower, regardless of the combination of parameters chosen for the channel permeabilities, pump, and transporter. We conclude that it is important to consider HCO3− when studying the electrophysiology of the HBE; the presence of voltage-gated K+ channels in the basolateral membrane does not impact the system under the experimental setups presented, and the basolateral Cl− channels modify the Isc transient response to forskolin.
Model Description
Overview
The model as applied to short-circuit experiments consists of a monolayer of polarized cells, separating the apical from the basolateral region, with no difference in electrical potential between them. Both regions are considered mathematically to be of infinite volume, maintaining constant concentrations. The ions cross the membranes via ion channels, the NaK pump, and transporters. Water is driven across the epithelium by osmotic forces, resulting in intracellular volume changes. Open-circuit and in vivo simulations will be treated in a subsequent work. The cells used for experimental measurements were required to have been maintained alive for >20 days, during which time the extracellular bath was changed every other day (16). Therefore, we assume in this study that the major physiological functions are intact. That includes mechanisms that consume energy, such as ATP use by the NaK pump, which is essential for maintenance of high intracellular K+ and low intracellular Na+.
Ion channels, pumps, and transporters included in the model
The CFTR functions as a Cl channel, but is also permeable to , with a selectivity ratio of ∼4:1 Cl/HCO3 (25). Low extracellular Cl results in decreased CFTR permeability to both Cl and HCO3 (26).When the CFTR is not stimulated, it still presents a residual permeability (9). The apical cation channels taken into account are of three kinds: a nonselective (equally permeable to Na+ and K+) amiloride-insensitive channel; a nonselective amiloride-sensitive channel; and a highly selective amiloride-sensitive Na+ channel.
Two transporters in the basolateral membrane are responsible for maintaining intracellular concentrations and membrane potentials: the NaK pump and the NKCC. The latter also plays a role in restoring the intracellular volume in several epithelia (27). The basolateral K+ permeability varies between secreting and nonsecreting states (3,4). In Calu cells, the total basolateral K+ permeability is a combination of basal, calcium-activated, and cAMP-stimulated voltage-gated potassium channels (KvLQT1) (15,24). The latter consists of a voltage-gated channel expressed in the lungs and several other tissues. Its permeability is enhanced by membrane depolarization, and doubled by forskolin (28).
Three transporters known to be present in ciliated cells of the HBE and related to pH regulation are the cation exchanger NHE1, extruding one proton per Na+ absorbed; the anion exchanger AE2 (8); and the sodium bicarbonate cotransporter NBC4 (6,7). The AE2 exchanges Cl− for in either direction and is finely regulated by intracellular pH. It is less sensitive to extracellular pH than to intracellular pH (29). CA inhibition reduces the fluxes of AEs (12) and NBCs (13,14). Based on Fischer et al. (21), three kinds of basolateral Cl− channels are included: an outward rectifier (BORC), sensitive to cellular volume; an inward rectifier (BIRC); and a small population of forskolin-sensitive CFTR-like channels (BCFTR). In a parallel study using Isc and transepithelial currents, Itani et al. (22) reported the presence of basolateral Cl currents that are not sensitive to volume, not CFTRs, and very sensitive to intracellular pH. These seem to be BIRCs.
In constructing the model, we sometimes refer to electrophysiological data for the particular transporter or channel type as expressed in cell types different from that modeled in this article. In those cases, we retain the dependence on concentrations, membrane potential, and pH that describe the original data, but modify the postulated density of the protein to fit the data in our tissue.
All pathways are shown in Fig. 1. Table S1 in the Supporting Material summarizes the passive flux membrane proteins and Table S2 lists the transporters included in the basolateral membrane.
Model equations
The transport of ions across animal cell membranes occurs due to electrochemical potential through ion channels, or is mediated by pumps and transporters. For many channels, the ionic currents are well described macroscopically using the constant-field flux equation (30).
| (1) |
where (mol m−2 s−1) is the passive flux for ion i from compartment x to y, zi is the valence of the ion i, F = 96,500 C mol−1 is the Faraday constant, Vm (V) is the membrane potential difference, R = 8.314 J mol−1 K−1 is the gas constant, T = 310 K is the temperature, and Ci,x (or Ci,y) (mol m−3) is the concentration of the ion i in compartment x (or y). The permeability, Pi (m s−1), is evaluated as a combination of several components:
| (2) |
where superscript “f” stands for fixed permeability, “r” for regulated channels, and “ns” for nonselective channels. The subscript j identifies the several nonselective channels, and, finally, αi,j is the coefficient that correlates the selectivity of the channel j to the ionic species i.
When evaluating transport mediated by the NaK pump or other transporters, the flux is dependent on the ionic concentrations in the compartment the ionic species are being carried from, the number of binding sites, the half-saturation constants, the membrane potential, and intracellular pH. The generic functional form used for all transporters is
| (3) |
The flux of the transporter Jtrp is evaluated as the product of four terms: the amplitude imposed by Jmax, proportional to the density of active membrane proteins; the contribution from the concentrations and binding site properties, represented by the Michaelis-Menten term; a linear relation with membrane potential prescribed by the coefficients A (1/V) and B; and, finally, the dependency on intracellular pH, expressed by the last term of Eq. 3. The exponent cfi is the Hill coefficient and stands for the number of binding sites, whereas K is the half-saturation constant. The constant Kp is equal to the value of pH for which half of the maximum flux occurs, whereas the coefficient ap represents the sensitivity of the transporter to intracellular pH change. The combination of coefficients as presented in Table S2 will maintain the same functional form used for the NKCC and NaK pump in our previous model (3,4). The pH dependence became necessary for better description of the AE2 (29). The flux of each ionic species i due to a transporter (trp) depends on the corresponding number of the specific ions carried by it:
| (4) |
The coefficient ni is the same as cfi in the case of independent binding sites. The use of two separate coefficients allows the implementation of transporters with electrophysiology not perfectly described by the Michaelis-Menten kinetics. The direction of each ionic species is dependent on the compartment of origin x. For example, if x corresponds to the basolateral region, the ion is being carried into the cell. In the case of bidirectional fluxes (complete reversibility), the transporter is defined twice (as if there were two), switching the index identifying the compartment of origin. That was the case for NKCC and AE2.
The regulatory mechanism for the NKCC was maintained as in the previous version of the model (3,4).
| (5) |
The superscripts t and t + 1 stand for integration steps and are Δt s apart. The regulatory constant Kr establishes the dynamics of the parametric change. The increment is directly proportional to the difference between the target cell volume, , and the current volume, . In other words, we use proportional feedback (31) to describe the change of NKCC Jmax in response to deviation of the cell volume from its resting condition, since the NKCC is well known for regulating cell volume in response to osmotic effects (27).
Next, we describe the regulation of the basolateral Cl channels. The current-flux relationship,
| (6) |
and Eq. 1 were used to extract the dependence of permeability on membrane potential (Vm) using the current voltage (I/V) curves reported by Fischer and colleagues (21) for outward (BORC) and inward rectifiers (BIRC), whereas the forskolin-stimulated basolateral Cl− channel (BCFTR) presents a linear I/V curve and is computed as having two open probabilities, according to its stimulation (five times greater after forskolin (21)). The functional forms are presented in the equations presented below, with the membrane potential inserted in volts and the constants Por (m s−1) and Pir (m s−1) dependent on the density of inward and outward rectifier channels, respectively, in the basolateral membrane.
| (7) |
| (8) |
Note that the dependence on volume and pH is computed as an instantaneous increment rather than a continuous increase/decrease, as in Eq. 5. In other words, whereas Eq. 5 imposes a regulatory mechanism, Eqs. 7 and 8 reproduce the sensitivity of the channels as described by their electrophysiological characterization (21,22). The distinction between regulation and sensitivity is as follows. The derivative of the regulatory flux (NKCC) with time is proportional to the difference between the instantaneous volume and the target volume. The instantaneous value (not the time derivative) of the volume-sensitive flux (BORC) is dependent on the instantaneous volume. In a similar way, the BIRC is pH-sensitive, i.e., it is determined by the instantaneous pH. Once again, the superscript tg represents the targeted value of the quantity to which it is appended.
The flux across the KvLQT1 is evaluated by combining Ohm's law with Eq. 6:
| (9) |
where (mol m−2 s−1) is the passive flux, Gi (S) the conductance to the ion i, and Ei (V) the reversal potential for the ion i (32). The conductance for the basolateral K+ channel is also dependent on membrane potential:
| (10) |
| (11) |
where GVm (S) is the final conductance due to the membrane potential, and the time τ (s) represents the delay effect. The fit was obtained using data from Yang and colleagues (28). The coefficient (S) is doubled under stimulation by cAMP, consequent to the addition of forskolin to the apical bath. Equations 10 and 11 reproduce the electrophysiology of the channel and should not be confused with a regulatory mechanism.
In summary, the functional form presented by Eq. 1 was used to evaluate the flux across all ion channels. For the mixed array of basolateral K+ channels only, in order to represent the ones corresponding to KvLQT1, an additional flux is evaluated using Eqs. 9–11. All fluxes through cotransporters, exchangers, and pump are evaluated using Eq. 3. Equations 5, 7, 8, 10, and 11 describe regulatory and sensitivity mechanisms.
Water transport is driven by osmotic forces. The water flux from compartment x to compartment y is given by
| (12) |
and is proportional to the water permeability, Pw, and the difference in osmolarity, S, between compartments x and y (mol m−3).
The system is integrated over time, accounting for all ionic and water fluxes across the boundaries of each compartment. Concentrations are updated using their definition (number of moles/volume).
| (13) |
The summation in Eq. 13 accounts for the net flux entering the cell, where compartments “in” and “o” correspond to intracellular and extracellular, respectively. The summation over the coefficient k accounts for the several membrane proteins, including ion channels, pump, and transporters present in either the basolateral or the apical membranes, of surface area Am. The time step in the simulation for water fluxes is 1000 times smaller than that used for ionic fluxes, a tactic necessitated by the fact that the water permeability is much higher than the permeability for ions. The intracellular volume changes are in proportion to the flux of water across the cell membranes, m:
| (14) |
where Vw = 1.8 × 10−5 m3 mol−1.
The pH is regulated by short- and long-term neutralizations due to buffering and H+/ transport, respectively. It is considered that CO2 permeates the cell membrane much faster than the ions (33); therefore, we consider its concentration constant. The intracellular buffering power, βin (M/pH units), is inferred from experimental data for pH regulation in Calu-3 cells (17):
| (15) |
The contribution of and CO2, βCO2, is expressed by the first term on the righthand side of Eq. 15, whereas the remaining terms represent contributions intrinsic to the intracellular environment.
Changes in the intracellular pH due to H+ and HCO3− fluxes and cell volume changes are computed using the definition of buffering power βin = d[ ]/dpH, where d[ ] stands for positive changes in basic ionic concentrations and negative changes in acidic ionic concentrations. It is assumed that the change in pH is completely governed by the intracellular buffer:
| (16) |
Equation 16 implies that unlike the other ions considered, can be consumed or produced within the cell, and in this case, Eq. 13 requires two extra terms. The first is due to the effect of the buffer on the ions entering/leaving the cell, which is measured by the difference between the H+ concentration (or number of intracellular moles, mH) corresponding to the evaluated pH and what would be the proton concentration in the absence of the buffer or chemical reactions with (i.e., number of intracellular moles evaluated considering change due to protons crossing the cell membrane only, mF) times the ratio between the /CO2 buffer, βCO2, and the total intracellular buffer, βin. That is because for every molecule of H+ consumed (or produced) due to βCO2, there is one corresponding molecule of being consumed (or produced). The second extra term is added because there may be extra production or consumption of in the cytoplasm, since the intracellular concentration of is not necessarily in equilibrium at all times, resulting in transient hydration/dehydration (κ1 = 0.0436 s−1 and κ2 = 5.5 × 104 M−1 s−1). The amount of charge on the impermeant intracellular anions also changes with pH. These relationships are embodied in the equation
| (17) |
The timescale for the membrane potential to adjust to new concentrations of permeant ions is approximately a millisecond, much smaller than the time step used in the simulations in this study. Therefore, it is assumed that the membrane potential instantly moves to its steady-state value for each new value set of concentrations and transport and permeation parameters. Calculation of the new steady state is iteratively, as follows: for each time step, the values for membrane potential are estimated using the reversal potential as an initial guess, and iterated including all transporters using Kirchhoff's loop and node laws. Therefore, there is no accumulation of charges in the intracellular environment due to membrane transport, and bulk electroneutrality is maintained in all compartments modeled throughout the transient simulations.
Fixed coefficients
Fixed coefficients for the transporters and basolateral Cl− channels are provided in the Supporting Material.
Parametric search
The parameters in the model that represent the density of channels (Pi; see Table S1) and transporters (Jmax; see Table S2) were estimated in the following manner.
First, the parameters were required to maintain the intracellular concentrations described in the previous version of the model under short-circuit conditions. Starting with Cl−, the apical flux matches the fluxes across the basolateral membrane due to the cotransporter and basolateral Cl− permeability, for a membrane potential of approximately −50 mV. This value has been computed for airway epithelium under short-circuit conditions (3,34) and is similar to that measured in HBE under open-circuit conditions (35). The K+ concentration is maintained by balancing the cotransporter, pump, permeability, and conductance fluxes. The Na+ is finally maintained by balancing apical flux with the cotransporter and pump fluxes. The and proton-related transporters are introduced. Initially, the parameters for the new transporters AE, NBC, and NHE are set to deliver small fluxes, to determine the necessary ratios to maintain the intracellular concentration and pH. The parameters are increased proportionally until the transient changes in Isc are able to reproduce the experiments. Refined adjustments to all parameters are made manually or after analysis of stochastic perturbations of the initial conditions. The set of parameters used in the simulations reported in the next section are reported in Table S1 and Table S2, and in Table 1.
Table 1.
Parameters used in set of case studies reported in Fig. 2
| Parameters | = 0 | × 2 | = 0 | × 2 | Reference | Concentrations (mM) | ||
|---|---|---|---|---|---|---|---|---|
| , S/m2 | 10 | 10 | 0 | 21 | 10 | Na+ | 20 | |
| , μ m/s | 8.0 e−2 | 8.0 e−2 | 10.5 e−2 | 5. e−2 | 8.0 e−2 | K+ | 140 | |
| , μ m/s | 0 | 1 e−1 | 5.2 e−2 | 5.2 e−2 | 5.2 e−2 | Cl− | 55 | |
| Jmax, mol/(m2s) | H+ | 4.2 e−5 | ||||||
| NaK pump | 1.33 e−5 | 1.75 e−5 | 1.6 e−5 | 1.6 e−5 | 1.6 e−5 | 13 | ||
| NKCC | 1.25 e−5 | 1.5 e−5 | 1.25 e−5 | 1.25 e−5 | 1.25 e−5 | |||
| NHE | 4.5 e−6 | 4.5 e−6 | 4.5 e−6 | 4.5 e−6 | 4.5 e−6 | |||
| AE | 1.22 e−5 | 1.24 e−5 | 1.24 e−5 | 1.24 e−5 | 1.24 e−5 | |||
| NBC | 1.1 e−6 | 1.1 e−6 | 1.1 e−6 | 1.1 e−6 | 1.1 e−6 | |||
Reference values are the set of parameters that best reproduce the experimental data. Numbers in bold bring attention to values that differ from those for the reference case. Modifications in Jmax were necessary to make all compared cases correspond to equivalent basal conditions. Values in the last column are the initial conditions for intracellular concentrations.
Experimental data used for validation
A common experimental technique is the culture of cells of the tissue of interest in Ussing chambers, combined with Isc measurements. The exposure of apical and basolateral regions to bath solutions with substances known to inhibit or stimulate the activity of specific cell membrane proteins is translated into temporal changes of the Isc. Simulation of the pharmacological intervention can be used to validate the model. Since variations in experimental Isc values are significant even within samples investigated under the same experimental conditions by the same lab, we seek to match qualitative behavior rather than precise quantitative behavior.
Certain pharmaceutical agents are known to act on specific ion channels or transporters: amiloride blocks ENaCs; forskolin stimulates the CFTR and the basolateral K+ channel KvLQT1; bumetanide blocks the basolateral NKCC; stilbene-insensitive 5-(N-ethyl-N-isopropyl)-amiloride (EIPA) EIPA blocks the NHE; and acetazolamide is a CA inhibitor. Devor and colleagues (16) report several experiments in which primary cultures of HBE cells were used.
Table S3 and Fig. 2 show the experimental values used for validation (16) (Fig. 1, a and b). We label the two sets of experimental conditions Experiment 1 and Experiment 2. Experiment 1 consists of monolayers under physiological saline bath solution (in mM, 120 NaCl, 25 NaHCO3, 3.3 KH2PO4, 0.8 K2HPO4, 1.2 MgCl2, and 10 glucose) exposed to sequential interventions by amiloride, forskolin, bumetanide, EIPA, and acetazolamide. Experiment 2 consists of experiments of monolayers under Cl−-free bath (gluconate is substituted for Cl−) exposed to amiloride, forskolin, bumetanide, and acetazolamide. In terms of temporal behavior, in Experiment 1, the response to forskolin consists of a peak followed by a lower-current plateau. For the Cl−-free bath, the same drug induces a steplike response. Also, bumetanide does not disturb the Isc in the absence of Cl− in Experiment 2. In Experiment 1, both EIPA and acetazolamide trigger mild decays, although the decay of acetazolamide is faster. Notice the large standard deviations in some of the measurements, and within groups of experiments. What becomes very clear is the trend set by the interventions: amiloride decreases Isc; forskolin and genistein increase Isc; bumetanide decreases Isc; and acetazolamide decreases Isc a little bit further.
Figure 2.
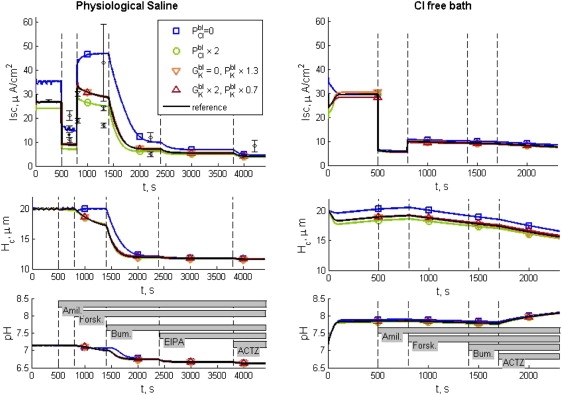
Simulations of short-circuit interventions for HBE in physiological saline (left column) and in Cl−-free bath (right column). The vertical dashed lines correspond to the times when the pharmacological interventions occur. The identification and order of the pharmacological interventions are indicated by the bars in the bottom panels: amil (amiloride), forsk (forskolin), bum (bumetanide), EIPA, and actz (acetazolamide). Plots of Isc, cell thickness (volume/surface area as projected on the plane of the epithelium), and intracellular pH are included. The reference simulation assumes basolateral Cl− permeability of 5.2 × 10−8 m s−1, whereas K+ permeates with a combination of fixed permeability of 8 × 10−8 m s−1 and voltage-sensitive conductance constant = 10 S m−2. Symbols indicate simulations in which different assumptions are made about the basolateral Cl− permeability and K+ conductance, so that the effects of these particular quantities can be seen. The reference Isc can be compared with error bars corresponding to data from Experiment 1 (16). Different symbols for the error bar correspond to different groups of data obtained sequentially (Table S3). For Experiment 2, fewer experimental data were reported (16) than for Experiment 1: in a group of 11 samples, forskolin increased Isc by 6.3 ± 1.3 μA cm−2, and in another group of five experiments, Isc values after amiloride and forskolin introduction were 3.4 ± 0.3 and 7.4 ± 1 μA cm−2, respectively. The other simulated results are features of the system not revealed by the experimental procedures. Thus, the top curves are validations of the model, whereas the other curves are new discoveries about the system behavior revealed in the simulations.
The simulated effects of amiloride on ENaC and of forskolin on CFTR are listed in Table S1. The effect of the CA inhibitor acetazolamide is computed by neglecting the effect of the CO2 buffer βCO2, combined with the reduction of the maximum flux, Jmax, for the anion exchanger to 45% of its initial value (12), and for the NBC to 50% of its initial value (13,14).
Results
Our simulations of Experiment 1 consist of a basal Isc up to time 500 s, at which time amiloride is apically added, followed by forskolin at 800 s, bumetanide at 1400 s, EIPA at 2400 s, and acetazolamide at 3800 s. Simulations of Experiment 2 differ in that they do not use EIPA, and acetazolamide is added at 1700 s. In Fig. 2, we compare five parametric studies: the reference state (parameters as described in previous sections); two studies of the effect of KvLQT1; and two studies on the effect of basolateral Cl− permeability. In Figs. 2 and 3, the vertical dashed lines mark the times of the pharmacological interventions. Random numerical perturbation of the reference set of parameters (permeabilities and conductance in Table S1, Jmax values in Table S2, and the ratio between and Cl− apical permeabilities) within ±10% showed that the qualitative behavior of the model is robust. More than 93% of the simulations with randomly varied parameters succeeded in regulating intracellular pH within the range 7.14 ± 0.05 pH units. The relative invariance of the results with the parameter variation suggests that the mechanisms contained in the model will provide a functioning epithelium over a wide range of parameters. From the simulations with varied parameters, we learned that the basal Isc is most sensitive to the magnitude of amiloride-sensitive Na+ permeabilities. After addition of amiloride, the Isc is most sensitive to the magnitude of the basal apical anionic permeability for both Experiment 1 and Experiment 2. The selectivity between Cl and HCO3 ions in the apical membrane will mostly affect the postamiloride Isc for the Cl-free study. Among the pH-related transporters, the one that has the greater impact on Isc is the NBC.
Figure 3.
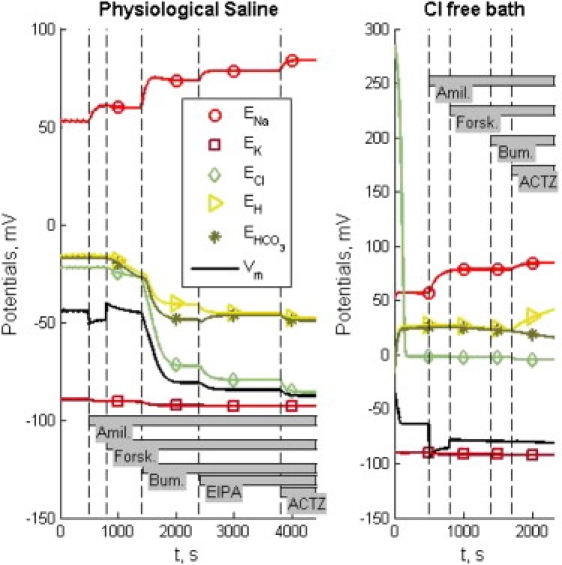
Reversal potentials (curves with symbols) and membrane potential (black line) for pharmacological interventions under physiological saline (left column) and Cl−-free bath (right column). Dashed vertical lines indicate the times of the pharmacological interventions as indicated by gray bars.
We address the relevance of the dependence of the KvLQT1 channels on membrane potential and forskolin by varying the channel population. Before stimulation, the percentage distribution of the passive basolateral K current between a fixed permeability, PK, and the KvLQT1 conductance are 100:0 ( = 0); 75:25 (reference); and 50:50 ( × 2) (see Table 1). The simulations show that the inclusion of a voltage-sensitive basolateral potassium channel, based on I/V curves for KvLQT1 (28), does not perturb the results significantly in comparison to having an unregulated permeability (Fig. 2).
To evaluate the effect of the basolateral Cl− permeability (), parameters for other transporters were adjusted so that the prestimulated intracellular concentrations were the same, both with and without the basolateral Cl− channels. The adjustments and intracellular concentrations are reported in Table 1. Simulation for = 0 required decreases of 17% and 2% for the Jmax NaK pump and AE, respectively. Simulation for × 2 required increases of 9% and 20% for the Jmax NaK pump and NKCC, respectively. Inclusion of basolateral Cl− channels results in a negative shift in Isc, noticed with greater amplitude before the addition of bumetanide. The absence of basolateral Cl− channels changes the temporal behavior of the response, most evident after the forskolin application (Fig. 2).
The cell volume (proportional to epithelial thickness, since the area as projected onto the plane of the epithelium remains constant) and intracellular pH are also presented in Fig. 2. For the set of simulations of Experiment 1 (Fig. 2, left column), the cell volume is well regulated until the addition of forskolin to the bath, for all cases studied. In the simulation in the absence of basolateral Cl− permeability ( = 0) the volume remains regulated until the addition of bumetanide. The addition of bumetanide triggers severe volume decrease for all five cases, due to inhibition of the NKCC. The intracellular pH is regulated toward intracellular alkalization by the combined contribution of the transporters NHE and NBC and toward acidification by AE. The magnitude of their contribution is validated with the simulation of Experiment 2 (Fig. 2, right column). Their transmembrane ionic fluxes are one order of magnitude lower than the pump or NKCC, in both Experiment 1 and Experiment 2 (Fig. S1 and Fig. S2). When the intracellular Cl− concentration is no longer sustained by the NKCC, the fluxes across the other transporters are not sufficient to sustain intracellular pH regulation, and acidification occurs for Experiment 1. In the absence of extracellular Cl−, the reversal potential ECl in Fig. 3 shows that the anion vanishes from the intracellular compartment within the simulation of basal conditions. Therefore, the AE is unable to contribute to cell acidification, and intracellular pH increases. There is still some contribution from the intracellular buffering power shown after the addition of acetazolamide. The drug partially reduces the influx of HCO3−, but also annuls the buffering power, βCO2, resulting in further alkalization.
Fig. 3 shows the membrane potentials (solid line) and specific ionic reversal potentials at each cell membrane (symbols) during simulations corresponding to Experiments 1 and 2, using the reference-set parameters. Notice that for Experiment 1, all potentials are constant during the first 500 s, representing the basal condition. In the course of the simulation, the reversal potentials change, but they maintain the same qualitative relationship to each other and to the membrane potentials. The reversal potentials for protons and are closely related.
For Experiment 2, the leak of Cl− is accompanied by hyperpolarization of the membrane potentials, and the increase of proton and reversal potentials. The further hyperpolarization due to addition of amiloride temporarily brings the membrane potential lower than the K+ reversal potential. The same effect was observed in all five parametric studies. The absence of Cl− eliminates the NKCC and AE fluxes, and the consequent intracellular alkalization eliminates the NHE flux. The remaining Isc is carried by the NaK pump on the basolateral membrane and the exiting through the CFTR on the apical membrane. The intracellular concentration is maintained by the NBC.
Discussion and Summary
We developed a model of the bronchial epithelium that closely emulates Isc for this tissue in response to a variety of pharmacological interventions. The array of experiments we consider provides sufficient constraints to largely determine the model. We therefore judge that the model provides a sound foundation for experimental design and further model refinement. Our goal is not to create the definitive model of epithelial function, but to provide a framework in which modeling can be joined with experiment to aid our understanding of epithelial function. To this end, the model is created in modular form in a widely used programming and modeling language (MATLAB, The MathWorks, Natick, MA) and will be freely shared. The one significant exception to the model's ability to account for experiment is that the reduction in Isc upon application of acetazolamide is not as pronounced in the simulation as in the experiments using Cl−-free bath. We note that acetazolamide appears also to be implicated in calcium signaling processes (36), so that may be the missing component of our model. However, we do not have access to data that would permit us to specify that action in the context of epithelia.
The key to the usefulness of the model is that it reveals details of mechanism for the epithelial response that are not yet readily available via experiment, such as time-varying fluxes, concentrations, apical and basolateral membrane potentials, and volume. Experiments to test these predictions could confirm or provide a basis for further refinement of the model, which could in turn lead to sharpening our understanding of the transport mechanisms underlying integrated epithelial function.
An example of using the model to focus on a particular mechanistic point has to do with basolateral Cl− permeability, which has been inferred by (21) and (22). In this case, we did simulations both with and without basolateral Cl− permeability, and found that when it is present, the simulated response to forskolin matches experiment much better (Fig. 2), reproducing a peak followed by decay, as observed by Devor et al. (16), whereas when it is absent, the time course of the experimental trace is simply an asymptote to a new value.
Regarding the previous version of our model, we noticed that when the and pH are not taken into account, the monolayer Isc after bumetanide is <4 μA cm−2 (results not shown), which is ∼30% of the experimental value (16). Variations of the permeability for Na+, K+, and Cl−, and the fluxes via the NaK pump or the NKCC, do not increase the transepithelial current after addition of bumetanide to the bath solution. This issue is resolved in the current extended version of the model, due to the inclusion of transporters that carry protons and (NHE, AE, and NBC) and the diffusion of HCO3− through the CFTR.
Comparison to previous models in the literature
Hartmann and Verkman (34) were pioneers in developing an electrokinetic model for the airway epithelium to understand the impact of stimulation and inhibition by specific transporters. The Cl− permeability was also stimulated by calcium, but that model did not consider osmotic forces and fluxes. Warren et al. (1) combined the water and ionic transport in a similar manner, as described by our previous model, and added calcium regulation of channels (apical Cl− and basolateral K+), evaluating the relation between calcium signaling and fluid movement. Larsen et al. (2) present a Na+ recirculation theory and model for epithelia that focuses on a description of the paracellular pathway, which is not involved in understanding short-circuit currents.
Compared to these models, our model adds coupling to pH regulation, which to our knowledge has not previously been done for airway epithelia, and also adds the following specific transporters and channels: basolateral Cl− channels, voltage-dependent K+ channels, NBC, NHE, and AE. We find that all of these, with the possible exception of the voltage dependence of the K+ channels, are necessary to accurately match the Isc in HBE.
In future work, we plan to incorporate the epithelial model presented in this article into a more complete model of the epithelium that includes the apical surface liquid (ASL). Modeling ASL interactions will provide insight into the detailed mechanisms by which an effective liquid film thickness is maintained, contributing to our understanding of the biomolecular basis of mucociliary clearance, and perhaps leading to more effective ways of fighting lung infections in a CF lung environment (37). It may be that such understanding would also be of benefit in the development of therapies for other pulmonary obstructive disease (38,39).
Supporting Material
Three tables and two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)06006-8. The coefficients for the transporters on the basolateral membrane are based on experiments in references (40–44), as listed in Table S2.
Supporting Material
Acknowledgments
We thank Dr. Shreedhar Natarajan for initially translating the Novotny-Jakobsson code from Fortran to MatLab, and Dr. Robert Bridges for useful discussions on parameterizing and validating the model.
This work was funded by the National Institutes of Health (grant 5PN2EY016570).
References
- 1.Warren N.J., Tawhai M.H., Crampin E.J. A mathematical model of calcium-induced fluid secretion in airway epithelium. J. Theor. Biol. 2009;259:837–849. doi: 10.1016/j.jtbi.2009.04.026. [DOI] [PubMed] [Google Scholar]
- 2.Larsen E.H.J.B.S., Sørensen J.B., Sørensen J.N. Analysis of the sodium recirculation theory of solute-coupled water transport in small intestine. J. Physiol. 2002;542:33–50. doi: 10.1113/jphysiol.2001.013248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Novotny J.A., Jakobsson E. Computational studies of ion-water flux coupling in the airway epithelium. I. Construction of a model. Am. J. Physiol. Cell Physiol. 1996;270:C1751–C1763. doi: 10.1152/ajpcell.1996.270.6.C1751. [DOI] [PubMed] [Google Scholar]
- 4.Novotny J.A., Jakobsson E. Computational studies of ion-water flux coupling in the airway epithelium. II. Role of specific transport mechanisms. Am. J. Physiol. Cell Physiol. 1996;270:C1764–C1772. doi: 10.1152/ajpcell.1996.270.6.C1764. [DOI] [PubMed] [Google Scholar]
- 5.Boucher R.C. Airway surface dehydration in cystic fibrosis: pathogenesis and therapy. Annu. Rev. Med. 2007;58:157–170. doi: 10.1146/annurev.med.58.071905.105316. [DOI] [PubMed] [Google Scholar]
- 6.Kreindler J.L., Peters K.W., Bridges R.J. Identification and membrane localization of electrogenic sodium bicarbonate cotransporters in Calu-3 cells. Biochim. Biophys. Acta. 2006;1762:704–710. doi: 10.1016/j.bbadis.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 7.Pushkin A., Abuladze N., Kurtz I. Cloning, characterization and chromosomal assignment of NBC4, a new member of the sodium bicarbonate cotransporter family. Biochim. Biophys. Acta. 2000;1493:215–218. doi: 10.1016/s0167-4781(00)00149-4. [DOI] [PubMed] [Google Scholar]
- 8.Dudeja P.K., Hafez N., Al-Bazzaz F.J. Expressionof the Na+/H+ and Cl−/HCO3- exchanger isforms in proximal and distal human airways. Am. J. Physiol. Lung Cell. Mol. Physiol. 1999;276:971–978. doi: 10.1152/ajplung.1999.276.6.L971. [DOI] [PubMed] [Google Scholar]
- 9.Johnson M.D., Bao H.F., Eaton D.C. Functional ion channels in pulmonary alveolar type I cells support a role for type I cells in lung ion transport. Proc. Natl. Acad. Sci. USA. 2006;103:4964–4969. doi: 10.1073/pnas.0600855103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mall M., Gonska T., Kunzelmann K. Modulation of Ca2+-activated Cl− secretion by basolateral K+ channels in human normal and cystic fibrosis airway epithelia. Pediatr. Res. 2003;53:608–618. doi: 10.1203/01.PDR.0000057204.51420.DC. [DOI] [PubMed] [Google Scholar]
- 11.Schwiebert E.M., Cid-Soto L.P., Cutting G.R. Analysis of ClC-2 channels as an alternative pathway for chloride conduction in cystic fibrosis airway cells. Proc. Natl. Acad. Sci. USA. 1998;95:3879–3884. doi: 10.1073/pnas.95.7.3879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alvarez B.V., Vilas G.L., Casey J.R. Metabolon disruption: a mechanism that regulates bicarbonate transport. EMBO J. 2005;24:2499–2511. doi: 10.1038/sj.emboj.7600736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Becker H.M., Deitmer J.W. Carbonic anhydrase II increases the activity of the human electrogenic Na+/HCO3- cotransporter. J. Biol. Chem. 2007;282:13508–13521. doi: 10.1074/jbc.M700066200. [DOI] [PubMed] [Google Scholar]
- 14.Loiselle F.B., Morgan P.E., Casey J.R. Regulation of the human NBC3 Na+/HCO3- cotransporter by carbonic anhydrase II and PKA. Am. J. Physiol. Cell Physiol. 2004;286:C1423–C1433. doi: 10.1152/ajpcell.00382.2003. [DOI] [PubMed] [Google Scholar]
- 15.Cowley E.A., Linsdell P. Characterization of basolateral K+ channels underlying anion secretion in the human airway cell line Calu-3. J. Physiol. 2002;538:747–757. doi: 10.1113/jphysiol.2001.013300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Devor D.C., Bridges R.J., Pilewski J.M. Pharmacological modulation of ion transport across wild-type and ΔF508 CFTR-expressing human bronchial epithelia. Am. J. Physiol. Cell Physiol. 2000;279:C461–C479. doi: 10.1152/ajpcell.2000.279.2.C461. [DOI] [PubMed] [Google Scholar]
- 17.Inglis S.K., Finlay L., Olver R.E. Regulation of intracellular pH in Calu-3 human airway cells. J. Physiol. 2002;538:527–539. doi: 10.1113/jphysiol.2001.012806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leroy C., Prive A., Brochiero E. Regulation of ENaC and CFTR expression with K+ channel modulators and effect on fluid absorption across alveolar epithelial cells. Am. J. Physiol. Lung Cell. Mol. Physiol. 2006;291:1207–1219. doi: 10.1152/ajplung.00376.2005. [DOI] [PubMed] [Google Scholar]
- 19.Shin J.-H., Son E.J., Yoon J.H. Molecular and functional expression of anion exchangers in cultured normal human nasal epithelial cells. Acta Physiol. (Oxf.). 2007;191:99–110. doi: 10.1111/j.1748-1716.2007.01731.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Su X., Li Q., Ji H.L. Interregulation of proton-gated Na+ channel 3 and cystic fibrosis transmembrane conductance regulator. J. Biol. Chem. 2006;281:36960–36968. doi: 10.1074/jbc.M608002200. [DOI] [PubMed] [Google Scholar]
- 21.Fischer H., Illek B., Widdicombe J.H. Basolateral Cl channels in primary airway epithelial cultures. Am. J. Physiol. Lung Cell. Mol. Physiol. 2007;292:L1432–L1443. doi: 10.1152/ajplung.00032.2007. [DOI] [PubMed] [Google Scholar]
- 22.Itani O.A., Lamb F.S., Welsh M.J. Basolateral chloride current in human airway epithelia. Am. J. Physiol. Lung Cell. Mol. Physiol. 2007;293:L991–L999. doi: 10.1152/ajplung.00077.2007. [DOI] [PubMed] [Google Scholar]
- 23.Bleich M., Warth R. The very small-conductance K+ channel KvLQT1 and epithelial function. Pflugers Arch. 2000;440:202–206. doi: 10.1007/s004240000257. [DOI] [PubMed] [Google Scholar]
- 24.Mall M., Wissner A., Kunzelmann K. Role of KVLQT1 in cyclic adenosine monophosphate-mediated Cl− secretion in human airway epithelia. Am. J. Respir. Cell Mol. Biol. 2000;23:283–289. doi: 10.1165/ajrcmb.23.3.4060. [DOI] [PubMed] [Google Scholar]
- 25.Poulsen J.H., Fischer H., Machen T.E. Bicarbonate conductance and pH regulatory capability of cystic fibrosis transmembrane conductance regulator. Proc. Natl. Acad. Sci. USA. 1994;91:5340–5344. doi: 10.1073/pnas.91.12.5340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wright A.M., Gong X., Gray M.A. Novel regulation of cystic fibrosis transmembrane conductance regulator (CFTR) channel gating by external chloride. J. Biol. Chem. 2004;279:41658–41663. doi: 10.1074/jbc.M405517200. [DOI] [PubMed] [Google Scholar]
- 27.Haas M., Forbush B. The Na-K-Cl cotransporter of secretory epithelia. Annu. Rev. Physiol. 2000;62:515–534. doi: 10.1146/annurev.physiol.62.1.515. [DOI] [PubMed] [Google Scholar]
- 28.Yang W.P., Levesque P.C., Blanar M.A. KvLQT1, a voltage-gated potassium channel responsible for human cardiac arrhythmias. Proc. Natl. Acad. Sci. USA. 1997;94:4017–4021. doi: 10.1073/pnas.94.8.4017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stewart A.K., Chernova M.N., Alper S.L. Regulation of AE2 anion exchanger by intracellular pH: critical regions of the NH2-terminal cytoplasmic domain. Am. J. Physiol. Cell Physiol. 2001;281:C1344–C1354. doi: 10.1152/ajpcell.2001.281.4.C1344. [DOI] [PubMed] [Google Scholar]
- 30.Hille B. Sinauer Associates; Sunderland, MA: 1992. Ionic Channels of Excitable Membranes. [Google Scholar]
- 31.Astrom K.J., Murray R.M. Princeton University Press; Princeton, NJ: 2008. Feedback Systems: An Introduction for Scientists and Engineers. [Google Scholar]
- 32.Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Al-Awqati Q. One hundred years of membrane permeability: does Overton still rule? Nat. Cell Biol. 1999;1:E201–E202. doi: 10.1038/70230. [DOI] [PubMed] [Google Scholar]
- 34.Hartmann T., Verkman A.S. Model of ion transport regulation in chloride-secreting airway epithelial cells. Integrated description of electrical, chemical, and fluorescence measurements. Biophys. J. 1990;58:391–401. doi: 10.1016/S0006-3495(90)82385-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kreindler J.L., Jackson A.D., Danahay H. Inhibition of chloride secretion in human bronchial epithelial cells by cigarette smoke extract. Am. J. Physiol. Lung Cell. Mol. Physiol. 2005;288:L894–L902. doi: 10.1152/ajplung.00376.2004. [DOI] [PubMed] [Google Scholar]
- 36.Shimoda L.A., Luke T., Swenson E.R. Inhibition of hypoxia-induced calcium responses in pulmonary arterial smooth muscle by acetazolamide is independent of carbonic anhydrase inhibition. Am. J. Physiol. Lung Cell. Mol. Physiol. 2007;292:L1002–L1012. doi: 10.1152/ajplung.00161.2006. [DOI] [PubMed] [Google Scholar]
- 37.Yoon S.S., Coakley R., Hassett D.J. Anaerobic killing of mucoid Pseudomonas aeruginosa by acidified nitrite derivatives under cystic fibrosis airway conditions. J. Clin. Invest. 2006;116:436–446. doi: 10.1172/JCI24684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cantin A.M., Hanrahan J.W., Durie P. Cystic fibrosis transmembrane conductance regulator function is suppressed in cigarette smokers. Am. J. Respir. Crit. Care Med. 2006;173:1139–1144. doi: 10.1164/rccm.200508-1330OC. [DOI] [PubMed] [Google Scholar]
- 39.Yoshida T., Tuder R.M. Pathobiology of cigarette smoke-induced chronic obstructive pulmonary disease. Physiol. Rev. 2007;87:1047–1082. doi: 10.1152/physrev.00048.2006. [DOI] [PubMed] [Google Scholar]
- 40.Levine S.A., Montrose M.H., Donowitz M. Kinetics and regulation of three cloned mammalian Na+/H+ exchangers stably expressed in a fibroblast cell line. J. Biol. Chem. 1993;268:25527–25535. [PubMed] [Google Scholar]
- 41.Humphreys B.D., Jiang L., Alper S.L. Functional characterization and regulation by pH of murine AE2 anion exchanger expressed in Xenopus oocytes. Am. J. Physiol. Cell Physiol. 1994;267:C1295–C1307. doi: 10.1152/ajpcell.1994.267.5.C1295. [DOI] [PubMed] [Google Scholar]
- 42.Pushkin A., Abuladze N., Kurtz I. Cloning, tissue distribution, genomic organization, and functional characterization of NBC3, a new member of the sodium bicarbonate cotransporter family. J. Biol. Chem. 1999;274:16569–16575. doi: 10.1074/jbc.274.23.16569. [DOI] [PubMed] [Google Scholar]
- 43.Miyamoto H., Ikehara T., Masuya T. Kinetic mechanism of Na+, K+, Cl− cotransport as studied by Rb+ influx into HeLa cells: effects of extracellular monovalent ions. J. Membr. Biol. 1986;92:135–150. doi: 10.1007/BF01870703. [DOI] [PubMed] [Google Scholar]
- 44.Westenfelder C., Earnest W.R., Al-Bazzaz F. Characterization of Na-K-ATPase in dog tracheal epithelium: enzymatic and ion transport measurements. J. Appl. Physiol. 1980;48:1008–1019. doi: 10.1152/jappl.1980.48.6.1008. [DOI] [PubMed] [Google Scholar]
- 45.Reference deleted in proof.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


