Wilcoxon-Mann-Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules

Abstract

In a mathematical approach to hypothesis tests, we start with a clearly defined set of hypotheses and choose the test with the best properties for those hypotheses. In practice, we often start with less precise hypotheses. For example, often a researcher wants to know which of two groups generally has the larger responses, and either a t-test or a Wilcoxon-Mann-Whitney (WMW) test could be acceptable. Although both t-tests and WMW tests are usually associated with quite different hypotheses, the decision rule and p-value from either test could be associated with many different sets of assumptions, which we call perspectives. It is useful to have many of the different perspectives to which a decision rule may be applied collected in one place, since each perspective allows a different interpretation of the associated p-value. Here we collect many such perspectives for the two-sample t-test, the WMW test and other related tests. We discuss validity and consistency under each perspective and discuss recommendations between the tests in light of these many different perspectives. Finally, we briefly discuss a decision rule for testing genetic neutrality where knowledge of the many perspectives is vital to the proper interpretation of the decision rule.

1. Introduction

In this paper we explore assumptions for statistical hypothesis tests and how several sets of assumptions may relate to the interpretation of a single decision rule (DR). Often statistical hypothesis tests are developed under one set of assumptions, then subsequently the DR is shown to remain valid after relaxing those original assumptions. In other situations the later conditions that the DR is studied under are not a relaxing of original assumptions, but an exploration of an entirely different pair of probability models which neither completely contain the original probability models nor are contained within them. In either case, both the original interpretations of the DR and the later interpretations are always available to the user each time the DR is applied, and the major point of this paper is that it may make sense to package a single DR with several sets of assumptions.

We use the term ‘hypothesis test’ to denote a DR coupled with a set of assumptions that delineate the null and alternative hypotheses. Some DRs will be approximately valid for several sets of assumptions, and we can package these assumptions together with the DR as a multiple perspective DR (MPDR), where each perspective is a different hypothesis test using the same DR.

The MPDR outlook is a way of looking at the assumptions of the statistical DR and how the DR is interpreted, so we start in Section 2 discussing assumptions in scientific research in general, showing how the MPDR assumptions (i.e., statistical assumptions) fit into scientific inferences. In Section 3 we formalize our notation and terminology surrounding MPDRs. In Section 4 we define the MPDR and discuss some useful properties. In Section 5 we detail some MPDRs for two sample tests of central tendency, formally stating many of the perspectives and the associated properties. This is the primary example of this paper and it fleshes out cases where some perspectives are subsets of other perspectives within the same MPDR. In Section 6.1 we discuss tests for interval censored data as an example of a different use of the MPDR. In this case, the MPDR outlook takes two different DRs developed under two different sets of assumptions and shows that either DR may be applied under the other set of assumptions, and we can compare the two decisions by looking at them from the same perspective (i.e., from the same set of assumptions). In Section 6.2 we discuss genetic tests of neutrality as an example of how having several perspectives on a DR may be vital to the proper interpretation of the decision.

2. Assumptions in scientific research

In order to show that the MPDR framework has practical value, we need to first outline how statistical assumptions fit into scientific research. Thus, although non-statistical assumptions for scientific research are not our main focus, we briefly discuss them in this section. Throughout this section we refer to the Physician's Health Study (PHS) (Hennekens, Eberlein for PHS Research Group, 1985; Sterring Committee of the PHS Research Group, 1988, 1989), as a specific example to clarify general concepts.

The Physician's Health Study was a randomized, 2 by 2 factorial, double blind, placebo-controlled clinical trial of male physicians in the US between the ages of 40 and 84. An invitational questionnaire was mailed to 261,248 individuals, and 33,211 were willing, eligible and started on a run-in phase of the study. Of these individuals, 22,071 adhered to their regimen sufficiently well to be enrolled in the randomized portion of the study, where each subject was randomized to either aspirin or aspirin-placebo and either β-carotene or β-carotene-placebo. We will focus on the aspirin aspect of the study which was designed to detect whether alternate day consumption of aspirin would reduce total cardiac mortality and death from all causes.

We begin our scientific assumption review with the influential book by Mayo (Mayo, 1996, see also Mayo and Spanos, 2004, 2006), which describes how hypothesis tests are used in scientific research, and it “successfully knots together ideas from the philosophy of science, statistical concepts, and accounts of scientific practice” (Lehmann, 1997). Mayo (1996) starts with a “primary model” which in her examples is often a fairly specific framing of the problem in a statistical model. In this aspect, Mayo (1996) matches closely with the typical presentation of a statistical model by a mathematical statistician. For example, Mayo (1996) goes into great detail on Jean Perrin's experiments on Brownian motion, describing the primary model as (Table 7.3):

Hypothesis: ℋ : the displacement of a Brownian particle over time t, S_t follows the Normal distribution with μ = 0 and variance= 2Dt.

This is a wonderful example of a statistical model that describes a scientific phenomenon. Although it is not framed as a null and alternative set of assumptions, Mayo's (1996) “primary model” is nonetheless framed as a statistical model. Mayo (1996) then defines the other models and assumptions which make up the particular scientific inquiry (models of experiment, models of data, experimental design, data generation). It is not helpful to go into the details of those models here, particularly since:

[Mayo does] not want to be too firm about how to break down an inquiry into different models since it can be done in many different ways (Mayo, 1996, p. 222).

The point of this paper is that although there are examples where the primary hypothesis that drives the experimental design can be stated within a clear statistical model (e.g., Perrin's experiments), often in the biological sciences the motivating primary theory is much more vague and perhaps many different statistical models could equally well describe the primary scientific theory. In other words, often the null hypothesis is meant to express that the data are somehow random, but that randomness may be formalized by many different statistical models. This vagueness and lack of focus on one specific statistical model is inherent in biological phenomena, since unlike the physical sciences, often there are several statistical models that can equally well describe for example, a male physician's response to aspirin or aspirin-placebo. Thus, Mayo's (1996) notion that the design of an experiment begins with a primary model which can be represented as a statistical model does not appear to describe many of the biological experiments we encounter in our work. If possible, a statistical model based on the science of the application is preferred; however, often so little is known about the mechanism of action of the effect to be measured that any of several different statistical models could be applied.

Note that although this paper emphasizes hypothesis testing and p-values, we are not implying that other statistics should not supplement the p-value. For example, if a meaningful confidence interval is available then it can add valuable information. Similarly, power calculations or severity calculations (see e.g., Mayo, 2003, or Mayo and Spanos, 2006) could also supplement the hypothesis test. The problem with all three of these statistics is that often more structure is required of the hypothesis test assumptions in order to define these statistics.

Let us outline a typical experiment in the biological sciences. Here, we will start with what we will call a scientific theory, which is less connected to a particular statistical model than Mayo's (1996) “primary model”. In the PHS a scientific theory is that prolonged low-dose aspirin will decrease cardiovascular mortality. This scientific theory is not attached to a particular statistical model; for example, that theory is not that low-dose aspirin will decrease cardiovascular mortality by the same relative risk for all people by the same parameter which is to be estimated from the study. The scientific theory is more vague than a detailed statistical model. Next the researchers make some assumptions to be able to study the scientific theory. Since these assumptions relate the study being done to some external theory that motivated the study, we will call them the external validity assumptions. In the PHS, the external validity assumptions include the assumption that people who are eligible, elect to participate, and sufficiently adhere to a regimen (i.e., those who actually could end up in the study) will be similar to prospective patients to whom we would like to suggest a prolonged low-dose aspirin regimen. Since the PHS is restricted to male physicians aged 40 to 84, an external validity assumption is that this population will tell us something about future prospective patients.

Assumptions related to the statistical hypothesis test should be kept separate from these external validity assumptions. This position was stated in a different way by Kempthorne and Doerfler (1969):

[T]here are two aspects of experimental inference. The first is to form an opinion about what would happen with repetitions of the experiment with the same experimental units, such repetitions being unrealizable because the experiment ‘destroys’ the experimental units. The second is to extend this ‘inference’ to some real population of experimental material that is of interest. (p. 235)

The classic example in which this dichotomy arises is with randomization tests (see e.g., Ludbrook and Dudley, 1998; Mallows, 2000). Ludbrook and Dudley (1998) emphasize the first point of view, arguing that randomization tests are preferred to t or F tests because they not only perform better for small sample sizes, but because “randomization rather than random sampling is the norm in biomedical research”. They point out, in keeping with the sentiments of Kempthorne and Doerfler (1969) and others, that the subsequent generalization to a larger population is separate and not statistical: “However, this need not deter experimenters from inferring that their results are applicable to similar patients, animals, tissues, or cells, though their arguments must be verbal rather than statistical. (p. 129)”

External validity assumptions are important, and they must be reasonable, otherwise one may design a very repeatable study which gives not very useful results. In the PHS the external validity assumptions seem reasonable since one would expect that although male physicians are different from the general population (especially females), it is not unreasonable to expect that results from the study would tell us something about non-physicians – at least for males of the same ages. The external validity assumption that allows us to apply the results to females is a bigger one, but this issue is separate from the internal results of the study and whether there was a significant effect for the PHS. In this paper we are emphasizing statistical hypothesis tests, which are tools to make inferences about the study that was performed and cannot tell us anything about the external validity of the study. For example, statistical assumptions have nothing to do with whether we can generalize the results of the PHS to females.

The next step in the process is that the researchers design an ideal study (either an experiment or an observational study) to test their theory. The term ideal refers to the study being done exactly according to the design. In the PHS the ideal study is a double-blind placebo-controlled study on male physicians aged 40 to 84. It is ideal in the sense that all inclusion criteria and randomization are carried out exactly as designed and all instruments are accurate to the specified degree, and the data are recorded correctly, etc. We call the assumptions needed to treat the actual study as the ideal study, the study implementation assumptions.

The study is carried out and data are observed. Then the researchers make some statistical assumptions in order to perform a statistical hypothesis test and calculate related statistics such as p-values and confidence intervals. For the PHS some statistical assumptions were that the individuals were independent, the randomization was a true and fair one, and that the rate of myocardial infarction (MI) events (heart attacks) under the null hypothesis was the same for the group randomized to the aspirin as the group randomized to aspirin-placebo. The PHS showed that the relative risk of aspirin to placebo for MI was significantly lower than 1. If the null hypothesis is rejected, then if all the assumptions are correct, chance alone is not a reasonable explanation of the results. What this statistical decision says about the scientific theory depends on all of the assumptions, the statistical assumptions, the study implementation assumptions, and the external validity assumptions.

In this paper we will focus on statistical assumptions. This focus should not be interpreted to imply that the other types of assumptions are not vital for the scientific process. However, often times the non-statistical assumptions are separated enough from the statistical ones that the statistical assumptions may be changed without modifying the non-statistical ones. Here we treat each possible set of statistical assumptions as a different lens through which we can look at the data. Through the lenses of the statistical assumptions and the accompanying DRs, we can see how randomness may play its role in the data. Each DR in our toolbox is associated with many lenses, and for any particular study some of those lenses may be more useful than others. It is even possible that using multiple lenses on the same study may clarify its interpretation. The usefulness of the DR depends on how clearly the lenses of the statistical assumptions help us see reality.

3. Terminology and properties for hypothesis tests and decision rules

Since we are associating a DR with many different hypotheses, we need to be clear about terminology and about what properties of hypothesis tests are associated with the DRs apart from the assumptions about the hypotheses.

Consider a study where we have observed some data, x. In order to perform a hypothesis test we need to make several assumptions. We assume the sample space, 𝒳, the (possibly uncountable) set of all possible values of new realizations of the data if the study could be repeated. Let X be an arbitrary member of 𝒳.

In the usual hypothesis testing framework, we assume that the data were generated from one of a set of probability models, 𝒫 = {P_θ|θ ∈ ϴ}, and we partition that set into two disjoint sets, the null hyphothesis, H = {P_θ|θ ∈ ϴ_H} and the alternative hypothesis, K = {P_θ|θ ∈ ϴ_K}, where θ may be an infinite dimensional parameter. Since we will compare many sets of assumptions, we bundle all the assumptions together as A = (𝒳, H, K). We often assign subscripts to different sets of assumptions.

Let α be the predetermined significance level, and let δ(·, α) = δ denote a DR (also called the critical function, see Lehmann and Romano, 2005) which is a function of α and either x or X. The function δ takes on values in [0, 1] representing the probability of rejecting the null hypothesis. In this paper we only consider non-randomized DRs, where δ(X, α) ∈ {0, 1}, for the X ∈ 𝒳. We call the set (δ, A) a hypothesis test. This terminology is a more formal statement of the standard usage for the term ‘hypothesis test’ where the assumptions are often implied or left unstated. For example, the Wilcoxon-Mann-Whitney (WMW) DR is often used without any explicit statement of what hypotheses are being tested.

Let the power of a DR under P_θ be denoted Pow[δ(X, α); θ] = Pr[δ(X, α) = 1; θ]. A test is a valid test (or an α-level test) if for any 0 < α < .5 the size of the test is less than or equal to α, where the size is ${\alpha }_n^{\ast }={\sup }_{\theta \in {ϴ}_H}\mathit{Pow}[\delta (X_n,\alpha );\theta ]$, where X = X_n with n indexing the sample size. There are two types of asymptotic validity (see Lehmann and Romano, 2005, p. 422). A test is pointwise asymptotically valid (PAV) (or pointwise asymptotically level α) if for any θ ∈ ϴ_H, lim sup_n→∞ Pow [δ(X_n, α); θ] ≤ α. Note that when a test is PAV, this does not mean that the size of the test will necessarily converge to a value less than α. This latter, more stringent property is the following: a test is uniformly asymptotically valid (UAV) (or uniformly asymptotically level α) if $\lim {\sup }_{n\to \infty }{\alpha }_n^{\ast }\le \alpha$. We give examples of these asymptotic validity properties with respect to two-sample tests in Section 5.2.1.

The classical approach to developing a hypothesis test is to set the assumptions, then choose the decision rule which produces a valid test with the largest power under the alternative. If the null and alternative hypotheses are simple (i.e., represent one probability distribution each) then the Neyman-Pearson fundamental lemma (see Lehmann and Romano, 2005, Section 3.2) provides a method for producing the (possibly randomized) most powerful test. For applications, the hypotheses are often composite (i.e., represent more than one probability distribution), and ideally we desire one decision rule which is most powerful for all θ ∈ ϴ_K. If such a decision rule exists, the resulting hypothesis test is said to be uniformly most powerful (UMP).

For some assumptions, A, there does not exist a UMP test, and extra conditions may be added so that among those tests which meet that added condition, a most powerful test exists. We discuss two such added conditions next, unbiasedness and invariance. A test is unbiased (or strictly unbiased) if the power under any alternative model is greater than or equal to (or strictly greater than) the size. A test that is uniformly most powerful among all unbiased tests is called UMP unbiased. Often we will wish the hypothesis test to be invariant to certain transformations of the sample space. A general statement of invariance is beyond the scope of this paper (see Lehmann and Romano, 2005, Chapter 6); however, one important case is invariance to monotonic transformations of the responses. A test invariant to monotonic transformations would, for example, give the same results regardless of whether we log transform the responses or not. Tests based on the ranks of the responses are invariant to monotonic transformations. Additionally, we may want to restrict our optimality consideration to the behavior of the tests close to the boundary between the null and alternative and study the locally most powerful tests, which are defined as the UMP tests within a region of the alternative space that is infinitesimally close to the null space (see Hájek and Šidák, 1967, p. 63).

A test is pointwise consistent in power (or simply consistent) if the power goes to one for all θ ∈ Θ_K. Because many tests may be consistent, in order to differentiate between them using asymptotic power results, we consider a sequence of tests that begin in the alternative space and approach the null hypothesis space. Consider the parametric case where θ is k dimensional. Let θ_n = θ₀ + hn^1/2, where h is a k dimensional constant with |h| > 0, θ_n ∈ Θ_K and θ₀ ∈ Θ_H. The test (δ, A) is asymptotically most powerful (AMP) if it is PAV and for any other sequence of PAV tests, say (δ*, A), we have lim sup_n→∞ {Pow[δ(X_n, α); θ_n] − Pow[δ*(X_n, α); θ_n]} ≥ 0 (see Lehmann and Romano, 2005, p. 541).

For the applied statistician, usually the asymptotic optimality criteria are not as important as the finite sample properties of power. At a minimum we want the power to be larger than α for some θ ∈ Θ_K, and practically we want the power to be larger than some large pre-specified level, say 1 − β, for some θ ∈ Θ_K.

Now consider some properties of DRs that require only the sample space assumption, χ, and need not be interpreted in reference to the rest of the assumptions in A. First we call a DR monotonic if for any 0 < α^′ < α < .5

$$\delta (X,{\alpha }^{\prime })\le \delta (X,\alpha )\text{for all}X\in 𝒳.$$

Non-monotonic tests have been proposed as a way to increase power for unbiased tests, but Perlman and Wu (1999) (see especially the discussion of McDermott and Wang, 1999) argue against using these tests. Although there are cases where the most powerful test is non-monotonic (see Lehmann and Romano, 2005, p. 96 prob 3.17, p. 105, prob 3.58), non-monotonic tests are rarely if ever needed in applied statistics.

The p-value is

$$p\left(X\right)=\inf \{\alpha :\delta (X,\alpha )=1\},$$

and is a function of the DR and χ only. The validity of the p-value depends on the assumptions. We say a p-value is valid if (see e.g., Berger and Boos, 1994)

$$\underset{\theta \in {ϴ}_H}{\sup }P{r}_{\theta }[p\left(X\right)\le \alpha ]\le \alpha$$

We will say a hypothesis test is valid if the p-value is valid. For non-randomized monotonic DRs, a valid hypothesis test (i.e., valid p-value) implies an α-level hypothesis test, and in this paper we will use the terms interchangeably. Most reasonable tests are at least PAV, asymptotically strictly unbiased, and monotonic.

4. Multiple perspective decision rules

We call the set (δ, A₁, … , A_k) a multiple perspective DR, with each of the hypothesis tests, (δ, A_i), i = 1, … , k called a perspective. We only consider perspectives which are either valid or at least PAV.

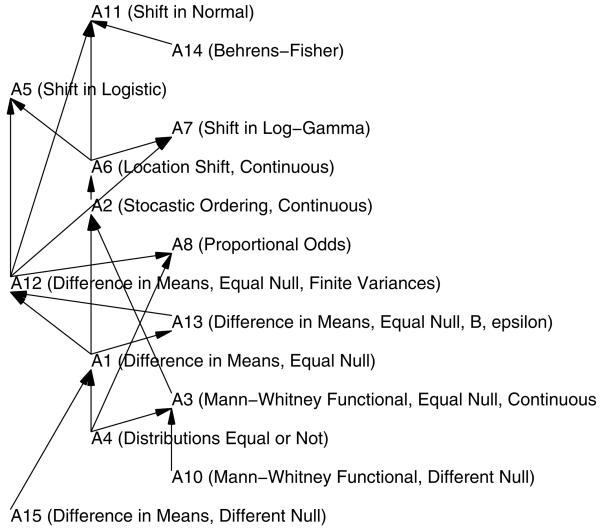
We say that A_i is more restrictive than A_j if χ_i ⊆ χ_j , H_i ⊆ H_j, K_i ⊆ K_j, and either H_i ∩ H_j ≠ H_j or K_i ∩ K_j ≠ K_j , and denote this as A_i ⊏ A_j. In other words, if both (δ, A_i) and (δ, A_j) are valid tests and A_i ⊏ A_j then (δ, A_j) is a less parametric test than (δ, A_i).

We state some simple properties of MPDR which are obvious by inspection of the definitions. If A_i ⊏ A_j then:

• if (δ, A_j) is valid then (δ, A_i) is valid (and if (δ, A_i) is invalid then (δ, A_j) is invalid),

• if (δ, A_j) is PAV then (δ, A_i) is PAV,

• if (δ, A_j) is UAV then (δ, A_i) is UAV,

• if (δ, A_j) is unbiased then (δ, A_i) is unbiased, and

• if (δ, A_j) is consistent then (δ, A_i) is consistent.

Note that the statements about validity only require H_i ⊆ H_j.

We briefly mention broad types of perspectives. First, an optimal perspective shows how the DR has some optimal property (e.g., uniformly most powerful test) under that perspective. Second, a consistent perspective delineates an alternative space whereby for each P_θ ∈ K, the DR has asymptotic power going to one. Sometimes the full probability space for consistent perspectives (i.e., 𝒫 = H ∪ K) is not a “natural” probability space in that it is hard to justify the assumption that the true model exists within the full probability space but not within some smaller subset of that space. This vague concept will become more clear through the examples given in Section 5. In cases where the full probability space is not natural in this sense, we call the perspective a focusing perspective, since it focuses the attention on certain alternatives. We now consider some real examples to clarify these broad types of perspectives and show the usefulness of the MPDR framework.

5. MPDRs for two-sample tests of central tendency

Consider the case where the researcher wants to know if group A has generally larger responses than group B. The researcher may think the choice between the Wilcoxon rank sum/Mann-Whitney U test (WMW test) and the t-test depends on the results of a test of normality (see e.g., Figure 8.5 of Dowdy, Weardon and Chilko, 2004). In fact, the issue is not so simple. In this section we explore these two DRs and the choice between them and some related DRs.

Let the data be x = x_n = {y₁, y₂, … , y_n, z₁, z₂ … , z_n} where y_i represents the ordinal (either discrete or continuous) response for the ⁱth individual, and z_i is either 0 (for n₀ individuals) or 1 (for n₁ = n − n₀ individuals) representing either of the two groups. Let X = X_n = {Y₁, Y₂, … , Y_n, Z₁, Z₂ … , Z_n} be another possible realization of the experiment. Throughout this section, for all asymptotic results we will assume that n₀/n → λ₀, where 0 < λ₀ < 1.

For all of the perspectives discussed in the following except Perspective 9, we assume the sample space is

$$𝒳=\{z,Y:Y\in 𝒴\},$$

where Y is a set of possible values of Y if the experiment were repeated. The z vector does not change for this sample space. Further, for all perspectives except Perspective 9, we assume that the Y_i are independent with Y_i ~ F if Z_i = 1 and Y_i ~ G if Z_i = 0. Failure of the independence assumption can have a large effect on the validity of some if not all the hypothesis tests to be mentioned. This problem exists for all kinds of distributions, but incidental correlation is not a serious problem for randomized trials (see Box, Hunter and Hunter, 2005, Table 3A.2, p. 118, and Proschan and Follmann, 2008).

5.1. Wilcoxon-Mann-Whitney and related decision rules

5.1.1. Valid perspectives for the WMW decision rule

Wilcoxon (1945) proposed the exact WMW DR allowing for ties presenting the test as a permutation test on the sum of the ranks in one of the two groups. Let δ_W be this exact DR, which can be calculated using network algorithms (see e.g., Mehta, Patel and Tsiatis, 1984). Wilcoxon (1945) does not explicitly give hypotheses which are being tested but talks about comparing the differences in means. We do not have a valid test if we only assume that the means of F and G are equal, since difference in variances can also cause the test statistic to be significant. Thus, for our first perspective we assume F = G under the null to ensure validity, and make no assumptions about the discreteness or the continuousness of the responses:

Perspective 1. Difference in Means, Same Null Distributions

$$\begin{array}{cc}\hfill & H_1=\{F,G:F=G\}\hfill \\ \hfill & K_1=\{F,G:E_F\left(Y\right)\ne E_G\left(Y\right)\}\hfill \end{array}$$

This is a focusing perspective, since P = H∪K is hard to justify in an applied situation because P is the strange set of all distributions F and G except those that have equal means but are not equal. This is not a consistent perspective.

Mann and Whitney (1947) assumed continuous responses and tested for stochastic ordering. Letting ψ_C be the set of continuous distributions, the perspective is:

Perspective 2. Stochastic Ordering:

$$\begin{array}{cc}\hfill & H_2=\{F,G:F=G;F\in {\Psi }_C\}\hfill \\ \hfill & K_2=\{F,G:F{<}_{\mathit{st}}G\mathrm{or}G{<}_{\mathit{st}}F;F,G\in {\Psi }_C\}\hfill \end{array}$$

where F <_st G denotes that G is stochastically larger than F , which is equivalent to G(y) ≤ F (y) for all y with strict inequality for at least some y.

Mann and Whitney (1947) showed the consistency of the WMW DR under the Stochastic Ordering (SO) perspective. Lehmann (1951) shows the unbiasedness under the SO perspective, and his result holds even without the continuity assumption. Lehmann (1951) also notes that the Mann and Whitney (1947) consistency proof shows the consistency for all alternatives under the following perspective:

Perspective 3. Mann-Whitney Functional (continuous, equal null distributions):

$$\begin{array}{cc}\hfill & H_3=\{F,G:F=G;F\in {\Psi }_C\}\hfill \\ \hfill & K_3=\{F,G:\varphi (F,G)\ne \frac{1}{2};F,G\in {\Psi }_C\}\hfill \end{array}$$

where ϕ is called the Mann-Whitney functional, defined (to make sense for discrete data as well) as

$$\begin{array}{cc}\hfill \varphi (F,G)& =\frac{1}{2}\left(1+\int G\left(y\right)\mathit{dF}\left(y\right)-\int F\left(y\right)\mathit{dG}\left(y\right)\right)\hfill \\ \hfill & =\mathit{Pr}[Y_F>Y_G]+\frac{1}{2}\mathit{Pr}[Y_F=Y_G]\hfill \end{array}$$

where Y_F ~ F and Y_G ~ G.

Similar to Perspective 1, the Mann-Whitney functional perspective is a focusing one since the full probability set, P is created more for mathematical necessity than by any scientific justification for modeling the data, which in this case does not include distributions with both ϕ(F, G) = 1/2 and F ≠ G. It is hard to imagine a situation where this complete set of allowable models, P, and only that set of models is justified scientifically; the definition K₃ acts more to focus on where the WMW procedure is consistent. A more realistic perspective in terms of P = H ∪ K is the following:

Perspective 4. Distributions Equal or Not

$$\begin{array}{cc}\hfill & H_4=\{F=G\}\hfill \\ \hfill & K_4=\{F\ne G\}\hfill \end{array}$$

Later we will introduce another realistic perspective (Perspective 10), for which the WMW procedure is invalid, but first we list a few more perspectives for which δ_W is valid.

Under the following optimal perspective, δ_W is the locally most powerful rank test (see Hettmansperger, 1984, section 3.3) as well as an AMP test (van der Vaart, 1998, p. 225):

Perspective 5. Shift in logistic distribution

$$\begin{array}{cc}\hfill & H_5=\{F,G:F=G;F\in {\Psi }_L\}\hfill \\ \hfill & K_5=\{F,G:G\left(y\right)=F(y+\Delta );\Delta \ne 0;F\in {\Psi }_L\}\hfill \end{array}$$

where ψ_L is the set of logistic distributions.

Hodges and Lehmann (1963) showed how to invert the WMW DR to create a confidence interval for the shift in location under the following perspective:

Perspective 6. Location Shift (continuous)

$$\begin{array}{cc}\hfill & H_6=\{F,G:F=G;F\in {\Psi }_C\}\hfill \\ \hfill & K_6=\{F,G:G\left(y\right)=F(y+\Delta );\Delta \ne 0;F\in {\Psi }_C\}\hfill \end{array}$$

Sometimes we observe responses, say $Y_i^{\ast }$, where $Y_i^{\ast }\in (0,\infty )$ and there are extreme right tails in the distribution. A general case is the gamma distribution, which has chi squared and exponential distributions as special cases. For the gamma distribution a shift in location does not conserve the support of the distribution (i.e., Y changes with location shifts), and a better model is a scale change. This is equivalent to a location shift after taking the log transformation. Let $Y_i={\log }_e\left(Y_i^{\ast }\right)$; then the scale change for the random variables $Y_i^{\ast }$ is equivalent to the location shift for Y_i, which has a log-gamma distribution.

Perspective 7. Shift in log-gamma distribution

$$\begin{array}{cc}\hfill & H_7=\{F,G:F=G;F\in {\Psi }_{\mathit{LG}}\}\hfill \\ \hfill & K_7=\{F,G:G\left(y\right)=F(y+\Delta );\Delta \ne 0;F\in {\Psi }_{\mathit{LG}}\}\hfill \end{array}$$

where ϕ_LG is the set of log gamma distributions.

Consider a perspective useful for discrete responses. Assume there exists a latent unobserved continuous variable for the ith observation, and denote it here as $Y_i^{\ast }$. Let F* and G* be the associated distributions for each group. All we observe is some coarsening of that variable, $Y_i=c\left(Y_i^{\ast }\right)$, where c(·) is an unknown non-decreasing function that takes the continuous responses and assigns them into k ordered categories (without loss of generality let the sample space for Y_i be {1, … , k}). We assume that for j = 1, … , k, c(Y*) = j if ξ_j−1 < Y* ≤ ξ_j for some unknown cutpoints −∞ ≡ ξ₁ < … ξ_k−1 < ξ_k ≡∞. Then F*(ξ_j) = F(j). Then a perspective that allows easy interpretation of this type of data is the proportional odds model, where

$$\frac{G^{\ast }\left(y^{\ast }\right)}{1-G^{\ast }\left(y^{\ast }\right)}=\left(\frac{F^{\ast }\left(y^{\ast }\right)}{1-F^{\ast }\left(y^{\ast }\right)}\right){\Delta }^{\ast }\text{for all}{y}^{\ast }\text{with}{\Delta }^{\ast }>0.$$

The observed data then also follows a proportional odds model regardless of the unknown values of ξ_j:

Perspective 8. Proportional Odds

$$\begin{array}{cc}\hfill & H_8=\{F,G:F=G;F\in {\Psi }_{D_k}\}\hfill \\ \hfill & K_8=\left\{F,G:\frac{G\left(y\right)}{1-G\left(y\right)}=\left(\frac{F\left(y\right)}{1-F\left(y\right)}\right)\Delta \mathrm{for}\mathrm{all}y;\Delta \ne 1;F\in {\Psi }_{D_k}\right\}\hfill \end{array}$$

where ψ_Dk is a set of discrete distributions with sample space 1, … , k.

Under the proportional odds model the WMW test is the permutation test on the efficient score, which is the locally most powerful similar test for one-sided alternatives (McCullagh, 1980, p. 117). Note that if we could observe $Y_i^{\ast }$ then the logistic shift perspective on $Y_i^{\ast }$ follows the proportional odds model, since the shifting of a logistic distribution by △_L, say, is equivalent to multiplying the odds by exp(△_L).

All of the above perspectives use a population model, i.e., postulate a distribution for the Y_i, i = 1, … , n. Another model is the randomization model that assumes that each time the experiment is repeated the responses y_i, i = 1, … , n will be the same, but the group assignments Z_i, i = 1, … , n may change. Notice how this perspective is very different from the other perspectives, which are all different types of population models (see Lehmann, 1975, for a comparison of the randomization and population models):

Perspective 9. Randomization Model

$$𝒳=\{y,Z:Z\in \Pi \left(z\right)\},$$

where ∏(z) is the set of all permutations of the ordering of z, which has N = n!/(n₁!(n − n₁)!) unique elements. Let ∏(z) = {Z₁, … , Z_N}.

$$H_9=\{\mathit{Pr}[Z={𝒵}_a]=N^{-1}\mathrm{for}\mathrm{all}a\}$$

The randomization model does not explicitly state a set of alternative probability models for the data, i.e., it is a pure significance test (see Cox and Hinkley, 1974, Chapter 3), although it is possible to define the alternative as any probability model not in H₉.

5.1.2. An invalid perspective and some modified decision rules

Here is one perspective for which the WMW procedure is not valid:

Perspective 10. Mann-Whitney Functional (Different null distributions):

$$\begin{array}{cc}\hfill & H_{10}=\left\{F,G:\varphi (F,G)=\frac{1}{2};\mathit{Var}\left(F\left(Y_G\right)\right)>0,\mathit{Var}\left(G\left(Y_F\right)\right)>0\right\}\hfill \\ \hfill & K_{10}=\left\{F,G:\varphi (F,G)\ne \frac{1}{2};\mathit{Var}\left(F\left(Y_G\right)\right)>0,\mathit{Var}\left(G\left(Y_F\right)\right)>0\right\}.\hfill \end{array}$$

Note that the conditions V ar(F(Y_G)) > 0 and V ar(G(Y_F)) > 0 are not very restrictive, allowing both discrete or continuous distributions. This perspective has also been called the nonparametric Behrens-Fisher problem (Brunner and Munzel, 2000), and under this perspective δ_W is invalid (see e.g., Pratt, 1964). Brunner and Munzel (2000) gave a variance estimator for φ(F̂, Ĝ) which allows for ties, where F̂ and Ĝ are the empirical distributions. Since for continuous data the variance estimator can be shown equivalent to Sen's jackknife estimator (Sen, 1967, see e.g., Mee, 1990), we denote this V_J. Brunner and Munzel (2000) showed that comparing

$$T_{\mathit{NBF}}=\frac{\varphi (\widehat{F},\widehat{G})-\frac{1}{2}}{\sqrt{V_J}}$$

to a t-distribution with degrees of freedom estimated using a method similar to Satterthwaite's gives a PAV test under Perspective 10. We give a slight modification of that DR in Appendix A, and denote it as δ_NBFa.

For the continuous random variable case, Janssen (1999) showed that if we perform a permutation test using a statistic equivalent to T_NBF as the test statistic, then the test is PAV under Perspective 10 with the added condition of F, G ∈ ψ_C. Neubert and Brunner (2007) generalized this to allow for ties, i.e., they created a permutation test based on Brunner and Munzel's T_NBF . We denote that DR as δ_NBFp. Since it is a permutation test, δ_NBFp is valid for finite samples for perspectives where F = G.

5.2. Decision rules for two-sample difference in means (t-tests)

5.2.1. Some valid t-tests

To talk about DRs for t-tests we introduce added notation. Let the sample means and variances for the first group be ${\widehat{\mu }}_1=n_1^{-1}{\Sigma }_{i=1}^n{Z}_i{Y}_i$ and ${\widehat{\sigma }}_1^2={(n_1-1)}^{-1}{\Sigma }_{i=1}^n{Z}_i{(Y_i-{\widehat{\mu }}_1)}^2$ and similarly define the sample mean (μ̂₀) and variance $\left({\widehat{\sigma }}_0^2\right)$ for the second group. Let ${\widehat{\sigma }}_t^2={(n-2)}^{-1}\left((n_1-1){\widehat{\sigma }}_1^2+(n_0-1){\widehat{\sigma }}_0^2\right)$ be the pooled sample variance used in the usual t-test DR, say δ_t Let

$$T_t\left(X\right)=\frac{{\widehat{\mu }}_1-{\widehat{\mu }}_0}{{\widehat{\sigma }}_t\sqrt{\frac{1}{n_1}+\frac{1}{n_0}}},$$

so the DR is

$${\delta }_t\left(X\right)=\{\begin{array}{cc}1\hfill & \text{if}\left|T_t\left(X\right)\right|>t_{n-2}^{-1}(1-\alpha ∕2)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

where $t_{n-2}^{-1}\left(q\right)$ is the qth quantile of the t-distribution with n − 2 degrees of freedom. The standard perspective for this DR is:

Perspective 11. Shift in Normal Distribution

$$\begin{array}{cc}\hfill & H_{11}=\{F,G:F=G;F\in {\Psi }_N\}\hfill \\ \hfill & K_{11}=\{F,G:G\left(y\right)=F(y+\Delta );\Delta \ne 0;F\in {\Psi }_N\}\hfill \end{array}$$

where ψ_N is the set of normal distributions.

Under this perspective, the associated test, (δ_t, A₁₁), is the uniformly most powerful unbiased test and can be shown to be asymptotically most powerful (see Lehmann and Romano, 2005, Section 5.3 and Chapter 13). Under the following perspective, the standard t-test is PAV (see Lehmann and Romano, 2005, p. 446):

Perspective 12. Difference in Means, (Finite Variances, Equal Null distributions)

$$\begin{array}{cc}\hfill & H_{12}=\{F,G:F=G;F\in {\Psi }_{\mathit{fv}}\}\hfill \\ \hfill & K_{12}=\{F,G:E\left(Y_G\right)\ne E\left(Y_F\right),F,G\in {\Psi }_{\mathit{fv}}\}\hfill \end{array}$$

where ψ_fv is the class of distributions with finite variances.

Note that the fact that a test is PAV does not guarantee that for sufficiently large n, the size of the test is close to α; for this we require UAV. In fact, (δ_t, A₁₂) is pointwise but not uniformly asymptotically valid (PNUAV). To see this, take F_n = G_n to be Bernoulli(p_n) such that np_n → λ. The numerator of the t-statistic behaves like a difference of Poissons, and the type I error rate can be inflated (see Appendix B for details).

We show in Appendix C that if we restrict the distributions to the following perspective then the t-test is UAV:

Perspective 13. Difference in Means, (Variance ≥ ε > 0 and E(Y⁴) ≤ B with 0 < B < ∞, Equal Null distributions)

$$\begin{array}{cc}\hfill & H_{13}=\{F,G:F=G;F\in {\Psi }_{B∊}\}\hfill \\ \hfill & K_{13}=\{F,G:E\left(Y_G\right)\ne E\left(Y_F\right),F,G\in {\Psi }_{B∊}\}\hfill \end{array}$$

where ψ_Bε is the class of distributions with V ar(Y) ≥ ε > 0 and E(Y⁴) ≤ B, with 0 < B < ∞.

Using different methods, Cao (2007) appears to show that only finite third moments are needed to show that the t-test is UAV.

Consider the exact permutation test for the difference in means. This DR is defined by enumerating all permutations of indices of the z_i, recalculating μ̂₁ − μ̂₀ for each permutation, and using the permutation distribution of that statistic to define the DR. Denote this DR as δ_tp. It is equivalent to the permutation test on the standard t-test (Lehmann and Romano, 2005, p. 180). Note that although δ_tp is asymptotically equivalent to δ_t under H_fv (Lehmann and Romano, 2005, p. 642), δ_tp is valid (and hence UAV) while δ_t is not UAV. This issue is discussed in Appendix D. Note that because δ_tp is a permutation test, it is valid for any n for any perspective for which F = G under the null.

Now consider a perspective where neither δ_t nor δ_tp is valid:

Perspective 14. Behrens-Fisher: Difference in Normal Means, Different Variances

$$\begin{array}{cc}\hfill & H_{14}=\{F,G:E_F\left(Y\right)=E_G\left(Y\right);F,G\in {\Psi }_N\}\hfill \\ \hfill & K_{14}=\{F,G:E_F\left(Y\right)\ne E_G\left(Y\right);F,G\in {\Psi }_N\}\hfill \end{array}$$

For this perspective, Welch's modification to the t-test is often used. Let the Behrens-Fisher statistic (see e.g., Dudewicz and Mishra, 1988, p. 501) be

$$T_{\mathit{BF}}\left(X\right)=\frac{{\widehat{\mu }}_1-{\widehat{\mu }}_0}{\sqrt{\frac{{\widehat{\sigma }}_1^2}{n_1}+\frac{{\widehat{\sigma }}_0^2}{n_0}}}.$$

Welch's DR is

$${\delta }_{\mathit{tW}}\left(X\right)=\{\begin{array}{cc}1\hfill & \text{if}\left|T_{\mathit{BF}}\left(X\right)\right|>t_{d_W}^{-1}(1-\alpha ∕2)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$

where

$$d_W=\frac{{\left(\frac{{\widehat{\sigma }}_1^2}{n_1}+\frac{{\widehat{\sigma }}_0^2}{n_0}\right)}^2}{\frac{{({\widehat{\sigma }}_1^2∕n_1)}^2}{n_1-1}+\frac{{({\widehat{\sigma }}_0^2∕n_0)}^2}{n_0-1}}.$$ (5.1)

Welch's DR, δ_tW , is approximately valid for the Behrens-Fisher perspective. If we replace d_W with min(n₁, n₀)−1 then the associated DR is Hsu's, δ_tH, which is a valid test under the Behrens-Fisher perspective (see e.g., Dudewicz and Mishra, 1988, p. 502). Both (δ_tW, A₁₄) and (δ_tH, A₁₄) are asymptotically most powerful tests (Lehmann and Romano, 2005, p. 558).

Finally, as with the rank test, we may permute T_BF to obtain a PAV test under Perspective 14 and a valid test whenever F = G; we denote this statistic δ_BFp. Janssen (1997) showed that δ_BFp is PAV under less restrictive assumptions than Perspective 14, replacing ψ_N with the set of distributions with finite means and variances.

5.2.2. An invalid perspective

Consider the seemingly natural perspective:

Perspective 15. Difference in Means, Different Null Distributions

$$\begin{array}{cc}\hfill & H_{15}=\{F,G:E_F\left(Y\right)=E_G\left(Y\right)\}\hfill \\ \hfill & K_{15}=\{F,G:E_F\left(Y\right)\ne E_G\left(Y\right)\}\hfill \end{array}$$

For this perspective, for any DR that has a power of 1 − β > α for some probability model in the alternative space, the size of the resulting hypothesis test is at least 1 − β. To show this, take any two distributions, F* and G*, for which the DR has a probability of rejection equal to 1 − β. Now create F and G as mixture distributions, where F = (1 − ε)F* + _εF^ε, G = (1 − ε)G* + _εG^ε and F^ε and G^ε are distributions which depend on ε that can be chosen to make E_F (Y) = E_G(Y) for all ε. More explicitly, let μ(·) be the mean functional, so that the mean of the distribution F is μ(F). Then for any constant u, we can create a F^ε which meets the above condition as long as μ(F^ε) = ε⁻1 {u − (1 − ε)μ(F*)}, and similarly for μ(G^ε). For any fixed n we can make ε close enough to zero, so that the the power of the test under this probability model in the null hypothesis space approaches 1 − β, and the resulting test is not an α–level test. Note that the above result holds even if we restrict the perspective so that F and G have finite variances. See Lehmann and Romano (2005), Section 11.4, for similar ideas but which focuses mostly on the one-sample case.

5.3. Comparing assumptions and decision rules

5.3.1. Relationships between assumptions

In Figure 1 we depict the cases where we can say that one set of assumptions is more restrictive than another. Most of these relationships are immediately apparent from the definitions; however, the relationships related to stochastic ordering (assumptions A₂) are not obvious. If G is stochastically larger than F (i.e., F <_st G) then for all nondecreasing real-valued functions h, E(h(Y_F)) < E(h(Y_G)) (see e.g., Whitt, 1988). Thus, stochastic ordering implies both ordering of the means (letting h be the identity function) and ordering of the Mann-Whitney function for continuous data (letting h = F), so that A₂ ⊏ A₁ and A₂ ⊏ A₃. We can use Figure 1 to show validity and consistency of DRs under various perspectives.

Fig 1.

Relationship between assumptions. A_i ← A_j denotes that A_i ⊏ A_j (i.e., A_i are more restrictive assumptions than A_j).

5.3.2. Validity and consistency

Table 1 summarizes the validity and consistency of the DRs introduced under different perspectives. For this table we assume finite variances for F and G (so Perspectives 6, 2, 3, 4, and 10 have this additional restriction), although both validity and consistency results hold for the rank tests without this additional assumption. The first symbol for each test answers the question “Is this test valid?” with either: y=yes (for all n), u=UAV, a = PAV, p = pointwise but not uniformly asymptotically valid (PNUAV), n=no (not even asymptotically). The symbol a for PAV, denotes an unsolved answer to the question of whether the perspective is UAV or PNUAV. For Perspective 9 there is no probability model for the responses so only permutation based DRs will be valid. Others will be marked as ‘-’ for undefined. Justifications for the validity symbols of Table 1 not previously discussed are given in Appendix D.1.

Table 1.

Validity and Consistency of Two Sample MPDRs

		Decision Rules
		WMW =Wilcoxon-Mann-Whitney (exact)
		NBFa =Nonparametric Behrens-Fisher (asymptotic)
		NBFp =Nonparametric Behrens-Fisher (permutation)
		t =t-test (pooled variance)
		tW =Welch's t-test (Satterthwaite's df)
		tH =Hsu's t-test (df=min(ni)-1)
		tp =permutation t-test
		tBFp =permutation test on Behrens-Fisher statistic
	Perspective	WMW	NBFa	NBFp	t	tW	tH	tp	tBFp
11.	Normal Shift	yy	uy	yy	yy	uy	yy	yy	yy
14.	Behrens-Fisher	n-	ay	ay	n-	uy	yy	n-	ay
5.	Shift in Logistic	yy	uy	yy	ay	ay	ay	yy	yy
7.	Shift in Log-Gamma	yy	uy	yy	ay	ay	ay	yy	yy
6*.	Location Shift, fv	yy	uy	yy	ay	ay	ay	yy	yy
2*.	Stochastic Ordering, SN, fv	yy	uy	yy	ay	ay	ay	yy	yy
8.	Proportional Odds, SN	yy	uy	yy	ay	ay	ay	yy	yy
12.	Diff in Means, SN,fv	yn	un	yn	py	py	py	yy	yy
13.	Diff in Means, SN, B∊	yn	un	yn	uy	uy	uy	yy	yy
3*.	Mann-Whitney Func., SN, fv	yy	uy	yy	an	an	an	yn	yn
4*.	Distributions Equal or Not, fv	yn	un	yn	an	an	an	yn	yn
15*.	Diff in Means, DN, fv	n-	n-	n-	n-	n-	n-	n-	n-
10*.	Mann-Whitney Func., DN, fv	n-	ay	ay	n-	n-	n-	n-	n-
9.	Randomization Model	y-	- -	y-	- -	- -	- -	y-	y-

^*Perspective numbers with have the additional assumption that F, G ∈ Ψ_fv in both H and K.

SN=Same Null Distns., DN=Different Null Distns., fv=Finite Var., B∊ = {E(Y⁴) ≤ B and Var(Y) ≥ ∊}

Each hypothesis test is represented by 2 sets of symbols representing the 2 properties: (i) validity, and (ii) (pointwise) consistency, where each character answers the question, This test has this property: y=yes, n=no, and – = not applicable.

For validity we also have the symbols: u=UAV, a = PAV, p =PNUAV.

The second symbol in Table 1 denotes consistency: y=yes or n=no, but will only be given for tests that are at least PAV, otherwise we use a ‘-’ symbol. Justification for the consistency results is given in Appendix D.2.

Besides the asymptotic results, there are many papers which simulate the size of the t-test for different situations. For example, for many practical situations when F = G (e.g., lumpy multimodal distributions, and distributions with digital preference), Sawilowsky and Blair (1992) show by simulation that the t-test is approximately valid for a range of finite samples. These simulations agree with the above.

5.3.3. Power and small sample sizes

We consider first the minimum sample size needed to have any possibility of rejecting the null. For simplicity we deal only with the case where there are equal numbers in both groups. It is straightforward to show that when α = 0.05, the sample size should be at least 4 per group (i.e., n = 8) in order for the WMW exact or the permutation t procedures to have a possibility of rejecting the null. In contrast, we only need 2 per group (i.e., n = 4) for Student's t and Welch's t. There are subtle issues on using tests with such small sample sizes. For example, a t-test with only 2 people per treatment group could be highly statistically significant, but the 2 treated patients might have been male and the two controls female so that sex may have explained the observed difference.

5.3.4. Relative efficiency of WMW vs. t-test

Since the permutation t-test is valid under the fairly loose assumptions of Perspectives 4 or 9, some might argue that it is preferred over the WMW because the WMW uses ranks which is like throwing some data away. For example, Edgington (1995), p. 85, states:

When more precise measurements are available, it is unwise to degrade the precision by transforming the measurements into ranks for conducting a statistical test. This transformation has sometimes been made to permit the use of a non-parametric test because of the doubtful validity of the parametric test, but it is unnecessary for that purpose since a randomization test provides a significance value whose validity is independent of parametric assumptions, while using the raw data.

Although this position appears to make sense on the surface, it is misleading because there are many situations where the WMW test has more power and is more efficient. For example, for distributions with heavy tails or very skewed distributions, we can get better power by using the WMW procedure rather than the t procedure. Previously, Blair and Higgins (1980) carried out some extensive simulations showing that in most of the situations studied, the WMW is more powerful than the t-test. Here we just present two classes of distributions: for skewed distributions we will consider the location tests on the log-gamma distribution (equivalent to scale tests on the gamma distribution) and for heavy tails we consider location tests on the t-distribution.

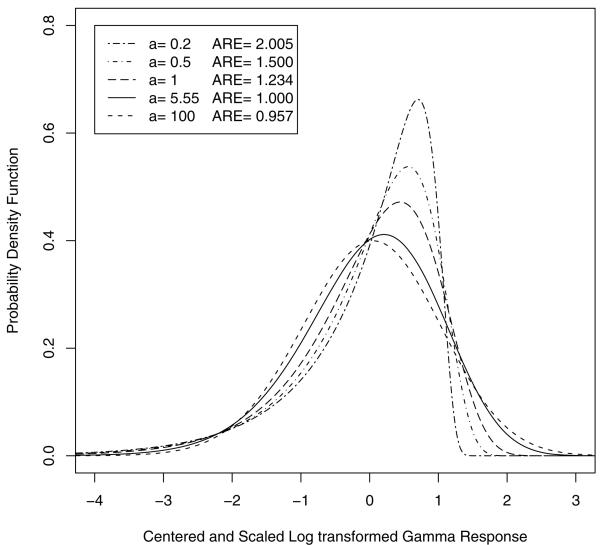
Consider first the location shift on the log gamma distribution (Perspective 7). Here is the pdf of the log transformed gamma distribution with scale=1 and shape=a.

$$f\left(y\right)=\frac{1}{\Gamma \left(a\right)}\exp (\mathit{ay}-e^y)$$ (5.2)

By changing the a parameter we can change the extent of the skewness. We plot some probability density functions standardized to have a mean 0 and variance 1 in Figure 2. Although all the tails are more heavy on the left, the results below would be identical if we had used −y so that the tails are skewed to the right. In the legend, we give the asymptotic relative efficiency (ARE) of the WMW compared to the t-test for different distributions. This ARE is given by (see e.g., Lehmann, 1999, p. 176)

$$\mathit{ARE}=12{\sigma }^2{\left(\int f^2\left(y\right)\mathit{dy}\right)}^2$$

where σ² is the variance associated with the distribution f(y). Now using f from equation 5.2 we get

$$\mathit{ARE}=\frac{12{\psi }^{\prime }\left(a\right){\Gamma }^2\left(2a\right)}{\Gamma \left(a\right)2^{4a}}$$

where ψ′ (a) is the trigamma function, ${\psi }^{\prime }\left(a\right)=\frac{{\partial }^2\left\{\log \left(\Gamma \left(a\right)\right)\right\}}{\partial a}$. We plot the ARE for different values of a in Figure 3.

Fig 2.

The probability density functions for some log transformed gamma distributions. All distributions are scaled and shifted to have mean 0 and variance 1. The value a is the shape parameter, and ARE is asymptotic relative efficiency. An ARE of 2 denotes that it will take twice as many observations to obtain the same asymptotic power for the t-test compared to the WMW-test.

Fig 3.

Relative efficiency of WMW test to t-test for testing for a location shift in log-gamma distribution. The value a is the shape parameter. The solid black line is the ARE. The dotted grey horizontal line is at 1, and is where both tests are equally asymptotically efficient, which occurs at the dotted grey vertical line at a = 5.55. The solid grey horizontal lines are at 3 and 3/π = .955, which are the limits as a → 0 and a → ∞. Points are simulated relative efficiency for shifts which give about 80% power for the WMW DR when there are about 20 in each group.

To show that these AREs work well enough for finite samples, we plot additionally the simulated relative efficiency for several values of a where the associated shift for each a is chosen to give about 80% power for a WMW DR with sample sizes of 20 in each group. The simulated relative efficiency (SRE) is the ratio of the expected sample size for the t (pooled variance) over that for the exact WMW, where the expected sample size for each test randomizes between the sample size, say n, that gives power higher than .80 and n − 1 that gives power lower than .80 such that the expected power is .80 (see Lehmann, 1999, p. 178). The powers are estimated by a local linear kernel smoother on a series of simulations at different sample sizes (with up to 10⁵ replications for sample sizes close to the power of .80).

Note that from Figure 2 the distribution where the ARE=1 looks almost symmetric. Thus, histograms for moderate sample sizes that look symmetric may still have some small indiscernible asymmetry which causes the WMW DR to be more powerful.

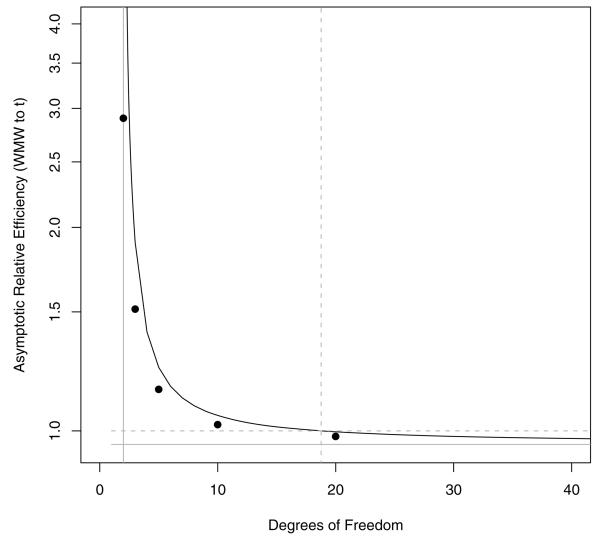
Now suppose the underlying data have a t-distribution, which highlights the heavy tailed case. The ARE of the WMW test to the t-test when the distribution is t with d degrees of freedom (d > 2) is

$$\mathit{ARE}=\frac{12{\Gamma }^4\left(\frac{d+1}{2}\right){\Gamma }^2\left(\frac{2d+1}{2}\right)}{\pi (d-2){\Gamma }^4\left(\frac{d}{2}\right){\Gamma }^2(d+1)}$$ (5.3)

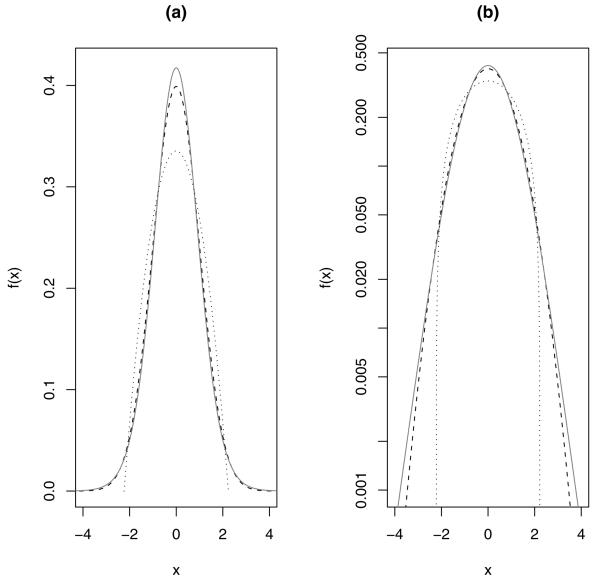
We can show that as d approaches 2 the ARE approaches infinity, and since the t-distribution approaches the normal distribution as d gets large, lim_d→∞ ARE = 3/π. From equation 5.3, if d ≤ 18 then the WMW test is more efficient, while if d ≥ 19 then the t-test is more efficient. We plot the scaled t-distribution with d = 18 (scaled to have variance equal to 1), and the standard normal distribution in Figure 4. In Figure 4a, we can barely see that the tails of the t-distribution are larger than that of the normal distribution, but on the log-scale (Figure 4b) we can see the larger tails. Further, there is a distribution for which the ARE is minimized (see e.g., Lehmann, 1975, p. 377) at 108/125 = .864, given by $f\left(Y\right)=\frac{3}{20\sqrt{5}}(5-y^2)\text{for}y\in (-\sqrt{5},\sqrt{5})$. We plot this distribution in Figure 4 as well.

Fig 4.

Standard normal distribution (black dashed) and scaled t-distribution with 18 degrees of freedom (grey solid), and the distribution with the minimum ARE (black dotted), where all distributions have mean 0 and variance 1. The plots are the same except the right plot (b), has the f(x) plotted on the log scale to be able to see the difference in the extremities of the tails.

In Figure 5 we plot the ARE and simulated relative efficiency for the case where 20 in each group give a power of about 80% for the WMW DR. Note that the ARE gives a fairly good picture of the efficiency even for small samples (although when d → 2 and the ARE → ∞, the SRE at d = 2 is only 2.3).

Fig 5.

Relative efficiency of WMW test to t-test for testing for location shift in t-distributions. The dotted grey horizontal line is at 1, and is where both tests are equally asymptotically efficient, which occurs at the dotted grey vertical line at 18.76. The solid grey lines denote limits, the vertical line shows ARE goes to infinity at df = 2, the horizontal line shows ARE goes to 3/π = .955 as df → ∞. Points are simulated relative efficiency for shifts which give about 80% power for the WMW DR when there are about 20 in each group.

In Figure 4 we see that the distribution with ARE=1 looks very similar to a normal distribution. If the tails of the distribution are much less heavy than the t with 18 degrees of freedom, then the t-test is recommended. This matches with the simulation of Blair and Higgins (1980) who showed that the uniform distribution had slightly better power for the t procedure than for the WMW.

5.3.5. Robustness

Robustness is a very general term that is used in many ways in statistics. Some traditional ways the term is used we have already discussed. We have seen that the classical t-test, i.e., (δ_t, A₁₁), is a UMP unbiased test, yet δ_t retains asymptotic validity (specifically UAV) when the normality assumption does not hold (i.e., it is asymptotically robust to the normality assumption), and all we require for this UAV is second and fourth moment bounds on the distributions (see Perspective 13 and Table 1). Similarly we can say that although the test given by (δ_W, A₆) is AMP, the validity of that test is robust to violations of the logistic distribution assumption (see Table 1).

We have addressed robustness of efficiency indirectly by focusing on the efficiency comparisons between the t-test and the WMW test with respect to location shift models as discussed in Section 5.3.4. We can make statements about the robustness of efficiency of the WMW test from those results. Since we know that (δ_t, A₁₁) is asymptotically most powerful, and we know that the t-distribution approaches the normal distribution as n → ∞, we can say that for large n the WMW test retains 95.5% efficiency compared to the AMP test against the normal shift.

Consider another type of robustness. Instead of wishing to make inferences about the entire distribution of the data, we may wish to make inferences about the bulk of the data. For example, consider a contamination model where the distribution F (G) may be written in terms of a primary distribution, F_p (G_p) and an outlier distribution, F_o (G_o) with ∊_f (∊_g) of the data following the outlier distribution. In other words,

$$\begin{array}{cc}\hfill & F=(1-{∊}_f)F_p+{∊}_f{F}_o\hfill \\ \hfill & \text{and}\hfill \\ \hfill & G=(1-{∊}_g)G_p+{∊}_g{G}_o\hfill \end{array}$$ (5.4)

In this setup, we want to make inferences about F_p and G_p, not about F and G, and the distributions F_o and G_o represent gross errors that we do not wish to overly influence our results. In this setup, the WMW decision rule outperforms the t-test in terms of robustness of efficiency. We can perform a simple simulation to demonstrate this point. Consider X₁, … , X₁₀₀ ~ N(0, 1) and Y₁, … , Y₉₉ ~ N(1, 1) and Y₁₀₀ = 1000 is an outlier caused by perhaps an error in data collection. When we simulate the scenario excluding Y₁₀₀, then all p-values for δ_t and δ_tW are less than 5 ×10⁻⁶ and all for δ_W are less than 3 ×10⁻⁵, while if we include Y₁₀₀ we get simulated p-values for δ_t and δ_tW between 0.26 and 0.29 and p-values for δ_W between 10⁻¹⁵ and 10⁻⁴. Clearly the WMW decision rule has much better power to detect differences between F_p and G_p in the presence of the outlier. Here we see that only one very gross error in the data may totally “break down” the power of the t-test, even when the outlier is in the direction away from the null hypothesis. A formal statement of this property is given in He, Simpson and Portnoy (1990).

There is an extensive literature on robust methods in which many more aspects of robustness are described in very precise mathematics, and although not a focus, robustness for testing is addressed within this literature (see e.g., Hampel, Ronchetti, Rousseeuw and Stahel, 1986; Huber and Ronchetti, 2009; Jureckova and Sen, 1996). Besides the power breakdown function previously mentioned, an important theoretical idea for limiting the influence of outliers is to find the maximin test, the test which maximizes the minimum power after defining the null and alternative hypotheses as neighborhoods around simple hypotheses (e.g., using equation 5.4 with F_p and G_p representing two distinct single distributions). Huber (1965) showed that maximin tests (also called minimax tests) are censored likelihood ratio-type tests (see also Lehmann and Romano, 2005, Section 8.3, or Huber and Ronchetti, 2009, Chapter 10). The problem with this framework is that it is not too convenient for composite hypotheses (Jureckova and Sen, 1996, p. 407). An alternative more general framework is to work out asymptotic robustness based on the influence function (see Huber and Ronchetti, 2009, Chapter 13). A thorough review of those robust methods and related methods and properties are beyond the scope of this paper.

5.3.6. Recommendations on choosing decision rules

The choice of a decision rule for an application should be based on knowledge of the application, and ideally should be done before looking at the data to avoid the appearance of choosing the DR to give the lowest p-value. To keep this section short, we focus on choosing primarily between δ_t (or δ_tW) and δ_W, although for any particular application one of the other tests presented in Table 1 may be appropriate. When using the less well known or more complicated DRs, one should decide whether their added complexity is worth the gains in robustness of validity or some other property.

The choice between t- and WMW DRs should not be based on a test of normality. We have seen that under quite general conditions the t-test decision rules are asymptotically valid (see Table 1), so even if we reject the normality assumption, we may be justified in using a t-test decision rule. Further, when the data are close to normal or the sample size is small it may be very difficult to reject normality. Hampel et al. (1986, p.23), reviewed some research on high-quality data and the departures from normality of that data. They found that usually the tails of the distribution are larger than the normal tails and t-distributions with degrees of freedom from 3 to 10 often fit real data better than the normal distribution. In light of the difficulty in distinguishing between normality and those t-distributions with moderate sample sizes, and in light of the relative efficiency results that showed that the WMW is asymptotically more powerful for t-distributions with degrees of freedom less than 18 (see Section 5.3.4), it seems that in general the WMW test will often be asymptotically more powerful than the t-test for real high quality data. Additionally, the WMW DR has better power properties than the classical t-test when the data are contaminated by gross errors (see Section 5.3.5).

In a similar vein to the recommendation not to test for normality, it is not recommended to use a test of homogeneity of variances to decide between the classical (pooled variance) t-test DR (δ_t) and Welch's DR (δ_tW), since this procedure can inflate the type I errors (Moser, Stevens and Watts, 1989).

One case where a t-test procedure may be clearly preferred over the WMW DR is when there are too few observations to produce significance for the WMW DR (see Section 5.3.3). Also, if there are differences in variance, then δ_tW (or some of the other decision rules, see Table 1) may be used while δ_W is not valid. In general, whenever the difference in means is desired for interpretation of the data, then the t-tests are preferred. Nonetheless, if there is a small possibility of gross errors in the data (see Section 5.3.5), then there may be better robust estimators of the difference in means which will have better properties (see References in Section 5.3.5).

6. Other examples and uses of MPDRs

In Section 5 we went into much detail on how some common tests may be viewed under different perspectives. In this section, we present without details two examples that show different ways that the MPDR framework can be useful.

6.1. Comparing decision rules: Tests for interval censored data

Another use of the MPDR outlook is to compare DRs developed under different assumptions. Sun (1996) developed a test for interval censored data under the assumption of discrete failure times. In the discussion of that paper, Sun states that his test “is for the situation in which the underlying variable is discrete” and “if the underlying variable is continuous and one can assume proportional hazards model, one could use Finkelstein's [1986] score test”. Although there can be subtle issues in differentiating between continuous and discrete models especially as applied to censored data (see e.g., Andersen, Borgan, Gill and Keiding, 1993, Section IV.1.5), in this case Sun's (1996) test can be applied if the underlying variable is continuous. If we look at Sun's (1996) DR as a MPDR then this extends the usefulness and applicability of his test, since it can be applied to both continuous and discrete data. In fact, under the MPDR outlook Finkelstein's (1986) test can be applied to discrete data as well. See Fay (1999) for details.

6.2. Interpreting rejection: Genetic tests of neutrality

In the examples of Section 5, the MPDR outlook was helpful in interpreting the scope of the decision. Some perspectives provide a fairly narrow scope with perhaps some optimal property (e.g., t-test of difference in normal means with the same variances is uniformly most powerful unbiased), while other perspectives provide a much broader scope for interpreting similar effects (e.g., the difference in means from the t-test can be asymptotically interpreted as a shift in location for any distribution with finite variance). In this section, we provide an example where the different perspectives do not just provide a difference between a broad or narrow scope of the same general tendency, but the different perspectives highlight totally different effects. In other words, from one perspective rejecting the null hypothesis means one thing, and from another perspective rejecting the null hypothesis means something else entirely.

The example is a test of genetic neutrality (Tajima's [1989] D statistic), and the original perspective on rejection is that evolution of the population has not been neutral (e.g., natural selection has taken place). This perspective requires many assumptions. Before mentioning these we first briefly describe the DR.

The data for this problem are n sequences of DNA, where each sequence is from a different member of a population of n individuals from the same species. The sequences have been aligned so that each sequence is an ordered list of w letters, where each letter represents one of the four nucleotides of the genetic code (A,T,C, and G). We call each position in the list, a site. Let S be the number of sites where not all n sequences are equal to the same letter. Let k̂ be the average number of pairwise differences between the n sequences. Tajima's D statistic is

$$D=\frac{\widehat{k}-\frac{S}{a_1}}{\sqrt{\widehat{V}}}$$

where $a_1={\Sigma }_{i=1}^{n-1}\frac{1}{i}$, and V̂ is an estimate of the variance of $\widehat{k}-\frac{S}{a_1}$ which is a function of S and some constants which are functions of n only (see Tajima, 1989, equation 38). We reject if D is extreme compared to a generalized beta distribution over the range D_min to D_max with mean equal to 0 and variance 1, and both range parameters are also functions of n only (see Tajima, 1989).

To create a probability model for D Tajima assumed (under the null hypothesis) that:

1. there is no selection (i.e., there is genetic neutrality),

2. the population size is not changing over time,

3. there is random mating in the population,

4. the species is diploid (has two copies of the genetic material),

5. there is no recombination (i.e., a parent passes along either his/her mother's or his/her father's genetic material in its entirety instead of picking out some from the mother and some from the father),

6. any new mutation happens at a new site where no other mutations have happened,

7. the mutation rate is constant over time.

If all the assumptions hold then Tajima's D has expectation 0 and the associated DR is an approximately valid test. The problem is that when we observe an extreme value of D, then it could be either due to (1) chance (but this is unlikely because it is an extreme value), (2) selection has taken place in that population (i.e., assumption 1 is not true), or (3) one of the other assumptions may not be true. This interpretation may seem obvious, but unfortunately, according to Ewens (2004), p. 348, the theory related to tests of genetic neutrality is often applied “without any substantial assessment of whether [the assumptions] are reasonable for the case at hand”.

The MPDR framework applied to this problem could define the same null hypothesis as listed above, but have a different alternative hypothesis for each perspective according to whether one of the assumptions does not hold. For intuition into the following, recall that D will be negative if each site on average has a lower frequency of pairwise nucleotide differences than would be expected. Now consider alternatives where one and only one of the assumptions of the null is false.

Selection

If Assumption 1 is false, then the associated alternative creates a perspective that is Tajima's original one, and that is why the test is called a test of genetic neutrality. When we reject the null hypothesis, then this is seen as implying that there is selection (i.e., there is not genetic neutrality). Specifically, if there has recently been an advantageous mutation such that variability is severely decreased in the population, this is a selective sweep and the expectation of D would be negative. Conversely, if there is balancing selection, then the expectation of D would be positive (see e.g., Durrett, 2002).

Non-constant Population Size

Consider when Assumption 2 is false under the alternative.

Growth of Population

If the population is growing exponentially then we would expect D to be negative (see e.g., Durrett, 2002, p. 154).

Recent Bottleneck

A related alternative view is that the genetic variation in the population happened within a fairly large population, but then the population size was suddenly reduced dramatically and the small remaining population grew into a larger one again. This is known as bottle-necking (see e.g., Winter, Hickey and Fletcher, 2002). Tajima (1989) warned that rejection of the null hypothesis could be caused by recent bottlenecking, and Simonsen, Churchill and Aquadro (1995) showed that Tajima's D has reasonable power to reject under the alternative hypothesis of a recent bottleneck.

Random Mating

Consider the alternative where Assumption 3 is false. If the mating is more common (but still random) within subgroups, then this can lead to positive expected values of D (see e.g., Durrett, 2002, p. 154, Section 2.3).

These results for Tajima's D are now ‘well known’, and a user of the method should be aware of all the possible alternative interpretations (different perspectives) when the null hypothesis is rejected. As with other MPDRs the p-value is calculated the same way, but the interpretation has very real differences depending on the perspective. But unlike the previous examples of Section 5 and 6.1, the different interpretations are not just an expansion or shrinkage of scope of applicability, but they describe qualitatively different directions for looking at rejection of the null.

7. Discussion

We have described a framework where one DR may be interpreted under many different sets of assumptions or perspectives. We conclude by reemphasizing two major points highlighted by the MPDR framework:

• Do not necessarily disregard results of a decision rule because it is obviously invalid from one perspective. Perhaps it is valid or approximately valid from a different perspective. For example, consider a hypothesis test comparing two HIV vaccines, where the response is HIV viral load in the blood one year after vaccination. Even if both groups have median HIV viral loads of zero even under the alternative (which is very likely), invalidating the location shift perspective and all more restrictive perspectives than that (see Figure 1), that does not mean that a WMW DR cannot be applied under a different perspective (e.g., Perspective 3). As another example, suppose that a large clinical trial shows a significant difference in means by t-test but the test of normality determines the data are significantly non-normal. Then the t-test p-value can still be used under the general location shift perspective instead of under the normal shift perspective. Finally, consider the tests for interval censored data developed for continuous data which could be shown to be valid for discrete data as well (see Section 6.1).

• Be careful of making conclusions by assumption. In Section 6.2 we showed how the rejection of a genetic test of neutrality could be interpreted many different ways depending on the assumptions made. Every time a genetic test of neutrality is used, all the different perspectives (sets of assumptions) should be kept in mind, since focusing on only one perspective could lead to the totally wrong interpretation of the decision rule.

Therefore, the fact that a decision rule can have multiple perspectives can be either good or bad for clarification of a scientific theory; the MPDR may help support the theory by offering multiple statistical formulations consistent with it, or the MPDR may highlight statistical formulations that may be consistent with alternative theories as well.

Appendix A: Nonparametric Behrens-Fisher decision rule of Brunner and Munzel

Let R₁, …, R_n be the mid-ranks of the Y_i values regardless of Z_i value, and let W₁, …, W_n be the within-group mid-ranks (e.g., if there are no ties and W_i = w and Z_i = 1 then Y_i is the wth largest of the responses with Z_i = 1). Let ${\stackrel{-}{R}}_1=\frac{1}{n_1}{\Sigma }_{i=1}^n{Z}_i{R}_i$ and ${\stackrel{-}{R}}_0=\frac{1}{n_0}{\Sigma }_{i=1}^n(1-Z_i)R_i$, and

$$\begin{array}{cc}\hfill & {\widehat{\tau }}_1^2=\frac{1}{n_0^2(n_1-1)}\underset{i=1}{\overset{n}{\Sigma }}{Z}_i{\left(R_i-W_i-{\stackrel{-}{R}}_1+\frac{n_1+1}{2}\right)}^2\hfill \\ \hfill & {\widehat{\tau }}_0^2=\frac{1}{n_1^2(n_0-1)}\underset{i=1}{\overset{n}{\Sigma }}(1-Z_i){\left(R_i-W_i-{\stackrel{-}{R}}_0+\frac{n_0+1}{2}\right)}^2.\hfill \end{array}$$

More intuitively, we can write ${\widehat{\tau }}_1^2$ and ${\widehat{\tau }}_0^2$ as

$$\begin{array}{cc}\hfill & {\widehat{\tau }}_1^2=\frac{1}{n_1-1}\underset{i=1}{\overset{n}{\Sigma }}{Z}_i{\left(\tilde{G}\left(Y_i\right)-\stackrel{-}{G}\right)}^2\hfill \\ \hfill & {\widehat{\tau }}_0^2=\frac{1}{n_0-1}\underset{i=1}{\overset{n}{\Sigma }}(1-Z_i){\left(\tilde{F}\left(Y_i\right)-\stackrel{-}{F}\right)}^2\hfill \end{array}$$

where $\tilde{F}\left(t\right)=n_1^{-1}{\Sigma }_{i=1}^n{Z}_i\{I(Y_i<t)+\frac{1}{2}I(Y_i=t)\}$ and $\stackrel{-}{F}=n_0^{-1}{\Sigma }_{i=1}^n(1-Z_i)\tilde{F}\left(Y_i\right)$, and similarly for G̃ and Ḡ. Then, let

$$\begin{array}{c}\hfill V_J=\sqrt{\frac{{\widehat{\tau }}_0^2}{n_0}+\frac{{\widehat{\tau }}_1^2}{n_1}}\hfill \\ \hfill T_{\mathit{NBF}}=\frac{n^{-1}({\stackrel{-}{R}}_1-{\stackrel{-}{R}}_0)}{\sqrt{V_J}}=\frac{\varphi (\widehat{F},\widehat{G})-\frac{1}{2}}{\sqrt{V_J}}.\hfill \end{array}$$

When there is no overlap between the two groups, then τ₀ = τ₁ = 0 and V_J = 0; in this case Neubert and Brunner (2007), p. 5197, suggest setting V_J equal to the lowest possible non-zero value: $\frac{1}{\sqrt{2n_0^2{n}_1^2}}$. We reject when $\left|T_{\mathit{NBF}}\right|>t_{d_B}^{-1}(1-\alpha ∕2)$ where d_B is given by d_W of equation 5.1 except that ${\tau }_0^2$ and ${\tau }_1^2$ replace ${\sigma }_0^2$ and ${\sigma }_1^2$.

Appendix B: Counterexample to uniform control of error rate for the t-test

Let Y₁, …, Y_n be iid Bernoulli random variables with parameter p_n = ln(2)/n. Suppose that the two groups have equal numbers so that n₀ = n₁ = n/2. Let $S_1={\Sigma }_{i=1}^n{Z}_i{Y}_i$ and $S_0={\Sigma }_{i=1}^n(1-Z_i)Y_i$. Then

$$T_t\left(X\right)=\frac{S_1-S_0}{\sqrt{\frac{n}{n-2}\left(S_1-\frac{2S_1^2}{n}+S_0-\frac{2S_0^2}{n}\right)}}.$$

When S₁ ≥ 1 and S₀ = 0 then

$$T_t\left(X\right)=\frac{S_1}{\sqrt{\frac{n}{n-2}\frac{S_1(n-2S_1)}{n}}}\ge \frac{S_1}{\sqrt{\frac{n}{n-2}\frac{S_1(n-2)}{n}}}=\sqrt{S_1}\ge 1$$

Now suppose that α = .16 one-sided. If n ≥ 100 then $t_{n-2}^{-1}\left(.84\right)\ge .9995$ and we would reject whenever S₁ ≥ 1 and S₀ = 0, which occurs with probability

$$\mathit{Pr}[S_1\ge 1\text{and}{S}_0=0]=(1-\mathit{Pr}[S_1=0])\mathit{Pr}[S_0=0]=(1-q_{n_1})q_{n_0}\approx 0.25$$

where $q_n={\left(1-\frac{\ln \left(2\right)}{n}\right)}^n$ and the approximation uses ${\lim }_{n\to \infty }{q}_n=\exp (-\ln \left(2\right))=\frac{1}{2}$; for n = 100 we get q₅₀(1−q₅₀) = 0.249994 and for n > 100 the approximation gets closer to .25. Therefore, for this sequence of distributions, with n > 100 the type I error rate is 0.249 or more instead of the intended 0.16.

Appendix C: Sufficient conditions for uniform control for the t-test

The test δ_t is UAV if we impose certain conditions on the common distribution function F. For example, for 0 < B < ∞ and ∊ > 0, consider the class Ψ_B,∊ of distribution functions such that V ar(Y) ≥ ∊ and E(Y ⁴) ≤ B. We will show that for every sequence of functions F_n ∈ Ψ_B,∊, assuming lim_n→∞ n₀/n = λ₀ and 0 < λ₀ < 1, the type 1 error rate has limit α. We do this in three steps: 1) we use the Berry-Esseen theorem to show that even though F_n may change with n, the distribution of the z-score associated with the sample mean converges uniformly to a normal distribution, 2) we show that the same is true of the z-score for the difference of two sample means, and 3) we show that the same is true for the t-score, which uses the sample variance instead of the population variance in the denominator.

Step 1

Consider a sequence of distribution functions F_n ∈ Ψ_B,∊ with associated mean and variance equal to μ_n and ${\sigma }_n^2$. In this appendix Y_n denotes a random variable from F_n and the sample means for each group are μ̂_1n and μ̂_0n. According to the Berry-Esseen theorem, for any sequence of distribution functions F_n ∈ Ψ_B,∊,

$$\underset{z}{\text{sup}}\left|\mathrm{Pr}\left\{\frac{{\widehat{\mu }}_{1_n}-{\mu }_n}{{\sigma }_n∕\sqrt{n_1}}\le z\right\}-\Phi \left(z\right)\right|\le \frac{33}{4}\frac{E{|Y_n-{\mu }_n|}^3}{{\sigma }_n^3\sqrt{n_1}},$$

for all n. Of course the same is true of the group with Z_i = 0 except with n₁ replaced by n₀, because they have the same distribution. Notice that E|Y_n − μ_n|³ ≤ {E|Y_n − μ_n|⁴}^3/4, and

$$\begin{array}{cc}\hfill {|Y_n-{\mu }_n|}^4& \le {(\left|Y_n\right|+\left|{\mu }_n\right|)}^4\le {\left\{2\max (\left|Y_n\right|,\left|{\mu }_n\right|)\right\}}^4\hfill \\ \hfill & =2^4{\left\{\max (\left|Y_n\right|,\left|{\mu }_n\right|)\right\}}^4\le 2^4({\left|Y_n\right|}^4+{\left|{\mu }_n\right|}^4)\hfill \\ \hfill & =16(Y_n^4+{\left|\mathrm{E}\left(Y_n\right)\right|}^4)\le 16(Y_n^4+\mathrm{E}\left(Y_n^4\right))\hfill \\ \hfill & \le 16(Y_n^4+B).\hfill \end{array}$$

It follows that $\mathrm{E}{|Y_n-{\mu }_n|}^4\le 16(\mathrm{E}\left(Y_n^4\right)+B)\le 32B$, so E|Y_n − μ_n|³ ≤ (32B)^3/4. Furthermore, because ${\sigma }_n^2\ge ∊$, the Berry-Esseen bound is no greater than A_n1 = (33/4)(32B)^3/4/{n₁∊³}^1/2 → 0. The same result holds for the second group.

Step 2

We next show that even though the distribution function F_n may change with n, $({\widehat{\mu }}_{1n}-{\widehat{\mu }}_{0n})∕{\left({\sigma }_n^2(1∕n_1+1∕n_0)\right)}^{1∕2}$ converges uniformly to a standard normal distribution. Specifically, we show that

$$\underset{z}{\text{sup}}\left|\mathrm{Pr}\left\{\frac{{\widehat{\mu }}_{1_n}-{\mu }_n}{{\sigma }_n{b}_n}-\frac{{\stackrel{-}{Y}}_n-{\mu }_n}{{\sigma }_n{b}_n}\le z\right\}-\Phi \left(z\right)\right|\le A_{n_1}+A_{n_0},$$

where b_n = (1/n₀ + 1/n₁)^1/2.

Let λ_0n = n₀/n and λ_1n = 1 − λ_0n = n₁/n, so that ${\lambda }_{0_n}^{1∕2}=b_n^{-1}{n}_1^{-1∕2}$, and assume that λ_0n → λ₀ and 0 < λ₀ < 1. Let H_n1 and H_n0 denote the distribution functions for $Z_{n_1}=({\widehat{\mu }}_{1n}-{\mu }_n)∕({\sigma }_n∕n_1^{1∕2})$ and $Z_{n_0}^{\prime }=({\widehat{\mu }}_{0n}-{\mu }_n)∕({\sigma }_n∕n_0^{1∕2})$, respectively. Then

$$\begin{array}{cc}\hfill & \mathrm{Pr}\left(Z_n\sqrt{{\lambda }_{0_n}}-Z_n^{\prime }\sqrt{{\lambda }_{1_n}}\le z\right)\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{H}_{n_1}\left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right){\mathit{dH}}_{n_0}\left(u\right)\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\{\Phi \left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right)+H_n\left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right)-\phantom{\}}\hfill \\ \hfill & \Phi \phantom{\{}\left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right)\}{\mathit{dH}}_{n_0}\left(u\right)\hfill \\ \hfill & =C_n+D_n,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & C_n={\int }_{\infty }^{\infty }\Phi \left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right){\mathit{dH}}_{n_0}\left(u\right),\hfill \\ \hfill & \text{and}\hfill \\ \hfill & D_n={\int }_{-\infty }^{\infty }\left\{H_{n_1}\left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right)-\Phi \left(\frac{z}{\sqrt{{\lambda }_{0_n}}}+u\sqrt{\frac{{\lambda }_{1_n}}{{\lambda }_{0_n}}}\right)\right\}{\mathit{dH}}_{n_0}\left(u\right).\hfill \end{array}$$

Note that $C_n=\mathrm{Pr}(V<\frac{z}{\sqrt{{\lambda }_{0n}}}+Z_{n_0}^{\prime }\sqrt{\frac{{\lambda }_{1n}}{{\lambda }_{0n}}})=\mathrm{Pr}(Z_{n_0}^{\prime }>V\sqrt{\frac{{\lambda }_{0n}}{{\lambda }_{1n}}}-\frac{z}{\sqrt{{\lambda }_{1n}}})$, where V is independent of $Z_{n_0}^{\prime }$ and has a standard normal distribution. We can therefore rewrite C_n as

$$\begin{array}{cc}\hfill C_n& =\int \left\{1-H_{n_0}\left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right\}\varphi \left(v\right)\mathit{dv}\hfill \\ \hfill & =\int \left\{1-\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right\}\varphi \left(v\right)\mathit{dv}+\hfill \\ \hfill & \int \left\{\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)-H_{n_0}\left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right\}\varphi \left(v\right)\mathit{dv}\hfill \\ \hfill & =\Phi \left(z\right)-\int \left\{\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)-H_{n_0}\left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right\}\varphi \left(v\right)\mathit{dv}\hfill \end{array}$$

To show the last step, notice that if we let V and V′ be independent standard normals, then $V\sqrt{{\lambda }_{0n}}-V^{\prime }\sqrt{1-{\lambda }_{0n}}$ is standard normal, so that

$$\begin{array}{cc}\hfill \int \left\{1-\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right\}\varphi \left(v\right)\mathit{dv}& =\mathit{Pr}\left[V^{\prime }>V\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right]\hfill \\ \hfill & =\mathit{Pr}\left[V\sqrt{{\lambda }_{0_n}}-V^{\prime }\sqrt{{\lambda }_{1_n}}\le z\right]=\Phi \left(z\right)\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill |C_n-\Phi \left(z\right)|& \le {\int }_{-\infty }^{\infty }\left|H_{n_0}\left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)-\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right|\varphi \left(v\right)\mathit{dv}\hfill \\ \hfill & \le {\int }_{-\infty }^{\infty }{A}_{n_0}\varphi \left(v\right)\mathit{dv}=A_{n_0},\hfill \end{array}$$

where A_n0 is as specified at the end of step 1. Also,

$$\begin{array}{cc}\hfill \left|D_n\right|& \le {\int }_{-\infty }^{\infty }\left|H_{n_1}\left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)-\Phi \left(v\sqrt{\frac{{\lambda }_{0_n}}{{\lambda }_{1_n}}}-\frac{z}{\sqrt{{\lambda }_{1_n}}}\right)\right|{\mathit{dH}}_{n_0}\left(u\right)\hfill \\ \hfill & \le {\int }_{-\infty }^{\infty }{A}_{n_1}{\mathit{dH}}_{n_0}\left(u\right)=A_{n_1}.\hfill \end{array}$$

In summary,

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(Z_n\sqrt{{\lambda }_{0_n}}-Z_n^{\prime }\sqrt{{\lambda }_{1_n}}\le z\right)& =\Phi \left(z\right)+C_n-\Phi \left(z\right)+D_n\hfill \\ \hfill \left|\mathrm{Pr}\left(Z_n\sqrt{{\lambda }_{0_n}}-Z_n^{\prime }\sqrt{{\lambda }_{1_n}}\le z\right)-\Phi \left(z\right)\right|& \le |C_n-\Phi \left(z\right)|+\left|D_n\right|\hfill \\ \hfill & \le A_{n_0}+A_{n_1}\to 0.\hfill \end{array}$$ (C.1)

Step 3

The next step is to show that the t-statistic, T_t, also converges to a standard normal distribution. To do so, we will show that ${\widehat{\sigma }}_{\mathit{pn}}^2∕{\sigma }_n^2$ converges to 1 in probability, where ${\widehat{\sigma }}_{\mathit{pn}}^2$ is the pooled variance. Because ${\widehat{\sigma }}_n^2\ge ∊$, this is equivalent to showing that ${\widehat{\sigma }}_{\mathit{np}}^2-{\sigma }_n^2\to 0$ in probability. It is clearly sufficient to show that this is true of each of the two sample variances, say ${\widehat{\sigma }}_{1n}^2$ and ${\widehat{\sigma }}_{0n}^2$, since ${\widehat{\sigma }}_{\mathit{pn}}^2$ is a weighted average of the two sample variances. In the following, we consider only the group with Z_i = 1 so all summations are over {i : Z_i = 1}, and further let _Yin ~ F_n for all i.

$$\begin{array}{cc}\hfill (n_1-1){\widehat{\Sigma }}_{n_1}^2& =\Sigma {(Y_{\mathit{in}}-{\mu }_n+{\mu }_n-{\widehat{\mu }}_{1_n})}^2\hfill \\ \hfill & =\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2+n_1{({\mu }_n-{\widehat{\mu }}_{n_1})}^2+2({\mu }_n-{\widehat{\mu }}_{n_1})\Sigma (Y\mathit{in}-{\mu }_n)\hfill \\ \hfill & =\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2+n_1{({\widehat{\mu }}_{n_1}-{\mu }_n)}^2-2n_1{({\widehat{\mu }}_{n_1}-{\mu }_n)}^2\hfill \\ \hfill & =\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2+n_1{({\widehat{\mu }}_{n_1}-{\mu }_n)}^2.\hfill \end{array}$$

That is, ${\widehat{\sigma }}_{1n}^2={(n_1-1)}^{-1}\{\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2-n_1{({\widehat{\mu }}_{1n}-{\mu }_n)}^2\}$. The proof is slightly easier if we replace n₁ − 1 with n₁. Therefore, we show that $\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2∕n_1-{({\widehat{\mu }}_{1n}-{\mu }_n)}^2-{\sigma }_n^2\to 0$ in probability. Use Markov's inequality to conclude that (μ̂_1n − μ_n)² converges to 0 in probability: $\mathrm{Pr}\{{({\widehat{\mu }}_{1n}-{\mu }_n)}^2>\eta \}\le \mathrm{E}{({\widehat{\mu }}_{1n}-{\mu }_n)}^2∕\eta =\mathrm{var}\left({\widehat{\mu }}_{1n}\right)∕\eta ={\sigma }_n^2∕\left(n_1\eta \right)$, and ${\sigma }_n^2=\mathrm{E}{(Y_n-{\mu }_n)}^2\le \sqrt{E{({\mathrm{Y}}_{\mathrm{n}}-{\mu }_{\mathrm{n}})}^4}\le \sqrt{32B}$ (from the calculations in step 1). Thus, (μ̂_1n − μ_n)² → 0 in probability. The only remaining task is to prove that $|\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2∕n_1-{\sigma }_n^2|$ converges in probability to 0. Note that

$$\begin{array}{cc}\hfill \mathrm{Pr}\left(\left|\frac{\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2}{n_1}-{\sigma }_n^2\right|>\eta \right)& \le \mathrm{var}\left(\Sigma {(Y_{\mathit{in}}-{\mu }_n)}^2∕n_1\right)∕{\eta }^2\hfill \\ \hfill & =\frac{\mathrm{var}{(Y_n-{\mu }_n)}^2}{n_1{\eta }^2}\hfill \\ \hfill & =\frac{E\left({(Y_n-{\mu }_n)}^4\right)-{\left\{E{(Y_n-{\mu }_n)}^2\right\}}^2}{n_1{\eta }^2}\hfill \\ \hfill & \le \frac{E\left({|Y_n-\mu |}^4\right)}{n_1{\eta }^2}\le \frac{32B}{n_1{\eta }^2}\to 0.\hfill \end{array}$$

Appendix D: Justifications for Table 1

D.1. Validity

All the permutation-based DRs (e.g., δ_W, δ_NBFp, δ_tp, and δ_J) are valid whenever each permutation is equally likely under all θ ∈ Θ_H. These DRs can be expressed by either permuting the Z values or permuting the Y values; therefore, all perspectives with F = G for all models in the null space, plus Perspective 9 (the randomization model) give valid tests.

Under H₁₂ then δ_t is asymptotically equivalent to δ_tp, so when δ_t is not valid for less restrictive hypotheses (e.g., Perspectives 14 and 15, see below), δ_tp is also not valid. Since we have assumed F, G ∈ Ψ_fv for all of Table 1, whenever δ_tp is valid then δ_t is at least PAV.

Since the denominator of T_BF can be written as σ̂_BF (1/n₁ + 1/n₀)^1/2 with ${\widehat{\sigma }}_{\mathit{BF}}^2=n^{-1}(n_0{\widehat{\sigma }}_1^2+n_1{\widehat{\sigma }}_0^2)$, and we see that ${\widehat{\sigma }}_{\mathit{BF}}^2$ is just a weighted average of the individual sample variances, then similar methods to Appendix C can be used to show that the other t-tests (δ_tW and δ_tH) are also UAV under Perspective 13.

The δ_t is valid under Perspective 11 and δ_tH is valid under Perspective 14 (see e.g., Dudewicz and Mishra, 1988, p. 502), so (δ_tH, A₁₁) is valid. Since δ_tW is equivalent to δ_tH except it has larger degrees of freedom (see e.g., Dudewicz and Mishra, 1988, p. 502), it is UAV under Perspectives 14 and 11. One can show that (δ_tW, A₁₁) is not valid for finite samples by simulation from standard normal with n₁ = 2 and n₀ = 30, which gives type I error of around 12%.

The rules δ_NBFa and δ_NBFp were shown to be PAV under H₁₀ (see Brunner and Munzel, 2000 and Neubert and Brunner, 2007 respectively).

For any null where F = G and F ∈ Ψ_C, any rank test that is PAV and only depends on the combined ranks is also UAV. To see that, note that such a DR is invariant to monotone transformations. Thus, if we let $Y_{\mathit{in}}^{\ast }=F_n\left(Y_{\mathit{in}}\right)$ for all i = 1, …, n, where F_n is the common distribution function regardless of Z_i, then the $Y_{\mathit{in}}^{\ast }\mathrm{s}$ are iid uniforms. The type I error rate of the rank test applied to the original data is the same as that applied to the uniforms, so the type I error rate is controlled uniformly over all continuous distributions.

Pratt (1964) showed that under the Perspective 14 (Behrens-Fisher), both the WMW and the t tests are not valid (not even PAV), so since A₁₄ ⊏ A₁₅ and and A₁₄ ⊏ A₁₀, both those DRs are not valid under Perspectives 15 and 10. However, note that when n₁ = n₀ then T_t = T_BF, and (δ_t, A₁₄) is UAV. We have previously shown in Section 5.2.2 that Perspective 15 is invalid for any DR which has power > α for some 𝒫 ∈ K₁₅. For Perspective 10 we can show the two simple discrete distributions with three values at (−1, 0, 2) and probability density functions at those three points as (.01, .98, .01) (associated with F) and (.48, .02, .48) (associated with G) are in H₁₀ but are not valid for δ_tW, δ_tH or δ_BFp.

D.2. Consistency

The consistency of δ_W was shown for Perspective 3 by Lehmann (1951) and Putter (1955) expanded this result showing consistency for discrete distributions. We can use the relationship among the assumptions (see Figure 1) to show consistency for most of Table 1. Brunner and Munzel (2000) showed the asymptotic normality of T_NBF whenever φ(F,G) = 1/2 and V ar(F (Y_G)) > 0 and V ar(G(Y_F)) > 0, and it is straightforward to extend this to show the asymptotic normality of

$$T_{\mathit{NBF}}\left(\varphi \right)=\frac{\varphi (\widehat{F},\widehat{G})-\varphi (F,G)}{\sqrt{\frac{{\widehat{\tau }}_0^2}{n_0}+\frac{{\widehat{\tau }}_1^2}{n_1}}},$$

even when φ(F,G) ≠ 1/2. Thus, δ_NBFa is consistent for Perspective 10 and all more restrictive assumptions. Neubert and Brunner (2007) showed the asymptotic normality of the permutation version T_NBF (φ) and hence δ_NBFp is consistent for the same perspectives as δ_NBFa. For all three rank DRs (δ_W, δ_NBFa and δ_NBFp), the associated tests are not consistent when there are alternatives which include probability models with φ(F,G) = 1/2.

The consistency of δ_t under K₁₂ is shown in e.g., Lehmann and Romano (2005), p. 466, and it is straightforward to extend this to δ_tW and δ_tH. Thus, for all more restrictive assumptions those tests are also consistent. Similar methods analogously show that both δ_tW and δ_tH are consistent for K₁₄. For alternatives that contain probability models with μ₀ = μ₁, all the t-tests are not consistent.

Under K₁₁ then δ_t is asymptotically equivalent to δ_tp (Lehmann and Romano, 2005, p. 683, problem 15.10); therefore δ_tp is consistent. Janssen (1997), Theorem 2.2, showed the consistency of δ_tBFp as long as μ₀ ≠ μ₁ under a less restrictive assumptions than A₁₄ which include A₆ and A₇. The DRs δ_tp and δ_BFp are consistent whenever respectively, δ_p and δ_W are consistent assuming finite variances (see van der Vaart, 1998, p. 188).