Vibrational Analysis of the Model Complex (μ-edt)[Fe(CO)₃]₂ and Comparison to Iron-only Hydrogenase: The Activation Scale of Hydrogenase Model Systems

Abstract

Research on simple [FeFe] hydrogenase model systems of type (μ-S₂R)[Fe(CO)₃]₂ (R = ethane, propane) which have been shown to function as robust electrocatalysts for proton reduction, provides a reference to understand the electronic and vibrational properties of the active site of [FeFe] hydrogenases and of more sophisticated model systems. In this study, the solution and solid Raman spectra of (μ-S₂R)[Fe(CO)₃]₂ (R = ethane) and of the corresponding ¹³CO-labeled complex are presented and analyzed in detail, with focus on the ν(C=O) and ν(Fe-CO)/δ(Fe-C=O) vibrational regions. These regions are specifically important as vibrations involving CO ligands serve as probes for the ‘electron richness’ of low-valent transition metal centers and the geometric structures of the complexes. The obtained vibrational spectra have been completely assigned in terms of the ν(C=O), ν(Fe-CO) and δ(Fe-C=O) modes, and the force constants of the important C=O and Fe-CO bonds have been determined using our Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA). In the 400–650 cm⁻¹ region, 15 mixed ν(Fe-CO)/δ(Fe-C=O) modes have been identified. The most prominent Raman peaks at 454, 456 and 483 cm⁻¹ correspond to a combination of ν(Fe-CO) stretching and δ(Fe-C=O) linear bending modes. The less intense peaks at 416 cm⁻¹ and 419 cm⁻¹ correspond to pure δ(Fe-C=O) linear bends. In the ν(C=O) region, the ν(C=O) normal modes at lower energy (1968 and 1964 cm⁻¹) are almost pure equatorial (eq) ν(C=O)_eq stretching vibrations, whereas the remaining four ν(C=O) normal modes show dominant (C=O)_eq (2070 and 1961 cm⁻¹) and (C=O)_ax (2005 and 1979 cm⁻¹; ax = axial) contributions. Importantly, an inverse correlation between the f(C=O)_ax/eq and f(Fe-CO)_ax/eq force constants is obtained, in agreement with the idea that the Fe(I)-CO bond in these types of complexes is dominated by π backdonation. Compared to the reduced form of [FeFe] hydrogenase (H_red), the ν(C=O) vibrational frequencies of (μ-edt)[Fe(CO)₃]₂ are higher in energy, indicating that the dinuclear iron core in (μ-edt)[Fe(CO)₃]₂ is less electron rich compared to H_red in the actual enzyme. Finally, quantum yields for the photodecomposition of (μ-edt)[Fe(CO)₃]₂ have been determined.

INTRODUCTION

Hydrogenases are a class of enzymes found in many microorganisms that catalyze reversible proton reduction to form molecular hydrogen. The two main classes of hydrogenases are [NiFe] and [FeFe] (diiron hydrogenase), the former of which is mainly involved in H₂ oxidation, while the latter is used mainly for H⁺ reduction.¹ [FeFe] hydrogenases are highly evolved for catalysis, producing 6000–9000 molecules of H₂/s per enzyme molecule at 30°C.² In comparison, [NiFe] hydrogenase is ~10–100 times less active.³ Hydrogenases and corresponding model complexes are currently intensively studied in light of designing chemical or biochemical systems for molecular hydrogen production and utilization,^4–17 which are more efficient and cheaper than the currently available platinum catalysts.¹⁸

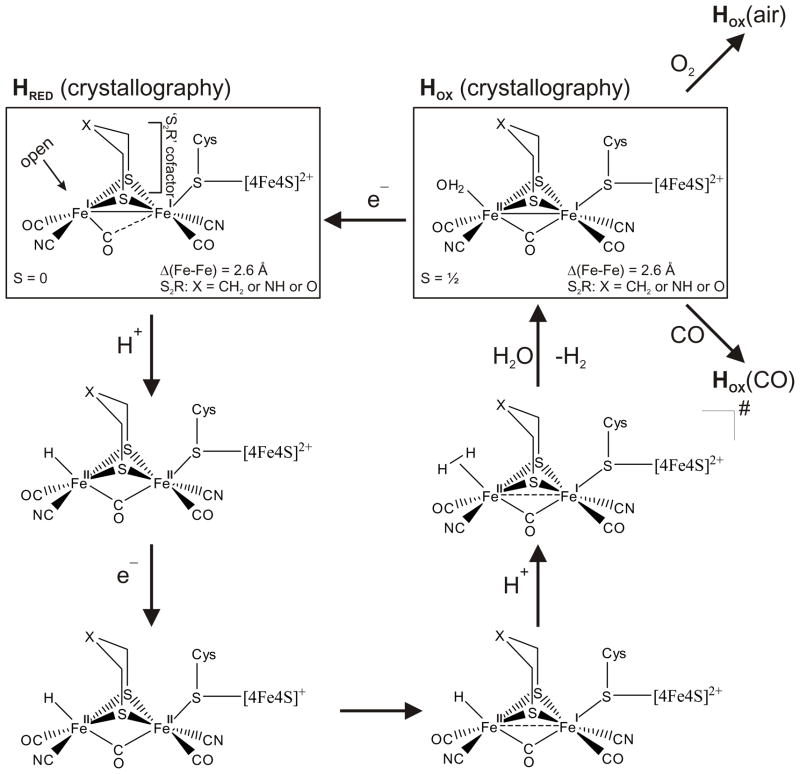
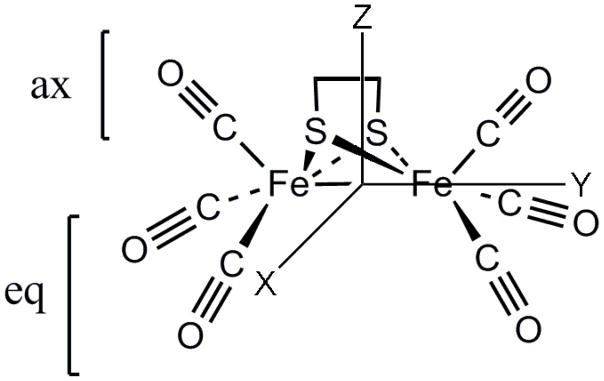
The catalytic site of [FeFe] hydrogenases consists of a dinuclear Fe-Fe center bridged by either a di(thiomethyl)amine, propanedithiolate or -ether non-proteic moiety.^19–22 Cyanide and CO ligands are also bound to the iron centers.^23–27 In the oxidized form (H_ox) of this catalytic site, a CO ligand bridges the two Fe centers, while in the reduced form (H_red) all CO ligands can be considered terminally bound as shown in Scheme 1.²¹ Along with the considerable advances involved in structure elucidation as well as understanding of the biochemical processes in [FeFe] hydrogenases, many synthetic complexes have been designed to closely resemble the active site of this enzyme, and some of these have been investigated with respect to their ability to catalyze proton reduction.^{9, 13, 14, 17, 28–61} One of the simplest [FeFe] hydrogenase models from which many of the more sophisticated mimics are derived is (μ-edt)[Fe(CO)₃]₂ (edt = ethanedithiolate; cf. Figure 1). This complex has an ideal C_2v symmetry where the CO ligands and hydrogens of the bridging methylenes are fully eclipsed leading to an axial-axial (aa) conformation of the Fe₂S₂(CO)₆ core with two axial and four equatorial carbonyl groups.^{62, 63} The isolation and characterization of this complex was first reported more than four decades ago.⁶⁴ (μ-edt)[Fe(CO)₃]₂ and the structurally similar compound (μ-pdt)[Fe(CO)₃]₂ (pdt = propanedithiolate) are still being studied as reference systems for a more complete understanding of the electronic and vibrational properties of [FeFe] hydrogenases and corresponding, more sophisticated model systems.^{29, 65, 66} In addition, (μ-pdt)[Fe(CO)₃]₂ has been shown to function as a robust electrocatalyst for proton reduction (although at a quite large overpotential of ~−1.2 volt),^{13, 16, 67–69} further stressing its important role in [FeFe] hydrogenase model studies. Hence, a detailed understanding of the properties of the simple model systems serves as a basis for the investigation of more complex [FeFe] hydrogenase model compounds. In this respect, vibrations involving the CO ligands are of particular interest because these ligands can serve as probes for the ‘electron richness’ of low-valent transition metal centers.^70–72 Correspondingly, probing vibrational modes in the simple model complex (μ-edt)[Fe(CO)₃]₂ contributes to a general understanding of these types of diiron cluster. Lastly, a detailed vibrational picture of (μ-edt)[Fe(CO)₃]₂ is particularly useful in calibrating DFT calculations frequently applied to gain insight into [FeFe] hydrogenase catalysis of H⁺ reduction.^{8, 49, 59, 73–83}

Scheme 1.

Catalytic mechanism of [FeFe] hydrogenase based on available crystallographic, spectroscopic data, DFT calculations, and insight obtained from model complex studies (references noted in the text).

Figure 1.

Structure of the (μ-edt)[Fe(CO)₃]₂ hydrogenase model complex. The molecule has C_2v symmetry.

The electronic and vibrational properties of (μ-pdt)[Fe(CO)₃]₂ were previously described by Brunold and co-worker using absorption, magnetic circular dichroism (MCD) and resonance Raman (rR) spectroscopies, coupled to DFT computations.⁶⁵ The electronic spectra of (μ-pdt)[Fe(CO)₃]₂ in CH₃CN show two bands at 21,700 cm⁻¹ and 30,400 cm⁻¹, which were assigned to the HOMO → LUMO [Fe(σ^b) → Fe(σ^*)] and HOMO-2 → LUMO [Fe(t_2g) → Fe(σ^*)] transitions, whereas Fe(I) → CO(σ^*) charge transfer transitions were assigned to broad features >32,000 cm⁻¹. The rR spectrum of (μ-pdt)[Fe(CO)₃]₂ (in CH₃CN)⁶⁵ focused on the 200–550 cm⁻¹ region where two intense peaks at 205 and 356 cm⁻¹ were assigned to ν(Fe-Fe) and ν(Fe-S) stretching modes, but the important 400–650 cm⁻¹ range specifically assigned to ν(Fe-CO) stretching and δ(Fe-C=O) bending modes was not analyzed, and no detailed assignment of the features observed in this region was reported. In addition, the ν(C=O) modes observed between 1900 and 2050 cm⁻¹ were not assigned. From Normal Coordinate Analysis (NCA), Fe-Fe, Fe-S and Fe-CO force constants of 1.20, 1.50 and 2.35 mdyn/Å, respectively, were reported for (μ-pdt)[Fe(CO)₃]₂. For the NCA fit, (μ-pdt)[Fe(CO)₃]₂ was simplified by eliminating the -C₃H₈- dithiol linkage, and by using a hypothetical “atomic” ligand with an effective mass of 28 amu substituting the CO ligands. Because of this approximation, no analysis of Fe-CO and C=O stretching and Fe-C=O bending modes could have been provided. In this study, we do not make any of these assumptions, but in contrast, use the complete molecule (μ-edt)[Fe(CO)₃]₂ in our analysis. This includes actual CO ligands and application of C_2v symmetry, where the axial and equatorial CO ligands are treated separately. We have analyzed all ν(C=O), ν(Fe-CO) and δ(Fe-C=O) vibrations in detail and in this way, we are expanding the previous studies⁶⁵ that focused on ν(Fe-Fe) and ν(Fe-S) modes only.

The goal of this study is to elucidate the vibrational properties of (μ-edt)[Fe(CO)₃]₂ focusing on the ν(C=O) (1900–2100 cm⁻¹) and ν(Fe-CO) stretching and δ(Fe-C=O) bending (400–650 cm⁻¹) regions. In fact, this is the first study on a hydrogenase model complex that analyzes the vibrational assignments of these modes in detail. These results provide a starting point for a complete understanding of the vibrational structure of the active site of the [FeFe] hydrogenase enzyme. Experimental IR and Raman spectra were obtained on the solid and solution forms of (μ-edt)[Fe(CO)₃]₂ and its corresponding ¹³CO-labeled complex. Calculated IR and Raman spectra were generated to help in spectral assignments. Based on these results, a Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA)^{84, 85} was then performed where a subset of force constants of the DFT-calculated force field is fit to reproduce the vibrational frequencies of interest with their corresponding isotope shifts. QCC-NCA generates experimentally calibrated force constants and potential energy distributions (PED’s) of selected vibrational frequencies, which gives a detailed description of the vibrational structure of the molecule of interest, here (μ-edt)[Fe(CO)₃]₂. The photochemistry of this molecule has also been investigated.

MATERIALS AND METHODS

Synthesis of (μ-edt)[Fe(CO)₃]₂ and (μ-edt)[Fe(¹³CO)₃]₂

The synthesis of (μ-edt)[Fe(CO)₃]₂ was performed from the reaction of 1,2-ethanedithiol with Fe₃(CO)₁₂ in toluene at ~80 °C as previously described.^{86, 87} Unlike the synthesis of the natural abundance sample, the corresponding ¹³CO-labeled complex was prepared without using preformed iron carbonyls. In this more recent method, (μ-edt)[Fe(¹³CO)₃]₂ was prepared from the reaction of FeCl₂ with Na₂S₂C₂H₄ under an atmosphere of ¹³CO with Zn as a reductant.⁸⁸ The samples were recrystallized from a saturated solution of hexane as reported by Hughes et al.⁶²

UV-Visible, Infrared and Raman spectroscopy

Room temperature absorption spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile were collected using a Varian Cary 5000 spectrophotometer. A 0.2 mM solution in a 1 cm × 1 cm quartz cuvette was photolyzed by exposure to UV light (applying a O.D 2.0 gray filter with 10% transmittance) at ~2cm distance (Intensity, I = 2.5 × 10⁻⁷ einsteins/min, after passing through the grey filter). The sample was exposed at 1 min intervals for 40 min to prevent it from thermal degradation, and the UV-Vis spectra were recorded after each minute. Standard actinometry was employed using ferrioxalate to determine the quantum yield, φ.⁸⁹

Infrared spectra were measured using a Perkin-Elmer Spectrum GX FTIR. For the IR solution studies of (μ-edt)[Fe(CO)₃]₂ and (μ-edt)[Fe(¹³CO)₃]₂, the following solvents were used: hexane, benzene, THF, butyronitrile, dichloromethane and acetonitrile. For the solid IR studies, diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) was performed on ~5 mg of powdered sample diluted with KBr.

The resonance Raman spectra were obtained on solids and saturated solutions of (μ-edt)[Fe(CO)₃]₂ and the corresponding ¹³CO-labeled complex in CH₃CN using 514, 568 and 647 nm excitation from a SpectraPhysics Beamlok 2060-RS Kr⁺-Ar⁺ laser. The excitation beam (20 mW) was focused onto ~30 mg or 0.2 mL of the sample in an EPR tube contained in an EPR coldfinger dewar with liquid N₂ to prevent thermal degradation. The scattered photons were dispersed by a Princeton Instruments two-stage TriVista 555 system and detected by a liquid N₂-cooled Princeton Instruments Spec-10:400B/LN CCD camera. A typical resolution in these experiments was 0.5 cm⁻¹.

Density Functional Theory (DFT) calculations

The geometry of (μ-edt)[Fe(CO)₃]₂ was fully optimized in the gas phase using a hybrid functional consisting of the three-parameter exchange functional of Becke⁹⁰ and the non-local correlation functional of Lee, Yang and Parr (B3LYP).⁹¹ All atoms were optimized using Ahlrich’s triple zeta valence polarization basis set (TZVP)⁹² as implemented in Gaussian 03.⁹³ The fully optimized structure was confirmed by following frequency calculations showing no imaginary modes. Geometry optimizations were performed in C₁ symmetry. The obtained structure of (μ-edt)[Fe(CO)₃]₂ shows the usual C_2v geometry as observed in the crystal structures of this class of compounds.^{62, 63} For comparison, the gradient-corrected functional BP86 was also applied to (μ-edt)[Fe(CO)₃]₂, combined with the TZVP basis set. The geometric structure of the complex was fully optimized and vibrational energies were calculated with BP86/TZVP. As shown in Tables 1 and S4, good agreement with experiment was also obtained in this case, in particular for the ν(C=O) stretching vibrations. On the other hand, B3LYP/TZVP is superior for the ν(Fe-CO)/δ(Fe-C-O) metal-ligand vibrational region, and hence, the B3LYP calculations provide a better starting point for the QCC-NCA simulation. We therefore focus mostly on the B3LYP/TZVP results in this paper.

Table 1.

Selected bond distances (Å) and angles (°) in (μ-edt)[Fe(CO)₃]₂

	X-ray crystallography		DFT calculationsb
(μ-edt)[Fe(CO)3]2a	Hughes et. al, 62	Messelhauser et. al63	B3LYP	BP86
Fe-Fe	2.497	2.502	2.525	2.540
Fe-S (mean)	2.245	2.239	2.297	2.279
Fe-Cax (mean)	n/a	1.798	1.801	1.784
Fe-Ceq (mean)	n/a	1.785	1.808	1.789
S···S	2.893	2.887	2.971	2.951
S-C (mean)	n/a	1.827	1.853	1.863
C-C	n/a	1.487	1.526	1.523
Fe-S-Fe (mean)	67.6	68.0	66.7	67.7
S-Fe-S (mean)	80.2	80.3	80.6	80.7
S-C-C (mean)	n/a	112.6	113.0	112.5

^aThe bond distances and angles represent the mean of two or more equivalents types of bonds or angles.

^bThis work using the basis set TZVP.

n/a = data not available.

Quantum Chemistry Centered Normal Coordinate Analysis (QCC-NCA)

The calculated force field from DFT was used to generate initial force constants in internal coordinates for the following NCA. A modified version of the program Redong (QCPE 628) was used to transform the DFT force field into internal coordinates.⁹⁴ In the QCC-NCA approach,^{84, 85} only a subset of the force constants in the f matrix is then adjusted to reproduce the vibrational frequencies and the corresponding isotope shifts in the specific subunit of interest in the molecule. The B3LYP/TZVP geometry-optimized structure of (μ-edt)[Fe(CO)₃]₂ was used without any modifications in the QCC-NCA treatment. In C_2v symmetry, the two axial C=O and four equatorial C=O ligands are symmetry equivalent. Correspondingly, two diagonal force constants for the axial and equatorial C=O stretching coordinates, and four non-diagonal elements were used to reproduce the six experimental vibrational ν(C=O) frequencies (1900–2100 cm⁻¹) obtained from Raman spectroscopy. The four non-diagonal elements are: f[(C=O)_ax/(C=O)_eq], f[(C=O)_eq/(C=O)_eq] for CO bound to the same Fe, f[(C=O)_eq/(C=O)_eq]_ss for CO ligands on the same side (ss) of the yz plane of the molecule, and f[(C=O)_eq/(C=O)_eq]_os on opposite sides (os) of the yz plane as shown in Figure 1. This six-parameter fit reproduced vibrational energies to a difference of 1 cm⁻¹ or less.

The force constants in the Fe-CO region were used to reproduce the experimentally observed fifteen of the eighteen ν(Fe-CO) and δ(Fe-CO) modes. Four diagonal and eight non-diagonal force constants were used to obtain a fit that differs from the experimental frequencies by at most 3 cm⁻¹. The four diagonal elements are the f(Fe-C=O)_ax, f(Fe-C=O)_eq linear bending and f(Fe-CO)_ax, f(Fe-CO)_eq stretching force constants. The eight non-diagonal elements are: f[(Fe-CO)_ax/(C=O)_ax], f[(Fe-CO)_eq/(C=O)_eq], f[(Fe-CO)/(Fe-S)] trans interaction, f[(Fe-CO)_ax/(Fe-CO)_eq], f[(Fe-CO)_eq/(C=O)_eq]_ss for CO ligands on the same side of the yz plane of the molecule (but at different Fe centers), f[(Fe-CO)_ax/(C=O)_eq], f[(Fe-CO)_eq/(C=O)_ax], and f[(Fe-CO)_eq/(C=O)_eq]_os for CO bound to the same Fe but on opposite sides (os) of the yz plane of the molecule (cf. Figure 1). The force constants for all (Fe-C=O)_ax and all (Fe-C=O)_eq were initially fit to just one diagonal force constant (0.4092 and 0.4626 mdyn/Å, respectively) on the assumption that each set of axial and each set of equatorial linear bends are equivalent, but this desymmetrized the vibrations of the molecule. This is due to the fact that the two orthogonal directions of Fe-C=O linear bending are not equivalent in the given geometry of the molecule. In order to incorporate this without inflating the number of parameters (force constants) in the fit, adjustments were made to preserve the percent differences between each set of linear bending force constants as predicted by the DFT calculation. This reduces the 12 total Fe-C=O bending force constants to only two parameters in the fit. A few other force constants were also manually adjusted, but not included in the fit to reproduce the experimental vibrational energies (Table S1, Supplementary Information). In all cases, the symmetry of the molecule was taken into account.

RESULTS

A. DFT geometry optimizations

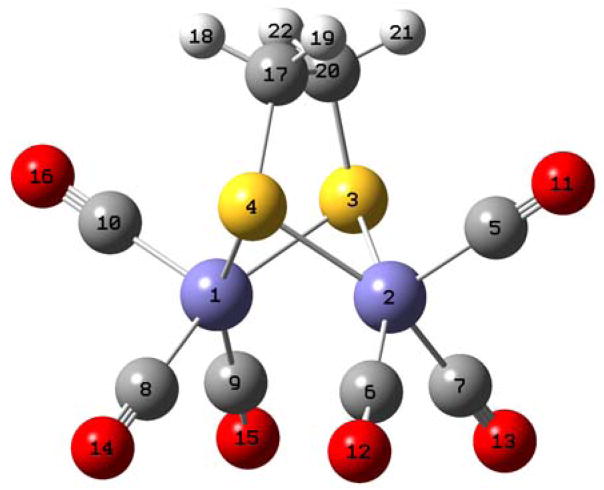
The B3LYP/TZVP geometry-optimized structure of (μ-edt)[Fe(CO)₃]₂ (Figure 2) shows very close resemblance of the actual crystal structure of this molecule in its axial/axial (aa) conformation, where the CO ligands and the bridging methylene groups in edt are fully eclipsed.^{62, 63} For example, the Fe-Fe distance in the crystalline form is 2.497 Å,⁶² which is comparable to 2.525 Å for the optimized structure. The Fe-S bond distances for the crystal and calculated structures are 2.245 Å⁶² and 2.297 Å, respectively. The axial and equatorial Fe-C distances in the crystal structure are 1.798 Å and 1.785 Å,⁶³ respectively, which is again comparable to the optimized structure (1.801 and 1.808 Å, respectively). Table 1 lists selected bond distances and angles of the experimental and B3LYP/TZVP optimized structure of (μ-edt)[Fe(CO)₃]₂ for comparison. The good agreement between the DFT calculated geometry of (μ-edt)[Fe(CO)₃]₂ and the crystal structure of this compound indicates that our DFT calculations are well suited to describe the electronic and vibrational properties of this complex. This is essential for the QCC-NCA method, which relies on a good description of the molecule under investigation (see Section C). Importantly, (μ-edt)[Fe(CO)₃]₂ shows an effective C_2v symmetry both in the optimized structure and the crystal structure, indicating that aa is the lowest-energy conformation of the dinuclear cluster.

Figure 2.

DFT (B3LYP/TZVP) optimized structure of (μ-edt)[Fe(CO)₃]₂. The atom numbers are referred to in the Supplementary Information (Table S2) showing the coordinates of the molecule.

The BP86/TZVP optimized structure of (μ-edt)[Fe(CO)₃]₂ shows comparable bond distances and angles as the B3LYP/TZVP optimized geometry (cf. Table 1), and hence, is also in excellent agreement with experiment. Interestingly, the DFT functional-dependence of the geometry of (μ-edt)[Fe(CO)₃]₂ is therefore unusually low.

B. Spectroscopic results

1. Infrared spectroscopy

The diffuse reflectance FTIR spectra of solid (μ-edt)[Fe(CO)₃]₂ and of the ¹³CO-labeled complex are shown in Figure S1. The spectrum of (μ-edt)[Fe(CO)₃]₂ is dominated by broad signals corresponding to ν(C=O) stretches in the 1850–2100 cm⁻¹ region. Here, three distinct bands and a shoulder are observed at 2074, 2028, 1987 and 1949 cm⁻¹, which are shifted to lower energy by ~50 cm⁻¹ in the ¹³CO-labeled complex (Figure S1). Vibrational energy shifts are also observed between both compounds in the 400–650 cm⁻¹ region where the ν(Fe-CO) stretching and δ(Fe-C=O) bending modes occur. In this region, prominent peaks at 453, 499, 569, and 616 cm⁻¹ are observed that shift by ~−10 cm⁻¹ in the ¹³CO-labeled compound.

The IR spectrum of (μ-edt)[Fe(CO)₃]₂ in hexane shows five bands in the ν(C=O) region at 2078, 2038, 2008, 1995, and 1985 cm⁻¹ (cf. Figure 3) that shift by ~50 cm⁻¹ to lower energy upon ¹³CO substitution, in agreement with the Raman results (vide infra; Table 2). These values for ν(C=O) are similar to the frequencies previously reported by Hughes et al.⁶² for the same compound and solvent (2084(s), 2044(s), 2012(s), 1997(vs), and 1988(m) cm⁻¹). In comparison, the IR spectrum of (μ-pdt)[Fe(CO)₃]₂ reflects the pseudo-C_2v symmetry of this compound, and shows five similar bands in hexane at 2076(s), 2035(s), 2006(s), 1992(s) and 1983(w) cm⁻¹,⁹⁵ and corresponding features in heptane.⁶⁶ The number of bands experimentally observed is consistent with the number of ν(C=O) modes predicted by group theory for this molecule. The symmetry assignments of these modes are discussed in Section C. Interestingly, two very weak peaks (referred to as signal “A”) are additionally observed at lower energy (1958 and 1955 cm⁻¹; cf. Figure 3) in (μ-edt)[Fe(CO)₃]₂, which we conclude are due to an impurity based on purification and experiments in different solvents. In the former case, the compound was purified on a silica gel column where a yellow band was observed to adhere to the column. The collected fraction of the purified sample showed a small reduction in the intensity of peak “A” as seen in the IR spectrum (not shown).

Figure 3.

Infrared spectrum of (μ-edt)[Fe(CO)₃]₂ in hexane at room temperature.

Table 2.

Assignment of the Infrared (IR) and resonance Raman (rR) spectra of (μ-edt)[Fe(CO)₃]₂ and (μ-edt)[Fe(¹³CO)₃]₂ focusing on the ν(C=O) and ν(Fe-CO)/δ(Fe-C=O) regions.

Mode	Symmetrya (ax ± eq)	Experimental/cm−1		Calculated/cm−1
		IRb (12CO/13CO)	rRc (12CO/13CO)	DFTd	NCAe (12CO/13CO)
ν(C=O)	A1 + A1	2078(2077)/2030	2070/2023	2153 m, IR; m, Raman	2069/2020
ν(C=O)	B2 + B2	2038(2037)/1991	2005/1959	2105 vs, IR; vw, Raman	2006/1959
ν(C=O)	A1 − A1	2008(1998)/1962	1979/1934	2095 s, IR; m, Raman	1980/1934
ν(C=O)	B1	1995/1950	1968/1924	2083 s, IR; m, Raman	1968/1922
ν(C=O)	A2	not observed	1964/1919	2076 na, IR; m, Raman	1963/1918
ν(C=O)	B2 − B2	1985/1940	1961/1917	2072 w, IR; m, Raman	1960/1915
ν(Fe-CO) + δ(Fe-C=O)	A1 + A1		630/615	636 w, IR; vw, Raman	628/617
ν(Fe-CO) + δ(Fe-C=O)	A1 − A1		592/579	601 w, IR; vw, Raman	594/578
ν(Fe-CO) + δ(Fe-C=O)	B1 − B1		572/562	578 w, IR; vw, Raman	573/562
ν(Fe-CO) + δ(Fe-C=O)	A2 − A2		565/556	571 na, IR; vw, Raman	567/556
δ(Fe-C=O)	B1 + B1		528/519	526 vw, IR; vw, Raman	528/518
ν(Fe-CO) + δ(Fe-C=O)	A1 − A1		503/495	507 w, IR; vw, Raman	506/496
ν(Fe-CO) + δ(Fe-C=O)	A2 + A2		494/485	496 na, IR; vw, Raman	496/482
ν(Fe-CO) + δ(Fe-C=O)	B1 − B1		483/474	481 vw, IR; w, Raman	482/475
ν(Fe-CO) + δ(Fe-C=O)	B2 − B2		470/462	471 vw, IR; vw, Raman	473/465
ν(Fe-CO) + δ(Fe-C=O)	A2		463/452	454 na, IR; vw, Raman	461/449
ν(Fe-CO) + δ(Fe-C=O)	A1 − A1		456/444	448 vw, IR; w, Raman	453/442
ν(Fe-CO) + δ(Fe-C=O)	B1		454/442	446 vw, IR; w, Raman	452/441
ν(Fe-CO) + δ(Fe-C=O)	B2 − B2		447/435	440 w, IR; vw, Raman	444/432
δ(Fe-C=O)	A2 + A2		419/406	416 na, IR; vw, Raman	422/408
δ(Fe-C=O)	B1 + B1		416/403	410 vw, IR; vw, Raman	416/403

^aSymmetry labels are given based on the C_2v symmetry of the molecule; ax = axial, eq = equatorial. In A₁+A₁, for example, the first symmetry label corresponds to the symmetry of the axial internal coordinate; the second corresponds to the equatorial internal coordinate that the normal mode is comprised of (+ = in-phase combination).

^bVibrational IR energies were obtained in hexane and acetonitrile (in parenthesis).

^cFrom resonance Raman measurements on a saturated solution in acetonitrile.

^dUsing B3LYP/TZVP. Intensities are classified as: vs = very strong; s = strong; m = medium; w = weak; vw = very weak.

^eVibrational energies obtained from Normal coordinate analysis (NCA) using vibrational frequencies from the rR spectra.

2. Resonance Raman spectroscopy

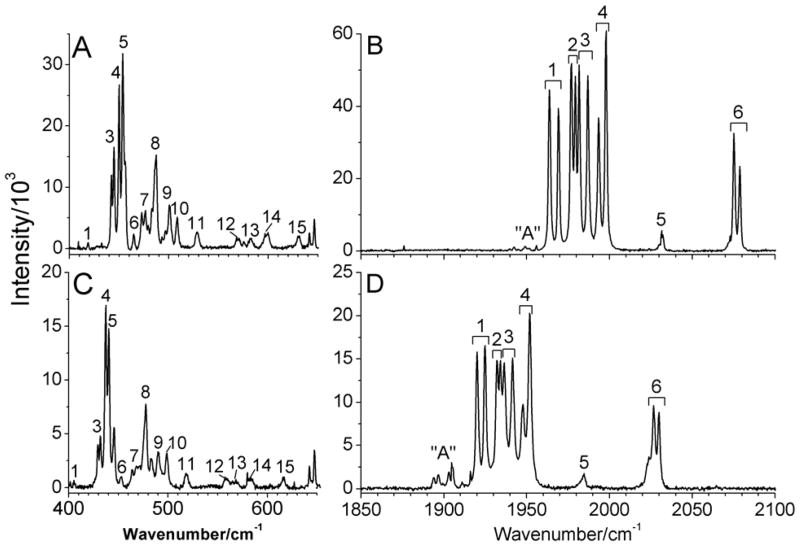
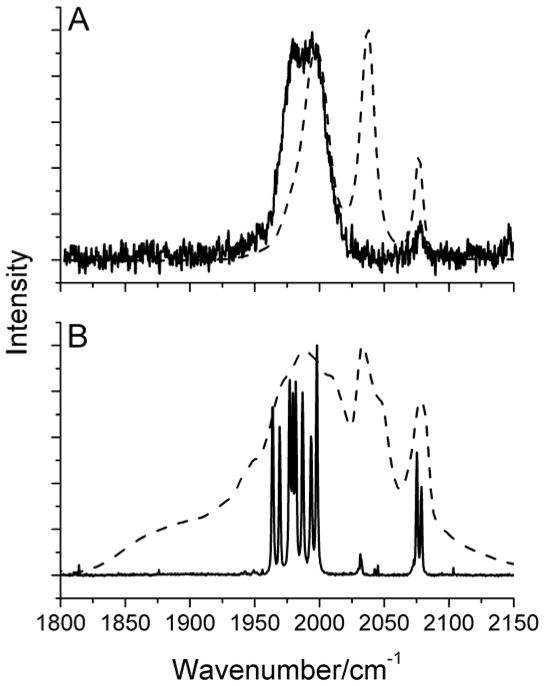
Figure 4 shows the resonance Raman spectra of solid (μ-edt)[Fe(CO)₃]₂ and (μ-edt)[Fe(¹³CO)₃]₂ in the ν(Fe-CO)/δ(Fe-C=O) (400–650 cm⁻¹) and ν(C=O) (1850–2100 cm⁻¹) regions at 77K. Interestingly, all observed features appear split into two components in the spectra with an average splitting of 5 cm⁻¹. The splittings are most distinct in the 1850–2100 cm⁻¹ region. These small splittings can be explained by the presence of two independent but virtually identical molecules in the crystalline unit cell of solid (μ-edt)[Fe(CO)₃]₂ that exhibit slightly different vibrational energies. The occurrence of two virtually identical molecules in crystals of (μ-edt)[Fe(CO)₃]₂ has previously been reported.^{62, 63}

Figure 4.

Raman spectra of solid (μ-edt)[Fe(CO)₃]₂ (A and B) and (μ-edt)[Fe(¹³CO)₃]₂ (C and D) at 77K. The peaks in the spectra are labeled according to the number of modes predicted by group theory in the ν(Fe-CO)/δ(Fe-C=O) and ν(C=O) regions. The spectra were obtained by exciting the samples at 568 nm. Peak “A” is attributed to impurities present in the sample, as indicated by the variable intensity of this feature relative to the signals of (μ-edt)[Fe(CO)₃]₂ in panels B and D.

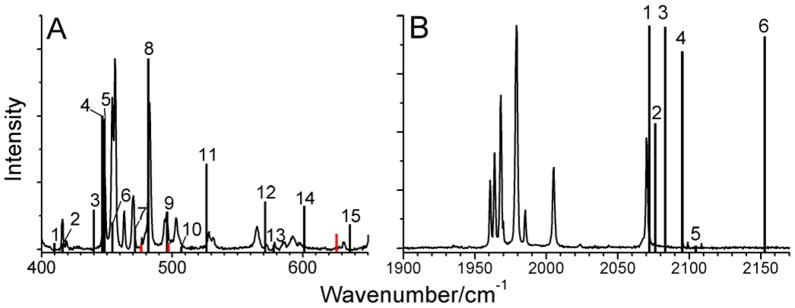
In the ν(Fe-CO)/δ(Fe-C=O) region, there are fifteen normal modes that can be identified from the spectra as (mixed) Fe-CO stretching and Fe-C=O bending vibrations. These features are labeled accordingly in Figure 4. The most intense peaks in this region are located in the 440–490 cm⁻¹ frequency range (Figure 4A). The prominent peaks 3 and 4 show clearly distinguishable splittings at 442, 445, and 450, 453 cm⁻¹, respectively, while the weaker vibrational features at higher energy are observed as single peaks at 529, 569, 582, 598, and 630 cm⁻¹. Upon ¹³CO labeling, all peaks in the ν(Fe-CO)/δ(Fe-C=O) region shift by ~10 cm⁻¹ to lower energy (Figure 4C).

In the ν(C=O) region, a group of intense vibrational features is observed at 1960–2000 cm⁻¹, and less intense isolated peaks are found at 2031, 2075, and 2078 cm⁻¹ for the natural abundance isotopes (n.a.i) complex (Figure 4B). The peaks labeled 1–6 in the spectra correspond to the six ν(C=O) normal modes of the complex (Figures 4B and 4D). These peaks shift by ~50 cm⁻¹ to lower energy upon ¹³CO labeling in agreement with the IR results. The overall appearance of the Raman spectra in the ν(C=O) region is similar for (μ-edt)[Fe(CO)₃]₂ and the ¹³CO-labeled complex, except for the more noticeable weak signals “A” in the lower energy region (at ~1900 cm⁻¹) for the ¹³CO-labeled complex, which are less intense in the n.a.i. complex (at ~1950 cm⁻¹; cf. Figures 4B and 4D). These additional peaks are also observed in the IR spectrum of (μ-edt)[Fe(CO)₃]₂ in hexane as discussed above (Figure 3). Interestingly, the Raman spectrum of the ¹³CO compound reveals that these features are actually split into two components by 3 cm⁻¹ (cf. Figure 4D), which becomes apparent due to the fact that these modes are more intense in the ¹³CO case. As discussed earlier, we conclude this to be a minor impurity.

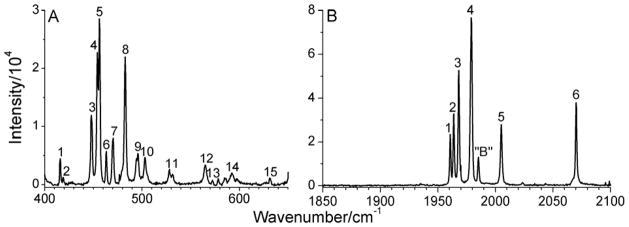
Compared to the rather complicated Raman spectrum of solid (μ-edt)[Fe(CO)₃]₂, the spectrum of a saturated acetonitrile solution of this compound shows well-resolved single peaks (Figure 5) that correlate well with the solid state data. This provides strong evidence that the observed splittings in solid (μ-edt)[Fe(CO)₃]₂ are due to a solid state effect, and not the presence of different conformers. In addition, the fact that the relative intensities of the peaks in solution and the solid state are similar indicates that most (if not all) of the compound exists in the form of the aa conformer in solution as observed in the crystal structure.

Figure 5.

Raman spectrum of a saturated solution of (μ-edt)[Fe(CO)₃]₂ in acetonitrile focusing on A) the ν(Fe-CO)/δ(Fe-C=O) and B) the ν(C=O) regions. The peaks in the spectra are labeled according to the number of modes predicted by group theory in the ν(Fe-CO)/δ(Fe-C=O) and ν(C=O) regions, respectively. Peak “B” does not correspond to a signal of (μ-edt)[Fe(CO)₃]₂ as indicated by the absence of this signal in the solid state Raman spectra (cf. Figure 4). The spectrum was obtained by exciting the samples at 568 nm.

Figure 5A shows well resolved, single vibrational bands attributed to ν(Fe-CO) and δ(Fe-C=O) modes of (μ-edt)[Fe(CO)₃]₂ in the 400–650 cm⁻¹ region. In order to obtain these well-resolved peaks, a saturated solution of (μ-edt)[Fe(CO)₃]₂ in acetonitrile was necessary. The use of a lower concentration resulted in broad, unresolved bands. For (μ-edt)[Fe(CO)₃]₂, group theory predicts eighteen ν(Fe-CO) and δ(Fe-C=O) vibrational modes, six of them correspond to Fe-CO stretches and twelve to Fe-C=O linear bends. Here, δ(Fe-C=O) of each Fe-C=O unit has two orthogonal components, which, due to the low symmetry of the complex, are not degenerate. In this study, we were able to assign fifteen of these vibrational modes based on comparison with the ¹³CO-labeled complex and DFT calculations. These bands are labeled 1–15 as shown in Figures 4A and 5A. These are observed as singlet peaks in the solution data in Figure 5A at 416, 419, 447, 454, 456, 463, 470, 483, 494, 503, 565, and 630 cm⁻¹. The two most intense peaks at 454 and 456 cm⁻¹ (peaks 4 and 5) are considered as two different modes based on the DFT calculations. Two additional weak features are observed between bands 13 and 14. These are not included in the assignment because they do not match well with any feature in the spectrum of the ¹³CO-labeled complex and the DFT calculations. A complete list of the ν(Fe-CO) and δ(Fe-C=O) vibrational frequencies along with the symmetries of these modes is given in Table 2 for both the natural abundance and ¹³CO-labeled complex. Note that ν(Fe-Fe) and a totally symmetric ν(Fe-S) stretching mode occur at 205 and 356 cm⁻¹, respectively, for (μ-pdt)[Fe(CO)₃]₂ as assigned by Brunold and co-worker.⁶⁵ In our case, two corresponding peaks that are insensitive to ¹³CO labeling are observed at 212 and 342 cm⁻¹. This is outside the range of the ν(Fe-CO) and δ(Fe-C=O) vibrational modes, so these features do not interfere with our analysis.

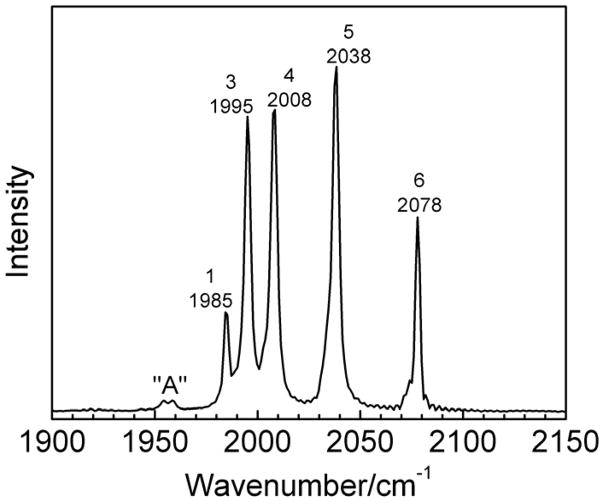
In the ν(C=O) region, the solution Raman spectrum of (μ-edt)[Fe(CO)₃]₂ shows single bands at 2070, 2005, 1979, 1968, 1964, and 1961 cm⁻¹ that shift by ~50 cm⁻¹ to lower energy in the ¹³CO-labeled complex (Figure 5B). Group theory predicts six Raman active peaks for (μ-edt)[Fe(CO)₃]₂. The Raman active peaks are labeled 1–6 in Figures 4B and 5B. Interestingly, a seventh vibrational feature is observed at 1985 cm⁻¹ (between peaks 4 and 5) which will be referred to as signal “B”. This feature is absent in the solid state data and possibly in the ¹³CO data.⁹⁶ Peak “B” (~1985 cm⁻¹) is not attributed to a photo-cleavaged product upon exposure of (μ-edt)[Fe(CO)₃]₂ to the 568 nm laser light as the relative intensity of this peak does not show any dependence on exposure time. In this respect, note that in (μ-pdt)[Fe(CO)₃]₂, peaks at ~1930 and ~1960 cm⁻¹ were observed upon 365 nm photolysis.⁹⁷

3. Comparison between the IR and Raman spectra

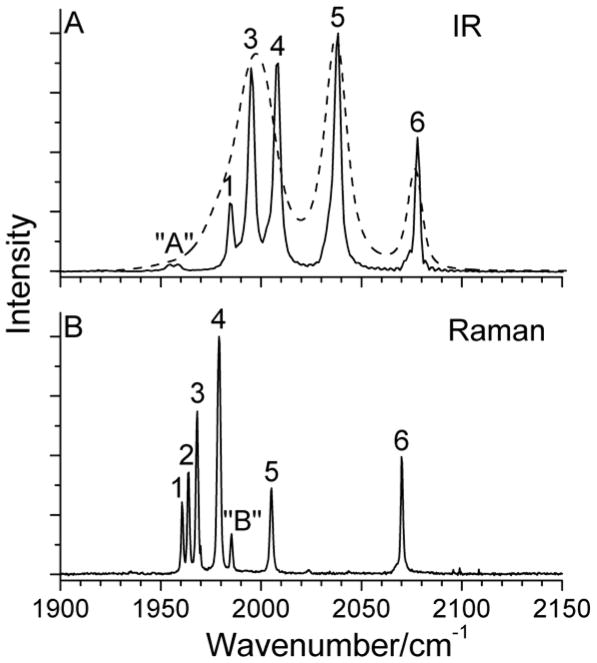
As mentioned earlier, group theory predicts five IR active and six Raman active peaks in the ν(C=O) region for (μ-edt)[Fe(CO)₃]₂. As shown in Figure 6, band 2 is the exclusively Raman active peak, which is not observed in the IR spectrum (A₂ symmetry). The symmetry assignment of each ν(C=O) mode is given in Table 2.

Figure 6.

A) IR and B) Raman spectra of (μ-edt)[Fe(CO)₃]₂. The IR spectra were taken in hexane (solid line) and acetonitrile (dashed line) for comparison. The Raman spectrum was recorded in a saturated acetonitrile solution with λ_ex = 568 nm. The peaks in the spectra are labeled according to the number of modes predicted by group theory in the ν(C=O) region. Peak “A” in the top panel is attributed to impurities (see Figure 4). The origin of peak “B” in the bottom panel is unclear (cf. Figure 5).

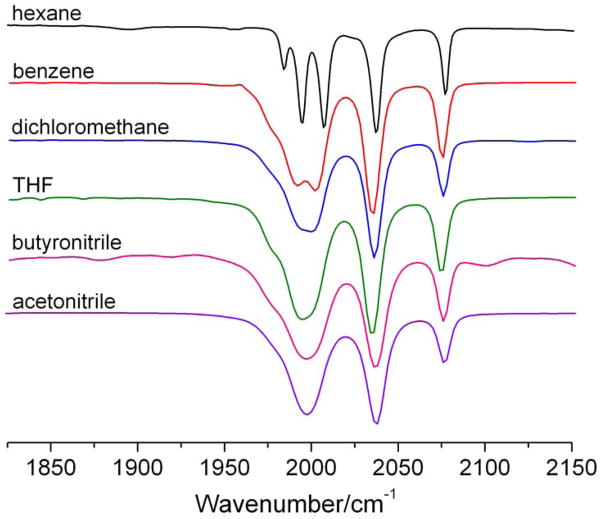
Another difference between the IR and Raman spectra of (μ-edt)[Fe(CO)₃]₂ is the distinct discrepancy in vibrational energies in the ν(C=O) region for the solution data (Figure 6). For example, a ~30 cm⁻¹ shift to lower energy of bands 1–5 in the Raman spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile (at 77K) is observed relative to bands 1,3–5 in the IR spectrum taken in hexane (at RT). In order to test whether this relates to the polarity of the solvent, the IR spectrum of (μ-edt)[Fe(CO)₃]₂ was taken in acetonitrile at RT for comparison. Figure 6A shows an overlay of the IR spectra of (μ-edt)[Fe(CO)₃]₂ in hexane and acetonitrile. Unlike in hexane where five well-resolved peaks are observed, only three peaks at 2077, 2037, and 1998 cm⁻¹ are noticeable in acetonitrile. This three-peak profile in acetonitrile is consistent with the FTIR spectrum of (μ-pdt)[Fe(CO)₃]₂ reported in the same solvent (observed energies: 2074, 2032, and 1995 cm⁻¹).⁶⁶ To further understand the effect of polarity on the ν(C=O) modes of (μ-edt)[Fe(CO)₃]₂, IR spectra were recorded in different polar and non-polar solvents (Figure 7). The IR spectrum in non-polar hexane exhibits the most resolution with five peaks, as described above. The peaks at lower frequency merge into one broad peak as the solvent polarity increases. There are no distinct shifts of ν(C=O) modes on going from non-polar to polar solvents. These generic spectral features (broadening of ν(C=O) bands and non-distinct shifts on going from polar to non-polar solvents) have previously been reported for (μ-pdt)[Fe(CO)₃]₂.⁹⁷

Figure 7.

IR spectra of (μ-edt)[Fe(CO)₃]₂ in hexane, acetonitrile, dichloromethane, benzene, THF, and butyronitrile at room temperature.

Although the overall appearance of the IR spectrum of (μ-edt)[Fe(CO)₃]₂ in hexane and acetonitrile is different, the vibrational energies are quite similar as shown in Figure 6 and 7. In order to test whether the frequency shift between solution IR and Raman spectra is due to the temperature difference at which these measurements were taken, we attempted to obtain room temperature Raman spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile. Figure 8 shows an overlay of the IR and Raman spectra taken at RT (top) in comparison to the IR and Raman spectra of solid (μ-edt)[Fe(CO)₃]₂ taken at RT and 77K, respectively (bottom). It is noted that (μ-edt)[Fe(CO)₃]₂ is photolabile, hence the RT Raman spectrum shown in Figure 8 is the best that we could obtain, but this spectrum has to be treated with some caution. The RT Raman spectrum of (μ-edt)[Fe(CO)₃]₂ shows a broad peak in the 1950–2025 cm⁻¹ region and a weaker signal at 2078 cm⁻¹ that overlay well with the corresponding bands in the RT IR spectrum. Unfortunately, the distinguishable peak in the IR spectrum at 2037 cm⁻¹ (band 5) is not observable in the RT Raman spectrum because it is too weak. Figure 8 shows that the solid IR and Raman spectra of (μ-edt)[Fe(CO)₃]₂ also line up well. In summary, the RT IR spectra taken in different solvents and in the solid state and the RT solution and low temperature solid state Raman spectra are all consistent. The inconsistency in terms of band positions of these data with the 77K Raman spectrum in acetonitrile in the ν(C=O) region therefore seems to be due to a temperature-effect in solution that is much smaller in the solid state. To test this hypothesis, IR spectroscopy at variable temperature was performed from RT to −35 °C, but no distinct shift of ν(C=O) was observed in this small temperature window. We believe that the discrepancy observed between the solution RT IR spectrum and the 77K Raman spectrum might actually relate to the freezing of the acetonitrile solution for the Raman measurements, but experimentally, this would be very difficult to probe using IR spectroscopy.

Figure 8.

A) Room temperature Raman (solid line) and IR (dashed line) spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile. B) Resonance Raman spectrum of solid (μ-edt)[Fe(CO)₃]₂ at 77K (solid line) and RT IR spectrum of solid (μ-edt)[Fe(CO)₃]₂.

Due to the fact that the ν(Fe-CO)/δ(Fe-C=O) region is not accessible by solution IR spectroscopy, the Raman spectra of (μ-edt)[Fe(CO)₃]₂ were used for NCA vibrational analysis to assign the spectra and obtain corresponding experimental force constants in the ν(Fe-CO)/δ(Fe-C=O) and ν(C=O) regions.

4. Quantum Yield Determination

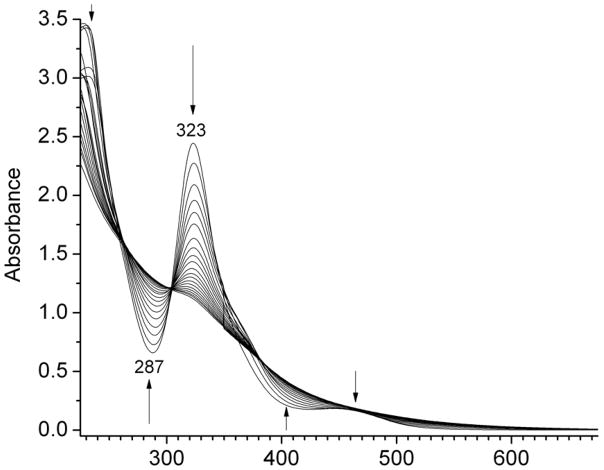
The absorption spectrum of (μ-edt)[Fe(CO)₃]₂ in acetonitrile shows an intense band at 323 nm and a shoulder with weak intensity at 455 nm (Figure 9). Upon exposure to UV light, the two bands decrease in intensity, while features at 287 and 400 nm appear. Four isosbestic points at 260, 305, 353, and 382 nm are observed upon photolysis. Interestingly, the formation of the isosbestic point at 353 nm stops at ~10% conversion, which is then followed by the appearance of another isosbestic point at 382 nm. This indicates the formation of a photolyzed product, potentially (μ-edt)[Fe₂(CO)₅(CH₃CN)], which then converts to another species, either by isomerization or by following photolysis of this acetonitrile complex. Previous photochemical studies on (μ-pdt)[Fe(CO)₃]₂ in acetonitrile and toluene support the formation of (μ-edt)[Fe₂(CO)₅(solv)] upon exposure to UV light.⁹⁷ Evidence for the formation of a mixture of (μ-pdt)[Fe₂(CO)₅]_ax-eq and (μ-pdt)[Fe₂(CO)₅]_eq-eq within 50 ps and generation of a weakly solvated by-product (μ-edt)[Fe₂(CO)₅(solv)] was obtained by ultrafast UV-pump IR-probe spectroscopy and DFT simulations.⁹⁸ More work is necessary to understand all the products of the photolysis of (μ-edt)[Fe(CO)₃]₂. The obtained quantum yield (φ₃₂₃) from our experiments for the photodissociation of CO is 0.15 ± 0.01.

Figure 9.

UV-Vis absorption spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile at different time intervals upon exposure to UV light.

5. DFT calculations

The DFT predicted IR spectrum of (μ-edt)[Fe(CO)₃]₂ shows five bands in the ν(C=O) region consistent with group theory and experimental data (cf. Figures S2 and S3). The vibrational energies predicted by B3LYP/TZVP overestimate the actual ν(C=O) frequencies by ~80 cm⁻¹ relative to the experimental IR spectrum. This suggests that B3LYP/TZVP does not accurately describe the C=O bond strength, but nevertheless, the relative energies of the different ν(C=O) modes are in good agreement with experiment. This is a common observation for B3LYP calculations as documented in the literature.^{66, 76, 80} The relative intensities in the DFT calculated IR spectrum (normalized to band 5) for bands 1, 3–6 are: 0.02, 0.41, 0.56, 1.0, and 0.22, which compares reasonably well with the experimental values of 0.28, 0.85, 0.86, 1.0 and 0.06 for these features. Alternatively, the vibrational energies predicted by BP86/TZVP underestimate the experimental ν(C=O) frequencies slightly by ~10 cm⁻¹ (cf. Figure S3 and Table S4), suggesting that this method describes the C=O bond strength more accurately than B3LYP/TZVP. In addition to this, the overall relative intensities in the DFT calculated IR spectra (with both B3LYP and BP86) compare well with experiment as shown in Figure S3. The DFT calculated IR spectrum in the ν(Fe-CO)/δ(Fe-C=O) region is not presented, since no high-resolution IR spectra are experimentally available for this spectral region.

Figure 10 shows an overlay of the B3LYP/TZVP calculated and experimental (solution) Raman spectrum of (μ-edt)[Fe(CO)₃]₂ in the ν(Fe-CO)/δ(Fe-C=O) and ν(C=O) regions. In the ν(Fe-CO)/δ(Fe-C=O) region (400–650 cm⁻¹), DFT predicts eighteen peaks, in agreement with group theory. All eighteen bands are shown in Figure 10A, but only fifteen of these were unambiguously identified experimentally (labeled 1–15) and used for NCA. The DFT-predicted spectrum correlates very well with experimental data (Figure 10A). For example, the prominent DFT-calculated peaks at 446 cm⁻¹ (peak 4) and 448 cm⁻¹ (peak 5) are consistent with the experimental frequencies at 454 and 456 cm⁻¹, respectively (Figure 10A). The intense band calculated at 481 cm⁻¹ (peak 8) corresponds to the experimental feature at 483 cm⁻¹. The DFT-predicted peak 9 at 496 cm⁻¹ is identified with the experimental band at 494 cm⁻¹. Peak 11 shows a larger deviation compared to experiment, which might be related to an admixture of ν(S-C) character that differs in magnitude from experiment. On the other hand, the sum of δ(Fe-C=O)_ax (16% from DFT and 21% from QCC-NCA) and δ(Fe-C=O)_eq (39% from DFT and 34% from QCC-NCA) contributions are quite similar. This is in addition to the admixture of ν(S-C) character. In summary, the accurate reproduction of the experimental vibrational frequencies and intensities suggests that B3LYP/TZVP describes ν(Fe-CO) and δ(Fe-C=O) vibrational modes well. The DFT-calculated frequencies for the ν(Fe-CO)/δ(Fe-C=O) vibrations are listed in Tables 2 and S4. In contrast, the BP86/TZVP-calculated frequencies in the ν(Fe-CO)/δ(Fe-C=O) region are clearly of lower quality and do not reproduce the experimental Raman spectra well (cf. Figure S4 and Table S4).

Figure 10.

Overlay of the B3LYP/TZVP calculated (column bars) and experimental (solid lines) Raman spectra of (μ-edt)[Fe(CO)₃]₂ in acetonitrile in the A) ν(Fe-CO)/δ(Fe-C=O) and B) ν(C=O) regions. The DFT calculated modes are labeled according to the corresponding experimental modes (refer to Figure 5).

In the ν(C=O) region, B3LYP/TZVP predicts six Raman-active bands consistent with group theory and experimental data, which are labeled accordingly in Figure 10B. As already mentioned above, the vibrational energies are overestimated by DFT. The calculated relative Raman intensities show larger deviations compared to the predicted IR intensities: whereas the experimental data show distinct intensity differences between bands 1–6, the DFT calculations predict more or less equal intensities for vibrations 1, 3, 4 and 6. On the other hand, the intensity of band 5 is underestimated by DFT. The BP86/TZVP-calculated frequencies predicted for this energy region compare well to experiment, and show closer agreement with the experimental peak positions than the B3LYP/TZVP results, as discussed for the IR spectra above. Tables 2 and S4 list the DFT-calculated ν(C=O) frequencies.

C. Normal Coordinate Analysis

1. ν(Fe-CO) stretching and δ(Fe-C=O) linear bending region

The DFT-calculated force field of (μ-edt)[Fe(CO)₃]₂ was used as a starting point for vibrational analysis in the spirit of the QCC-NCA approach.^{84, 85} A total of fifteen peaks were identified in the ν(Fe-CO)/δ(Fe-C=O) region (Table 2) and fit by varying four diagonal and eight off-diagonal force constants as described in the Experimental Section. A list of the force constants of each axial and equatorial Fe-C=O linear bending and Fe-CO stretching internal coordinate is given in Table 3. The experimental force constants of the Fe-C=O linear bends differ by only ~0.02 mdyn·Å from the DFT-calculated values, whereas larger deviations are observed for the Fe-CO internal coordinates. The force constants generated from QCC-NCA are 2.685 and 2.795 mdyn/Å for the axial and equatorial Fe-CO bonds, respectively. This indicates that the equatorial Fe-CO bonds are stronger than their axial counterparts. A previous study reported a force constant of 2.35 mdyn/Å for the Fe-CO bonds of (μ-pdt)[Fe(CO)₃]₂ based on NCA.⁶⁵ However, in this case the CO ligands were represented by atoms of mass 28, the linear bends were excluded, couplings with C=O stretching and linear bending coordinates could not be considered, and no distinction was made between axial and equatorial internal coordinates.⁶⁵ The off-diagonal force constants for the (Fe-CO)_ax/(C=O)_ax and (Fe-CO)_eq/(C=O)_eq interactions are surprisingly large at 0.768 and 0.785 mdyn/Å, respectively, but are in agreement with the DFT calculated values of 0.814 and 0.826 mdyn/Å. Another substantial non-diagonal force constant involves the trans interaction between Fe-CO and Fe-S bonds, obtained at a value of 0.314 mdyn/Å (calculated: 0.113 mdyn/Å). Other off-diagonal force constants are listed in Table 3.

Table 3.

Force constants obtained from the normal coordinate analysis of (μ-edt)[Fe(CO)₃]₂ and (μ-edt)[Fe(¹³CO)₃]₂

Diagonal/Off-diagonal elementsa	DFT calculatedb	QCC-NCA
C=O stretching,
f(C=O)ax	17.765	16.037
f(C=O)eq	17.886	15.972
Interactionc
f[(C=O)ax/(C=O)eq]	0.157	0.304
f[(C=O)eq/(C=O)eq]	0.151	0.205
f[(C=O)eq/(C=O)eq]ss	0.183	0.056
f[(C=O)eq/(C=O)eq]os	0.085	0.233
Fe-CO stretching
f(Fe-CO)ax	2.698	2.685
f(Fe-CO)eq	2.613	2.795
Fe-C-O bending
f(Fe2-C5=O11)ax	0.39636	0.41487
f(Fe2-C5=O11)ax	0.39066	0.40917
f(Fe1-C10=O16)ax	0.39069	0.40920
f(Fe1-C10=O16)ax	0.39797	0.41648
f(Fe2-C6=O12)eq	0.45150	0.46260
f(Fe2-C6=O12)eq	0.45426	0.46537
f(Fe2-C7=O13)eq	0.44555	0.45665
f(Fe2-C7=O13)eq	0.46017	0.47128
f(Fe1-C8=O14)eq	0.44387	0.45498
f(Fe1-C8=O14)eq	0.46248	0.47359
f(Fe1-C9=O15)eq	0.46124	0.47235
f(Fe1-C9=O15)eq	0.44512	0.45622
Interactionc
f[(Fe-CO)ax/C=O)ax]	0.814	0.768
f[(Fe-CO)eq/(C=O)eq]	0.826	0.785
f[(Fe-CO)/(Fe-S)trans]	0.113	0.314
f[(Fe-CO)ax/(Fe-CO)eq]	0.060	0.104
f[(Fe-CO)eq/(C=O)eq]ss	−0.087	−0.219
f[(Fe-CO)ax/(C=O)eq]	−0.081	0.213
f[(Fe-CO)eq/(C=O)ax]	−0.077	−0.192
f[(Fe-CO)eq/(C=O)eq]os	−0.070	−0.166

^aThe units for the force constants of stretching and linear bending coordinates, and stretching/linear bending interactive matrix elements are mdyn/Å, mdyn·Å, and mdyn, respectively.

^bThe DFT calculated force constants of the (C=O)_ax, (C=O)_eq, (Fe-CO)_ax, and (Fe-CO)_eq internal coordinate differ by only + 0.001 mdyn/Å, respectively, and hence, are considered equivalent (average value shown).

^cOff-diagonal elements are listed according to how they are described in the Experimental Section.

Table 4 lists the vibrational frequencies and the corresponding symmetries and potential energy distributions in the ν(Fe-CO)/δ(Fe-C=O) region. Figure 8 and Tables 2 and 4 are suggested as a reference point for the following analysis. The most intense Raman peaks at 454 cm⁻¹ (53% δ(Fe-C=O), B₁ symmetry), 456 cm⁻¹ (55% δ(Fe-C=O), A₁) and 483 cm⁻¹ (65% ν(Fe-CO), B₁) are composed of a combination of ν(Fe-CO) stretching and δ(Fe-C=O) linear bending coordinates. The medium intense band at 470 cm⁻¹ (B₂) has a dominant ν(Fe-CO) stretching contribution of 86%. The less intense peaks at 416 cm⁻¹ (B₁) and 419 cm⁻¹ (A₂) correspond to pure δ(Fe-C=O) linear bends (94% and 95% contribution, respectively). The B₁ mode at 528 cm⁻¹ shows a dominant contribution from δ(Fe-C=O) linear bends (55%), no ν(Fe-CO) stretching character, but a 19% ν(S-C) stretching admixture. In comparison, the DFT-calculated ν(S-C) contribution is 14%, which is somewhat underestimated.

Table 4.

Potential energy distribution (P.E.D) of the normal modes in the ν(C=O) and ν(Fe-CO)/δ(Fe-C=O) vibrational energy regions of (μ-edt)[Fe(CO)₃]₂

Mode	QCC-NCAa/cm−1	Symmetryb (ax ± eq)	P.E.Dc
ν(C=O)	2069	A1 + A1	18.3 % C=O (ax) 75.9 % C=O (eq)
ν(C=O)	2006	B2 + B2	60.2 % C=O (ax) 34.3 % C=O (eq)
ν(C=O)	1980	A1 − A1	76.2 % C=O (ax) 18.2 % C=O (eq)
ν(C=O)	1968	B1	0 % C=O (ax) 94.3 % C=O (eq)
ν(C=O)	1963	A2	0 % C=O (ax) 94.5 % C=O (eq)
ν(C=O)	1960	B2 − B2	34.4 % C=O (ax) 60.0 % C=O (eq)
δ(Fe-C=O) + ν(Fe-CO)	628	A1 + A1	4.6 % Fe-CO (ax) 9.1 % Fe-CO(eq) 11.2 % Fe-C=O (ax) 45.7 % Fe-C=O (eq)
δ(Fe-C=O) + ν(Fe-CO)	594	A1 − A1	14.8 % Fe-CO (ax) 4.6 % Fe-CO (eq) 1.2 % Fe-C=O (ax) 62.8 % Fe-C=O (eq)
δ(Fe-C=O) + ν(Fe-CO)	573	B1 − B1	0 % Fe-CO (ax) 30.7 % Fe-CO (eq) 22.9 % Fe-C=O (ax) 28.0 % Fe-C=O (eq)
δ(Fe-C=O) + ν(Fe-CO)	567	A2 − A2	0 % Fe-CO (ax) 41.3 % Fe-CO (eq) 27.5 % Fe-C=O (ax) 20.5 % Fe-C=O (eq)
δ(Fe-C=O)	528	B1 + B1	0 % Fe-CO (ax) 0 % Fe-CO (eq) 21.0 % Fe-C=O (ax) 33.7 % Fe-C=O (eq)
ν(Fe-CO) + δ(Fe-C=O)	506	A1 − A1	46.0 % Fe-CO (ax) 12.9 % Fe-CO (eq) 23.3 % Fe-C=O (ax) 7.5 % Fe-C=O (eq)
ν(Fe-CO) + δ(Fe-C=O)	496	A2 + A2	0 % Fe-CO (ax) 22.3 % Fe-CO (eq) 16.4 % Fe-C=O (ax) 51.2 % Fe-C=O (eq)
ν(Fe-CO) + δ(Fe-C=O)	482	B1 − B1	0 % Fe-CO (ax) 65.4 % Fe-CO (eq) 4.4 % Fe-C=O (ax) 9.9 % Fe-C=O (eq)
ν(Fe-CO)	473	B2 − B2	41.5 % Fe-CO (ax) 44.7 % Fe-CO (eq) 0 % Fe-C=O (ax) 9.1 % Fe-C=O (eq)
ν(Fe-CO) + δ(Fe-C=O)	461	A2	0 % Fe-CO (ax) 54.3 % Fe-CO (eq) 1.4 % Fe-C=O (ax) 41.3% Fe-C=O (eq)
δ(Fe-C=O)+ ν(Fe-CO)	453	A1 − A1	15.7 % Fe-CO (ax) 22.5 % Fe-CO (eq) 36.5 % Fe-C=O (ax) 18.6 % Fe-C=O (eq)
δ(Fe-C=O)+ ν(Fe-CO)	452	B1	0 % Fe-CO (ax) 22.8 % Fe-CO (eq) 1.4 % Fe-C=O (ax) 52.4 % Fe-C=O (eq)
δ(Fe-C=O)+ ν(Fe-CO)	444	B2 − B2	10.2 % Fe-CO (ax) 32.7 % Fe-CO (eq) 28.0 % Fe-C=O (ax) 25.5 % Fe-C=O (eq)
δ(Fe-C=O)	422	A2 + A2	0 % Fe-CO (ax) 0.7 % Fe-CO (eq) 29.9 % Fe-C=O (ax) 64.7 % Fe-C=O (eq)
δ(Fe-C=O)	416	B1 + B1	0.1 % Fe-CO (ax) 0 % Fe-CO (eq) 31.5 % Fe-C=O (ax) 62.9 % Fe-C=O (eq)

^aQuantum Chemistry Centered-Normal Coordinate Analysis.

^bSymmetry labels are given based on the effective C_2v symmetry of the molecule and use the xyz plane designation shown in Figure 1; ax = axial, eq = equatorial. In A₁+A₁, for example, the first symmetry label corresponds to the symmetry of the axial internal coordinate; the second corresponds to the equatorial internal coordinate that the normal mode is comprised of (+ = in-phase combination).

^cPotential energy distribution matrix.

2. ν(C=O) stretching region

In the 1900–2100 cm⁻¹ region where the ν(C=O) stretching modes of (μ-edt)[Fe(CO)₃]₂ occur, six different force constants are required to obtain a good agreement between the NCA-simulated and experimental vibrational frequencies. These include two diagonal force constants for the axial, f(C=O)_ax, and equatorial, f(C=O)_eq, C=O bonds, respectively. In addition, four off-diagonal force constants are required as described in the Experimental Section. The f(C=O)_ax and f(C=O)_eq experimental force constants are 16.037 and 15.972 mdyn/Å, respectively, suggesting the (C=O)_ax bonds to be slightly stronger than the (C=O)_eq bonds. The f[(C=O)_ax/(C=O)_eq] off-diagonal parameter contributes as the most significant interaction between C=O stretching coordinates with a force constant of 0.304 mdyn/Å, which is 0.15 mdyn/Å larger than its DFT-predicted value. The three remaining interaction force constants are f[(C=O)_eq/(C=O)_eq], f[(C=O)_eq/(C=O)_eq]_ss, and f[(C=O)_eq/(C=O)_eq]_os, which all fall in the 0.06–0.23 mdyn/Å range. A complete list of the DFT-predicted and experimentally calibrated force constants is presented in Table 3.

The symmetry labels and potential energy distributions (PED) for the six ν(C=O) normal modes are shown in Table 4. The mode at highest energy is observed at 2070 cm⁻¹ and has A₁ symmetry. This totally symmetric mode contains large contributions (76%) from the (C=O)_eq stretching coordinates. The next two ν(C=O) modes found at 2005 cm⁻¹ (B₂) and 1979 cm⁻¹ (A₁) show dominant (C=O)_ax stretching character with 60% and 76% contribution, respectively. DFT calculations predict the modes at 2005 and 1979 cm⁻¹ to have B₂ and B₁ symmetry, respectively, similar to calculations by Brunold and co-worker.⁶⁵ However, in the QCC-NCA fit of the data, the third and fourth mode change order. The fourth mode at 1968 cm⁻¹ (B₁) shows dominant (C=O)_eq stretching character with 94% contribution, and the same applies to the IR inactive ν(C=O) stretch at 1964 cm⁻¹ (A₂, 95% (C=O)_eq). The lowest energy ν(C=O) stretch at 1962 cm⁻¹ (B₂) has major contributions from (C=O)_eq coordinates at 60%. Importantly, these potential energy distributions show that the mixing of (C=O)_eq and (C=O)_ax internal coordinates is limited in the resulting ν(C=O) normal modes of (μ-edt)[Fe(CO)₃]₂.

DISCUSSION

In this study, the vibrational properties of (μ-edt)[Fe(CO)₃]₂ are analyzed in detail with respect to ν(C=O), ν(Fe-CO) and δ(Fe-C=O) vibrations. Solid and solution resonance Raman and IR spectra are presented and the observed six ν(C=O) and fifteen ν(Fe-CO)/δ(Fe-C=O) normal modes are assigned with respect to their symmetries, and detailed mode decompositions are reported for all features. This is achieved with the aid of ¹³CO isotope labeling and QCC-NCA simulations of the obtained data. In (μ-edt)[Fe(CO)₃]₂, the ν(Fe-CO)/δ(Fe-C=O) modes are observed in the 400–650 cm⁻¹ region. These results can be compared to a previous study by Spiro and co-worker⁹⁹ on vibrational assignments in (μ-S₂)[Fe(CO)₃]₂, a complex whose S₂Fe₂ cluster models iron sulfur proteins of class 2Fe-2S. Here, ν(Fe-CO)/δ(Fe-C=O) features were also observed in the 400–600 cm⁻¹ frequency range. The main interest in this study was to define the vibrational modes of the S₂Fe₂ cluster, hence the force constants that describe the C=O and Fe-CO coordinates are of lower quality. Noticeable differences are observed between our data and those obtained for (μ-S₂)[Fe(CO)₃]₂. In particular, the Raman spectrum on polycrystalline (μ-S₂)[Fe(CO)₃]₂ shows less resolution compared to our Raman results on solid (μ-edt)[Fe(CO)₃]₂. For (μ-S₂)[Fe(CO)₃]₂, the major feature in this region is a quartet of Raman bands at 447, 463, 475, and 495 cm⁻¹, the latter two of which are polarized and have dominant ν(Fe-CO) character. These bands might correspond to the peaks observed at 503 and 483 cm⁻¹ for (μ-edt)[Fe(CO)₃]₂ that also have large contributions from the ν(Fe-CO) stretch. In addition, Spiro and co-worker⁹⁹ identified a peak at 554 cm⁻¹ that exhibits 23% Fe-C=O bending, and 54% S-S and 23% Fe-S stretching character. This feature can be correlated with the band at 528 cm⁻¹ in (μ-edt)[Fe(CO)₃]₂ that is of pure Fe-C=O bending character, but lacks Fe-S character. The force constants reported for (μ-S₂)[Fe(CO)₃]₂ do not distinguish between the two independent sets of ν(Fe-CO) and δ(Fe-C=O) axial and equatorial coordinates, but were constrained to a single value of f(Fe-CO) = 2.59 mdyn/Å and f(Fe-C=O) = 0.87 mdyn·Å. This restriction is reflected in the ~5–10 cm⁻¹ discrepancy between the experimental and NCA frequencies in the ν(Fe-CO)/δ(Fe-C=O) region for (μ-S₂)[Fe(CO)₃]₂.⁹⁹ In contrast, our force constants of f(Fe-CO)_ax = 2.685 mdyn/Å and f(Fe-CO)_eq = 2.795 mdyn/Å suggest a stronger Fe-CO bond in the equatorial position. The f(Fe-C=O) linear bending force constants are quite similar for equatorial and axial Fe-C=O units. The average value is 0.43 mdyn·Å, which is distinctively smaller than the reported value for (μ-S₂)[Fe(CO)₃]₂. With these parameters (cf Table 3), we were able to fit the experimental frequencies of (μ-edt)[Fe(CO)₃]₂ to a difference of ~3 cm⁻¹ or less. Our current work therefore represents the most sophisticated assignment of the ν(Fe-CO)/δ(Fe-C=O) vibrations of a hydrogenase model complex available so far, based on the use of independent sets of f(Fe-CO) and f(Fe-C=O) equatorial and axial force constants, as well as the consideration of interaction force constants between these internal coordinates.

The ν(C=O) region of (μ-edt)[Fe(CO)₃]₂ shows six Raman and five IR active bands, with the peak at 1964 cm⁻¹ (A₂ symmetry) being IR inactive. As described earlier and shown in Table 4, the mixing of (C=O)_ax and (C=O)_eq coordinates is quite limited as evidenced by the potential energy distributions of the ν(C=O) normal modes. The peaks at 2005 and 1979 cm⁻¹ have mostly (C=O)_ax stretching character, while the remaining peaks at 2070, 1968, 1964, and 1961 cm⁻¹ are dominated by (C=O)_eq stretching contributions. The importance of distinguishing between axial and equatorial CO ligands to obtain the best fit in the ν(C=O) region is emphasized. For example, in a previous work on (μ-S₂)[Fe(CO)₃]₂, a force constant of 16.20 mdyn/Å was obtained for C=O, but the discrepancy between the experimental and calculated frequencies is 32–43 cm⁻¹ due to the fact that axial and equatorial CO ligands were not distinguished in the analysis. Our current analysis requires that f(C=O)_ax = 16.037 mdyn/Å and f(C=O)_eq = 15.973 mdyn/Å, and that off-diagonal elements between (C=O)_ax and (C=O)_eq should be taken into account to fit vibrational energies to a difference of 1 cm⁻¹ or less. The fact that the axial C=O bond is slightly stronger than its equatorial counterpart, and the observation of the inverse trend for the axial and equatorial Fe-CO bonds, has implications in π-backbonding as discussed below. This could not have been observed if the C=O axial and equatorial bonds were not individually accounted for. This underscores the need to distinguish between the axial and equatorial C=O coordinates when analyzing experimental data in the ν(C=O) region of hydrogenase models.

The complex (μ-edt)[Fe(CO)₃]₂ studied here does not have the staggered or “rotated” structure (“ae”; where one of the carbonyls is semi-bridging the iron centers) found in [FeFe] hydrogenase, but instead has the eclipsed (aa) structure as observed from X-ray crystallography. The aa conformation of (μ-edt)[Fe(CO)₃]₂ is supported by our solid and solution Raman data and the DFT-optimized structure. The experimental IR spectrum in hexane shows good agreement with the DFT-calculated IR spectrum in terms of relative vibrational frequencies and intensities (Figure S2). The close correspondence of solution and solid state spectra also shows that the C_2v structure of (μ-edt)[Fe(CO)₃]₂ is preserved in solution. A similar conclusion has been drawn from the experimental and theoretical IR spectra of (μ-pdt)[Fe(CO)₃]₂.^{76, 100} Interestingly, the “rotated” isomer of (μ-pdt)[Fe(CO)₃]₂ and of corresponding derivatives is favored in the one-electron oxidized cationic form.¹⁰⁰ In the protein, the overall geometric structure of the [FeFe] active site can tune the binding mode of the hydride and/or influence the redox and reorganizational energy enabling fast electron transfer. Thus, two factors are of primary importance for the enzyme’s ability to optimally catalyze the reduction of H⁺: (a) the rotated structure of the active site which promotes terminal hydride formation (kinetic control via an entatic state), and (b) the electron richness of the diiron core, which controls the basicity of the active site (thermodynamic control). In the following, we will focus on the active site’s electron richness as a critical parameter for (electro)catalysis of H⁺ reduction in the protein and corresponding model systems. In this regard, we consider the vibrational properties of the Fe-C=O units of (μ-edt)[Fe(CO)₃]₂ in comparison to more complex models as well as the protein active site.

Ideally, force constants, and not vibrational frequencies, are the best indicators of bond strengths since they are devoid of contributions from mode mixing.⁸⁵ However, information on force constants remains limited, specifically for C=O and Fe-CO bonds, in [FeFe] model complexes. Therefore, the following discussion focuses mainly on vibrational ν(C=O) and ν(Fe-CO) frequencies. The vibrational ν(C=O) and ν(Fe-CO) frequencies reflect π-backbonding changes, as has been intensively studied for various ferrous heme carbonyl complexes.¹⁰¹ Here, an inverse correlation is predicted between ν(C=O) and ν(Fe-CO), which is attributed to the Fe(d_π) → CO(π^*) backdonation: as the strength of this backbond increases, the Fe-CO bond becomes stronger whereas the C=O bond becomes weaker. In five- and six-coordinate ferrous heme complexes, the f(Fe-CO) force constant typically falls in the range of 2.30–2.65 mdyn/Å.^101–103 For (μ-edt)[Fe(CO)₃]₂, the NCA results show the expected inverse correlation between ν(C=O) and ν(Fe-CO) for the axial and equatorial Fe-C=O units. In the axial case, f(C=O)_ax = 16.037 mdyn/Å and f(Fe-CO)_ax = 2.685 mdyn/Å, whereas f(C=O)_eq = 15.972 mdyn/Å and f(Fe-CO)_eq = 2.795 mdyn/Å in the equatorial case. This is also consistent with the pattern obtained from the DFT calculations. Therefore, the inverse correlation between ν(C=O) and ν(Fe-CO) also holds true for [FeFe] hydrogenase model complexes indicating that the Fe(I)-CO bond (as expected) is also dominated by π-backbonding. The oxidation state of Fe in a given carbonyl complex correlates with the ν(C=O) frequency, and the inverse correlation with ν(Fe-CO) is usually observed, although the availability of Fe-CO frequencies and force constants is very limited. For example, on going from [Fe^−II(CO)₄]²⁻ (ν(C=O)_ave = 1815 cm⁻¹)¹⁰⁴ to [Fe⁰(CO)₅] (2030 cm⁻¹)¹⁰³ and to [Fe^+II(CO)₆]²⁺ (2215 cm⁻¹),¹⁰⁵ an increase of ~200 cm⁻¹ in the average ν(C=O)_ave vibrational frequency is observed for every increase in the Fe oxidation state by +2, respectively. In addition, the f(C=O) and f(Fe-CO) force constants appear to move in opposite directions. These observations are explained by a decrease in π-backbonding as the oxidation state of Fe increases from −2 to +2. The active site of [FeFe] hydrogenase which is proposed to exist in three oxidation states, H_red [Fe(I)Fe(I)], H_ox [Fe(II)Fe(I)], and H_ox^air [Fe(II)Fe(II)] (Scheme 1) shows consistent trends in ν(C=O) vibrational frequencies upon an increase in oxidation state as evident from reported IR spectra (see below).^{3, 20, 21, 106}

In general, the ν(C=O) vibrational frequencies can be used to access the electron richness of the diiron center upon substitution of CO ligands. The following discussion will first focus on comparing reported ν(C=O) vibrational frequencies of selected [Fe(I)Fe(I)] hydrogenase models, a number of which have been synthesized.^{28–30, 43, 55, 56} For (μ-edt)[Fe(CO)₃]₂, the average ν(C=O)_ave IR frequency is 2021 cm⁻¹. Upon substitution of two CO by CN⁻ ligands as in the case of (μ-pdt)[Fe₂(CO₄)(CN)₂]²⁻ and (μ-edt)[Fe₂(CO)₄(CN)₂]²⁻, ν(C=O)_ave drops to 1922 (in THF) and 1907 cm⁻¹ (KBr),^{28, 29} respectively, showing that cyanide is a strong donor, increasing the electron density at the iron centers. [Fe(I)Fe(I)] hydrogenase models with two phosphine ligands show C=O frequencies at somewhat higher energy with ν(C=O)_ave of 1940 cm⁻¹ for [Fe₂(μ-pdt)(CO)₄(PMe₃)₂]⁹ and 1935 cm⁻¹ for the phosphine-bridged complex (μ-pdt)[Fe₂(CO)₄(μ-(Ph₂P)₂CH₂)].⁵⁶ Given this set of model complexes with similar, bridging dithiolate ligands, the complex with the two CN⁻ ligands displays ν(C=O)_ave about 20 cm⁻¹ lower in energy, indicating that CN⁻ is a somewhat stronger donor than phosphine, as opposed to what has been previously reported.¹⁰⁷ A model complex with three phosphine donors, (μ-pdt)[Fe₂(CO)₃(μ,κ-P,κ²-P′, P″-triphos)] (triphos = bis(2-diphenylphosphinoethyl)phenylphosphine)) exhibits ν(C=O)_ave = 1918 cm⁻¹,⁵⁵ which is ~20 cm⁻¹ lower than the compounds having two phosphines. Finally, a model complex with four coordinated phosphine donors, (μ-edt)[Fe₂(CO)₂(dppv)₂] (dppv = cis-1,2-bis(diphenylphosphino)ethene), shows ν(C=O)_ave at 1878 cm⁻¹,⁴⁴ which is ~40 cm⁻¹ lower in frequency compared to (μ-pdt)[Fe₂(CO)₃(μ,κ-P,κ²-P′, P″-triphos)].

In the above discussion, comparison has been made between complexes that contain slightly different bridging dithiolate ligands (edt and pdt). This is justified as it has been shown in the literature that variation of the dithiolate between edt and pdt has only a minor effect on the properties of the complexes. For example, the reported ν(C=O)_ave vibrational energies for (μ-pdt)[Fe₂(CO)₄(dppv)], (μ-adt)[Fe₂(CO)₄(dppv)] (adt = azadithioloate), and (μ-edt)[Fe₂(CO)₄(dppv)] are 1961, 1963, and 1964 cm⁻¹, respectively.⁵⁹

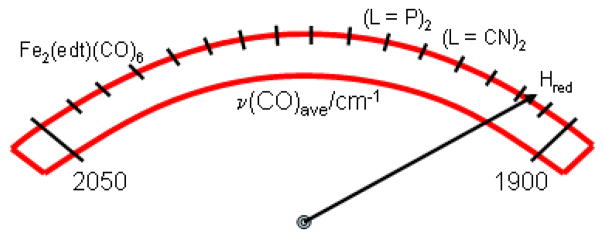
In comparison, the ν(C=O) stretching frequencies for H_red, as obtained from FTIR data on D. vulgaris and D. desulfuricans, are 1965, 1916, and 1894 cm⁻¹,^{20, 108} which indicates a relatively electron-rich environment when compared to the model complexes containing phosphine ligands. Compared to ν(C=O) obtained on (μ-edt)[Fe(CO)₃]₂ from our study, the ν(C=O) stretching frequency in H_red is ~70–100 cm⁻¹ lower. This indirectly shows that due to the presence of six C=O ligands and correspondingly, six Fe-CO backbonds in the model complex (μ-edt)[Fe(CO)₃]₂, this compound has much more electron-poor iron centers than H_red. This has important implications for the (electro)catalysis of H⁺ reduction as the more electron-rich or basic species are prone to accepting a proton in the initial step of catalysis forming a hydride complex. From the enumerated set of model complexes with varying numbers of phosphine ligands (see above), it can be concluded that at least three phosphine groups must be present to attain similar ν(C=O) vibrational frequencies as the [FeFe] model compounds containing two CN⁻ or the H_red form of [FeFe] hydrogenase itself. This implies that the presence of at least three phosphine ligands is a pre-requisite for a model complex to be basic enough to accept a proton, as shown on the activation scale in Scheme 2.

Scheme 2.

The activation scale of hydrogenase diiron active sites.

The mixed valent forms H_ox of D. desulfuricans Hildenborough and D. vulgaris show low ν(C=O) stretching frequencies at 1965, 1940, and 1802 cm⁻¹.²¹ In comparison, the mixed-valent model complex (μ-pdt)[Fe^II(CO)₂IMes][Fe^I(CO)₂PMe₃]PF₆⁻ exhibits terminal ν(C=O) stretching frequencies at 2037, 1997, and 1886.¹⁰⁹ Just like H_red, H_ox indicates a relatively electron-rich environment in the protein on the basis of the abovementioned frequencies. Finally, the ν(C=O) frequencies in the H_ox^air [Fe(II)Fe(II)] state of D. vulgaris are 1965 and 1940 cm⁻¹, which corresponds to an ~40 cm⁻¹ shift to higher energy compared to H_red (vide supra). Model complexes that resemble H_ox^air and exhibit the [Fe(II)Fe(II)] core have been synthesized and their corresponding ν(C=O) frequencies have also been determined.^{36, 110} An example of such a model complex is Fe₂(S₂C₂H₄)(μ-CO)(CN)₂(PPh₃)₂(CO)₂, where terminal ν(C=O) stretching frequencies at 2039, 1993, and a bridging ν(C=O) stretching frequency at 1904 cm⁻¹ have been determined.³⁶

SUMMARY AND CONCLUSIONS

The solution and solid state resonance Raman and IR measurements, DFT calculations, and QCC-NCA simulations performed on the aa conformer of (μ-edt)[Fe(CO)₃]₂ and its corresponding ¹³CO-labeled complex have allowed for the complete assignment of ν(C=O), ν(Fe-CO) and δ(Fe-C=O) vibrational modes, and the determination of the diagonal and off-diagonal force constants of the corresponding axial and equatorial internal coordinates C=O, Fe-CO, and Fe-C=O. Discrepancies between the 77K solution Raman spectrum and the RT solution IR spectrum of (μ-edt)[Fe(CO)₃]₂ were observed, but were attributed to temperature effects (freezing) of the solution sample. Six Raman active peaks in the ν(C=O) region and fifteen of the eighteen possible vibrations in the ν(Fe-CO)/δ(Fe-C=O) region were identified for this molecule. From QCC-NCA, an inverse correlation between the f(C=O)_ax/eq and f(Fe-CO)_ax/eq was obtained, which is consistent with an Fe-CO bond that is dominated by π-backdonation. Results from this study provide a complete picture of all vibrational aspects in the ν(C=O), ν(Fe-CO) and δ(Fe-C=O) regions of (μ-edt)[Fe(CO)₃]₂. Comparison to the reduced form of the [FeFe] active site in hydrogenase shows that the dinuclear core in (μ-edt)[Fe(CO)₃]₂ is distinctively less reduced compared to H_red. Introduction of at least three phosphine ligands is required to generate an Fe-Fe core that has similar properties to H_red, judging from the C=O stretching frequencies. This is mostly attributed to the fact that CN⁻ present in the enzyme is an overall stronger donor than phosphine. Given the ν(C=O) stretching frequencies of the different aforementioned model complexes in their [Fe(I)Fe(I)], [Fe(II)Fe(I)], and [Fe(II)Fe(II)] oxidation states, and comparing them to their [FeFe] hydrogenase counterpart, a range of ~1880–1960 cm⁻¹ is needed for a [FeFe] model complex to accurately reflect the electron richness of the diiron core in hydrogenases.