The Rate of Intramolecular Loop Formation in DNA and Polypeptides: The Absence of the Diffusion-Controlled Limit and Fractional Power-Law Viscosity Dependence

Abstract

The problem of determining the rate of end-to-end collisions for polymer chains has attracted the attention of theorists and experimentalists for more than three decades. The typical theoretical approach to this problem has focused on the case where a collision is defined as any instantaneous fluctuation that brings the chain ends to within a specific capture distance. In this paper, we study the more experimentally relevant case, where the end-to-end collision dynamics are probed by measuring the excited state lifetime of a fluorophore (or other lumiphore) attached to one chain end and quenched by a quencher group attached to the other end. Under this regime, a “contact” is defined not by the chain ends approach to within some sharp cutoff but, instead, typically by an exponentially distance-dependent process. Previous theoretical models predict that, if quenching is sufficiently rapid, a diffusion-controlled limit is attained, where such measurements report on the probe-independent, intrinsic end-to-end collision rate. In contrast, our theoretical considerations, simulations, and an analysis of experimental measurements of loop closure rates in single-stranded DNA molecules all indicate that no such limit exists, and that the measured effective collision rate has a nontrivial, fractional power-law dependence on both the intrinsic quenching rate of the fluorophore and the solvent viscosity. We propose a simple scaling formula describing the effective loop closure rate and its dependence on the viscosity, chain length, and properties of the probes. Previous theoretical results are limiting cases of this more general formula.

1. Introduction

The two ends of a polymer chain that diffuses freely in solution are occasionally found in close proximity. The problem of determining the time scale over which such collisions take place has received considerable attention over the last three decades.^1–15 This problem arises in a number of different contexts. In particular, diffusional search for certain native contacts has been proposed to be the rate limiting step in protein folding,^16–19 thus suggesting that the loop closure rate of polypeptides ultimately determines the folding “speed limit”.^20,21 Thus motivated, this problem has received the attention of several experimental groups, who have measured loop closure times for a range of unstructured polypeptides^6,20,22,23 and single-stranded DNAs.^24–26

Despite its apparent simplicity, calculation of polymer loop closure times remains an open theoretical problem. The two most commonly used approximations, the Szabo–Schulten–Schulten (SSS) theory²⁷ and the Wilemski–Fixman (WF) approximation,¹⁵ utilize two different local equilibrium approximations for the polymer dynamics and cannot be systematically improved in any straightforward way. Computer simulations^2,3,6–9,12 have provided further insights and revealed the limitations inherent in these approximations. A recent paper by Thirumalai and co-workers¹² presents a comprehensive comparison of various theories with the results of such simulations.

In addition to the above-mentioned approximations inherent in existing theories of polymer loop closure, there remains an additional, fundamental inconsistency between theoretical models of the process and the experimental measurements commonly used to test them. Experimental studies of polymer loop closure rates generally employ probes attached to the chain termini (Figure 1). These typically consist of an optically excited probe (a fluorophore or other lumiphore) at one end that is quenched when it approaches a quenching group on the opposite terminus. The rate of quenching k = k(R) depends on the distance R between the ends. For example, when the quenching mechanism involves electron transfer, this dependence is given by an exponential function

Figure 1.

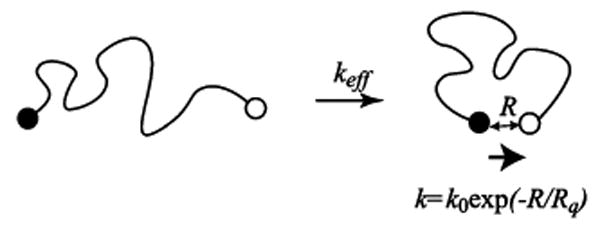
The effective end-to-end collision rate is typically measured by monitoring the quenching of a fluorescent probe (or other lumiphore) upon its collision with a quencher attached to the other end of the polymer chain. For electron-transfer-based quenching, which is commonly employed experimentally, the efficiency of the quenching mechanism depends exponentially on the end-to-end distance.

$$k(R)=k_0\text{exp}(-R/R_q)$$ (1)

where k₀ is a parameter describing the intrinsic quenching rate and R_q sets a length scale over which quenching can take place. Typically, this length is on the order of 1 Å. In the following, we will refer to eq 1 as the “exponential quenching model” (EQM). In contrast to the experimental approach, theoretical studies and computer simulations commonly assume an idealized situation where a collision between the polymer ends takes place when R falls below a certain capture radius. This corresponds to

$$k(R)=k_0\theta (R_q-R)$$ (2)

where θ(x) is the Heaviside step function and k₀ → ∞. We will refer to this model as the “contact quenching model” model (CQM) and will consider the more general situation of finite k₀. In CQM, the overall rate becomes independent of k₀ when k₀ is large enough: the quenching itself is effectively instantaneous as the distance R_q is reached. Therefore, the overall rate is determined by the diffusive dynamics of the polymer ends rather than by the kinetics of quenching.

Here, we show that the difference between the idealized CQM and more realistic experimental scenarios such as EQM is not merely quantitative. In the latter case, the time scales of the probe quenching cannot be decoupled from those of polymer dynamics. As a result, although such a limit is well-defined for the idealized CQM case, the commonly assumed diffusion-controlled limit, in which the measured quenching rate becomes independent of k₀, does not in fact exist in any experimentally relevant situation. By contrast, the standard SSS and WF approximations, which are widely invoked to interpret experimental data, cannot differentiate between the two cases: They correctly predict the existence of a diffusion-controlled limit for CQM but erroneously predict the same limit for the more realistic EQM. We note that these findings are independent of the exponential form assumed for the distance-dependent quenching in EQM and are valid for any k(R) that does not identically vanish at any finite distance (as in eq 2).

The finding that the WF/SSS approximations break down at large values of k₀ is not new. In fact, Wilemski and Fixman anticipated such a possibility in their original work.¹⁵ Numerical studies by Srinivas et al.¹¹ and by Barzykin et al.¹ report significant deviations from the WF result at large values of k₀ for the extreme (and somewhat obvious) experimental case in which k(R) describes the relatively long-range R⁻⁶ distance dependence of fluorescence resonance energy transfer (FRET). Specifically, in the FRET case, the spatial range of k(R) is often comparable with the polymer length scales, leading to significant and obvious competition between energy transfer and polymer dynamics. Here, however, we address this same issue for cases in which the end-to-end “collisions”, as reported by the quenching rate k(R), are well localized spatially (i.e., for which the quenching mechanism exhibits a more realistically strong distance dependence). Under these conditions, which are true of most of the reported experimental studies of loop closure, the quenching length scale R_q is much shorter than the typical length scale for the polymer's end-to-end distance. The lack of a diffusion-controlled limit and the failure of the standard approximations is far less obvious in this case. Nevertheless, we will show that replacing the commonly employed, finite-range transfer model (eq 2) by a model capturing a more realistic distance dependence (eq 1) leads to a qualitatively different dependence of the observed collision rate on the properties of the quencher, the polymer, and the solvent.

Our findings make it imperative to reconcile previous experimental data, which were analyzed in terms of WF or SSS theories and/or by using CQM, with the present theoretical predictions. If the diffusion-controlled limit is not achieved experimentally, is it meaningful at all to fit experimental data to approximate theories that predict such a limit? Likewise, since most of the computer simulations reported to date were based on the assumption of hard-shell contact quenching,^7,8,12 where the diffusion-controlled limit is well-defined, do they have any bearing on the results of experimental loop closure studies? To answer these questions, it is useful to consider our results from a different perspective. The value of k₀ is normally not an experimentally adjustable parameter. Instead, the existence of the diffusion-controlled rate is commonly ascertained by examining the dependence of the measured effective end-to-end collision rate, k_eff, on the solvent viscosity, η. In the diffusion-controlled limit, one expects k_eff ∝ η⁻¹. More generally, WF and SSS theories predict that the rate is given by

$$k_{\text{eff}}^{-1}=k_{\text{D}}^{-1}+k_{\text{R}}^{-1}$$ (3)

where k_D ∝ η⁻¹ is the diffusion-controlled rate and k_R is the reaction-controlled rate that is proportional to k₀ and is independent of the viscosity. This suggests that the effective collision time ${\mathit{\text{k}}}_{\text{eff}}^{-1}$ should depend linearly on η, while the intercept of the ${\mathit{\text{k}}}_{\text{eff}}^{-1}$ vs η plot yields the reaction-controlled rate.⁶ We will show that, for CQM, this equation adequately captures the viscosity dependence of the rate. That is, as the viscosity (or k₀) is increased, one continuously goes from the reaction-controlled regime (where k_eff is proportional to the intrinsic quenching rate k₀ and is independent of viscosity) to the diffusion-controlled limit, where k_eff is independent of k₀ and is inversely proportional to the viscosity.

We will further demonstrate that the viscosity (and k₀) dependence of the overall rate is more complicated when the more realistic EQM is considered. As the viscosity (or k₀) is increased, three regimes are encountered. In regime I, the WF approximation holds, as described by eq 3. Note that regime I should not be used synonymously with a diffusion-limited regime: As will be seen below, the system commonly leaves regime I and enters regime II before the diffusion-controlled limit is attained. In regime II, which thus replaces the familiar diffusion-limited regime expected for CQM, the effective end-to-end collision rate exhibits a power-law dependence on η and k₀ which is of the form

$$k_{\text{eff}}\propto k_0^{\delta }{\eta }^{-(1-\delta )}$$ (4)

Note that the scaling exponents for k₀ and η are related. We will show that this is necessarily the case as long as the polymer dynamics are overdamped. Finally, in regime III, the solvent is effectively frozen, the quenching kinetics are no longer exponential, and the overall quenching time scales as ${\mathit{\text{k}}}_0^{-1}$ and is independent of viscosity.

The scaling exponent δ observed in regime II is central to the present study. It is not universal but rather depends on the properties of both the polymer and the quenchers. We will show that it generally becomes smaller when the quenching length scale R_q becomes shorter. When δ is close to 0, it becomes difficult to distinguish between the fractional power law of eq 4 and the 1/η dependence expected in the diffusion-controlled limit. Thus, fitting the experimental data with eq 3 can appear adequate even when the interpretation of the data in terms of the simple CQM is not, a cautionary note that is a key result of the work presented here.

Although simulations can be used to estimate the value of the scaling exponent, they are not always practical. Thus, it is desirable to have a simple estimate of δ based on experimental parameters. In the following, we will present evidence that δ exhibits a universal dependence on the ratio of the polymer's quadratic mean end-to-end distance and the quenching length R_q. This enables us to estimate the values of δ for various experiments and to reanalyze the experimental data from the point of view of eq 4.

For a theorist, our study highlights the observation that efforts to generate more realistic theory/simulations may lead to additional complications. If, instead of the idealized CQM, one adopts a more realistic spatial dependence of the quenching rate, then additional information regarding the time scale of the intrinsic quenching rate is required. In contrast to the case with CQM, in this case, the limit of an infinitely fast quenching rate produces a physically meaningless result.

The rest of this paper is organized as follows. In section 2, we present our theoretical arguments and simulation results and explore the dependence of the loop closure rates on the solvent viscosity, and on the spatial range and the intrinsic quenching rate of the probe. In section 3, we compare our predictions with several experimental studies. Finally, section 4 summarizes our main findings, outlines possible extensions, and discusses implications of our results for experimental loop closure studies.

2. Theory and Simulation Results

2.1. The Absence of a Diffusion-Controlled Limit

To demonstrate that a breakdown of diffusion-limited kinetics is mathematically inevitable (except for very special cases), consider first the extreme limit of infinite intrinsic quenching rate, k₀ → ∞. Suppose we start with an equilibrium ensemble of terminally labeled polymer chains free in solution. A laser pulse excites the fluorophores so that at t = 0 we have an ensemble of electronically excited molecules with an equilibrium distribution p(R) for the end-to-end distance R (see Figure 2a). To measure the overall quenching rate k_eff, we monitor the population of excited molecules, which is related to the survival probability S(t) that a fluorophore is still excited at time t.

Figure 2.

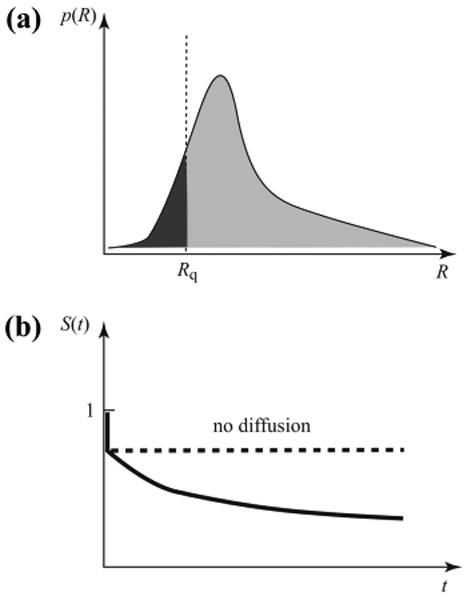
(a) In the contact quenching model (CQM), fluorescence quenching takes place instantaneously for all fluorophores for which R < R_q. This instantaneously depletes the dark shaded area in the probability distribution of the end-to-end distance for the excited molecules. (b) In the CQM, the survival probability for the excited probe undergoes a sharp drop at short times due to fluorophores that are within R_q of the quencher during excitation. This is followed by diffusion-controlled decay as other fluorophores diffuse into the quenching radius.

Let us first consider the CQM case (eq 2), in which quenching occurs whenever the chain ends happen to be within a capture distance R_q. In the k₀ → ∞ limit, the molecules with R < R_q will be quenched instantly (dark shaded area in Figure 2a). Thus, S(t) will exhibit a sudden drop from 1 to $1-{\mathit{\int }}_0^{R_q}p(R)\text{d}R$ (see Figure 2b). The population of excited molecules at t = 0+ will thus have a “hole” at short distances (as described by the lightly shaded area in Figure 2a). If diffusional rearrangement of the chains is neglected, the molecules with fluorophores outside this “hole” will remain excited indefinitely (in our idealized model) because their rate of quenching, according to eq 2, is identically zero. Thus, S(t) will remain constant (as shown by a dashed line in Figure 2b). When polymer diffusion is present, however, the fluorophores originally outside of this hole will eventually approach to within R < R_q, resulting in a decreasing survival probability. It is clear from this argument that the measured overall quenching rate is diffusion limited. If the survival probability decays exponentially

$$S(t)\propto \text{exp}(-k_{\text{D}}t)$$ (5)

then eq 5 defines the diffusion-controlled rate constant k_D, which vanishes in the limit of infinitely slow diffusion.

The situation is different when the quenching rate is finite (no matter how small) at any finite R. In this case, the survival probability will decay to zero even in the absence of any polymer motion. Moreover, S(t) will decay instantaneously to zero in the limit k₀ → ∞. To see this, we write the exact expression for the survival probability:^1,28–30

$$S(t)=\langle \text{exp}\{-{\int }_0^{t}k\left[R(t)\right]\text{d}t\}\rangle$$ (6)

where the angular brackets denote averaging over the trajectories R(t) of the polymer chain starting with the equilibrium distribution. Since the exponent is proportional to k₀(cf. eq 1), the survival probability will vanish in the k₀ → ∞ limit for any finite time t.

Given these arguments, we should expect that, depending on the extent to which the quenching rate is poorly approximated as a step-function of distance, we will not observe well-defined, diffusion-controlled kinetics in experimental measurements of polymer dynamics. In contrast to this argument, the two most commonly employed approximations for describing polymer loop closure kinetics, SSS and WF theory, predict a well-defined, diffusion-controlled rate for any quenching mechanism. WF theory, in particular, predicts k_eff to approach the diffusion-limited constant value k_D given by the expression¹⁵

$$k_{\text{D}}^{-1}=k_{\text{R}}^{-2}{\int }_0^{\infty }\langle \mathrm{\Delta }k\left[R(t)\right]\mathrm{\Delta }k\left[R(0)\right]\rangle \text{d}t$$ (7)

where

$$k_{\text{R}}={\int }_0^{\infty }k(R)p(R)\text{d}R$$ (8)

is the reaction-controlled rate and

$$\mathrm{\Delta }k(R)=k(R)-k_{\text{R}}$$ (9)

The factor k₀ cancels out in eq 7, thus giving a value that is independent of the intrinsic quenching rate. We note that the possibility of a breakdown of the WF approximation at large values of k₀ has been anticipated (although not further explored) by Wilemski and Fixman in their original work.¹⁵

2.2. In the Limits of Slow and Rapid Diffusion, the Effective Time of Quenching Scales as ${\mathit{\text{k}}}_0^{-1}$

When the quenching rate k(R) is a continuous function of R, quenching takes place even in the absence of polymer motion. For example, in the limit of very high solvent viscosity (when the polymer is essentially frozen), the survival probability is given by²⁸

$$S(t)\approx \langle \text{exp}(-kt)\rangle ={\int }_0^{\infty }\text{exp}[-k(R)t]p(R)\text{d}R$$ (10)

It is known^1,11 that the kinetics are strongly nonexponential in this limit and so the survival probability S(t) does not predict a single unique time scale for quenching. Nevertheless, it is possible to define an effective time scale τ_F for quenching in this limit by considering the first passage time

$${\tau }_{\text{F}}\equiv k_{\text{F}}^{-1}={\int }_0^{\infty }S(t)\text{d}t={\int }_0^{\infty }p(R)k^{-1}(R)\text{d}R=\langle 1/k\rangle$$ (11)

which can be estimated analytically if we assume that the polymer obeys Gaussian statistics such that p(R) is given by

$$p(R)=4\pi R^2{\left(\frac{3}{2\pi l^{2}n}\right)}^{3/2}\text{exp}\left(-\frac{3R^2}{2l^{2}n}\right)$$ (12)

where l is the Kuhn length and n is the number of statistical segments. Substituting eqs 1 and 12 into eq 11, we find

$$k_{\text{F}}^{-1}=\frac{k_0^{-1}}{\sqrt{54\pi }}\{6g+\sqrt{6\pi }{e}^{g^2/6}(3+g^2)[1+\text{erf}(g/\sqrt{6})]\}$$ (13)

where

$$g=l\sqrt{n}/R_q=\sqrt{\langle R^2\rangle }/R_q$$ (14)

The dimensionless parameter g is a measure of the characteristic polymer length scale relative to the quenching length scale. For typical experimental peptide/DNA loop closure measurements,^6,20,23 the quenching rate drops off very rapidly over the relevant polymer length scales. Therefore, the case g ≫ 1 is of interest, where the following asymptotic expression is obtained:

$$k_{\text{F}}\approx \frac{3}{2}{k}_0{g}^{-2}{e}^{-g^2/6}$$ (15)

Note that k_F is proportional to k₀. Also note that the chain length and the quencher properties enter into the result only as the dimensionless combination g.

The parameter k_F provides an estimate of the rate of the “direct” process in which quenching occurs without polymer reconfiguration. As an example, consider the experiments of Lapidus et al.,^6,23 who measured the end-to-end collision rates of polypeptides containing N = 5–20 residues. The root-mean-square end-to-end distance for these polypeptides was estimated²³ to be in the range 〈R²〉^1/2 ≈ 1.11–2.22 nm. Using the value³¹ R_q = 0.025 nm, g corresponds to 44–100, and according to eq 13, k_F = (5 × 10⁻⁵⁷³ − 5 × 10⁻¹⁴⁶)k₀. This leads, under the “no diffusion” assumption we are exploring here, to astronomically long quenching time scales for any reasonable k₀.

In the opposite limit, the limit of rapid diffusion, the overall rate is given by eq 8, which, again, is proportional to k₀. For Gaussian chains described by eq 12,

$$k_{\text{R}}=\frac{k_0}{\sqrt{54\pi }}\{-6\text{g}+e^{g^2/6}(3+g^2)\sqrt{6\pi }(1-\text{erf}(g/\sqrt{6}))\}$$ (16)

Here, too, the chain length and quenching length dependencies enter into this result only through the dimensionless parameter g. Finally, we note that the rate k_R provides an upper bound on the observed collision rate k_eff while k_F gives a lower bound.^1,28

2.3. Comparison of Simulated Rates with the Wilemski–Fixman Approximation

Having discussed the limiting conditions of slow and rapid diffusion, we now turn to the general case. Here, however, we do not report an analytical solution. Instead, we report our results for the overall rate k_eff as a function of the intrinsic quenching rate k₀ obtained using Langevin dynamics simulations of a simple bead-and-spring polymer model (see the Appendix for technical details of the simulations). For the EQM, we find that at very low values of k₀ the reaction-controlled limit takes place and the dependence is linear (Figure 3a), in accord with the WF approximation given by eqs 3, 7, and 8. At higher, though still low, values of k₀, the WF approximation remains accurate. As noted above, we call this regime I. As the intrinsic quenching rate is further increased, however, the WF approximation predicts k_eff to approach a constant plateau value k_D (given by eq 7). Instead, the rate observed in our simulations continues to increase, although it exhibits a weaker dependence on k₀. We call this regime II. The departure of k_eff from the predictions of WF theory at high values of k₀ is observed regardless of the quenching length scale. For example, shortening R_q by ∼2-fold leads to a similar dependence (compare Figure 3b with Figure 3a).

Figure 3.

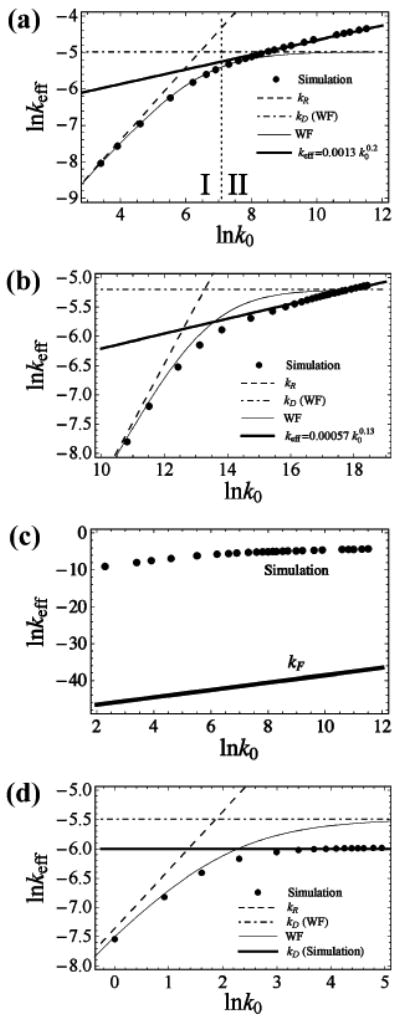
For the exponential quenching model (EQM), the Wilemski–Fixman (WF) theory (eq 3) is qualitatively incorrect in its prediction that the overall quenching rate k_eff attains a diffusion-controlled limit k_D (eq 7) that is independent of the intrinsic quenching rate k₀ at large values of k₀. In contrast, simulation results exhibit a power-law k₀ dependence. At low values of k₀, a reaction-controlled limit k_R is attained (eq 8), where k_eff is directly proportional to k₀. (a) Various theoretical predictions are compared with simulation data for N = 14 and R_q = 0.2σ, where σ is the polymer bond length. The dotted vertical line provides a rough boundary between regime I (where the WF approximation holds) and regime II (where the kinetics remains exponential and a power law holds). Regime III (where the polymer is effectively frozen) is well outside the range of k₀ plotted and occurs at ln k₀ ≥ 20. (b) Various theoretical predictions are compared with the simulation data for N = 14 and R_q = 0.091σ, where σ is the polymer bond length. (c) The direct rate k_F is many orders of magnitude lower than the actual quenching rate k_eff determined from simulations (same data as in Figure 3a). Therefore, the onset of the direct quenching mechanism per se cannot explain the deviations from the WF behavior observed in regime II. (d) The WF theory predicts a qualitatively correct behavior of the overall quenching rate k_eff as a function of the intrinsic quenching rate k₀ for CQM, unlike the EQM case. Here, the WF approximation is compared with simulation data for N = 14 and R_q = 2^1/6σ, where σ is the polymer bond length. The value of R_q chosen here corresponds to the spatial range of the repulsive Lennard-Jones potential acting between monomers. The diffusion limited value k_D predicted by the WF theory agrees with the k₀ → ∞ limit found from simulations to within a factor of ∼1.7.

Importantly, the departure from the WF theory cannot be explained simply by the onset of the slow diffusion limit described in section 2.2. Indeed, in such a limit, the direct quenching mechanism not involving any polymer reconfiguration would dominate. However, the direct rate k_F estimated from eq 11 remains many orders of magnitude (e.g., a factor of 10¹⁶ for the data of Figure 3a) smaller than the observed rate k_eff (Figure 3c). Thus, regime II must result from a more subtle interplay between polymer dynamics and quenching kinetics.

As k₀ is further increased, the direct quenching mechanism will eventually become important. Indeed, the direct rate k_F is proportional to k₀, while the regime II rate exhibits a weaker, power-law dependence (see section 2.4). Therefore, the curves representing these two dependences (Figure 3c) must cross at some k₀. It is evident from Figure 3c that the direct rate will become dominant only at k₀'s that are many orders of magnitude higher than those explored in Figure 3a. At such high values of k₀, the polymer may be viewed as effectively frozen. In this limit, which we call regime III, the overall rate k_eff is not well-defined because the kinetics (which are described by eq 10) are no longer exponential. Nevertheless, a corresponding time scale can still be defined as described in section 2.2. In the intermediate regime, regime II, the survival probability still shows exponential behavior and the rate constant k_eff can be estimated from the computed survival probability S(t).

While the WF approximation fails to predict the dependence of k_eff on k₀ at high values of k₀ in the more realistic EQM case (shown in Figure 3a and b), it remains qualitatively correct for any k₀ in the CQM case. Specifically, it predicts a diffusion-limited plateau k_eff → k_D at large values of k₀ (Figure 3d). Although the numerical value of k_D predicted by the WF approximation differs from the exact value found in the simulations, they agree to within an order of magnitude, as previously discussed by Pastor et al.⁷ Again, we emphasize that the difference between the performance of the WF approximation in the CQM and EQM cases (Figure 3d versus Figure 3a,b) is not just a matter of numbers: while in the former case it gives a qualitatively correct behavior for k_eff as a function of k₀, in the latter case, the WF approximation fails to capture even the qualitative observation that the quenching rate k_eff continues to rise as k₀ is increased.

2.4. Regime II: The Power Law for k_eff as a Function of k₀ and Viscosity

We now focus on the EQM case in regime II (see Figure 3a), where exponential kinetics are still observed despite the fact that the rate significantly deviates from the WF approximation. In this regime (see Figure 3a,b), the dependence of k_eff on k₀ is well described by a power law:

$$k_{\text{eff}}=A{k}_0^{\delta }$$ (17)

We now show that the validity of eq 17 necessitates that the viscosity dependence of k_eff should also be a power law and not, as commonly assumed,^6,12 inversely proportional. This can be seen from the following argument: Assuming an overdamped limit, the equations governing the polymer dynamics are of the general form

$$\gamma \frac{\mathbf{\text{dr}}}{\text{d}t}=\mathbf{\text{F}}(\mathbf{\text{r}},t)$$ (18)

where γ is a friction coefficient (proportional to the solvent viscosity), r is the vector describing the configuration of the polymer, and F is the force (which includes the usual stochastic component). For a given polymer trajectory r(t), the survival probability $S(t)=\text{exp}\{-{\int }_0^{t}k[\mathbf{\text{r}}(t)]\text{d}t\}$ satisfies the equation

$$\frac{\text{d}S}{\text{d}t}=-k[\mathbf{\text{r}}(t)]S=-k_0\kappa [\mathbf{\text{r}}(t)]S$$ (19)

where κ[r] = exp (−R/R_q) is a dimensionless function that describes the distance dependence of the quenching rate constant (see eq 1). Introducing dimensionless time units τ = k₀t, eqs 18 and 19 become

$$\begin{array}{l}\gamma k_0\frac{\mathbf{\text{dr}}(\tau )}{\text{d}\tau }=\mathbf{\text{F}}(\mathbf{\text{r}},\tau )\\ \frac{\text{d}S}{\text{d}\tau }=-\kappa [\mathbf{\text{r}}(\tau )]S(\tau )\end{array}$$ (20)

According to eq 20, the dynamics of the system depend on the “reduced” friction parameter γk₀ rather than on γ or k₀ individually. More importantly, the rate at which the survival probability decays to zero, measured in dimensionless units, also depends only on this reduced friction coefficient. Reverting to the original time units, we conclude that the overall rate must be of the form

$$k_{\text{eff}}=k_{0}f(k_0\gamma )$$ (21)

where f(x) is some yet unknown function. Thus, the γ dependence and the k₀ dependence of the rate are interrelated. We emphasize that the only assumption made in eq 21 is that the dynamics are overdamped.

We now can take advantage of the fact that in the regime of interest the k₀ dependence is a power law (eq 17). The function f(k₀γ) must thus also be a power law. Specifically, to satisfy eq 17, it has to be given by f(k₀γ) ∝ (k₀γ)^δ−1, leading to

$$k_{\text{eff}}\propto k_0^{\delta }{\gamma }^{-(1-\delta )}$$ (22)

which is equivalent to eq 4. If, for example, δ = 0, then k_eff ∝ 1/γ and the overall rate is inversely proportional to the friction coefficient (and viscosity) and is independent of k₀. This is the standard diffusion-controlled limit. If, on the other hand, δ = 1, the rate is directly proportional to k₀ and is independent of viscosity. This dependence is observed both in the reaction-controlled and frozen limits (regimes I and III). The cases δ = 0 and δ = 1 represent two extremes, where the measured quenching kinetics are controlled, respectively, by the diffusive dynamics of the polymer and by the intrinsic quenching time scale. The fractional power law, 0 < δ < 1, represents the more general case where the two time scales compete.³² Such fractional power-law viscosity dependence has been previously observed in the simulations of Srinivas and co-workers¹¹ for the case where k(R) described fluorescence resonance energy transfer between the ends of a Rouse chain. Given the long length scale of FRET, this is perhaps not surprising. As we note below, however, fractional power-law dependencies have also been observed experimentally even when much more strongly distance-dependent quenching mechanisms have been employed.

What can be said about the proportionality coefficient in eq 22? There are two characteristic time scales in the problem. The first one is associated with the intrinsic quenching rate ${\mathit{\text{k}}}_0^{-1}$. The second one is the polymer's inherent time scale. Although polymer fluctuations generally exhibit a spectrum of time scales, the slowest one usually dominates long time dynamics. The relevant characteristic time can be estimated as^33,34

$${\tau }_{\text{r}}=\frac{\gamma N\langle R^2\rangle }{k_{\text{B}}T}$$ (23)

Note that we have omitted any numerical factors in our definition of τ_r. For example, the longest relaxation time within the Rouse model of polymer dynamics^33,34 differs from the above equation by a factor of 3π². Equation 22 suggests that the exponent δ describes the partitioning of the overall relaxation time between these two time scales. In other words, we can rewrite eq 22 in the form

$$k_{\text{eff}}=a{k}_0^{\delta }{(1/{\tau }_{\text{r}})}^{1-\delta }$$ (24)

where a is a dimensionless coefficient. If R_q is longer than the polymer's Kuhn length, a should depend only on the ratio of the polymer's characteristic length scale 〈R²〉^1/2 and R_q. In other words, a is a function of the parameter g =〈R²〉^1/2/R_q defined in section 2.2. Remarkably, most known analytic approximations to k_eff are limiting cases of eq 24. For example, it is straightforward to check that the SSS approximation^6,27 for CQM is obtained by assuming δ = 0 and a = c/g, where c is a numerical constant. In contrast, Doi⁴ and Friedman and O'Shaughnessy⁵ predicted that k_eff should be proportional to 1/τ_r. Their result is recovered if one assumes that δ = 0 and a is a constant. Likewise, the expressions for the quenching rate in the limits of rapid and slow polymer diffusion (eqs 13 and 16) are also of the form of eq 24, where δ = 1. These, however, are all limiting cases that do not rigorously describe real experimental systems. In the following sections, we will explore how the exponent δ and the proportionality coefficient a depend on the properties of the experimental system at hand.

2.5. The Dependence of the Exponent δ on the Properties of the Polymer and Probe

While the viscosity dependence of the rate k_eff is readily measured via experiment, its dependence on k₀ is not, since the value of k₀ is generally fixed by the physical properties of the probes employed. From a computational perspective, however, it is actually quite easy to determine δ from the k₀ dependence of k_eff, more so, in fact, than from its friction coefficient dependence. This is because a single polymer trajectory obtained at one value of the friction coefficient is sufficient to compute k_eff for any value of k₀. In view of eq 22, both approaches contain the same information and yield the same value of δ. Indeed, we have verified the validity of eq 22 by performing simulations over a range of viscosities (data not shown).

The value of the exponent δ generally depends on the specific polymer and on the probes employed to monitor its kinetics. Our goal here is to explore this dependence and to establish simple estimates of δ that would be applicable for various experimental conditions. As R_q decreases and quenching becomes increasingly short ranged, the exponent δ also decreases (Figure 4a). This is consistent with previous simulation results¹¹ obtained for the kinetics of fluorescence resonance energy transfer between the ends of an ideal Rouse chain. In the case of infinitely short-range quenching (R_q → 0), the 1/η scaling of the diffusion-controlled limit is recovered, which is intuitively expected, as in this limit quenching occurs upon contact (R ≈ 0) and the difference between the CQM and EQM disappears. In practice, of course, this limit is of only academic interest, since the probability of such a contact would become vanishingly small.

Figure 4.

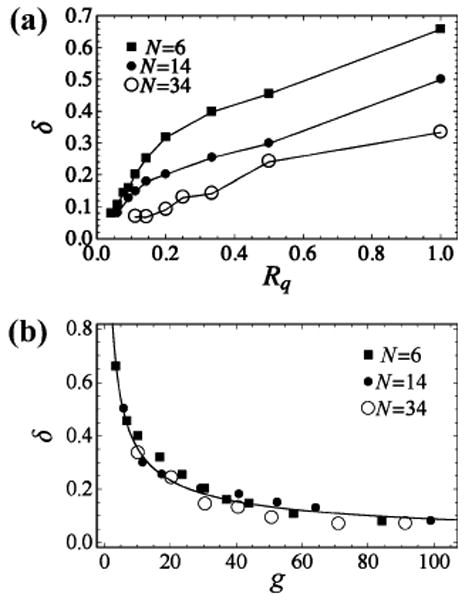
(a) The scaling exponent δ varies strongly as a function of the length scale of quenching and with polymers of different lengths. (b) The scaling exponent δ approaches a universal curve when plotted as a function of the dimensionless parameter g = 〈R²〉^1/2/R_q. The solid line represents a power-law fit of this curve given by the equation δ ≈ 1.416g^−0.602.

In order to establish the dependence of δ on the properties of the polymer itself, we have also performed simulations for chains of different length N. These simulations show that the exponent δ decreases with increasing chain length (Figure 4a).

The above findings regarding the dependence of δ on N and R_q were obtained for an idealized bead-and-spring polymer system. We can employ them, however, to estimate the numerical values of the exponent δ for various experiments without having to use a more realistic polymer model in each case. In the limit of sufficiently long chains and for the values of R_q that are larger than the Kuhn length of the chain, this is to be expected; in this limit, only two length scales are relevant, the quenching length scale R_q and the polymer's characteristic dimension 〈R²〉^1/2. Thus, the dimensionless exponent δ should depend on the ratio of the two, g = 〈R²〉^1/2/R_q, as it does in the two limiting cases discussed in section 2.2. Fortuitously, a near universal relationship between δ and g holds even in the (more experimentally relevant) regime where R_q is comparable to or smaller than the chain Kuhn length. Indeed, when the data of Figure 4a is replotted as δ versus g, it falls close to a single curve (Figure 4b). The rather small deviations from a universal relationship presumably arise from finite size effects. The (nearly) universal curve δ(g) computed here can be used to analyze a variety of experimental systems as long as enough is known about them to estimate the value of g.

2.6. The Dependence of the Proportionality Coefficient A on the Properties of the Polymer and Probe

The proportionality coefficient A between k_eff and $k_0^{\delta }$ (cf. eq 17) strongly depends on chain length and R_q and spans several orders of magnitude, as these parameters are varied in our simulations (Figure 5). As suggested by eq 24, we can write this proportionality coefficient as A(R_q,N) = a(1/τ_r)^1−δ, where τ_r is the polymer's inherent characteristic time (eq 23). The dimensionless parameters a and δ should become universal functions of the dimensionless parameter g defined in eq 14 in the asymptotic limit where both R_q and 〈R²〉^1/2 are much larger than the Kuhn length. Consistent with this, for the largest values of R_q studied here, the dependence A(R_q,N) is well described by eq 24 with a constant value of a ≈ 0.5 (Figure 5). As R_q is decreased, deviations from the simple scaling formula of eq 24 are observed, although this formula still correctly describes the qualitative trend for A to decrease with decreasing R_q or with increasing chain length. These deviations are not surprising, since in this range of parameters we do not expect the parameter a to be constant or, more generally, to be any universal function of g. Nevertheless, eq 24, with a ≈ 0.5, predicts the overall quenching time scale to within less than an order of magnitude across the entire range of R_q and N studied here.

Figure 5.

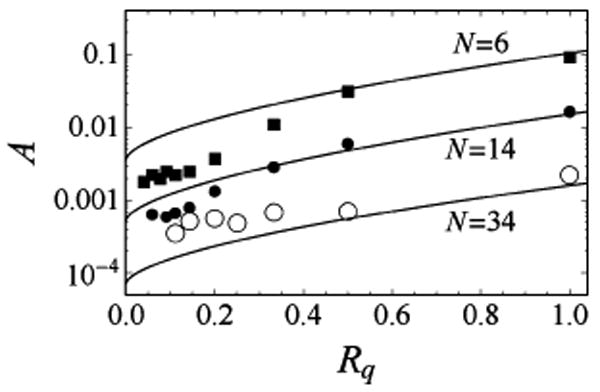
The proportionality coefficient A in the relationship $k_{\text{eff}}=A{k}_0^{\delta }$ varies strongly as a function of the length scale of quenching and polymer length. Much of this variation is captured by the approximate formula A = a(1/τ_r)^1−δ, where τ_r is the polymer's inherent relaxation time (eq 23), a = 0.5, and the scaling exponent δ is estimated using the universal curve δ(g) of Figure 4b. The predictions of this formula are plotted as solid lines.

In the limit R_q → 0, our results suggest that A should approach a finite value (Figure 5). This may appear counterintuitive, since one naturally expects the overall quenching rate to vanish in this limit. It is however important to remember that A represents the proportionality coefficient between k_eff and $k_0^{\delta }$ in the range of k₀'s such that the power law holds (i.e., in regime II). If R_q is decreased, the range of k₀ where the power law is valid gets shifted toward larger values (cf. Figure 3a and b). On the other hand, k_eff indeed vanishes in the limit R_q → 0 for any fixed value of k₀.

3. Comparison with Experimental Data

Fractional viscosity dependence has been observed by Bieri et al.²⁰ in their measurements of the end-to-end collision rates in short polypeptides. They found that k_eff ∝ η^δ−1 with δ close to 0.2 except for the shortest peptide studied, for which δ is ∼0.04. Since the chains used in that study were rather short (3 ≤ N ≤ 10), we do not necessarily expect the universal behavior described here (Figure 4b) to hold. Nevertheless, if we assume it to be true, the value δ = 0.2 corresponds to g = 20–40. Estimating 〈R²〉^1/2 ∼ 1.5 nm for a polypeptide with N = 10 bonds, this corresponds to R_q ∼ 0.4–0.8 Å.

In contrast to the nonlinear relationship predicted here, and reported by Bieri et al.,²⁰ Lapidus et al.⁶ report a linear relationship between ${\mathit{\text{k}}}_{\text{eff}}^{-1}$ and viscosity and interpret the intercept as the value associated with the reaction-controlled rate k_R (see eq 3). In section 2.2, however, we have estimated g = 44–100 for their system, thus corresponding to δ < 0.15. Although a power-law fit was not attempted by Lapidus et al., it appears that it would be difficult to distinguish between the $k_{\text{eff}}^{-1}\propto {\eta }^{1-\delta }={\eta }^{0.85}-{\eta }^{0.9}$ predicted here and the linear ${\mathit{\text{k}}}_{\text{eff}}^{-1}$ vs η dependence expected on the basis of the WF or SSS approximations.

As yet another example, we have recently studied the end-to-end collision rates of single-stranded DNA.²⁵ For a 15-base polythymine chain, deviations from a linear dependence of ${\mathit{\text{k}}}_{\text{eff}}^{-1}$ on the viscosity are readily apparent (Figure 6). Specifically, a power-law fit $k_{\text{eff}}^{-1}\propto {\eta }^{1-\delta }$ employs the same number of adjustable parameters as the linear fit predicted by the CQM and provides a statistically significantly improved fit (Figure 6). The value of δ obtained from this fit, δ ≈ 0.524, is higher than the value estimated using the universal curve (Figure 4b). Specifically, assuming a Kuhn length of 4 nm for a single-stranded DNA³⁵ and using a bond length of σ = 0.34 nm for single-stranded DNA,³⁶ we estimate 〈R²〉^1/2 ≈ (Nσl)^1/2 ≈ 4.6 nm. Using the value³⁷ R_q = 0.725 Å, we estimate g ∼ 60, which corresponds to δ ≈ 0.14 (Figure 4b). The discrepancy between the observed and predicted values of the exponent, however, is not surprising because the contour length of the chain is not much longer than the Kuhn length and so the experimental conditions are rather far from the flexible chain assumed in this analysis. Moreover, our recent study²⁵ demonstrates that electrostatic interactions within rather short single-stranded DNAs such as this lead to significant finite size effects that cannot be captured by simple analytic polymer models.

Figure 6.

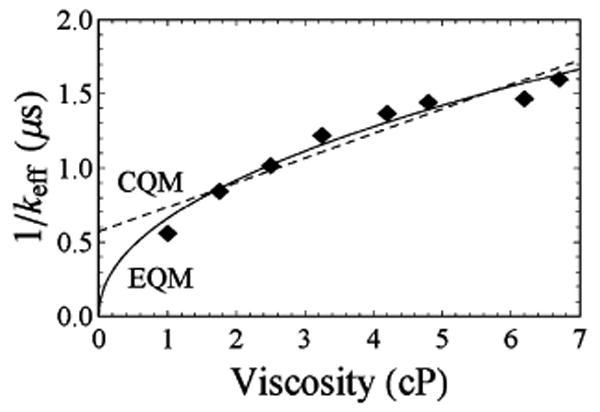
The EQM predicts a nonlinear, power-law relationship between solvent viscosity and the end-to-end collision rate of a polymer (here a 15-base single-stranded DNA comprised of polythymine) when probed using a long-lived lumiphore (ruthenium tris(bipy)) quenched via electron transfer (to methyl-ethyl-viologen). While the difference in the two fits may appear subtle, both models entail only two fitted coefficients and thus the differences in the residuals of the two fits are statistically significant (R² = 0.96 versus 0.90 for the EQM and CQM, respectively).

Given the approximations still inherent in our model, and its inability to model the specific details of each of these experimental setups, even the limited degree of correlation observed between theory and experiment appears heartening. Moving forward, a more realistic model for the end-to-end collision dynamics would also have to take into account the effect of flexible linkers connecting DNA to the probes.²⁵ One could attempt to capture the effect of the linkers with a naïve model, in which k(R) represents the overall rate of two processes: The first one consists of a diffusional approach between the fluorophore and the quencher groups subject to the constraint imposed by tethering those probes to the ends of the DNA chain. The second process is the fluorophore quenching. The effect of the flexible linkers is thus to effectively increase the spatial range of the quenching process. The characteristic length scale for k(R) would then be comparable with the typical end-to-end distances for the linkers and would be longer than the assumed value of R_q. It then appears plausible that the presence of the linkers would lead to an effectively lower value of g and thus a higher value of δ, consistent with our experimental findings.

4. Concluding Remarks

Experimental methods for measuring end-to-end collision dynamics of polypeptides and DNA commonly utilize the quenching of an optically excited probe attached to one chain end upon its collision with a quencher attached to the other end. The main message of this study is that the time scales of quenching and of the polymer conformational dynamics are inherently inseparable in such measurements. As a consequence, even their qualitative theoretical interpretation requires explicit consideration of the quenching mechanism of the experimentally employed probes.

Mathematically, the inseparability of the time scales of quenching and of the polymer conformational dynamics arises from the distance dependence of the quenching rate k(R), which is a decreasing function of the distance between the chain ends. Even if this rate is so rapid that quenching is effectively instantaneous at sufficiently short distances, the time scale of quenching becomes comparable with that of polymer reconfiguration at larger values of R. Using simple scaling arguments, we have then shown that if the polymer dynamics are overdamped then the overall quenching time scale τ is given by

$${\tau }^{-1}=k_{\text{eff}}=k_{0}f(k_0{\tau }_{\text{r}})$$ (25)

where k₀ is the intrinsic quenching rate, τ_r is the polymer's intrinsic reconfiguration time (eq 23), and f(x) is some function that depends parametrically on the chain length and R_q. Equation 25 is exact and may serve as a starting point for developing various useful approximations for k_eff through mapping out of the function f(x).

Simulations of model polymer chains performed here indicate that in the regime of moderately high values of k₀ where the quenching kinetics remains exponential this function is close to a power law, f(x) ∝ x^δ−1, thus necessitating that the dependence of k_eff on both viscosity and intrinsic quenching rate be a power law. The fractional power-law viscosity dependence is consistent with earlier observations for other systems.^{11,29,30,32,38} According to those studies, such a dependence is a common signature of the competition between the time scales of diffusion and reaction kinetics. Although our own simulations here employed a particular functional form for the quenching rate k(R), in view of those studies, we anticipate that the power law found here for EQM would be more general and would not require an exponential dependence of eq 1. In fact, Srinivas et al.¹¹ report a fractional power law in the viscosity dependence for k(R) = k₀/[1 +(R/R₀)⁶], where R₀ is a constant.

Using dimensional analysis, we have further shown that the dependence of the measured loop closure rate on the properties of the probes and on the polymer length can be recast as the scaling law given by eq 24, where a = a(g) and δ = δ(g) are universal in the asymptotic limit where the chain dimensions and the quenching length are much longer than the monomer size. We also found that near universality persists even outside this asymptotic limit, where the quenching length is comparable with the monomer size.

The scaling exponent δ describes how the overall time scale of quenching is partitioned between the inherent time scales of quenching and polymer dynamics. If, for example, δ = 0, then polymer dynamics is rate limiting and k_eff becomes independent of the quenching kinetics and inversely proportional to viscosity. In the opposite extreme, δ = 1 and k_eff is independent of the polymer dynamics and is proportional to k₀, as in the reaction-controlled limit (where polymer dynamics are infinitely rapid) and the limit where the polymer is effectively frozen. Moreover, standard analytic approximations are recovered as various limiting cases of the scaling relationship of eq 24. For example, the SSS approximation⁶ corresponds to a ∝ g⁻¹, δ = 0, while the Doi result⁴ (described above) is obtained if δ = 0 and a is constant.

The scaling prediction of eq 24 allows us to estimate the error incurred when using the standard approximations (such as the CQM) that do not explicitly take into account the quenching mechanism and predict a diffusion-controlled limit that is independent of k₀. This approximation corresponds to choosing δ = 0 and underestimates the more accurate (EQM-predicted) rate by a factor of $k_{\text{eff}}^{(\text{EQM})}/k_{\text{eff}}^{(\text{CQM})}\sim {(k_0{\tau }_{\text{r}})}^{\delta }$. When δ is close to zero and/or when the intrinsic quenching rate k₀ does not significantly exceed ${\tau }_{\text{r}}^{-1}$, then the interpretation of the experimental data in terms of the approximate CQM does not lead to significant errors.

Finally, we note that the characteristic polymer reconfiguration time scale τ_r has attracted considerable attention from experimentalists in the context of the dynamics of unfolded proteins (see, e.g., refs 39–41). If the intrinsic quenching rate k₀ can be measured independently, eq 24 provides another method for measuring τ_r.

Here, we provide technical details of our simulations and experiments.

Langevin Dynamics Simulations of Polymer Chains

We used a simple polymer model that consisted of N + 1 beads of mass m connected by N springs. The interaction potential between a pair of beads separated by a distance r consists of a harmonic bond interaction for two covalently linked beads

$$V_{\text{bond}}(r)=k_{\text{bond}}{(r-\sigma )}^2/2$$ (26)

and a repulsive Lennard-Jones potential between nonbonded beads

$$V_{\text{nonbonded}}(r)=4\epsilon [{(\sigma /r)}^{12}-{(\sigma /r)}^6]\theta (2^{1/6}\sigma -r)$$ (27)

Here, the parameter ε sets the energy scale, σ represents the equilibrium bond distance, k_bond = 100ε/σ², and θ(x) is the Heaviside step function used to truncate the attractive part of the Lennard-Jones potential. The dynamics of each bead was described by the Langevin equation

$$m{\ddot{\mathbf{\text{r}}}}_i(t)=-\frac{\partial V}{\partial {\mathbf{\text{r}}}_i}-\gamma {\dot{\mathbf{\text{r}}}}_i(t)+{\mathbf{\text{R}}}_i(t)$$ (28)

where r_i is the position of the bead, V is the total potential, γ is the friction coefficient, and R_i(t) is the random force satisfying the fluctuation–dissipation theorem. All simulations reported here were performed for γ = 2.0 (σ²/mε)^−1/2 and a temperature of T = 1.0 ε/k_b. In reporting our data, we use the bond length σ as the unit of distance and τ₀ = (mσ²/ε)^1/2 as a unit of time so that the reported rate constants are normalized by the factor (mσ²/ε)^−1/2.

To obtain the overall quenching rate, we computed the survival probabilities S(t) defined by eq 6 using R(t) from Langevin trajectories. In the range of parameters reported here, S(t) was found to be close to exponential, S(t) ≈ exp(−k_efft), thus yielding the values of the overall quenching rate k_eff.

Experimental Measurements of End-to-End Collision Dynamics in Single-Stranded DNA

To probe the end-to-end collision dynamics of a single-stranded DNA, we employed the quenching of a modified ruthenium tris(bipyridine) by electron transfer to methyl ethyl viologen (N-methyl-N′-ethyl bipyridine, MV) as previously described.²⁵ The effective end-to-end collision rate was determined from fluorescence lifetime measurements performed using time-correlated single photon counting.²⁵ The viscosity of glucose in pH 7, 100 mM NaCl/20 mM sodium phosphate buffer was estimated via its relationship with the index of refraction,⁴² which was measured using an Abbe-3 L refractometer (Thermo Spectronic).