Estimation of Selection Intensity under Overdominance by Bayesian Methods

Abstract

A balanced pattern in the allele frequencies of polymorphic loci is a potential sign of selection, particularly of overdominance. Although this type of selection is of some interest in population genetics, there exists no likelihood based approaches specifically tailored to make inference on selection intensity. To fill this gap, we present Bayesian methods to estimate selection intensity under k-allele models with overdominance. Our model allows for an arbitrary number of loci and alleles within a locus. The neutral and selected variability within each locus are modeled with corresponding k-allele models. To estimate the posterior distribution of the mean selection intensity in a multilocus region, a hierarchical setup between loci is used. The methods are demonstrated with data at the Human Leukocyte Antigen loci from world-wide populations.

1. Introduction

Selection reshapes patterns of variation in the genome leaving its signature on allele frequencies. Different selective mechanisms produce a variety of patterns. A balancing selection pattern arises when heterozygous genotypes are favored, a mechanism known as overdominance (see [Maruyama, 1981] and references therein for background). Contrary to mechanisms which work by eliminating the genetic variability, overdominance actively maintains allelic polymorphism in populations. Consequently, exceptional levels of polymorphism are expected to mark prototypical loci under overdominance. In this paper, methods to estimate selection intensity in such genomic regions are presented.

While mathematically well grounded frameworks have been advanced to model overdominance, equally well grounded statistical methods, linking the observed patterns of variability to the estimates are yet to be developed. This inference problem has some unique aspects. A notable one is that both elevated mutation rates and selection promote genetic diversity. This fact implies that allele frequencies reshaped by both processes do not carry distinctive information about the respective parameters. In statistical terms, parameters representing mutation and selection are unidentifiable. Another point arises in estimation. A relatively detailed and well understood class of population genetic models that can accommodate overdominance is k-allele models with selection [Watterson, 1977, Wright, 1949]. Nevertheless, it has been shown that the maximum likelihood estimates cannot be reliably coupled with bootstrap to assess the error of estimates under k-allele models with selection [Buzbas and Joyce, 2009]. Intensive resampling of the allele frequency space creates a numerical instability, which causes the estimates to be both unreliable and inaccurate. Therefore, obtaining good interval estimates is a challenge. Further, polymorphic systems may span a number of genetic loci, sometimes with large number of alleles. This makes the scalability of computational methods an issue. To our knowledge, there exists no likelihood based methods that can handle data from multiple polymorphic loci to make inference on the strength of overdominance. Our main contribution is to provide such methods which overcome all the aforementioned problems.

We alleviate the problem of identifiability by defining two classes of “alleles” which capture two types of variation, “neutral” versus “selected”. We build two classes of k-allele models. One to identify plausible mutation rates using the neutral variation. Another to use this information and the selected variation to recover the signal due to overdominance. We solve the instability issue in estimation by taking a Bayesian view. Since posterior inference fixes the data and searches only the parameter space, it avoids pitfalls arising due to resampling of the data space. Our model can accommodate arbitrary number of loci and alleles. This flexibility allows us to obtain estimates of mean selection intensity for groups of loci using a hierarchical model setting.

As a real data application we consider the polymorphism in the Major Histo-compatibility Complex (MHC) region of vertebrates. In humans, each major MHC locus has sufficient variability to be a good candidate for overdominance. However, there is extensive functional similarity and cooperation of molecular products encoded by different MHC loci. In such systems, handling information from the whole group of loci is a reasonable first approximation for an assessment of the intensity of selection in the region. Methods are demonstrated using Human Leukocyte Antigen data from world-wide populations. Data sets published in the Proceedings of the 13^th International Histocompatibility Workshop and Conference (see [Meyer et al., 2007] and references therein) are analyzed across loci for signals of overdominance.

2. Model

The k-allele model with symmetric overdominance is described using a Wright-Fisher population (see [Donnelly and Kurtz, 1999, Ethier and Griffiths, 1987, Ethier and Kurtz, 1993, Ewens, 2004] for background). It assumes a panmictic population of N diploid individuals at a non recombinant locus with non overlapping generations. There are k possible alleles. Each generation 2N genes are randomly paired to form N gene pairs or genotypes. Thus, (assuming large N) the genotype frequency of A_mA_l will be 2x_mx_l. The genotypes are then sampled to form the next generation. The probability of sampling a genotype is proportional to its fitness, w_ml = 1 + s_ml, with s_ml = 0 if m ≠ l and s_ml = −s, (s > 0) otherwise. A randomly chosen allele within each sampled genotype is subjected to mutation with probability u before it is included into the next generation’s allele pool. This process is Markovian and there exists a stationary distribution of the allele frequencies, x = [x₁ ... x_k], given by

$$f\left(x|\theta ,\sigma \right)=\frac{e^{-\sigma }{\sum }_{i=1}^k{x}_i^2}{c\left(\theta ,\sigma \right)}\prod _{i=1}^k{x}_i^{(\theta /k-1)}$$ (1)

where θ = 4Nu, σ = 2Ns are mutation and selection parameters and

$$c\left(\theta ,\sigma \right)=\frac{\Gamma {\left(\theta /k\right)}^k}{\Gamma \left(\theta \right)}\int \cdots \int e^{-\sigma {\sum }_{i=1}^k{x}_i^2}f\left(x|\theta \right)dx$$ (2)

is the normalizing constant. Efficient numerical methods to compute c(θ, σ) are given in [Genz and Joyce, 2003] and [Joyce et al., 2009]. Here, f (x|θ) is the stationary distribution under neutrality which is appropriate when all genotypes have equal fitness. It can be obtained as a special case of equation 1 by setting σ = 0, which gives

$$f\left(x|\theta \right)=\frac{\Gamma \left(\theta \right)}{\Gamma {\left(\theta /k\right)}^k}\prod _{i=1}^k{x}_i^{(\theta /k-1)}.$$ (3)

In the next two subsections, we describe our approach to jointly estimating θ, σ using both equations 1 and 3, with selected and neutral variability respectively.

2.1. Allelic Variability

The data from single locus are summarized in Table 1. The first column identifies selectively distinct alleles, k of them in total. These alleles differ by a non synonymous mutation at least at one site in their sequence and constitute the “selected variation”. Each line in the second column gives the frequency vector of neutral variants, for the corresponding selectively distinct allele. Elements of a vector differ from each other by synonymous substitutions only. For example, the j_i neutral variants associated with the i^th allele in the first column are denoted by [x_i1 ... x_iji]. These alleles are subject to the same selection and thus differ from each other by a “neutral” substitution. The third column gives the frequency of selected alleles which are then collected in the vector x = [x₁ x₂ ... x_k]. Finally, in the last column are the normalized frequencies of neutral variants, to be used with the neutral model. These are collected in the vector of vectors Y.

Table 1:

Partitioning the allelic variability at a locus.

Number of selected alleles	Frequency of neutral variants	Frequency of selected alleles	Normalized frequency of neutral variants
1	[x11 ... x1j1]	$x_1={\sum }_{i=1}^{j_1}{x}_{1i}$	y1 = [x11 ... x1j1]/x1
2	[x21 ... x2 j2]	$x_2={\sum }_{i=1}^{j_2}{x}_{2i}$	y2 = [x21 ... x2j2]/x2
.	.	.	.
.	.	.	.
.	.	.	.
k	[xk1 ... xk jk]	$x_k={\sum }_{i=1}^{j_k}{x}_{ki}$	yk = [xk1 ... xk jk]/xk

Vector of selected allele frequencies x = [x₁ x₂ ... x_k].

Vector of vectors for neutral allele frequencies Y = [y₁ y₂ ... y_k].

As we justify in section 5, if only x is available, θ and σ are statistically unidentifiable. This problem can be circumvented however, by observing that variation encapsulated in Y is reshaped by mutation only and it can be used to extract information about θ. The variation in x on the other hand, can be used to extract information about both parameters. The two types of data, x and Y are modeled as follows.

2.2. Single Locus Model

The neutral variation does not affect fitness, hence it is subject to equation 3. Assuming a constant mutation rate within a locus, Appendix A shows that the joint likelihood of the allele frequencies can be written as

$$P\left(Y|\theta \right)\propto \prod _{i=1}^{k}f\left(y_i|\theta \right).$$ (4)

Using Bayes’ rule we obtain

$$P\left(\theta |Y\right)\propto P\left(Y|\theta \right)P\left(\theta \right),$$ (5)

where P(θ) is a prior for the mutation parameter.

On the other hand, the selected variation results from fitness differences and under overdominance it follows equation 1. Denote the likelihood by P(x|θ, σ), which is the density in equation 1 evaluated at the data x as a function of θ, σ. Assuming the prior independence of θ, σ and using Bayes’ rule we link neutral and selected models by

$$P\left(\theta ,\sigma |x,Y\right)\propto P\left(\text{x}|\theta ,\sigma \right)P\left(\theta |Y\right)P\left(\sigma \right)$$ (6)

where P(σ) is prior for the selection parameter. In this way, the information obtained using the density in equation 3 and the data Y are fused with that from equation 1 and x. In practice, we first estimate the posterior distribution of the mutation parameter, P(θ|Y) = P(Y|θ)P(θ), then use this information to obtain the posterior in equation 6. The second analysis is still joint estimation, that is, our view of the mutation parameter from the first step is not fixed but subject to re-evaluation using the new evidence. Throughout we use proper uniform priors with diffuse bounds both for θ and σ.

2.3. Extension to Multiple Loci

To extend the single locus model to multiple loci we adopt a hierarchical normal model as a robust choice (see [Bustamante et al., 2002] for an application in population genetics and [Gelman et al., 2004] pp. 74–77 for a detailed treatment in general settings). Given i = 1, 2, ..., m loci, we assume that selection parameters σ_i are normally distributed with group specific common mean μ and variance τ. Conditional on the normal distribution, the process at each locus is identical, corresponding to a (conditionally) independent Wright-Fisher population. From the Bayesian perspective, the normality has the interpretation of a prior on the selection parameters. Next, we derive posterior distributions of the mutation and selection parameters.

There are m conditionally independent posteriors, one for each selection parameter. Let x_i and Y_i denote the selected and the neutral frequencies for i^th locus. Appendix B shows that the conditional distribution of σ_i and θ_i are given respectively by

$$P\left({\sigma }_i|x_i,{\theta }_i,\mu ,\tau \right)\propto P\left(x_i|{\theta }_i,{\sigma }_i\right)P\left({\sigma }_i|\mu ,\tau \right),$$ (7)

$$P\left({\theta }_i|{\sigma }_i,x_i,Y_i\right)\propto P\left(x_i|{\theta }_i,{\sigma }_i\right)P\left(Y_i|{\theta }_i\right)P\left({\theta }_i\right).$$ (8)

We assign diffuse priors to hyperparameters. We use a uniform distribution on μ and an inverse chi-squared distribution on τ, which is conjugate for the normal model variance [Gelman et al., 2004]. We write, τ ∼ Inv –χ²(ν₀, τ₀) where Inv – χ² denotes an inverse χ² distribution. Prior parameters are chosen so that this distribution is uninformative (i.e., large τ₀ and small ν₀). The joint posterior for (μ, τ) is given by

$$P\left(\mu ,\tau |\sigma \right)\propto \frac{1}{{\tau }^{\left(m+v_0+2\right)/2}}{e}^{-\frac{{\sum }_{i=1}^m{\left({\sigma }_i-\mu \right)}^2-v_0{\tau }_0}{2\tau }},$$ (9)

where σ = [σ₁ ... σ_m]. The total number of parameters to be estimated is 2m + 2, mutation and selection parameters for 2m loci in addition to μ, τ. In particular, our interest lies with μ, the group specific mean selection parameter.

The above treatment of the normal hierarchical model is a common one. However, the hard to compute integration constant in the stationary distribution of the allele frequencies creates difficulties in sampling the target posterior distributions. Below we present algorithms to accomplish this task.

3. Methods

3.1. Single Locus

The posterior distribution of θ under the neutral model and the joint posterior distribution of (θ, σ) under overdominance are obtained with the following (Metropolis-Hastings) algorithms respectively [Hastings, 1970, Metropolis et al., 1953].

Algorithm 1

1. Start with an arbitrary initial value, θ⁽⁰⁾.

2. Generate θ^* independently, from θ* ∼ Unif(0, θ_max) where θ_max is a fixed constant.

3. Generate U ∼ Unif(0, 1).

4. Set θ⁽¹⁾ = θ^* with probability $\alpha =\text{min}\left\{1,{\prod }_{i=1}^k\frac{f(y_i|{\theta }^{*})}{f(y_i{|}^{(0)})}\right\}$.

5. Iterate from step 2.

Algorithm 2

1. Start with arbitrary initial values (σ⁽⁰⁾, θ⁽⁰⁾).

2. Generate (θ*, σ*) independently, from θ* ∼ P(θ|Y) and σ* ∼ Unif(–σ_max, σ_max) where σ_max > 0 is a fixed constant.

3. Generate U ∼ Unif(0, 1).

4. Set σ⁽¹⁾ = σ*, θ⁽¹⁾ = θ* with probability $\alpha =\text{min}\left\{1,\frac{f({\sigma }^{*},{\theta }^{*}|x,Y)}{f({\sigma }^{(0)},{\theta }^{(0)}|x,Y)}\right\}$.

5. Iterate from step 2.

If diffuse limits for θ_max and σ_max are used, the priors will be uninformative.

3.2. Multiple Loci

Under the hierarchical model of section 2.3, a relatively easy strategy to simulate from the joint posterior distribution of the parameters is as follows [Bustamante et al., 2002, Gelman et al., 2004]:

1. Simulate τ from its marginal posterior distribution and μ from its conditional distribution given τ.

2. Given the values of the hyperparameters and the data, generate the selection and mutation parameters for each locus from their conditional distributions respectively.

To perform Step 1 we exploit

$$P\left(\mu ,\tau |\sigma \right)=P\left(\mu |\sigma ,\tau \right)P\left(\tau |\sigma \right).$$ (10)

The posterior distribution of the mean selection parameter conditional on τ is given by (μ|τ, σ) ∼ N (σ̄, τ/m), where σ̄ denotes the mean of selection parameters and m is the number of loci. The marginal distribution of the variance is given by

$$\left(\tau |\sigma \right)\sim Inv-{\chi }^2(v_0+m,\hspace{0.17em}\frac{v_0{\tau }_0+\left(m-1\right)s_{\sigma }}{v_0+m})$$

where sσ is the sample variance of selection parameters.

The posterior distributions of θ and σ to be sampled in Step 2 do not have familiar forms and simulating directly from these conditionals is not possible with standard methods. One way to sample them is via the inverse method using empirical cumulative distribution functions evaluated on a grid, but this is computationally expensive under k-allele models. In the rest of this section we describe efficient methods to sample from these distributions. These methods are embedded in a Gibbs sampler including all the parameters and hyperparameters.

We start with the selection parameter. Using equation 7 without subscripts for notational convenience, the conditional distribution of σ can be written as

$$P\left(\sigma |x,\theta ,\mu ,\tau \right)\propto \frac{e^{-\sigma F}{G}^{\left(\theta /k-1\right)}}{c\left(\theta ,\sigma \right)}{e}^{-{\left(\sigma -\mu \right)}^2/2\tau }$$ (11)

where $F={\sum }_{i=1}^k{x}_i^2$, $G={\prod }_{i=1}^k{x}_i$. Completing the square and collecting the exponential terms we get

$$P\left(\sigma |x,\theta ,\mu ,\tau \right)\propto \left[\frac{1}{\sqrt{2\pi \tau }}{e}^{-\frac{{\left(\sigma -\left(\mu -\tau F\right)\right)}^2}{2\tau }}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\frac{1}{c\left(\theta ,\sigma \right)}\right].$$ (12)

The first term on the right is the familiar normal density with mean μ – τF and variance τ. The second term is a normalizing constant from the stationary distribution under selection which we know how to compute numerically [Genz and Joyce, 2003, Joyce et al., 2009]. To sample the density in equation 12 we use a result due to Damien et al. [Damien et al., 1999]. Put in our context, the result states that if c(θ, σ) is invertible and non-negative, then there exists a Gibbs sampler for P(σ|x, θ, μ, τ). The condition is satisfied since c(θ, σ) > 0 for all θ, σ and it follows from equation 2 that c(θ, σ) is a decreasing function in σ for fixed θ. To build the Gibbs sampler, an auxiliary variable U is introduced such that the conditional distribution U|σ is uniform on (0, c(σ, θ)⁻¹). On the other hand, the conditional distribution σ|U is the normal distribution given in equation 12, restricted to the set B_σ = {σ : c(θ, σ)⁻¹ > u}. Hence, the conditional of σ is a truncated normal with truncation point updated at each iteration of the Gibbs sampler. The truncation is from the left and for strong selection the set B_σ consists of large values of σ. This involves drawing from extreme tails of a normal distribution, a difficult feat using the standard inverse method due to the cumulative distribution function approaching to unity. We circumvent this problem using an accept-reject algorithm that is efficient for hard to draw values from truncated normal distributions [Geweke, 1991]. The choice of the instrumental distribution depends on the truncation point. For the hard to draw region described above a truncated exponential distribution with rate min(B_σ) on σ > min(B_σ) is used, where min(B_σ) is the truncation point.

The posterior distribution of the mutation parameter, θ, is given by

$$P\left(\theta |x,Y,\sigma \right)\propto \frac{G^{\left(\theta /k-1\right)}}{c\left(\theta ,\sigma \right)}P\left(Y|\theta \right)P\left(\theta \right).$$ (13)

To obtain a workable form we fit a gamma distribution (with parameters λ, α), to P(θ|Y) = P(Y|θ)P(θ). After some algebra we get

$$P\left(\theta |x,\sigma ,\lambda ,\alpha \right)\propto \left[\frac{{\left(\lambda -\text{log}G/k\right)}^{\alpha }{\theta }^{\alpha -1}{e}^{-\left(\lambda -\text{log}G/k\right)\theta }}{\Gamma \left(\alpha \right)}\right]\hspace{0.17em}\left[\frac{1}{c\left(\theta ,\sigma \right)}\right].$$ (14)

The first term on the right is a gamma density with parameters λ – logG/k and α, whereas the second term is again the normalizing constant of the density under selection. Similar to the case of σ, one way to sample the posterior distribution of θ is by first finding the restriction set for θ and then drawing from the truncated version of the gamma given by the first term of equation 14. There exist efficient accept-reject algorithms to sample a truncated gamma density to obtain draws in this way [Dagpunar, 1978, Phillippe, 1997]. Here we opt for an alternative, the inverse cumulative distribution function method coupled with a truncated exponential density [Damien and Walker, 2001]. There is little difference between the two methods from computational point of view. We let B_θ = {θ : θ^α−1 c(θ, σ)⁻¹ > u}. Now, generating from the posterior distribution of θ is equivalent to generate from P(θ|λ, x) = (λ – logG/k)e^{−(λ − logG/k)θ} I(θ > min(B_θ)), which is a truncated exponential distribution with parameter (λ − logG/k). We use the inverse method to generate θ by

$$\theta =-\text{log}\left(U/\left(\lambda -\text{log}\hspace{0.17em}G/k\right)\right)/\left(\lambda -\text{log}\hspace{0.17em}G/k\right)+\text{min}\left(B_{\theta }\right),$$

where U ∼ Unif(0, 1).

To sample posterior distributions of all the parameters and hyperparameters we setup a Gibbs sampler as follows.

Algorithm 3

1. Start with initial values for the parameter vector

   $${\mu }^{(0)},{\tau }^{(0)},{\sigma }^{(0)}=\left[{\sigma }_1^{(0)},\cdots ,{\sigma }_k^{(0)}\right],{\theta }^{(0)}=\left[{\theta }_1^{(0)},\cdots ,{\theta }_k^{(0)}\right].$$
2. Iterate for all i :

   1. Draw u = U from Unif(0, 1) and find the set

      $$B_{\sigma }=\{\sigma :c{\left({\theta }_i^{(0)},\sigma \right)}^{-1}>uc{({\theta }_i^{(0)},{\sigma }_i^{(0)})}^{-1}\}.$$
   2. Sample ${\sigma }_i^{(1)}\sim TN\left(({\mu }^{(0)}-{\tau }^{(0)}{F}_i),{\tau }^{(0)}\right)$ where TN denotes a truncated normal distribution with truncation point given by min(B_σ).
   3. Draw u = U from Unif(0, 1) and find the set

      $$B_{\theta }=\{\theta :{\theta }_i^{\alpha -1}c{({\theta }_i,{\sigma }_i^{(0)})}^{-1}>u{({\theta }_i^{(0)})}^{\alpha -1}c{({\theta }_i^{(0)},{\sigma }_i^{(0)})}^{-1}\}.$$
   4. Draw u = U from Unif(0, 1) and find ${\theta }_i^{(1)}=-\text{log}(u/(\lambda -\text{log}\hspace{0.17em}G/k))/(\lambda -\text{log}\hspace{0.17em}G/k)+\text{min}(B_{\theta })$.

3. Given σ⁽¹⁾, sample from τ ∼ Invχ²(m − 1, sσ₍₁₎).

4. Given τ⁽¹⁾, sample from μ ∼ N (σ̄⁽¹⁾, τ⁽¹⁾/m), where σ̄⁽¹⁾ is the sample mean of σ⁽¹⁾.

5. Iterate from Step 2.

Before moving to specific examples let us recapitulate the above procedures. Given a set of loci, considered as a group for purposes of estimating the intensity of selection under overdominance, we adopt the following strategy.

1. Identify neutral and selected frequencies at each locus as defined in table 1.

2. Use neutral variation and Algorithm 1 to construct a prior view of the mutation parameter at each locus.

3. Use this prior, selected variation and Algorithm 3 to sample the posterior distribution for the mean and variance of the selection parameter for each group.

4. Method Validation and Examples

4.1. Simulations

The focus of our simulations is two fold. First, we explore the effect of the distribution of information among loci on the estimates of μ. Second, we assess the amount of data required to obtain reasonable error bounds on μ under appreciable selection. In the same context, we also analyze the simulated data with fixed θ, to assess the quality of joint estimation with respect to the known mutation parameter case.

Consider data sets with

$$(m,k)=\{(3,32),\hspace{0.17em}\hspace{0.17em}(4,24),\hspace{0.17em}\hspace{0.17em}(6,16),\hspace{0.17em}\hspace{0.17em}(8,12),\hspace{0.17em}\hspace{0.17em}(12,8),\hspace{0.17em}\hspace{0.17em}(16,6),\hspace{0.17em}\hspace{0.17em}(24,4),\hspace{0.17em}\hspace{0.17em}(32,3)\}$$

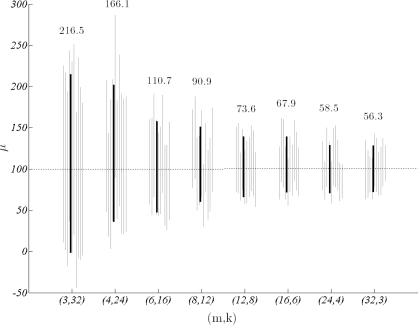
all generated under σ = 100. Each data set has 96 allele frequencies in total, however, the organization of information is quite different. We simulated thirty replicates under each parameter combination and obtained posterior distributions as explained in Algorithm 3. Credible intervals for μ show that data sets with fewer alleles distributed in many loci yield smaller variance estimates in comparison to those with large number of alleles distributed over a few loci (figure 1). This result is not totally unexpected and it can be interpreted as a realization of the fact that data from different loci are treated as (conditionally) independent. In other words, an allele at a new locus has more information (due to independence) than an additional allele within a locus (where the frequencies are correlated).

Figure 1:

95% credible intervals of μ for data sets with m = 3, 4, 6, 8, 12, 16, 24, 32 loci and k = 32, 24, 16, 12, 8, 6, 4, 3 alleles respectively, all generated under σ = 100. For each parameter vector the mean credible interval based on thirty replicates (black) and ten individual intervals are shown (shades). Interval lengths for means are given on top.

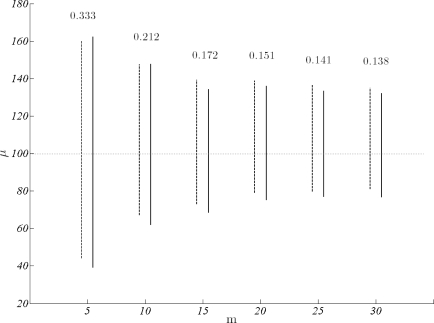
As can be deduced from the analysis just presented, single locus data are not expected to provide precise estimates. Note that, a multivariate x is actually sample of size 1 for each locus. Combined information from multiple loci on the other hand, is expected to improve the precision considerably. Accordingly, we now fix k and turn to answer how many loci yield a reasonable precision on the mean selection parameter. The data have m = 5, 10, 20, 25, 30, k = 10 and σ = 100. The improvement in precision with the number of loci are illustrated as the mean of thirty replicates in terms of 95% credible intervals and coefficient of variation in μ. A comparison of these intervals with corresponding intervals from the analysis with fixed θ show very little difference (figure 2). Hence, prior distributions of θ obtained using neutral variation are pretty informative and do an excellent job in recovering information about individual mutation parameters.

Figure 2:

The decrease in 95% credible intervals of μ with m. For all data k = 10 and σ =100. Interval estimates from joint estimation (solid lines) and fixed θ estimation (dotted lines) show little difference. Coefficient of variation for each μ from joint estimation is given on top of the corresponding interval.

4.2. Human Leukocyte Antigen

As an application of the methods we consider data from the Human Leukocyte Antigen (HLA) loci, a most intensively studied region of the human genome. HLA genes code for molecular products that regulate and control immune system functions. High levels of genetic variability is observed in these genes. Complex adaptive processes that resulted in diversification of functional regions such as HLA are yet to be resolved [Black and Hedrick, 1997] and the astounding1 variability in these regions has many implications. A widely stated hypothesis is that the high genetic variability at HLA is a result of overdominance. The molecular products coded by HLA help detect foreign agents such as pathogens, bacteria, virus etc. Briefly, these molecular products are attached on the cell surface and they either remain inactive if they recognize an agent as “self” (i.e., produced by the body itself) or signal to the immune system if they recognize it as “non-self”. Higher genetic variability is promoted since the production of different molecules gives an opportunity to recognize a wider range of non-self pathogenic agents. Therefore, heterozygous individuals are hypothesized to have a selective advantage over homozygous ones.

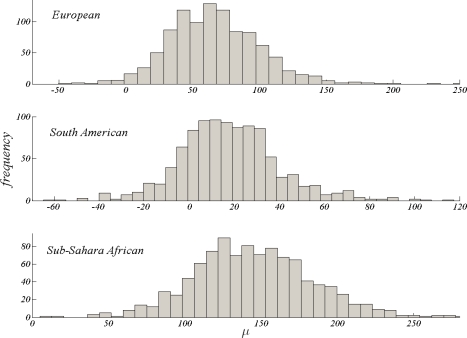
There exist analyses of single locus HLA data sets in the literature aiming at estimating the selection intensity from allele frequency data. For example, Muirhead and Slatkin [2000] analyzed large data sets of HLA from world wide populations for signals of balancing selection. Their model is essentially the same as the single locus model presented in this paper, however, they used simpler estimators of selection intensity since current methods and computational power were not available at that time. Here, we use some of the data on HLA loci provided by the Proceedings of the 13^th International Histocompatibility Workshop and Conference [Meyer et al., 2007] to illustrate our methods. We use data from three Class I loci (i.e., A, B and C) and two Class II loci (i.e., DRB and DQB) consisting of three geographical populations: European, South American and Sub-Sahara African. The most polymorphic of these is the Sub-Sahara African population, with an exceptional variability both in neutral and selected variation, whereas the least polymorphic is the South American population (Table 2). We analyze the data using the hierarchical model with the goal of estimating the mean selection intensity in the HLA region of the genome, for each of these populations. Since there exists sufficient variability at serotype groups, we assume that selection acts at the antigen level and identify the selected alleles accordingly. High variability in the neutral data for each locus provided informative prior distributions of θ. Posterior samples of μ for European and Sub-Sahara African populations (figure 3), indicate that overdominance might be a plausible hypothesis for the HLA loci in these populations, since 95% credible intervals do not include zero, the neutral case. On the other hand, South American population frequencies are not inconsistent with neutrality. For this population, one would fail to conclude a signal for overdominance. Note that this result is consistent with our observation that this is the least polymorphic of the three populations.

Table 2:

The HLA data (modified from 13^th Histocompatibility workshop proceedings [Meyer et al., 2007]). Only loci that provide sufficient variation at synonymous level are used. Populations/Loci not used for the analysis are indicated by (*). The first figure in each cell is the number of serologically differing alleles (selected variability). The neutral variation is given parenthetically: aⁿ denotes that there are n groups with a neutral alleles each.

Pop./ Locus	A	B	C	DRB	DQB
European	17, (2, 3)	28, (24, 3)	13, (24, 3)	13, (27)	5, (22)
South American	9, (2)	10, (23)	7, (23)	10, (2)	*
Sub-Sahara African	21, (22, 32)	30, (25, 32)	14, (25, 3, 4)	13, (28, 3)	5, (25, 3)

Figure 3:

Posterior samples for the mean selection intensity, μ, under selective overdominance model for European, South American and Sub-Sahara African populations.

5. Discussion

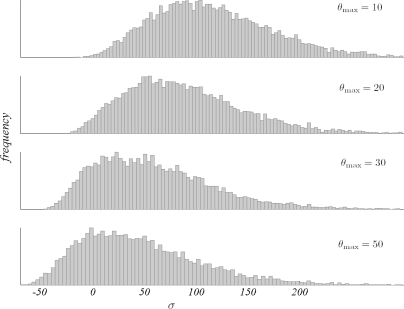
In this paper, we presented an overdominance model that can accommodate data from multiple loci with multiple alleles and likelihood based methods to estimate the selection intensity under this model. Our methods use two types of genetic variability: neutral and selected. The necessity of neutral variability as part of the data has been mentioned several times hitherto. Its crucial role is to restrict the mutation parameter to a range consistent with the data such that unrealistically large values are not considered consistent with the data. If only selected variation is used, large mutation rates are able to account for the variation actually produced by selection. Consequently, selection intensities would be biased towards lower values leading to erroneous inference. In fact, under the k-allele model, mutation and selection parameters turn out to be statistically unidentifiable if the data consist only of allele frequencies reshaped by both forces (figure 4). Therefore, some external data limiting the mutation rates are necessary for meaningful inference.

Figure 4:

The effect of θ, on the posterior distribution of σ illustrating the identifiability problem.

A large number of loci might not always be available for the biological system of interest. For example the HLA system has six major Class I and Class II genes. Data consisting of 32 loci such as ones considered in the simulations seem overly optimistic. When the number of loci is small, interval estimates can be too wide to be useful even if there is appreciable signal for selection.

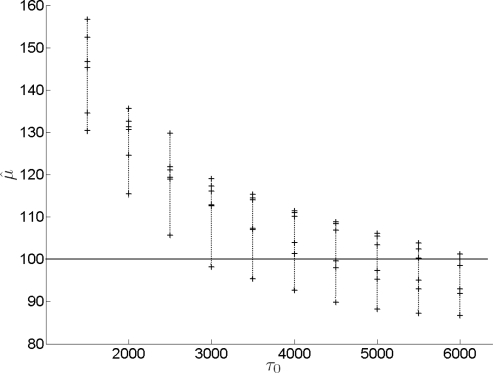
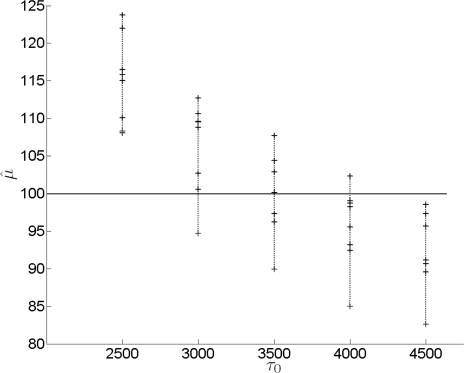
Importantly, when m,k (i.e., the number of loci and allele frequencies in the data) are small to moderate, the estimates of σ and μ will be sensitive to the prior parameter τ₀ for the variance. This effect is due to the fact that τ is a parameter in the posterior distributions of σ and μ. In such cases, τ₀ should be chosen carefully to minimize its effect on inference. For the conjugate prior considered above, the Inv − χ² prior is uninformative when τ₀ is large. However, for a given pair of m,k, a too large τ₀ introduces a negative bias in the estimates, whereas a too small τ₀ creates a positive bias. To minimize the effect in either direction, τ₀ can be optimized based on the number of loci and allele frequencies for the loci of interest. Note that, these quantities are constants in the model and not part of the data, legitimizing their role to optimize the prior parameter. An optimal τ₀ for a given m,k pair has on average a minimal biasing effect. A good way to determine such a τ₀ is as follows. First, we generate a large sample of data sets with the m and k of the actual data. (The actual value of μ under which the data are generated, has a negligible effect on the bias.) We choose an arbitrary τ₀ and obtain the posterior distribution of μ. If the mode is above the true value, we decrease, otherwise increase τ₀ and reiterate until an acceptable level of bias is achieved. The effect of prior parameter τ₀ on the estimates is shown by mean estimates of μ, based on 10 independent simulated data sets for each m,k combination and a range of τ₀ values (figure 5 and 6).

Figure 5:

Mean μ̂ for a range of τ₀ for data with increasing number of loci (k = 10 constant). For each τ₀, marks indicate estimates for (from top to bottom) m = 5, 10, 15, 20, 25, 30. Each estimate is the mean of 10 data sets. The unbiased point estimates corresponding to the given number of loci are obtained respectively at optimal τ₀ = 6100, 6000, 5500, 4450, 4100, 2850 (not shown).

Figure 6:

Mean μ̂ for a range of τ₀ for data with different (m,k) combinations. From top to bottom: (m,k) = {(3, 32), (4, 24), (6, 16), (8, 12), (12, 8), (16, 6), (24, 4), (32, 3)} The unbiased point estimates corresponding to the given number of loci are obtained respectively at τ₀ = 4350, 3900, 3850, 3800, 3800, 3500, 3250, 3050, 2700. Note that, in the given range of (m,k) values, all but very extreme pairs have similar optimal τ₀ (approximately 3500–4000). That is, when both m and k are relatively large, optimal τ₀ stays constant.

A certain amount of genetic linkage is expected in a set of loci located on the same chromosome. Linkage affects a multi locus system by creating correlation in the allele frequencies between loci. In this case, the joint distribution of data across loci currently given by equations 18 through 21 in Appendix A, would no longer be the product of the likelihoods, but would be more complex. To derive such a likelihood one would have to know specific information concerning the linkage between loci. However, if these adjustments are possible, the rest of the hierarchical Bayesian setup would remain unchanged. Yet, this strategy is not useful unless a realistic correlation structure about the system is available. However, if locus i and locus j are linked, one would expect the estimated selection coefficients to be closer than if they were unlinked. From an estimation perspective, the consequence of correlation between allele frequencies is decreased variance of the estimates of σ; which in turn decreases τ.

Our model assumes no population demography. Under balancing selection, migration turns out to be one of the confounding demographic effects [Hudson, 1991]. In the diffusion approximation to Wright-Fisher model, if included, the effect of migration on the allele frequencies is similar to that of mutation. Both migration and mutation affect the allele frequencies linearly, whereas selection affects the allele frequencies non-linearly. In particular, under our model, symmetric migration can be incorporated by replacing the mutation parameter θ by θ + M where M = 4Nm is the population scaled migration parameter and m is the migration rate. It is also possible to introduce asymmetric migration structures where the rate of migration is different for each allele, although such a model will be data hungry since the number of parameters increases. On the other hand, if there is some migration ignoring it will inflate the mutation parameter estimates. The selection parameter estimates however, will not be affected unless migration is much stronger than mutation or it has a highly asymmetric structure.

The hierarchical model is a first pass to make inference from a multiple loci system with a high number of alleles. As such, it does not take into account allele frequency changes due to epistatic interactions between loci. This is not surprising for a model of additive effects. A model capturing more biological detail such as epistasis is necessarily more complicated than the one presented in this paper. Under the framework presented here such a model implies a more intricate hierarchy. From an inference perspective, epistasis might be easier to handle with a model able to treat the multi locus allele frequencies without appealing to a hierarchical structure. For example, the mathematical machinery of the multiple loci k-allele diffusion can be also established in the presence of epistasis, as shown by new theoretical developments [Fearnhead, 2006]. Fearnhead extended the theory of single locus diffusion approximations to the multiple loci case, where a group of genes act as a single unit of selection. Using this result, overdominance can be modeled in the presence of epistatic interactions between loci. This avenue is particularly appealing for inference on loci related to immune system, where there is evidence for epistatic interactions between loci. Therefore, a future direction is to develop statistical methods for such models, a problem which we tackle in a subsequent paper.

Appendix A.

We are interested in the joint density of θ, σ given the two data sets, x, Y. Apply Bayes’ rule

$$P\left(\theta ,\sigma |x,Y\right)\propto P\left(x,Y|\theta ,\sigma \right)P\left(\sigma ,\theta \right)$$ (15)

$$=P\left(Y|\theta ,x\right)P\left(x|\theta ,\sigma \right)P\left(\theta ,\sigma \right)$$ (16)

$$=\left(\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right)\right)P\left(x|\theta ,\sigma \right)P\left(\theta ,\sigma \right).$$ (17)

The last equality follows from

$$P\left(Y|\theta ,x\right)=P\left(Y,x|\theta \right)/P\left(x|\theta \right)=\prod _{i=1}^{k}P\left(y_i,x_i|\theta \right)P\left(x|\theta \right)$$ (18)

$$=\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right)P\left(x_i|\theta \right)/P\left(x|\theta \right)$$ (19)

$$=\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right)P\left(x|\theta \right)/P\left(x|\theta \right)$$ (20)

$$=\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right).$$ (21)

The second equality in equation 18 follows from the fact that given the i^th sum, x_i, the synonymous allele frequencies for that class y_i are independent of the other sums. The result in equation 17 says that the joint posterior of θ, σ has three pieces: The joint likelihood under neutrality, where only the synonymous data are used, the joint likelihood under selection, where only the non-synonymous data are used and the prior. This formulation is equivalent to use the posterior of θ from the synonymous data analysis as the prior of θ for the analysis under selection. This can be seen by expressing equation 17 as

$$\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right)P\left(x|\theta ,\sigma \right)P\left(\theta \right)P\left(\sigma \right)$$ (22)

$$=\prod _{i=1}^{k}P\left(y_i|x_i,\theta \right)P\left(\theta \right)P\left(x|\theta ,\sigma \right)P\left(\sigma \right)$$ (23)

$$\propto P\left(\theta |x,Y\right)P\left(x|\theta ,\sigma \right)P\left(\sigma \right).$$ (24)

Appendix B.

The joint distribution of all the parameters for i^th locus is given by

$$f\left({\sigma }_i,{\theta }_i,x_i,\mu ,\tau \right)=f\left({\sigma }_i|{\theta }_i,x_i,\mu ,\tau \right)f\left({\theta }_i,x_i,\mu ,\tau \right)$$ (25)

$$=f\left(x_i|{\sigma }_i,{\theta }_i,\mu ,\tau \right)f\left({\sigma }_i,{\theta }_i,\mu ,\tau \right).$$ (26)

By the second equality we get

$$f\left({\sigma }_i|{\theta }_i,x_i,\mu ,\tau \right)=\frac{f\left(x_i|{\sigma }_i,{\theta }_i,\mu ,\tau \right)f\left({\sigma }_i,{\theta }_i,\mu ,\tau \right)}{f\left({\theta }_i,x_i,\mu ,\tau \right)}.$$ (27)

Using the fact that the hyperparameters affect the data only through the parameters and conditioning we have

$$f\left({\sigma }_i|{\theta }_i,x_i,\mu ,\tau \right)=\frac{f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left({\sigma }_i|{\theta }_i,\mu ,\tau \right)f\left({\theta }_i,\mu ,\tau \right)}{f\left(x_i|{\theta }_i,\mu ,\tau \right)f\left({\theta }_i,\mu ,\tau \right)}.$$ (28)

Noting that μ and τ fully specify the distribution of σ_i, we write

$$f\left({\sigma }_i|{\theta }_i,x_i,\mu ,\tau \right)=\frac{f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left({\sigma }_i|\mu ,\tau \right)}{f\left(x_i|{\theta }_i,\mu ,\tau \right)}.$$ (29)

and finally

$$f\left({\sigma }_i|{\theta }_i,x_i,\mu ,\tau \right)\propto f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left({\sigma }_i|\mu ,\tau \right).$$ (30)

The first term is the stationary distribution of the allele frequencies under selection from the single locus model and the second term is the normal density.

Similarly for θ_i we get

$$f\left({\theta }_i|{\sigma }_i,x_i,Y_i,\mu ,\tau \right)f\left({\theta }_i,x_i,Y_i,\mu ,\tau \right)=f\left(x_i|{\sigma }_i,{\theta }_i,\mu ,\tau \right)f\left({\sigma }_i,Y_i,{\theta }_i,\mu ,\tau \right).$$ (31)

$$f\left({\theta }_i|{\sigma }_i,x_i,Y_i,\mu ,\tau \right)=\frac{f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left({\theta }_i|{\sigma }_i,Y_i,\mu ,\tau \right)f\left({\sigma }_i,\mu ,\tau \right)}{f\left(x_i|{\sigma }_i,\mu ,\tau \right)f\left({\sigma }_i,\mu ,\tau \right)}.$$ (32)

$$f\left({\theta }_i|{\sigma }_i,x_i,Y_i,\mu ,\tau \right)=\frac{f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left(Y_i|\theta \right)f\left({\theta }_i\right)}{f\left(x_i|{\sigma }_i,\mu ,\tau \right)}.$$ (33)

So we have

$$f\left({\theta }_i|{\sigma }_i,x_i,Y_i\right)\propto f\left(x_i|{\sigma }_i,{\theta }_i\right)f\left(Y_i|\theta \right)f\left({\theta }_i\right).$$ (34)

Again, the first term is the stationary distribution of the allele frequencies under selection from the single locus model and the second term is the prior distribution of θ_i which is the posterior obtained from the neutral model analysis for i^th locus.