Counter-Intuitive Stochastic Behavior of Simple Gene Circuits with Negative Feedback

Abstract

It has often been taken for granted that negative feedback loops in gene regulation work as homeostatic control mechanisms. If one increases the regulation strength a less noisy signal is to be expected. However, recent theoretical studies have reported the exact contrary, counter-intuitive observation, which has left a question mark over the relationship between negative feedback loops and noise. We explore and systematically analyze several minimal models of gene regulation, where a transcriptional repressor negatively regulates its own expression. For models including a quasi-steady-state assumption, we identify processes that buffer noise change (RNA polymerase binding) or accentuate it (repressor dimerization) alongside increasing feedback strength. Moreover, we show that lumping together transcription and translation in simplified models clearly underestimates the impact of negative feedback strength on the system's noise. In contrast, in systems without a quasi-steady-state assumption, noise always increases with negative feedback strength. Hence, subtle mathematical properties and model assumptions yield different types of noise profiles and, by consequence, previous studies have simultaneously reported decrease, increase or persistence of noise levels with increasing feedback. We discuss our findings in terms of separation of timescales and time correlations between molecular species distributions, extending current theoretical findings on the topic and allowing us to propose what we believe new ways to better characterize noise.

Introduction

Negative feedback loops have long been thought of as dynamic stabilizers in cell-signaling pathways, possibly due to their prototypical role in engineering design (1). A biology equivalent is a simple gene circuit in which a protein (a transcriptional repressor) negatively regulates its own expression (Fig. 1). This is an interesting and well-studied case because gene expression is an inherently noisy business (2), a fact that is backed by numerous findings on the topic (3–5). The key question is to clarify the relations between feedback structures and noise characteristics of the regulated system. It has been addressed in several theoretical and experimental studies (1,6–13), with contradicting results. In this study, we elucidate the reasons for such discrepancies by development, simulation, and analysis of mathematical models for simple negative feedback circuits.

Figure 1.

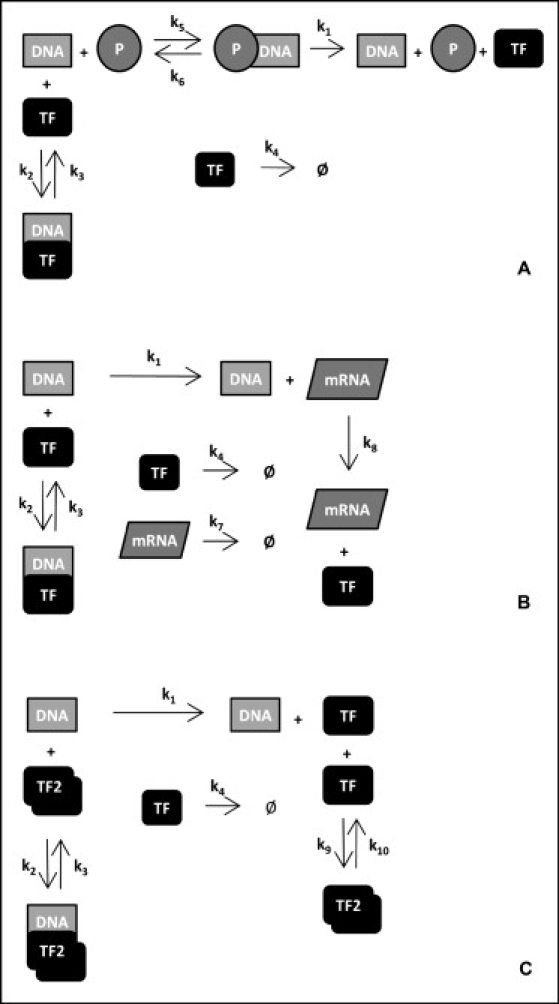
The basic modules of gene regulation modeling including (A) RNA polymerase binding to the gene, (B) making a clear distinction between mRNA transcription and protein translation, and (C) including repressor dimerization.

Early experimental and theoretical studies such as the one by Becskei and Serrano (6) showed that protein levels will be more tightly controlled—less noisy—with increasing strength of the feedback loop. However, the experimental results refer to variability of protein levels of cellular populations, rather than to variations in single-cell time courses. Moreover, many of these theoretical analyses lump transcription and translation into a single process and they do not use a full stochastic treatment of the noise-generating processes in gene expression. More recent studies treat transcription and translation as distinct processes (Fig. 1 B) where, after linearization of the self-regulation, the noise appears to be reduced as the feedback is increased (13). Yet, without linearization of the feedback, and considering a wider range of feedback values, noise actually increases. This makes the noise at high-level feedback greater than that of unregulated systems (1), a result that is consistent with reports using different approaches (9,11).

Most published models use a QSS assumption on the possible states of the gene, primarily to reduce computational costs. However, the QSS assumption breaks down at high feedback levels (1). By consequence, the noise behavior of the system will also depend on whether a QSS assumption holds or not. Fortunately, the biggest proportion of biologically feasible (e.g., typically observed) parameter values lies within areas where the QSS may actually be a reasonable assumption. Nevertheless, it is important to understand when this is so, and what the differences between both cases are.

For all the above reasons, it is not clear if, even in the simplest biological contexts, negative feedback loops reduce noise and, if not, what the exact relations between circuit design and noise characteristics are. To tackle both issues, we analyzed seven minimalist models of gene expression, some of them resembling partial or full models considered previously in literature (1,6,11,13). As is standard in prokaryotic gene expression models, we will assume molecular species to be well-mixed, and use the common nomenclature of temporal stochastic models (cf. Supporting Material). There exist delayed or spatially-resolved stochastic techniques, however, and these are indispensable when spatial information is essential for the correct understanding of a cellular process (14–16). This is particularly important when modeling gene expression in eukaryotes due to explicit and more substantial time delays (17), a topic that lies outside the scope of this study. Nevertheless, we want to stress that retorting to spatial/delayed modeling schemes is inevitable whenever spatial/delay effects deem to affect any considered cellular process within the studied time frame.

Another important aspect relates to the quantitative characterization of stochastic noise. Except for a few studies (18–20), gene expression noise has been assessed through measurements based on the first two moments of the protein/mRNA distributions. The CV is a measure used commonly. It is defined as the variance of the observations divided by their squared mean, CV(X) = σ²(X)/μ(X)², allowing for a clean separation of different noise sources if models are weakly nonlinear (5). However, the CV and similar measures cannot capture deviant effects, such as nonclassical behavior or deterministic models being closer to the mode rather than the average of stochastic dynamics (20). Additionally, mRNA and protein distributions need not be symmetric nor unimodal (19); multimodal distributions are often, but not always, related to the breakdown of the QSS approximation. Hence, the interpretation of noise varies significantly depending on the applied methodology.

To systematically study the effect of feedback, we characterize model assumptions and conditions under which noise in simple negative feedback circuits is bound to increase, decrease, or remain unchanged when tuning negative feedback strength. We then focus on the relationship between typical noise measurements and emergent properties of the system due to separation of timescales, such as protein bursts and multimodal behavior. This shows that noise measurements based on the first two moments of the molecular species distributions can be dangerously misleading. We suggest using a combination of techniques to assess noise sources and scaling (e.g., the CV in conjunction with time-correlation measures). Alternatively, if noise is to be assessed within individual expression patterns, we suggest a modified CV weighted by the frequency/mode of nonclassic behaviors. Our results agree to a certain extent with recent reports based on separation of timescales (18,19,21,22), extending the observable ranges and types of correlation between mRNA transcripts and synthesized proteins.

Methods

Parameters for simulations

For each model, we specified the TF steady-state and obtained all involved kinetic rate constants (Table S1, Table S2, and Table S3), one by one, while keeping all other kinetic rate constants fixed. The initial conditions considered were 1, 10, 100, and 1000 molecules of the repressor, TF, in a typical Escherichia coli volume of 10⁻¹⁵ L. We refer to these as initial TF levels, corresponding to distinct deterministic steady-states. A state for mRNA was also calculated when transcription and translation were treated separately. The feedback parameter a = k₂/k₃ is equivalent to the parameter k_r in Becskei and Serrano (6) on a QSS assumption for the bound and unbound gene states, and it is also the reciprocal of the parameter K_d used in most references (i.e., K_d = 1/α). Parameter α was varied in a large range (10⁻²⁰–10¹⁵ M⁻¹; see Stekel and Jenkins (1) and Slutsky and Mirny (32)) given experimental results and previous criticisms on the lack of consideration of strong feedback scenarios. In a few cases, kinetic rate constants yielded negative parameter values. In such cases, simulations were not run and we explicitly point out when this happens.

We carried out single cell simulations (Fig. S3) using the SSA. Each individual stochastic simulation started from the deterministic steady-state protein number and ran for a time T such that T = 10^{−(Ln(k4)/Ln(10 − 1)} > 10 × Ln(2)/k₄ (T = 10⁵ s when varying k₄), the RHS being an expected time for the system to reach steady-state (13). For each of these single simulations we collected 10⁵ equally spaced time points and computed the CV, where the mean was calculated from each TF time course. However, even when considering 10⁵ sample points, noise measurements varied for high feedback gain. Hence, we decided to analyze our results by obtaining statistics of 100 CVs for each feedback value, for each case (cf. Supporting Material). By doing this, we attempt to rule out noise stemming from lower molecular concentrations.

Matrix formulation of the CME and the FSP

For the purposes of this study, the models are both bounded and finite, so we restrict our notation to N dimensions. If we define a vector $\mathit{p}\in {\mathcal{R}}^{\text{n}}$ such that each entry corresponds to the probability P(x;t) for each reachable state x, we can think of its time evolution as $\dot{\mathit{p}}\left(t\right)=\mathit{Ap}\left(t\right)$, where the matrix A = [a_ij] contains the propensities and a_jj = −∑_i≠j a_ij, which basically means that each row of the matrix sums up to zero and the probability is conserved. Given an initial distribution p(0), the solution at time t is p(t) = exp(tA)p(0), where the matrix exponential is generally defined through its Taylor series expansion. If the reachable state space is large it may come in handy to consider the FSP (28), in which matrix A is replaced by A_k, a k × k submatrix of the true operator A, the corresponding indexed systems states form the finite state projection and p(t_f) ≈ exp(t_fA_k)p_k(0) is the approximation to p(t) = exp(tA)p(0) at time t_f. An approximation can be gradually improved by adding reachable states up to a prespecified tolerance level.

Results

The paradigm of noise attenuation

It is often taken for granted that strong negative feedback results in less noisy signals. A classical example is the study by Becskei and Serrano (6), where the model structurally corresponds to our scheme in Fig. 1 A. In their study, a noise-mitigating effect of negative feedback was inferred from the responses of a deterministic model to perturbations of TF at varying feedback gains. Normalized concentrations showed clearly that the unregulated system has a broader distribution of TF molecules than the autoregulated system (6).

This model, however, assumes a QSS, lumping RNA polymerase binding, transcription, and translation into a single first-order reaction. In addition, stochastic trajectories of the CME do not necessarily resemble solutions of a perturbed ODE system. Such perturbations are not equivalent to solving the corresponding SDE system and, even when the noise term is introduced correctly, an SDE approach would not be appropriate when dealing with low reactant concentrations. Here, we only have one gene copy and its state changes dynamically. Therefore, we obtained independent exact trajectories of the CME through the SSA (23). Our results show that, contrary to Becskei and Serrano (6), there is no noticeable noise mitigation by negative feedback (cf. Supporting Material).

Having this observation at hand, what can be expected from negative feedback regulation? For a more systematic analysis of the key factors controlling noise in simple feedback systems, we will now consider three core modules consisting of RNA polymerase binding to the gene (Fig. 1 A), separate processes of transcription and translation (Fig. 1 B), and dimerization of the TF (Fig. 1 C). For simplicity, we will refer to these as RNAP, TT, and DM modules. The seven possible module combinations summarize the range of models used commonly, making the most complete story the one that comprises them all (Fig. S4). We will analyze these models first under a QSS assumption, and drop this assumption later on.

Oversimplified models do not show strong noise attenuation

We analyzed the three QSS models that lump transcription and translation into a single first-order process: the RNAP module, the DM module, and their corresponding combination. Models were parameterized for given feedback gains a = k₂/k₃ and fixed steady-state levels of transcription factor (see Methods and Supporting Material). For the sake of transparency we did not use any coarse-graining technique or approximation (22). Instead, we solely obtained exact trajectories of the system's CME through the SSA and, due to the lack of nonclassical behavior in the observed protein time courses, we measured noise by the CV solely.

In line with our findings for the model from Becskei and Serrano (6), none of the systems displayed noise increase nor, counter intuitively, extreme noise attenuation with increasing gain of the negative feedback (cf. Supporting Material). The steepest noise attenuation was achieved when tuning the RNA polymerase binding/unbinding rates (k₅, k₆) followed by the TF degradation rate (k₄). Tuning rates that capture TF dimerization (k₉, k₁₀) showed no noticeable noise variation with respect to increasing feedback (Fig. 2, A and B). Hence, detailed analyses of parameter spaces are required for characterizing noise behavior even of simple gene circuits.

Figure 2.

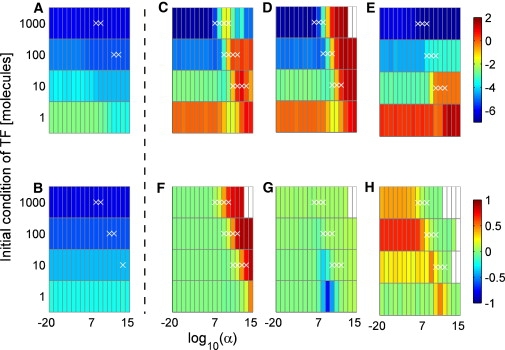
(A and B) Feedback-dependent noise of the RNAP + DM module. (C–H) Correlation behavior of the TT module. Initial TF levels were fixed by tuning the (A) RNA polymerase binding rate (k₅), (B) TF dimerization rate (k₉), (C and F) mRNA degradation rate (k₇), (D and G) the protein translation rate (k₈), and (E and H) the protein degradation rate (k₄), respectively. Colors show the log₁₀(CV) of protein numbers (A–E) and time correlations between mRNA and TF (F–H). White crosses indicate cases where all kinetic parameters are within typical biological ranges.

Next, we investigated the influences of circuit topologies (Fig. S6). Compared to the model based on the RNAP module, the DM module achieved slightly greater noise reductions. The system resulting from the combination of these two modules showed intermediary levels of noise reduction. Especially for the DM module—that introduces nonlinearities and switch-like behavior that could increase noise (24)—these findings were unexpected, but consistent with the parametric studies for repressor dimerization (k₉, k₁₀) above. Moreover, such differences cannot be deduced from a deterministic analysis because the eigenvalues of the system are strictly negative and real, leading to stable steady-states (see Supporting Material). Hence, apparent inconsistencies between earlier studies on the effects of negative feedback (1,6,11–13) might stem from subtle differences in the analysis approaches used (e.g., stochastic versus deterministic, exact model structures, and parameterizations).

Noise increase by separate transcription and translation

Transcription and translation are distinct biochemical processes, and models that consider them separately are closer to reality (25). Most importantly, the time delays implied in these two sequential steps are well-known sources of oscillations and other more complicated systems behaviors (26). Therefore, we will now explore the TT module (equivalent to the system in Thattai and van Oudenaarden (13)), a minimal system that distinguishes the processes of transcription and translation. In combination with the modules discussed previously, it gave rise to three additional, composite models: the TT along with RNAP modules, TT along with DM modules, or the combination of all modules.

As above, we carried out exact stochastic simulations to measure the CV in these four models under a QSS assumption. The most striking difference to the behavior of the lumped transcription-translation model was that noise always increased with increasing feedback gain when tuning the mRNA degradation constant k₇, the translation constant k₈ (Fig. 2, C and D) or the protein degradation rate (k₄, Fig. 2 E). Adjusting k₇ yielded much less pronounced noise amplification than tuning k₈. Noticeably, the latter generated high noise even for high steady-state TF numbers, where stochastic effects are not necessarily expected. This difference required further explanation because, when tuning k₇, the associated deterministic systems exhibit complex eigenvalues (spirals) at steady-state for some feedback values, whereas tuning k₈ always yielded negative eigenvalues (stable fixed points). Hence, the deterministic analysis would result in opposite predictions on the influences of the parameters.

In addition, the systematic analysis showed substantial differences between model structures (Fig. S7). Compared to the noise profile of the TT module alone, incorporating the RNAP module attenuates noise increase by postponing it to higher feedback values. Such buffering is not due to unreasonably large concentrations of the RNA polymerase as we considered a concentration of 100 nM, equivalent to 60 mol/cell (6). In contrast, the addition of the DM module accentuates noise increase, by shifting it to lower feedback values. This behavior is diametrically opposite to the effects of TF-TF interactions in the simpler lumped models where the addition of a DM module resulted in preponed noise decrease. Finally, for the set of kinetic parameters considered, the effects of the RNAP and DM modules approximately balance out.

Two obvious questions arise. Why do QSS lumped models yield decrease of noise, as opposed to models that distinguish transcription and translation? And, why do certain rates accentuate noise increase more than others? To answer these questions, we analyze the behavior of the system resulting from tuning mRNA degradation (k₇) and protein translation (k₈) in the TT module, separately. Our simulations suggest that the addition of other modules (Fig. 1, A and C) does not produce abrupt qualitative changes in the noise profile (data not shown) and we expect that similar results hold for the more complex cases.

Stochastic discrete effects

In all models where transcription and translation were treated as separate processes, our simulations showed behavior that resembles stochastic focusing—fluctuations that can make a gradual response mechanism work as a threshold mechanism (27)—while fixing the number of TF molecules and tuning rate k₇ according to increasing feedback (Fig. S8 and Fig. S11). The protein level shifted to a generally higher state than would be expected from a deterministic analysis and, in certain parameter ranges, this behavior was tightly correlated with the mRNA concentration (Fig. 3, A and B). Discrete random changes at the mRNA level lead to a protein scaling behavior according to the difference between the integer numbers of mRNA molecules and their deterministic steady-state. Such protein scaling behavior results from protein distributions that follow the mRNA distributions (using the terminology of Iyer-Biswas et al. (18)). Moreover, the mRNA time courses can be multimodal or they can settle at the initial condition for very high feedback levels—i.e., they gradually relax to the steadiest state, the reason why high TF levels on the noise profile may display an inverted U-shape (Fig. 2 C and Fig. S7, A–D).

Figure 3.

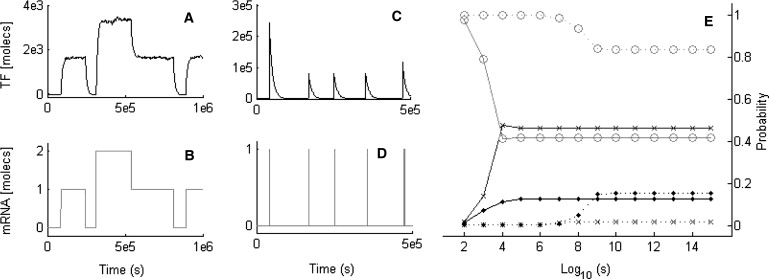
Protein and mRNA time courses in the TT module, portraying TF (A and B) multimodal behavior and (C and D) bust-like synthesis, using a feedback of α = 10¹³ in parameter set 2 and initial TF level of 100 molecules. FSP analysis (E), with fixed feedback α = 10¹⁰ (solid line) and α = 10¹⁵ (dotted line). Probabilities are evaluated for times between 10² and 10¹⁵ s, time represented in log scale. Labels refer to the probability of having 0 (cross), 1 (circle), and 2 (dot) molecules of mRNA, respectively.

To explore how and when the mRNA level is able to switch between stable states in the TT module, we used the FSP (see Methods and Munsky and Khammash (28)). Moreover, we focused on the establishment of a dynamic equilibrium (cf. Supporting Material). Our simulations highlight the dependency of numbers of mRNA molecules on both the parameters and feedback level of the system. Moreover, they show how predetermined mRNA distributions can be constructed through appropriate selection of parameter sets. The mRNA probability distributions of the TT module with two different nominal parameter sets (Table S2 and Table S3) and two feedback strengths (α = 10¹⁰ and α = 10¹⁵) differ significantly (Fig. 3 E). When the feedback and time range are both increased, the probability of observing one mRNA molecule is always higher than that of observing no mRNA. Noticeably, with sufficiently high feedback one can lower the probability of observing no mRNA at all times by using a tailored nominal parameter set (Table S3, Fig. 3 E, and Fig. S13).

Additionally, the sum of state probabilities in the FSP is always less or equal to one. For high feedback levels, the sum slightly deviates from one, implying that other states not considered are probable. On comparison with the corresponding SSA time courses, we found that discrete jumps of more than one mRNA molecule are possible, resembling transcriptional bursts (21), a recent experimental observation. Interestingly, for the model we did not allow several mRNAs to be produced in a single transcription reaction while the gene is active, as in Raj et al. (21) and Golding et al. (29). Such jumps can also be obtained by strong regulation solely.

Protein bursts

Protein bursts have been observed experimentally (30) and cannot be considered mere numerical artifacts. They can be thought of as special cases of discrete stochastic effects, but we treated this case separately as the underlying mRNA profiles are somewhat distinctive. When tuning the protein degradation or translation rate (k₄, k₈) in the TT module, one obtains rather high numbers of mRNA molecules for low feedback levels, and an almost-zero mRNA level with the exception of a few pulses for high feedback levels. These pulses induce the sudden burst-like production of TF (Fig. 3, C and D, and Fig. S12), the bursts being enormous when the initial TF level (and, by consequence, k₈) are highest. In contrast to the discrete stochastic effects, TF distributions in protein bursts scenarios are no longer multimodal nor do they follow those of mRNA, and they are largely asymmetric (19). Noticeably, the multimodality observed when tuning k₇ can also be replaced by protein bursts at particularly low TF levels.

Moreover, early studies such as the one by Thattai and van Oudenaarden (13) have described pulses to occur with an average frequency that is inversely proportional to the mRNA transcription rate, inducing a sudden burst-like production of TF that scales as k₈/k₇. Although on average this scaling seems reasonable, individual time courses can show protein bursts up to two orders of magnitude below and above this estimate (data not shown). Hence, the size of the protein bursts is also distributed.

A matter of separation of timescales

We have observed the CV to increase alongside feedback strength. While tuning k₇, such increase was due to the emergent multimodality in the protein time courses. On the other hand, tuning k₄ and k₈ produced protein bursts. Under either circumstance, the CV does not assess noise behavior correctly. Interestingly, many prior studies have missed this fact and have used the linear noise approximation. Such an approach has several shortcomings, the first of which is its inability to describe multimodality or antisymmetric distributions. Furthermore, unless one studies a relatively rare linear system, one has to introduce a bias by moment-closure approximations of the CME.

One way around this has been the analysis of minimal gene expression circuits, where a gene is either always active (two-stage model) or fluctuates between active and inactive states (three-stage model) in accordance to specified constant rates (18,19,25). Here, DNA activation/inactivation involves explicit molecular binding events, the nonlinearity of which does not allow an exact analytic solution, or a generating function method without approximation. Nevertheless, we find it useful to compare our results to previously published criteria based on separation of timescales between different reactions.

To explore these perspectives, we computed the average correlation coefficient of all model combinations of the TT module. We did not use the Shannon entropy or the Kullback-Leibler divergence because we wanted to assess how TF distributions follow those of mRNA, both in distribution and in time. This will yield nonzero correlations when TF follows mRNA, including multimodality. In all other feedback values and cases, the correlation is close to zero. This includes protein burst scenarios because as soon as the TF levels peak in a burst, relaxation to an inactive gene TF state begins. This implies that for the same mRNA state there will be large numbers of possible TF states. By combining computed CV and correlation values, we can get more informative descriptions of protein time courses.

In the following, we will compare our results with criteria published previously for predicting different types of nonclassical behavior. In our simulations, variations in k₇ and k₄ yield correlations between the mRNA and TF time courses (Fig. 2, F and H). This confirms earlier studies showing that TF distributions will follow mRNA distributions when a TF degrades faster than its parent mRNA (k₄ > k₇) (21) or when the sum of DNA activation and inactivation rates is <k₄, and k₄ < k₇ (18). However, we observe such behavior at considerably extended ranges of parameters (Fig. S15) because we consider the nonlinearity of the binding reaction explicitly. For variations in k₇, the correlation increases with feedback strength, implying that TF levels are proportional to mRNA levels at all times. Coincidences with increasing CV indicate when mRNA and TF exhibit multimodality, extending the ranges of parameters predicting bimodality whenever gene activation/inactivation rates are <k₇ (18). Significant correlations obtained while tuning k₄ have a different interpretation: the TF distributions follow the mRNA distributions at low feedback values, but not in a multimodal sense as indicated by the lower CV values. Moreover, almost-zero correlations for very low TF levels coincide with very high CVs, indicating protein bursts. Quite surprisingly, negative correlations appear while tuning k₈ at low TF levels (Fig. 2 G and Fig. S15). In those cases, mRNA production immediately shuts off whenever TF is abundant—the TF distributions still follow those of mRNA, albeit in a cat and mouse manner. To our knowledge, such an in silico behavior has never been noticed before.

In Shahrezaei and Swain (19) and Mehta et al. (22) it has been shown that whenever k₇ >> k₄, protein expression profiles will exhibit bursts. Even though our analyses somewhat agree while varying k₄, two important differences should be noted. First, multimodal behavior is labeled as bursts when varying k₇ while omitting all relevant cases stemming from variations in k₈, and second, that our parameter ranges are again much broader. The same holds when comparing our results with those in Schultz et al. (17), where the authors explore a lumped transcription-translation model and predict a bimodal TF distribution whenever the DNA inactivation rate is slower than k₄. Because the bimodality is achieved through discrete active gene changes, we compared it to our TT module, where the bimodality corresponds to discrete mRNA changes. Interestingly, all of the above mentioned criteria overlooked the observed protein bursts obtained when varying k₄ at low TF levels and no criterion faithfully portrayed the occurrence all types of nonclassical behavior. For a more visual perspective, we highlight how treating nonlinearities explicitly in the TT module can extend the observable ranges of nonclassical behavior in gene expression (Fig. S14 and Fig. S15).

Noise increase without QSS

At very high feedback levels, namely when the DNA-repressor complex rarely dissociates, the QSS assumption of a model breaks down (1,9). Formally, a QSS assumption implies a hyperbolic term in the reaction propensities that provides a smooth transition between the bound and unbound states of the gene. With high feedback, this may yield longer and more frequent open windows of active gene. As a result, the model predicts mRNA transcripts that would otherwise not be observed, making it an inaccurate representation of the physical phenomena. To study these effects, we removed the QSS assumption and considered only first- and second-order elementary reactions in our basic modules.

Models without QSS displayed CV increase irrespective of separating or lumping transcription and translation, the increase being mild/intermediate for the latter. For instance, when varying k₁ in lumped models, the increase in CV results from full depletion of TF (increasing variance alongside decreasing mean) or from small scale protein burst-like behavior, stemming from pulses of gene activity that are no longer masked by a hyperbolic function (Fig. S16). Except for rates k₄ and k₉ in the lumped transcription-translation models, no other rate variation displayed significant correlations between TF and active gene time courses. For k₉, this corresponded to a behavior tending toward multimodality (without sharp transitions) for high TF values, whereas k₄ displayed moderate protein bursts that, quite interestingly, corresponded to high correlations. In this case, the relaxation to the inactive gene TF state is not gradual, but simply imitates the activation/inactivation events.

Tuning rates k₇ and k₈ in the TT module alone yielded qualitatively similar noise profiles with or without a QSS assumption (Fig. 4 and Fig. S17). Up to intermediate values of the feedback parameter, protein bursts were of equivalent magnitude and frequency. However, higher feedback values in systems without QSS still yielded protein bursts, albeit at much lower frequencies (Fig. S18). Interestingly, the range of feedback parameters associated with discrete effects resembling stochastic focusing is reduced, most cases being replaced by small scale protein bursts. This is consistent with the shorter and less frequent open windows for the unrepressed gene. We observe milder negative correlations while tuning k₈, corresponding to the loss of cat and mouse multimodality. Tuning rate k₇ still yielded positive correlations, albeit lower than those obtained with a QSS, corresponding to the above mentioned multimodality without sharp transitions.

Figure 4.

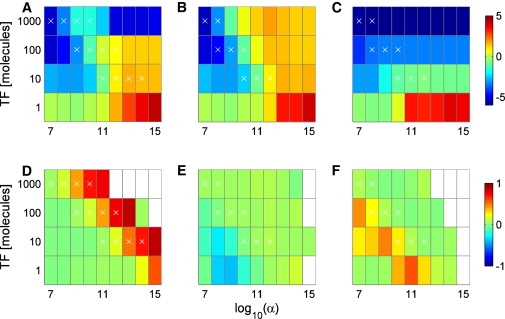
Feedback-dependent noise (CV) and correlation behavior of the TT module, without a QSS assumption. All labels are identical to Fig. 2, C–H.

Our noise pattern criterion needs some modifications once the QSS assumption is removed. In this case, transcriptional and translational bursts can be tightly correlated and display a high CV at low TF levels. The CV associated with uncorrelated protein bursts and multimodality is similar, yet lower than that of correlated bursts. Comparing our results with all the above cited timescale separation criteria yielded similar conclusions to those obtained when assuming a QSS (Fig. S19 and Fig. S20). The combination of the CV and time-correlations pointed at parameter sets where moderate protein bursts and multimodality without sharp transitions can be observed. Also, the ranges of observable nonclassical behavior in gene expression are, again, larger than previously expected.

Last, adding the RNAP and DM modules did not yield apparent clear-cut patterns, unlike models assuming a QSS. Depending on TF initial conditions, the topology of the system, and parameterization, both extensions accentuate and buffer noise changes. For instance, adding the DM module to the TT module while tuning the transcription rate k₁ resulted in noise buffering for high TF initial number of molecules (Fig. S16). In this case, high propensities of TF dimerization and dissociation render new transcription events rare. Hence, the protein level slowly decreases and, with it, the computed CV. Unfortunately, acute stiffness of the systems without QSS assumption prevented us from studying all cases of the combined modules, especially when incorporating the DM module.

Discussion

Computational predictions of protein expression patterns heavily depend on the choice of network topology, model parameterization, assumption of a QSS or not, and the use of a stochastic or deterministic approach. Furthermore, noise interpretation will depend on the adopted metric for its quantification. As a consequence, some particular noise and protein time course profiles can be constructed from predefined sets of assumptions.

In this study, we have aimed at highlighting that a noise analysis is only complete when considering the underlying source of variation. The same holds for assessing the emergence of any nonclassical behavior in gene expression through changes in regulation strength. Two examples of the latter are multimodality and burst-like protein synthesis, for which commonly used measures based on the variance and mean are insufficient. For assessing single nonclassical cases, we propose a modified CV based on the protein distributions and the frequency of relevant discrete events. For multimodality, one can separate the data into sets revolving around the distinct modes and compute a weighted CV, corresponding to the frequency with which each mode is visited in the entire time course. In the case of protein bursts one could in turn measure variations revolving around the natural relaxation to the inactive gene state. Such a measure should be again weighted by the frequency of the events, for which a combination with a frequency-domain analysis such as that in Cox et al. (10) could be more suitable. However, when comparing different types of protein-courses or describing emergent patterns of strong feedback regulation, one can benefit from analyzing the regular CV (representing protein variation and scaling behavior) alongside time-correlations between protein and mRNA/active gene distributions.

Much remains to be discussed on what can and cannot be termed noise. For practical purposes, we have referred to noise as the scale of time course variations, but we note that noise might be an abuse of terminology in some cases. Protein bursts provide an obvious example: they indeed stem from discrete random events, but variations in the protein time courses contain structure that is not entirely random.

We focused exclusively on discrete stochastic negative regulation models that incorporate modules of RNA polymerase binding to the gene, repressor dimerization, and lumped/separate processes of mRNA transcription and protein translation. We measured noise intensity by means of the CV and, whenever individual time courses displayed a nonclassical behavior (e.g., distribution asymmetry or multimodality), we compared our CV measurements with time correlations between protein and mRNA/active gene time courses. This simultaneous analysis of the CV and time correlations provides a bigger and more intuitive picture of characteristic behaviors attainable when tuning negative feedback strength in all these scenarios. A full summary of noise and protein scaling behavior is presented in Fig. 5.

Figure 5.

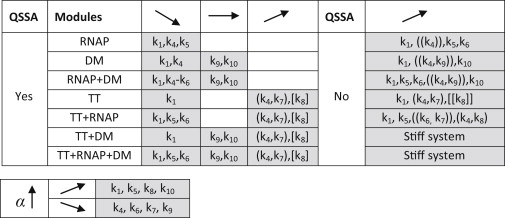
Summary of observed CV behavior as negative feedback strength is increased. Observations were classified according to the model and whether a QSS assumption was included or not. Tuned kinetic rates are specified in each box; arrows indicate the form of dependency. Round/squared brackets show positive/negative time correlation of TF and mRNA time courses, double brackets portray mild correlations. The lower panel shows rate parameterization behavior with increasing feedback.

When including the QSS assumption, models that lump transcription and translation together showed none to slight decrease of noise with increasing negative feedback strength. On the other hand, models that make a clear separation between these processes showed noticeable noise increase within typical ranges of biological parameters. This noise increase is associated with discrete stochastic effects, such as protein bursts or behavior resembling stochastic focusing. Moreover, our simulations suggest that the addition of RNA polymerase binding in a model buffers noise increase or decrease, whereas the addition of repressor dimerization accentuates noise variations.

In contrast to all QSS models, describing all module combinations through elementary reactions resulted in slight to moderate increase of noise when increasing negative feedback strength. This was independent of treating mRNA transcription and repressor translation as lumped or separate processes, and it was most common for low TF concentrations. Moreover, noise increase was obtained while varying all possible rates, stemming from unmasked discrete changes in the active gene state. Unfortunately, we did not find any clear-cut pattern of noise accentuation or buffering for these cases and, in many cases, multimodal behavior was replaced by noisy synthesis or protein bursts.

By comparing noise measurements with analysis focused on separation of timescales, we extended reported parameter ranges for the appearance of protein bursts and distribution correlations (18,19,21,22) due to the explicit treatment of the binding reactions' nonlinearity. Moreover, subtle yet substantial differences in TF profiles arise in accordance to each tuned rate, irrespective of considering a system at QSS or not. Namely, the protein can change alongside mRNA levels without any apparent modality (when tuning protein degradation) or in a multimodal fashion while switching states rather infrequently (when tuning protein translation or mRNA degradation). In the multimodal case, TF increases proportionally to mRNA while varying mRNA degradation. However, variations in the protein translation rate surprisingly yield negative correlations when assuming a QSS, indicating that the mRNA production shuts off whenever the protein is abundant, and vice versa. Finally, further analysis of simple negative feedback systems seems essential, especially when models with and without QSS disagree. For this, a sensible distinction between slow and fast reactions that yield accurate dynamics is necessary (31). Should the latter be insufficient, new stochastic simulation algorithms may have to be developed, in particular, to tackle the stiffness of the system.

Supporting Material

Additional methods, discussion, analytic derivations and notes, three tables, and 20 figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00149-9.