Elongational Flow Induces the Unfolding of von Willebrand Factor at Physiological Flow Rates

Abstract

The unfolding of von Willebrand Factor (vWF), one of the largest multimeric proteins in our body, has been shown to be a crucial step in the process of blood clotting. Here we show that elongational flows, which appear during vasoconstriction or stenosis, are the primary activation mechanisms of vWF, and unfold the multimeric protein at flow rates that are two orders-of -magnitude below those corresponding to pure shear. The findings presented here complement the current understanding of blood clotting from the molecular to the physiological level, and provide new physical insights into the connection between clotting anomalies, such as Heyde's syndrome and stenosis. These findings also represent a new paradigm in the function and activation of vWF.

There is a large body of work that has attempted to elucidate the mechanism of blood clotting from the molecular to the physiological level, with a large focus on the large multimeric protein von Willebrand Factor (vWF) (1–4). The overall globular structure of vWF has been shown to unfold under different kinds of stresses (e.g., shear stress) (2,3). Once unfolded, the molecule can adhere to the surface of a wounded vessel and start the formation of the plug. The unfolding pathways of VWF are mediated through a broad spectrum of hierarchies. In particular, it has been shown that unfolding is intimately related to the expression of adhesion proteins (5,6), flow conditions surrounding the protein (2,7–9), and the molecular structure of vWF itself (3,4). If the balance of these three parameters is lost, the function of vWF is mitigated or overly enhanced, resulting in von Willebrand's disease or embolism formation, respectively (9,10).

The mechanism by which vWF self-assembles with platelets at the sites of vascular injury has recently received significant attention from the polymer physics community (2,11,12,13). A large amount of recent speculation has focused on the ability of the overall globular structure of vWF to unfold under the influence of shear flows, and we have developed physical models to explain this phenomenon (11–14). Although it appears that pure shear can induce the blood clotting process by itself, it is worthwhile to explore other mechanisms that might dominate under physiological conditions. Recent work by Nesbitt et al. (7) has suggested that shear gradients are responsible for thrombus formation, and Zhang et al. (3) have proposed that elongational flows could play a major role in vWF regulation. Here, we use numerical simulations to further elaborate on this observation from a polymer physics perspective to demonstrate that elongational flows, which naturally appear at regions with shear gradients, are the most prominent mechanism in the regulation of vWF, and consequently one of the primary triggers in blood clotting. Interestingly, this kind of flow seems to be ubiquitous in the blood vessel system, particularly at locations of vasoconstriction and stenosis.

Elongational flow in a biological system is manifested most commonly in a transition in vessel size. This is schematically shown in Fig. 1, where conservation laws dictate that the velocity in the smaller tube must be faster than in the larger tube. In the transition from a larger tube to a smaller tube, the fluid requires an acceleration such that locally a suspended protein will feel an elongational pulling force as the forward portion of the protein gets carried away at a faster rate than the back portion (see the Supporting Material for a more thorough treatment). The approximate rate of elongation in this case can be written as

$$\dot{\epsilon }=\frac{\Delta v}{D}=\frac{v_1\left(\frac{{\text{r}}_1^2}{{\text{r}}_2^2}-1\right)}{D},$$ (1)

where v is the maximum velocity (at the center of the tube), r₁ and r₂ are the tube radius before and after a transition, and D is the distance over which this radius changes. In a typical blood vessel during injury, the process of vasoconstriction causes the vessel to constrict to a smaller radius (15,16) (see Fig. 1 for a diagram that portrays the fluid velocity field in such a system). This provides a way to locally induce elongation, and as shown below, it can also induce a clotting response with a threshold much lower than that for a constant shear rate.

Figure 1.

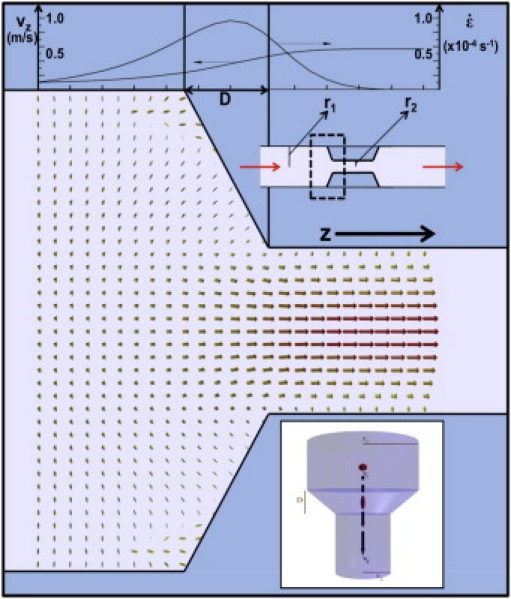
A typical flow profile for the case of stenosis or vasoconstriction (an approximate schematic is shown in the center-top-right area). The entry to such a blockage results in elongational flow (see the Supporting Material for discussion). On the top, there is a graph of both the fluid velocity and the velocity gradient (or elongational flow rate ɛ) along the center of the tube. The maximum elongational rate clearly occurs in the transition region between the different radii (that are bounded by D) and tends toward zero in the regimes where the vessel radius remains constant. The bottom right shows the effect of placing a protein (the red globule) in this sort of flow: in the transition region d, the protein is elongated by the flow field.

Our model uses a Brownian dynamics approach to study the dynamics of vWF in an arbitrary flow field, and takes into account the hydrodynamic interactions between the different units in vWF (see the Supporting Material). The structure of vWF consists of a series of large dimers, each consisting of a number of protein domains (10). We represent these dimers as effective spheres, or beads, which are connected by springlike forces. The hydrophobic interactions and self-association between dimers are represented by an effective interaction energy between two different beads Δu, which collapses the protein into a dense globule. This type of simulation has been used for simple shear flow in previous works that elucidated the mechanism for unfolding of collapsed globules in shear flow (11,12).

Following the coordinate system employed in Fig. 1, the flow field to which a molecule is exposed (in the reference frame of the molecule itself) while passing through the transition region D is well approximated by (see the Supporting Material for a detailed analysis)

$$\overrightarrow{v}=\dot{\epsilon }\left(z{\widehat{e}}_{\text{z}}-\frac{1}{2}x{\widehat{e}}_{\text{x}}-\frac{1}{2}y{\widehat{e}}_{\text{y}}\right),$$ (2)

where ${\widehat{e}}_{\text{x},\text{y},\text{z}}$ is the unit vector in the corresponding Cartesian coordinate direction and $\dot{\epsilon }$ is the elongation rate. Diagrams of the flow field and a typical unfolding polymer from the simulations are shown in Fig. 2 a. Fig. 2 b represents the behavior of a vWF-type polymer by considering the mean extension versus the elongation rate $\dot{\epsilon }$. This demonstrates that there is a critical flow rate at which the globule (Fig. 2 a, far-left conformation) unfolds to a fully extended chain (Fig. 2 a, far-right conformation). We also include unfolding as a function of shear rate $\dot{\gamma }$, and obtain results similar to previous studies on vWF in shear flows (11,12). There are striking differences between the two data sets, most noticeably in that the shear case demonstrates a much broader transition at rates two orders-of-magnitude larger than the elongation case. The dynamics of the two cases suggest that these differences are due to the rotational nature of shear flow—the extension of polymers in shear is ultimately limited by what is known as tumbling behavior, which causes the globule to continuously transition between collapsed and stretched states (17). Furthermore, the regulation of vWF is believed to be force-dependent, and we show in Fig. 2 c for mixed elongation-shear flows that the globule-stretch transition does induce a large change in the maximum tensile force along the chain. However, this figure again emphasizes the differences between elongation and shear, with the former displaying a large, discrete jump in tensile force per monomer while the latter shows a much more broad and continuous increase at rates two orders-of-magnitude above pure elongation.

Figure 2.

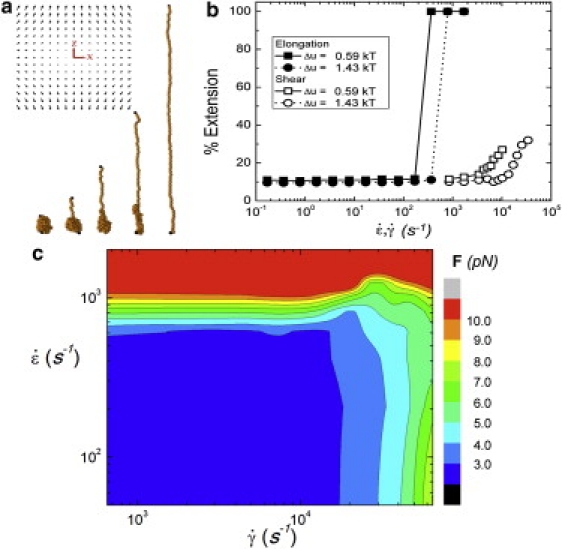
(a) The elongational flow (profile shown: z is the stretching axis as per Eq. 2 and Fig. 1, whereas x is an arbitrary transverse axis) imposed on a collapsed vWF molecule has the ability to stretch the protein. This opens up the quaternary structure to allow for bonding with other molecules. The snapshots shown represent the unfolding over time seen in simulations of vWF in elongational flow. (b) The average percent extension of vWF as a function of the elongation/shear rate $\dot{\epsilon }/\dot{\mathrm{\gamma }}$ for simulation using two different interaction energies Δu and a dimer size of ∼50 nm (see text for discussion). (c) The maximum tensile force along the chain F mapped as a function of elongation versus shear rates (u = 1.5 kT). We note that this maximum, for an extended chain, occurs at the center of the chain as predicted in Zhang et al. (3). This force quickly increases into the biologically relevant regime as elongational flow is applied, whereas application of shear flow demonstrates a much more broad transition.

The physical model presented above can be directly translated to the case of vWF in the bloodstream by considering typical parameters for the collapsed globule. If we consider a monomer size of ∼50 nm (a typical vWF dimer size), an effective interaction energy of Δu ∼ 0.5 – 1.5 kT (the typical strength of van der Waals/hydrophobic type interactions), and room temperature T ∼300 K, we obtain critical flow rates of ${\dot{\epsilon }}_{\text{c}}\sim 3\times {10}^2-6\times {10}^2{\text{s}}^{-1}$. To compare this flow rate to what would be found in a typical blood flow, we consider the model described by Eq. 1. Assuming a change in radius of ∼20%, a typical preconstriction blood velocity in the microcirculation of ∼0.1 m/s, and D ∼10 μm, the typical elongation rate is $\dot{\epsilon }\sim 5.6\times {10}^3{\text{s}}^{-1}$, which is an order-of-magnitude beyond the critical rate at which the unfolding process will occur. Alternatively, significant amplification of the vWF response and platelet aggregation upon stenosis was seen in the work by Nesbitt et al. (7). The values utilized in that work indicate that an elongation rate of ∼2 × 10⁴ s⁻¹ was more than sufficient to induce thrombus formation (7). Both results are well above the simulated threshold for elongational induced vWF stretching, and indicate that the application of an elongational flow is a strong regulator vWF activation. For comparison, simulations place the pure shear flow-induced stretching transition near 10⁴ s⁻¹ (see Fig. 2 b), which is in the uppermost side in our circulatory system, perhaps only occurring during stenosis. Hence, pure shear requires a much more exclusive set of conditions than elongational flow (7).

Our results indicate that the unfolding of vWF in the bloodstream before clotting is regulated very strongly by elongational flow fields, particularly compared to shear flow, which is weaker by two orders-of-magnitude and does not demonstrate the necessary sharp transition that would mediate the on-off biological functionality required for blood clotting. This could also aid clotting at the molecular level, because it has been shown that the vWF binding is strongly dependent on the application of strong forces along the protein chain (8). Our results also agree quantitatively with the maximum tensile force per monomer necessary to cleave vWF by ADAMTS13 determined by Zhang et al. (3), with the maximum force along the chain exceeding ∼10 pN upon unfolding in an elongational flow.

The results presented here provide a further understanding of the dynamics of VWF and could be translated into the development of treatments for a wide variety of diseases associated with blood clotting, such as von Willebrand's disease, ischemic stroke, and acute coronary syndromes. In addition, these results provide insights into other somewhat counterintuitive diseases such as Heyde's syndrome, in which arterial stenosis induces clotting disorders. Clearly, by having an stenotic vessel, the activation of vWF becomes prominent due to the strong elongational component that appears in the flow, inducing either complexation of vWF with platelets to promote a local thrombotic thrombocytopenic purpura, or it gets degraded by ADAMTS13 and becomes nonfunctional. Both of these processes lead to bleeding, as observed. In summary, we have presented a convincing case that implies that elongational flow under pathophysiological conditions strongly supplements shear flow, and could be the main mechanism to induce unfolding and activation of vWF. These findings represent a new paradigm in the function of vWF.

Supporting Material

Four equations and two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00197-9.